Оглавление:
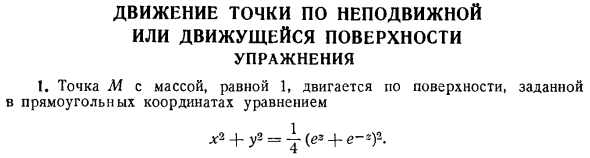





Движение точки по неподвижной или движущейся поверхности. Упражнения
- Точка M, масса которой равна 1, движется вдоль поверхности, определяемой в декартовых координатах следующим уравнением: x2 + y2 = 1 ex + e 2. Это притягивается к каждому элементу оси z с силой, равной отношению 4 й степени длины элемента и расстояния до точки M. Исследуйте движения, которые может получить точка, выясните проекцию локуса на плоскость xy. Мы исследуем случай, когда точка существует в первый момент на оси X и скорость равна 1 угол угол ху лицензии, Кан. 2. Нулевая точка обычно направлена в плоскость xy и под действием силы mk2, равной, перемещает сферу x2 j y2z2 R2 0. Где k2 константа. Найдите движение и нормальную реакцию.
Орбита представляет собой сферическую коническую секцию. 3.Рассмотрим материальная точка м массой 1.Масса M находится под действием силы F, проекция которой на 3 прямоугольные координатные оси равна частной производной силовых функций U x, y, z .Уравнение U = const представляет собой горизонтальную поверхность, где точка пересечения с любой поверхностью S может быть названа линией уровня на поверхности S. Эта последняя поверхность определяется так, что точка M, обеспечиваемая силой M без начальной скорости, описывает траекторию C, ортогональную всем линиям уровня. Например, если вес действует только на точку M, то он должен падать вдоль линии максимального наклона к нужной поверхности.
Движущаяся точка выходит из положения х0 и приходит в начало координат за промежуток времени, который мы можем принять равным единице. Людмила Фирмаль
Докажите, что синус угла, под которым горизонтальная плоскость пересекает поверхность S, изменяется в разных точках линии пересечения относительно обратной силы F A. de Saint Germain, Journal de Math.1876, 10 ноября. 4.Свободная точка, находящаяся под влиянием только сопротивления среды, представляет собой прямую line. It движется вдоль поверхности, доказывая, что точка под воздействием только сопротивления и трения среды представляет собой геодезическую. 5.Тяжелые материальные точки, оставшиеся на поверхности сферы радиуса a, притягиваются пропорционально расстоянию неподвижной точкой B, которая находится на вертикальной оси Oz и проходит через центр o сферы. Расстояние OB B.
Рассмотрим величину p. начальное расстояние от точки до горизонтальной плоскости Oxy, которое принято считать горизонтальным, и, наконец, от точки до центра сферы. 1 Найти границу, где z Координата точки изменяется во время движения. 2 определить движение неподвижной точки B в центре сферы в определенных случаях, когда притяжение равно и противоположно весу. 6.Перемещайтесь по сфере и находите движение точек, которые притягиваются к плоскости диаметра пропорционально расстоянию. Задача сводится к интегралу уравнения хромого. Кобб, Конт rendus, т. CVIII 7.Геодезический Ан ellipse.
В результате соотношения pD = const, которое доказывается в теле 279, доказываются следующие предложения: Если O и O это 2 сферические точки эллипса, которые не превышают одного диаметра, то LJ и LJ геодезические линии, соединяющие точку L4 с этими точками, и эти 2 линии одинаково наклонены к каждой кривизне, проходящей через точку M. Если точка M представляет собой линию кривизны, то сумма или разность дуг геодезического MO MO постоянна. См. журнал де Liouvillc, 1846. 8.Найдите геодезическую карту Тельца. Рэз, Конт rendus, т. X. p. s. 937.
Найти геодезическую поверхность, образованную вращением цепной линии вокруг основания 0, по r, определяется 1 м видом эллиптического интеграла, который сразу приобретает стандартную форму. 9а. Найти 1 гиперболические геодезические, образованные вращением гиперболы = 1 e отображение по эксцентриситету Получаем следующее уравнение для тергеничности гиперболы, проекции геодезической. kdr г e2g в р в Р2 А2 Р2 К2 Итак, 0 представляется Интегралом и сводится к эллипсу. Форма кривой аналогична форме, указанной в пункте 275.если k= a, то если k= , то она приближается к горловому кругу r = a асимптотически, и кривая становится генератором.
Геодезическая кривизна плоскости вращения. R и R , где r радиус главной кривизны точки на плоскости вращения, r радиус соответствующей параллельной линии, I наклон обзорной линии относительно меридиана, а p ее радиус кривизны. Тип печати Р2. К г Где k в тексте постоянная величина произведения r slni вдоль рассматриваемой геодезической. Re для е Нувель Ле Анналов, 1887 2 11.Тяжелые пятна движутся вдоль surface. To докажите, что можно взять очень большую начальную скорость, траектория на некотором расстоянии от начального положения точки сколь угодно мало отличается от геодезической.
Найти геодезическую плоскость вращения Ifa2 х + Йи = З2 2А2 З2.Смогите быть помещено, И и G = COStt, Z = alslny COS 1. Эти геодезические линии имеют вид пространственной фигуры 8.Все они закрыты и имеют одинаковую длину. Таннер и matheniatiques Вестник науки, 1892, стр. 190. 13. 2 тяжелые точки даны и притягиваются друг к другу пропорционально расстоянию. Первые из них движутся вертикально, а другие по плоскости, образующей горизонтальную линию и угол. Найдите движение этой 2 х точечной системы. А m = m 6 рассмотрим частный случай, когда начальное положение совпадает с положением равновесия.
- В проекция начальной скорости 2 й точки на горизонтальную и максимальной наклонной линии на плоскость равна начальной скорости 1 й точки соответственно. г грех а=. Также рассмотрим случай, когда плоскость горизонтальна, то есть a = 0. 14.Движение точки На сфере под действием постоянной силы в плоскости меридиана, проходящего через точку движения. Радиус сферы равен 1, а положение точки это угол с долготой 0 Предполагается, что он определяется в дополнение к широтам. Сила, постоянно действующая на плоскости Меридиана, действует на точку. Проекция силы на плоскость контакта сферы показана в F.
F, эта составляющая Значение считается положительным или отрицательным в зависимости от того, направлено ли оно на увеличение или уменьшение значения. Докажите справедливость следующих уравнений, которые аналогичны соответствующим уравнениям теории центральной силы, в частности уравнению виньетки. т. Л = , Вопрос sin2 П. Серр, Theorie geometriquc et mecanique и др. С. С. 195. Образцы.
Если скорость точки обратится в нуль до того, как она достигнет положения Е, то она упадет в первый притягивающий центр. Людмила Фирмаль
Если F важно, то орбита будет сферической Конусное сечение, ориентированное на полюса аналогия с движением планет. 15.Установите выражение того же характера, что и в примере 14 для перемещения точки на вращающейся плоскости под действием силы, постоянно находящейся в плоскости меридиана движущейся точки. 16.Трансформация movement. In дана неподвижная плоскость, массовая Точка 1.Масса точки 1 находится на полу под действием силы F, а ее проекции X и Y являются лишь функцией координат X и y движущейся точки. Уравнение движения ПХ = Л =Ю.
Замену независимой переменной T на переменную Т, связанные с T с соотношением Второзаконие 1 А х + ь у + С У Вы можете использовать этот инструмент для выполнения томографического преобразования топор Джей с С А х б усь х 1 А х 4 Б г + С Л = А х 4 Б г + с Точки xy, yO перемещаются как масса 1 точка во времени 1e, Xv Yt оказывается подверженной влиянию проекционной силы Fb, которая зависит только от Xj и yt. Точечный локус xb yj, point x, y Force Fx томографическое преобразование направления силы F. Если сила F центрирована, то сила Fx также параллельна центру или постоянному направлению. Аппель, Конт rendus, т.
Доказательство обратного: когда нужно найти наиболее распространенное преобразование форм 1 = м у У1 = г, ДТИ = .Y Новая сила Fx зависит только от координат xr и yt, и это происходит что угодно: если сила F зависит от x и y, то получается только вышеупомянутое томографическое преобразование. Американский журнал, том. ДВЕНАДЦАТЫЙ. 18.Преобразование сферического движения В а plane. It дана сфера ы с радиусом 1 и плоскостью Р, находящейся в контакте с ней. Каждая точка Afj на сфере связана с проекцией M на плоскость P этой точки, используя радиус от центра до Afx.
Это так называемая Центральная проекция, хорошо известная в теории географических карт, которая связывает большую окружность S на сфере с произвольной прямой плоскостью P .С точки зрения анализа, если точка соприкосновения плоскости P и сферы S является полярным координатным полюсом плоскости и сферы, a Через p и w, которые являются полярными координатами точек M на плоскости, и через f и 0, которые являются полярными координатами точек на сфере p дополнение широты и долготы, мы получаем следующую формулу преобразования: Р = тг г = 6. Уравнение Лагранжа плоского движения = =.
Аналогично, если рассматривать на сфере точку массы 1, которая движется во времени, то уравнение движения выглядит следующим образом: Где и 6 функции cp и 0.Если мы произведем преобразование центральной проекции, определяемой формулой а для уравнения б движения плоскости, и установим связь между t и tt = cos2 ст1 СР ДТ Уравнение b принимает форму уравнения c. cos2 p гребаная вода cos2 Поэтому движение на плоскости соответствует движению на сфере. Траектория 1 точки будет преобразована с использованием центральной проекции траектории 2 й точки Appel, American Journal, vol. ТРИНАДЦАТЫЙ. Присоедините это преобразование к примеру 14.
Точно так же движение точки на поверхности определенной кривизны может быть преобразовано в движение на плоскости, доказывая более общее положение. До этих вилл, в 1890 году, Annales de i Ecole Normale superieure. 20.Точка, на которую данная сила не действует, всегда движется по плоскости, которая вращается с постоянной угловой скоростью o вокруг неподвижной оси, которая соединена. Найдите движение и рассчитайте реакцию де Сен Жермен. 21.Гринхилл стр. 280 Greenhill найти длину кривой, описываемой сферическим маятником в горизонтальной и стереографической проекциях. 22.Установите уравнение движения точки на поверхности с трением. См.
Аппель, Конт rendus, 1892 2 15 Майер, Sachsische Гезельшафт, 1893 6 5 23.Найти движение за счет трения тяжелой точки о цилиндр с вертикальной осью. Сен Жермен, Вестник науки mathematiques, 1892 8. 24.Если точка, движущаяся по поверхности без трения, находится под действием силы в определенном направлении, то это доказывает наличие точки перегиба в проекции траектории на плоскость, перпендикулярную силе. 2 если контактная поверхность дорожки качения перпендикулярна поверхности de Sparr, т.
Смотрите также:
Решение задач по теоретической механике
| Теорема Гринхилла | Уравнения Лагранжа для свободной точки |
| Бесконечно малые колебания | Интеграл кинетической энергии |
