Оглавление:






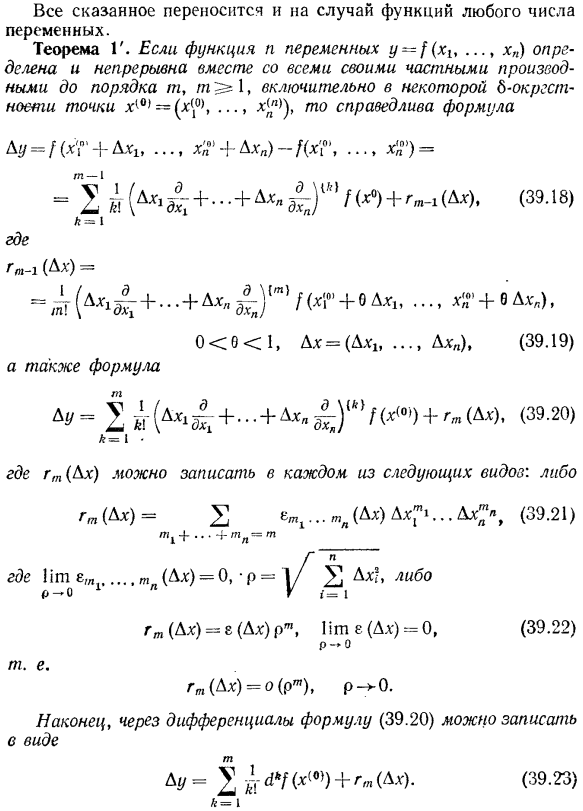


Формула Тейлора для функций многих переменных
Формула Тейлора для функций многих переменных. Если функция многих переменных имеет достаточное количество непрерывных производных в окрестности точки, то функция может быть выражена в указанной окрестности (как это делается с функцией 1 переменной) как сумма определенных многочленов и, в некотором смысле,»мала». Теорема 1.Определить функцию r = f (x, y) и континуум со всеми частными производными до степени m (m) в окрестности 8 (x0, y0).Тогда условие p=] / » Ax2 + Au2 C. Для всех Ax и a y, удовлетворяющих b, существует 6 = 0 (Ax, a y), 0 0 1, поэтому выражение АР =(Ahdh + Ауду) {к)КХ°е)+ РМ-1(а, г), (39.1) Куда? РМ-Лос-Ас)= ^ [топор ^ с-О ^ 1м)} (х0 + Бакс, У0 + залив). (39.2).
Величина полученного смешанного дифференциала в частных производных не зависит от порядка производны. Людмила Фирмаль
- Выражение (39.1) называется выражением функции / Тайлера (порядок m〜1), функция rt_x (Ax, Ay) является его остаточным членом, а выражение в форме (39.2) является остаточным членом выражения Тейлора в Лагранжевой форме. 39.1.Формула Тейлора для многих переменных функций Пять Для m = (39.1) 1 значение первого члена в правой части должно быть clear. In в этом случае общий индекс вверху равен zero. In в этом случае, по определению, этот член равен нулю, то есть формула (39.1) имеет вид ДТ = Р0(Л1; а г). В будущем, когда выражение записывается с использованием символа 2, где значение более высокого суммарного индекса меньше значения более низкого индекса, предположим, что это выражение равно нулю.
Доказательство. Зафиксируйте Ax и AY, p = YAx2 + Ay2 b, все точки вида (xn + 1Ax, y0 + 1Ay), здесь 0 = / / = ^ 1, находятся на отрезке, соединяющем точки (x0, yo) и (l’o Ax, yo + Au), поэтому все они принадлежат контексту точки (xc, y0). А я нет sure. As в результате, состав функций имеет смысл. Р = Ф(*.y) И затем x = x0 + 1Ax, y = y0 + 1Ay, 0 * 1, или комплексная функция P (1)= [(x0 + 1Ax, Y0 + * Ay), 0 ^ 1. (39.3) Очевидно.、 ДТ = Ф(х0 + Ах, У0 + Ау)-Ф (*О, как v0)= Р(1)-П(0)-(39.4) Поскольку функция является непрерывной производной от m в окрестности точки B (xa, y°), то в соответствии с теоремой о производной комплексной функции (см.§ 20.3) функция также также имеет непрерывную производную от M в интервале[0, 1].Поэтому справедлива формула Тейлора порядка m-1, содержащая остаток Лагранжевой формы. P(1)-P (0)= P ’(0) 1 Р » (0)»■, п, Т1 ’(0) 1,п»п) т, м 2! * Т \ 1 (39.5) o 0 1.
- В окрестности рассматриваемой точки (x0, y0) функция(39.3) может быть дифференцирована m раз по производному правилу комплексной функции (см. раздел 20.4, замечание 2). х (см. раздел). 21.1). Производная P (k) (I) выражается производной функции [(x, y) и выражением(39.5)1 = 1((39.4)вы получаете формулу Тейлора, необходимую для функции f (x, y).Конечно. От 6 до 39.Формула Тейлора и ряд Тейлора многих 3 функций. От (39.3) Р’_ d1I д(_ Ау _ ЦТ, ЦН ли Йи = д [(ху +(Ах, У0 + ^ Ау), Г / + + М…, Г, -, Нау) д 5л. » к」 Р «(1)= д [ ё (\ДХ О! ■а * 4 „) К и dhg Dx2 + 2 Д * 1 dhdu Ахау + ^ Ау2.
Отсюда, для P “ {I), опустите обозначение аргумента, чтобы сделать его кратким, и получите: (39.6) В общем случае, по индукции, P (k) {1)^ [^ x ^Auyy} ’ k)!{Хо + 1 топор, У0 +(топор)、 Поставим формулу (39.6)^ 0 = k = 1, 2,…М-1 Р ’(0)= Ах +?/ ..(*Йо) Ду. ДХ делать du2 Р ’(0)= Ax2 + 2〜; ^ о) топор Ау + г ^%п ^ а У2、 И вообще Р *(0)=(ДХ!+ Д ^)1 ′ р} /(.Р0, Е),* = 1, 2,…, М-1 (39,7) если k = m, заменить I на 0、 РМ) у = [Ax1x + AUD и УТ]1(x0yYAx, йо + Б (Ас) 39.8) Здесь заменить (39.7) и (39.8) на (39.5) и заменить I-1.Затем, благодаря отношениям(39.4) Т-1 Lg_t-р (о)= 1У&+ э = А = и Т-1 = 2 \ м а-dх + Ауду) {к)^ Хоу°)+ к = 1 + ^(х * | + о-ут) [(х0 + 0 dх, у + Dу 0), 0 01.Результат. Уравнение в предположении теоремы 1 т. ДГ = 2 г {Ах ТХ + АС ДУ){к)Я(х° * е)+ ТМ(а * „’ 39-9) 39.1.
Формула Тейлора для многих переменных функций Семь Кроме того, остальные разделы rm (Ax, Au) могут быть записаны в следующих форматах: т. РМ(Ах, Ау)= 2?А (ДХ, Ау) AhiAut-к (39.10)) к = 0 Куда? Eddx по ТМ, Ас)= 0, к = 0, 1,…. т, п = п, rAx2 + Au2 П-О Или РМ (Ах, Ау)= Р (Ах, Ау) РМ (39.11) Fri e (Dx, Au)= 0, то есть О ТМ (Ах, Ау)= о (РТ). (39.12) Доказательство. Поставь (39.13) А./, Л “ л ДТ ((х0 + 0 У0 + в АУ) ст1 (*о. Уд б * ’ ТП ^ у * ’dup-б ДХ’dup-Б на ЦТ Для непрерывности всех частных производных порядка M Пте * (Дх, Ду)=0. р * * о _ {Ах, Ау) к-о ■К ДТ [(х» + б топор, У0 + вай) не dhkdutk.
Оставшееся представление формулы Тейлора в виде (39.12) называется обозначением формы Пеано. Людмила Фирмаль
- Средство выход-к = Преобразуйте остаток rm_1 (Dx, Au) (см. (39.2)), используя следующее уравнение (39.13): Средство Выход-К + В ГК ДТ /(* а. Г «) т \ т \ смотрите игру DHK дут \ т \ т \ т \ т \ т \ т к = 0 + Ш 2 с-ОВОС * с) б * kyut〜к = к = 0 т. (39.15)) (39.14) =〜(Топор ^ + Ау (р) и tx0, йо)+ ЕК (Ах, Ау) средство аут-к、 е = 0 Ck где *(Дх, ду)= -■? e *(Ah, Du), следовательно Пятница*(Ax, Du) = 0. Р-О Подставляя (39.14), получаем (39.1) выражение Тейлора (39.9), где остальные члены имеют вид.
Смотрите также:
Решение задач по математическому анализу
