Оглавление:
Достаточные условия экстремума
Теорема 9.2 (первое достаточное условие экстремума). Пусть функция 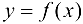 дифференцируема в некоторой проколотой окрестности точки
дифференцируема в некоторой проколотой окрестности точки 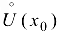 и непрерывна в точке
и непрерывна в точке 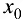 . Тогда, если
. Тогда, если 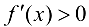 при
при 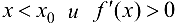 при
при 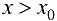 , то в точке
, то в точке 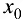 функция имеет локальный максимум; если
функция имеет локальный максимум; если 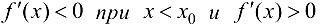 при
при 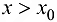 , то в точке
, то в точке 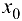 функция имеет локальный минимум.
функция имеет локальный минимум.
Доказательство следует из теоремы 9.1.
Теорема 9.3 (второе достаточное условие экстремума). Если в критической точке 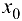 функции
функции 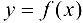 существует
существует 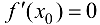 , а
, а 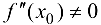 , то при
, то при 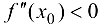 функция имеет локальный максимум, при
функция имеет локальный максимум, при 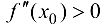 — локальный минимум.
— локальный минимум.
Доказательство.
Если в точке 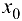 существует вторая производная
существует вторая производная 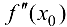 , то первая производная
, то первая производная 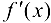 существует в некоторой окрестности этой точки
существует в некоторой окрестности этой точки 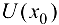 . Тогда
. Тогда 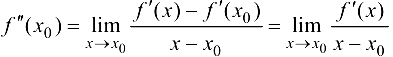 .
.
Пусть 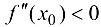 . Тогда
. Тогда 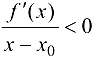 .
.
При 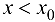 производная
производная 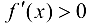 , т. е., согласно теореме 9.1, функция
, т. е., согласно теореме 9.1, функция 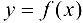 возрастает; при
возрастает; при 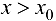 производная
производная 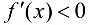 , т. е. функция
, т. е. функция 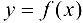 убывает. На основании теоремы 9.2; в точке
убывает. На основании теоремы 9.2; в точке 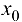 функция имеет локальный максимум.
функция имеет локальный максимум.
Случай 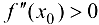 рассматривается аналогично. ■
рассматривается аналогично. ■
Замечание 9.2. Так как теорема формулирует только достаточное условие, то при 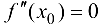 , функция может как иметь, так и не иметь экстремум.
, функция может как иметь, так и не иметь экстремум.
Пример 9.2.
Функция 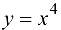 имеет в точке
имеет в точке 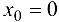 минимум, при этом
минимум, при этом 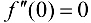 . Функция
. Функция 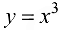 не имеет в точке
не имеет в точке 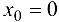 экстремума, при этом также
экстремума, при этом также 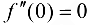 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
