Оглавление:
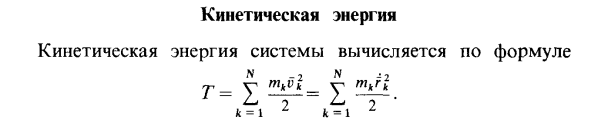




Кинетическая энергия
- Кинетическая энергия системы рассчитывается по формуле В случае системы с двумя степенями свободы, в которой наложены стационарные, идеальные, голономные и несвободные связи, радиус-вектор в каждой точке rk является функцией только обобщенных координат qt и q2. Когда система движется, обобщенные координаты qt и q2 зависят от времени. Следовательно, производная по времени от радиус-вектора Подставляя это в выражение кинетической энергии, Где введены обозначения 22 _ де Сумма A] равна qt Это не зависит от qt × q2.
Каждая из этих функций раскрывается в степенных рядах qt и q2 вблизи положения равновесия и принимает положение равновесия ^ i = <72 = 0. У нас есть для LP Индекс 0 ниже показывает, что эти значения необходимо рассчитать для Ц1 = 22 = -. Такое же разложение может быть получено для A12 и A22. Вводит следующие обозначения: w = (l) o; «12 = примерно (-412); a22 = (L22) 0 Постоянные значения a, a12 и a22 называются системными коэффициентами инерции. Если отбросить члены третьего и более высокого порядка для qt, q2, qt и q2, получим следующее уравнение для кинетической энергии: T = il1 (ailq2i + 2al2qlq2 + a22q22).
Момент инерции однородного тела вращения, ограниченного плоскостями двух параллелей, относительно его оси. Разобьем тело плоскостями, перпендикулярными к оси, на элементарные цилиндры. Людмила Фирмаль
Однородная квадратичная форма двух переменных x и x2 является выражением вида F = Biix2l + 2Bilxlx2 + B22x22, Где Vi, B12 и B22 — постоянные значения, а не все ноль. Квадратичная форма, которая принимает только положительные значения в области переменных переменных x1 и x2 и равна нулю только при нулевом значении переменной, называется полностью положительной. Не обращая внимания на третий и более высокие члены, кинетическая энергия системы вблизи положения равновесия имеет однородную квадратичную форму с обобщенной скоростью q2.
- Поскольку кинетическая энергия всегда положительна и равна нулю только при нулевом значении обобщенной скорости, она представлена вблизи положения равновесия системы явно положительной квадратичной формой обобщенной скорости. Чтобы обеспечить положительную квадратичную форму F, необходимо и достаточно, чтобы ее коэффициенты удовлетворяли условиям. W> 0; B22> 0; Bn Br1-B} 2 = | ^ 12 |> 0. (58) Получите эти условия. Убедитесь, что F в положительной квадратичной форме. Далее, если F> 0 для x2 = 0, x, x0, то Bj> 0. Точно так же B22> 0 из условия, что F> 0 для x2 # 0, x, = 0.
Это необходимые условия для определенных положительных квадратичных форм, но их недостаточно, потому что B12 достаточно отрицателен, чтобы F был отрицательным. Если x2 не равен нулю в рассматриваемой области, переменная x = Xj / x2 вводится для преобразования квадратичной формы. В противном случае вы можете обменять xt и x2.
Допустим, что маятники совершают круговое движение, и обозначим через Т продолжительность обращения каждого из маятников, а через т — промежуток времени, отделяющий начала их движений. Людмила Фирмаль
Вторичная форма F принимает форму: B = x ^ (Vih2 + 2B12x + B22). Квадратичное уравнение необходимо и достаточно, чтобы F был положительным всюду в рассматриваемой области значений x. Вих2 + 2В12х + V22 = 0 Не было настоящего корня, то есть параболы y = Bin2 + 2B12x + B22, Когда Bc> 0 и B22> 0, он был полностью выше горизонтальной оси. По этой причине дискриминант квадратного уравнения должен быть отрицательным. Bh-BuB22 <0 или BnB22-B | 2> 0. Условие (58) доказано. Поскольку кинетическая энергия вблизи равновесия представляется явной положительной квадратичной формой, ее коэффициент должен удовлетворять условию (58).
Следовательно, для an, ai2 и a2r Для систем с любой конечной степенью свободы n кинетическая энергия вблизи положения равновесия выражается в однородной квадратичной форме. T = 42 (ailql + al2qiq2 + auq2qi + a22ql + … + amqi). Ясные положительные условия:
Смотрите также:
Задачи по теоретической механике
| Математический и физический маятники | Потенциальная энергия |
| Малые колебания системы с двумя степенями свободы (результаты для общего случая) | Диссипативная функция |
