Монотонность. Точки экстремума
Теорема 1 (признак монотонности). Для того, чтобы функция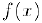 
, определенная и дифференцируемая в некотором интервале 
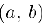была невозрастающей (неубывающей) в этом интервале, необходимо и достаточно, чтобы се производная была неположительной (неотрицательной) в этом интервале, т.е. 
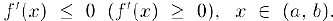Если же 
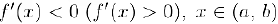, то функция убывает (возрастает) в интервале .
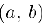Доказательство. Предположим, для определенности, что данная функция является невозрастающей. Тогда для любой точки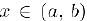 
при малом приращении 
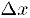аргумента в точке x
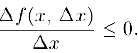
Воспользовавшись теперь дифференцируемостью функции в точке x b свойством 5) предела функции (глава IV, §4, пункт 2), заключаем:
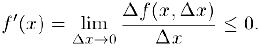
Наоборот, пусть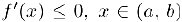 
. Возьмем произвольные точки 
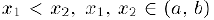и применим к отрезку 
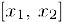теорему Лагранжа (§3). В результате получим:
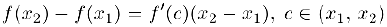
откуда следует, что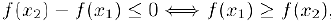 
т. е. функция 
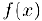нс возрастает.
Из рассуждений предыдущего абзаца при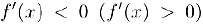 
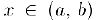следует, что 
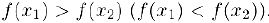. Теорема доказана.
Геометрически последнее утверждение теоремы означает, что, если во всех точках графика функции касательная образует тупой (острый) угол с положительным направлением осп Ох. то эта функция является убывающей (возрастающей).
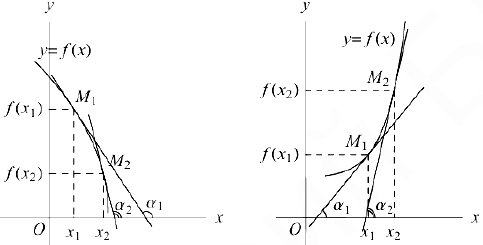
Всюду в дальнейшем в этом пункте мы будем предполагать, что функция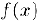 
определена в некотором интервале, содержащем точку 
.
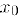Точка .то называется точкой локального минимума (максимума) данной функции. если при всех х из достаточно малого интервала, включающего точку 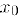, выполняется неравенство
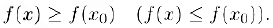
Если, кроме того,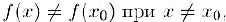 
то будем говорить, ото в точке то функция имеет строгий локальный минимум (максимум).
Точки локального минимума или максимума функции называются точками се локального экстремума, соответственно, точками ее строгого локального экстремума.
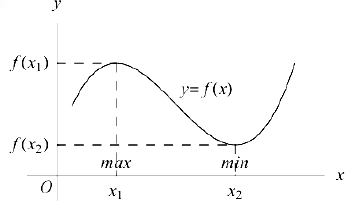
Теорема 2 (необходимый признак экстремума). В точке экстремума производная функции обращается в нуль или не существует.
Действительно, если 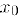— точка экстремума функции 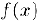, то в случае, когда производная 
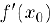существует, повторяя рассуждения, которые мы использовали при доказательстве теоремы Ролля (§3), получим,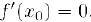 
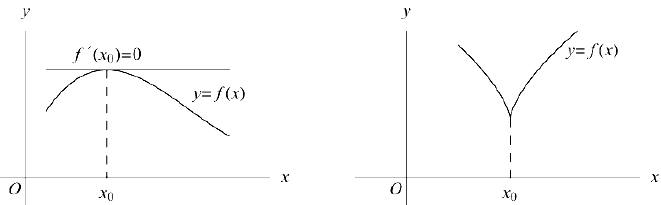
Обратное, вообще говоря, неверно, т.е. из того, что производная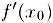 
не существует или равна нулю, еще не следует, что 
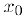— точка экстремума функции 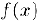, в чем мы убедимся на примерах. Рассмотрим функции
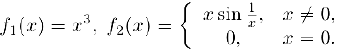
Для первой из них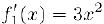 
и, следовательно, 
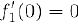, а производная 
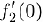не существует, так как не существует предел
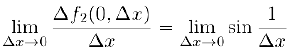
(глава TV . §5, пункт 2. с)). В то же время точка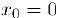 
не является точкой экстремума данных функций, так как первая из них возрастает, а вторая меняет знак в любом сколь угодно малом интервале, содержащем эту точку.
Точка, в которой производная данной функции равна пулю или не существует, называется критической точкой функции. Теорема 2 утверждает, что каждая то’гка экстремума является кригической точкой, а приведенные выше примеры убеждают нас в том, чго не всякая критическая точка является точкой экстремума. Сформулируем условия, при которых в критической точке функция будет иметь экстремум.
Теорема 3 (достаточный признак экстремума I). Предположим, что функция 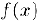дифференцируема в некотором малом интервале, содержащем критическую точку 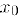, кроме, возможно, самой этой точки. Тогда, если при. 
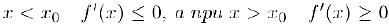или наоборот, то 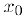— точка локального минимума или, наоборот, локального максимума данной функции. Если указанные выше неравенства для производной строгие, то и соответствующий экстремум является строгим, иначе говоря, в критической точке функция имеет строгий экстремум, если при переходе через эту критическую точку производная, функции меняет знак на противоположный.
Доказательство этой теоремы очевидным образом следует из теоремы 1.
Замечание 1. Из теоремы 1 также следует, ‘гго, если при переходе через критическую точку производная функции не меняет знак на противоположный, то функция не имеет экстремума в этой точке.
Теорема 4 (достаточный признак экстремума II). Пусть функция 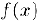дифференцируема в некотором малом интервале, содержащем критическую точку 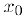и дважды дифференцируема в точке 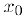. Тогда, если 
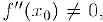функция имеет строгий экстремум в точке 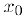. а именно, если 
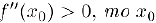— точка строгого локального минимума, если же 
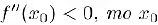— точка, строгого локального максимума данной функции.
Доказательство. Поскольку функция дифференцируема в критической точке 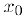. то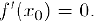 
Запишем для данной функции формулу Тейлора второго порядка в точке 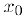с остатком в форме Пеано (§5. пункт 1):
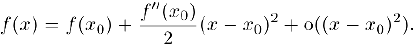
Отсюда
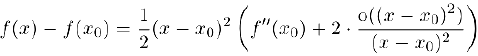
Выберем положительное число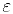 
так. чтобы 
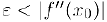Поскольку
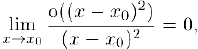
то существует число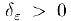 
такое, что при всех 
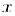из интервала 
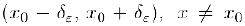выполняется неравенство
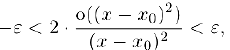
откуда,
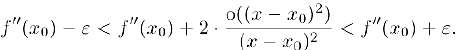
Если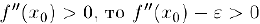 
за счет выбора 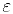и, следовательно
при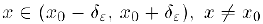 
и поэтому для всех таких 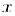справедливо неравенство
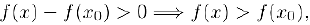
т. е. 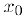—точка строгого минимума функции 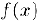. Аналогично, если 
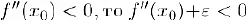и поэтому
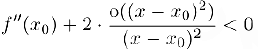
для всех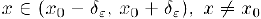 
. Следовательно.
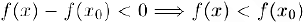
и, значит, 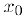— точка строгого максимума данной функции. Теорема доказана.
Замечание 2. Если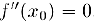 
, то экстремум в критической точке 
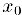может как быть, гак и отсутствовать. Рассмотрим, например, функции 
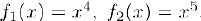. Здесь
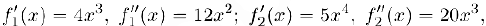
следовательно, для обеих этих функций точка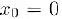 
является критической и в ней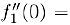 
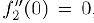, однако первая функция имеет минимум в точке 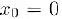. а вторая экстремума не имеет.
Из вышеизложенного следует, что для исследования функции на экстремум необходимо найти критические точки этой функции и проверить каждую из них на экстремум с помощью одного из достаточных признаков.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
