Оглавление:


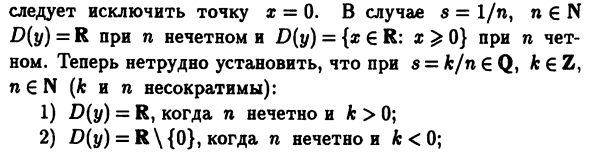






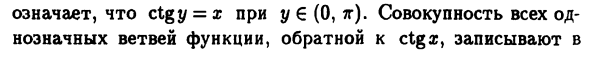

Основные элементарные функции
- Среди огромного количества разрабатываемых функций Математика постепенно присваивалась небольшому населению Особенно распространенная относительно простая функция Самое разнообразное применение математического анализа Поэтому было проведено самое подробное расследование. Функции, содержащиеся в этой коллекции, называются основными Элементарная функция Или признак общего принципа. При изучении других людей, Обычно более сложные функции уже широко используются Известны характеристики основных базовых функций, Большинство из них рассматриваются в школьных курсах Математика.
Степенная функция Y = x>, (3.14) Где 8 6 R — постоянное действительное число. Поведение этой функции сильно зависит от показателя Степень с. Когда s∈Z, (3.14) является рациональной функцией. Где 8 = k / n∈Q (k∈Z, n∈N, а k и n Общий делитель, и, следовательно, неприводимый), и x8 = hk1n = #? (3.15) Функция (3.15) назначена иррациональной функции. Не так просто рассчитать его стоимость Рациональное значение функции. Это трудно сделать Функция (3.14), если само число s иррационально (например, s =% / 2). Однако этот вопрос требует особого рассмотрения.
Поэтому ограничьте эти функции следующим списком: Небольшой комментарий. Людмила Фирмаль
Область (y) функции (3.14) Существенно зависит от набора Номер 8. Если s∈N, D (y) = R. Когда s является целым числом Если отрицательно, D (y) = R \ {0}, то есть от числовой линии Точка x = 0 должна быть исключена, если s = 1 / n, n € N D (y) = R нечетно, D (y) = {x∈R: a; ^ 0} n Но. s = fc / n∈Q, k∈Z, n 6 N (& и n неприводимы): 1) Если n нечетно и k> 0, D (y) = R. 2) Если η нечетно и fc <0, D (y) = R \ {0}. 3) D (y) = {x € R: £ ^ 0}, когда η четно и A:> 0. 4) D (y) = {x∈R: a;> 0}, когда n чётно и KO. Иррациональный случай 8 рассмотрен ниже ( Логарифмическая функция). Экспоненциальные функции называются функциями o> 0, af . (3.16) а> \ а> \ Область этой функции — целое число Непосредственно.
Эта функция положительна и монотонно возрастает Когда a> 1, 0 0, выполняется уравнение a0 = 1, Любое значение х этой функции Не может быть рассчитано Окончательная помощь Алгебраическая последовательность (Сложение, вычитание, Умножение, деление и монтаж Общая степень). так Эта функция Неалгебраический, или Трансцендентальная функция (от Латинское выражение Gebrae Vires Transcendit — это превышает силу алгебры). Г. Лейбниц впервые использовал термин «трансцендентность». 1686. Срок был назначен на I в 1724 году. Ноль.
- Рисунок 3.16 Логарифмическая функция показывает (3,17) Где a — положительная постоянная, отличная от 1. Определяется как число, и обратная величина экспоненты Функция Это x = ay из (3.17), подробности : Любое число с x> 0 имеет уникальный номер y, Удовлетворяет отношения ау-х. С этим номером у называется логарифмом числа х в нижней части, лог # поэтому Так знаком со школьного курса Логарифмическая идентичность по сути является определением Логарифмическая функция (3.17). Определение D домен (у) = = {x € R: x> 0}. Эта функция монотонно возрастает при> 1 0 <a <1 уменьшается монотонно.
Во всяком случае ее график Пройдите через точку (1, 0) на координатной плоскости, Симметричен относительно графика функции a * относительно прямой y = x (См. Рисунок 3.16). с того времени logas = -log1 / aa: Графики функций logax и log ^ ax симметричны. Ось ах. Где общая степенная функция (3.14) и Реальное значение s € R определяется равенством x9 = (alo * «* y = a *» ° ge *? a € (0, 1) U (1, + oo). Экспоненциальный диапазон и диапазон значений Логарифмические функции совпадают (это целочисленная строка). Таким образом, область их определения суперпозиции
В области определения логарифмической функции, т.е. ‘) = (0} + оо). Людмила Фирмаль
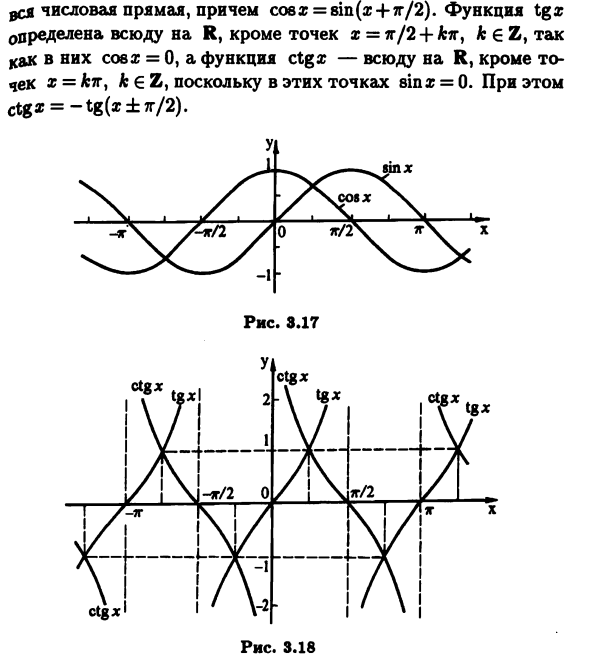
Подумайте о синусе от тригонометрических функций sin z, косинус C0S2, тангенс tgx = (sinz) / cosz и Котангенс ctgz = (coss) / грехи. Характерные особенности этих функций Они периодические в sinx и cosz Период составляет 2 тг (рисунок 3.17), тгк и ктга. -Период р (Рисунок 3.18). Сфера греха. Кроме того, cosx функционирует как числовая строка, cos £ = sin (z + 7r / 2). Функция Tgx Точка x = η / 2 + kit, определенная в любом месте R, кроме fc € Z. Как и их, потому что x = 0, функция ctgg всюду в R, Поскольку K является обратной функцией тригонометрической функции, точка x = & π, k∈Z Вызовите arcsinz, arccosx, arctgx, arcctgx. Арк синус, арккосинус, арктангенс, Arco касательным. Функция <р (х)
Является ли противоположность для данной функции f (x) ) Z = f (y). Для функции ах, наоборот ». Однако эта функция может иметь обратную многозначную функцию. Таким образом, обратная функция у = х2 Есть две уникальные ветви, y = l / x и y = -l / x. Из этих двух соотношений х = у2 ( Пример 3.7). Для каждой тригонометрической функции Наоборот, с уникальным бесконечным множеством Отделение. Произвольный интервал [—tr / 2-h Ar7r, tr / 2 + for], fc € Z, функция Грех а; строго монотонный и потому инъективный. И поэтому У каждого из этих сегментов есть измена Функция. Другими словами, я существую ради греха Обратная функция с уникальным бесконечным множеством Отделение.
Указано в Arcsina; Из этого набора Одна ветвь назначает то, что соответствует сегменту [-7g / 2, 7g / 2], это называется основным значением Обозначает арксинус x и арксинус; Очистить область Диапазон функции arcsina: sin a: Сегмент [-1, 1] и диапазон, указанный над сегментом [-tg / 2, tg / 2]. Итак арчина, заключенный между [-tg / 2, tg / 2] Угол (в радианах), где синус равен x. тогда Целое все однозначные ветви многозначной функции, может быть написано как обратная сторона греха а; Arcsinx = для + (-l) * arcsina;, k € Z. (3,18) Аналогично, введите противоположную функцию для других функций Тригонометрическая функция.
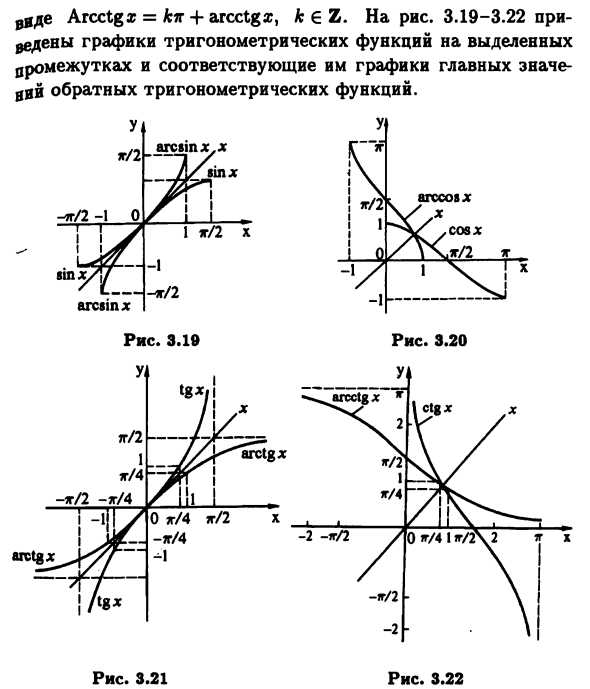
Например, arccosa; -значение Угол заключен в [0,7d] с косинусом x, и Целое все однозначные ветви многозначной функции, Записано как обратная сторона Cosx, Arccosa. = 2 для арккозы; k € Z. Обозначение y = arctga; по определению tgt / = = х для у € (-7 г / 2, 7 г / 2). Все ясно целое Ветвь многозначной функции, обратной к tgx, имеет вид Вид на Арктгу. = А? Mr + arctga;, k £ Z. Наконец, обозначение y = arcctga; ctgy = x для y € (0,7 г). Все в целом Прозрачная ветвь обратной функции ctgx написана Arcctgx = для + arcctgx, k € Z. 3.19-3.22, когда- График выбранной тригонометрической функции Основной 0 интервал и соответствующее расписание Значение обратной тригонометрической функции.
Смотрите также:
| Четные и нечетные функции | Некоторые элементарные функции |
| Ограниченные функции | Законы композиции |
