Оглавление:
Основные теоремы дифференциального исчисления
Теорема Ферма
Если функция 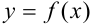 дифференцируема в точке
дифференцируема в точке 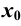 и имеет в этой точке экстремум, то ее производная при
и имеет в этой точке экстремум, то ее производная при 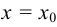 обращается в нуль, т. е.
обращается в нуль, т. е. 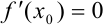 .
.
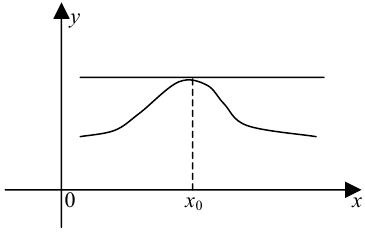
Доказательство. Пусть для определенности 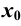 — точка максимума. Тогда для достаточно малых
— точка максимума. Тогда для достаточно малых 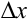 имеет место неравенство:
имеет место неравенство: 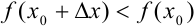 или
или 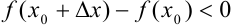 . Разделим обе части неравенства на
. Разделим обе части неравенства на 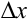 .
.
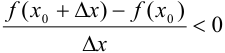 при
при 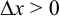 ,
,
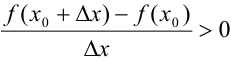 при
при 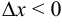 .
.
По условию 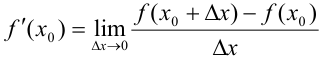 существует. Поэтому при
существует. Поэтому при 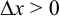
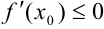 , при
, при 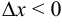
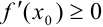 . Значит,
. Значит, 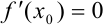 .
.
Теорема Ролля
Если функция 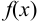 непрерывна на
непрерывна на 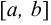 и дифференцируема в интервале
и дифференцируема в интервале 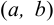 , а на концах отрезка имеет равные значения
, а на концах отрезка имеет равные значения 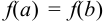 , то в интервале
, то в интервале 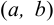 найдется хотя бы одна точка
найдется хотя бы одна точка 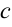 , в которой производная равна нулю.
, в которой производная равна нулю.
Доказательство. Поскольку функция непрерывна на отрезке 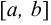 , то она принимает на нем свое наибольшее и наименьшее значения:
, то она принимает на нем свое наибольшее и наименьшее значения: 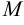 и
и 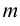 . Если
. Если 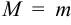 , то функция постоянна на данном отрезке и
, то функция постоянна на данном отрезке и 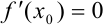 в любой точке отрезка. Значит
в любой точке отрезка. Значит 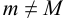 . Ясно, что либо
. Ясно, что либо 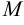 , либо
, либо 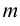 отлично от
отлично от 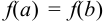 . Пусть
. Пусть 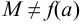 и
и 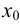 — значение, при котором
— значение, при котором 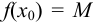 . Так как
. Так как 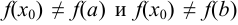 , то
, то 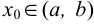 и в этой точке дифференцируемая функция имеет максимум. По теореме Ферма
и в этой точке дифференцируемая функция имеет максимум. По теореме Ферма 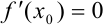 . Положив
. Положив 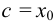 , получим:
, получим: 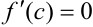 .
.
Теорема Лагранжа
Если функция 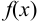 непрерывна на
непрерывна на 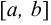 и дифференцируема в интервале
и дифференцируема в интервале 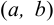 , то в интервале
, то в интервале 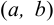 найдется хотя бы одна точка
найдется хотя бы одна точка 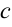 , в которой
, в которой
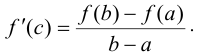
Доказательство. Запишем уравнение хорды 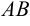 , проходящей через точки
, проходящей через точки 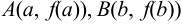 :
:
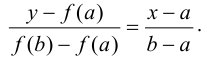
Отсюда
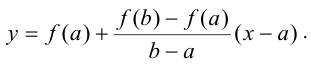
Рассмотрим вспомогательную функцию:
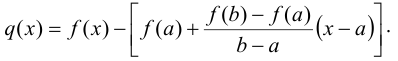
Эта функция удовлетворяет условиям теоремы Ролля. Она непрерывна на 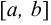 и имеет в
и имеет в 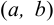 производную
производную
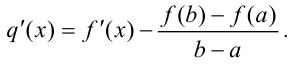
Кроме того, 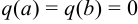 . По теореме Ролля в интервале
. По теореме Ролля в интервале 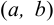 найдется точка
найдется точка 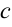 , в которой
, в которой 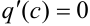 .
.
Теорема Коши
Если 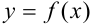 и
и 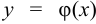 — две функции, непрерывные на
— две функции, непрерывные на 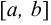 и дифференцируемые на
и дифференцируемые на 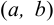 , причем
, причем 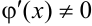 для всех
для всех 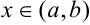 , то между
, то между 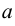 и
и 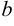 найдется точка с такая, что
найдется точка с такая, что
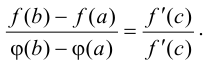
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
