Оглавление:




Свойства и характеристики распределения случайных погрешностей
- Характеристики и характеристики распределения случайных ошибок При рассмотрении характеристик и характеристик распределения случайных ошибок случайные ошибки измерений обычно распределяются нормально, поэтому ограничивайте их только нормальным распределением. Эти свойства, заданные теорией вероятностей, а также выводы и доказательства свойств здесь не приводятся.
Для ясности рассмотрим характеристики и характеристики нормального распределения, используя график (см. Рисунок 20). Обратите внимание, что эти характеристики и характеристики отражены в формуле (UP.4). Наибольшее значение (плотность вероятности (т.е. наибольшая ордината) соответствует ошибке 6 = 0. Увеличение как положительного, так и отрицательного значения ошибки уменьшает ординату кривой, то есть ошибку 6.
Сменные преобразователи могут использоваться с любым конструктивным прибором и любым источником измерений при условии совпадения входных и выходных характеристик преобразователя. Людмила Фирмаль
Чем больше значение, тем ниже его плотность вероятности (встречается реже) и, по мере ее уменьшения, кривая асимптотически приближается к горизонтальной оси, что означает, что плотность вероятности появления очень больших ошибок Значит очень маленький. Кривая нормального распределения симметрична относительно оси y, то есть вертикальной линии, проходящей через точку, соответствующую 6 = 0. Это означает, что ошибки одинаковы, но разные знаки имеют одинаковую плотность вероятности. Кривая в форме колокола. Выпуклость кривой увеличивается вблизи средней точки.
Существует точка перегиба для этой кривой на определенном расстоянии симметрично от центра, ниже которого выпуклость кривой уменьшается. Высота ординат различных кривых и абсцисса точки перегиба различны и отражают характеристики (параметры) нормального распределения. Математическое ожидание случайной величины — это окружающее значение, вокруг которого группируются отдельные наблюдения. Математическое ожидание дискретной случайной величины M (x) определяется как сумма произведений всех возможных значений случайной величины из-за вероятности этих значений М (х).
Для непрерывных случайных величин вы должны полагаться на интеграцию. Поэтому необходимо знать зависимость плотности вероятности от x, то есть p (x). тогда М (х) = + ^ ° хр (х) ^ х. Это выражение означает, что ожидаемое значение равно сумме произведений бесконечно большого числа всех возможных значений случайной величины x на бесконечно малую область p (x) xx. Где o (x) — координата каждого x, а 1x — базовый сегмент горизонтальной оси. Если наблюдается нормальное распределение случайных ошибок, математическое ожидание случайных ошибок равно нулю (см. Рисунок 20).
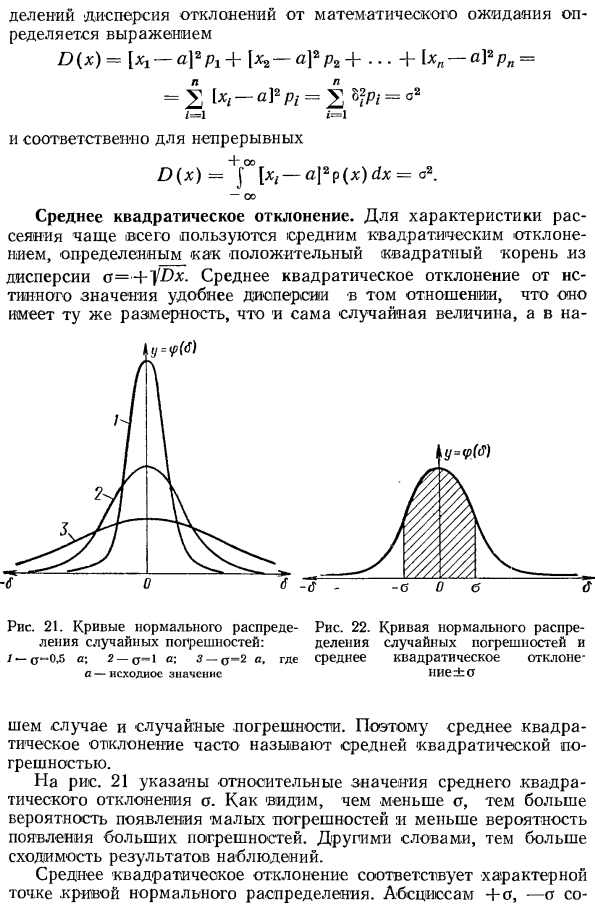
Учитывая нормальное распределение результатов (см. Рисунок 19), математическое ожидание соответствует истинному значению измеренной величины и обозначается как. В будущем для простоты мы будем использовать обозначение a для математического ожидания меры таким же образом, как и для истинных значений. Дисперсия. На рисунке 21 показаны несколько кривых с нормальным распределением (ошибка. Как и выше, (вся площадь под кривой распределения всех кривых соответствует 1. Это потому, что кривая является случайной величиной). Для охвата всех значений, т. Е. Всех наблюдений и суммы вероятностей.
- Наличие всех возможных результатов равно 1. То есть, если какой-либо результат получен во время измерения, Природа будет выше. Как вы можете охарактеризовать нормальную кривую распределения Они имеют одинаковую ограниченную площадь и разный внешний вид Сравнение кривых, показанных на фигуре Как показано на фигуре 21, на кривой 1 можно подтвердить, что почти вся область сосредоточена вблизи центральной ординаты. Это означает, что большинство результатов почти совпадают с математическими ожиданиями. То есть большинство ошибок практически не отличаются от 0.
В этих случаях вариация (или вариация) в результатах наблюдения невелика, и существует высокая вероятность того, что произойдет значение, близкое к математическому ожиданию. Распределение кривой 2 характеризуется большой дисперсией. Здесь вероятность большой ошибки увеличилась, но вероятность почти нулевой ошибки также уменьшилась. Рассеяние распределения вдоль кривой 3 еще больше. Вероятность возникновения большой ошибки значительно выше, чем распределение по кривой 2. Дисперсия O (x), равная O2, служит мерой изменения значения случайной величины.
В случае рассмотрения заявки на разработку специального измерительного прибора необходимо учитывать взаимное влияние контролируемых параметров на соответствующие погрешности измерений. Людмила Фирмаль
Для дискретного (теоретического) распределения Дисперсия отклонения от математического ожидания определяется по формуле O (x) = l, -a 2P1 + 1 * 2 — a 2p2 + … + 1xa — a 2p = Поэтому постоянно O (x) = +; ° ° x -a12P (x) dx = oa. Стандартное отклонение Для характеристики рассеяния чаще всего используется среднеквадратичное отклонение, определяемое как положительный квадратный корень дисперсии o = + yDx. Среднеквадратичное отклонение от истинного значения более удобно, чем дисперсия, в том смысле, что оно имеет те же размеры, что и сама случайная величина.
В этом случае случайная ошибка. Поэтому стандартное отклонение часто называют стандартным отклонением. На фиг.21 показана относительная величина среднеквадратичного отклонения o. Как видите, чем меньше значение a, тем выше вероятность возникновения небольшой ошибки и ниже вероятность возникновения большой ошибки. Другими словами, сходимость результатов наблюдений больше. Стандартное отклонение соответствует характерной точке кривой нормального распределения. Абсцисса + о, -а- Соответствует точке перегиба кривой.
Вероятность того, что случайная погрешность измерения не превысит ± 0, составляет приблизительно 0,6826 S-22 Это соответствует входу в заштрихованную область, примерно в два раза больше, чем незатененная область. Формула (UP.Z) содержит две величины, значения которых полностью определяют закон распределения для каждого конкретного случая. Это a = L1 (x) (математическое ожидание) и o (стандартное отклонение). Рассмотренное нормальное распределение случайных величин, включая случайные ошибки, является теоретическим.
Поэтому описанное нормальное распределение следует рассматривать как идеальный взлом, теоретическую основу для изучения случайных ошибок и их влияния на результаты измерений. Вот как на самом деле применить это распределение с различной степенью приближения: Другое распределение, используемое для небольших наблюдений (распределение студентов *), также рассматривается.
Смотрите также:
