Оглавление:
Свойства основных классов векторных полей
Соленоидальное поле
Напомним, что векторное поле  называется соленоидальным, если во всех точках его дивергенция поля равна нулю, т. е.
называется соленоидальным, если во всех точках его дивергенция поля равна нулю, т. е. 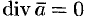 .
.
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела (см. пример 71.4); магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и другие.
Приведем некоторые свойства соленоидального поля.
1. В соленоидальном поле  поток вектора черта любую замкнутую поверхность равен нулю. Это свойство непосредственно вытекает из формулы (71.8). Таким образом, соленоидальное поле не имеет источников и стоков.
поток вектора черта любую замкнутую поверхность равен нулю. Это свойство непосредственно вытекает из формулы (71.8). Таким образом, соленоидальное поле не имеет источников и стоков.
2. Соленоидальное поле является полем ротора некоторого векторного поля, т. е. если 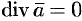 , то существует такое поле
, то существует такое поле 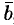 , что
, что 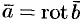 . Вектор
. Вектор 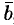 называется векторным потенциалом поля
называется векторным потенциалом поля  .
.
Любое из свойств 1-2 можно было бы взять в качестве определения соленоидального поля.
Доказывать свойство 2 не будем. Отметим лишь, что обратное утверждение — поле ротора векторного поля есть соленоидальное — нами доказано (выше мы показали, что 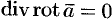 ).
).
3. В соленоидальном поле  поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение (называемое интенсивностью трубки).
поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение (называемое интенсивностью трубки).
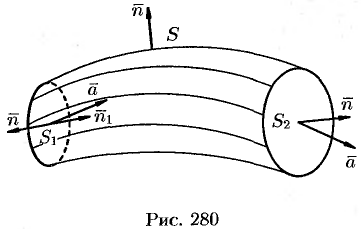
Рассмотрим векторную трубку между двумя ее произвольными сечениями 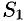 и
и 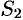 ; боковую поверхность трубки обозначим через
; боковую поверхность трубки обозначим через  (см. рис. 280). Поток вектора через замкнутую поверхность, состоянию из
(см. рис. 280). Поток вектора через замкнутую поверхность, состоянию из 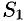 ,
, 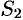 и
и  , равен нулю. Следовательно,
, равен нулю. Следовательно,
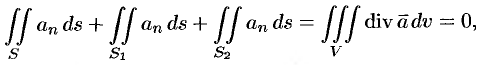
где 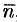 — внешняя нормаль.
— внешняя нормаль.
Так как на боковой поверхности векторной трубки нормаль 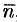 перпендикулярна к векторам поля, то
перпендикулярна к векторам поля, то 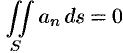 и, следовательно,
и, следовательно,
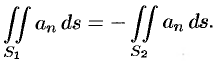
Переменив направление нормали на площадке 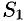 , т. е. взяв внутреннюю нормаль
, т. е. взяв внутреннюю нормаль 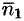 , получим:
, получим:
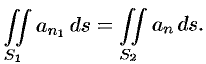
В поле скоростей текущей жидкости полученный результат означает, что количество жидкости, втекающей в трубку за единицу времени, равно количеству жидкости, вытекающей из нее.
Потенциальное поле
Векторное поле  называется потенциальным (или безвихревым, или градиентным), если во всех точках поля ротор равен нулю, т. е.
называется потенциальным (или безвихревым, или градиентным), если во всех точках поля ротор равен нулю, т. е. 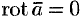 . Примером потенциального поля является электрическое
. Примером потенциального поля является электрическое
поле напряженности точечного заряда (и другие).
Приведем основные свойства потенциального поля.
Свойство 1. Циркуляция потенциального поля  по любому замкнутому контуру в этом поле равна нулю.
по любому замкнутому контуру в этом поле равна нулю.
Это непосредственно вытекает из формулы (71.14). Следовательно, 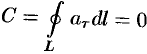 .
.
В частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости равенство 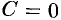 означает, что в потоке нет замкнутых струек, т. е. нет водоворотов.
означает, что в потоке нет замкнутых струек, т. е. нет водоворотов.
Свойство 2. В потенциальном поле  криволинейный интеграл
криволинейный интеграл 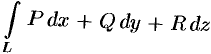 вдоль любой кривой
вдоль любой кривой  с началом в точке
с началом в точке 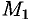 и концом в точке
и концом в точке 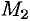 зависит только от положения точек
зависит только от положения точек 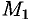 и
и 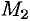 и не зависит от формы кривой.
и не зависит от формы кривой.
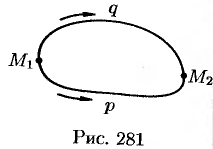
Это свойство вытекает из свойства 1. Действительно, взяв в поле две точки 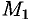 и
и 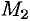 , соединим их двумя кривыми
, соединим их двумя кривыми 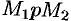 и
и 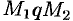 так, чтобы контур
так, чтобы контур 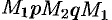 лежал внутри поля (см. рис. 281). Тогда, в силу свойства 1, имеем
лежал внутри поля (см. рис. 281). Тогда, в силу свойства 1, имеем
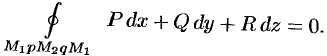
Учитывая свойства криволинейного интеграла, получаем:
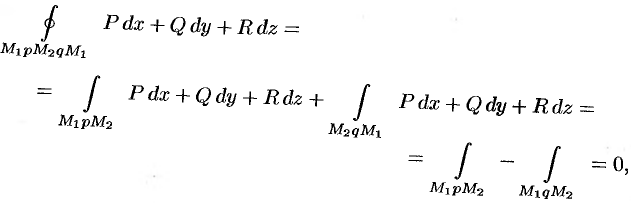
т.е.
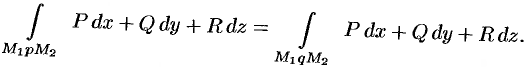
Свойство 3. Потенциальное поле является полем градиента некоторой скалярной функции 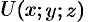 , т. е. если
, т. е. если 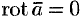 , то существует функция
, то существует функция 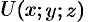 такая, что
такая, что 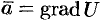 .
.
Из равенства 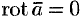 вытекает, что
вытекает, что 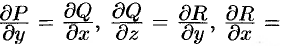
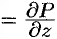 , т. e. выражение
, т. e. выражение 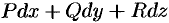 является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции 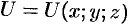 (следствие 56.1). Эту функцию называют потенциалом векторного поля
(следствие 56.1). Эту функцию называют потенциалом векторного поля 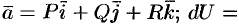
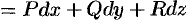 .
.
Отсюда: 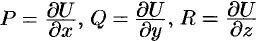 . Следовательно,
. Следовательно,
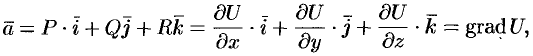
т. e. вектор поля  является градиентом скалярного поля.
является градиентом скалярного поля.
Замечание. Из равенства 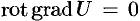 следует обратное утверждение — поле градиента скалярной функции
следует обратное утверждение — поле градиента скалярной функции 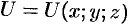 является потенциальным.
является потенциальным.
Из равенства 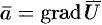 следует, что потенциальное поле определяется заданием одной скалярной функции
следует, что потенциальное поле определяется заданием одной скалярной функции 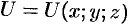 — его потенциала. Потенциал векторного поля может быть найден по формуле
— его потенциала. Потенциал векторного поля может быть найден по формуле
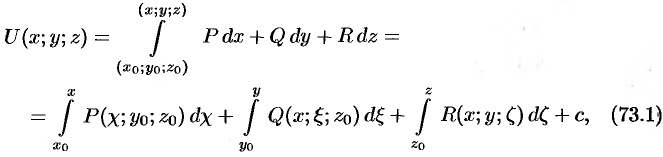
где 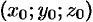 — координаты фиксированной точки,
— координаты фиксированной точки, 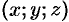 — координаты произвольной точки. Потенциал определяется с точностью до произвольного постоянного слагаемого (из-за того, что
— координаты произвольной точки. Потенциал определяется с точностью до произвольного постоянного слагаемого (из-за того, что 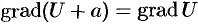 ).
).
Произвольное же векторное поле требует задания трех скалярных функций (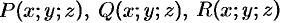 — проекции вектора поля на оси координат).
— проекции вектора поля на оси координат).
Замечание. Определение потенциального поля может быть дано иначе — векторное поле  называется потенциальным, если оно является градиентом некоторого скалярного поля, т. е.
называется потенциальным, если оно является градиентом некоторого скалярного поля, т. е. 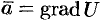 . (Иногда пишут
. (Иногда пишут 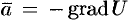 ; знак «минус» пишут для удобства, обычно векторные линии направлены в сторону убывания
; знак «минус» пишут для удобства, обычно векторные линии направлены в сторону убывания  : поток жидкости направлен туда, где давление меньше; теплота перемещается от более нагретого места к менее нагретому и т. д.)
: поток жидкости направлен туда, где давление меньше; теплота перемещается от более нагретого места к менее нагретому и т. д.)
Пример №73.1.
Установить потенциальность поля
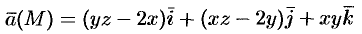
и найти его потенциал.
Решение:
Имеем:
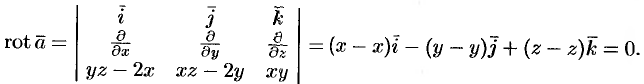
Следовательно, поле вектора  потенциальное.
потенциальное.
Найдем потенциал  по формуле (73.1), выбирая в качестве фиксированной точки начало координат, т. е.
по формуле (73.1), выбирая в качестве фиксированной точки начало координат, т. е. 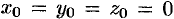 . Так как
. Так как 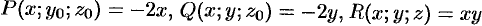 , то
, то
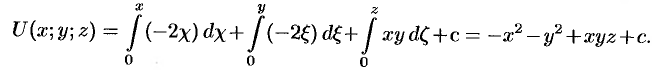
Гармоническое поле
Векторное поле  называется гармоническим (или лапласовым), если оно одновременно является потенциальным и соленоидальным, т. е. если
называется гармоническим (или лапласовым), если оно одновременно является потенциальным и соленоидальным, т. е. если 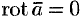 и
и 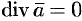 .
.
Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.
Так как поле  потенциально, то его можно записать в виде
потенциально, то его можно записать в виде 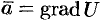 , где
, где 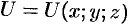 — потенциал поля.
— потенциал поля.
Но так как поле одновременно и соленоидальное, то
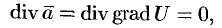
или, что то же самое,
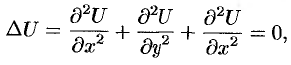
т. е. потенциальная функция  гармонического поля
гармонического поля  является решением дифференциального уравнения Лапласа. Такая функция называется, как уже упоминали, гармонической.
является решением дифференциального уравнения Лапласа. Такая функция называется, как уже упоминали, гармонической.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Циркуляция векторного поля |
| Ротор векторного поля. Формула Стокса |
| Дифференцирование функции комплексного переменного |
| Аналитическая функция тфкп |
