Оглавление:










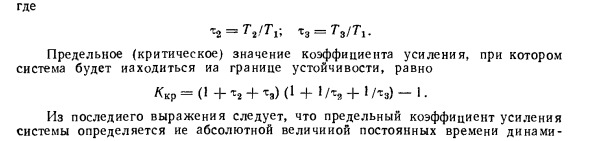
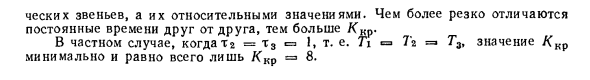
Алгебраические критерии устойчивости
- Алгебраические критерии устойчивости С помощью алгебраических критериев устойчивости об устойчивости системы можно судить по коэффициентам характеристического уравнения. D (p) = a0pn + a1Pn’x + ••. + an = 0. (3.30) Из критериев алгебраической устойчивости наиболее широко используются критерии устойчивости Рауса и Флуитца. Прежде чем знать их, обратите внимание, что условия, необходимые для устойчивости системы любого порядка, являются положительными для всех коэффициентов характеристического уравнения (3.30) a0> 0, a,> 0, …,> 0. (3,31) Фактически, согласно теореме Безу, уравнение (3.30) можно выразить как произведение факторов, включающих корни p, p2 ….. pn. n0 (P-Pi) (p-Pi) (P-Pn) = 0 (3,32) Если все корни характеристического уравнения отрицательны, то все факторы в уравнении (3.32) имеют вид МР + я I I a2 |) … (p + | a „|) = 0, (3.33) Где p {= — | a * | -корневое значение.
Умножение (3.33) дает (3.30). Где все коэффициенты определяются положительными условиями. * * выражение (3.33), то есть положительное. Пример 3.2 Системное характеристическое уравнение ! 2p4-b 2P2 + 4p + 50 = 0. Система нестабильна, потому что коэффициент а \ = 0. Пример 3.3. Системное характеристическое уравнение Зр3 + Юр4 + 5 / т3- + р + 100 = О Система нестабильна, потому что a3 = —7 <0. Пример 3.4. Системное характеристическое уравнение 2p * + 6p2-b \ 0p + 15 = 0 Все коэффициенты в этом характеристическом уравнении положительны, а определитель Гурвица с четным индексом Да a1a3 a0a2 -aha2-a0a.j = 6 • 10-2 • 15 = 30> 0.
Это особенно полезно при изучении устойчивости систем автоматического управления высшего порядка, в которых характеристическое уравнение (3.30) имеет сложные корни с отрицательными действительными частями. Людмила Фирмаль
Поэтому система стабильна. Пример 3.5 Системное характеристическое уравнение D (p) «(l + 7» (1 + rtP) (1-й Гцр) 4-AC = 0, Где К — усиление открытой системы. Tlf Tg, постоянная времени индивидуальной динамической связи T3-System. Используйте критерий Гурвица, чтобы найти предел усиления для системы LCR с обратной связью как функцию постоянных времени T1, Tg и T3. Перепишите характеристическое уравнение в виде D (p) = TJJzp * + (TJ, + T, T3 + G2G3) p2 + (T1 + G2 + T3) p + 1 + K = = a0rd + ahrg + atf -f fls = 0, Здесь AO ^ TW. <* i-TxTt + TtT9 + Γ, Gv; a2 = 7 *, + T2 + T8-a, = l + / (. Согласно критерию устойчивости Гурвица кубическая система устойчива, если выполняется следующее неравенство: a0> 0, a,> 0, a2> 0,> 0, a, a8-a ^ a9> 0.
В этом случае все коэффициенты в характеристическом уравнении положительны, поэтому система устойчива, когда: (TgT2 + T1T3 + TgT3) (T, + T, + 7 * s)> TJtT3 (1 + K). Последнее неравенство можно переписать как К <(1 + 4-13) (1 + 1 / та + 1 / т3) -1 TJ = T ^ / T1j; x3 = T3 / Ti. Пределы усиления (критические) значения, при которых система находится на устойчивых границах: Kk p = (1 + m, + *,) <1 4,1 / m8 +! / M3) -I. Из последнего уравнения видно, что ограничение усиления системы не определяется абсолютным значением постоянной времени динамики Единицы и их относительные значения. Чем больше постоянные времени отличаются друг от друга, тем больше / скр.
Предмет теория автоматического управления тау
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В конкретном случае T1 = m3 c => 1, то есть T1 = 7’r = T3, значение / Ckr является наименьшим и равно только Kkr = 8. Установить как (P + I a, |) (p-А a21- / co,) (p + | a21 + / © J … (p + I a |) = 0 или flo (P + I a «I) \ (P + I a21) 2 + U … (P -f-1 st |) = 0 (3,34) Уравнение (3.34) также принимает форму уравнения (3.30) с положительным коэффициентом. Для первичных и вторичных систем требуемые условия устойчивости также являются достаточными. Это потому, что все корни остались в положительном коэффициенте характеристического уравнения. Однако для систем третьего и более высокого порядка положительный коэффициент в характеристическом уравнении является необходимым условием устойчивости, но его недостаточно.
В этом случае все действительные корни характеристического уравнения (если таковые имеются) остаются, но сложные корни находятся справа. Критерии устойчивости Рауса и Гурвица позволяют использовать коэффициенты характеристического уравнения (3.30) для определения устойчивости системы без вычисления корней. Стандарты устойчивости рта.
Этот критерий устойчивости был предложен в 1877 году английским математиком Э. Раутом в виде определенных правил (алгоритмов). Людмила Фирмаль
Это легче всего объяснить в таблице. 3.1. и Си си а. , = C21 a3 = cr2 C23 — aA — r3a C2b = C39 gc 34 С1. (= C3. 1-2 ~ T1 ^ 3. «-1 Ги-цис / медь s \ b ~ sg — ss, si C1.1 = C2, от -2 до -1C2, I-1 -c1. 1-2 fCl, I-1 RfO и RH • Таблица 3.1 колонка Коэффициент г (Строка 1 2 3 4 аа = ^ 31 0, они были положительными. Поэтому, если Oo> 0, следующие условия необходимы и достаточны для стабильности системы: 0, D2 = a’az> 0, a0a.2 a ^ a0a2a4 0 a, a3> 0, a, a3a5 … 0 a0a2a4 … 0 0 a, a3 … 0 0 0 0 0th> 0. Например, выявляя определитель Гурвица характеристических уравнений первого, второго, третьего и четвертого порядка, можно получить следующее условие устойчивости: 1) Линейное уравнение (n = 1), то есть a0p — + — = 0, условие устойчивости a0> 0, a,> 0; (3,41) 2) Квадратичное уравнение (n = 2), т.е. a0p2 + a (p + — + — a2 = 0, условие устойчивости a0> 0, a,> 0, a2> 0; (3.42) 3) В случае кубического уравнения (n = 3) a0> 0, a,> 0, a2> 0, a3> 0, (3.43) а, а2-а0а3> 0; (3,44) 4) Четвертичное уравнение (n = 4), то есть a0p4 + a2rr a3p -} — a4 = 0, условие устойчивости (3,40) ао> 0, а,> 0, а2> 0, а3> 0, а4> 0, (3.45) (3,46) a3 (a, a2-a0a3) -a1a4> 0.
Поэтому необходимым и достаточным условием устойчивости систем первого и второго порядка является положительный коэффициент характеристического уравнения. Для кубических и квартичных уравнений, помимо положительных коэффициентов, должны соблюдаться дополнительные неравенства (3.44) и (3.46). Когда n> 5, число таких дополнительных неравенств увеличивается, что делает процесс раскрытия детерминанта довольно громоздким и громоздким. Поэтому критерий устойчивости Гурвица обычно применяется к n 4. Если n> 5, мы рекомендуем применять критерии устойчивости Лиенара — Шипара, сформулированные ниже, или перейти к компьютерному численному методу при использовании критериев устойчивости Гурвица.
В последнем столбце основного определителя Гурвица (3.38) только один коэффициент а отличается от нуля, Дя = аА-. (3,47) Как видно из (3.47), если a> 0, достаточно найти только определитель Гурвица от D до D , чтобы проверить устойчивость системы. Все детерминанты Гурвица низкого порядка положительны, поэтому, если основной определитель равен нулю, система находится на устойчивой границе = (3-48) Последнее уравнение возможно в двух случаях: ann-0 или Дя, = = 0. В первом случае система находится на границе апериодической устойчивости (один из корней характеристического уравнения равен нулю). Во втором случае на границе устойчивости колебаний (два комплексных сопряженных корня характеристического уравнения находятся на мнимой оси).
Используя критерий Гурвица, для определенного параметра системы вы можете выбрать один параметр как неизвестный (например, коэффициент усиления, постоянная времени и т. Д.) И определить критическое значение (критическое), при котором система находится на устойчивой границе. Поскольку стандарт Гурвица можно получить из стандарта Рауса, стандарт Гурвица иногда называют стандартом Рауса-Гурвица. Критерии устойчивости Лиенарда-Шипара. Для проверки устойчивости систем автоматического управления с порядками характеристического уравнения n> -5 полезно использовать одну из модификаций критерия алгебраической устойчивости Гурвица, предложенную П. Лиенаром и Р. Шипаром в 1914 г. ,
Тот факт, что все определители D, D3, D5 являются положительными, доказывает, что все коэффициенты характеристического уравнения (3.30) положительны (a0> ax> 0, …, a71> 0) , Использование нечетного индекса следует за положительным индексом определителей Гурвица D2, D4, De, … и наоборот при использовании четного индекса. Таким образом, если выполняется требуемое условие устойчивости, то есть a0> 0, o,> 0, …, a> 0, необходимым и достаточным условием устойчивости является индекс ДД …., индекс Дп между определителями Гурвица
Все детерминанты с четным числом (или все нечетные числа) были положительными. Поэтому необходимо и достаточно, чтобы система автоматического управления была стабильной, чтобы выполнялось следующее неравенство: ao> 0, a >> 0, …, a „> Oj или ao> 0, a,> 0, …, al> 0 J A2> 0, A4> 0, A6> 0 ….. J. (3,49) (3.50) Окончательная формулировка критерия устойчивости, называемая критерием устойчивости Лиенара-Шипара, требует раскрытия меньшего числа определителей, чем нормальный критерий Гурвица.
В этом случае все действительные корни характеристического уравнения (если таковые имеются) остаются, но сложные корни находятся справа. Критерии устойчивости Рауса и Гурвица позволяют использовать коэффициенты характеристического уравнения (3.30) для определения устойчивости системы без вычисления корней. Стандарты устойчивости рта. Этот критерий устойчивости был предложен в 1877 году английским математиком Э. Раутом в виде определенных правил (алгоритмов). Это легче всего объяснить в таблице. 3.1. и Си си а. , = C21 a3 = cr2 C23 — aA — r3a C2b = C39 gc 34 С1. (= C3. 1-2 ~ T1 ^ 3. «-1 Ги-цис / медь s \ b ~ sg — ss, si C1.1 = C2, от -2 до -1C2, I-1 -c1. 1-2 fCl, I-1 RfO и RH • Таблица 3.1 колонка Коэффициент г (Строка 1 2 3 4 аа = ^ 31 0, они были положительными.
Поэтому, если Oo> 0, следующие условия необходимы и достаточны для стабильности системы: 0, D2 = a’az> 0, a0a.2 a ^ a0a2a4 0 a, a3> 0, a, a3a5 … 0 a0a2a4 … 0 0 a, a3 … 0 0 0 0 0th> 0. Например, выявляя определитель Гурвица характеристических уравнений первого, второго, третьего и четвертого порядка, можно получить следующее условие устойчивости: 1) Линейное уравнение (n = 1), то есть a0p — + — = 0, условие устойчивости a0> 0, a,> 0; (3,41) 2) Квадратичное уравнение (n = 2), т.е. a0p2 + a (p + — + — a2 = 0, условие устойчивости a0> 0, a,> 0, a2> 0; (3.42) 3) В случае кубического уравнения (n = 3) a0> 0, a,> 0, a2> 0, a3> 0, (3.43) а, а2-а0а3> 0; (3,44) 4) Четвертичное уравнение (n = 4), то есть a0p4 + a2rr a3p -} — a4 = 0, условие устойчивости (3,40) ао> 0, а,> 0, а2> 0, а3> 0, а4> 0, (3.45) (3,46) a3 (a, a2-a0a3) -a1a4> 0.
Поэтому необходимым и достаточным условием устойчивости систем первого и второго порядка является положительный коэффициент характеристического уравнения. Для кубических и квартичных уравнений, помимо положительных коэффициентов, должны соблюдаться дополнительные неравенства (3.44) и (3.46). Когда n> 5, число таких дополнительных неравенств увеличивается, что делает процесс раскрытия детерминанта довольно громоздким и громоздким. Поэтому критерий устойчивости Гурвица обычно применяется к n 4. Если n> 5, мы рекомендуем применять критерии устойчивости Лиенара — Шипара, сформулированные ниже, или перейти к компьютерному численному методу при использовании критериев устойчивости Гурвица.
В последнем столбце основного определителя Гурвица (3.38) только один коэффициент а отличается от нуля, Дя = аА-. (3,47) Как видно из (3.47), если a> 0, достаточно найти только определитель Гурвица от D до D , чтобы проверить устойчивость системы. Все детерминанты Гурвица низкого порядка положительны, поэтому, если основной определитель равен нулю, система находится на устойчивой границе = (3-48) Последнее уравнение возможно в двух случаях: ann-0 или Дя, = = 0. В первом случае система находится на границе апериодической устойчивости (один из корней характеристического уравнения равен нулю).
Во втором случае на границе устойчивости колебаний (два комплексных сопряженных корня характеристического уравнения находятся на мнимой оси). Используя критерий Гурвица, для определенного параметра системы вы можете выбрать один параметр как неизвестный (например, коэффициент усиления, постоянная времени и т. Д.) И определить критическое значение (критическое), при котором система находится на устойчивой границе. Поскольку стандарт Гурвица можно получить из стандарта Рауса, стандарт Гурвица иногда называют стандартом Рауса-Гурвица. Критерии устойчивости Лиенарда-Шипара.
Для проверки устойчивости систем автоматического управления с порядками характеристического уравнения n> -5 полезно использовать одну из модификаций критерия алгебраической устойчивости Гурвица, предложенную П. Лиенаром и Р. Шипаром в 1914 г. , Тот факт, что все определители D, D3, D5 являются положительными, доказывает, что все коэффициенты характеристического уравнения (3.30) положительны (a0> ax> 0, …, a71> 0) , Использование нечетного индекса следует за положительным индексом определителей Гурвица D2, D4, De, … и наоборот при использовании четного индекса.
Таким образом, если выполняется требуемое условие устойчивости, то есть a0> 0, o,> 0, …, a> 0, необходимым и достаточным условием устойчивости является индекс ДД …., индекс Дп между определителями Гурвица Все детерминанты с четным числом (или все нечетные числа) были положительными. Поэтому необходимо и достаточно, чтобы система автоматического управления была стабильной, чтобы выполнялось следующее неравенство: ao> 0, a >> 0, …, a „> Oj или ao> 0, a,> 0, …, al> 0 J A2> 0, A4> 0, A6> 0 ….. J. (3,49) (3.50) Окончательная формулировка критерия устойчивости, называемая критерием устойчивости Лиенара-Шипара, требует раскрытия меньшего числа определителей, чем нормальный критерий Гурвица.
