Оглавление:


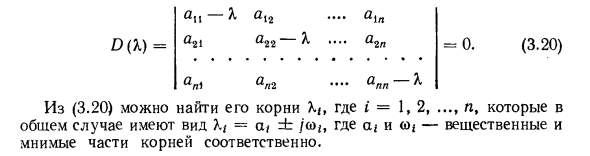

Теоремы к. М. Ляпунова об устойчивости движения по первому приближению
- Теорема К. М. Ляпунова об устойчивости движения в приближении первого порядка Если общее решение дифференциального уравнения движения (3.1) известно, значение переменной движения возмущения yi (f) определяется непосредственно и строится вариация xt-yt (t) -y * (t). Вы можете изучить их и решить проблему невозмущенной устойчивости двигателя y * {t). Однако в принципе исследования устойчивости движения выполняются с использованием методов, основанных на качественном анализе дифференциальных уравнений движения возмущения, удовлетворяемых отклонениями (вариациям), а не на анализе общих решений.
Чтобы вывести уравнение возмущения, найдите переменные yt (t) = y * (i) + *, (/) из (3.9) и подставьте эти значения * /, (дифференциальное уравнение движения (3.1) из о) dy] (it) / dt + dx, (ty’dt-V, (y \ + x „y \ + x2 ….. y \ + xnt /). (3.15) Если правая часть уравнения (3.15) допускает расширение до степенного ряда Тейлора, то после этого расширения степени xt: (T) 4-d * i (0 _ V /, / u-, / / \, (LL X + 4- ++ (ZL6) Где / ^ (Xj, x2, …, *) — набор терминов в большей степени, чем первый, в зависимости от отклонения xx. Учитывая (3.5), dxi (t) / dt-anXl + altxt + … + ailtxlt + Rllxl9 x2, …, xp). (3.17) В уравнении (3.17) коэффициент Общий случай является функцией времени /, в частности, он может быть постоянным.
В дальнейшем коэффициент алк константы будет учитываться, если не указано иное. Людмила Фирмаль
Уравнение (3.17) называется дифференциальным уравнением с двухлетним возмущением. Если отклонение xt достаточно мало, игнорирование Ri приводит к линеаризованному уравнению. dxjdt = ati xt + al2 x2 + … -f- allt * n (* e 1 »2> ••• .n)» (3.19) Называется уравнение первого приближения. Во многих случаях устойчивость движения исследуется уравнением первого приближения. Это объясняется не только простотой этого метода, но также и тем фактом, что зачастую только первый линейный член может быть надежно определен путем знания процессов, происходящих в реальной системе. Однако уравнение первого приближения может дать совершенно неверный вывод об устойчивости движения.
Таким образом, конечно, возникает проблема, заключающаяся в том, что уравнение первого приближения определяет условия, которые дают правильный ответ для устойчивости движения. Это очень важная и фундаментальная проблема для теории автоматического управления А. Впервые предложено и разрешено М. Ляпуновым. Уравнения одновременности (3.19) соответствуют характеристическим уравнениям и могут быть описаны следующим образом: al {-X a12 …. a (p D () = arg- * … a2n = 0 (3,20) …. app- \ Из (3.20) вы можете найти маршрут с i = 1,2. Это в общем случае = = a, = b / a> |, где a * и <0 — действительная и мнимая части корня соответственно. А для изучения устойчивости системы по линеаризованному уравнению.
Предмет теория автоматического управления тау
| Понятие устойчивости | Условия устойчивости линейных систем автоматического управления |
| Общая постановка задачи устойчивости по А. М. Ляпунову | Алгебраические критерии устойчивости |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Следующая теорема М. Ляпунова принципиально важна. Теорема 1. Если действительная часть всех корней характеристического уравнения первого приближения (3.20) отрицательна, невозмущенное движение асимптотически устойчиво. Теорема 2. Если в корне Kt характеристического уравнения первого приближения (3.20) имеется хотя бы один корень с положительной вещественной частью, невозмущенное движение неустойчиво. Этот случай называется критическим, если в корне характеристического уравнения имеется один или несколько нулевых корней, а действительная часть оставшегося корня отрицательна. Как показал Ляпунов, при критической устойчивости устойчивость непертурбативного движения (неустойчивость) зависит от вида нелинейной функции Ri (xi, x, x, xl), поэтому используется уравнение первого приближения.
Не может быть оценено. Поэтому исходная форма движения учитывает дифференциальное уравнение возмущения (3.17). Теорема Ляпунова очень важна, потому что линеаризованное уравнение (уравнение первого приближения) может определять устойчивость нелинейной системы.
