Оглавление:







Условия устойчивости линейных систем автоматического управления
- Условия устойчивости линейных систем автоматического управления. На основе приведенного выше определения устойчивости А. М. Ляпунова показано, как найти условия устойчивости для линейных (линеаризованных) систем автоматического управления. Дифференциальное уравнение линейной системы автоматического управления, записанное для регулируемой выходной величины x \ t) при наличии управляющего воздействия g (t), имеет вид (AQpn + fli P «-1 + — + an) x (i) = (b0p»> + bx pt to> + … + bm) g (t), (3.21) Где a0, ai …, an и bQy b [y …, bn — постоянные коэффициенты, а p = d / dt — дифференциальный оператор.
Изменение управляющей переменной * (/) при любом внешнем воздействии g (t) является решением уравнения (3.21) * (/) = *. (0 + * «</) • (3.22) В (3.22) первый член xH (t) является вынужденной компонентой, которая имеет те же характеристики, что и правая часть уравнения (3.21). Определяется как конкретное решение гетерогенного дифференциального уравнения (3.21) с правой стороны (A0p »+ ax pn˜1 + … + an) xv (t) = (bQp * + bxp ^ + … + bm) g (t). (3,23)
Второе слагаемое xCB (t) является свободной (переходной) компонентой и определяется общим решением однородных производных. (А0Ря + в1Ря «1 + … + *») * „(0 = 0. Людмила Фирмаль
Обычно теория автоматического управления заинтересована в устойчивости вынужденной составляющей * (() переходного процесса, поэтому непертурбативное движение системы должно получить вынужденную составляющую x ^ (() переходного процесса). Возмущающее движение является управляющей переменной x (t) в системе, а свободная компонента xCB (t) = x (t) -xB (t). Согласно А. М. Ляпунову, возмущение является начальным значением xcb, которое произошло в момент t-t0 под действием дополнительной внешней силы, действующей внезапно, т. Е. Начального значения xcBo, в данном случае производной возмущения первого приближения. Уравнение есть уравнение (3.24). (3,24)
Уравнение без правой части (3.21) Согласно определению устойчивости А. М. Ляпунова, система становится асимптотически устойчивой во времени, когда свободный состав материала стремится к нулю при t ®, т.е. xcB (() 0). Формула (3.24) (3,26) + dn ~ \ * C * + «. + I„ * sv (0 «0. (3.25) Решение уравнения (3.25) получается как xCb (t) = Сех /. После дифференцирования этого уравнения n раз, отменив с помощью общего множителя Cex и подставив его в (3.25), a0Xn + a, H / » 1 + … + ay = 0 Полученное алгебраическое уравнение (3.26) называется характеристическим уравнением. Маршрут X! E Kp определяет характер миграционного процесса в системе.
Предмет теория автоматического управления тау
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Легко видеть, что левая часть уравнения (3.26) соответствует дифференциальному оператору выходного значения уравнения (3.21). Поэтому характеристическое уравнение обычно получается путем установки дифференциального оператора выходного значения исходного дифференциального уравнения (3.21) на ноль. е. (3,27) Однако обратите внимание, что буква p- «K» в характеристическом уравнении (3.27) означает комплексное число, а не дифференциальный символ. Решение характеристического уравнения порядка n включает n корней.
Корень характеристического уравнения нормального линейного дифференциального уравнения с постоянными коэффициентами может быть действительным, комплексным, мнимым или нулевым. Общий случай (3,58) pl = ai ± Io) t. На рисунке 3.4 показаны возможные положения корней в комплексной плоскости корня p. P = a2-f / a> 2; p3 = a2-p4 = 0; p5 = -a5; pb = -a6 + / co6; p7 = -a0-; Cho6. Если все маршруты разные, их называют простыми. Если есть одинаковые маршруты, они называются множественными. объединенная комиссия по океанографии J (V6 РБ * » P JU} 2 р 6 Рисунок 3.4.
Корень с отрицательной вещественной частью обычно располагается в комплексной плоскости корня с левой стороны мнимой оси, а корень с положительной вещественной частью — это правый корень, поэтому его обычно называют левым. Людмила Фирмаль
Условие устойчивости линейной системы формулируется как Для того чтобы другие системы были асимптотически устойчивыми, необходимо и достаточно, чтобы все корни их характеристического уравнения (3.27) оставались. Это условие устойчивости легко объяснить, рассмотрев решение однородного уравнения (3.25). Если нет многократных корней, однородное уравнение (3,29) * cb (0 = 2C ‘, 1 = 1 Где Pi — корень характеристического уравнения (3.27). C / — интегральная постоянная, определенная из начальных условий. Отметим, что корень характеристического уравнения pt зависит только от левой формы дифференциального уравнения (3.21) линейной системы. Константа интегрирования C / также зависит от формы справа.
Таким образом, скорость распада и форма переходного процесса определяются как левой, так и правой сторонами исходного дифференциального уравнения (3.21). Однако, поскольку понятие устойчивости включает только наличие или отсутствие переходного затухания, устойчивость линейной системы не зависит от формы правой части дифференциального уравнения (3.21) и определяется только характеристическим уравнением (3.27). При составлении (3.21) предполагалось, что внешнего воздействия не будет. Если вы запишите дифференциальное уравнение движения системы относительно возмущающего действия, в этом случае левая часть (3.21) не изменится, а правая часть будет иметь другой вид.
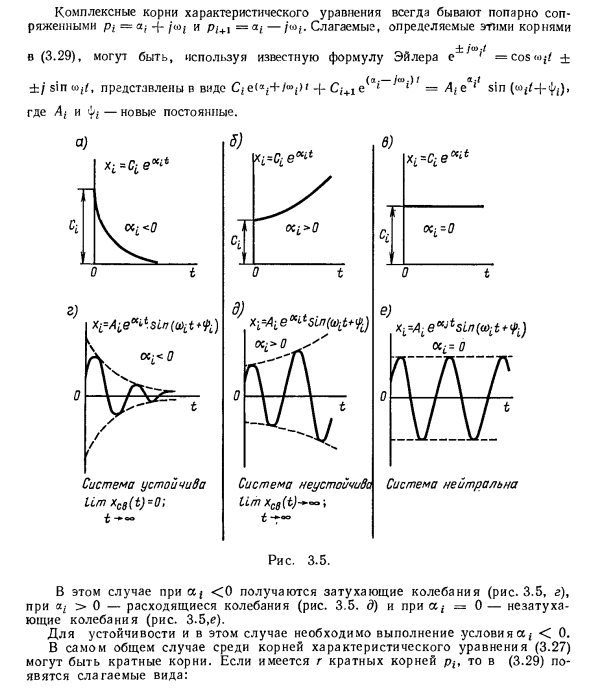
Поскольку характер переходного процесса линейной системы определяется только левой формой дифференциального уравнения (3.21), качественная схема переходного процесса определяет, записывать ли исходное дифференциальное уравнение для эффектов управления или помех Это практически безразлично. Действительный корень характеристического уравнения pi = at в (3.29) соответствует члену, представляющему показатель степени Ясно, что отрицательные (левые) корни при <0 соответствуют экспоненциальному затуханию (рис. 3.5, а), положительные (правые) корни а, -> 0 соответствуют экспоненциальному увеличению (рис. 3.5.6) Когда нулевой корень = 0, он представляет собой линейную параллельную ось слагаемого времени (рис. 3.5, в).
Комплексный корень характеристического уравнения всегда является попарно сопряженным pi = -f / o> | и pi + 1 = at -jiOf. Термины, определенные этими маршрутами (3.29), используя известную формулу Эйлера, o ± / u> » = cos <. » ± // ± / d __ / a> -) ‘ ± / см wf / выражается как Cl +. 1 1 = -4, е ‘sin fy), Где Ai и <| <| -Новые константы. 0 Система нейтральна x ^ e ^ siniayj + ty0СС = О Рисунок 3.5. В этом случае, если aj <0, получается затухающая вибрация (рис. 3.5, d), если oi> 0, расходящаяся вибрация получается (рис. 3.5.E), если a = 0 — вибрация без демпфирования (Рис. 3.5, е). В этом случае условие <0 должно выполняться для устойчивости.
В самом общем случае корень характеристического уравнения (3.27) имеет несколько корней. Если имеется несколько корневых ям, в (3.29) будут отображены следующие термины.(C, <r «1 + … + C, 1 / + C | c) eP <f. Если root = a, — ± / cf <0 и имеет отрицательную вещественную часть, коэффициент ePlt уменьшается со временем. Поскольку коэффициент в скобках бесконечно велик, существует неопределенность оо-0. Однако e −l®kK стремится к нулю быстрее, чем выражение C |, T-1X X / 1, поэтому, если cti <0, эта группа терминов также стремится к нулю с течением времени. Таким образом, в самом общем случае ясно, что необходимо и достаточно, чтобы все корни характеристического уравнения (3.27) были оставлены для устойчивости линейной системы.
Расчет корня очень прост только для характеристических уравнений первого и второго порядка. Существуют общие выражения для корней кубических и квартичных уравнений, но эти выражения громоздки и используются редко. Для уравнений более высокого порядка, как правило, невозможно написать общее уравнение для корня в терминах коэффициентов характеристического уравнения. Поэтому правила, которые могут определять стабильность системы без расчета маршрутов, очень важны. Эти правила называются критериями устойчивости.
Используя критерии стабильности, вы можете не только проверить стабильность системы, но и исследовать, как определенные параметры и структурные изменения в системе влияют на стабильность. Критерии устойчивости можно разделить на алгебру и частоту. С математической точки зрения все критерии устойчивости эквивалентны, но если вы выберете тот или иной критерий устойчивости соответствующим образом при решении конкретной проблемы, вы можете взглянуть на стабильность самым простым способом Вы можете
