Оглавление:



Аналитическое представление кривых на плоскости
Аналитическое представление кривых на плоскости. Эта глава, в качестве примера, затрагивает некоторые приложения дифференциального исчисления к геометрии-главным образом в плоскости. Эти приложения подробно изучаются в области дифференциальной геометрии, которая является самостоятельной математической дисциплиной. Во-первых, вспомним различные методы аналитического выражения кривых на плоскости (известные читателю из аналитической геометрии), предполагая, что в качестве основы используются некоторые Декартовы системы. 1°.Мы перебираем уравнения вида Y = Px) 1 или X-8 (Y)(!) Мы рассмотрели соответствующие кривые. coordinate.
Задача такой кривой вызывает явную задачу (или представление) кривой, когда одна из текущих координат точки непосредственно представлена как однозначная функция другой. Людмила Фирмаль
- It обладает особой простотой и четкостью. Примером может служить парабола y = ax. 2°.Однако в аналитической геометрии кривые часто задавались уравнениями, которые не были бы решены ни относительно x>, ни относительно Y. Р(х, _y)= 0,(2) Это называется неявным уравнением кривой. ( • ) Как только мы заявляем, что функции, описанные в этой главе, обычно считаются непрерывными и имеют непрерывные производные по отношению к их аргументам. При необходимости она требует непрерывности и наличия дальнейших производных. y * Пример Helene-1-0.Иногда мы можем Чтобы представить 1 переменную из другой переменной (например, от y до x) из выражения (2、 Представляет кривую (или ее (Часть) по явному уравнению(1).
- В других случаях, например, зависимость y от x определяется уравнением (2), но при определенных условиях*)-существует однозначная функция (которая удовлетворяет уравнению (2), и можно утверждать, что эта»неявная»функция непрерывна и имеет непрерывную производную, но в случае декартовой, например, невозможно написать явное выражение: xYY-3axu = 0 (рис.95). 3°.Наконец, в предыдущем представлении были упомянуты уравнения формы: * * = Р(0. У = Х0.(3) Устанавливает зависимость от текущих координат точки для заданного параметра 1, а также определяет кривую на плоскости. Первый пример-параметрическое представление эллипса. х = Асо $ 1,у = $ ТТ *.
Подобное уравнение называется параметрическим. Обеспечивает параметрическое представление кривой. Людмила Фирмаль
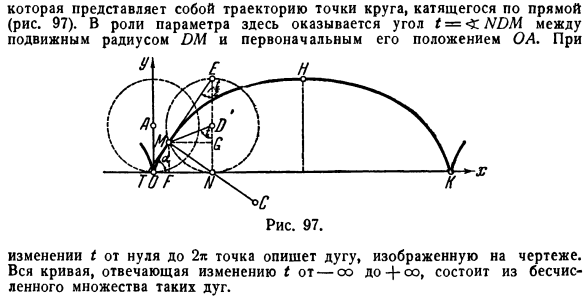
- Если параметр I(его геометрический смысл ясен из рисунка 96) изменяется от нуля до 2π, то эллипс описывается против часовой стрелки от края длинной оси A (a, 0). В качестве 2-го примера мы упомянем циклоид, встречающийся более 2 раз. х = а(1 $ 1л Д), Г = О(1-соѕ)、 *) См. главу по этому вопросу в Томе 2 XIX. Это локус точки в окружности, которая перекатывается по прямой (рис. 97). в роли параметра выступает угол между подвижным радиусом OM и его начальным положением ОА* =л^) м. Если вы измените его с нуля на 2n, точка будет представлять дугу, нарисованную на чертеже. вся кривая, соответствующая изменению I от oo до+ oo, состоит из такого множества Дуг.
Смотрите также:
Решение задач по математическому анализу
| Нахождение статических моментов и центра тяжести плоской фигуры. | Касательная к. плоской кривой. |
| Механическая работа | Положительное направление касательной. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.
