Оглавление:


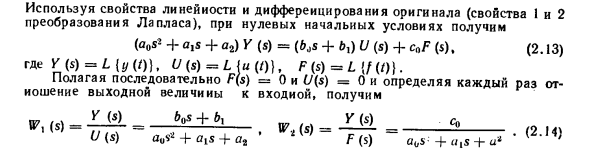


Формы записи линейных дифференциальных уравнений. Передаточные функции
- Форма для написания линейных дифференциальных уравнений. Передаточная функция При описании автоматических систем управления магией широко используются символические формы, описывающие линейные дифференциальные уравнения. Рассмотрим пример из уравнения (2.5). Чтобы уменьшить нотацию, опустите символ A и перепишите его, оставив только левый член, содержащий выходную переменную и ее производную. «OY + a \ Y + ayU = b0 и 4-bx4-c0f. (2.6) Вводит обозначение p для дифференциальных операций. didt = pt df / dtl = pl Используя это, уравнение (2.6) можно записать в виде: a Q (p) (* oP2 4-flip + <22 Используя передаточную функцию, уравнение (2.6) становится + (2.12) Это выражение представляет условно более компактный формат описания исходного выражения (2.6).
Уравнения (2.8), (2.9) и (2.12) называются уравнениями в символической или операторной форме описания. Используя обозначения дифференциальных уравнений в символической форме (2.8) или (2.9) и формально рассматривая свой собственный оператор и оператор действия как нормальный алгебраический фактор, передаточная функция формы оператора Это также может быть определено как отношение количества продукции. Наряду с операторной формой передаточной функции широко используется форма изображения Лапласа передаточной функции.
Передаточная функция или передаточная функция в форме изображения Лапласа — это отношение изображения выходной величины к изображению входной величины при начальном условии нуля. Людмила Фирмаль
Если ссылка (система) имеет несколько входов, оставшаяся входная величина принимается равной нулю при определении передаточной функции для одной входной величины. Найти передаточную функцию в виде изображения Лапласа ссылки, описанной в примере 2.3 (2.6). Преобразуйте обе части этого уравнения в изображение Лапласа. L (a0 V + окси-b ° * /) = L (b0 и -f-bxu -f cj I. Используя исходную линейность и производные характеристики (характеристики 1 и 2 преобразования Лапласа), при начальном условии нуля получаем: (A0s * + a, s + a2) Y (s) = (b, s + b}) U (s) + cnF ($), (2.13) Где K (s) = M </ (‘) b U (s) = L} ((/)), F (s) = /. {/ (/)}.
Каждый раз, когда F (s) = 0 и U (s) = 0 устанавливаются непрерывно, и определяется отношение выходной величины к входной величине, Сравнивая уравнения (2.10), (2.11) и (2.14), легко увидеть, что передаточная функция и операторная форма формы изображения Лапласа соответствуют обозначениям. Передаточная функция в виде изображения Лапласа может быть получена из передаточной функции оператора cfopMe. В последнем случае замена p = s сделана. В общем случае это происходит из-за того, что исходная производная (символическое умножение на исходное p), когда начальное условие равно нулю, соответствует умножению изображения на комплексное число s.
Предмет теория автоматического управления тау
| Уравнения динамики и статики. Линеаризация | Частотные характеристики |
| Основные свойства преобразования Лапласа | Временные характеристики |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Сходство между формой изображения Лапласа и передаточной функцией операторной формы чисто внешнее и имеет место только с фиксированными связями (системами). Уравнение (2.14) ложно, если связь нестационарная, т.е. множитель (2.6) зависит от времени. Передаточная функция (2.14) может быть использована для описания уравнения изображения Лапласа (2.13). Y (s) = Wt (s) U (s) + Wt (s) F (s). (2.15) Это уравнение, как и уравнение (2.13), подходит для исходного дифференциального уравнения (2.6) только тогда, когда начальное состояние равно нулю. Если начальное условие не равно нулю, уравнения (2.13) и (2.15) не могут использоваться в качестве математического описания начальной ссылки.
Как правило, линейные дифференциальные уравнения с постоянными коэффициентами, меньшими или равными второму порядку, записываются в стандартном виде. Кроме того, термины, которые включают в себя вывод и е Напишите производную в левой части уравнения и все остальные члены в правой части. Коэффициент выходного значения равен 1. Если справа есть производная, любая отдельная входная величина и термин, содержащий производную, объединяются в группу, а соответствующие входные количественные коэффициенты берутся из скобок.
Стандартный формат для описания линейных дифференциальных уравнений. Людмила Фирмаль
Стандартная формула формулы (2.6) принимает следующую форму: + Tree + y = kx (7> + u) + kj, (2.16) Здесь k = c0 / a. В уравнении (2.16) постоянные T0, G и T2 имеют временную размерность, они называются постоянными времени, а коэффициент и кг — коэффициенты передачи. Если исходное уравнение (2.6) не содержит y (a.g = 0), в стандартной форме производная y должна иметь коэффициент, равный 1. Обе части уравнения делятся на коэффициент а. В символической форме уравнение (2.16) принимает вид: (Подсказка * + 7> = + + kj.
