Оглавление:


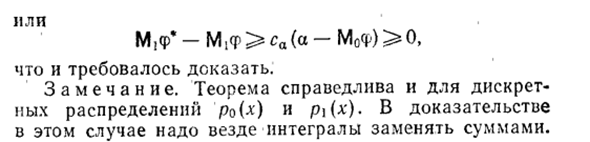

Оптимальный критерий Неймана-Пирсона
- Оптимальные критерии Неймана-Пирсона po (x) -p (x) bq), Pi () = f> (; 0j), M0p = »= 5ΦWo (x) dx, M1 == фΦ (() p, (x) dx. Оптимальный критерий (7) можно искать по критерию, определяемому отношением мощностей p1 (x) / p0 (x). Теорема 1. (Теорема Неймана-Пирсона.)
- В случае 0 ^ a ^ 1, поскольку существует 0 и 0 ^ e ^ 1, критерий φ функции равен 1, p \ (x)> cp0 (x) tφ * 9, если M = e, P \ (x) = cp (x). 0, если Pi (a) <gr0 (l), Определить оптимальный критерий, которому удовлетворяет уровень значимости (7). Доказательство. 0 <a <1. Случаи a = 0 и a = 1 проверяются отдельно и здесь не рассматриваются.
Думаю, функция g(c) = P {Pl G)> cp0tt) l / f0} При условии, что гипотеза H0 верна. Людмила Фирмаль
Функция Является полностью непрерывным и g (<»), потому что это функция распределения случайных величин Pi (l) / Po (l) t. (3) -0, ((0 -) = 1. Определите ca из условия. <г (около-0). Если £ (Ca) <g (f «-0) _ q-g (<q) ^ (Ca-O) — // ^) • Если g (ca) = g (c <z-, то установите ea = 0. Если g (c) 5 = ct — весь сегмент C \ <c2, то ca может быть любой точкой в этом сегменте, например.
- Возьмем левый конец (8) и построим функцию φ *, предполагая, что c и in равны значениям ca и e. Mof * = $ p0 (x) dx + Px (x)> caP0 (x) , A- £ G (са) G / ч, + i (G.-0) -й (g.) J Pd *) dx = P | C *) -feP0C *) = 6 (С «> + Д (с’-0 ^ (с.) ■ << ■ -0) — * <* >> =« • Пусть φ — еще один критерий для Mc ^ a. M.fF> M, ф. Думаю, что цельный J (Φ * (*) — Φ ())) {px (x) -syro (.v)) Ac. (9)
Разделенный на два термина \ (Φ’-φ) (| | — «Lock / * + J (φ * φ) (p | capo) dx. (10)» В первом члене, поскольку интегрирование выполняется в точке xy, где φ * (x)> q> (x)> 0, это интегрирование p \ (a) <saro (x), то есть подынтегральное выражение является отрицательным Существует нет.
Аналогично, для второго интеграла (10) φ * (π ‘) <1 и, следовательно, p) (x) <^. с <хРо (х). Людмила Фирмаль
Подынтегральное выражение также не является отрицательным. Следовательно, интеграл (9) неотрицателен, ^ (Ф * -Ф) Р \ dx> ca $ (ф * -Ф) р№> или M, Φ * -MjT> ca (a-MoF)> 0, Если вам нужно доказать. Замечания. Теорема также применима к дискретным распределениям po (x) и p \ (x). Доказательство в этом случае требует замены всех интегралов суммами.
Смотрите также:
Решение задач по теории вероятностей
| Статистические гипотезы | Оптимальные критерии для проверки гипотез о параметрах нормального и биномиального распределений |
| Уровень значимости и мощность критерия | Критерии для проверки сложных гипотез |
Если вам потребуется помощь по теории вероятности вы всегда можете написать мне в whatsapp.
