Оглавление:
Основные понятия, относящиеся к системам уравнений. Системы линейных уравнений
Решение системы, равносильность и следствие, совокупность систем.
а) Будем рассматривать системы с двумя и тремя неизвестными (переменными). Систему двух уравнений с двумя неизвестными 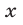 и
и 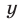 можно записать в виде
можно записать в виде
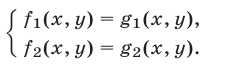
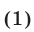
Если левые и правые части уравнений системы (1) являются многочленами от 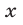 и
и 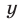 или их можно представить в виде отношения многочленов, то систему (1) называют алгебраической.
или их можно представить в виде отношения многочленов, то систему (1) называют алгебраической.
Решением системы (1) называется пара чисел 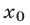 ,
, 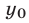 , при подстановке которых соответственно вместо
, при подстановке которых соответственно вместо 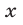 и
и 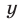 каждое уравнение системы (1) становится верным числовым равенством. Множество решений системы может быть, в частности, пустым. В этом случае говорят, что система не имеет решений (несовместна).
каждое уравнение системы (1) становится верным числовым равенством. Множество решений системы может быть, в частности, пустым. В этом случае говорят, что система не имеет решений (несовместна).
Решить систему — значит найти все ее решения или установить, что система не имеет решений.
б) Процесс решения системы обычно состоит в последовательном переходе с помощью некоторых преобразований от данной системы к другим, более простым, которые мы умеем решать. При этом нужно внимательно следить за тем, чтобы не потерять решения. Что касается посторонних для данной системы решений, которые могут появиться при преобразовании системы, то их обычно отсеивают с помощью проверки.
Если в результате преобразований системы (1) получена система
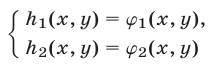
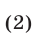
такая, что каждое решение системы (1) является решением системы (2), то система (2) называется следствием системы (1). Аналогично, уравнение
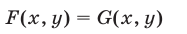
называют следствием системы (1), если равенство
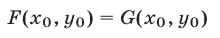
верно для каждой пары чисел 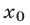 ,
, 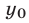 . образующих решение системы (1).
. образующих решение системы (1).
Если система (2) является следствием системы (1), а система (1) также является следствием системы (2), то эти системы называются равносильными. Иначе говоря, системы называют равносильными, если множества их решений совпадают. В частности, две системы, не имеющие решений, являются равносильными.
Используя определения равносильности и следствия, можно утверждать, что:
1) если в системе уравнений заменить какое-либо уравнение на равносильное ему, а остальные уравнения оставить без изменения, то полученная при этом система будет равносильна исходной;
2) если к данной системе присоединить уравнение, являющееся следствием этой системы, то полученная система будет равносильна исходной;
3) если какое-либо уравнение данной системы заменить его следствием, а остальные уравнения оставить без изменения, то полученная система будет следствием исходной.
в) При решении систем уравнений нередко приходится применять такие преобразования систем, как умножение обеих частей уравнения на одно и то же число (или одну и ту же функцию), почленное сложение, вычитание, умножение и деление уравнений системы, возведение обеих частей уравнения в 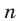 —ю степень.
—ю степень.
Сформулируем утверждения, связанные с этими преобразованиями, опустив в записи системы неизвестные.
1°. Система
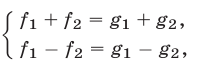
полученная почленным сложением и вычитанием уравнений системы (1), равносильна системе (1).
2°. Система
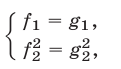
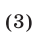
является следствием системы (1). Если же функции 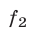 и
и 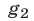 принимают неотрицательные значения в области определения системы (1), т.е. на множестве, где определены функции
принимают неотрицательные значения в области определения системы (1), т.е. на множестве, где определены функции 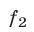 и
и 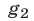 , то система (3) равносильна системе (1).
, то система (3) равносильна системе (1).
3°. Система
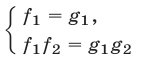
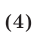
является следствием системы (1). Если же не существует таких пар чисел 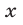 ,
, 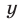 , при которых обе функции
, при которых обе функции 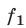 и
и 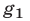 обращаются в нуль, то система (4) равносильна системе (1).
обращаются в нуль, то система (4) равносильна системе (1).
4°. Если не существует таких пар чисел 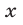 и
и 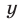 , при которых обе функции
, при которых обе функции 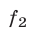 и
и 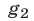 одновременно обращаются в нуль, то система
одновременно обращаются в нуль, то система
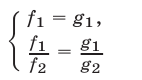
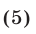
является следствием системы (1), а при дополнительном требовании, что одновременно не обращаются в нуль функции 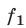 и
и 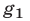 , система (5) равносильна системе (1).
, система (5) равносильна системе (1).
Эти свойства преобразований систем, доказательство которых легко можно получить самостоятельно, широко применяются при решении систем с двумя и тремя переменными.
г) Введем еще одно понятие, играющее важную роль при решении систем уравнений.
Пусть система уравнений имеет вид
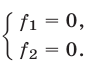
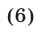
Будем говорить, что система (6) равносильна совокупности систем
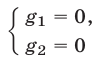
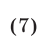
и
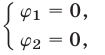

если каждое решение системы (6) является решением хотя бы одной из систем (7), (8) и всякое решение каждой из систем (7), (8) есть решение системы (6).
Это означает, что множество решений системы (6) совпадает с объединением множеств решений систем (7) и (8). Поэтому
вместо слов «система (6) равносильна совокупности систем (7) и (8)» говорят, что «система (6) распадается на системы (7) и (8)».
Обычно это понятие применяется в случае, когда левую часть одного из уравнений системы (6) удается разложить на множители. Пусть, например, 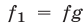 где
где 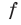 и
и 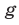 — многочлены (или функции, которые определены на одном и том же множестве).
— многочлены (или функции, которые определены на одном и том же множестве).
Тогда система
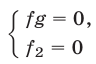
равносильна совокупности систем
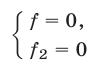
и
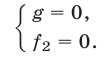
Методы решения систем.
а) При решении систем уравнений часто применяется метод подстановки (метод исключения неизвестного), с помощью которого решение системы с двумя неизвестными сводится к решению уравнения с одним неизвестным. В основе этого метода лежит следующее утверждение.
Система уравнений
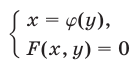
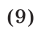
равносильна системе
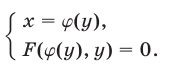
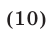
б) Одним из эффективных методов решения систем уравнений является метод замены переменной, который состоит в следующем. Пусть левые части уравнений системы
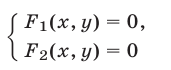
записываются в виде 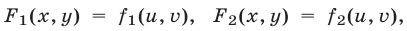 где
где 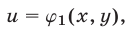
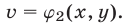 Тогда система примет вид
Тогда система примет вид
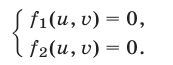
Если 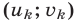 —все решения этой системы,
—все решения этой системы, 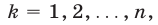 то, решив
то, решив 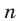 систем уравнений
систем уравнений
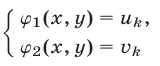
и объединив эти решения, найдем все решения исходной систе-
Системы двух линейных уравнений с двумя неизвестными. Определители второго порядка. Правило Крамера.
Рассмотрим систему двух уравнений с двумя неизвестными
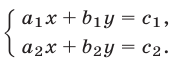
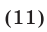
Предполагая, что хотя бы один из коэффициентов при неизвестных в каждом уравнении системы (11) отличен от нуля, будем решать эту систему способом алгебраического сложения. Уравняем коэффициенты при 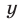 в обоих уравнениях системы, умножив обе части первого уравнения на
в обоих уравнениях системы, умножив обе части первого уравнения на 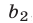 , а второго — на
, а второго — на 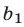 . Получим систему
. Получим систему
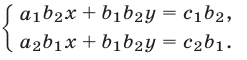
Вычитая почленно из первого уравнения этой системы второе уравнение, имеем
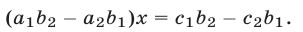
Уравнение (12) не содержит 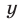 . Чтобы получить уравнение, не содержащее
. Чтобы получить уравнение, не содержащее 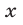 , умножим обе части первого уравнения системы (11) на
, умножим обе части первого уравнения системы (11) на 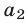 , а второго — на
, а второго — на 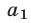 . Получим систему
. Получим систему
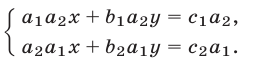
Вычитая из второго уравнения этой системы первое, имеем
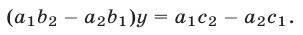
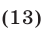
Заметим, что коэффициент при 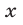 в уравнении (12) равен коэффициенту при
в уравнении (12) равен коэффициенту при 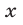 в уравнении (13), и предположим, что этот коэффициент не равен нулю, т. е.
в уравнении (13), и предположим, что этот коэффициент не равен нулю, т. е.
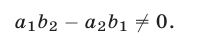
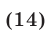
Тогда из уравнений (12) и (13) получаем
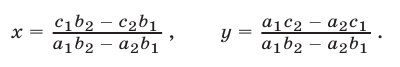
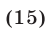
Если выполняется условие (14), то система (11) имеет единственное решение, которое можно найти по формулам (15). В самом деле, если 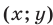 — решение системы (11), то каждое из равенств (12), (13), (15) является верным, т. е. решение системы (11) определяется формулами (15). Легко проверить, что если выполняется условие (14), то пара чисел
— решение системы (11), то каждое из равенств (12), (13), (15) является верным, т. е. решение системы (11) определяется формулами (15). Легко проверить, что если выполняется условие (14), то пара чисел 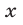 ,
, 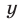 , которые определяются формулами (15), удовлетворяет системе (11).
, которые определяются формулами (15), удовлетворяет системе (11).
Установим правило, по которому образованы правые части равенств (15). Пусть  — общий знаменатель дробей (15), т.е.
— общий знаменатель дробей (15), т.е.
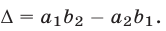
Число  назовем определителем системы (11) и обозначим его символом
назовем определителем системы (11) и обозначим его символом
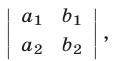
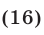
а числа 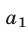 ,
, 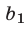 ,
, 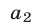 ,
, 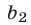 назовем элементами этого определителя. В первом и втором столбцах определителя (16) расположены соответственно коэффициенты при неизвестном
назовем элементами этого определителя. В первом и втором столбцах определителя (16) расположены соответственно коэффициенты при неизвестном 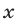 и неизвестном
и неизвестном 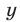 системы (11). Диагональ, на которой расположены элементы
системы (11). Диагональ, на которой расположены элементы 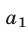 и
и 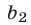 , называют главной, а диагональ, на которой стоят элементы
, называют главной, а диагональ, на которой стоят элементы 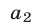 и
и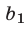 определителя (16), называют побочной.
определителя (16), называют побочной.
Из равенства
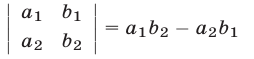
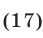
следует, что определитель  равен разности произведений элементов, стоящих на главной и побочной диагоналях.
равен разности произведений элементов, стоящих на главной и побочной диагоналях.
Обозначим числители в формулах (15) через 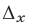 и
и 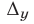 . Тогда, пользуясь правилом (17), получаем
. Тогда, пользуясь правилом (17), получаем
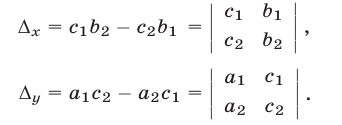
Следовательно, равенства (15) можно записать так:
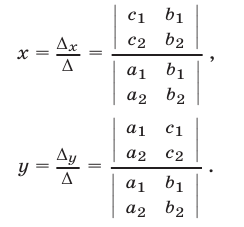

Заметим, что определители 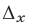 и
и 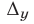 можно получить из определителя
можно получить из определителя  заменой столбца из коэффициентов соответственно при
заменой столбца из коэффициентов соответственно при 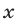 и
и 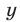 системы (11) столбцом свободных членов этой системы.
системы (11) столбцом свободных членов этой системы.
Определители  ,
, 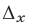 ,
, 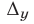 , имеющие две строки и два столбца, называют определителями второго порядка.
, имеющие две строки и два столбца, называют определителями второго порядка.
Формулы (18), (19) выражают правило Крамера для нахождения решения системы (11) в том случае, когда определитель этой системы 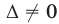
Заметим, что каждое уравнение системы (11) геометрически представляет прямую на координатной плоскости. Если 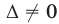 и
и 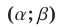 — решение системы (11), то это означает, что прямые
— решение системы (11), то это означает, что прямые 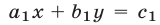 и
и 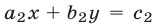 пересекаются в точке с координатами
пересекаются в точке с координатами 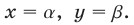
Примеры с решениями
Пример №164.
Решить систему уравнений
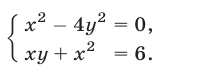
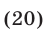
Решение:
Так как 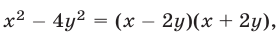 то система (20) равносильна совокупности двух систем
то система (20) равносильна совокупности двух систем
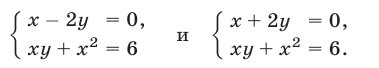
Решим первую систему. Подставляя 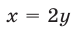 во второе уравнение этой системы, получаем
во второе уравнение этой системы, получаем 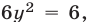 откуда
откуда 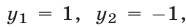
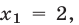

Следовательно, первая система имеет два решения, которые будем записывать так: 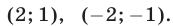 Аналогично, решив вторую систему, найдем еще два решения
Аналогично, решив вторую систему, найдем еще два решения 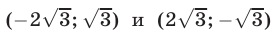 исходной системы.
исходной системы.
Ответ. 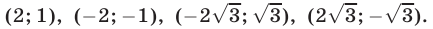
Пример №165.
Решить систему уравнений
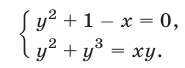
Решение:
Так как первое уравнение системы равносильно уравнению 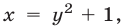 то, заменяя во втором уравнении
то, заменяя во втором уравнении 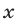 на
на 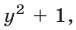 получаем уравнение
получаем уравнение 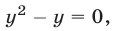 имеющее корни
имеющее корни 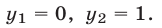 Тогда из равенства
Тогда из равенства 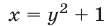 находим
находим 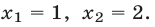
Ответ. 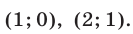
Пример №166.
Решить систему уравнений
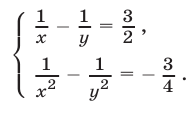
Решение:
Введем новые неизвестные 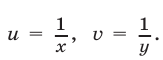 Тогда система примет вид
Тогда система примет вид
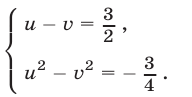
Эта система равносильна системе
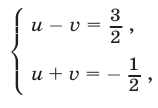
имеющей единственное решение 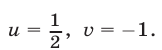
Следовательно, 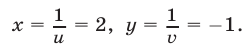
Ответ. 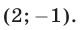
Пример №167.
Пользуясь правилом Крамера, решить систему уравнений
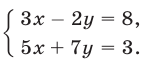
Решение:
Здесь
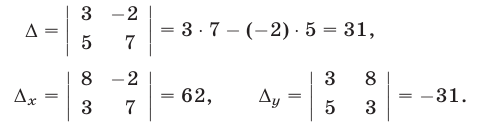
По формулам (18), (19) находим 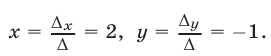 Следовательно, система имеет единственное решение
Следовательно, система имеет единственное решение 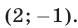
Ответ. 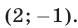
На рис. 15.1 дана геометрическая интерпретация системы из примера 4.
Замечание. Если определитель системы (11) равен нулю, то эта система либо не имеет решений, либо имеет бесконечное множество решений.
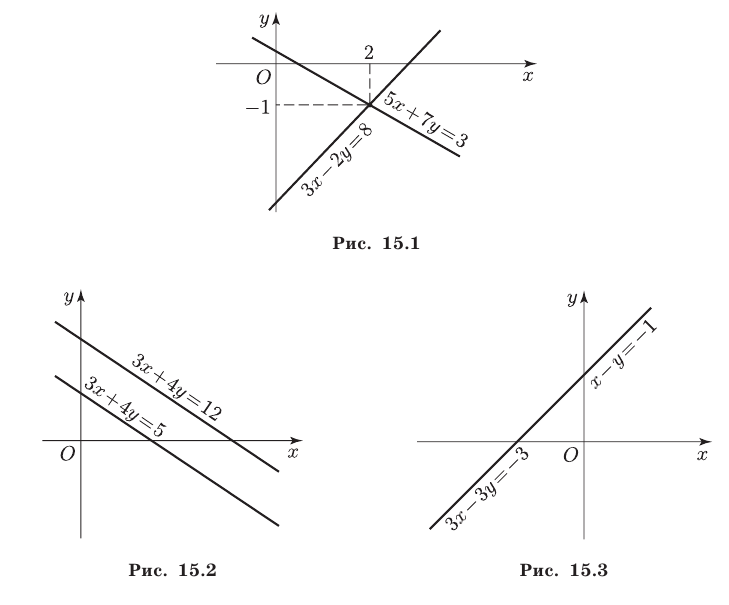
Так, система
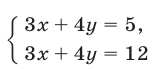
не имеет решений. Этой системе соответствует пара параллельных прямых (рис. 15.2), не имеющих общих точек. Система
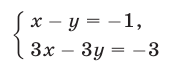
имеет бесконечное множество решений. Этой системе соответствует пара совпадающих прямых (рис. 15.3).
Можно показать, что если хотя бы один из коэффициентов при неизвестных в системе (11) отличен от нуля, то эта система:
а) не имеет решений, когда ее определитель 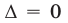 , а хотя бы один из определителей
, а хотя бы один из определителей 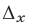 ,
, 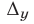 не равен нулю;
не равен нулю;
б) имеет бесконечное множество решений при
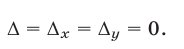
Пример №168.
Найти все пары значений 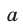 ,
, 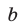 , при каждой из которых система уравнений
, при каждой из которых система уравнений
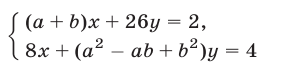
имеет бесконечное множество решений.
Решение:
Система имеет бесконечное множество решений тогда и только тогда, когда оба ее уравнения являются уравнением одной и той же прямой. Умножив обе части первого уравнения на 2 и приравняв коэффициенты при 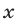 и
и 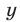 полученного уравнения и второго уравнения исходной системы, имеем
полученного уравнения и второго уравнения исходной системы, имеем
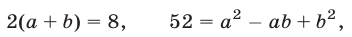
или
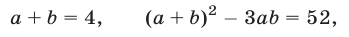
откуда 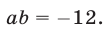 Решив систему
Решив систему
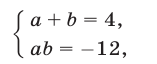
находим два ее решения 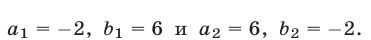
Ответ.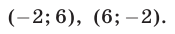
Обращаясь к линейным системам с 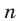 неизвестными, где
неизвестными, где 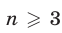 , рассмотрим один из способов решения таких систем.
, рассмотрим один из способов решения таких систем.
Пример №169.
Решить систему уравнений
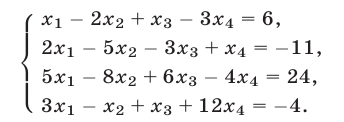
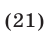
Решение:
Умножим первое уравнение системы (21) на 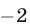 и сложим полученное уравнение со вторым. Затем умножим первое уравнение на
и сложим полученное уравнение со вторым. Затем умножим первое уравнение на 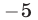 и сложим полученное уравнение с третьим. Наконец, умножим первое уравнение на
и сложим полученное уравнение с третьим. Наконец, умножим первое уравнение на 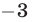 и полученное уравнение сложим с четвертым. Тогда система (21) примет вид
и полученное уравнение сложим с четвертым. Тогда система (21) примет вид
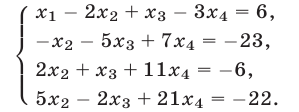
Цель этих преобразований состоит в том, чтобы получить систему, которая не содержит неизвестное 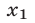 во всех уравнениях, кроме первого.
во всех уравнениях, кроме первого.
Далее преобразуем последние три уравнения системы (22) так, чтобы третье и четвертое уравнения новой системы не содержали неизвестное 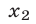 . Для этого умножим второе уравнение системы (22) на
. Для этого умножим второе уравнение системы (22) на  и полученное уравнение сложим с третьим, а затем умножим второе уравнение на
и полученное уравнение сложим с третьим, а затем умножим второе уравнение на 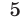 и полученное уравнение сложим с четвертым. В результате придем к системе
и полученное уравнение сложим с четвертым. В результате придем к системе
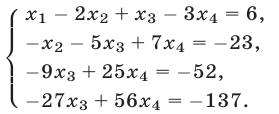
Умножим третье уравнение системы (23) на 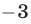 и полученное уравнение сложим с четвертым. Тогда система примет вид
и полученное уравнение сложим с четвертым. Тогда система примет вид
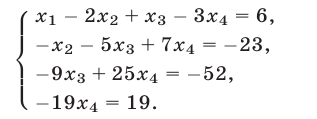
Из последнего уравнения системы (24) находим 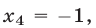 затем из третьего уравнения получаем
затем из третьего уравнения получаем 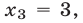 из второго имеем
из второго имеем 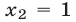 и, наконец, из первого находим
и, наконец, из первого находим 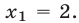 Итак, система (24) имеет следующее решение:
Итак, система (24) имеет следующее решение: 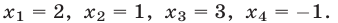
Заметим, что если одно из уравнений системы (21) заменить уравнением, которое получено почленным сложением этого уравнения и любого другого уравнения, умноженного на некоторое число, а остальные уравнения оставить без изменения, то новая система имеет то же множество решений, что и первоначальная система (равносильна системе (21)). Отсюда следует, что каждая из систем (22), (23), (24) равносильна системе (21).
Таким образом, система (21) имеет единственное решение 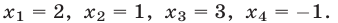
При решении системы (21) она преобразована к треугольному виду (24) методом Гаусса.
Пример №170.
Решить методом Гаусса систему уравнений
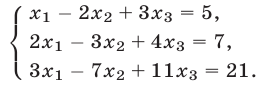
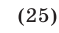
Решение:
Умножим первое уравнение системы (25) на 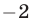 и прибавим полученное уравнение ко второму уравнению. Затем умножим первое уравнение на
и прибавим полученное уравнение ко второму уравнению. Затем умножим первое уравнение на 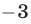 и прибавим полученное уравнение к третьему. Тогда придем к системе
и прибавим полученное уравнение к третьему. Тогда придем к системе
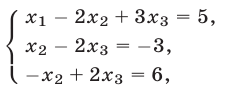
равносильной системе (25). Система (26) не имеет решений. В самом деле, третье уравнение можно записать так: 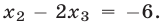 С другой стороны, в силу второго уравнения,
С другой стороны, в силу второго уравнения,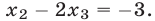
Эти равенства не могут одновременно быть верными. Итак, система (26) несовместна, а поэтому несовместна и система (25).
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
