Оглавление:


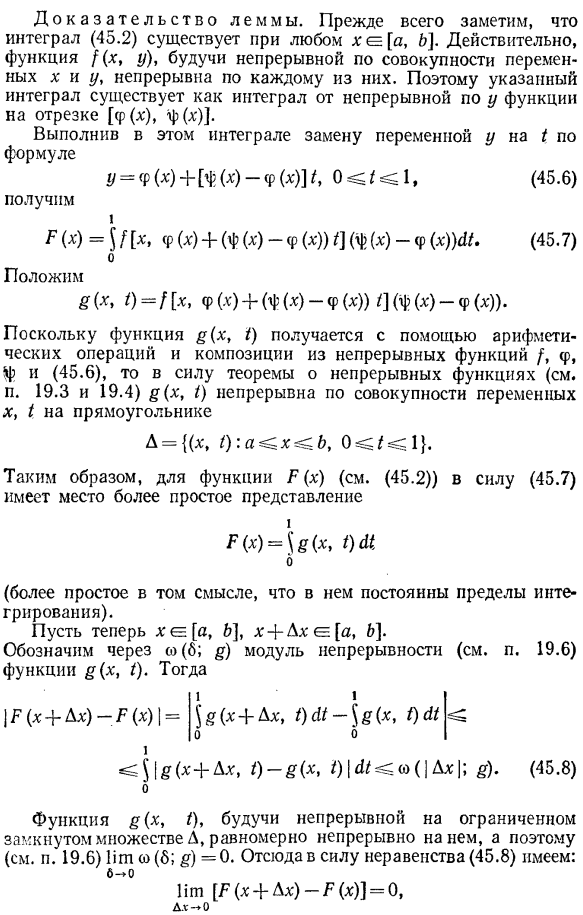





Сведение двойного интеграла к повторному
Сведение двойного интеграла к повторному. Далее обратимся к свойствам кратных интегралов, которые связаны с определенными функциями, различающими многомерные и одномерные случаи. Часто эти свойства значительно облегчают вычисление конкретного кратного интеграла. Полное доказательство выполняется только для функций 2 переменных. Идеологически общий n-мерный случай ничем не отличается от плоского случая, но аргумент там принимает форму, которая выглядит более громоздкой и сложной. 45.1.Уменьшение двойного интеграла для повторения. Во-первых, мы определяем понятие повторяющегося интеграла.
В этом разделе показано, что можно свести интеграцию функций многих переменных к последовательной интеграции функций 1 переменной. Людмила Фирмаль
- Непрерывные функции p(x) и φ (x) задаются в интервале[a, 6], p (x)^φ (x), a ^ x ^ b, предполагая, что в множестве (рис. 173) Е = {(х, г).А ^ х ^ в, р (х)= РЦ / ^φ(х)} (45.1) Определена функция f (x, y). Если функция f (x, y) как функция переменной y интегрируема на интервале [p (x), φ (x)] для фиксированного ke ke[b, b]、 § 45.Уменьшение кратных интегралов для повторения Сто пятьдесят восемь То есть для x∈[a, b] существует Интеграл/ / (π, y) Ax、 ?() Особенности Р(х)= 5!{Х, у) Ау (45.2) F(х) Б РФ(я) Пять АПХ(х) 1 (х, у) Ау Да. (45.3) Может быть интегрирован в интервале[a, b], Б ф(х) \ Топор ^ 1 (х, у) Ау. (45.4) И Ф() Это называется повторной интеграцией.、 Функция P (x), определенная в (45.2), называется интегральной в зависимости от параметра X. So, итерационный Интеграл(45.4) является Интегралом интеграла в зависимости от параметров (см. также§ 53, 54).
Заметим, что множество задав, определенное в (45.1), измеримо и замкнуто в смысле плоского Жордана measure. In дело в том, что непрерывность функций φ и φ на интервале[a, b] подразумевает их ограниченность, и поэтому множество огранич равно bounded. In кроме того, его граница qE обозначается функцией fn |и, скорее всего, отрезками X = A и X-b. Каждое из этих множеств имеет меру 0 (см. теорему§ 44.2 3), и поэтому граница gE E также имеет меру 0.Наконец, множество дается определяется с помощью нестрогих неравенств a ^ x ^ b, φ (X) ^ Y ^φ (X).Поскольку функция φ непрерывна, эти неравенства сохраняются даже при прохождении ограничений, что означает замыкание E. следовательно, E является измеримым компактом.
- Достаточные условия для приведения двойного интеграла ко 2-му интегралу задаются следующей теоремой: Теорема 1.Продолжите функцию f (x, y) с набором зад, определенным выражением (45.1).И затем… Б ф(х) 1 \ НХ г) AxAy = \ топора $ / (, у) Ау. (45.5) Е А F(х) Перед доказательством теоремы поставьте следующую лемму. Лемма 1.В предположении теоремы 1 функция (45.2) непрерывна на интервале[a, b. 45.1.Свести двойной интеграл к повторному Сто пятьдесят девять Доказательство леммы. Прежде всего заметим, что интеграл (45.2) существует в любом xe [a, b].фактически функция x(y, y) непрерывна во всех переменных x и y и в каждой из них непрерывна.
Изменение переменной y В этом Интеграле(по формуле у =φ(χ)-}-[φ(х) СР(х)] ^,(45.6) Мы получаем Один Р(х)= !IxΦ (x)+(Φ (X) φ(x)) 1](φ (x) φ (x)) c11. (45.7) О Поставь Е(Х, 0 = ф [.Φ (+ +(Φ (x) Φ (x)) 0 (Φ (x) Φ (x))Так как функции§(x, I) получены по теореме непрерывной функции, то с помощью арифметических операций и синтеза непрерывных функций f, φ, φ и (45.6) (см.§ 19.3 и 19.4)§(x, 1) множество переменных x и множество непрерывных прямоугольных I-функций. Д = {(х, я). а ^ х ^ ь, 0 я » с 1}. Таким образом, в случае функции P(x) (см. (45.2)), по (45.7), существует более простое представление. Р(Х)= \§(Х, О М О (Это просто в том смысле, что границы интеграции в нем постоянны). скажем, e [a, k], l. x ^ [a, 6]. Укажите коэффициент непрерывности функции§(x, 1) (см.§ 19.6) с помощью a (b; y).И затем… \ П(х + ьх)-П(Х)\ = ^(х + ДХ, 1) м\ §{х, 1) с $ | ^(х + ДХ, 1) е {х, 0 | У ^(О| / ДХ|;§).(45.8) Поскольку непрерывная функция μ (x,/) в ограниченном замкнутом множестве Д равномерно непрерывна, то (см.§ 19.6) тω(8; y)= 0.
Таким образом, указанный Интеграл существует как Интеграл непрерывной функции относительно y на интервале [φ(x), φ(x)]. Людмила Фирмаль
- Таким образом, по неравенству (45,8)、 Золото[P (x + Dx) P (x)] = 0、 § 45.Уменьшение кратных интегралов для повторения 160. Это означает непрерывность функции P (x), которая определена в Формуле (45.2). Я не уверен. Доказательство теоремы. Во-первых, правый Интеграл равенства (45.5), то есть в 6 ф (ЛГ) \ Р (х) топор = \ УГ $ Техас, гг、 Б А ф(л.) Является Интегралом непрерывной функции (см. лемму) и поэтому существует. Установите на на деталь EL1, i,/ = 1, 2 следующим образом… разделите его на K. рассмотрим разбиение xk =для интервала [a, b] K равных отрезков. 4 ОЭ Т * На самом деле, как уже было сказано, функции φ и φ ограничены интервалом[a, b], обусловленным их непрерывностью. То есть существует постоянная M 0, например|. φ (χ)\ <М и[φ (x) / » использовать M для всех x e [a, b].Таким образом, диаметр каждого набора.
Смотрите также:
Решение задач по математическому анализу
| Свойства кратного интеграла. | Обобщение на n-мерный случай. |
| Критерии интегрируемости функций Римана и Дарбу и их следствия. | Обобщенное интегральное неравенство Минковского. |
