Изучим теперь основные свойства пределов сходящихся последовательностей.
Последовательность 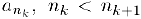 при всех
при всех 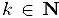 называется подпоследовательностью последовательности
называется подпоследовательностью последовательности
1) Любая подпоследовательность сходящейся последовательности сходится к пределу последовательности.
Доказательство очевидным образом следует из определения предела последовательности.
2) Сходящаяся последовательность имеет единственный предел.
Действительно, предположим, что у последовательности 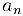 существуют два различных предела
существуют два различных предела 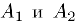 . Выберем число
. Выберем число 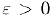 столь малым, чтобы интервалы
столь малым, чтобы интервалы 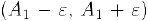 и
и 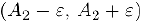 не пересекались. По определению предела найдется номер
не пересекались. По определению предела найдется номер 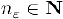 такой, что
такой, что
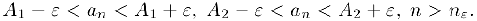
Полученное противоречие и доказывает утверждение.
Это свойство можно использовать доя того, чтобы доказать, что последовательность не имеет предела. В качестве примера рассмотрим упоминавшуюся в пункте 1 периодическую последовательность
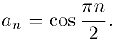
Рассмотрим две ее подпоследовательности. При 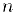 нечетном мы имеем:
нечетном мы имеем: 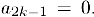 Следовательно,
Следовательно, 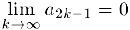 . Аналогично, если
. Аналогично, если 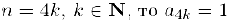 и, стало быть,
и, стало быть, 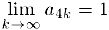 .
.
Таким образом, пределы двух подпоследовательностей данной последовательности различны и, следовательно, она нс может быть сходящейся, так как иначе по предыдущему свойству пределы всех подпоследовательностей совпадали бы с пределом последовательности.
3) Сходящаяся последовательность ограничена.
Действительно, пусть 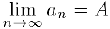 . Тогда найдется такое натуральное число
. Тогда найдется такое натуральное число 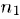 что
что
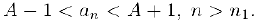
Полагая теперь 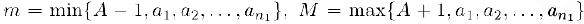 будем иметь при всех натуральных
будем иметь при всех натуральных 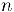 :
:
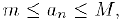
т. е. последовательность ограничена.
Последовательность 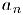 называется возрастающей (we убывающей), или убывающей (не возрастающей), если при всех натуральных
называется возрастающей (we убывающей), или убывающей (не возрастающей), если при всех натуральных 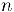 выполняется неравенство
выполняется неравенство 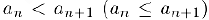 или неравенство
или неравенство 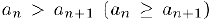 . Возрастающая или убывающая последовательность называется монотонной.
. Возрастающая или убывающая последовательность называется монотонной.
1) Монотонная, ограниченная последовательность сходится.
Пусть для определенности последовательность 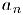 не убывает и ограничена сверху. По теореме 1, §2 последовательность
не убывает и ограничена сверху. По теореме 1, §2 последовательность 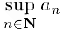 имеет верхнюю грань sup Докажем, что
имеет верхнюю грань sup Докажем, что
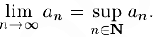
Зафиксируем произвольное 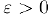 . Так как верхняя грань является минимальной из мажорант, то при всех
. Так как верхняя грань является минимальной из мажорант, то при всех 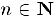 справедливо неравенство
справедливо неравенство 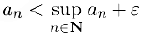 и существует натуральное
и существует натуральное 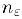 для которого
для которого 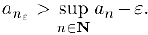 Поскольку последовательность
Поскольку последовательность  не убывает, то последнее неравенство выполняется и при всех
не убывает, то последнее неравенство выполняется и при всех  , что и завершает доказательство.
, что и завершает доказательство.
5) Если две последовательности сходятся к общему пределу, то к тому же пределу сходится и заключенная между ними последовательность.
Пусть 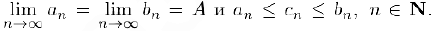 . По заданному
. По заданному 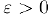 найдется номер
найдется номер 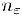 , после которого
, после которого 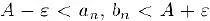 а, следовательно, и
а, следовательно, и 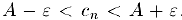 . Свойство доказано.
. Свойство доказано.
6) Если последовательность 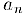 сходится и
сходится и 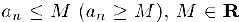 при всех
при всех 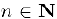 , то
, то 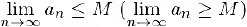 .
.
Пусть, для определенности, 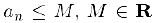 . Предположим, что, наоборот,
. Предположим, что, наоборот, 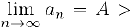
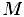 . Выберем
. Выберем 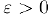 столь малым, чтобы выполнялось неравенство
столь малым, чтобы выполнялось неравенство 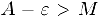 . Тогда, начиная с некоторого номера
. Тогда, начиная с некоторого номера 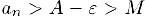 . Противоречие.
. Противоречие.
Сформулируем теперь свойства пределов последовательностей, связанные с арифметическими операциями над элементами этих последовательностей.
7) Если две последовательности 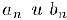 сходятся, то сходятся также и последовательности
сходятся, то сходятся также и последовательности 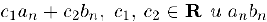 причем
причем
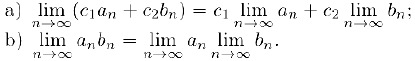
Если, кроме того. 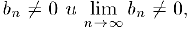 , то последовательность
, то последовательность 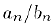 также сходится и
также сходится и
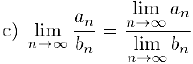
Докажем, например, последнее из этих свойств. Пусть 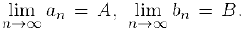 . Так как
. Так как 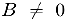 , то, интервал
, то, интервал 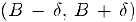 можно выбрать столь малым, чтобы он не содержал нуля. Ввиду сходимости последовательности
можно выбрать столь малым, чтобы он не содержал нуля. Ввиду сходимости последовательности 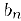 для всех
для всех 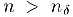 имеет место неравенство
имеет место неравенство 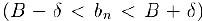 . Отсюда, учитывая, что все
. Отсюда, учитывая, что все 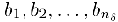 также отличны от нуля, мы заключаем, что последовательность
также отличны от нуля, мы заключаем, что последовательность 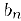 отделена от нуля, т. е. существует положительное число m такое,
отделена от нуля, т. е. существует положительное число m такое, 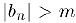 . Так как
. Так как
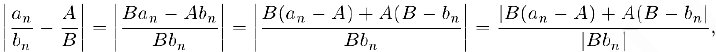
то. учитывая известное из курса элементарной математики неравенство 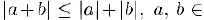
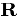 и отделенность от нуля последовательности
и отделенность от нуля последовательности 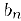 . получим:
. получим:
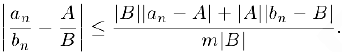
Зафиксируем произвольное положительное число 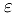 . Для числа
. Для числа 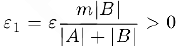 существует номер
существует номер 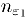 начиная с которого
начиная с которого 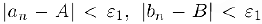 , поэтому из неравенства (1) при
, поэтому из неравенства (1) при 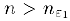 следует, что
следует, что
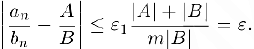
Утверждение доказано.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
| Числовые множества |
| Предел последовательности |
| Число e |
| О неопределенностях, возникающих при вычислении пределов |
