Формула полной вероятности и формула Байеса с примерами решения и образцами выполнения

Следствием обеих основных теорем—теоремы сложения
вероятностей и теоремы умножения вероятностей — является так называемая формула полной вероятности.

Пусть требуется определить вероятность некоторого события А,
которое может произойти вместе с одним из событий: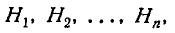

образующих полную группу несовместных событий. Будем эти
события называть гипотезами.

Докажем, что в этом случае

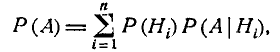(3.4,1)

т. е. вероятность события А вычисляется как сумма произведений
вероятности каждой гипотезы на вероятность события при этой
гипотезе.

Формула (3.4.1) носит название формулы полной вероятности.
Доказательство. Так как гипотезы H1, H2. …. Нn ,
образуют полную группу, то событие Л может появиться только в
комбинации с какой-либо из этих гипотез:

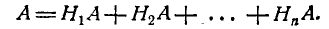
Так как гипотезы Н1, Н2, …. Нn, несовместны, то и комбинации
Н1А, Н2А, …, НnА , также несовместны; применяя к ним теорему
сложения, получим:

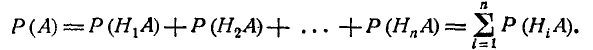
Применяя к событию H1A теорему умножения, получим: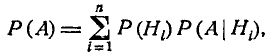

что и требовалось доказать.

Пример:

Имеются три одинаковые на вид урны; в первой урне два
белых и один черный шар; во второй — три белых и один черный; в третьей — два белых и два черных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.
Решение:

Рассмотрим три гипотезы:

H1 — выбор первой урны,
Н2 — выбор второй урны,
Н3 — выбор третьей урны
и событие А — появление белого шара.

Так как гипотезы, по условию задачи, равновозможны, то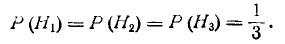

Условные вероятности события А при этих гипотезах соответственно равны:

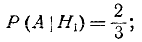
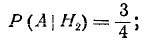
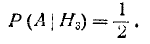
По формуле полной вероятности

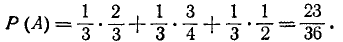
Пример:

По самолету производится три одиночных выстрела.
Вероятность попадания при первом выстреле равна 0,4, при втором — 0,5, при третьем—0,7. Для вывода самолета из строя заведомо достаточно трех попаданий; при одном попадании самолет выходит из строя с вероятностью 0,2, при двух попаданиях с вероятностью 0,6. Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя.
Решение:

Рассмотрим четыре гипотезы:

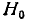— в самолет не попало ни одного снаряда,

H1 — в самолет попал один снаряд,

Н2 — в самолет попало два снаряда,

Н3 — в самолет попало три снаряда.

Пользуясь теоремами сложения и умножения, найдем вероятности этих гипотез:

Условные вероятности события А (выход самолета из строя) при этих
гипотезах равны:

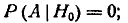
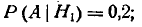
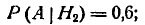
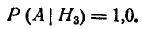
Применяя формулу полной вероятности, получим:

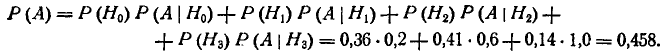
Заметим, что первую гипотезу 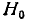можно было бы не вводить в
рассмотрение, так как соответствующий член в формуле полной вероятности обращается в нуль. Так обычно и поступают при применении формулы полной вероятности, рассматривая не полную группу несовместных гипотез, а только те из них, при которых данное событие возможно.

Пример:

Работа двигателя контролируется двумя регуляторами.
Рассматривается определенный период времени t, в течение которого желательно обеспечить безотказную работу двигателя. При наличии обоих регуляторов двигатель отказывает с вероятностью q1,2 , при работе только первого из них—с вероятностью q1 при работе только второго — с вероятностью q2, при отказе обоих регуляторов — с вероятностью q0. Первый из регуляторов имеет надежность Р1,а второй—Р2. Все элементы выходят из строя независимо друг от друга. Найти полную надежность (вероятность безотказной работы) двигателя.

Решение:

Рассмотрим гипотезы:
Н1, 2 — работают оба регулятора,
H1 —работает только первый регулятор (второй вышел из строя),
Н2 —работает только второй регулятор (первый вышел из строя), Но —оба регулятора вышли из строя

и событие

А — безотказная работа двигателя.

Вероятности гипотез равны:

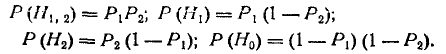
Условные вероятности события А при этих гипотезах заданы: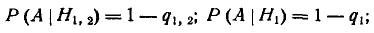

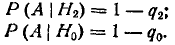
По формуле полной вероятности получим:

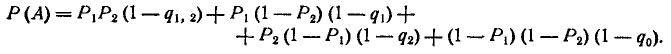
Формула полной вероятности:

Смотрите также:

Предмет теория вероятностей и математическая статистика

Геометрические вероятности	Формула Байеса
Условные вероятности	Независимость событий

Формула полной вероятности

Предположим, что в результате опыта может произойти одно из п событий, во-первых, несовместных и, во-вторых, составляющих полную группу событий 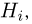т. е. 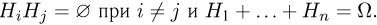События, удовлетворяющие этим двум требованиям, будем называть

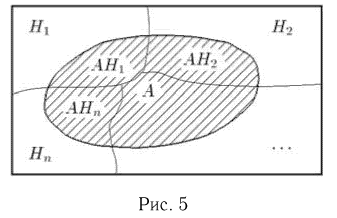
гипотезами. Пусть также имеется некоторое событие А, и нам известны 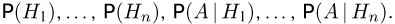Задача состоит в определении безусловной вероятности Р(А). Для решения представим событие А в следующем виде:

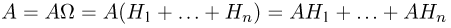
(см. рис. 5). Тогда

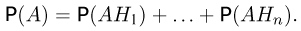
По формуле умножения вероятностей

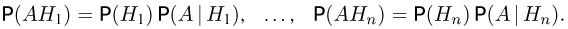
Поэтому

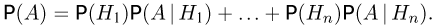
Выведенная формула носит название формулы полной вероятности. При всей своей простоте она играет весьма существенную роль в теории вероятностей.

Пример:

Частица пролетает мимо трех счетчиков, причем она может попасть в каждый из них с вероятностями 0,3, 0.2 и 0,4. В свою очередь, если частица попадает в первый счетчик, то она регистрируется с вероятностью 0,6, во второй — с вероятностью 0,5 и в третий — с вероятностью 0,55. Найдем вероятность того, что частица будет зарегистрирована (событие А). В нашем случае гипотеза 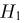— частица попадает в первый счетчик 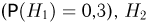— во второй 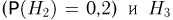— в третий 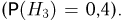События 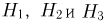не пересекаются, однако они не составляют полной группы событий. Для того чтобы получить полную группу событий, нужно добавить событие 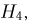заключающееся в том, что частица не попадет ни в один счетчик. Ясно, что 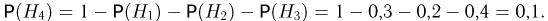Условные вероятности событя А при условии каждой гипотезы равны: 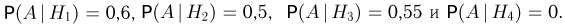По формуле полной вероятности имеем

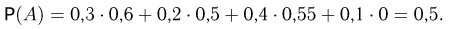
Формула Байеса

Во многих приложениях теории вероятностей встречается следующая задача. Пусть до опыта имеются гипотезы 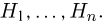После опыта становится известной информация о его результатах, но не полная. А именно, результаты наблюдений показывают, не какой конкретно элементарный исход 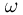из пространства элементарных исходов 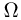произошел, а что наступило некоторое событие А. Считая, что до опыта были известны (априорные) вероятности гипотез 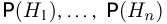и условные вероятности 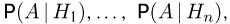необходимо определить (апостериорные) вероятности гипотез 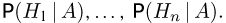Для решения поставленной задачи вспомним, что по определению условной вероятности

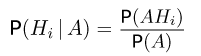
и по формуле умножения вероятностей

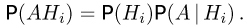
Поэтому

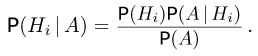
Полученное выражение носит название формулы Байеса.

Подставляя вместо вероятности Р(А) ее значение, вычисленное по формуле полной вероятности, формулу Байеса можно переписать также в виде

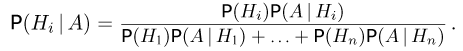
Формула Байеса находит широкое применение в математической статистике.

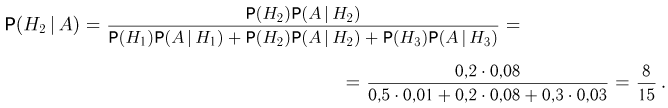
Пример:

Три завода выпускают одинаковые изделия, причем первый завод производит 50%, второй — 20% и третий — 30% всей продукции. Первый завод выпускает 1 % брака, второй завод — 8% и третий — 3%. Наудачу выбранное изделие оказалось бракованным (событие А). Найдем вероятность того, что оно изготовлено на втором заводе. У нас имеется три гипотезы: 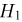— изделие изготовлено на первом заводе, 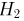— на втором заводе и 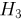-на третьем. По условию задачи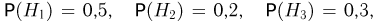 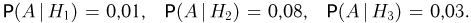Условная вероятность того, что бракованное изделие изготовлено на втором заводе, определяется формулой Байеса:

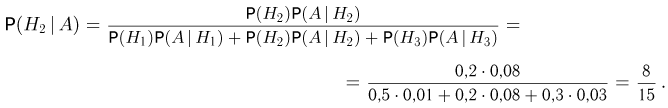
Итак, несмотря на то что продукция второго завода составляет 1/5, его доля в браке больше половины.

Пример:

Два охотника одновременно стреляют одинаковыми пулями в медведя. В результате медведь был убит одной пулей (событие .4). Как охотники должны поделить шкуру убитого медведя, если известно, что вероятность попадания у первого охотника 0,3, а у второго — 0,6? Снова воспользуемся формулой Байеса. Однако предварительно определим гипотезы. Гипотеза 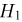попал первый охотник, второй промахнулся; гипотеза 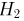: попал второй, первый промахнулся. События 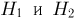несовместны, однако не составляют полной группы событий. Поэтому введем еще две гипотезы: 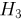— попали оба охотника и 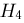— оба промахнулись. Заметим, что событие А может происходить тогда и только тогда, когда произошла либо гипотеза 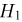либо гипотеза 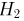т. е. 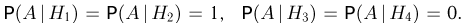Кроме того, делая естественное предположение, что попадания охотников в медведя не зависят друг от друга, получаем: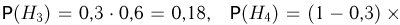

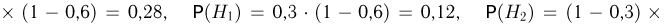
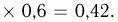
Теперь мы в состоянии применить формулу Байеса, согласно которой

Таким образом, при справедливом дележе первый охотник должен получить 2/9 шкуры, т.е. меньше 1/4, в то время как, на первый взгляд, казалось, что ему причитается 1/3 шкуры.

Пример:

В группе 15 студентов. Из них: 5 «отличников», 7 «четверочников» и 3 «троечника». Известно, что «отличник» с вероятностью 0,9 получает на каждом экзамене «отлично» и с вероятностью 0.1 — «хорошо». Аналогично, «четверочник» с вероятностью 0,1 получает «отлично», с вероятностью 0,7 — «хорошо» и с вероятностью 0,2 — «удовлетворительно». Наконец, «троечник» получает с вероятностью 0,1 «отлично», с вероятностью 0,2 — «хорошо» и с вероятностью 0,7 — «удовлетворительно». Один из студентов из этой группы получил на первом экзамене «хорошо». Найдем вероятность того, что на следующем экзамене он получит «отлично». Итак, опыт состоит в последовательной сдаче двух экзаменов. Событие А — студент сдал первый экзамен на «хорошо», событие В — второй экзамен на «отлично». Ясно, что в качестве гипотез надо взять: 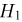— студент «отличник», 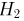— «четверочник» и 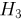— «троечник». Если бы нам необходимо было найти просто безусловную вероятность события В, то нужно было бы воспользоваться формулой полной вероятности, в которой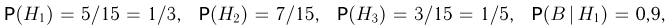 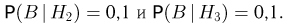Однако нас интересует условная вероятность события В при условии А, поэтому мы сначала с помощью формулы Байеса найдем условные вероятности гипотез 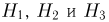при условии А. Поскольку 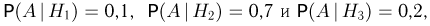то имеем:

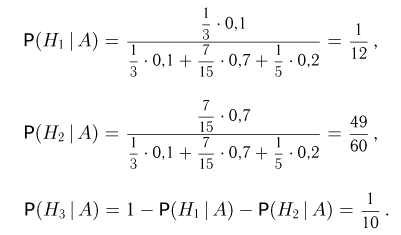
Таким образом, по полученной на первом экзамене оценке мы обязаны приписать нашему студенту новые вероятности 1/12, 49/60 и 1/10 того, что он «отличник», «четверочник» и «троечник». Теперь для вычисления условной вероятности 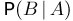воспользуемся формулой полной вероятности:

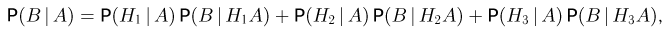
в которой вместо вероятностей 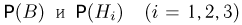взяты условные вероятности 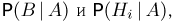а вместо условных вероятностей 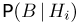— условные вероятности 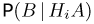(справедливость этой формулы мы предлагаем читателю проверить самостоятельно). Тогда, предполагая, что для студента одной успеваемости результат следующего экзамена не зависит от результата предыдущего, т.е. 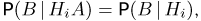получаем окончательно

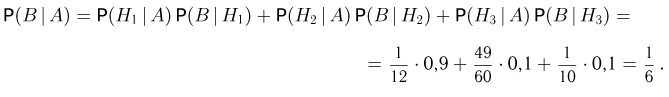
Для лучшего усвоения этого примера рекомендуем читателю построить пространство элементарных исходов 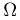(в данном случае оно будет состоять из 27 «троек» — «успеваемость-оценка на первом экзамене-оцснка на втором экзамене») и определить на нем вероятность. При определении вероятности нужно учитывать, что оценки на каждом экзамене для студентов одной успеваемости независимы.

Вообще говоря, можно отказаться и от условия независимости оценок на каждом экзамене. Тогда в формуле полной вероятности нужно вместо условных вероятностей 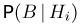использовать условные вероятности 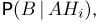т.е. учитывать не только успеваемость студента, но и его предыдущую оценку. Разумеется, модель экзаменов должна быть тоже более тонкой, т. е. необходимо задать для студента каждой успеваемости вероятность получения им любых оценок на двух последовательных экзаменах.

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Теорема о повторении опытов
13. Нормальный закон распределения
14. Определение законов распределения случайных величин на основе опытных данных
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность