Статистическое исследование зависимостей с примерами решения и образцами выполнения

Рассмотрим несколько часто встречающихся задач, связанных с восстановлением зависимостей между наблюдаемыми в эксперименте переменными.

Статистическое исследование зависимостей

Общая структура задач, о которых пойдет речь ниже, такова: наблюдаются две группы переменных — объясняющая (или исходная), описываемая вектором 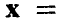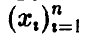и итоговая (или выходная), описываемая скаляром у. Следует дать ответы на вопросы:
— есть ли связь между переменными х и у?
— если связь есть, то какова возможная форма этой связи?
— каковы качественные характеристики этой связи?

Ответы на перечисленные вопросы (да и сами вопросы) могут выглядеть по разному в зависимости как от природы переменных х и у, наблюдаемых в эксперименте, так и от условий проведения измерений.

Различают следующие три основные модели.

Переменные х — детерминированные, а переменная 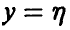— случайная величина.

Мы будем говорить что у зависит от х, если изменение переменных х влечет за собой изменение закона распределения случайной величины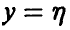

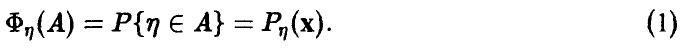
Если при этом математическое ожидание случайной величины 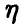может быть описано некоторой функцией переменных X

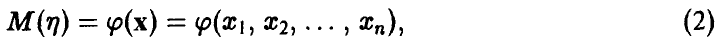
то мы, следуя сложившейся традиции, будем называть такую зависимость регрессионной.

Широкий класс регрессионных моделей описывается следующим примером.

Пример:

Пусть 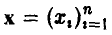— неслучайный вектор, у =f(х). В эксперименте измеряются значения у так, что

Здесь 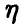— измеренное значение переменной у, 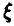— ошибка измерения с 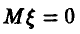(последнее означает отсутствие систематических ошибок измерения).

Соотношение (3) — модель измерений — доставляет нам пример регрессионной зависимости, так как из сделанных выше предположений следует, что

Как правило, в рассматриваемой ситуации вид линии регрессии 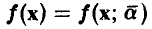бывает известен с точностью до вектора параметров 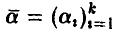и задача установления наличия зависимости между х и у не стойт. Требуется только определить возможные значения параметров 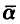и установить «качество» описания величины у посредством функции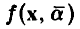

2. Переменные 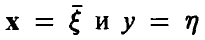— случайные величины, совместный закон распределения которых дается функцией 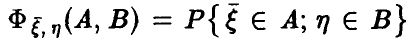. Известно, что случайные величины 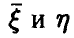независимы тогда и только тогда, когда выполняется соотношение

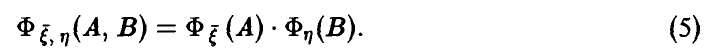
Если же равенство (5) не имеет места, то случайные величины зависимы. При этом, как и выше, выделим специальный случай, когда изменение математического ожидания случайной величины 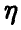описывается некоторой функцией от ,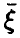

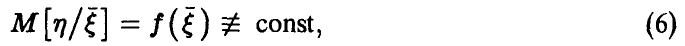
и будем говорить, что соотношение (6) описывает регрессию 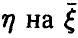. (Естественно, предполагается, что условные средние (6) существуют.)

Идентификация наличия или отсутствия зависимости между 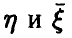представляет в рассматриваемом случае содержательную задачу, равно как и проблема установления формы регрессионной связи (6).

Важным для приложений частным случаем рассмотренной ситуации является случай совместной нормальности 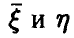. В этом случае проблема определения формы связи (6) не стоит — регрессия 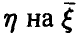является линейной и дается соотношением

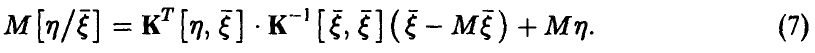
Здесь 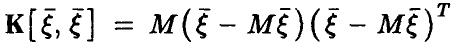— ковариационная матрица вектор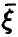а , а 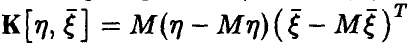— ковариационная матрица .

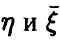Как следует из соотношения (7), регрессия 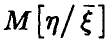полностью определяется корреляционными характеристиками совместного распределения величин .

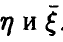Конечно, регрессия может оказаться линейной не только для совместно нормальных случайных величин. В любом случае мы будем называть соответствующую связь между переменными корреляционной.

Переменные х и у — детерминированные, неслучайные переменные и в эксперименте измеряются абсолютно точно. При этом уже факт наблюдения пар конкретных значений (X, У) в одном и том же опыте определяет положительный ответ на первый вопрос, и речь может идти только об установлении формы зависимости у и х.

Здесь возможны различные постановки и способы решения — интерполяция, сглаживание и т. п. Это задачи классического анализа и мы на них останавливаться не будем.

Ниже будут рассмотрены статистические процедуры, исследующие ситуации 1 и 2. Учитывая важность для приложений случая совместной нормальности изучаемых случайных величин и их линейных описаний, основное внимание будет уделено исследованию корреляционных связей.

Случайные переменные. Корреляционные связи

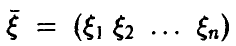Пусть в эксперименте наблюдаются случайные переменные и 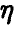. Проведено N опытов и получена выборка из совместного закона распределения величин ,

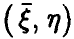Здесь

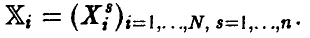
Требуется по выборке (1) сделать заключение о наличии или отсутствии зависимости между переменными 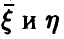и оценить эту зависимость.

Значимость коэффициента корреляции

Исследование вопроса о наличии связей между 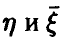мы начнем с простейшего случая n = 1. Тогда 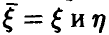— скалярные случайные величины, а выборка (1) — это выборка 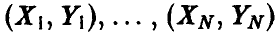из совместного закона распределения пары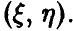

Отличие от нуля коэффициента корреляции 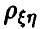пары 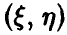является достаточно надежным показателем наличия зависимости между 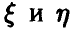. Эта зависимость носит корреляционный характер, т. е. может быть удовлетворительно описана линейной функцией в том смысле, что имеется четко выраженная тенденция к линейному изменению 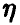относительно 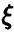. Точнее, в этом случае величина 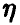представима в виде

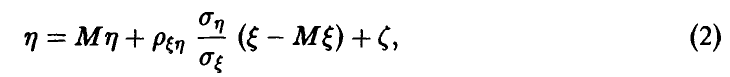
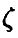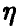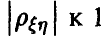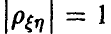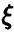и вклад остатка в рассеяние тем меньше, чем ближе . В случае между и 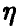имеется жесткая линейная связь, позволяющая с вероятностью восстанавливать неизвестные значения 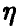по измеренным значениям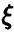

Если 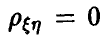, то это, вообще говоря, еще не свидетельствует об отсутствии зависимости между 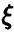и 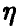, но является надежным свидетельством в пользу отсутствия линейной зависимости.

Значит, для идентификации наличия или отсутствия линейном связи между скалярными случайными величинами достаточно уметь по выборке (1) делать заключение о равенстве или неравенстве нулю коэффициента корреляции 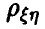пары .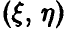

Пусть 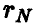— выборочный (эмпирический) коэффициент корреляции пары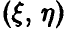

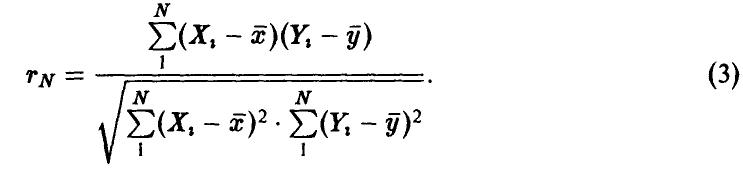
Он является оценкой истинного, но неизвестного коэффициента корреляции 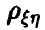. Если 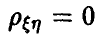, то чисто случайные колебания 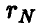могут привести к значению 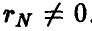. Как же выяснить, равен или не равен нулю коэффициент корреляции р по наблюдению за значением 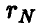, вычисленному по формуле (3)?

Теорема:

Пусть 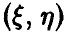— двумерная нормальная случайная величина, 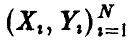— выборка значений 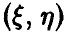, полученная в эксперименте, и 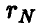— выборочный коэффициент корреляции (3). Тогда, если р = 0, то величина 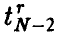, даваемая соотношением

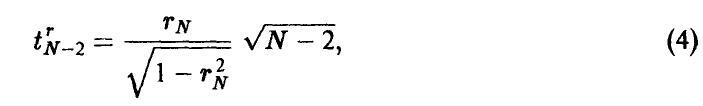
имеет распределение Стьюдента с N — 2 степенями свободы.

Эта теорема дает возможность построить процедуру статистической проверки гипотезы о значимости коэффициента корреляции (т. е. гипотезы об отличии р от нуля) следующим образом. Так как при фиксированном значении N > 2 величина (4) монотонно возрастает (рис. 1), то «маленьким» значениям 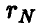отвечают «маленькие» значения 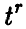. Если истинный коэффициент корреляции р равен нулю, то его эмпирический аналог 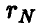в подавляющем большинстве случаев будет «маленьким», а, следовательно, в подавляющем большинстве случаев должна быть маленькой и величина 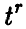. Зададим некоторый (близкий к нулю) уровень значимости к и найдем значение 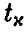такое, что

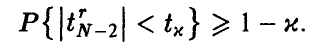
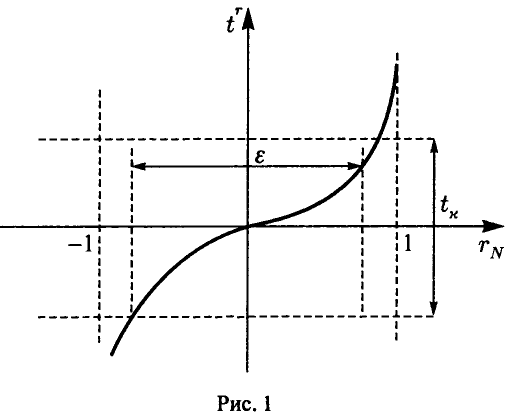
При этом для 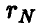будет иметь место соотношение

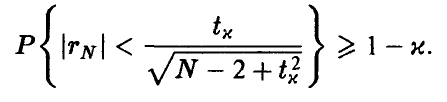
Если окажется, что 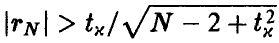, то гипотеза о равенстве нулю коэффициента корреляции должна быть признана не согласующейся с экспериментальными данными. Если же 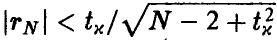, то можно считать, что р = 0 и, следовательно, величины 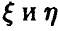независимы (напомним, что мы рассматриваем случай совместной нормальности 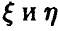, когда равенство нулю коэффициента корреляции эквивалентно независимости).

Если совместное распределение 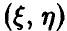не является нормальным, то основная теорема, позволившая построить критерий значимости для коэффициента корреляции, уже оказывается неверной. В этом случае рекомендуется использовать статистику Фишера Z, определяемую соотношением

Установлено, что уже при достаточно небольших значениях N величина Z приближенно нормальна с параметрами

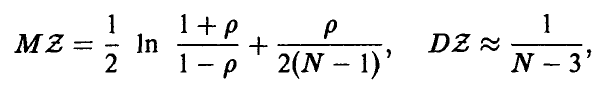
где р — истинный коэффициент корреляции величин 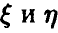. Учитывая монотонность функции Z = Z(r) на промежутке (-1, 1), мы можем, как и выше, построить процедуру статистической проверки гипотезы о значимости коэффициента корреляции.

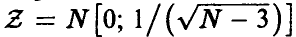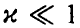Пусть р = 0. Тогда . Для определим 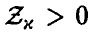так, что

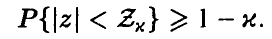
При этом

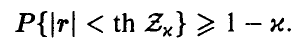
Гипотеза р = 0 принимается на уровне значимости х, если выполняется неравенство 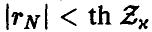; в противном случае признается значимым отличие коэффициента корреляции от нуля.

Таким образом, если предложенные выше критерии признали коэффициент корреляции значимо отличным от нуля, то можно сделать вывод о наличии зависимости между случайными величинами 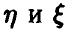, и чем ближе значения коэффициента корреляции к единице, тем лучше идентифицируемая зависимость описывается линейным соотношением (2).

Если отличие от нуля коэффициента корреляции признано незначимым, то в случае совместной нормальности это, как уже отмечалось выше, свидетельствует о независимости наблюдаемых случайных величин. В случае же, когда совместное распределение отличается от нормального, между наблюдаемыми случайными величинами возможно наличие зависимости, причем не исключается даже жесткая функциональная связь.

Множественная регрессия. Метод наименьших квадратов

Пусть теперь 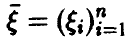— векторная случайная величина.

Если 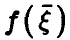— некоторая неслучайная функция п переменных, описывающая связь между 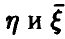так, что 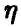представима в виде

то естественно оценивать качество описания случайной величины 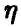функцией 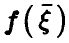с помощью «остатка» — чем меньше (в точно определенном смысле) , тем лучше 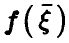описывает величину 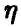. Если в качестве критерия малости 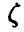взять ее дисперсию, то наилучшей из всех функций 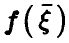будет удовлетворяющая условию

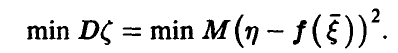
Оказывается, что при достаточно естественных предположениях о законе распределения совокупности 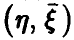, наилучшая (в смысле минимума дисперсии остатка) функция 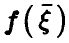существует и, как и в одномерном случае, совпадает с условным средним случайной величины 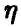относительно .

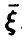Теорема:

Если существует условное среднее 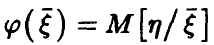, то

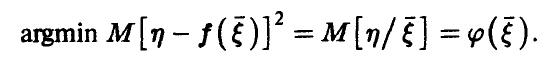
◄ Рассмотрим

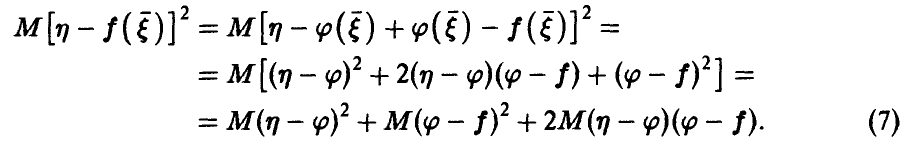
Последнее слагаемое равно нулю. Чтобы не загромождать изложение выкладками, покажем это для частного случая, когда 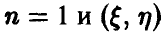непрерывна.

Пусть 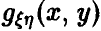— совместная плотность величин 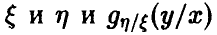— условная плотность 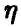относительно 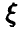. Тогда

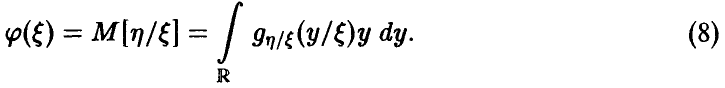
С учетом 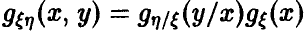получаем, что

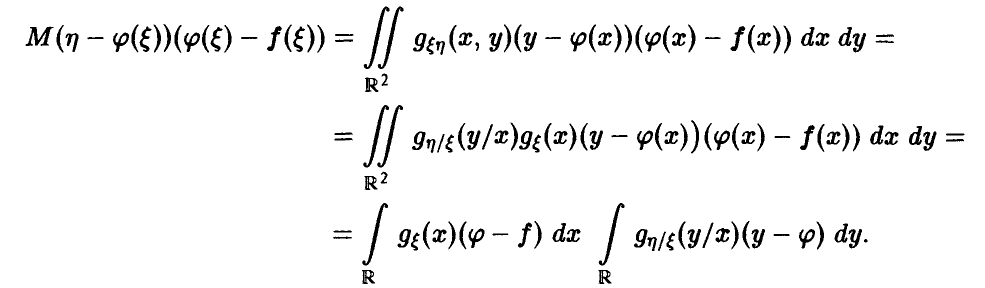
Но в силу соотношения (8) внутренний интеграл равен нулю, откуда и следует искомое.

Теперь соотношение (7) принимает вид

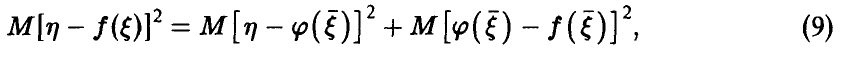
откуда (в силу неотрицательности 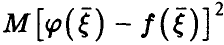) немедленно заключаем, что

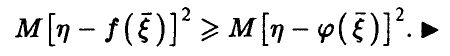
Таким образом, с точки зрения критерия минимума дисперсии остатка 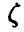, наилучшее описание зависимости 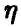от 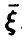дается линией регрессии 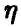на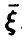

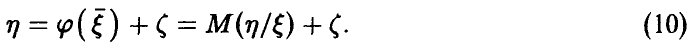
Отметим, что соотношению (10) отвечает дисперсионное соотношение, позволяющее оценивать степень тесноты связи между 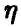и 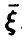. Имеет место следующее утверждение.

Теорема:

О разложении дисперсии. В условиях предыдущей теоремы

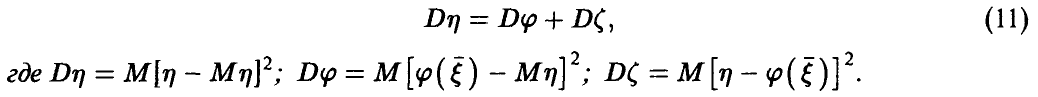
◄ Для доказательства соотношения (11) подставим в тождество (9) 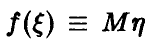и заметим, что

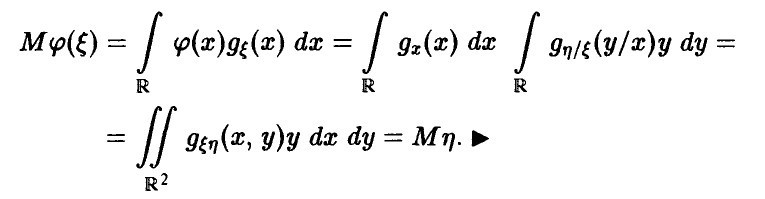
Разделим обе части соотношения (11) на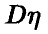

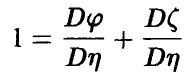
и введем величину 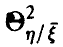— корреляционное отношение величины 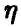относительно 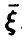— равенством

Тогда соотношение (11) запишется в виде

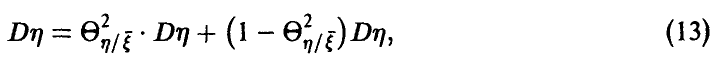
откуда видно, что если показатель (12) близок к единице — связь между 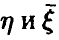достаточно тесная в том смысле, что среднее значение 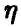закономерно меняется с изменением 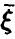, если же 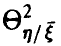близко к нулю, то такой тенденции нет — основной вклад в изменение 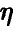вносит случайный остаток .

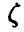Важным случаем регрессионных связей (10) являются линейные зависимости

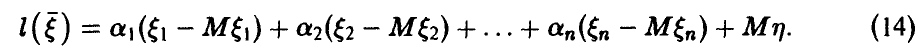
Как уже отмечалось выше (см. соотношение (7)), в случае совместной нормальности 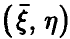регрессия всегда линейна. Она может оказаться таковой и в других случаях.

Поскольку любая регрессия 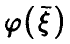, независимо от того, линейна она или нет, должна удовлетворять условию 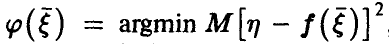, то коэффициенты 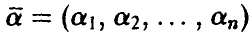линейной регрессии (14) могут быть найдены следующим образом. Положив 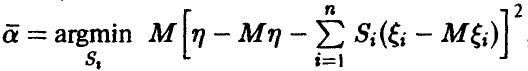, заметим, что

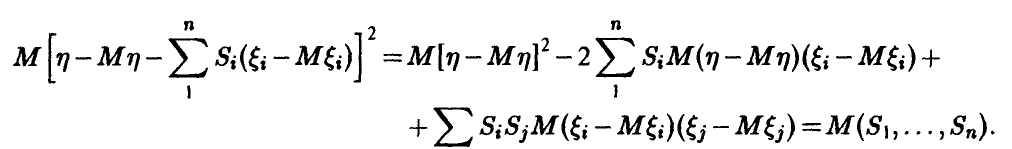
Необходимое условие экстремума описывается набором условий

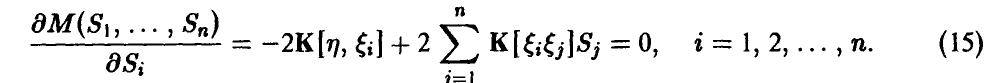
Если воспользоваться матричными обозначениями, то система линейных уравнений (15) может быть представлена в виде

где 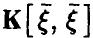— ковариационная матрица вектора 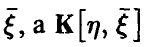— матрица ковариаций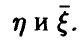

Лемма:

Пусть компоненты вектора 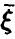линейно независимы. Тогда ковариационная матрица 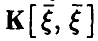невырождена и вектор коэффициентов линейной регрессии дается соотношением

◄ Пусть компоненты вектора 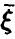линейно зависимы, тогда существует ненулевой вектор 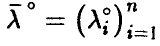такой, что

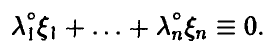
При этом

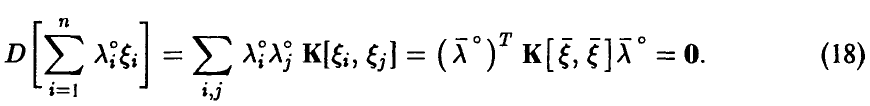
Заметим, что функция 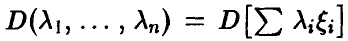неотрицательна и (в силу (18)) достигает в ненулевой точке 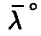своего наименьшего значения. Поэтому однородная система (необходимое условие экстремума!)

имеет ненулевое решение, а отсюда следует вырожденность ковариационной матрицы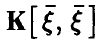

Пусть теперь матрица 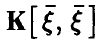вырождена. Тогда система (19) имеет ненулевое решение 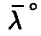. Умножая соотношение (19) на 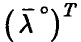, заключаем, что

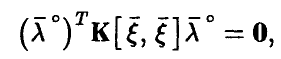
откуда (см. соотношение (18))

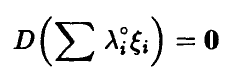
и значит с вероятностью единица компоненты 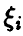линейно зависимы. ►

Еще раз отметим, что независимо от того, линейна регрессия или нет, мы можем попытаться описать связь величины 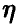с величинами 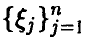линейным соотношением (14), коэффициенты которого даются равенством (17). Это будет наилучшее с рассматриваемой точки зрения линейное приближение к линии регрессии 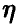на 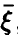, совпадающее с ней в случае, когда регрессия линейна.

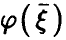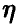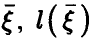Пусть — регрессия на — линейная функция (14) с коэффициентами (17). Рассмотрим корреляцию 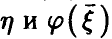. Оказывается, функция регрессии 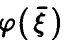дает наилучшее описание случайной величины 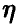не только с точки зрения минимума дисперсии остатка, но и имеет наибольший коэффициент корреляции с .

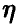Теорема:

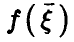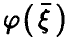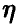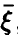Пусть — произвольная функция, — регрессия на Тогда

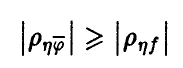
при этом 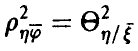(см. соотношение (12)).

Рассмотрим корреляцию случайной величины 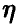и линейной функции 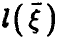(соотношение (14)) и заметим, что если регрессия 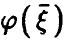— линейна, т.е.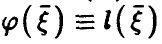, то

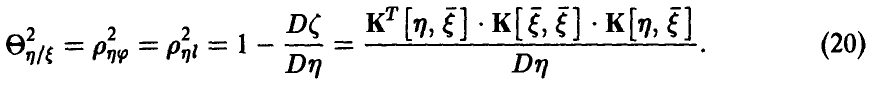
Если же регрессия 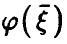линейной не является, то, как уже было отмечено выше, 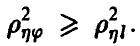Величина 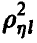определяемая правой частью соотношения (20), в этом случае описывает качество представления случайной величины 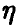линейной функцией переменных 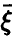и называется множественным коэффициентом корреляции.

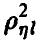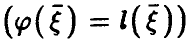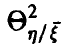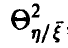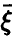Таким образом, множественный коэффициент корреляции в случае линейной регрессии совпадает с корреляционным отношением , Если же регрессия нелинейна, то он отличен от заключен между 0 и 1 и характеризует степень представимости линейной комбинацией величин — при 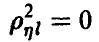корреляционная связь между 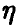и линейными комбинациями 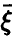отсутствует, при 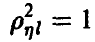— имеется жесткая функциональная связь между 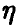и компонентами 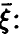с вероятностью 1 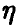является линейной комбинацией компонент .

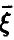Значимость множественного коэффициента корреляции

В практической ситуации, имея дело с выборочными значениями из закона распределения совокупности 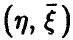, мы не имеем возможности определить точное значение множественного коэффициента корреляции 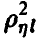, а можем лишь найти его выборочный аналог. При этом, как и в случае с парным коэффициентом корреляции, возникает задача установления значимости выборочного коэффициента множественной корреляции, для решения которой необходимо знание закона распределения последнего.

Пусть в эксперименте получена выборка из закона распределения совокупности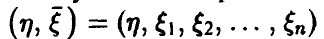

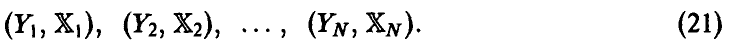
Эмпирический аналог 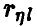множественного коэффициента корреляции 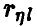может быть построен на основе соотношения (20) заменой фигурирующих там дисперсий их выборочными аналогами, найденными по выборке (21)

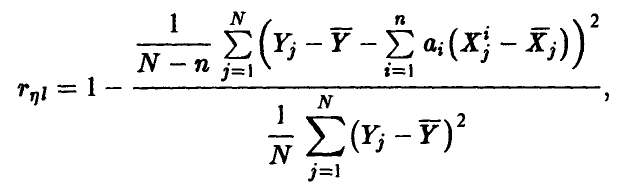
где 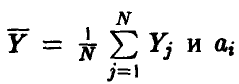— оценки (17) коэффициентов регрессии (14), полученные методом наименьших квадратов.

В предположении совместной нормальности 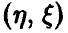установлено, что если множественный коэффициент корреляции равен нулю, то квадрат его эмпирического аналога имеет известное распределение. Этим можно воспользоваться для построения процедуры проверки значимости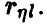

◄ Пусть компоненты вектора 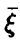линейно зависимы, тогда существует ненулевой вектор 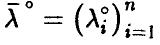такой, что

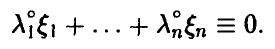
При этом

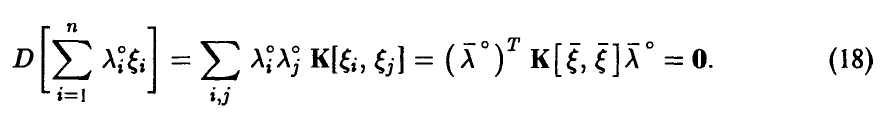
Заметим, что функция 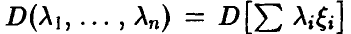неотрицательна и (в силу (18)) достигает в ненулевой точке 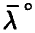своего наименьшего значения. Поэтому однородная система (необходимое условие экстремума!)

имеет ненулевое решение, а отсюда следует вырожденность ковариационной матрицы .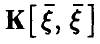

Пусть теперь матрица 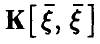вырождена. Тогда система (19) имеет ненулевое решение 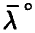. Умножая соотношение (19) на 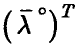, заключаем, что

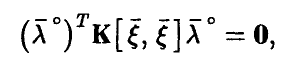
откуда (см. соотношение (18))

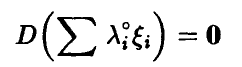
и значит с вероятностью единица компоненты 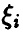линейно зависимы. ►

Еще раз отметим, что независимо от того, линейна регрессия или нет, мы можем попытаться описать связь величины 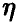с величинами 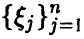линейным соотношением (14), коэффициенты которого даются равенством (17). Это будет наилучшее с рассматриваемой точки зрения линейное приближение к линии регрессии 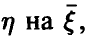совпадающее с ней в случае, когда регрессия линейна.

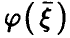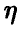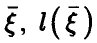Пусть — регрессия на — линейная функция (14) с коэффициентами (17). Рассмотрим корреляцию 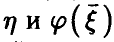. Оказывается, функция регрессии 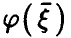дает наилучшее описание случайной величины 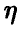не только с точки зрения минимума дисперсии остатка, но и имеет наибольший коэффициент корреляции с .

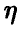Теорема:

Пусть 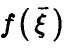— произвольная функция, 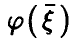— регрессия 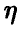на 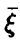.Тогда

при этом 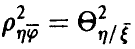(см. соотношение (12)).

Рассмотрим корреляцию случайной величины 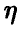и линейной функции 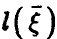(соотношение (14)) и заметим,что если регрессия 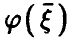— линейна,т.е. 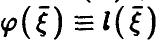, то

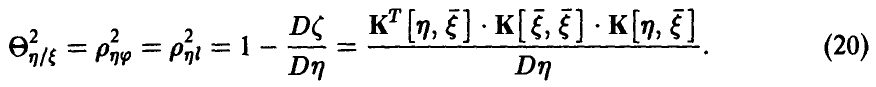
Если же регрессия 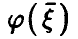линейной не является, то, как уже было отмечено выше, 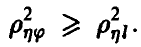Величина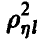, определяемая правой частью соотношения (20), в этом случае описывает качество представления случайной величины 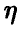линейной функцией переменных 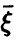и называется множественным коэффициентом корреляции.

Таким образом, множественный коэффициент корреляции 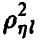в случае линейной регрессии 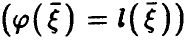совпадает с корреляционным отношением 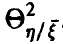, Если же регрессия нелинейна, то он отличен от 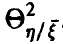, заключен между 0 и 1 и характеризует степень представимости 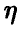линейной комбинацией величин 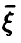— при 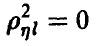корреляционная связь между 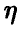и линейными комбинациями 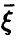отсутствует, при 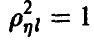— имеется жесткая функциональная связь между 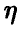и компонентами 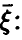с вероятностью 1 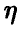является линейной комбинацией компонент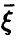

Значимость множественного коэффициента корреляции

В практической ситуации, имея дело с выборочными значениями из закона распределения совокупности 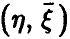, мы не имеем возможности определить точное значение множественного коэффициента корреляции 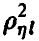, а можем лишь найти его выборочный аналог. При этом, как и в случае с парным коэффициентом корреляции, возникает задача установления значимости выборочного коэффициента множественной корреляции, для решения которой необходимо знание закона распределения последнего.

Пусть в эксперименте получена выборка из закона распределения совокупности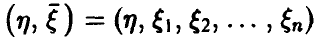

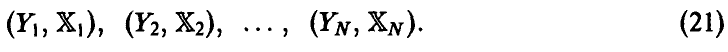
Эмпирический аналог 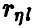множественного коэффициента корреляции 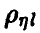может быть построен на основе соотношения (20) заменой фигурирующих там дисперсий их выборочными аналогами, найденными по выборке (21)

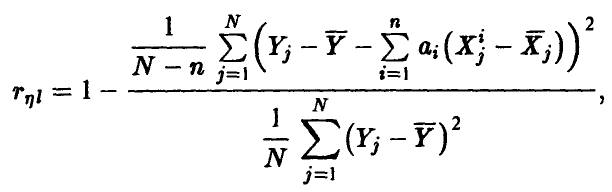
где 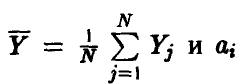— оценки (17) коэффициентов регрессии (14), полученные методом наименьших квадратов.

В предположении совместной нормальности 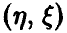установлено, что если множественный коэффициент корреляции равен нулю, то квадрат его эмпирического аналога имеет известное распределение. Этим можно воспользоваться для построения процедуры проверки значимости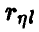

На практике для установления значимости отличия эмпирического коэффициента множественной корреляции от нуля пользуются тем, что величина

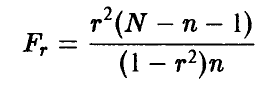
имеет распределение Фишера с (n, N — n — 1) степенями свободы при условии справедливости сделанных выше предположений о равенстве нулю 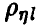и совместной нормальности .

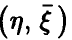По заданному уровню значимости х определяют величину 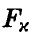такую, что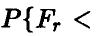 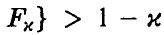. Если расчетное значение 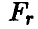оказывается меньше табличного 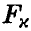— гипотеза о незначимом отличии 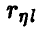от нуля считается согласующейся с результатами эксперимента и 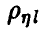полагается равным нулю. В противном случае считается, что коэффициент 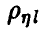отличен от нуля и множественная регрессия (14) дает представление о характере изменения величины 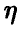с изменением .

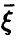Случайные переменные. Нелинейные зависимости

Пусть 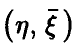— наблюдаемые в эксперименте случайные переменные. Предположим, что на основе рассмотрений предыдущих пунктов сделан вывод о незначимом отличии от нуля выборочного коэффициента корреляции (парного или множественного). Как уже неоднократно было отмечено, это дает основание для вывода об отсутствии линейной зависимости между 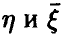, но не исключает возможного наличия зависимостей нелинейных (в том числе и жестких функциональных) между ними.

Для идентификации этих зависимостей изучим корреляционное отношение 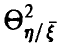, введенное соотношением (12). Оно обладает следующими свойствами:

1. Величина корреляционного отношения 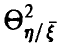заключена между нулем и единицей. Если отношение 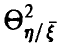близко к нулю — закономерное изменение переменной в зависимости от отсутствует. Если же 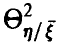близко к 1 — средние значения 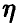с высокой степенью надежности могут быть найдены по известным значениям .

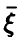2. Корреляционное отношение 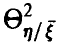не меньше квадрата коэффициента корреляции (теорема пункта 3.1.2)

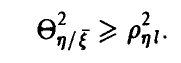
Знак равенства достигается тогда и только тогда, когда между переменными 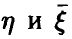имеется корреляционная (т. е. хорошо описываемая линейными соотношениями) связь.

Как и при анализе линейных зависимостей, достаточно уметь строить эмпирический аналог 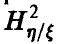величины 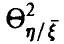по выборке (21) и оценивать значимость отличия этого выборочного аналога от нуля. Обе задачи оказываются технически более сложными, чем аналогичные для парного и множественного коэффициентов корреляции. Уже процедура построения эмпирического аналога 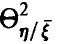предъявляет специальные требования к выборке (21) — в соответствии с (12) мы должны быть в состоянии вычислить эмпирический аналог (оценку) величины 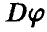, описывающей рассеяние 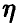относительно линии регрессии 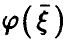. А для этого необходимо, чтобы экспериментальные данные позволяли строить линию условных средних 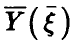. Возможность построения линии

условных средних может быть обеспечена, например, наличием в выборке (21) повторных измерений величины 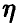: каждому из наблюденных значений 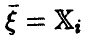, отвечает несколько измерений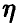

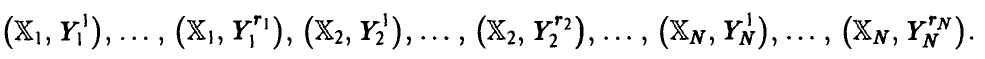
Либо выборочные данные должны допускать объединение наблюденных значений переменной 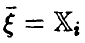, в группы так, чтобы каждому групповому выборочному среднему отвечало несколько значений переменной .

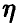В любом из указанных случаев эмпирическое корреляционное отношение может быть подсчитано по формуле

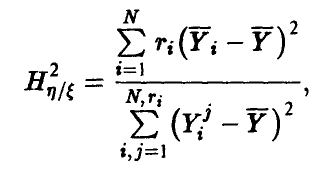
где 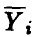— среднее наблюденных в i-й точке значений 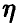(либо групповое среднее игреков),

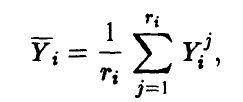
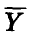— среднее всех наблюденных значений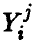

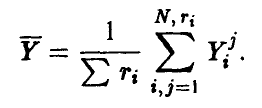
Для проверки гипотезы о значимом отличии от нуля величины 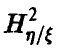воспользуемся тем фактом, что статистика 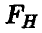, задаваемая соотношением

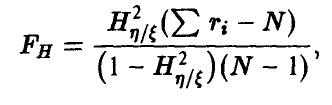
и мест приближенно распределение Фишера с 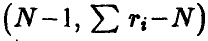степенями свободы при условии, что все сечения (групповые данные) нормальны с одинаковой дисперсией, и в предположении, что 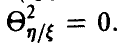В силу монотонности 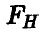как функции переменной 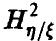это обстоятельство дает возможность обычным образом строить процедуру проверки интересующей нас гипотезы.

По заданному уровню значимости х определяем 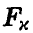так, что

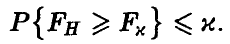
При этом

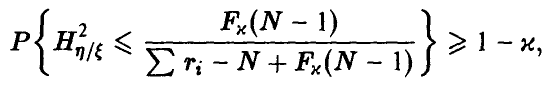
и гипотеза о значимом отличии от нуля эмпирического корреляционного отношения признается согласующейся с опытными данными, если

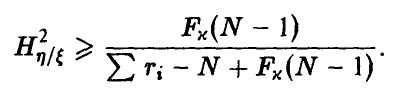
В этом случае можно считать, что переменные 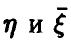связаны некоторой зависимостью, вообще говоря, нелинейной. Представление о ней может дать линия условных средних, построенная по экспериментальным точкам

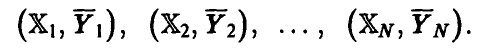
В противном случае корреляционное отношение признается равным нулю и, следовательно, можно считать, что закономерного изменения среднего значения переменной в связи с изменением значений переменных 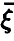нет.

Неслучайные переменные.
Линейные по параметрам регрессионные модели

3.1. Основные допущения

Пусть теперь 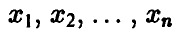— неслучайные переменные, связанные с неслучайной переменной у соотношением

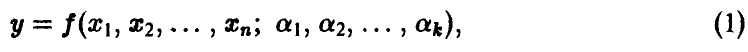
где функция 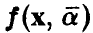известна с точностью до параметров. В эксперименте получены значения (У, X) переменных (у, х). Предполагается, что модель измерений аддитивна относительно ошибки измерений є и каждое измерение У складывается из значения f(X) и ошибки измерения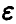

При этом допускается проведение нескольких измерений в одной и той же точке X, так что выборка измеренных значений имеет вид

Здесь нижний индекс показывает точку, в которой проведено измерение 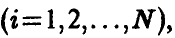верхний — номер измерения в i-й точке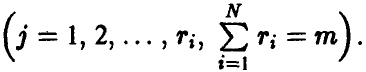

Требуется найти оценки неизвестных параметров 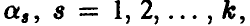и высказать некоторое обоснованное суждение о качестве найденного описания зависимости величины у от переменных

Последняя задача ниже будет уточнена, однако сразу заметим, что проблему подбора наилучшего класса параметрических функций 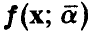, выбираемых для построения зависимости (1), мы здесь не обсуждаем. Предполагается, что этот класс определен из внестатистических соображений.

В дальнейшем ограничимся, чтобы избежать технических осложнений в выкладках, линейными по параметрам функциями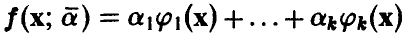. Функции 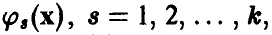будем предполагать линейно независимыми. Тогда модель измерений (3) запишется в виде

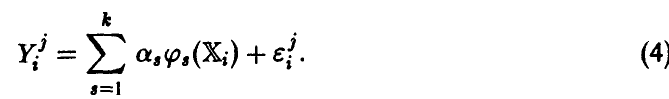
Считая ошибки 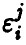попарно некоррелированными случайными величинами (что соответствует предположению о независимости измерений) с нулевым математическим ожиданием (отсутствие систематических ошибок) и одинаковой дисперсией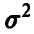

(равноточность измерений), будем искать неизвестные параметры 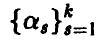, исходя из принципа минимизации суммы квадратов ошибок

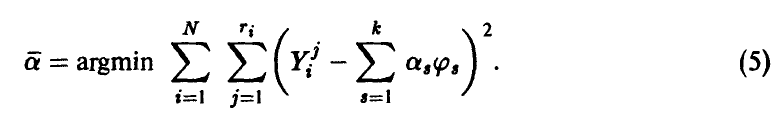
Заметим, что в силу предположения об отсутствии систематических ошибок измерения 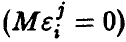из соотношения (2) следует

В соответствии с принятой терминологией соотношение (6) позволяет назвать функцию 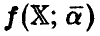функцией регрессии, параметры 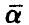— параметрами регрессии; в частности, для линейной по параметрам модели (4), параметры 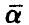будем называть коэффициентами регрессии.

Оценивание коэффициентов регрессии методом наименьших квадратов

Для удобства дальнейшего изложения и обозримости выкладок перейдем от скалярной формы записи задачи (5) к векторно-матричной, для чего введем следующие обозначения: Y — вектор измерений значений переменной 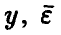— вектор ошибок измерений, 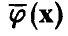— вектор параметров. Все векторы — матрицы-столбцы,

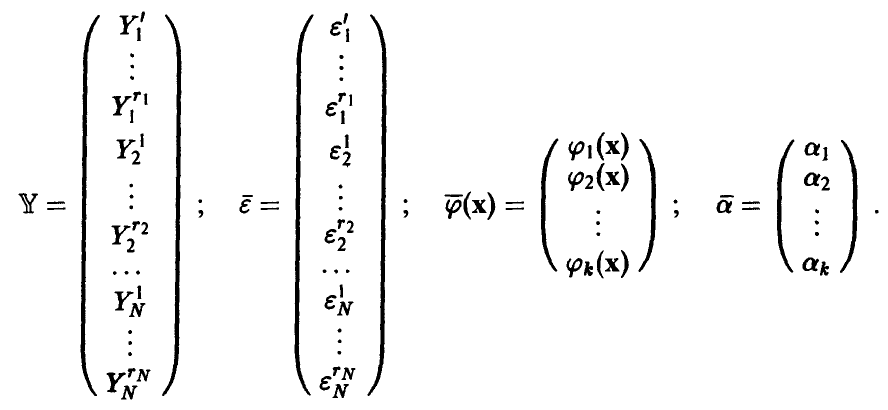
Тогда исследуемая зависимость (1) представима в виде

где символом 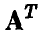обозначена матрица, транспонированная по отношению к А (в данном случае 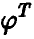— матрица-строка).

Модель измерений (4) запишется так

где F — матрица формата 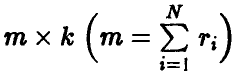, имеющая следующую структуру

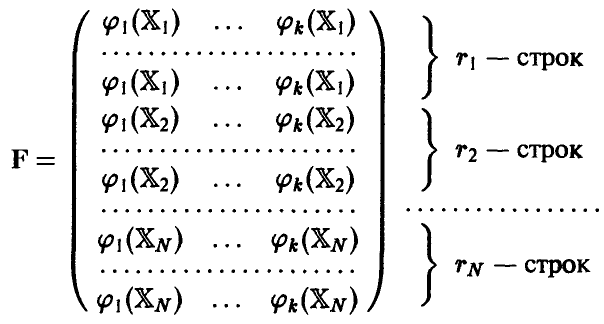
Метод наименьших квадратов (5) в матричной форме примет вид

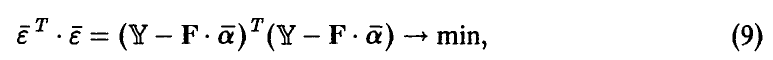
а необходимое условие экстремума

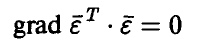
после несложных выкладок приводит к соотношению

Отметим, что функция 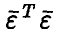как функция параметров 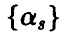является неотрицательно определенной квадратичной функцией, а потому достигает своего наименьшего значения. Поэтому argmin 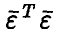содержится среди решений системы (10). Система линейных относительно 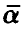уравнений (10) носит название системы нормальных уравнений метода наименьших квадратов. Если матрица 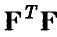оказывается невырожденной, то (10) имеет единственное решение, задаваемое соотношением

которое определяет оценки метода наименьших квадратов коэффициентов регрессии.

Отметим, что линейная независимость функций 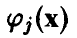не гарантирует невырожденности матрицы 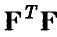, в то время как их линейная зависимость приводит к вырожденности указанной матрицы. Связано это с тем, что вырожденность или невырожденность 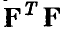определяется наличием или отсутствием линейной зависимости системы столбцов матрицы F, которые представляют собой упорядоченные значения базисных функций 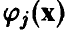в точках, где проводятся измерения, с учетом их кратности

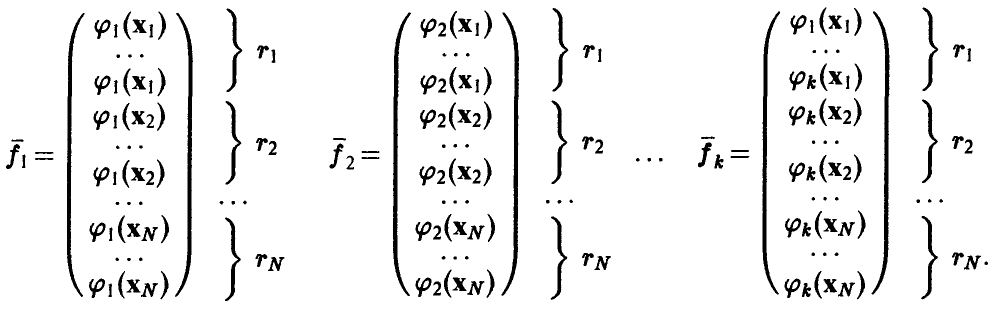
Матрица 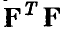является матрицей Грама векторов 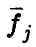— ее элементами являются скалярные произведения 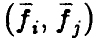. Она невырождена тогда и только тогда, когда векторы 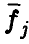линейно независимы.

Ясно, что для линейно зависимых функций 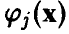векторы 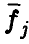линейно зависимы. Линейная независимость 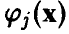, как показывает следующий простой пример

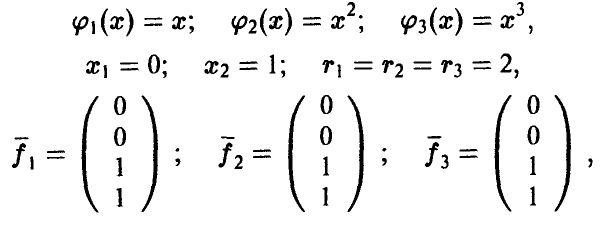
линейной независимости векторов 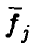не гарантирует.

Однако, даже если матрица 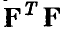— вырождена, система нормальных уравнений (10) все равно разрешима, и ее решение (т. е. оценки коэффициентов регрессии) могут быть найдены с помощью обобщенного обращения матрицы .

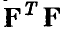Свойства оценок коэффициентов регрессии

Пусть ошибки измерений 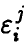совместно нормальны с нулевым средним и ковариационной матрицей 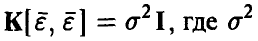— величина, характеризующая точность каждого отдельного измерения, I — единичная матрица порядка 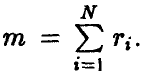Тогда статистические свойства оценок (11) коэффициентов регрессии описываются следующим утверждением.

Теорема:

Оценки (11) коэффициентов регрессии совместно нормальны с вектором средних 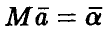и ковариационной матрицей .

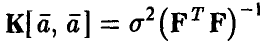◄ В силу модели (8) из формулы (11) получаем, что

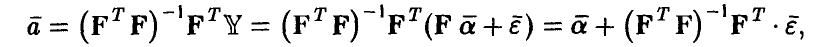
откуда следует совместная нормальность компонент вектора оценок 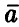, так как они являются линейными комбинациями нормальных величин. Далее

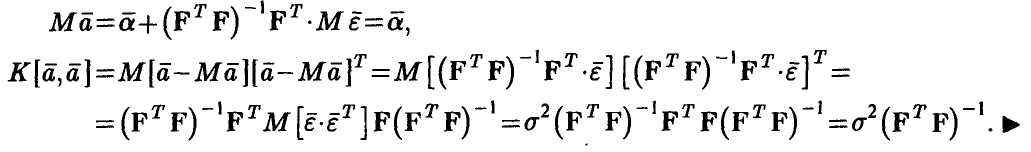
Заметим, что утверждения теоремы о несмещенности оценок (11) и о корреляционной матрице не зависит от предположения о нормальности ошибок. Точно так же не зависит от этого предположения некоторое свойство оптимальности оценок (4), описываемое теоремой Гаусса—Маркова.

Теорема Гаусса—Маркова:

Среди всех линейных несмещенных оценок коэффициентов регрессии оценки (11) — наилучшие в том смысле, что обладают наименьшим рассеянием.

Оценивание параметра

Оценивание параметра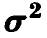

Как правило, параметр 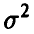, характеризующий точность каждого отдельного измерения при построении регрессионных зависимостей не известен и подлежит оцениванию по тем же исходным данным, по которым была построена модель. Это можно сделать различными способами. Некоторые из них мы приведем ниже.

Если 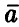— вектор оценок (11), то модель принимает вид

при этом сумма квадратов ошибок, допущенных при замене экспериментальных данных 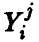, данными, рассчитанными по модельному соотношению (7), дается соотношением 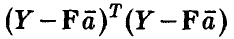— минимальным значением суммы квадратов отклонений модели от расчетных данных. Имеет место следующая теорема.

Теорема об оценивании :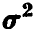

Величина

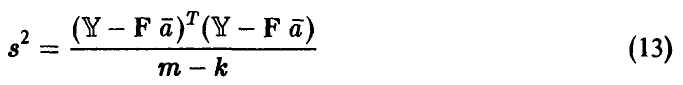
является несмещенной оценкой неизвестной дисперсии .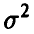

◄ В силу

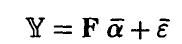
и

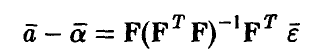
числитель соотношения (13) может быть представлен в виде

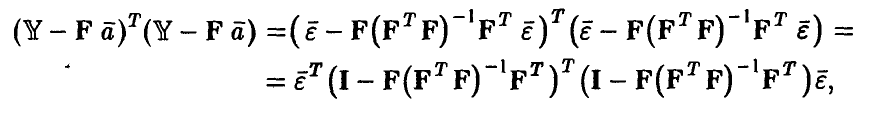
где I — единичная матрица формата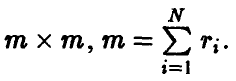

Далее

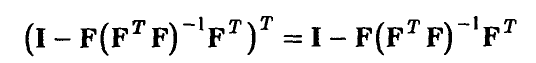
и

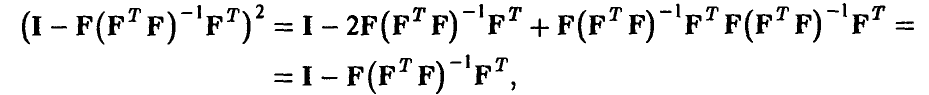
поэтому

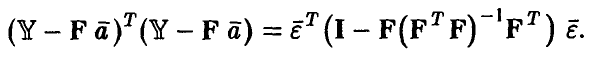
Вычисляя математическое ожидание обеих частей последнего соотношения и учитывая некоррелированность компонент вектора ошибок 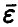, получим, что

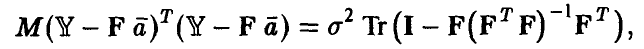
где Тr A — след матрицы А, обладающий следующими свойствами

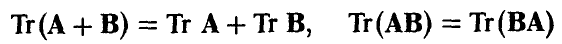
последнее — (для согласованных относительно умножения матриц).

Отсюда немедленно следует, что

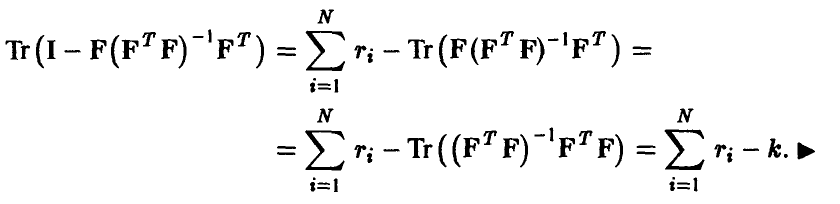
Если дополнительно вектор ошибок измерений считать нормальным с нулевым вектором средних и ковариационной матрицей , то, используя метод максимального правдоподобия, можно получить отличную от (13) оценку параметра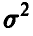

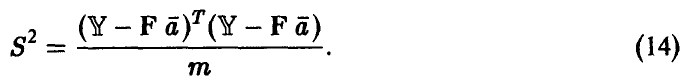
Оценка (14) свойством несмещенности обладать уже не будет, однако можно показать, что она несмещена асимптотически.

3.5. Адекватность модели

Пусть 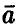— оценки коэффициентов регрессии (11), а зависимость переменной у от переменных 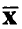х принимается в виде

Важный вопрос (о соответствии построенной нами модели (15) исследуемому процессу) — насколько удачно соотношение (15) позволяет прогнозировать значения переменной у по известным значениям переменных ?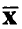

Мы не задаемся целью установить, является ли найденная нами зависимость «истинной» или «правильной» — исследование этого вопроса лежит вне плоскости наших рассмотрений, а мы просто хотим получить ответ на вопрос о том, насколько хорошо найденная нами зависимость заменяет реальный эксперимент.

Уточним постановку задачи. Будем называть остаточной ошибкой модели величину 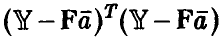, т. е. сумму квадратов отклонений наблюденных в эксперименте значений Y переменной у от прогнозируемых в этих же точках значений, полученных с помощью соотношения (15). Если через 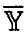обозначить вектор, составленный из средних значений измерений переменной у в точках 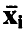, компоненты которого

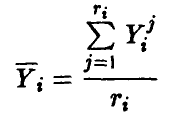
повторяются столько раз, какова кратность (т. е. количество ) измерений в і -й точке, то остаточная ошибка может быть представлена в виде

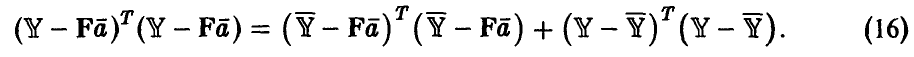
◄ Положим 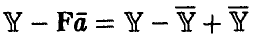рассмотрим

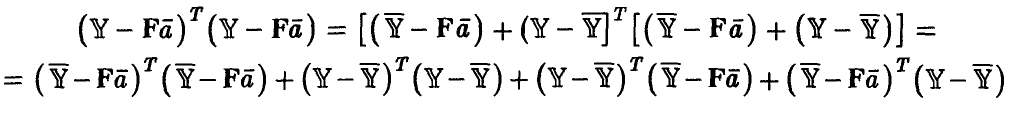
Легко убедиться в том, что два последних слагаемых равны нулю. Например,

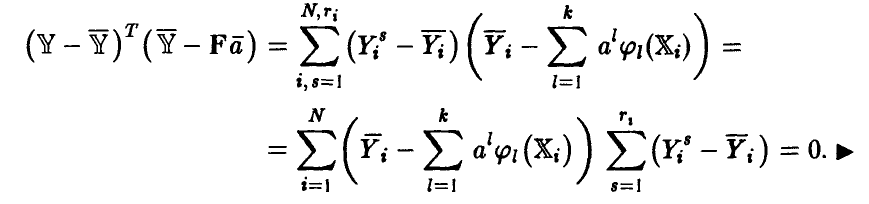
В полученном разложении остаточной ошибки модели первое слагаемое описывает отличие найденной нами зависимости от эмпирической регрессии, второе — рассеяние экспериментальных данных относительно эмпирической регрессии, т. е. ошибку эксперимента. Ясно, что модель тем лучше, чем меньше первое слагаемое и чем ближе остаточная ошибка модели ко второму слагаемому. Остаточная ошибка, описывает рассеяние экспериментальных данных относительно модели и не может быть меньше второго слагаемого — ошибки эксперимента. Чем меньше разница между остаточной ошибкой и рассеянием экспериментальных данных относительно эмпирической регрессии, тем лучше модель представляет наблюденные в эксперименте значения у.

Будем говорить что модель адекватно описывает результаты эксперимента, или просто, что модель адекватна, если в подавляющем большинстве случаев остаточная ошибка модели близка к ошибке эксперимента.

Статистические свойства слагаемых из соотношения (16) описываются следующей теоремой.

Теорема:

Пусть ошибки измерений совместно нормальны с нулевым вектором средних и ковариационной матрицей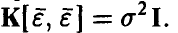

Тогда
— статистики 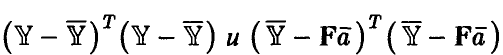независимы;
— статистика 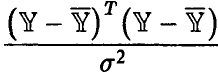имеет распределение 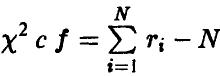степенями свободы, при этом величина

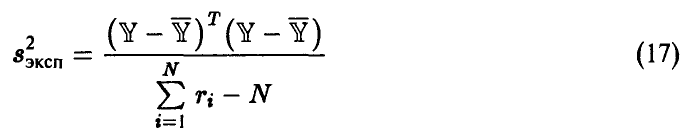
является несмещенной оценкой параметра .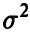

Если гипотеза об адекватности модели (15) справедлива, то дополнительно статистика

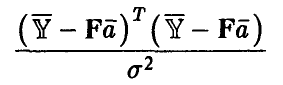
имеет 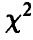-распределение с N — k степенями свободы.

Сформулированная теорема позволяет установить, что величина 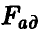, описываемая отношением

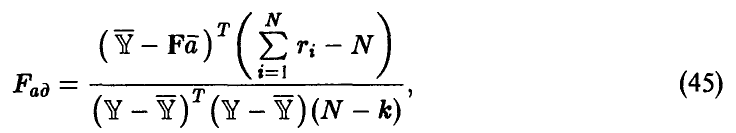
в случае справедливости гипотезы об адекватности имеет распределение Фишера с 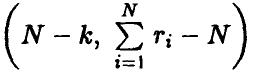степенями свободы.

Задавая уровень значимости х, определяем величину 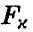так, что 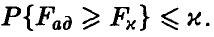. Если рассчитанная по результатам эксперимента величина (18) окажется меньше, чем 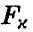, то гипотезу об адекватности следует признать согласующейся с опытными данными, так как в этом случае с надежностью, не худшей чем 1-х, остаточная ошибка модели ненамного превышает ошибку эксперимента. В противном случае гипотезу об адекватности следует признать плохо согласующейся с опытными данными, а в постулируемую модель внести изменения.

Точность и надежность оценивания коэффициентов регрессии

Для адекватных моделей представляет интерес вопрос о качестве оценок (11) коэффициентов регрессии: как велик может быть диапазон их надежного (для заданной степени надежности) варьирования? Поскольку оценки коэффициентов регрессии являются, вообще говоря, зависимыми случайными величинами, то желательно уметь получать информацию не только об индивидуальной, но и о совместной точности их оценивания.

Мы рассмотрим ниже процедуры определения точности оценивания коэффициентов регрессии как в предположении, что параметр 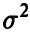известен точно, так и считая, что он оценен по результатам эксперимента.

1. Из результатов п. 3.2.3 следует, что вектор оценок 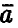нормален с вектором средних 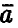и ковариационной матрицей 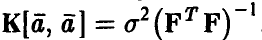. При точно известной величине 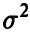этой информации достаточно для построения доверительных интервалов для каждого из коэффициентов регрессии в отдельности и для совместного определения точности их оценивания.

Индивидуальные доверительные интервалы

Каждая из компонент 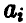, вектора а нормальна со средним 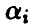и дисперсией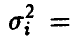 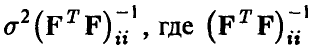— i-й диагональный элемент матрицы 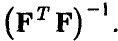Задавая уровень доверия х, легко находим (см. п. 1.3.1) доверительные границы для коэффициентов регрессии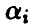

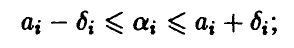
величины 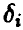определяются из условия 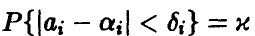и задаются равенством

где 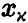— решение уравнения 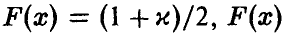— функция стандартного нормального с параметрами (0,1) распределения.

Совместные доверительные границы

Вообще говоря (если матрица 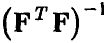не является диагональной), оценки коэффициентов регрессии зависимы.

Назовем главным эллипсоидом рассеяния случайного вектора 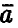относительно 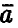эллипсоид 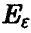, задаваемый неравенством

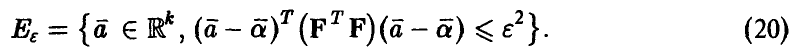
Величина є называется радиусом эллипсоида. Заметим, что уравнение

при заданной х однозначно разрешимо относительно .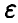

◄ В силу совместной нормальности компонент вектора 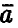, уравнение (21) имеет вид

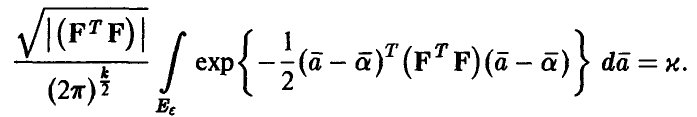
Сделаем в интеграле замену переменных, приводящую квадратичную форму, стоящую в показателе степени у экспоненты, к сумме квадратов. Последнее соотношение примет вид

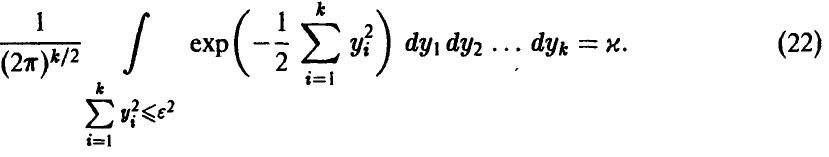
Переходя к сферическим координатам в и полагая

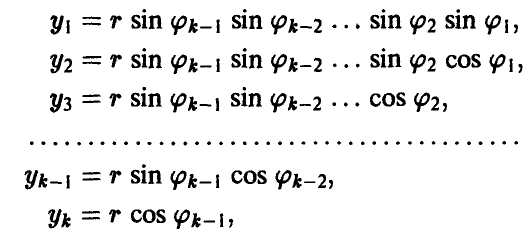
где 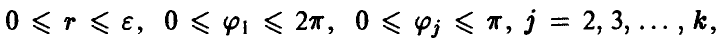из соотношения (22)
получим

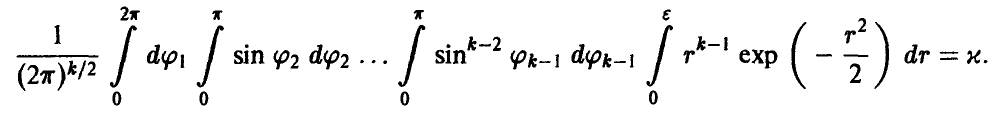
Учитывая, что

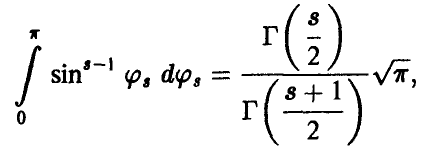
где Г(s) — гамма-функция Эйлера, для определения радиуса главного эллипсоида рассеяния 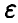получаем соотношение

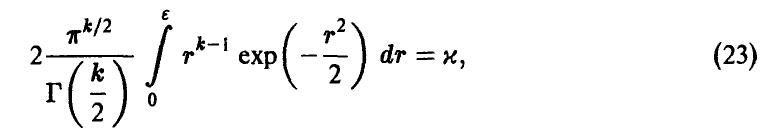
которое доказывает утверждение. ►

Если задать доверительную вероятность х (х близка к единице) и из уравнения (23) найти соответствующий ей радиус є, то совместное рассеяние оценок 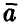коэффициентов регрессии будет описываться главным эллипсоидом .

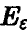2. Если величина параметра 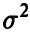неизвестна, то, заменив в полученных выше соотношениях для индивидуальных или совместных доверительных областей значение параметра 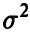какой-нибудь его оценкой, мы подучим приближенные индивидуальные или совместные доверительные области.

Построение точных доверительных областей в этом случае может быть осуществлено следующим образом.

Индивидуальные доверительные границы

Рассмотрим величины 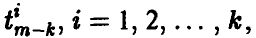определяемые отношением

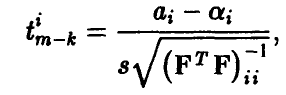
где s — оценка параметра 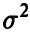, даваемая соотношением (13). Так же, как и в п. 1.3.1, можно установить, что каждая из этих величин имеет распределение Стьюдента с 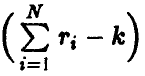степенями свободы. Отсюда для заданной доверительной вероятности х обычным образом получаем, что точность оценивания і-го коэффициента регрессии 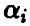описывается двойным неравенством

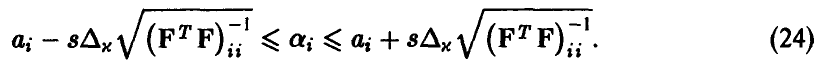
Величина 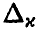находится по заданному значению х из условия

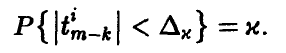
Совместные доверительные границы

Индивидуальные доверительные интервалы (24) не дают исчерпывающей информации о совместной оценке точности определения коэффициентов регрессии из-за возможной зависимости последних.

Для получения доверительной области в этом случае заметим, что в силу совместной нормальности компонент 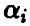вектора оценок 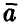величина

имеет распределение 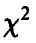с k степенями свободы. По теореме из предыдущего пункта величина

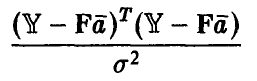
имеет распределение 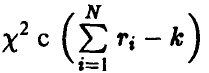степенями свободы и не зависит от величины, даваемой формулой (25).

Следовательно их отношение

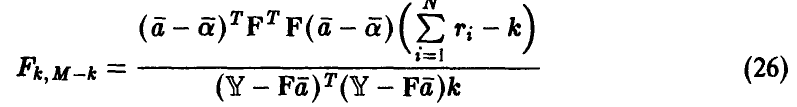
имеет распределение Фишера с 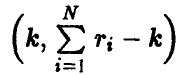степенями свободы. Зададим доверительную вероятность х и определим величину 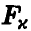так, что

Перепишем неравенство (27) с учетом (26)

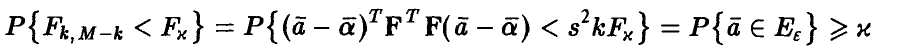
(здесь 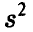— оценка (13) параметра 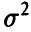). Искомой совместной доверительной областью для коэффициентов регрессии 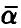будет главный эллипсоид рассеяния 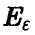радиуса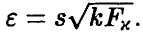

Прогнозирование результатов эксперимента. Точность и надежность прогноза

В предыдущих разделах мы показали, как по результатам эксперимента можно найти зависимость (1) между переменными 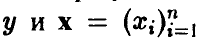, и описали эту зависимость соотношением (12)

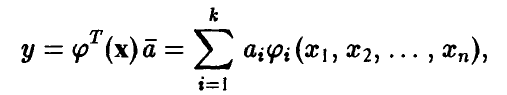
где 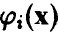— известные функции, а оценки 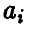— даются формулой (11)

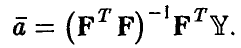
Эти формулы могут быть использованы теперь для прогнозирования результатов эксперимента. При этом, конечно, предполагается, что новые измерения подчиняются тем же закономерностям и структура взаимодействия переменных в новых экспериментах такая же, какой она была в экспериментах, послуживших источником информации для построения модели.

Пусть 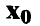— точка, в которой мы хотим спрогнозировать значение переменной 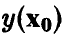. Отметим, что 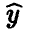— предсказываемое моделью (12) значение переменной у в точке ,

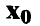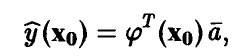
является несмещенной оценкой математического ожидания прогнозируемого измерения 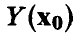. Дисперсия этой оценки легко находится

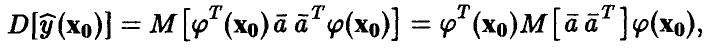
откуда, учитывая равенство 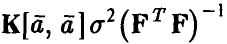, заключаем, что

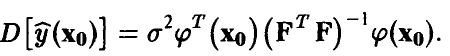
В соответствии с принятыми допущениями прогнозируемое измерение 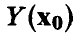складывается из значения 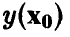и ошибки измерения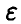

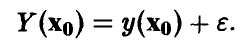
Разница между прогнозируемым значением и предсказанным с помощью модели (12) является нормальной случайной величиной с нулевым средним

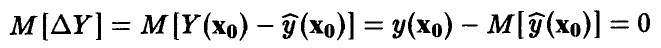
и дисперсией

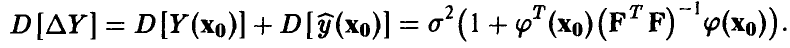
Отсюда, как и выше, заключаем, что отношение

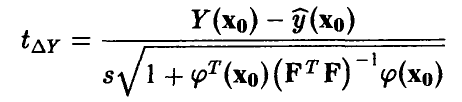
имеет распределение Стьюдента 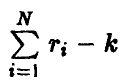степенями свободы. Это позволяет нам оценивать точность прогноза стандартным образом — задаем надежность х, близкую к единице, и находим значение 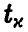такое, что 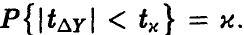С вероятностью,
не меньшей х, при этом выполняется соотношение

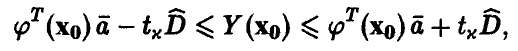
указывающее границы, в которых с надежностью, не худшей х, находится прогнозируемое значение 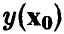переменной у.

Здесь 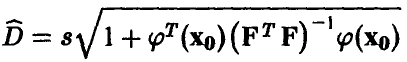— оценка дисперсии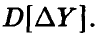

Заключение

Завершая обсуждение простейших задач статистического анализа экспериментальных данных отметим, что рассмотренные нами проблемы допускают широкое обобщение, как с точки зрения постановок, так и с точки зрения используемых методов исследования. Одним из важнейших обстоятельств, определяющих успех в постановке и решении статистических задач, является четкое осознание исследователем того, каким фактическим исходным материалом он обладает, какие цели он перед собой ставит и чего в конечном итоге хочет добиться. Постановка задачи определяет, как правило, не только аппарат, необходимый для ее решения, но, зачастую, и способы получения экспериментального материала.

Не менее существенной является и интерпретация результатов применения тех или иных статистических процедур.

Только компетентность исследователя и корректность статистика являются гарантией содержательной и безошибочной интерпретации. Сами по себе статистические процедуры не решают реальных прикладных проблем, однако правильно понятые и объясненные результаты их применения являются надежным ориентиром для прикладника.

Примеры решения задач

1. Случайные величины 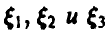независимы и нормальны с одинаковым средним, равным 2. Известно, что их дисперсии относятся соответственно как 3:4:2. Найти ковариационную матрицу этих случайных величин, если известно, что

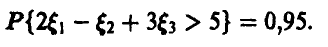
Решение:

Поскольку случайные величины 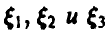— независимы, то они некоррели-рованы. Следовательно, искомая ковариационная матрица диагональна и ее диагональные элементы — дисперсии случайных величин 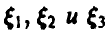соответственно:

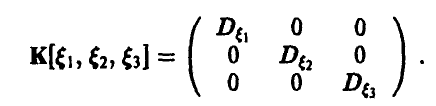
Далее, из независимости и нормальности заключаем, что любая линейная комбинация этих случайных величин — нормальная случайная величина. В частности

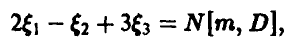
где

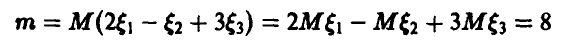
и

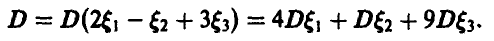
Пусть дисперсия случайной величины 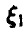равна 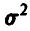. Тогда из условия задачи получим, что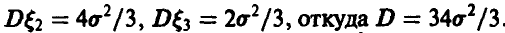

Для нахождения величины 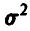используем последнее условие задачи

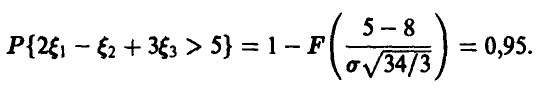
Отсюда

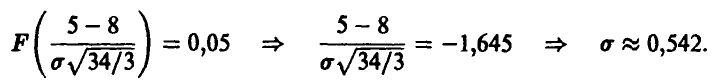
Искомая ковариационная матрица

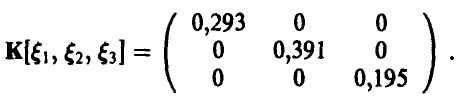
2. Пара случайных величин имеет совместное нормальное распределение с вектором математических ожиданий {-2,-1} и ковариационной матрицей К

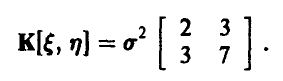
Известно, что 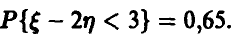Найти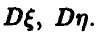

Решение:

Совместная нормальность пары случайных величин 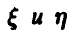обеспечивает нормальность каждой из них и любой их линейной комбинации, в частности величина 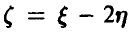нормальна с параметрами

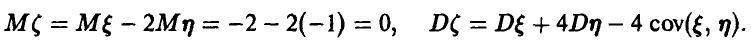
Подставляя в последнее соотношение элементы ковариационной матрицы:

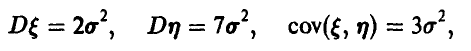
получим

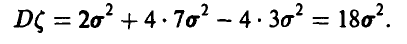
По условию 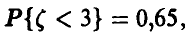, откуда, используя нормальность ,

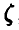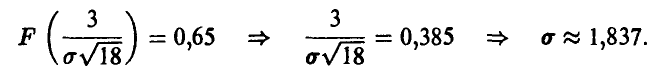
Искомые дисперсии равны, соответственно,

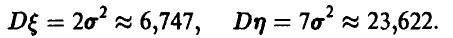
3. Найти ковариацию ординаты и абсциссы точки 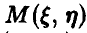, равномерно распределенной в квадрате К с вершинами 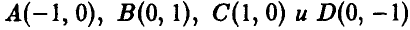Зависимы ли эти случайные величины?

Решение:

Пара 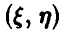равномерно распределена в квадрате, значит, ее плотность задается соотношением

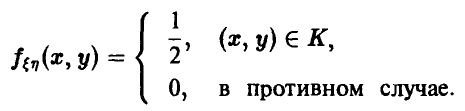
Для ковариации получаем

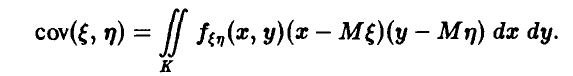
Поскольку

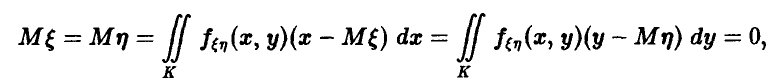
постольку

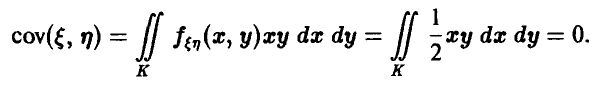
Тем не менее случайные величины зависимы, так как изменение значения одной из них вызывает изменение диапазона значений другой .

4. Двумерная случайная величина имеет вектор математических ожиданий {0, -1} и ковариационную матрицу

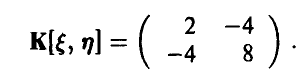
Достаточно ли этих данных, чтобы спрогнозировать значения компоненты 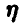при известных значениях компоненты ?

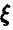Решение:

Заметим, что

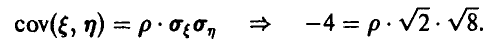
Отсюда 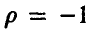, и это значит, что между случайными величинами 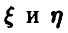имеется линейная функциональная зависимость, описываемая соотношением

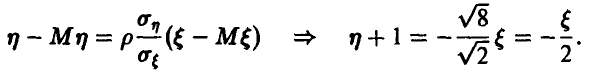
Следовательно, при известных значениях компоненты 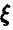значения компоненты 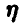могут быть спрогнозированы с вероятностью 1.

5. Случайные величины 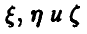связаны соотношением

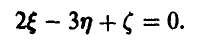
Известно, что 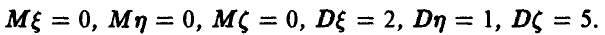Найти ковариационную матрицу этих случайных величин.

Решение:

Умножая данное в условии линейное соотношение последовательно на 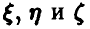и находя математические ожидания от обеих частей получающихся равенств, получим

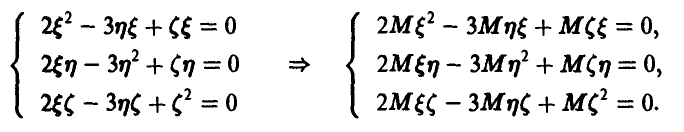
В силу равенства нулю математических ожиданий случайных величин, математические ожидания квадратов будут равны дисперсиям, а математические ожидания произведений — ковариациям. Для элементов ковариационной матрицы приходим к системе

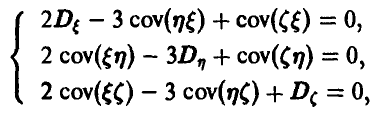
или, подставляя известные дисперсии рассматриваемых случайных величин

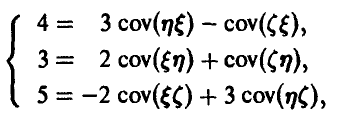
Решая эту систему, получим искомую ковариационную матрицу

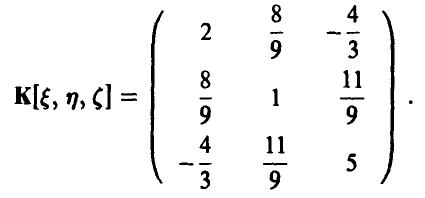
Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Теории игр
9. Вероятность события
10. Теорема умножения вероятностей
11. Формула полной вероятности
12. Теорема о повторении опытов
13. Нормальный закон распределения
14. Определение законов распределения случайных величин на основе опытных данных
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность