Определение законов распределения случайных величин на основе опытных данных

Математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономерностей, фактически существующих в массовых случайных явлениях природы.

До сих пор, говоря о законах распределения случайных величин, мы не затрагивали вопроса о том, откуда берутся, на каком основании устанавливаются эти законы распределения. Ответ на вопрос вполне определенен — в основе всех этих характеристик лежит опыт; каждое исследование случайных явлений, выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные. Оперируя такими понятиями, как события и их вероятности, случайные величины, их законы распределения и числовые характеристики, теория вероятностей дает возможность теоретическим путем определять вероятности одних событий через вероятности других, законы распределения и числовые характеристики одних случайных величин через законы распределения и числовые характеристики других. Такие косвенные методы позволяют значительно экономить время и средства, затрачиваемые на эксперимент, но отнюдь не исключают самого эксперимента. Каждое исследование в области случайных явлений, как бы отвлеченно оно ни было, корнями своими всегда уходит в эксперимент, в опытные данные, в систему наблюдений. Разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специальной науки — математической статистики.

Все задачи математической статистики касаются вопросов обработки наблюдений над массовыми случайными явлениями, но в зависимости от характера решаемого практического вопроса и от объема имеющегося экспериментального материала эти задачи могут принимать ту или иную форму.

Типичные задачи математической статистики

Охарактеризуем вкратце некоторые типичные задачи математической статистики, часто встречаемые на практике.

Задача определения закона распределения случайной величины (или системы случайных величин) по статистическим данным

Мы уже указывали, что закономерности, наблюдаемые в массовых случайных явлениях, проявляются тем точнее и отчетливее, чем больше объем статистического материала. При обработке обширных по своему объему статистических данных часто возникает вопрос об определении законов распределения тех или иных случайных величин. Теоретически при достаточном количестве опытов свойственные этим случайным величинам закономерности будут осуществляться сколь угодно точно. На практике нам всегда приходится иметь дело с ограниченным количеством экспериментальных данных; в связи с этим результаты наших наблюдений и их обработки всегда содержат больший или меньший элемент случайности. Возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, устойчивым и действительно присущи ему, а какие являются случайными и про- проявляются в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. Естественно, к методике обработки экспериментальных данных следует предъявить такие требования, чтобы она, по возможности, сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного материала. В связи с этим возникаем характерная для математической статистики задача сглаживания или выравнивания статистических данных, представления их в наиболее компактном вида с помощью простых аналитических зависимостей.

Задача проверки правдоподобия гипотез

Эта задача тесно связана с предыдущей; при решении такого рода задач мы обычно не располагаем настолько обширным статистическим материалом, чтобы выявляющиеся в нем статистические закономерности были в достаточной мере свободны от элементов случайности. Статистический материал может с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы. Например, может возникнуть такой вопрос: согласуются ли результаты эксперимента с гипотезой о том, что данная случайная величина подчинена закону распределения F (х)? Другой подобный вопрос: указывает ли наблюденная в опыте тенденция к зависимости между двумя случайными величинами на наличие действительной объективной зависимости между ними или же она объясняется случайными причинами, связанными с недостаточным объемом наблюдений? Для решения подобных вопросов математическая статистика выработала ряд специальных приемов.

Задача нахождения неизвестных параметров распределения

Часто при обработке статистического материала вовсе не возникает вопрос об определении законов распределения исследуемых случайных величин. Обыкновенно это бывает связано с крайне недостаточным объемом экспериментального материала. Иногда же характер закона распределения качественно известен до опыта, из теоретических соображений; например, часто можно утверждать заранее, что случайная величина подчинена нормальному закону. Тогда возникает более узкая задача обработки наблюдений — определить только некоторые параметры (числовые характеристики) случайной величины или системы случайных величин. При небольшом числе опытов задача более или менее точного определения этих параметров не может быть решена; в этих случаях экспериментальный материал содержит в себе неизбежно значительный элемент случайности; поэтому случайными оказываются и все параметры, вычисленные на основе этих данных. В таких условиях может быть поставлена только задача об определении так называемых «оценок» или «подходящих значений» для искомых параметров, т. е. таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие. С задачей отыскания «подходящих значений» числовых характеристик тесно связана задача оценки их точности и надежности. С подобными задачами мы встретимся в главе 14.

Таков далеко не полный перечень основных задач математической статистики. Мы перечислили только те из них, которые наиболее важны для нас по своим практическим применениям. В настоящей главе мы вкратце познакомимся с некоторыми, наиболее элементарными задачами математической статистики и с методами их решения.

Простая статистическая совокупность. Статистическая функция распределения

Предположим, что изучается некоторая случайная величина X, закон распределения которой в точности неизвестен, и требуется определить этот .закон из опыта или проверить экспериментально гипотезу о том, что величина X подчинена тому или иному закону. с этой целью над случайной величиной X производятся ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина X принимает определенное значение. Совокупность наблюденных значений величины и представляет собой первичный статистический материал, подлежащий обработке, осмыслению и научному анализу. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». Обычно простая статистическая совокупность оформляется в виде таблицы с одним входом, в первом столбце которой стоит номер опыта i, а во втором — наблюденное значение случайной величины.

Пример:

Случайная величина 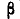— угол скольжения самолета в момент сбрасывания бомбы 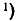. Произведено 20 бомбометаний, в каждом из которых зарегистрирован угол скольжения 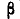в тысячных долях радиана. Результаты наблюдений сведены в простой статистический ряд:

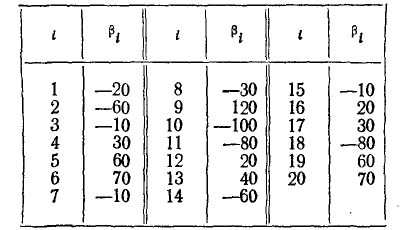
Простой статистический ряд представляет собой первичную форму записи статистического материала и может быть обработан различными способами. Одним из способов такой обработки является построение статистической функции распределения случайной величины.

Статистической функцией распределения случайной величины X называется частота события X < х в данном статистическом материале:

F* (х) = Р* (X < х). (7.2.1)

Для того чтобы найти значение статистической функции распре- распределения при данном х, достаточно подсчитать число опытов, в которых величина X приняла значение, меньшее чем х, и разделить на общее число n произведенных опытов.

Пример:

Построить статистическую функцию распределения для случайной величины 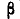, рассмотренной в предыдущем примере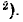

Под углом скольжения подразумевается угол, составленный вектором скорости и плоскостью симметрии самолета.

Здесь и во многих случаях далее, при рассмотрении конкретных практических примеров, мы не будем строго придерживаться правила — обозначать случайные величины большими буквами, а их возможные значения — соответствующими малыми буквами. Если это не может привести к недоразумениям, мы в ряде случаев будем обозначать случайную величину и ее возможное значение одной и той же буквой.

Решение:

Так как наименьшее наблюденное значение величины равно -100, то F(—100) = 0. Значение —100 наблюдено один раз, его частота равна 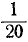следовательно, в точке —100 F* (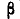) имеет скачок, равный 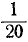. В промежутке от—100 до —80 функция F*(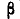) имеет значение 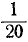; в точке 2 —80 происходит скачок функции F *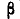) на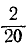 , так как значение —80 наблюдено дважды, и т. д.

График статистической функции распределения величины представлен на рис. 7.2.1.

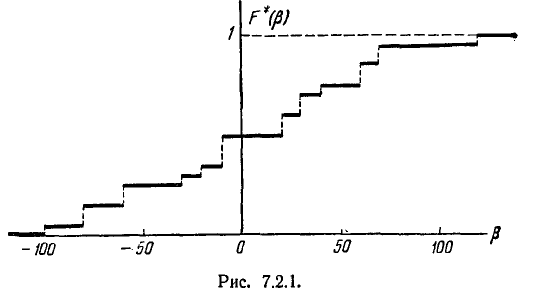
Статистическая функция распределения любой случайной вели- величины— прерывной или непрерывной — представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений. Если каждое отдельное значение случайной величины X было наблюдено только один раз, скачок статистической функции распределения в каждом наблюденном значении равен —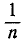, где n— число наблюдений.

При увеличении числа опытов n , согласно теореме Бернулли, при любом х частота события X < х приближается (сходится по вероятности) к вероятности этого события. Следовательно, при увеличении n статистическая функция распределения F * (х) приближается (сходится по вероятности) к подлинной функции распределения F*(x) случайной величины X.

Если X — непрерывная случайная rpличина, то при увеличении числа наблюдений п число скачков функции F* (х) увеличивается, самые скачки уменьшаются и график функции F* (х) неограниченно приближается к плавной кривой F*(x) — функции распределения величины X.

В принципе построение статистической функции распределения уже решает задачу описания экспериментального материала. Однако при большом числе опытов п построение F* (х) описанным выше способом весьма трудоемко. Кроме того, часто бывает удобно — в смысле наглядности — пользоваться другими характеристиками статистических распределений, аналогичными не функции распределения F*(x), а плотности f(х). С такими способами описания статистических данных мы познакомимся в следующем параграфе.

Статистический ряд. Гистограмма

При большом числе наблюдений (порядка сотен) простая статистическая совокупность перестает быть удобной формой записи статистического материала — она становится слишком громоздкой и мало наглядной. Для придания ему большей компактности и наглядности статистический материал должен быть подвергнут до- дополнительной обработке — строится так называемый «статистический ряд».

Предположим, что в нашем распоряжении результаты наблюдений над непрерывной случайной величиной X, оформленные в виде про- простой статистической совокупности. Разделим весь диапазон наблюденных значений X на интервалы или «разряды» и подсчитаем количество значений 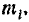приходящееся на каждый i-й разряд. Это число разделим на общее число наблюдений п и найдем частоту, соответствующую данному разряду:

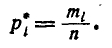(7.3.1)

Сумма частот всех разрядов, очевидно, должна быть равна единице.

Построим таблицу, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты. Эта таблица называется статистическим рядом:

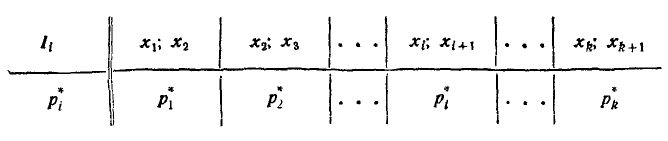
Здесь 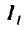— обозначение i-го разряда; 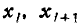— его границы; 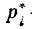соответствующая частота; k — число разрядов.

Пример:

Произведено 500 измерений боковой ошибки наводки при стрельбе с самолета по наземной цели. Результаты измерений (в тысячных долях радиана) сведены в статистический ряд:

Здесь 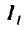обозначены интервалы значений ошибки наводки; 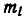—число наблюдений в данном интервале, 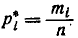— соответствующие частоты.

При группировке наблюденных значений случайной величины по разрядам возникает вопрос о том, к какому разряду отнести значение, находящееся в точности на границе двух разрядов. В этих случаях можно рекомендовать (чисто условно) считать данное значение принадлежащим в равной мере к обоим разрядам и прибавлять к числам 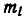того и другого разряда по .

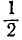Число разрядов, на которые следует группировать статистический материал, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Практика показывает, что в большинстве случаев рационально выбирать число разрядов порядка 10 — 20. Чем богаче и однороднее статистический материал, тем большее число разрядов можно выбирать при составлении статистического ряда. Длины разрядов могут быть как одинаковыми, так и различными. Проще, разумеется, брать их одинаковыми. Однако при оформлении данных о случайных величинах, распределенных крайне неравномерно, иногда бывает удобно выбирать в области наибольшей плотности распределения разряды более узкие, чем в области малой плотности.

Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из раз- разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь ее равна единице.

В качестве примера можно привести гистограмму для ошибки наводки, построенную по данным статистического ряда, рассмотрен- рассмотренного в примере 1 (рис. 7.3.1).

Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь,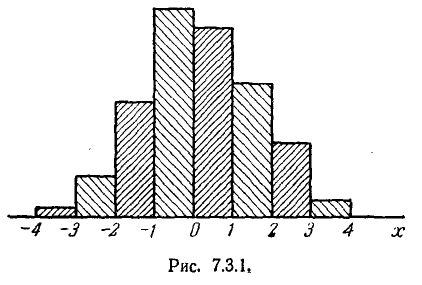

равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины X.

Пользуясь данными статистического ряда, можно приближенно построить и статистическую функцию распределения величины X. Построение точной статистической функции распределения с несколькими сотнями скачков во всех наблюденных значениях X слишком трудоемко и себя не оправдывает. Для практики обычно достаточно построить статистическую функцию распределения по нескольким точкам. В качестве этих точек удобно взять границы 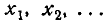разрядов, которые фигурируют в статистическом ряде. Тогда, очевидно,

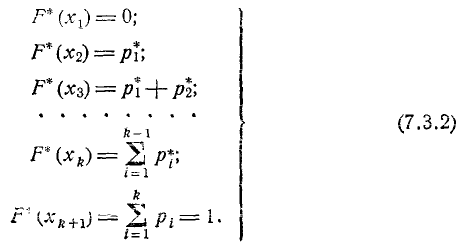
Соединяя полученные точки ломаной линией или плавной кривой, получим приближенный график статистической функции распределения.

Пример:

Построить приближенно статистическую функцию распределения ошибки наводки по данным статистического ряда примера 1.

Решение:

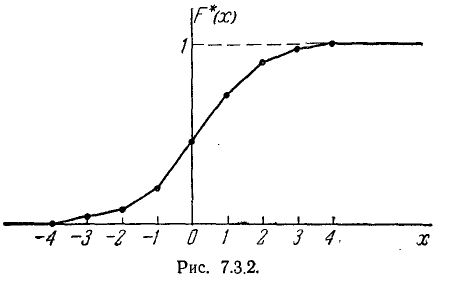
Применяя формулы (7.3.2), имеем

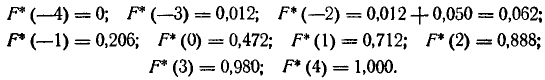
Приближенный график статистической функции распределения дан на рис. 7.3.2.

Числовые характеристики статистического распределения

Мы ввели в рассмотрение различные числовые характеристики случайных величин: математическое ожидание, дисперсию, начальные и центральные моменты различных порядков. Эти числовые характеристики играют большую роль в теории вероятностей. Аналогичные числовые характеристики существуют и для статистических распределений. Каждой числовой характеристике случайной величины Х соответствует ее статистическая аналогия. Для основной характеристики положения — математического ожидания случайной величины—такой аналогией является среднее арифметическое наблюденных значений случайной величины:

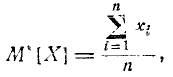(7.4.1)

где 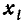значение случайной величины, наблюдаемое в i — м опыте, п — число опытов.

Эту характеристику мы будем в дальнейшем называть статистическим средним случайной величины.

Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При достаточно большом п статистическое среднее может быть принято приближенно равным математическому ожиданию. При ограниченном числе опытов с статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.

Подобные статистические аналогии существуют для всех числовых характеристик. Условимся в дальнейшем эти статистические аналогии обозначать теми же буквами, что и соответствующие числовые характеристики, но снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она представляет собой математическое ожидание случайной величины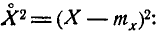

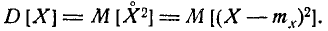(7.4.2)

Если в этом выражении заменить математическое ожидание его статистической аналогией — средним арифметическим, мы получим статистическую дисперсию случайной величины X: 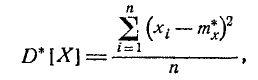(7.4.3)

где 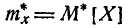— статистическое среднее.

Аналогично определяются статистические начальные и централь- центральные моменты любых порядков:

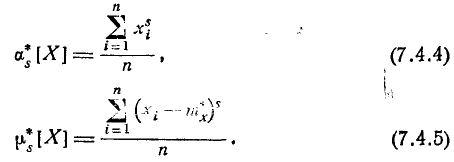
Все эти определения полностью аналогичны данным в главе 5 определениям числовых характеристик случайной величины, с той разницей, что в них везде вместо математического ожидания фигу- фигурирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном п могут быть приняты приближенно равными им.

Нетрудно доказать, что для статистических начальных и центральных моментов справедливы те же свойства, которые были выведены в главе 5 для математических моментов. В частности, статистический первый центральный момент всегда равен нулю: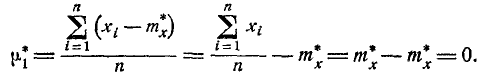

Соотношения между центральными и начальными моментами также сохраняются:

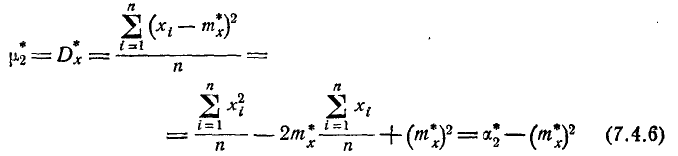
и т. д. При очень большом количестве опытов вычисление характеристик по формулам (7.4.1) — (7.4.5) становится чрезмерно громоздким, и можно применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характеристики будут выражаться приближенными формулами:

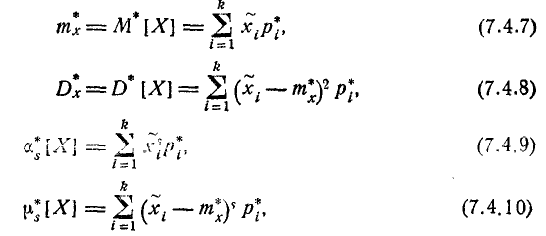
где 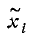— «представитель» i-го разряда, 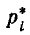— частота i-го разряда, k — число разрядов.

Как видно, формулы (7.4.7) — (7.4.10) полностью аналогичны формулам п° п° 5.6 и 5.7, определяющим математическое ожидание, дисперсию, начальные и центральные моменты прерывной случайной величины Х с той только разницей, что вместо вероятностей 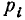в них стоят частоты 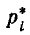вместо математического ожидания 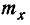статистическое среднее 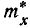, вместо числа возможных значений случайной величины — число разрядов.

В большинстве руководств по теории вероятностей и математической статистике при рассмотрении вопроса о статистических аналогиях для характеристик случайных величин применяется терминология, несколько отличная от принятой в настоящей книге, а именно, статистическое среднее именуется «выборочным средним», статистическая дисперсия—«выборочной дисперсией» и т. д. Происхождение этих терминов следующее. В статистике, особенно сельскохозяйственной и биологической, часто приходится исследовать распределение того или иного признака для весьма большой совокупности индивидуумов, образующих статистический коллектив (таким признаком может быть, например, содержание белка в зерне пшеницы, вес того же зерна, длина или вес тела какого-либо из группы животных и т. д.). Данный признак является случайной величиной, значение которой от индивидуума к индивидууму меняется. Однако, для того, чтобы составить представление о распределении этой случайной величины или о ее важнейших характеристиках, нет необходимости обследовать каждый индивидуум данной обширной совокупности; можно обследовать некоторую выборку достаточно большого объема для того, чтобы в ней были выявлены существенные черты изучаемого распределения. Та обширная совокупность, из которой производится выборка, носит в статистике название генеральной совокупности. При этом предполагается, что число членов (индивидуумов) N в генеральной совокупности весьма велико, а число членов п в выборке ограничено. При достаточно большом N оказывается, что свойства выборочных (статистических) распределений и характеристик практически не зависят от N; отсюда естественно вытекает математическая идеализация, состоящая в том, что генеральная совокупность, из которой осуществляется выбор, имеет бесконечный объем. При этом отличают точные характеристики (закон распределения, математическое ожидание, дисперсию и т. д.), относящиеся к генеральной совокупности, от аналогичных им «выборочных» характеристик. Выборочные характеристики отличаются от соответствующих характеристик генеральной совокупности за счет ограниченности объема выборки п; при неограниченном увеличении п, естественно, все выборочные характеристики приближаются (сходятся по вероятности) к соответствующим характеристикам генеральной совокупности. Часто возникает вопрос о том, каков должен быть объем выборки п для того, чтобы по выборочным характеристикам можно было с достаточной точностью судить о неизвестных характеристиках генеральной совокупности или о том, с какой степенью точности при заданном объеме выборки можно судить о характеристиках генеральной совокупности. Такой методический прием, состоящий в параллельном рассмотрении бесконечной генеральной совокупности, из которой осуществляется выбор, и ограниченной по объему выборки, является совершенно естественным в тех областях статистики, где фактически приходится осуществлять выбор из весьма многочисленных совокупностей индивидуумов. Для практических, задач, связанных с вопросами стрельбы и вооружения, гораздо более характерно другое положение, когда над исследуемой случайной величиной (или системой случайных величин) производится ограниченное число опытов с целью определить те или иные характеристики этой величины, например, когда с целью исследования закона рассеивания при стрельбе производится некоторое количество выстрелов, или с целью исследования ошибки наводки производится серия опытов, в каждом из которых ошибка наводки регистрируется с помощью фотопулемета, и т. д. При этом ограниченное число опытов связано не с трудностью регистрации и обработки, а со сложностью и дороговизной каждого отдельного опыта. В этом случае с известной натяжкой можно также произведенные п опытов мысленно рассматривать как «выборку» из некоторой чисто условной «генеральной совокупности», состоящей из бесконечного числа возможных или мыслимых опытов, которые можно было бы произвести в данных условиях. Однако искусственное введение такой гипотетической «генеральной совокупности» при данной постановке вопроса не вызвано необходимостью и вносит в рассмотрение вопроса, по существу, излишний элемент идеализации, не вытекающий из непосредственной реальности задачи.

Поэтому мы в данном курсе не пользуемся терминами «выборочное среднее», «выборочная дисперсия», «выборочные характеристики» и т. д., заменяя их терминами «статистическое среднее», «статистическая дисперсия», «статистические характеристики».

Выравнивание статистических рядов

Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем, что число наблюдений ограничено, что произведены именно те, а не другие опыты, давшие именно те, а не другие результаты. Только при очень большом числа наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает в полной мере присущую ему закономерность. На практике мы почти никогда не имеем дела с таким большим числом наблюдений и вынуждены считаться с тем, что любому статистическому распределению свойственны в большей или меньшей, мере черты случайности. Поэтому при обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

Задача выравнивания заключается в том, чтобы подобрать теоретическую плавную кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое распределение (рис. 7.5.1).

Задача о наилучшем выравнивании статистических рядов, как и вообще задача о наилучшем аналитическом представлении эмпирических функций, есть задача в значительной мере неопределенная, и решение ее зависит от того, чтоб условиться считать «наилучшим». Например, при сглаживании эмпирических зависимостей очень часто исходят из так называемого принципа или метода наименьших квадратов (см. п° 14.5), считая, что наилучшим приближением к эмпирической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из соображений, связанных с физикой решаемой задачи, с учетом характера полученной эмпирической кривой и степени точности произведенных наблюдений. Часто принципиальный характер функции, выражающей исследуемую зависимость, известен заранее из теоретических соображений, из опыта же требуется получить лишь некоторые численные параметры, входящие в выражение функции; именно эти параметры подбираются с помощью метода наименьших квадратов.

Аналогично обстоит дело и с задачей выравнивания статистических рядов. Как правило, принципиальный вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи,

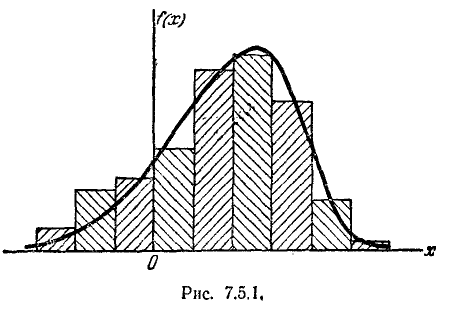
а в некоторых случаях просто с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров; задача выравнивания статистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим.

Предположим, например, что исследуемая величина X есть ошибка измерения, возникающая в результате суммирования воздействий множества независимых элементарных ошибок; тогда из теоретических соображений можно считать, что величина X подчиняется нормальному закону:

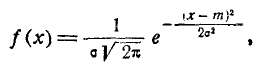(7.5.1)

и задача выравнивания переходит в задачу о рациональном выборе параметров m и в выражении 7.5.1).

Бывают случаи, когда заранее известно, что величина X распределяется статистически приблизительно равномерно на некотором интервале; тогда можно поставить задачу о рациональном выборе параметров того закона равномерной плотности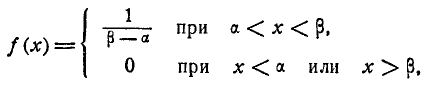

которым можно наилучшим образом заменить (выровнять) заданное статистическое распределение.

Следует при этом иметь в виду, что любая аналитическая функция f (х), с помощью которой выравнивается статистическое распределение, должна обладать основными свойствами плотности распределения:

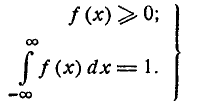(7.5.2)

Предположим, что, исходя из тех или иных соображений, нами выбрана функция f(x), удовлетворяющая условиям (7.5.2), с помощью которой мы хотим выровнять данное статистическое распределение; в выражение этой функции входит несколько параметров а, Ь, …; требуется подобрать эти параметры так, чтобы функция f(x) наилучшим образом описывала данный статистический материал. Один из методов, применяемых для решения этой задачи, — это так называемый метод моментов.

Согласно методу моментов, параметры а, b, … выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны соответствующим статистическим характеристикам. Например, если теоретическая кривая f (х) зависит только от двух параметров а и b, эти параметры выбираются так, чтобы математическое ожидание 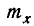и дисперсия 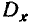теоретического распределения совпадали с соответствующими статистическими характеристикам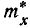и и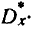 Если кривая f (х) зависит от трех параметров, можно подобрать их так, чтобы совпали первые три момента, и т. д. При выравнивании статистических рядов может оказаться полезной специально разработанная система кривых Пирсона, каждая из которых зависит в общем случае от четырех параметров. При выравнивании эти параметры выбираются с тем расчетом, чтобы сохранить первые четыре момента статистического распределения (математическое ожидание, дисперсию, третий и четвертый моменты).

Оригинальный набор кривых распределения, построенных по иному принципу, дал Н. А. Бородачев. 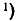Принцип, на котором строится система кривых Н. А. Бородачева, заключается в том, что выбор типа теоретической кривой основывается не на внешних формальных признаках, а на анализе физической сущности случайного явления или процесса, приводящего к тому или иному закону распределения.

Следует заметить, что при выравнивании статистических рядов нерационально пользоваться моментами порядка выше четвертого, так как точность вычисления моментов резко падает с увеличением их порядка.

Пример:

В п° 7.3 (стр. 137) приведено статистическое распределение боковой ошибки наводки X при стрельбе с самолета по наземной цели. Требуется выровнять это распределение с помощью нормального закона:

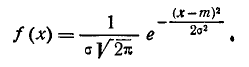
Решение:

Нормальный закон зависит от двух параметров: m и . Подберем эти параметры так, чтобы сохранить первые два момента—математическое ожидание и дисперсию — статистического распределения.

Вычислим приближенно статистическое среднее ошибки наводки по формуле (7.4.7), причем за представителя каждого разряда примем его середину:

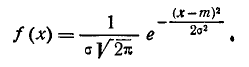
Для определения дисперсии вычислим сначала второй начальный момент по формуле (7.4.9), полагая s = 2, k = 8

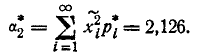
Пользуясь выражением дисперсии через второй начальный момент (формула (7.4.6)), получим:

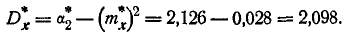
Выберем параметры m и нормального закона так, чтобы выполнялись условия:

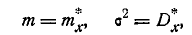
то есть примем:

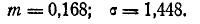
Напишем выражение нормального закона:

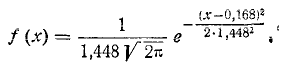
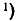Н. А. Бородачев, Основные вопросы теории точности производства, АН СССР, М. —Л., 1950.

Пользуясь в табл. 3 приложения, вычислим значения f(x) на границах разрядов

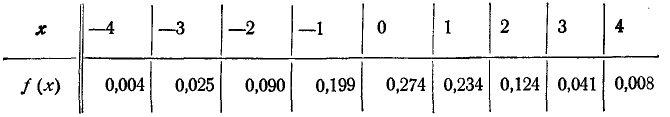
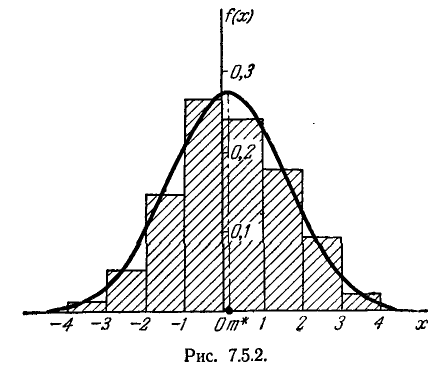
Построим на одном графике (рис. 7.5.2) гистограмму и выравнивающую ее кривую распределения.

Из графика видно, что теоретическая кривая распределения f (х), сохраняя, в основном существенные особенности статистического распределения, свободна от случайных неправильностей хода гистограммы, которые, по-видимому, могут быть отнесены за счет случайных причин; более серьезное обоснование последнему суждению будет дано в следующем параграфе.

Примечание:

В данном примере при определении 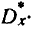мы воспользовались выражением (7.4.6) статистической дисперсии через второй начальный момент. Этот прием можно рекомендовать только в случае, когда математическое ожидание 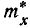исследуемой случайной величины X сравнительно невелико; в противном случае формула (7.4.6) выражает дисперсию 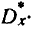как разность близких чисел и дает весьма малую точность. В случае, когда это имеет место, ре- рекомендуется либо вычислять 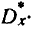непосредственно по формуле (7.4.3), либо перенести начало координат в какую-либо точку, близкую к 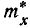, и затем применить формулу G.4.6). Пользование формулой (7.4.3) равносильно перенесению начала координат в точку 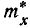; это может оказаться неудобным, так как выражение 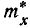может быть дробным, и вычитание 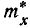из каждого 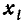при этом излишне осложняет вычисления; поэтому рекомендуется переносить начало координат в какое-либо круглое значение х, близкое к .

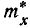Пример:

С целью исследования закона распределения ошибки измерения дальности с помощью радиодальномера произведено 400 измерений дальности. Результаты опытов представлены в виде статистического ряда:

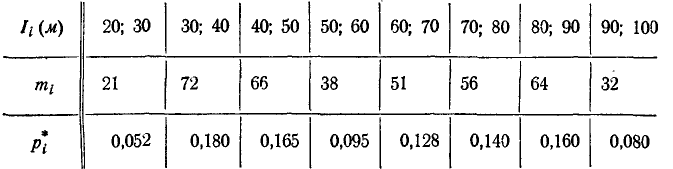
Выровнять статистический ряд с помощью закона равномерной плотности.

Решение:

Закон равномерной плотности выражается формулой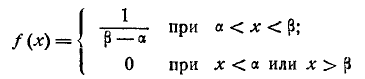

зависит от двух параметров а и 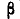. Эти параметры следует выбрать так, Чтобы сохранить первые два момента статистического распределения — математическое ожидание 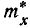и дисперсию 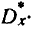. Из примера п°5.8 имеем выражения математического ожидания и дисперсии для закона равномерной плотности:

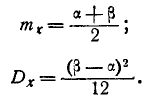
Для того чтобы упростить вычисления, связанные с определением статистических моментов, перенесем начало отсчета в точку 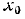= 60 и примем за представителя каждого разряда его середину. Ряд распределения примет вид:

где 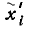— среднее для разряда значение ошибки радиодальномера 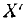при новом начале отсчета.

Приближенное значение статистического среднего ошибки 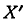равно: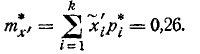

Второй статистический момент величины 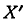равен: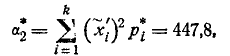

откуда статистическая дисперсия:

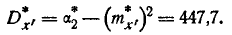
Переходя к прежнему началу отсчета, получим новое статистическое среднее:

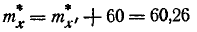
и ту же статистическую дисперсию:

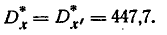
Параметры закона равномерной плотности определяются уравнениями:

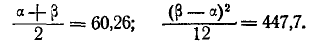
Решая эти уравнения относительно а и 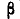,имеем:

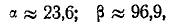
откуда

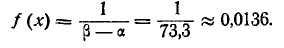
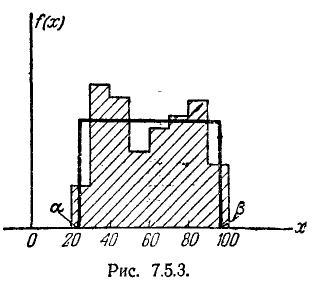
На рис. 7.5.3. показаны гистограмма и выравнивающий ее закон равномерной плотности f (х).

Критерии согласия

В настоящем п° мы рассмотрим один из вопросов, связанных с проверкой правдоподобия гипотез, а именно—вопрос о согласованности теоретического и статистического распределения.

Допустим, что данное статистическое распределение выравнено с помощью некоторой теоретической кривой f (х) (рис. 7.6.1). Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Естественно возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат так называемые «критерии согласия».

Идея применения критериев согласия заключается в следующем.

На основании данного статистического материала нам предстоит проверить гипотезу Н, состоящую в том, что случайная величина X подчиняется некоторому определённому закону распределения. Этот закон может быть задан в той или иной форме: например, в виде функции распределения F(x) или в виде плотности распределения f(x), или же в виде совокупности вероятностей 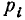, где 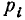— вероятность того, что величина X попадёт в пределы i-го разряда.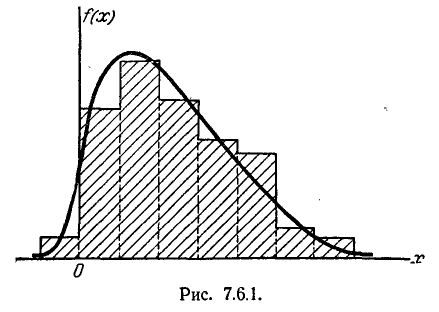

Так как из этих форм функция распределения F (х) является наиболее общей и определяет собой любую другую, будем формулировать гипотезу Н, как состоящую в том, что величина X имеет функцию распределения F (х).

Для того чтобы принять или опровергнуть гипотезу Н, рассмотрим некоторую величину U, характеризующую степень расхождения теоретического и статистического распределений. Величина U может быть выбрана различными способами; например, в качестве U можно взять сумму квадратов отклонений теоретических вероятностей 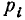от соответствующих частот 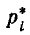или же сумму тех же квадратов с некоторыми коэффициентами («весами»), или же максимальное отклонение статистической функции распределения F*(x) от теоретической F(x) и т. д. Допустим, что величина U выбрана тем или иным способом. Очевидно, это есть некоторая случайная величина. Закон распределения этой случайной величины зависит от закона распределения случайной величины X, над которой производились опыты, и от числа опытов n. Если гипотеза Н верна, то закон распределения величины U определяется законом распределения величины X (функцией F(х)) и числом n.

Допустим, что этот закон распределения нам известен. В результате данной серии опытов обнаружено, что выбранная нами мера

расхождения U приняла некоторое значение а. Спрашивается, можно ли объяснить это случайными причинами или же это расхождение слишком велико и указывает на наличие существенной разницы между теоретическим и статистическим распределениями и, следовательно, на непригодность гипотезы Н? Для ответа на этот вопрос предположим, что гипотеза Н верна, и вычислим в этом предположении вероятность того, что за счет случайных причин, связанных с недостаточным объемом опытного материала, мера расхождения U окажется не меньше, чем наблюденное нами в опыте значение u, т. е. вычислим вероятность события:

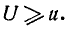
Если эта вероятность весьма мала, то гипотезу Н следует отвергнуть как мало правдоподобную; если же эта вероятность значительна, следует признать, что экспериментальные данные не противоречат гипотезе Н.

Возникает вопрос о том, каким же способом следует выбирать меру расхождения U ? Оказывается, что при некоторых способах ее выбора закон распределения величины U обладает весьма простыми свойствами и при достаточно большом n практически не зависит от функции F(x). Именно такими мерами расхождения и пользуются в математической статистике в качестве критериев согласия.

Рассмотрим один из наиболее часто применяемых критериев согласия— так называемый «критерий » Пирсона.

Предположим, что произведено n независимых опытов, в каждом из которых случайная величина X приняла определённое значение. Результаты опытов сведены в k разрядов и оформлены в виде статистического ряда:

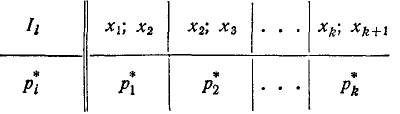
Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина X имеет данный закон распределения (заданный функцией распределения F(x) или плотностью f(x)). Назовём этот закон распределения теоретическим».

Зная теоретический закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов:

Проверяя согласованность теоретического и статистического распределений, мы будем исходить из расхождений между теоретическими вероятностями 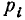и наблюденными частотами 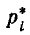. Естественно выбрать в качестве меры расхождения между теоретическим и статистическим распределениями сумму квадратов отклонений 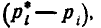взятых с некоторыми «весами»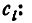 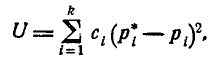(7.6.1)

Коэффициенты 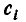(«веса» разрядов) вводятся потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Действительно, одно и то же по абсолютной величине отклонение может быть мало значительным, если сама вероятность 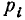велика, и очень заметным, если она мала. Поэтому естественно «веса» 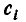взять обратно пропорциональными вероятностям разрядов .

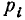Далее возникает вопрос о том, как выбрать коэффициент пропорциональности.

К. Пирсон показал, что если положить

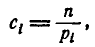(7.6.2)

то при больших п закон распределения величины U обладает весьма простыми свойствами: он практически не зависит от функции распределения F (х) и от числа опытов п, а зависит только от числа разрядов k, а именно, этот закон при увеличении я приближается к так называемому «распределению » .

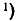При таком выборе коэффициентов 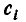мера расхождения обычно обозначается :

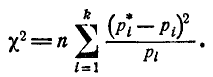(7.6.3)

Для удобства вычислений (чтобы не иметь дела с дробными величинами с большим числом нулей) можно ввести n под знак суммы

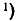Распределением с r степенями свободы называется распределение суммы квадратов r независимых случайных величин, каждая из которых подчинена нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Это распределение характеризуется плотностью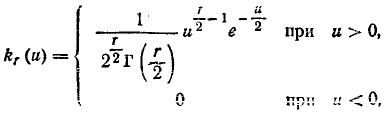

где 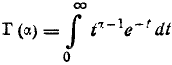— известная гамма-функция.

и, учитывая, что 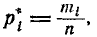, где 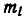, — число значений в i-м разряде, привести формулу (7.6.3) к виду:

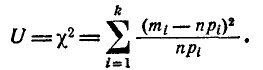(7.6.4)

Распределение зависит от параметра г, называемого числом «степеней свободы» распределения. Число «степеней свободы» r равно числу разрядов k минус число независимых условий («связей»), наложенных на частоты 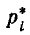. Примерами таких условий могут быть

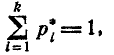
если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);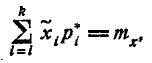

если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое и статистическое средние значения;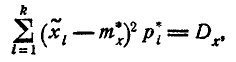

если мы требуем, кроме того, совпадения теоретической и статистической дисперсий и т. д.

Для распределения составлены специальные таблицы (см. табл. 4 приложения), Пользуясь этими таблицами, можно для каждого значения и числа степеней свободы r найти вероятность р того, что величина, распределенная по закону превзойдет это значение. В табл. 4 входами являются: значение вероятности р и число степеней свободы r. Числа, стоящие в таблице, представляют собой соответствующие значения .

Распределение даёт возможность оценить степень согласованности теоретического и статистического распределений, Будем исходить из того, что величина X действительно распределена по закону F(x). Тогда вероятность р, определённая по таблице, есть вероятность того, что за счёт чисто случайных причин мера расхождения теоретического и статистического распределений (7.6.4) будет не меньше, чем фактически наблюдённое в данной серии опытов значение .Если вероятность р весьма мала (настолько мала, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе Н о том, что закон распределения величины X есть F(x). Эту гипотезу следует отбросить как неправдоподобную. Напротив, если вероятность р сравнительно велика, можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счёт случайных причин. Гипотезу Н о том, что величина X распределена по закону F(x), можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.

Таким образом, схема применения критерия к оценке согласованности теоретического и статистического распределений сводится к следующему:

1) Определяется мера расхождения по формуле (7.6.4). 2) Определяется число степеней свободы r как число разрядов k минус число наложенных связей s:

r = k — s.

3) По r и с помощью табл. 4 определяется вероятность того, что величина, имеющая распределение с r степенями свободы, превзойдёт данное значение . Если эта вероятность весьма мала, гипотеза отбрасывается как неправдоподобная. Если эта вероятность относительно велика, 4 гипотезу можно признать не противоречащей опытным данным.

Насколько мала должна быть вероятность р для того, чтобы отбросить или пересмотреть гипотезу,—вопрос неопределённый; он не может быть решён из математических соображений, так же как и вопрос о том, насколько мала должна быть вероятность события для того, чтобы считать его практически невозможным. На практике, если р оказывается меньшим чем 0,1, рекомендуется проверить эксперимент, если возможно — повторить его и в случае, если заметные расхождения снова появятся, пытаться искать более подходящий для описания статистических данных закон распределения.

Следует особо отметить, что с помощью критерия (или любого другого критерия согласия) можно только в некоторых случаях опровергнуть выбранную гипотезу Н и отбросить ее как явно несогласную с опытными данными; если же вероятность р велика, то этот факт сам по себе ни в коем случае не может считаться доказательством справедливости гипотезы Н, а указывает только на то, что гипотеза не противоречит опытным данным.

С первого взгляда может показаться, что чем больше вероятность р, тем лучше согласованность теоретического и статистического распределений и тем более обоснованным следует считать выбор функции F(x) в качестве закона распределения случайной величины. В действительности это не так. Допустим, например, что, оценивая согласие теоретического и статистического распределений по критерию мы получили р=0,99. Это значит, что с вероятностью 0,99 за счёт чисто случайных причин при данном числе опытов должны были получиться расхождения большие, чем наблюдённые. Мы же получили относительно весьма малые расхождения, которые слишком малы для того, чтобы признать их правдоподобными. Разумнее признать, что столь близкое совпадение теоретического и статистического распределений не является случайным и может быть объяснено определёнными причинами, связанными с регистрацией и обработкой опытных данных (в частности, с весьма распространённой на практике «подчисткой» опытных данных, когда некоторые результаты произвольно отбрасываются или несколько изменяются).

Разумеется, все эти соображения применимы только в тех случаях, когда количество опытов п достаточно велико (порядка нескольких сотен) и когда имеет смысл применять сам критерий, основанный на предельном распределении меры расхождения при 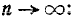Заметим, что при пользовании критерием достаточно большим должно быть не только общее число опытов n, но и числа наблюдений 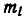, в отдельных разрядах. На практике рекомендуется иметь в каждом разряде не менее 5—10 наблюдений. Если числа наблюдений в отдельных разрядах очень малы (порядка 1 —2), имеет смысл объединить некоторые разряды.

Пример:

Проверить согласованность теоретического и статистического распределений для примера 1 п° 7.5 (стр. 137, 146).

Решение:

Пользуясь теоретическим нормальным законом распределения с параметрами

находим вероятности попадания в разряды по формуле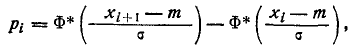

где 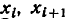—границы i-ro разряда.

Затем составляем сравнительную таблицу чисел попаданий в разряды 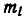, и соответствующих значений npи 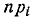(n = 500).

По формуле (7.6.4) определяем значение меры расхождения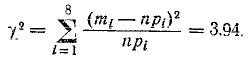

Определяем число степеней свободы как число разрядов минус число наложенных связей s (в данном случае s = 3):

r = 8 — 3 = 5,

По табл. 4 приложения находим для г = 5:

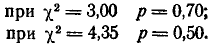
Следовательно, искомая вероятность р при = 3,94 приближенно равна 0,56. Эта вероятность малой не является; поэтому гипотезу о том, что величина X распределена по нормальному закону, можно считать правдоподобной.

Пример:

Проверить согласованность теоретического и статистического распределений для условий примера 2 п° 7.5 (стр. 149).

Решение:

Значения pi вычисляем как вероятности попадания на участки (20; 30), (30; 40) и т. д. для случайной величины, распределенной по закону равномерной плотности на отрезке (23,6; 96,9). Составляем сравнительную таблицу значени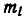й и 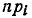(n = 400):

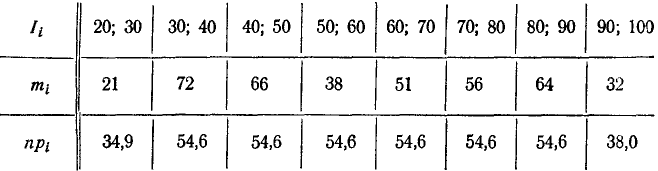
По формуле (7.6.4) находим :

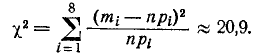
Число степеней свободы:

r= 8-3 = 5.

По табл. 4 приложения имеем:

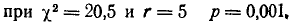
Следовательно, наблюдённое нами расхождение между теоретическим и статистическим распределениями могло бы за счёт чисто случайных причин появиться лишь с вероятностью 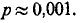Так как эта вероятность очень мала, следует признать экспериментальные данные противоречащими гипотезе о том, что величина X распределена по закону равномерной плотности.

Кроме критерия , для оценки степени согласованности теоретического и статистического распределений на практике применяется ещё ряд других критериев. Из них мы вкратце остановимся на критерии А. Н. Колмогорова.

В качестве меры расхождения между теоретическим и статистическим распределениями А. Н. Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F* (х) и соответствующей теоретической функцией распределения:

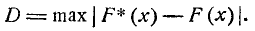
простой закон распределения. А. Н, Колмогоров доказал, что, какова бы ни была функция распределения F (х) непрерывной случайной величины X, при неограниченном возрастании числа независимых наблюдений n вероятность неравенства

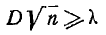
стремится к пределу

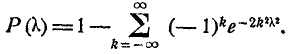(7.6.5)

Значения вероятности 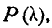подсчитанные по формуле (7.6.5), приведены в таблице 7.6.1.

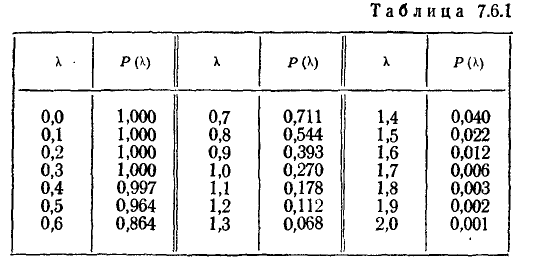
Схема применения критерия А. Н. Колмогорова следующая: строятся статистическая функция распределения F* (х) и предполагаемая теоретическая функция распределения F (х), и определяется макси- максимум D модуля разности между ними (рис. 7.6.2).

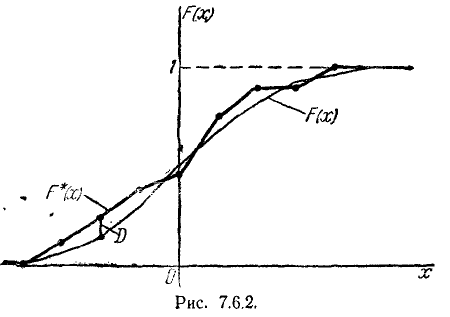
Далее определяется величина

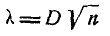
и по таблице 7.6.1 находится вероятность 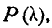Это есть вероятность того, что (если величина X действительно распределена по закону F (х)) за счет чисто случайных причин максимальное расхож- расхождение между F* (х) и F (х) будет не меньше, чем фактически наблюденное. Если вероятность 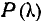весьма мала, гипотезу следует отвергнуть как неправдоподобную; при сравнительно больших 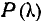ее можно считать совместимой с опытными данными.

Критерий А. Н. Колмогорова своей простотой выгодно отличается от описанного ранее критерия ; поэтому его весьма охотно применяют на практике. Следует, однако, оговорить, что этот критерий можно применять только в случае, когда гипотетическое распределение F (х) полностью известно заранее из каких-либо теоретических соображений, т. е. когда известен не только вид функции распределения F (х), но и все входящие в неё параметры. Такой случай сравнительно редко встречается на практике. Обычно из теоретических соображений известен только общий вид функции F (х), а входящие в неё числовые параметры определяются по данному статистическому материалу. При применении критерия это обстоятельство учитывается соответствующим уменьшением числа степеней свободы распределения . Критерий А. Н. Колмогорова такого согласования не предусматривает. Если все же применять этот критерий в тех случаях, когда параметры теоретического распределения выбираются по статистическим данным, критерий даёт заведомо завышенные значения вероятности 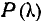; поэтому мы в ряде случаев рискуем принять как правдоподобную гипотезу, в действительности плохо согласующуюся с опытными данными.

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Теорема о повторении опытов
14. Нормальный закон распределения
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность