Теории игр — основные понятия и определения с примерами решения и образцами выполнения

В практической деятельности весьма часто приходится рассматривать явления и ситуации, в которых участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными, или просто конфликтами.

Типичный конфликт характеризуется тремя основными составляющими:
1) заинтересованными сторонами,
2) возможными действиями этих сторон,
3) интересами сторон.

Конфликтная ситуация, взятая из реальной жизни, как правило, довольно сложна. К тому же ее изучение затруднено наличием многих разных обстоятельств, часть из которых не оказывает сколь-либо существенного влияния ни на развитие конфликта, ни на его исход. Поэтому для того, чтобы анализ конфликтной ситуации оказался возможным, необходимо отвлечение от этих второстепенных факторов, при удачном стечении обстоятельств позволяющее построить упрощенную формализованную модель конфликта, которую и принято называть игрой. От реальной конфликтной ситуации игра отличается еще и тем, что ведется по вполне определенным правилам.

Необходимость изучения и анализа конфликтов, представляемых в виде упрощенных математических моделей (игр), вызвала к жизни специальный математический аппарат — теорию игр.

Введение в теорию игр

Опишем некоторые основные понятия, используемые в этой теории.

Заинтересованные стороны называются игроками. Любое возможное для игрока действие (в рамках заданных правил игры) называется его стратегией. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией. Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней.

В этих условиях протекание конфликта состоит в выборе каждым игроком своей стратегии и в получении им в сложившейся ситуации выигрыша из некоторого источника. На этом пути создается теория игр с выигрышами.

Однако оценка игроком ситуации путем указания его выигрыша, вообще говоря, не всегда возможна практически и даже не всегда имеет смысл. В подобных случаях иногда удается вместо прямых численных оценок ситуаций указывать на их сравнительную предпочтительность для отдельных игроков. На этом пути создается теория игр с предпочтениями, включающая в себя как частный случай и теорию игр с выигрышами. В дальнейшем мы ограничимся рассмотрением только игр с выигрышами.

Изучение игр можно проводить с различных точек зрения. Мы будем стремиться к
— выработке принципов оптимальности, то есть того, какое поведение игроков следует считать оптимальным (разумным, целесообразным),
— выяснению реализуемости этих принципов, то есть установлению существования оптимальных в выработанном смысле ситуаций,
и
— отысканию этих реализаций.

Одной из плодотворных форм реализации представлений об оптимальности можно считать понятие равновесия, при котором складывается такая (равновесная) ситуация, в нарушении которой не заинтересован ни один из игроков.

Именно ситуации равновесия могут быть предметом устойчивых договоров между игроками (ни у одного из игроков не будет мотивов к нарушению договора). Кроме того, ситуации равновесия являются выгодными для каждого игрока: в равновесной ситуации каждый игрок получает наибольший выигрыш (разумеется, в той мере, в какой это от него зависит).

Если в игре ситуации равновесия (в пределах отпущенных возможностей) нет, то, оставаясь в условиях стратегий, имеющихся у игроков, мы сталкиваемся с неразрешимой задачей. При возникновении подобных случаев естественно ставить вопрос о таком расширении первоначального понятия стратегии, чтобы среди ситуаций, составленных из новых, обобщенных стратегий, заведомо нашлись бы равновесные. Если такие обобщенные стратегии существуют, то обычно они представляются некоторыми комбинациями исходных стратегий (при этом, естественно, предполагается, что игра повторяется многократно). Для того, чтобы отличать прежние стратегии от новых, первые называют чистыми, а вторые — смешанными стратегиями.

Весьма плодотворным является представление смешанной стратегии как случайного выбора игроками их чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша. Игра, преобразованная таким образом, обычно называется смешанным расширением исходной игры.

Проиллюстрируем сказанное на примере одного из самых простых, но одновременно и наиболее изученных классов игр, на так называемыхлипиричных играх. Исследование матричных игр интересно еще и потому, что к ним могут быть приближенно сведены многие игры более общего вида.

Затем мы кратко остановимся на вопросе классификации игр и рассмотрим еще два вида игр — позиционные игры и биматричные игры.

Матричные игры

Рассмотрим игру, в которой участвуют два игрока, причем каждый из игроков имеет конечное число стратегий. Обозначим для удобства одного из игроков через А, в другого — через В.

Предположим, что игрок А имеет m стратегий — 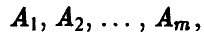а игрок В имеет n стратегий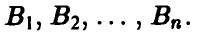

Пусть игрок А выбрал стратегию 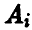, а игрок В стратегию 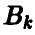. Будем считать, что выбор игроками стратегий 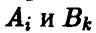однозначно определяет исход игры — выигрыш 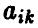игрока А и выигрыш 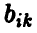игрока В, причем эти выигрыши связаны равенством

(отрицательный выигрыш на бытовом языке обычно называют проигрышем).

Последнее условие показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с противоположным знаком. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будут, например, выигрыши игрока А.

Если нам известны значения выигрыша при каждой паре стратегий (в каждой ситуации) 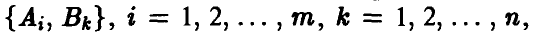то их удобно записывать или в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрока А,
а столбцы — стратегиям игрока В:

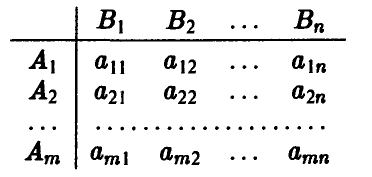
или в виде матрицы

Полученная матрица имеет размер m х n и называется матрицей игры, или платежной матрицей (отсюда и название игры — матричная).

Рассматриваемую игру часто называют игрой m х n или m х n игрой.

Замечание:

Матричные игры относятся к разряду так называемых антагонистических игр, то есть игр, в которых интересы игроков прямо противоположны.

Пример:

Каждый из двух игроков А и В одновременно и независимо друг от друга записывает нв листе бумаги любое целое число. Если выписанные числа имеют одинаковую четность, то игрок А получает от игрока В 1 рубль, а если разную, то наоборот — игрок А платит 1 рубль игроку В.

У игрока А две стратегии: 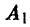— записать четное число и 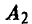— записать нечетное число. У игрока В такие же две стратегии. 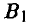— записать четное число и 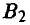— записать нечетное число. Выбор игроками соответственно стратеги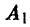й и 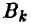однозначно определяет исход игры — выигрыш игрока А.

Матрица этой 2×2 игры имеет следующий вид

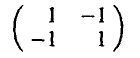
(здесь строки соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В).

Равновесная ситуация

Рассмотрим следующий пример.

Пример:

Два игрока Л и В, не глядя друг на друга, кладут на стол по картонному кружку красного (r), зеленого (g) или синего (b) цветов, сравнивают цвета кружков и расплачиваются друг с другом так, как показано в матрице игры

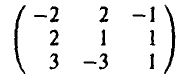
(напомним, что у этой 3 х 3-матрицы строки соответствуют стратегиям игрока A, а столбцы — стратегиям игрока В).

Считая, что эта 3×3 игра повторяется многократно, попробуем определить оптимальные стратегии каждого из игроков.

Начнем с последовательного анализа стратегий игрока A, не забывая о том, что, выбирая стратегию игрока A, должно принимать в расчет, что его противник В может ответить на нее той из своих стратегий, при которой выигрыш игрока A будет минимальным.

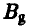Так, на стратегию он ответит стратегией (минимальный аыигрыш равен -2, что на самом деле означает проигрыш игрока Л, равный 2), на стратегию — стратегией или 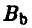(минимальный выигрыш игрока A равен 1), а на стратегию 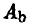— стратегией 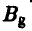(минимальный выигрыш игрока А равен -3).

Запишем эти минимальные выигрыши в правом столбце таблицы:

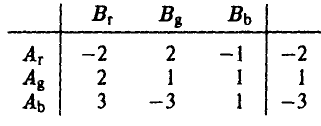
maxmin. Неудивительно, что игрок A останавливает свой выбор на стратегии 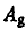, при которой его минимальный выигрыш максимален (из трех чисел —2, 1 и —3 максимальным является 1):

Если игрок A будет придерживаться этой стратегии, то ему гарантирован выигрыш, не меньший 1, при любом поведении противника в игре.

Аналогичные рассуждения можно провести и за игрока В. Так как игрок В заинтересован в том, чтобы обратить выигрыш игрока Л в минимум, то ему нужно проанализировать каждую свою стратегию с точки зрения максимального выигрыша игрока A.

Выбирая свою стратегию, игрок В должен учитывать, что при этом стратегией его противника A может оказаться та, при которой выигрыш игрока A будет максимальным. Так, на стратегию 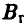он ответит стратегией 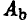(максимальный выигрыш игрока A равен 3), на стратегию 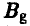— стратегией 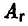(максимальный выигрыш игрока A равен 2), а на стратегию 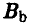— стратегие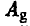й или 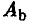(максимальный выигрыш игрока A равен 1). Эти максимальные выигрыши записаны в нижней строке таблицы

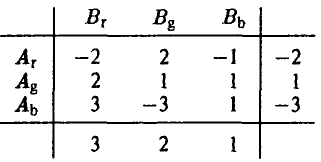
minmax. Неудивительно, если игрок В остановит свой выбор на стратегии 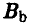, при которой максимальный выигрыш игрока А минимален (из трех чисел 3, 2 и 1 минимальным является 1):

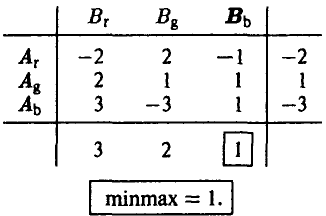
Если игрок В будет придерживаться этой стратегии, то при любом поведении противника он проиграет не больше 1.

В рассматриваемой игре числа maxmin и minmax совпали:

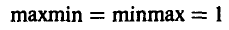
(соответствующие элементы в таблице

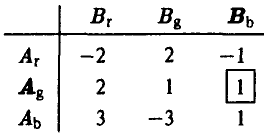
выделены жирным шрифтом).

Выделенные стратегии 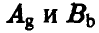являются оптимальными стратегиями игроков А и В,

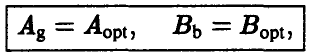
в следующем смысле:

при многократном повторении игры отказ от выбранной стратегии любым из игроков уменьшает его шансы на выигрыш (увеличивает шансы на проигрыш).

В самом деле, если игрок А будет придерживаться не стратегии 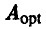, а выберет иную стратегию, например, 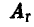, то вряд ли стоит рассчитывать на то, что игрок В этого не заметит. Конечно, заметит и не преминет воспользоваться своим наблюдением. Ясно, что в этом случае он отдаст предпочтение стратегии 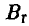. А на выбор 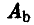игрок В ответит, например, так — 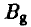. В результате отказа от стратегии 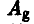выигрыш игрока A уменьшится.

Если же от стратегии 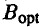отказывается игрок В, выбирая, например, стратегию 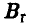, то игрок A может ответить на это стратегией 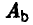и, тем самым, увеличить свой выигрыш. В случае стратегии 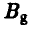ответ игрока A — .

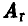Тем самым, ситуация 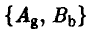оказывается равновесной.

Еще раз подчеркнем, что элементами матрицы игры являются числа, описывающие выигрыш игрока А. Более точно, выигрыш соответствует положительному элементу платежной матрицы, а отрицательный указывает на проигрыш игрока А.

Матрица выплат игроку В получается из матрицы игры заменой каждого ее элемента на противоположный по знаку.

Рассмотрим теперь произвольную матричную игру

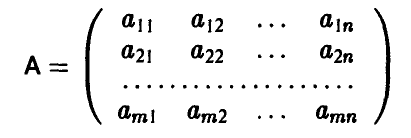
(строки заданной m х n-матрицы соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В) и опишем общий алгоритм, посредством которого можно определить, есть ли в этой игре ситуация равновесия или ее нет.

В теории игр предполагается, что оба игрока действуют разумно, то есть стремятся к получению максимального выигрыша, считая, что соперник действует наилучшим {для себя) образом.

Действия игрока А

1-й шаг. В каждой строке матрицы А ищется минимальный элемент

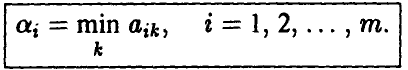
Полученные числа

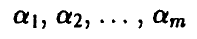
приписываются к заданной таблице в виде правого добавочного столбца

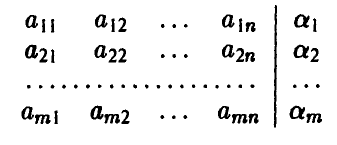
Пояснение:

Выбирая стратегию 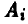, игрок А вправе рассчитывать на то, что в результате разумных действий противника (игрока В) он выиграет не меньше чем .

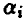2-й шаг. Среди чисел

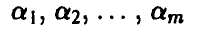
выбирается максимальное число

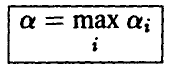
или, подробнее,

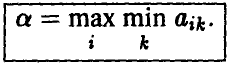
Специально отметим, что выбранное число а является одним из элементов заданной матрицы А.

Пояснение:

Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок А должен остановиться на той стратегии 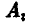, для которой число 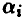является максимальным.

Если игрок А будет придерживаться стратегии, выбранной описанным выше способом, то при любом поведении игрока В игроку А гарантирован выигрыш, не меньший а.

Число а называется нижней ценой игры.

Принцип построения стратегии игрока А, основанный на максимизации минимальных выигрышей, называется принципом максимина, а выбираемая в соответствии с этим принципом стратегия 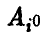— максиминной стратегией игрока А.

Действия игрока В

1-й шаг. В каждом столбце матрицы А ищется максимальный элемент

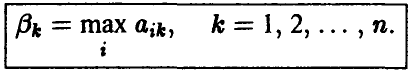
Полученные числа

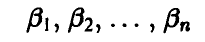
приписываются к заданной таблице в виде нижней добавочной строки

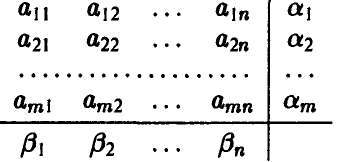
Пояснение:

Выбирая стратегию 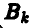, игрок В должен рассчитывать на то, что в результате разумных действий противника (игрока A) он проиграет не больше чем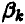

2-й шаг. Среди чисел

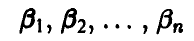
выбирается минимальное число

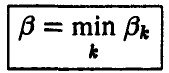
или, подробнее,

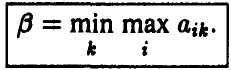
Выбранное число 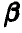также является одним из элементов заданной матрицы А.

Пояснение:

Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок В должен остановиться на той стратегии 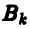, для которой число 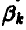является минимальным.

Если игрок В будет придерживаться стратегии, выбранной описанным выше способом, то при любом поведении игрока А игроку В гарантирован проигрыш, не больший .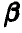

Число 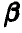называется верхней ценой игры.

Принцип построения стратегии игрока В, основанный на минимизации максимальных потерь, называется принципом минимакса, а выбираемая в соответствии с этим принципом стратегия 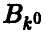— минимаксной стратегией игрока В.

Нижняя цена игры а и верхняя цена игры 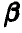всегда связаны неравенством

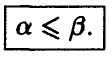
Замечание:

Реализация описанного алгоритма требует 2mn — 1 сравнений элементов матрицы А:

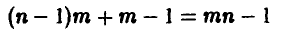
сравнений для определения а,

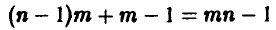
сравнений для определения 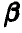и одно сравнение полученных чисел а и .

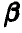Если

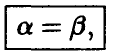
или, подробнее,

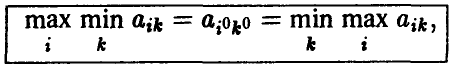
то ситуация 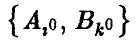оказывается равновесной, и ни один из игроков не Ійи’нте-ресован в том, чтобы ее нарушить (в этом нетрудно убедиться путем рассуждений, подобных проведенным при анализе игры в примере 2)

В том случае, когда нижняя цена игры равна верхней цене игры, их общее значение называется просто ценой игры и обозначается через v

Цена игры совпадает с элементом 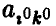матрицы игры А, расположенным на пересечении 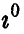-й строки (стратегия 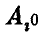игрока А) и 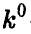-го столбца (стратегия 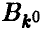игрока В) — минимальным в своей строке и максимальным в своем столбце

Этот элемент называют седловой точкой матрицы А, или точкой равновесия, а про игру говорят, что она имеет седловую точку

Стратегии 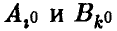, соответствующие седловой точке, называются оптимальными, а совокупность оптимальных ситуаций и цена игры — решением матричной игры с седловой точкой

Замечание:

Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение

Матричные игры с седловой точкой важны и интересны, однако более типичным является случай, когда применение описанного алгоритма приводит к неравенству

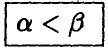
Как показывает следующий пример, в этом случае предложенный выбор стратегий уже, вообще говоря, к равновесной ситуации не приводит, и при многократном ее повторении у игроков вполне могут возникнуть мотивы к нарушению рекомендаций, основанных на описанном алгоритме действий игроков A и В

Пример:

Рассмотрим 3×3 игру, заданную матрицей

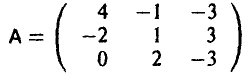
Применив предложенный алгоритм

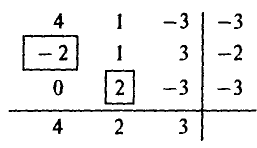
находим нижнюю цену игры а = — 2 и соответствующую ей стратегию 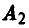, и верхнюю цену игры 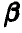= 2 и соответствующую ей стратегию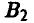

Нетрудно убедиться в том что пока игроки придерживаются этих стратегий, средний выигрыш при многократном повторении игры равен 1 Он больше нижней цены игры, но меньше верхней цены

Однако если игроку В станет известно, что игрок А придерживается стратегии 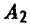, он немедленно ответит стратегией 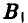и сведет его выигрыш к проигрышу —2 В свою очередь, на стратегию 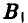у игрока A имеется ответная стратегия 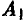, дающая ему выигрыш 4

Тем самым, ситуация 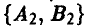равновесной не является

Смешанные стратегии

В случае, когда нижняя цена игры а и верхняя цена игры 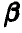не совпадают,

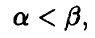
игрок А может обеспечить себе выигрыш, не меньший а, а игрок В имеет возможность не дать ему больше, чем 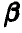Возникает вопрос — а как разделить между игроками разность

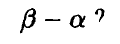
Предыдущие построения на этот вопрос ответа не дают — тесны рамки возможных действий игроков. Поэтому довольно ясно, что механизм, обеспечивающий получение каждым из игроков как можно большей доли этой разности, следует искать в определенном расширении стратегических возможностей, имеющихся у игроков изначально.

Оказывается, что компромиссного распределения разности 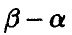между игроками и уверенного получения каждым игроком своей доли при многократном повторении игры можно достичь путем случайного применения ими своих первоначальных, чистых стратегий. При таких действиях
— во-первых, обеспечивается наибольшая скрытность выбора стратегии (результат выбора не может стать известным противнику, поскольку он неизвестен самому игроку),
— во-вторых, при разумном построении механизма случайного выбора стратегий, последние оказываются оптимальными.

Случайная величина, значениями которой являются стратегии игрока, называется его смешанной стратегией.

Тем самым, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его первоначальные стратегии.

Основные определения:

Рассмотрим произвольную m х n игру, заданную m х n-матрицей

Так как игрок А имеет m чистых стратегий, то его смешанная стратегия может быть описана набором m неотрицательных чисел

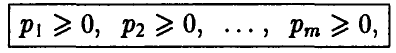
сумма которых равна 1,

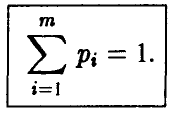
Смешанная стратегия второго игрока В, имеющего n чистых стратегий, описывается набором n неотрицательных чисел

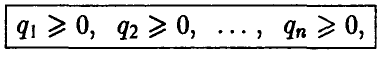
сумма которых равна 1,

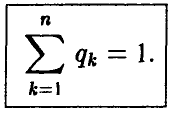
Замечание:

Каждая чистая стратегия является частным случаем смешанной стратегии: в частности, чистая стратегия 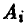является смешанной стратегией, описываемой набором чисел 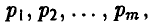в котором

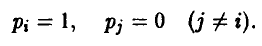
Подчеркнем, что для соблюдения секретности каждый из игроков применяет свои стратегии независимо от другого игрока.

Таким образом, задав два набора

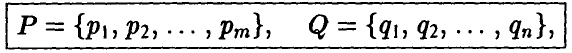
мы оказываемся в ситуации в смешанных стратегиях. В этих условиях каждая обычная ситуация (в чистых стратегиях) 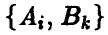по определению является случайным событием и, ввиду независимости наборов Р и Q, реализуется с вероятностью 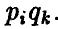В этой ситуации 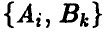игрок А получает выигрыш 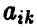. Тем самым, математическое ожидание выигрыша игрока А в условиях ситуации в смешанных стратегиях (Р, Q) равно

Это число и принимается за средний выигрыш игрока А при смешанных стратегиях

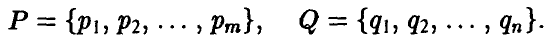
Определение:

Стратегии

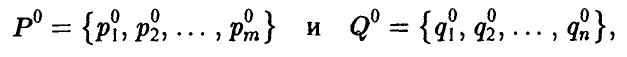
называются оптимальными смешанными стратегиями игроков А и В соответственно, если выполнено следующее соотношение

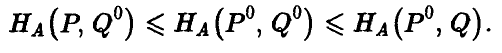
Пояснение:

Выписанные неравенства означают следующее:

левое неравенство — отклонение игрока А от оптимальной стратегии Р° при условии, что игрок В придерживается стратегии Q°, приводит к тому, что выигрыш отклонившегося игрока А может только уменьшиться,

правое неравенство — отклонение игрока В от оптимальной стратегии Q° при условии, что игрок А придерживается стратегии Р°, приводит к тому, что выигрыш игрока А может только возрасти, и значит, выигрыш игрока В — только уменьшиться.

Приведенное условие оптимальности равносильно тому, что

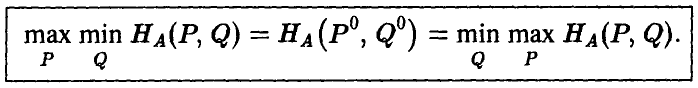
Величина

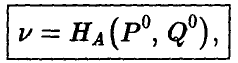
определяемая последней формулой, называется ценой игры.

Набор (Р°, Q°, v), состоящий из оптимальных смешанных стратегий игроков А и В и цены игры, называется решением матричной игры.

Пример:

Рассмотрим 2×2 матричную игру из примера 1. Матрица этой игры имеет следующий вид

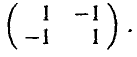
Как нетрудно убедиться, седловой точки у нее нет.

Смешанные стратегии игроков А и В могут быть описаны парами чисел

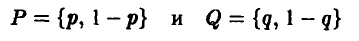
соответственно.

Средний выигрыш игрока А вычисляется так:

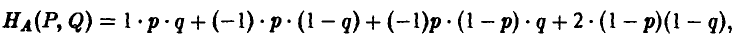
откуда легко следует, что

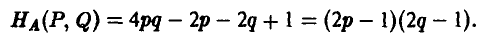
Последнее удобно записать так

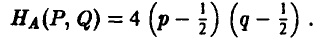
Полученная формула показывает, что если игрок А в половине случаев записывает на листе бумаге четное (нечетное) число (выбирает р = 1/2), то независимо от того, что делает игрок В, ожидаемый (средний) выигрыш игрока А в каждой партии будет нулевым.

Если же игрок А выберет р > 1/2 (так что разность р — 1/2 будет положительной), то узнaв об этом, игрок В мoжет выбрать q < 1/2 (так что разность q — 1/2 будет отрицательной) и, тем самым, еделaть средний выигрыш игрока А отрицательным, то есть заставит его проиграть. Если же игрок А выберет р < 1/2 (так что разность р — 1/2 будет отрицательной) и игрок В узнает об этом, то он может выбрать q > 1/2 (так что разность q-1/2 будет положительной) и вновь сделать выигрыш игрока А отрицательным, то есть опять заставит его проиграть.

Исследуем теперь эту формулу с точки зрения игрока В.

Если игрок А выбирает р = 1/2, то ожидаемый (средний) выигрыш игрока В независимо от его действий будет нулевым в каждой партии. Но если игрок В выберет q > 1/2 (так что разность q — 1/2 будет положительной), то, узнав об этом, игрок А может выбрать р < 1/2 (так что разность р — 1/2 будет отрицательной), и тогда игрок В будет проигрывать в каждой партии. Если же игрок В выберет q < 1/2 (так что разность q -1/2 будет отрицательной) и игрок А узнает об этом, то он может выбрать р > 1/2 (так что разность р — 1/2 будет положительной) и вновь заставит игрока В проиграть.

Тем самым, наборы

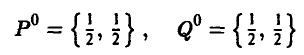
являются оптимальными, а исход игры ничейным:

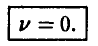
Замечание:

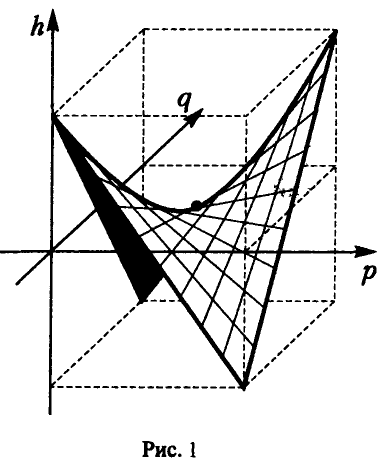
На рисунке 1 показано, как устроена поверхность, описываемая функцией

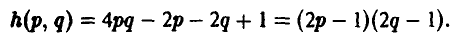
Точка

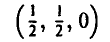
является седловой точкой (точкой перевала) этой поверхности. Именно эта точка и дает решение рассматриваемой матричной игры.

Естественно возникают два ключевых вопроса:
1- й — какие матричные игры имеют решение в смешанных стратегиях?
2- й — как находить решение матричной игры, если оно существует?

Ответы на эти вопросы дают следующие две теоремы.

Основная теорема теории матричных игр

Теорема Дж. фон Неймана:

Для матричной игры с любой матрицей A величины

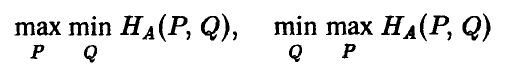
равны между собой,

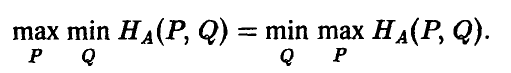
Более того, существует хотя бы одна ситуация в смешанных стратегиях (Р°, Q°), для которой выполняется соотношение

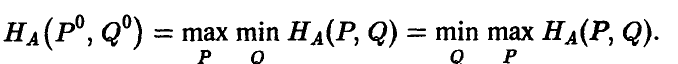
Иными словами, любая матричная игра имеет решение в смешанных стратегиях. Поиск этого решения опирается на следующие установленные факты.

2.3. Основные свойства оптимальных смешанных стратегий

Теорема:

Пусть

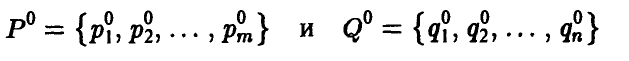
— оптимальные смешанные стратегии и v — цена игры.

Оптимальная смешанная стратегия Р° игрока А смешивается только из тех чистых стратегий 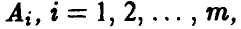то есть отличными от нуля могут быть вероятности 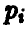только с теми номерами 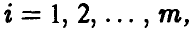для которых выполнены равенства

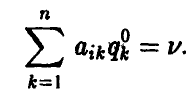
Это означает, что смешиваются не все чистые стратегии. Аналогично,

в оптимальной смешанной стратегии 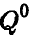игрока В отличных от нуля могут быть только те вероятности 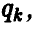для номеров 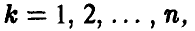которых выполнены равенства

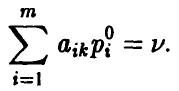
Кроме того, имеют место соотношения

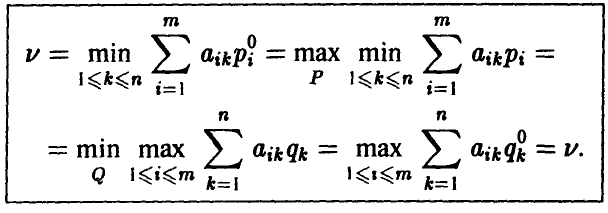
В этом последнем скоплении равенств, по существу, и лежат истоки, питающие методы построения решений матричных игр. Опишем простейшие из них.

Методы решения матричных игр

Наши рассмотрения мы начнем с матричных игр, число стратегий хотя бы одного из игроков в которых равно двум.

Для построения решений 2 х n и m х 2 игр существует эффективный метод, основанный на простых геометрических соображениях. Этот метод называют графическим.

3.1. игры

Пусть

— платежная матрица 2 х n игры.

Согласно теореме о двойном описании игры (теорема 2) нахождение цены игры и оптимального значения р° для игрока А равносильно разрешению уравнения

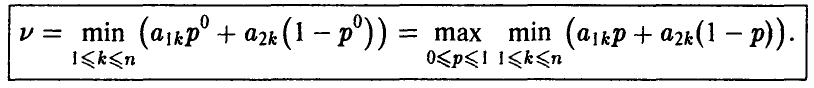
Опишем общую схему, приводящую к искомому результату.

Максимум функции

проще всего найти, построив ее график. Для этого поступают следующим образом.

Предположим, что игрок А выбрал смешанную стратегию Р = {р, 1 — р}, а игрок В — k-ю чистую стратегию, k = 1, 2, … , n. Тогда средний выигрыш игрока А в ситуации {Р, k} оказывается равным

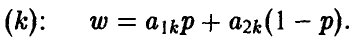
На плоскости (р, w) уравнение (k) описывает прямую. Тем самым, каждой чистой стратегии игрока В на этой плоскости соответствует своя прямая.

Поэтому сначала на плоскости (w, р) последовательно и аккуратно рисуются все прямые

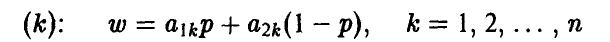
(рис. 2). Затем для каждого значения 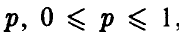, путем визуального сравнения соответствующих ему значений w на каждой из построенных прямых определяется и отмечается минимальное из них (рис. 3). В результате описанной процедуры получается ломаная, которая и является графиком функции (*) (выделена жирным на рис. 4). Эта ломаная как бы огибает снизу все семейство построенных прямых,

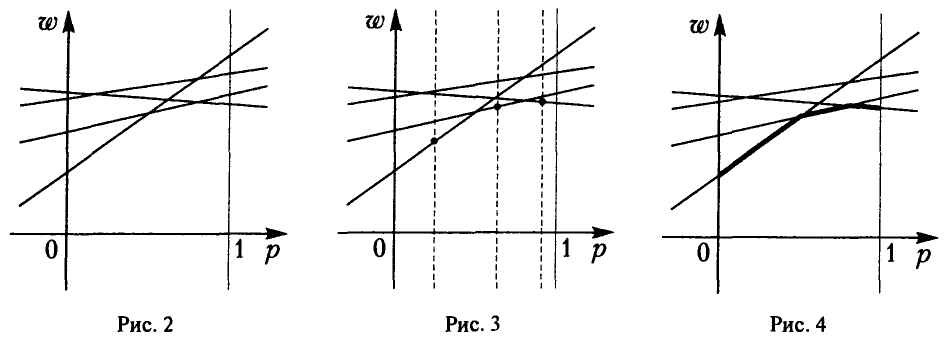
и по этой причине ее принято называть нижней огибающей этого семейства. Верхняя точка построенной нижней огибающей определяет и цену игры — v и оптимальную стратегию игрока А — Р° = {р°, 1 — р°} (рис. 5).

Замечание:

Описанная процедура может рассматриваться как некоторый аналог максиминного подхода при отсутствии седловой точки.

Опробуем описанную схему решения 2 х n игры на конкретном примере.

Пример:

Рассмотрим игру, заданную 2×6 матрицей

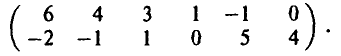
Решение:

1-й шаг. Анализ игры на наличие седловой точки.

Нижняя цена игры равна —1, верхняя цена игры равна 1. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

2- й шаг. Вычисление средних выигрышей игрока А (проводится при условии, что игрок В выбирает только чистые стратегии).

Из таблицы

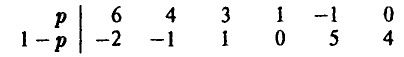
легко получаем:

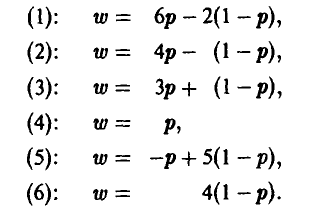
3-й шаг. Построение нижней огибающей.

Аккуратно строим на координатной плоскости (р, w) все шесть прямых, уравнения которых получены на 2-м шаге (рис. 6), и находим их нижнюю огибающую.

4- й шаг. Отыскание цены игры и оптимальной смешанной стратегии игрока А.

При аккуратном построении нижней огибающей, нетрудно определить, точкой пересечения каких двух из построенных шести прямых является ее наивысшая точка. В данном случае это прямые (4) и (5), заданные уравнениями w = р и w = -р + 5(1 — р) соответственно. Решая систему уравнений

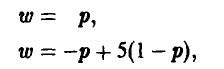
получаем

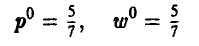
(рис. 7).

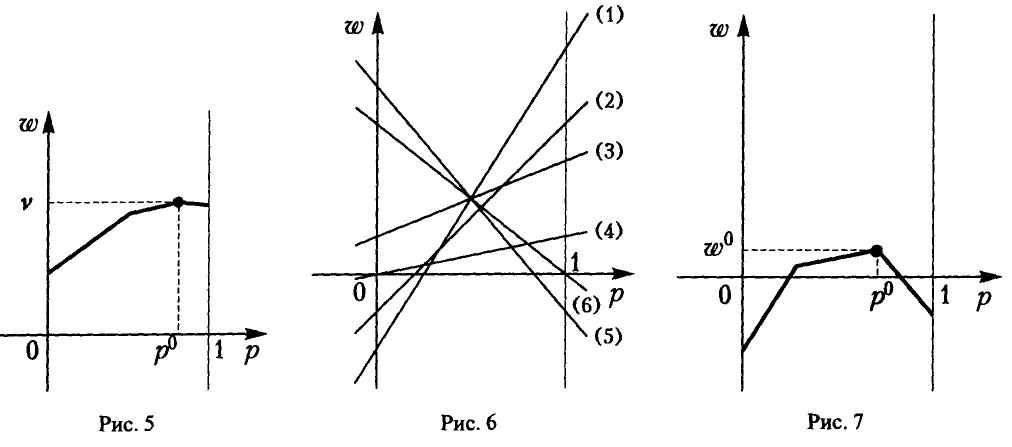
‘Тем самым, цена игры и и оптимальная стратегия Р° игрока А соответственно равны

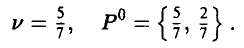
Собственно, этим и заканчивается решение игры для игрока А, поскольку его в первую очередь интересует отыскание собственной оптимальной стратегии и ожидаемого наилучшего гарантированного результата.

Замечание:

Решающий матричную игру обычно отождествляет себя с одним из игроков (как правило, это игрок А), считая другого своим противником. Это связано еще и с тем, что в некоторых случаях основное внимание уделяется поиску оптимальных стратегий только игрока А, а стратегии противника могут вообще не интересовать исследователя.

Однако в целом ряде случаев оказывается важным знать оптимальные смешанные стратегии обоих игроков.

Как ищется оптимальная смешанная стратегия игрока А, мы уже описали. Покажем теперь, как отыскать оптимальную смешанную стратегию игрока В.

Здесь, в зависимости от формы нижней огибающей, может представиться несколько случаев.

А. Нижняя огибающая имеет ровно одну наивысшую точку (р°, w°):

1) Если р° = 0 (оптимальная стратегия игрока А — чистая стратегия 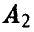), то игроку В выгодно применять чистую стратегию, соответствующую номеру прямой, проходящей через точку (0, w°) и имеющей наибольший отрицательный наклон (рис. 8).

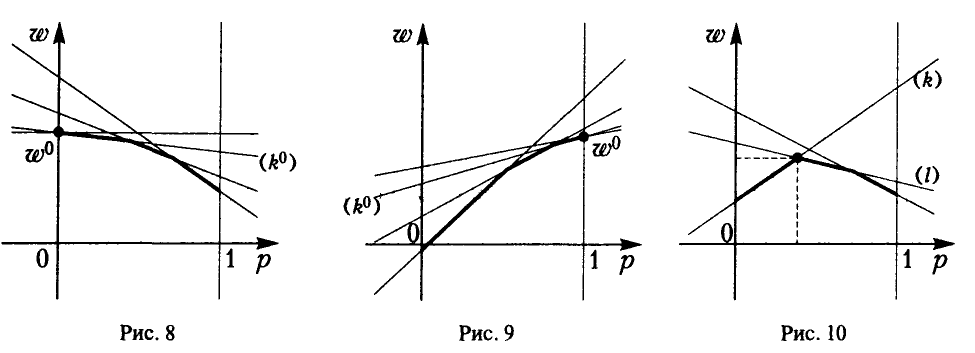
2) Если 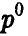= 1 (оптимальная стратегия игрока А — чистая стратегия ), то оптимальной для игрока В является чистая стратегия, соответствующая номеру прямой, проходящей через точку (1, w°) и имеющей наименьший положительный наклон (рис. 9).

3) Если 0 < р° < 1, то в наивысшей точке нижней огибающей пересекаются, по меньшей мере, две прямые, одна из которых (k-я) имеет положительный наклон, а другая (l-я) — отрицательный (рис. 10), и оптимальная смешанная стратегия игрока В получается, если положить

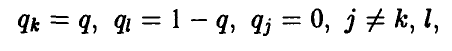
где q — решение уравнения

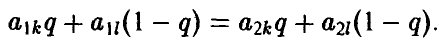
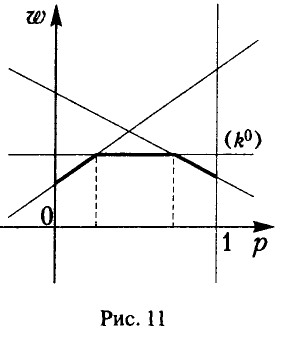
Б. Нижняя огибающая содержит горизонтальный участок, соответствующий чистой стратегии k° игрока В, которая и является оптимальной для него (рис. 11).

Пример:

Покажем теперь, как найти полное решение игры, то есть еще и оптимальную смешанную стратегию

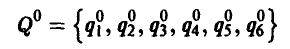
игрока В.

Для этого поступают так:

1) полагают

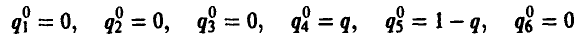
(выделяя тем самым из шести чистых стратегий игрока В стратегии 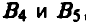, которым соответствуют прямые (4) и (5), определяющие наивысшую точку нижней огибающей),

2) приравнивают любой из двух средних выигрышей игрока В (игрок А выбирает только чистые стратегии), отвечающих предложенной смешанной стратегии

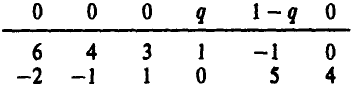
к цене игры

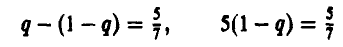
и

3) получают (в обоих случаях), что

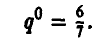
Полное решение игры имеет следующий вид

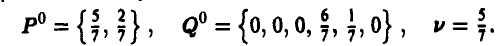
Замечание:

Ситуация с наличием лишь двух конкурирующих стратегий игрока А нельзя считать надуманной. Она возникает сравнительно часто. Например, в случае, если нужно сравнить два образца некоторого изделия (скажем, старого и модернизированного) с целью выяснения возможности замены, это весьма удобно сделать при помощи платежной матрицы 2 х n.

m х 2 игры

Пусть теперь в матричной игре две чистые стратегии имеет игрок В, а число чистых стратегий у игрока А произвольно (равно m). Это означает, что платежная матрица такой игры имеет вид

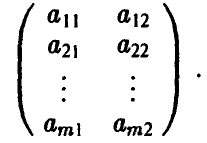
Анализ такой игры во многом напоминает рассуждения, описанные для игры 2 х n.

Пусть Q = {q, 1 — q} — произвольная смешанная стратегия игрока В. Если игрок А выбирает і-ю чистую стратегию, і = 1, 2,… , m, то средний выигрыш игрока В в ситуации {i, Q} будет равным

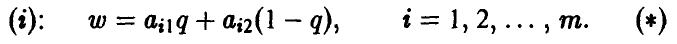
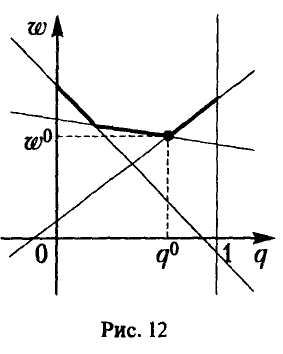
Зависимость этого выигрыша от переменной q описывается прямой.

Графиком функции

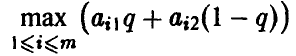
является верхняя огибающая семейства прямых (*), соответствующих чистым стратегиям игрока А (рис. 12).

Абсциссой нижней точки полученной ломаной будет значение q°, определяющее оптимальную смешанную стратегию игрока В, а ординатой w° — цена игры.

Замечание:

Отыскание оптимальной смешанной стратегии игрока А проводится по той же схеме, которая позволяет находить оптимальную смешанную стратегию игрока В в игре 2 х n.

Рассмотрим конкретный пример.

Пример 6. 3 х 2 игра задана матрицей

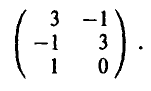
Решение:

1-й шаг. Анализ игры на наличие седловой точки.
Нижняя цена игры равна 0, верхняя цена игры равна 3. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.
2- й шаг. Вычисление средних выигрышей игрока В (проводится при условии, что игрок А выбирает только чистые стратегии).

Из таблицы

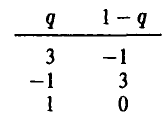
получаем:

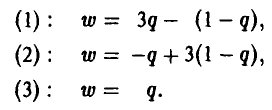
3- й шаг. Построение верхней огибающей.
Построим на координатной плоскости (q, w) все три прямых, а затем и их верхнюю огибающую (рис. 13).

4-й шаг. Отыскание цены игры и оптимальной смешанной стратеги игрока В.

Нижняя точка верхней огибающей является точкой пересечения прямых (1) и (2). Решая систему уравнений

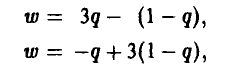
получаем

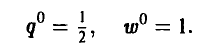
5-й шаг. Отыскание оптимальной смешанной стратегии игрока А.

Полагая

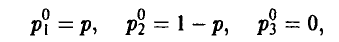
приравниваем средние выигрыши игрока А, соответствующие чистым выигрышам игрока В,

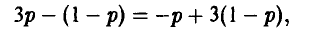
и находим р° = 1/2.

Таким образом, цена игры и оптимальные смешанные стратегии игроков А и В соответственно равны

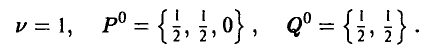
m*n игры

игры

В принципе решение любой матричной игры сводится к решению стандартной задачи линейного программирования и, тем самым, может быть найдено методами линейного программирования. При этом требуемый объем вычислений напрямую зависит от числа чистых стратегий игроков (растет с его увеличением и, значит, с увеличением размеров матрицы игры). Поэтому любые приемы предварительного анализа игры, позволяющие уменьшать размеры ее платежной матрицы или еще как-то упрощать эту матрицу, не нанося ущерба решению, играют на практике весьма важную роль.

Правило доминирования
В целом ряде случаев анализ платежной матрицы обнаруживает, что некоторые чистые стратегии не могут внести никакого вклада в искомые оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную матрицу на матрицу выигрышей меньших размеров.

Опишем одну из таких возможностей более подробно.
Пусть

— произвольная m х n матрица. Будем говорить, что i-я строка матрицы А

не больше j -й строки этой матрицы

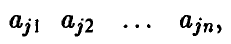
если одновременно выполнены следующие n неравенств

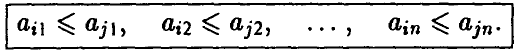
При этом говорят также, что j -я строка доминирует i-ю строку, или что стратегия 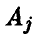игрока А доминирует стратегию .

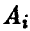Замечание:

Игрок А поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые строки.

Если в матрице А одна из строк (j -я) доминирует другую строку (i-ю), то число строк в матрице А можно уменьшить путем отбрасывания доминируемой строки (i-й).

Далее, будем говорить, что k-й столбец матрицы А

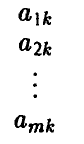
не меньше lго столбца этой матрицы

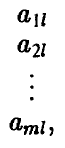
если одновременно выполнены следующие m неравенств

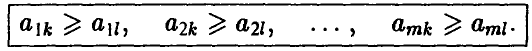
При этом говорят также, что l -й столбец доминирует k-й столбец, или что стратегия 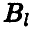игрока В доминирует стратегию .

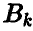Замечание:

Игрок B поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые столбцы.

Если в матрице А один из столбцов (l-й) доминирует другой столбец (к-й), то число столбцов в матрице А можно уменьшить путем отбрасывания доминируемого столбца (k-ro).

Важное замечание:

Оптимальные смешанные стратегии в игре с матрицей, полученной усечением исходной за счет доминируемых строк и столбцов, дадут оптимальное решение в исходной игре: доминируемые чистые стратегии игроков в смешении не участвуют — соответствующие им вероятности следует взять равными нулю.

Пример:

Рассмотрим игру с матрицей

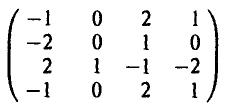
Сравнивая строки матрицы, видим, что 1-я строка совпадает с 4-й строкой, или, что то же, стратегия 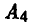дублирует стратегию 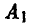. Тем самым, одну из этих строк можно вычеркнуть, не нанося ущерба решению

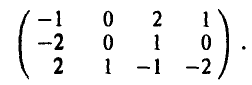
Поэлементно сравнивая 1-ю и 2-ю строки, замечаем, что 1-я строка доминирует 2-ю строку, или, что то же, стратегия 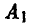доминирует стратегию 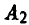. Это вновь позволяет уменьшить число строк матрицы

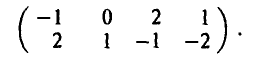
Замечая, что 4-й столбец полученной матрицы доминирует ее 3-й столбец, приходим к игре с 2 х 3-матрицей

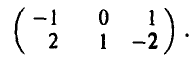
Решая эту 2×3 игру графическим методом, находим ее решение — цену игры и оптимальные смешанные стратегии игроков А и В:

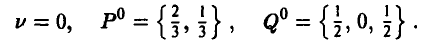
Возвращаясь к исходной 4×4 игре, получаем окончательный ответ:

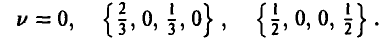
Замечание:

При отбрасывании доминируемых строк и столбцов некоторые из оптимальных стратегий могут быть потеряны. Однако цена игры не изменится, и по усеченной матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий.

Аффинное правило

При поиске решения матричных игр часто оказывается полезным следующее свойство.

Допустимые преобразования матрицы игры и ее цена. Оптимальные стратегии у матричных игр, элементы матриц A и С которых связаны равенствами

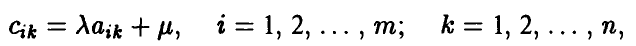
где 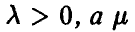— произвольно, имеют одинаковые равновесные ситуации (либо в чистых либо в смешанных стратегиях), а их цены удовлетворяют следующему условию

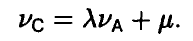
Пример:

Элементы матриц

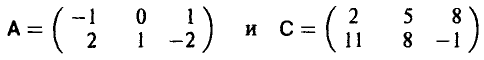
связаны равенством

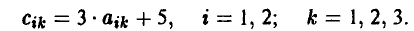
Поэтому цена игры с матрицей С легко вычисляется

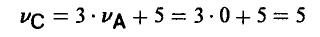
(см. пример 7).

Основные этапы поиска решения матричной игры

1- й этап — проверка наличия (или отсутствия) равновесия в чистых стратегиях (при наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры).

2- й этап — поиск доминирующих стратегий (в случае успеха этого поиска — отбрасывание доминируемых строк и столбцов в исходной матрице игры).

3-й этап — замена игры на ее смешанное расширение и отыскание оптимальных смешанных стратегий и цены игры.

Итерационный метод решения матричных игр

Опишем метод отыскания решения матричной игры — цены игры и оптимальных смешанных стратегий, в известной степени верно отражающий некоторую реальную ситуацию накопления опыта постепенной выработки игроками хороших стратегий в результате многих повторений конфликтных ситуаций. Основная идея этого метода заключается в том, чтобы мысленно как бы смоделировать реальное практическое «обучение» игроков в ходе самой игры, когда каждый из игроков на собственном опыте прощупывает способ поведения противника и старается отвечать на него наиболее выгодным для себя образом. Иными словами, всякий раз при возобновлении игры игрок выбирает наиболее выгодную для себя стратегию, опираясь на предыдущий выбор противника.

Проиллюстрируем этот метод на примере игры, заданной матрицей

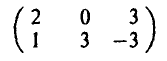
(здесь maxmin = 0, minmax = 2 => седловой точки нет).

Опишем правила выбора ходов игроками,-предположив, для определенности, что начинает игрок А:

игрок В выбирает свою стратегию так, чтобы выигрыш игрока А был минимален (отмечен полужирным шрифтом):

игрок А выбирает свою стратегию так, чтобы его выигрыш при стратегии 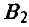игрока В был максимален (отмечен полужирным шрифтом):

игрок В выбирает свою стратегию так, чтобы «накопленный» выигрыш игрока А при стратегиях 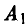и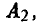

был минимален:

игрок А выбирает свою стратегию так, чтобы его «накопленный» выигрыш при стратегиях 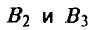игрока В,

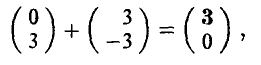
был максимален:

игрок В выбирает свою стратегию так, чтобы «накопленный» выигрыш игрока А при стратегиях 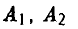и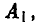

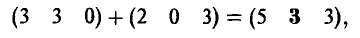
был минимален:

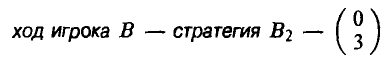
и т.д.

Разобьем последовательные ходы игроков А и В на пары

(ход игрока А, ход игрока В)

и запишем результаты в таблице

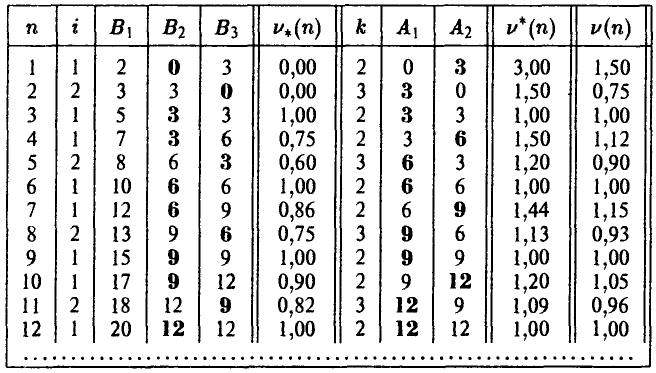
требующей некоторых пояснений.

Описание таблицы

1- й столбец — номер п шага (пары последовательных ходов игроков А и В),
2- й столбец — номер і стратегии, выбранной игроком А,

6- й столбец — минимальный средний выигрыш игрока А, равный минимальному накопленному им выигрышу за первые n шагов, деленному на число этих шагов,

7- й столбец — номер k стратегии, выбранной игроком В,

10- й столбец — максимальный средний выигрыш игрока А, равный максимальному накопленному им выигрышу за первые п шагов, деленному на число этих шагов,

11- й столбец — среднее арифметическое минимального среднего выигрыша и максимального среднего выигрыша игрока А.

Решение игры определяется приближенно по окончании любого из шагов.

Например, за приближенную цену игры можно взять среднее арифметическое v(n), полученное на n-м шаге. Смешанные стратегии противников определяются частотами появления чистых стратегий.

После 9-го шага имеем

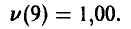
При этом игрок А 6 раз использовал стратегию 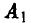и 3 раза стратегию 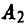. В свою очередь игрок В 6 раз применял стратегию 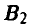, 3 раза стратегию 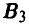, а стратегией 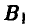не пользовался вообще. Отсюда получаем, что

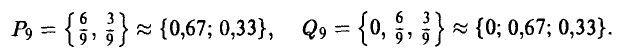
Соответственно, после 10-го шага получаем —

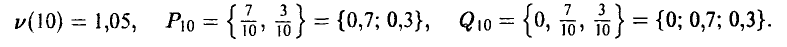
Данная игра легко решается графически. Вот точный ответ:

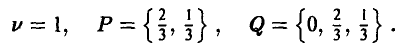
Сравнивая результаты, полученные на 9-м, 10-м, а также 11-м и 12-м шагах:

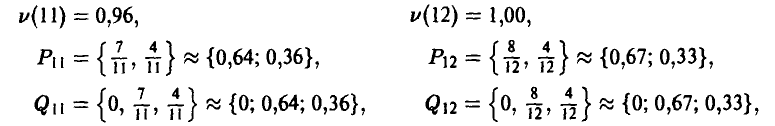
замечаем, что по мере увеличения числа шагов значения все меньше отличаются от точных.

Сделаем несколько замечаний:

Замечание:

При увеличении числа шагов все три величины 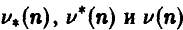будут приближаться к цене игры v, но среднее арифметическое v(n) будет приближаться к и сравнительно быстрее.

Замечание:

Хотя сходимость итераций весьма медленна, тем не менее, даже такой небольшой расчет всегда дает возможность находить ориентировочное значение цены игры и доли чистых стратегий.

Замечание:

Сравнительно медленная скорость сходимости можно объяснить целым рядом причин. Укажем одну из них, психологически наиболее интересную. Если, к примеру, игрок А уже получил оптимальную смешанную стратегию, то он не склонен останавливаться на ней. Отнюдь нет — он продолжит попытки выиграть у противника В побольше, особенно если последний еще не достиг оптимальной смешанной стратегии. Тем самым, игрок А может невольно ухудшить свое положение.

Замечание:

Отметим два основных преимущества описанного метода:
1) итерационный метод прост и одновременно универсален (при его помощи можно легко найти приближенное решение любой матричной игры),
2) объем и сложность вычислений сравнительно слабо растут по мере увеличения числа стратегий игроков (размеров матрицы игры).

Сведение матричной игры к задаче линейного программирования

Рассмотрим m х n игру с платежной матрицей

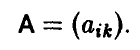
Без ограничения общности будем считать, что все элементы матрицы А положительны (этого всегда можно добиться, пользуясь аффинным правилом, преобразующим заданную матрицу игры, но не изменяющим оптимальных смешанных стратегий игроков). Тем самым, искомая цена игры v — положительное число.

Интересы игрока А

Из теоремы о свойствах оптимальных смешанных стратегий игроков вытекает, что при любой чистой стратегии 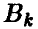игрока В, k = 1, 2, … , n, оптимальная смешанная стратегия 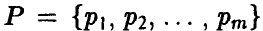игрока А обеспечивает его средний выигрыш, не меньший и. Иными словами, выполняются соотношения

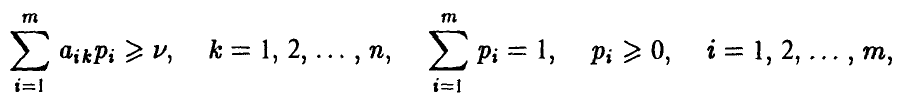
которые с учетом обозначений

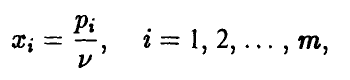
можно записать так

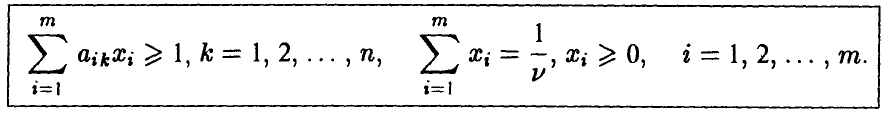
Поскольку игрок А стремится сделать свой гарантированный выигрыш максимально возможным, то задача отыскания решения матричной игры сводится к следующей задаче:

найти неотрицательные величины 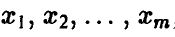удовлетворяющие неравенствам

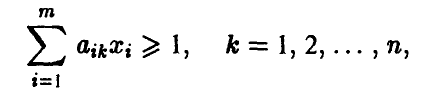
и такие, что их сумма минимальна

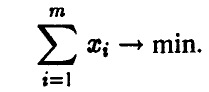
Интересы игрока В

Аналогичным образом заключаем, что оптимальная смешанная стратегия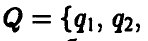 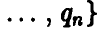игрока В при любой чистой стратегии 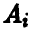, игрока А, і = 1, 2,… , m, обеспечивает его средний проигрыш, не больший v. Иными словами, выполняются соотношения

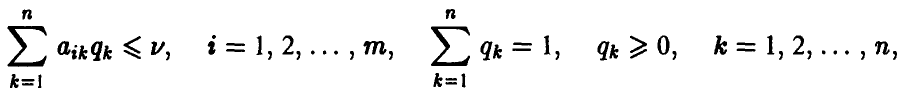
которые с учетом обозначений

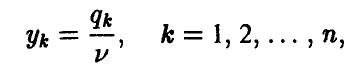
можно записать так

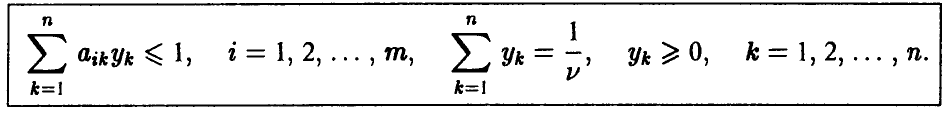
Поскольку игрок В стремится сделать свой гарантированный проигрыш минимально возможным, то задача отыскания решения матричной игры сводится к следующей задаче:

найти неотрицательные величины 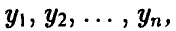удовлетворяющие неравенствам

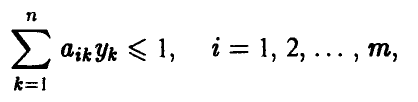
и такие, что их сумма максимальна

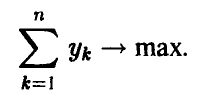
Тем самым, мы получаем следующий важный результат.

Теорема:

Решение матричной игры с положительной платежной матрицей 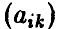равносильно решению двойственных задач линейного программирования

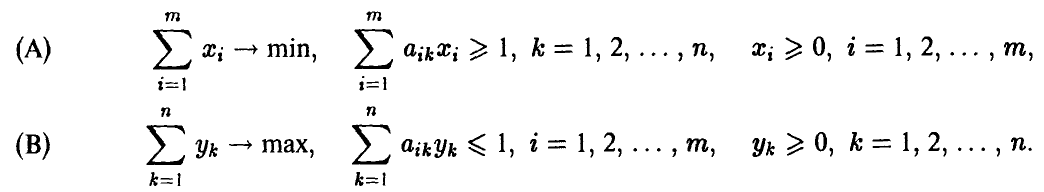
При этом цена игры

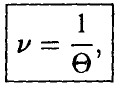
где 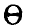— величина, обратная общему значению оптимальных сумм,

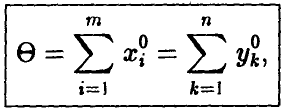
а оптимальные значения 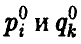связаны с оптимальными 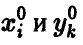посредством равенств

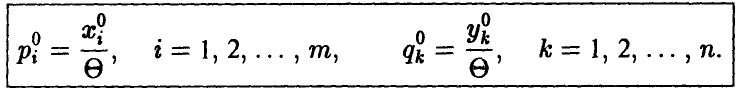
Алгоритм решения матричной игры

1- й шаг. Ко всем элементам исходной матрицы игры прибавляется одно и то же положительное число 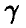так, чтобы все элементы новой матрицы были строго положительны.

2-й шаг. Решаются двойственные задачи линейного программирования (А) и (В) (например, симплекс-методом, или как-нибудь иначе). Находятся наборы 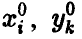и число .

3- шаг. Строятся оптимальные смешанные стратегии игроков Ап В соответственно

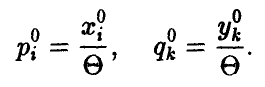
4- й шаг. Вычисляется цена игры

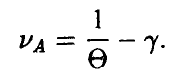
Пример:

Рассмотрим 2×2 игру с матрицей

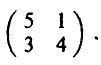
Соответствующие ей задачи линейного программирования имеют вид

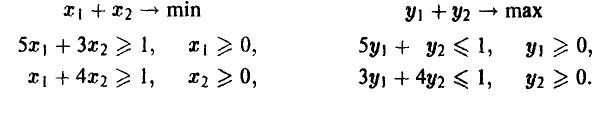
Решение:

1-й шаг. Все элементы платежной матрицы положительны.

2-й шаг. Строим решения обеих задач линейного программирования, пользуясь графическим методом. В результате получаем, что

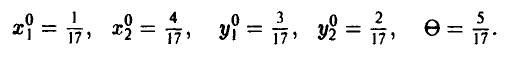
3-й шаг.

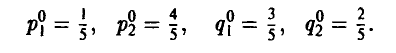
4-й шаг.

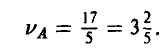
Примеры задач, сводимых к матричным играм

В чистом виде антагонистические конфликты встречаются редко (разве только в боевых действиях и в спортивных состязаниях). Однако довольно часто конфликты, в которых интересы сторон противоположны, при допущении, что множество способов действия сторон конечно, можно моделировать матричными играми.

Рассмотрим несколько конкретных ситуаций.

Пример:

«Планирование посева». Сельскохозяйственное предприятие имеет возможность выращивать две культуры — 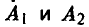. Необходимо определить, как сеять эти культуры, если при прочих равных условиях их урожаи зависят от погоды, а план посева должен обеспечить наибольший доход (прибыль от реализации выращенной культуры определяется полученным объемом). В зоне рискованного земледелия (а таковой является большая часть России) планирование посева должно осуществляться с учетом наименее благоприятного состояния погоды.

Таким образом, одной из сторон выступает сельскохозяйственное предприятие, заинтересованное в том, чтобы получить наибольший доход (игрок А}, а другой стороной — природа, способная навредить сельскохозяйственному предприятию в максимальной степени (от нее зависят погодные условия) и преследующая тем самым прямо противоположные цели (игрок В).

Принятие природы за противника равносильно планированию посева с учетом наиболее неблагоприятных условий; если же погодные условия окажутся благоприятными, то выбранный план даст возможность увеличить доход.

Налицо антагонистический конфликт, в котором у игрока А две стратегии — 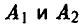, а у игрока В три — 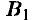(засушливое лето), 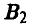(нормальное лето) и 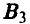(дождливое лето).

В качестве выигрыша игрока Л возьмем прибыль от реализации и будем считать, что расчеты прибыли сельскохозяйственного предприятия (в млрд руб.) в зависимости от состояний погоды сведены в следующую матрицу

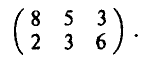
Нетрудно заметить, что седловой точки у этой матрицы нет. Поэтому оптимальная стратегия игрока A будет смешанной. Применяя графический метод, получаем

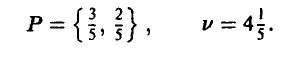
Замечание:

Здесь мы столкнулись со сравнительно редкой ситуацией, когда оптимальная смешанная стратегия одного из игроков допускает так называемую «физическую» реализацию. Полученное решение сельскохозяйственное предприятие может использовать так:

на 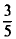всех площадей выращивать культуру ,

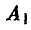на 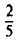всех площадей выращивать культуру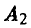

и получать прибыль в размере, не меньшем 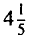млрд руб.

Пример:

«Переговоры о заключении контракта между профсоюзом и администрацией». Рассмотрим фирму, администрация которой ведет переговоры с профсоюзом рабочих и служащих о заключении контракта.

Предположим, что платежная матрица, отражающая интересы договаривающихся сторон, имеет следующий вид

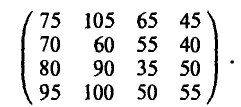
Выплаты указаны в центах в час и представляют собой среднюю зарплату служащего фирмы вместе со всеми добавками. Тем самым, заданная матрица описывает прибыль профсоюза (игрок А) и затраты администрации фирмы (игрок В).

Ясно, что профсоюз стремится максимизировать доходы рабочих и служащих, в то время как администрации хотелось бы минимизировать собственные потери.

Нетрудно заметить, что седловой точки у платежной матрицы нет. Кроме того, для дальнейшего анализа существенными являются лишь стратегии 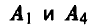игрока А и стратегии 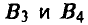игрока В (в этом нетрудно убедиться, воспользовавшись правилом доминирования стратегий). В результате соответствующего усечения получим матрицу

Элементы матрицы

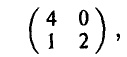
связаны с элементами предыдущей матрицы соотношениями

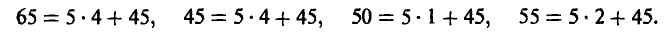
Воспользовавшись графическим методом, в итоге получим

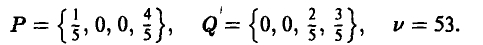
Тем самым, профсоюзу следует выбирать стратегию 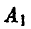в 20 % случаев и стратегию 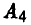в 80 %. Что касается администрации, то ей следует выбирать стратегию 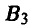с вероятностью 0,4 и стратегию 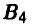с вероятностью 0,6. При этом ожидаемая цена игры равна 53.

Замечание:

Следует отметить, что если процесс переговоров будет повторяться много раз, то среднему должно сходиться к ожидаемому значению 53. Если же переговоры пройдут лишь единожды, то реальный результат получится при выборе каждым игроком некоторой своей чистой стратегии. Поэтому один из игроков, профсоюз или администрация, будет неудовлетворен.

Пример:

«Локальный конфликт». Рассмотрим войну между двумя небольшими государствами А и В, которая ведется в течение 30 дней.

Для бомбардировки небольшого моста — важного военного объекта страны В — страна А использует оба имеющихся у нее самолета. Разрушенный мост восстанавливается в течение суток, а каждый самолет совершает один полет в день по одному из двух воздушных маршрутов, соединяющих эти страны. У страны В есть два зенитных орудия, при помощи которых можно сбивать самолеты страны А. Если самолет собьют, то некая третья страна в течение суток поставит стране А новый самолет.

Страна А может послать самолеты либо по одному маршруту, либо по разным. Страна В может поместить либо обе зенитки на одном маршруте, либо по одной зенитке на каждый маршрут.

Если один самолет летит по маршруту, на котором расположена одна зенитка, то этот самолет будет сбит. Если два самолета летят по маршруту, на котором расположены две зенитки, то оба самолета будут сбиты. Если два самолета летят по маршруту, на котором расположена одна зенитка, то сбит будет только один самолет. Если самолет доберется до цели, то мост будет уничтожен.

У страны А есть две стратегии:

послать самолеты по разным маршрутам —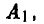

послать самолеты по одному маршруту —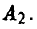

У страны В — также две стратегии:

поместить зенитки на разных маршрутах —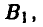

поместить зенитки на одном маршруте —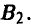

Если страна А выберет стратегию 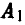, а страна В — стратегию 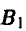, то страна А получит нулевой выигрыш, так как ни один из самолетов не достигнет цели.

Если страна А выберет стратегию 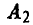, а страна В — стратегию 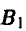, то хотя бы один самолет достигнет цели и вероятность разрушения моста будет равна 1.

Если страна А выберет стратегию 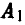, а страна В — стратегию 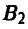, то вновь хотя бы один самолет достигнет цели и вероятность разрушения моста будет равна 1.

Если страна А выберет стратегию 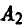, а страна В — стратегию 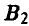, то страна А с вероятностью 1/2 выберет маршрут, на котором установлены зенитки, и, следовательно, цель будет уничтожена с вероятностью 1/2.

Оформим результаты проведенного анализа в стандартной игровой форме:

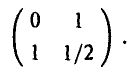
При помощи графического метода получаем оптимальные смешанные стратегии игроков и цену игры

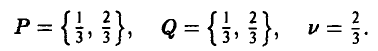
Это означает, что если страна А будет посылать самолеты по разным маршрутам в течение десяти дней из тридцати, отпущенных на войну (и, значит, по одному маршруту в течение двадцати дней), то в среднем страна А будет иметь 66,7 % удачных случаев (мост будем находиться в нерабочем состоянии). Воспользовавшись для своих зениток предложенным выбором, страна В не позволит бомбить мост чаще, чем в 66,7 % случаев.

Несколько слов в заключение

Матричные игры моделируют конфликтные ситуации, в которых каждая из сторон-участниц делает свой ход одновременно со второй стороной. При этом наибольший интерес представляет случай, когда игра не заканчивается сразу же после совершения игроками одной такой пары одновременных ходов, а повторяется многократно. Причем считается, что перед каждым возобновлением игры игроки не получают никаких новых сведений ни о конфликте, ни о возможных действиях противной стороны. Иными словами, при многократном повторении матричной игры каждая из сторон всякий раз оказывается перед выбором некоторой стратегии из одного и того же множества стратегий, неизменного у каждого из игроков.

Тем не менее, в таких многократно повторяющихся обстоятельствах большую роль играет анализ игры, как предварительный, так и промежуточный.

В результате разумно проведенного предварительного анализа матричной игры заинтересованная в анализе сторона может определить свою линию поведения (правило выбора стратегий) на всю серию игр. Разумеется, описанный нами выше максимин-ный подход является далеко не единственным средством. Однако не следует забывать, что принципиальной особенностью этого подхода является то обстоятельство, что игрок, придерживающийся выводимого на его основе правила выбора стратегий, заранее может довольно точно оценить нетривиальные размеры своего гарантированного выигрыша. Кроме того, максиминный подход позволяет сводить задачу поиска решения игры к рассмотрению сравнительно несложных задач линейного программирования и, тем самым, получать эффективные рекомендации по тому, как лучше выбирать стратегии в конкретной игре при многократном ее повторении.

Если игра повторяется много раз, то некоторые дополнительные сведения — какие именно стратегии выбирает противная сторона и какими правилами выбора стратегий она руководствуется — игрок все же получает. На основании этих сведений и результатов предварительного анализа игры он может довольно точно оценить противника и, если тот не придерживается компромиссного максиминного подхода, внести соответствующие изменения в собственную линию поведения и увеличить выигрыш.

О классификации игр

Реальные конфликтные ситуации приводят к различным видам игр. К настоящему времени общепризнанной классификации игр пока не сложилось. Тем не менее, легко заметить, что игры различаются по целому ряду признаков: по количеству участвующих в них игроков, по количеству возможных стратегий, по характеру взаимоотношений между игроками, по характеру выигрышей, по виду функций выигрышей, по количеству ходов, по характеру информационной обеспеченности игроков и т. д.

Остановимся на этих различиях чуть подробнее.

В зависимости от количества игроков определяют игры трех типов: игры одного игрока (в теории игр, как правило, не рассматриваются), игры двух игроков (наиболее изученный класс игр) и игры n игроков (успехов в изучении которых сравнительно немного вследствие возникающих принципиальных трудностей).

По количеству стратегий игроков игры делятся на конечные (каждый из игроков имеет конечное число возможных стратегий) и бесконечные (где хотя бы один из игроков имеет бесконечное количество возможных стратегий).

По характеру взаимоотношений между игроками игры делятся на бескоалиционные (в которых игроки не имеют права вступать в соглашения и образовывать коалиции), коалиционные (в которых игроки могут вступать в соглашения и образовывать коалиции) и кооперативные (в которых соглашения, связывающие игроков, определены наперед и обязательны).

По характеру выигрышей различают игры с нулевой суммой (общий капитал игроков не изменяется, а просто перераспределяется между игроками в зависимости от получающихся исходов) и игры с ненулевой суммой.

Игру двух игроков с нулевой суммой часто называют антагонистической, вследствие того, что цели игроков в них прямо противоположны: выигрыш одного из игроков происходит только за счет проигрыша другого.

По виду функций выигрышей игры делятся на: матричные игры (рассмотренные выше), биматричные игры, игры типа дуэлей, непрерывные игры, выпуклые игры и др.

По количеству ходов игры делятся на одношаговые (завершающиеся после одного хода каждого из игроков) и многошаговые, которые, в свою очередь, делятся на позиционные игры (каждый из игроков может последовательно во времени делать несколько ходов), стохастические игры (где при выборе новых позиций имеется определенная вероятность возврата на предшествующую позицию), дифференциальные игры (в которых допускается делать ходы непрерывно и подчинять поведение игроков условиями, описываемыми дифференциальными уравнениями), игры типа дуэлей (характеризующиеся моментом выбора хода и вероятностями получения выигрышей в зависимости от времени, прошедшего от начала игры до момента выбора).

По характеру информационной обеспеченности игроков различают игры с полной информацией (на каждом ходе игры каждому игроку известно, какие выборы были сделаны ранее всеми игроками) и игры с неполной информацией (если в игре не все известно о предыдущих выборах).

Существуют, разумеется, и другие виды игр.

В зависимости от вида игры разрабатывается и метод ее решения. Однако читатель, видимо, уже заметил, что структура предложенного выше описания основных направлений различения игр не является древовидной: одни и те же виды игр оказываются в разных классах.

Впрочем, возможны и иные подходы к разбиению игр.

Далее мы рассмотрим некоторые из указанных видов игр, а именно позиционные и биматричные игры.

Позиционные игры

Во многих практически важных конфликтных ситуациях, располагая той или иной информацией об их прошлом развитии, стороны-участницы совершают свой выбор не раз и навсегда, а последовательно во времени, шаг за шагом. Тем самым, они используют стратегии, отражающие как динамику конфликта, так и степень собственной информированности о фактически складывающейся обстановке в развитии этого конфликта.

Структура позиционной игры

Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются так называемые позиционные игры.

Позиционная игра — это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.

Процесс самой игры состоит в последовательном переходе от одного состояния игры к другому состоянию, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом (случайный ход).

В качестве примеров позиционных игр можно привести крестики-нолики, шашки, шахматы, карточные игры, домино и др. Интересно, что право выбора первого хода в этих играх часто определяется случайным образом.

Состояния игры принято называть позициями (отсюда и название — позиционные игры), а возможные выборы в каждой позиции — альтернативами.

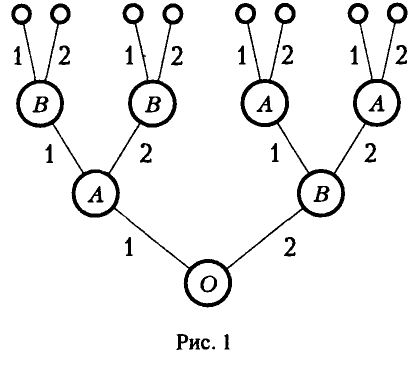
Характерной особенностью позиционной игры является возможность представления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры (рис. 1).

Для определенности мы будем рассматривать позиционные игры, в каждой позиции которых, кроме окончательных, ровно две альтернативы — первая и вторая.

Замечание:

Символ О, А или В в кружке указывает, кто из игроков (О, А или В) делает очередной ход в заданной позиции. При этом символом О обычно обозначается ход в игре, осуществляемый не игроком, а каким-нибудь случайным механизмом (иногда его называют природой). Например, в позиционной игре, представленной на рис. 1 своим деревом, первый ход производится случайно. Пользуясь графическим описанием игры, можно сказать, что процесс игры состоит в переходе от начальной позиции к окончательной через непосредственно следующие одна за другой промежуточные позиции.

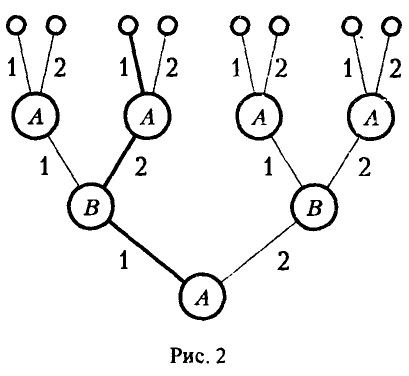
Каждая окончательная вершина определяет единственную цепь (последовательность идущих друг за другом звеньев), связывающую начальную вершину с данной (рис. 2). Такая цепь называется партией. На рис. 2 одна из партий выделена жирными линиями. Число различных партий равно числу окончательных вершин (позиций).

В каждой окончательной позиции задан числовой выигрыш игрока А.

Замечание:

Мы будем рассматривать здесь только антагонистические позиционные игры.

В шахматах функция выигрышей игрока А (белых) определяется так:

+1 на выигрываемых партиях,
О на ничейных партиях,
-1 на проигрываемых партиях.

Функция выигрышей игрока В (черных) отличается от функции выигрышей белых только знаком.

Различают позиционные игры с полной информацией и позиционные игры с неполной информацией.

В позиционных играх с полной информацией (пример — шашки, шахматы) каждый игрок при своем ходе знает ту позицию дерева игры, в которой он находится.

В позиционных играх с неполной информацией (пример — домино) игрок, делающий ход, не знает точно, в какой именно позиции дерева игры он фактически находится. Этому игроку известно лишь некоторое множество позиций, включающее в себя его фактическую позицию. Такое множество позиций называется информационным множеством.

Таким образом, в игре с неполной информацией игрок при своем ходе знает, в каком информационном множестве он находится, но ему неизвестно, в какой именно позиции этого множества.

Позиции, принадлежащие одному и тому же информационному множеству, объединяются пунктирными линиями.

Рассмотрим примеры двух игр, состоящих из двух ходов, которые последовательно делают участвующие в ней игроки А и В. Начинает игрок А: он выбирает одну из двух возможных альтернатив — число х, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива). На ход игрока А игрок В отвечает своим ходом, выбирая одну из двух возможных альтернатив — число у, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива).

И в результате игрок А получает вознаграждение или вынужден платить штраф.

Пример:

1- й ход. Игрок А выбирает число х из множества двух чисел {1,2}.
2- й ход. Игрок В выбирает число у из множества двух чисел {1,2}, зная выбор числа х игроком А.

Функция W(x, у) выплат игроку А за счет игрока В задается так

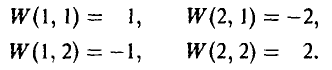
На рис. 3 показаны дерево игры и информационные множества.

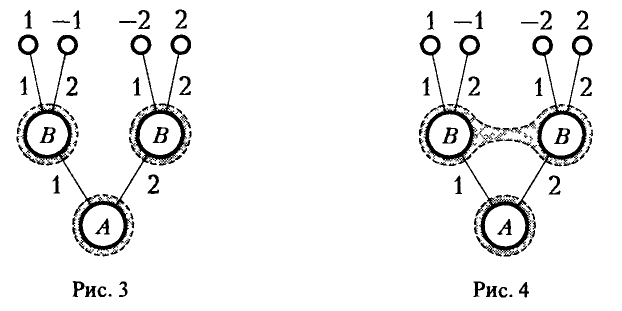
Пример:

В случае, если выполнены все условия предыдущего примера, кроме одного — хода игрока В,

2-й ход — игрок В выбирает число у из множества двух чисел {1, 2}, не зная выбора числа х игроком А, информационные множества выглядят так, как показано на рис.4.

Нормализация позиционной игры

Заранее определенную последовательность ходов игрока, выбранную им в зависимости от информации о ходах другого игрока и ходах игрока О (природы), будем называть чистой стратегией этого игрока.

В том случае, если в игре нет случайных ходов (игрок О в игре не участвует), выбор игроком А и игроком В чистых стратегий однозначно определяет исход игры — приводит к окончательной позиции, где игрок А и получает свой выигрыш. Это обстоятельство позволяет сводить позиционную игру к матричной игре.

Процесс сведения позиционной игры к матричной называется нормализацией позиционной игры.

Покажем на нескольких примерах, как это делается.

Пример:

Опишем стратегии игроков.

Стратегию игрока А можно задать одним числом х, показывающим, какую альтернативу, первую или вторую, выбрал игрок.

Тем самым, у игрока А две чистых стратегии:

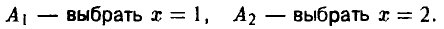
Стратегию игрока В, принимая во внимание, что выбор игрока А на 1-м ходе ему известен, удобно описывать упорядоченной парой

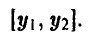
Здесь 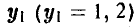— альтернатива, выбираемая игроком В при условии, что игрок А выбрал первую альтернативу, 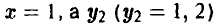— альтернатива, выбираемая игроком В при условии, что игрок А выбрал вторую альтернативу, х = 2.

Например, выбор игроком В стратегии [2, 1] означает, что если на 1-м ходе игрок А выбрал х = 1, то игрок В на своем ходе должен выбрать у = 2. Если же на 1-м ходе игрок А выбрал х = 2, то согласно этой стратегии игрок В на своем ходе должен выбрать у = 1.

Таким образом, у игрока В четыре чистых стратегии:
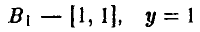при любом выборе х;
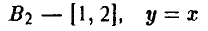при любом выборе x’,
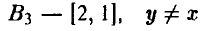при любом выборе х;
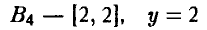при любом выборе x.

Покажем теперь, как рассчитываются выигрыши игрока А в зависимости от примененных стратегий.

Пусть, например, игрок А выбрал стратегию 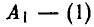, а игрок В — стратегию 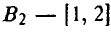. Тогда х = 1, а из стратегии [1, 2] вытекает, что у = 1. Отсюда

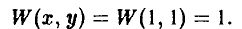
Остальные выигрыши рассчитываются совершенно аналогично.

Результаты расчетов записываются обычно или в виде таблицы выигрышей игрока А

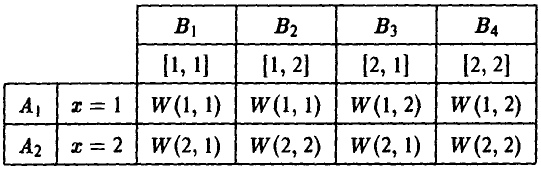
или в виде матрицы игры

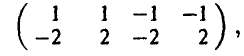
где, как обычно, строки соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В.

Полученная матрица имеет седловую точку. Оптимальные стратегии игроков: 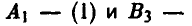[2, 1]. Тем самым, игрок А на 1-м ходе выбирает х = 1, а игрок В на 2-м ходе выбирает у = 2. Цена игры v=— 1.

Пример:

Опишем стратегии игроков.

У игрока А они те же, что и в предыдущем примере:

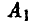— выбрать х = 1, 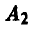— выбрать х = 2.

Так как игроку В выбор игрока А неизвестен, то есть игрок В не знает, в какой именно из двух позиций он находится (см. рис. 4), то у него те же две стратегии:

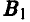— выбрать у = 1, 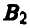— выбрать у = 2.

Соответствующие таблица выигрышей игрока А и матрица игры имеют следующий вид

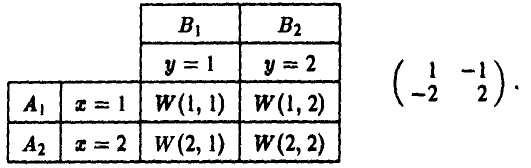
Полученная матрица седловой точки не имеет. Оптимальные смешанные стратегии игроков; Р = {2/3,1/3} и Q = {1/2,1/2}. Цена игры v = 0.

Замечание:

На этих двух примерах хорошо видно, что результат сведения позиционной игры к матричной напрямую зависит от степени информированности игроков. В частности, отсутствие у игрока В сведений о выборе, сделанном игроком А, приводит к уменьшению количества его возможных стратегий. Сравнивая ответы, полученные в примерах 13 и 14, замечаем, что снижение уровня информированности игрока (в данном случае — игрока В) делает для него исход игры менее благоприятным.

Замечание:

Приведенные выше примеры не исчерпывают всех возможных вариантов даже в этом, самом простом, случае двухходовых позиционных игр.

Рассмотрим теперь несколько примеров сведения к матричным играм позиционных игр, состоящих из трех ходов, сосредоточив при этом основное внимание на одном из наиболее ответственных шагов нормализации — описании стратегий игроков.

Пример:
1- й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}.
2- й ход делает игрок В: зная выбранное игроком А число х, он выбирает число у из множества двух чисел {1,2}.
3- й ход делает игрок А: не зная о выбранном игроке В числе у на 2-м ходе и забыв выбранное им самим на 1 -м ходе число х, он выбирает число z из множества двух чисел {1, 2}.

После этого игрок А получает вознаграждение W(х, у, z) за счет игрока В, например, такое:

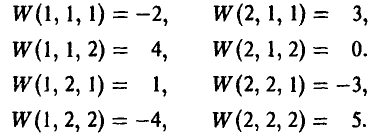
На рис. 5 показаны дерево игры и информационные множества.

Нормализуем эту игру.

Поскольку игроку В выбор игрока А на 1-м ходе известен, то у игрока В те же четыре стратегии, что и в примере 13:

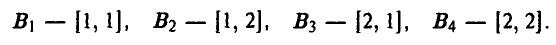
Игрок А на 3-м ходе не знает предыдущих выборов — ни значения х, ни значения у. Поэтому каждая его стратегия состоит просто из пары чисел (х, z), где х (х = 1, 2) — альтернатива, выбираемая игроком А на 1-м ходе, a z (z = 1, 2) — альтернатива, выбираемая игроком А на 3-м ходе.

Например, выбор игроком А стратегии (2, 1) означает, что на 1-м ходе он выбирает х = 2, а на 3-м ходе — z = 1.

Таким образом, у игрока А четыре стратегии:

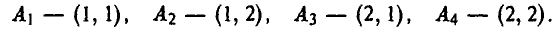
Покажем теперь, как рассчитываются выигрыши игрока А в зависимости от стратегий, применяемых в данной игре. Пусть, например, игрок А выбрал стратегию 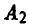— (1, 2), а игрок В — стратегию 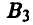— [2, 1]. Тогда х = 1, откуда вытекает, что у = 2. Значение z = 2 выбрано игроком А независимо от выбора игрока В. Вычисляя значение функции выигрышей для этого набора, получаем

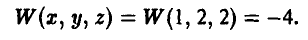
В результате подобных рассуждений получаются и остальные пятнадцать выигрышей. Это позволяет построить таблицу выигрышей игрока А. Имеем

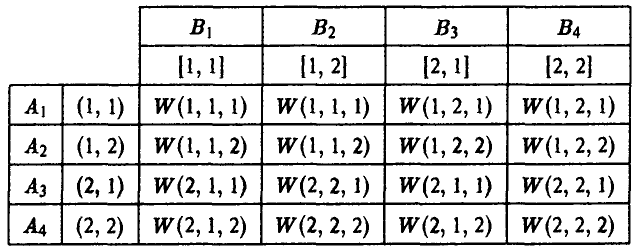
или

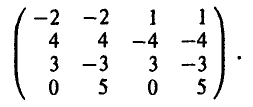
Пример:
1- й ход делает игрок А: он выбирает число х из множества двух чисел {1,2}.
2- й ход делает игрок В; не зная о выборе игрока А на 1-м ходе, он выбирает число у из множества двух чисел {1, 2}.
3- й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, не зная ни значения х, ни значения у.

После этого игроки расплачиваются по правилу, указанному в примере 15.

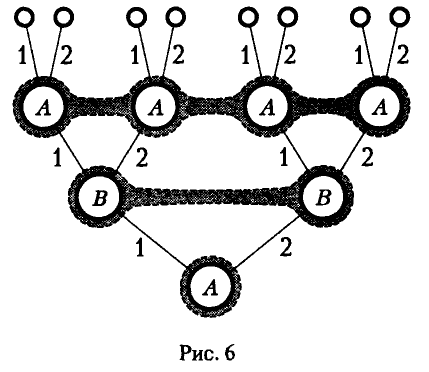
Графическое представление этой игры показано на рис. 6.
Ясно, что у игрока А те же четыре стратегии, что и в примере 15:

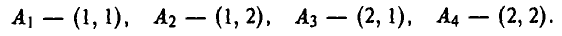
У игрока В всего две стратегии:

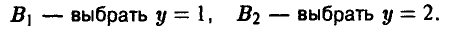
В этом случае (весьма слабой информированности игроков) таблица выигрышей игрока А и соответствующая матрица строятся совсем просто. Имеем

Оптимальные смешанные стратегии игроков и цена игры соответственно равны.

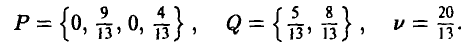
В следующем примере информационные множества выглядят немного иначе.

Пример:
1- й ход делает игрок А : он выбирает число х из множества двух чисел {1,2}.
2-й ход делает игрок В; не зная о выборе игрока А на 1-м ходе, он выбирает число у из множества двух чисел {1, 2}.
3- й ход делает игрок А : он выбирает число z из множества двух чисел {1, 2}, зная выбор у игрока В на 2-м ходе, но не помня собственного выбора х на 1-м ходе.

После этого игроки расплачиваются по правилу, указанному в примере 15.

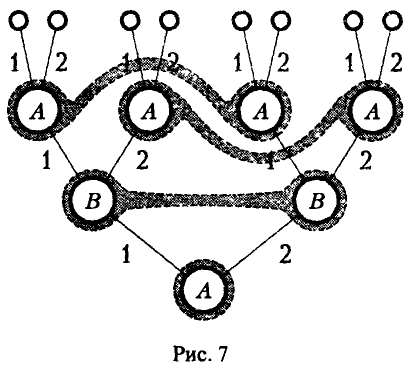
Графическое представление этой игры показано на рис. 7.

Поскольку игроку В неизвестен выбор игрока А на 1-м ходе, то, выполняя свой ход, он не знает, в какой именно из двух возможных позиций он находится. Поэтому у игрока В всего две стратегии:

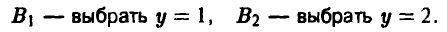
При описании стратегий игрока А нужно исходить из того, что к 3-му ходу игрок А утратил сведения о собственном выборе на 1-м ходе, но ему известен выбор игрока В на 2-м ходе. Поэтому выбор числа z игроку А следует связать с известным ему к 3-му ходу значением у. Удобнее всего это сделать по аналогии с расчетом стратегий игрока В в примерах 13 и 15, т. е. при помощи упорядоченной пары

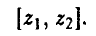
Здесь 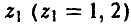— альтернатива, выбираемая игроком А при условии, что игрок В выбрал первую альтернативу, у = 1, a 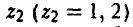— альтернатива, выбираемая игроком А при условии, что игрок В выбрал вторую альтернативу, у = 2.

Чистую стратегию игрока А в данной игре можно записать так

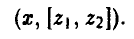
Здесь х (х = 1, 2) — альтернатива, которую игрок А выбирает на 1-м ходе, 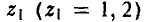— альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал выбрал первую альтернативу (у = 1) и 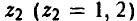— альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал вторую альтернативу (у = 2).

Например, выбор игроком А стратегии (2, [2, 1]) означает, что на 1-м ходе игрок А выбирает х = 2, а на 3-м z = 2, если игрок В выбрал у = 1, и z = 1, если игрок В выбрал у = 2.

Тем самым, у игрока А восемь чистых стратегий:

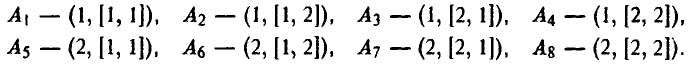
Покажем теперь, как в зависимости от применяемых стратегий определяются элементы таблицы выигрышей игрока А.

Пусть, например, игрок А выбрал стратегию 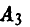— (1, [2, 1]), а игрок В — стратегию 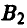— (2) Тогда х = 1, у = 2, а из [2, 1] вытекает, что z = 1. Отсюда

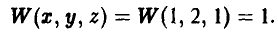
По этой же схеме вычисляются и остальные элементы таблицы.

В результате получаем

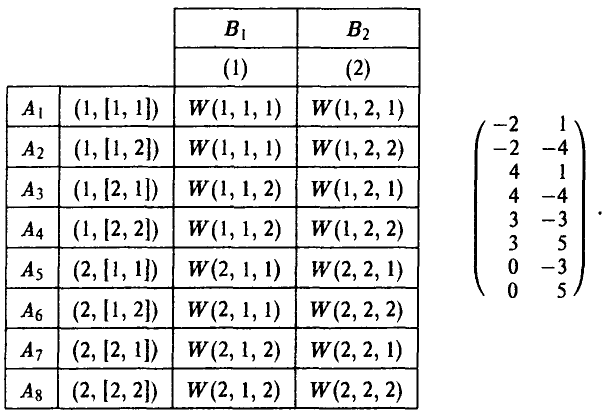
Оптимальные смешанные стратегии игроков и цена игры соответственно равны:

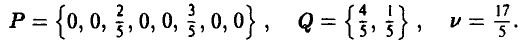
Рассмотрим позиционную игру со случайным ходом.

Пример:
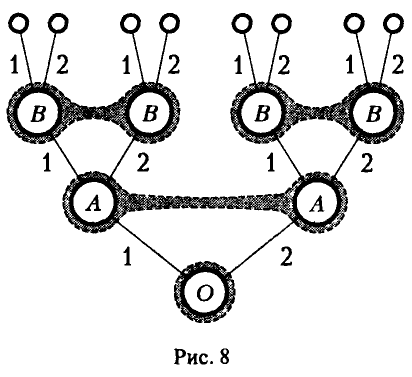
1- й ход производится случайно: игрок О выбирает число х, равное 1, с вероятностью 0,5 и равное 2 с такой же вероятностью.
2-й ход делает игрок А : он выбирает число у из множества двух чисел {1, 2}, не зная результатов случайного выбора на 1-м ходе.
3-й ход делает игрок В: он выбирает число z из множества двух чисел {1, 2}, зная о том, какое именно число х случайно выбрано игроком О на 1-м ходе и не зная выбора у игрока А на 2-м ходе.

После этого игроки расплачиваются, используя функцию W(x, у, z), ту же, что и в предыдущих примерах.

Графическое представление этой игры показано на рис. 8.

Опишем стратегии игроков

Поскольку игроку А исход случайного испытания неизвестен, то он имеет всего две стратегии:

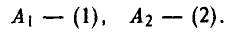
При построении своих стратегий игроку В естественно воспользоваться имеющейся у него информацией о результате 1-го хода. Это позволит ему описать свою стратегию упорядоченной парой

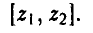
Здесь 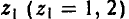— альтернатива, выбираемая игроком В при условии, что х = 1, a 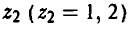— альтернатива, выбираемая игроком В при условии, что х — 2.

Тем самым, у игрока В четыре стратегии:

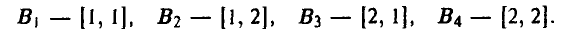
Покажем теперь, как определяются элементы таблицы выигрышей игрока А.

Пусть, например, игрок А выбрал стратегию 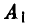— (1), а игрок В — стратегию 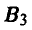— [2, 1]. Различаются два случая

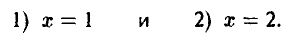
Если х — 1, то стратегия 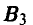указывает игроку В его выбор z = 2. А так как у = 1, то в результате имеем

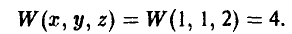
Если х = 2, то стратегия 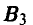указывает игроку В его выбор z = 1. А так как у = 1, то в результате имеем

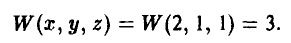
Поскольку первая и вторая альтернативы на 1-м ходе выбираются с вероятностями 0,5 и 0,5, то и вышеуказанные выигрыши появляются с теми же вероятностями и, следовательно, средний выигрыш игрока А при этих стратегиях определяется так

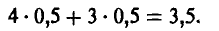
Аналогичным образом рассчитывая остальные средние выигрыши, получаем при x = 1

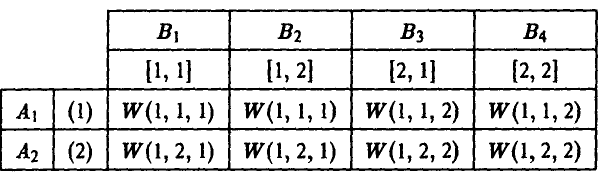
или

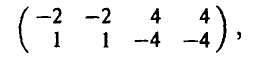
при х = 2

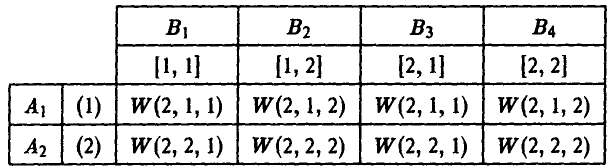
или

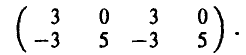
Искомая матрица игры имеет следующий вид

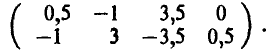
Наконец, рассмотрим пример позиционной игры со случайным разыгрыванием права первого хода.

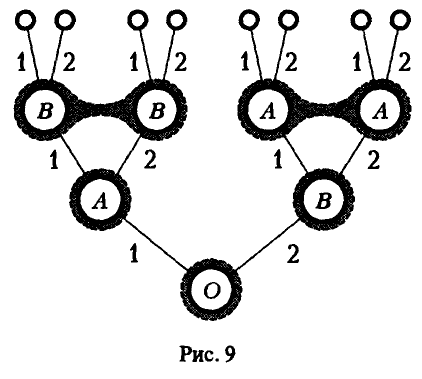
Пример:
1-й ход делает игрок О, выбирая число х, равное 1 с вероятностью 2/3 и равное 2 с вероятностью 1/3.

Если х = 1, то на 2-м ходе игрок А выбирает число у из множества двух чисел {1,2}, зная результат случайного выбора на 1-м ходе, а на 3-м ходе игрок В выбирает число z из множества двух чисел {1, 2}, зная х, но не зная у.

Если х = 2, то на 2-м ходе игрок В выбирает число у из множества двух чисел {1, 2}, зная результат случайного выбора на 1-м ходе, а на 3-м ходе игрок А выбирает число z из множества двух чисел {1, 2}, зная х, но не зная у.

После этого игроки расплачиваются, используя функцию W(x, у, r), ту же, что и в предыдущих примерах.

Графическое представление этой игры показано на рис. 9.

Чистую стратегию игрока А в данной игре можно описать упорядоченной парой

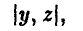
где у (у = 1, 2) — выбор игрока А на 2-м ходе, если на 1-м ходе выбрано х = 1, a z (z = 1, 2) — выбор игрока А на 3-м ходе, если на 1-м ходе выбрано х = 2.

Например, стратегия | 1, 2| означает, что на 2-м ходе игрок А выбирает у = 1, а на 3-м ходе — z = 2.

Тем самым, у игрока А четыре стратегии:

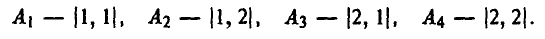
У игрока В те же четыре стратегии:

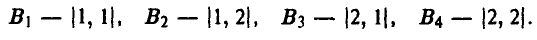
Покажем теперь, как находятся элементы матрицы выигрышей игрока А.

Пусть, например, игрок А применяет стратегию 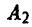— |1, 2|, а игрок В — стратегию 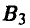— (2, 1|.

Различаются два случая

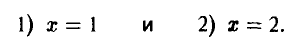
По условию при х = 1 игрок А имеет возможность сделать только 2-й ход (выбрать у), а игрок В — только 3-й (выбрать z). При х = 2 их возможности меняются местами: игроку В предоставлено право 2-го хода (выбрать у}, а игроку А — 3-го (выбрать z).

Если х = 1, то стратегия указывает игроку А при 2-м ходе взять у = 1, а стратегия указывает игроку В при 3-м ходе взять z = 1. В результате

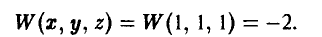
Если х = 2, то стратегия 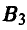указывает игроку В при 2-м ходе взять у = 2, а стратегия 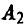указывает игроку А при 3-м ходе взять z = 2. В результате

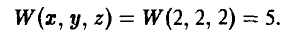
Поскольку первая и вторая альтернативы на 1-м ходе выбираются соответственно с вероятностями 2/3 и 1/3, то и найденные выигрыши появляются с теми же вероятностями. Следовательно, математическое ожидание выигрыша игрока А при таких стратегиях рассчитывается так

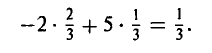
Итак,
при х= 1

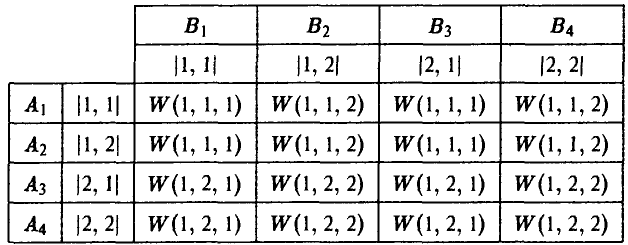
или

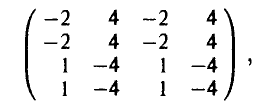
при х = 2

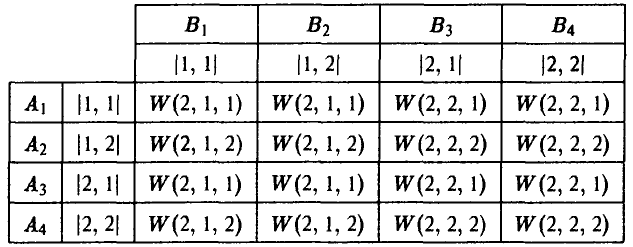
или

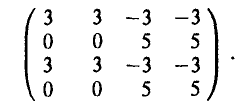
Отсюда получаем искомую матрицу игры

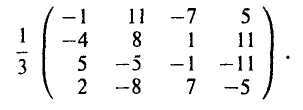
Замечание:

Графическое представление и функция выигрышей полностью определяют позиционную игру. В рассмотренных выше примерах 16-19 мы пользовались одной и той же функцией и одним и тем же деревом. Отличие было только в маркировке вершин дерева и информационных множествах. При построении последних необходимо соблюдать два правила:

1) в одно информационное множество могут входить позиции только одного игрока,

2) цепь, определяющая партию игры, может иметь с информационным множеством не более одной общей позиции.

Как показывает рис. 10, и при таких ограничениях информационные множества могут выглядеть довольно необычно.

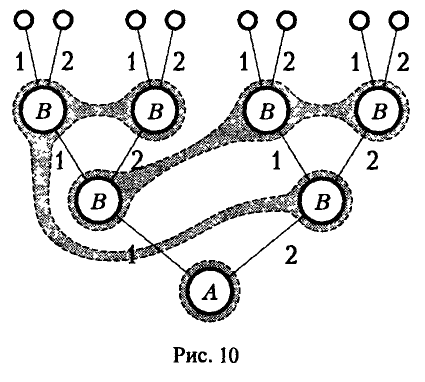
Позиционные игры с полной информацией

Позиционная игра называется игрой с полной информацией, если в каждой позиции любой ее партии игрок, делающий ход, знает, какие альтернативы были выбраны на предыдущих ходах. В графическом описании каждая вершина дерева такой игры представляет собой отдельное информационное множество.

Примерами позиционных игр с полной информацией могут служить крестики-нолики, шашки и шахматы.

Основная особенность позиционной игры с полной информацией состоит в том, что соответствующая ей матрица выигрышей всегда имеет седловую точку, то есть в игре с полной информацией существуют оптимальные чистые стратегии и, значит, равновесная ситуация.

Сказанное означает, что в шахматах (крестиках-ноликах, шашках) уже в начальной позиции либо имеется способ выигрыша за белых, либо способ выигрыша за черных, либо как та, так и другая сторона способна форсировать ничью.

Однако известное доказательство существования равновесной ситуации неконструктивно и не дает эффективных приемов фактического нахождения решения игры.

И такие способы (стратегии) в шахматах не найдены до сих пор, и даже неизвестно, какая из перечисленных возможностей имеет место на самом деле.

Иное дело с игрой крестики-нолики: стратегий в ней немного и она разобрана до самого конца — существуют оптимальные чистые стратегии, ведущие игроков к ничьей.

Рассмотрим несколько примеров.

1. Как нетрудно заметить, двухходовая игра из примера 11 является игрой с полной информацией. Ее нормализация приводит к матрице с седловой точкой (см. пример 13).

2. «Выкладывание монет на стол». Два игрока поочередно кладут монеты одинаковых размеров на обыкновенный стол, всякий раз выбирая произвольное доступное место для монеты (взаимное накрывание монет не допускается). Тот из игроков, кто положит монету, не оставляющую места для новых монет, выигрывает.

Это игра с полной информацией. Существует вполне определенная стратегия, обеспечивающая выигрыш тому из игроков, кто начинает игру. А именно, начинающий игру должен положить первую монету точно в центр стола и на каждый ход противника отвечать симметричным ходом. Исход игры от стратегии второго игрока не зависит.

3. «Переговоры». В переговорах участвуют две стороны А и В. В слегка идеализированном варианте это может выглядеть, например, так.

Сначала сторона А высказывает одно из нескольких предложений, способных заинтересовать сторону В. Затем сторона В, ознакомившись с предложением стороны А, высказывает одно из нескольких встречных предложений, способных, по ее мнению, заинтересовать сторону А. В свою очередь, сторона А, ознакомившись с реакцией стороны В на сделанные предложения, высказывает ей новое предложение, внеся одну из нескольких возможных корректировок в свое первоначальное предложение с учетом мнения стороны В и т. д.

Если предмет переговоров сложен, то подобный обмен ходов может затянуться. Однако любые переговоры непременно заканчиваются. И там, на финише, ждет функция выигрышей.

Попробуем смоделировать короткий переговорный процесс трехходовой позиционной игрой.

Предположим, что переговоры заканчиваются через три хода, на каждом из которых соответствующая сторона имеет возможность выбора из двух альтернатив, и опишем соответствующую позиционную игру.

1-й ход делает сторона А. она выбирает одно из двух возможных предложений — число х из множества двух чисел {1, 2}.

2-й ход делает сторона В: она выбирает число у из множества двух чисел {1, 2}, зная число х, предложенное стороной А.

3- й ход делает сторона А: она выбирает число z из множества двух чисел {1, 2}, зная о предложении стороны В на 2-м ходе и помня собственное предложение на 1-м ходе.

После этого сторона А либо получает вознаграждение (например, в виде кредита от стороны В), либо выплачивает стороне В штраф.

Все эти возможности описываются функцией выигрышей W(x, у, r), заданной следующей таблицей

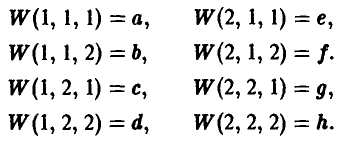
Графическое представление этой игры показано на рис. 11.

Ясно, что описанная позиционная игра является игрой с полной информацией.

Начнем с описания возможных стратегий игрока В.

Поскольку игроку В выбор игрока А на 1-м ходе известен, то у игрока В те же четыре стратегии, что и в примере 13.

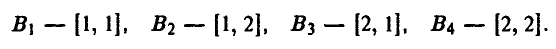
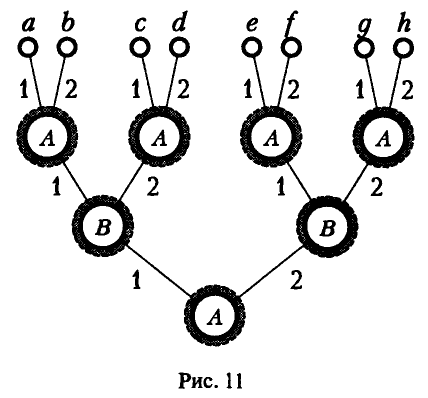
С описания возможных стратегий игрока А дело обстоит немного посложнее — их восемь.

Чистая стратегия игрока А в данной игре описывается упорядоченной тройкой

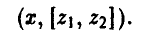
Здесь х (х = 1, 2) — альтернатива, которую игрок А выбирает на 1-м ходе, 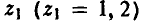— альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал выбрал первую альтернативу (у = 1) и 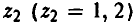— альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал вторую альтернативу (у = 2).

Например, выбор игроком А стратегии (1, [2, 1]) означает, что на 1-м ходе игрок А выбирает х = 1, а на 3-м z = 2, если игрок В выбрал у = 1, и z = 1, если игрок В выбрал у = 2.

Тем самым, у игрока А восемь чистых стратегий:

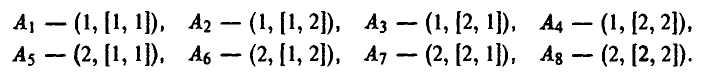
Покажем теперь, как в зависимости от применяемых стратегий определяются элементы таблицы выигрышей игрока А.

Пусть, например, игрок А выбрал стратегию — (2, [1, 2]), а игрок В —стратегию — [2,1]. Тогда х = 2. Из [2, 1] вытекает, что у = 1, а из (2, [1, 2]), что z = 1. Отсюда

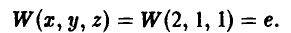
Рассчитывая по этой же схеме все остальные элементы таблицы выигрышей, в итоге получим

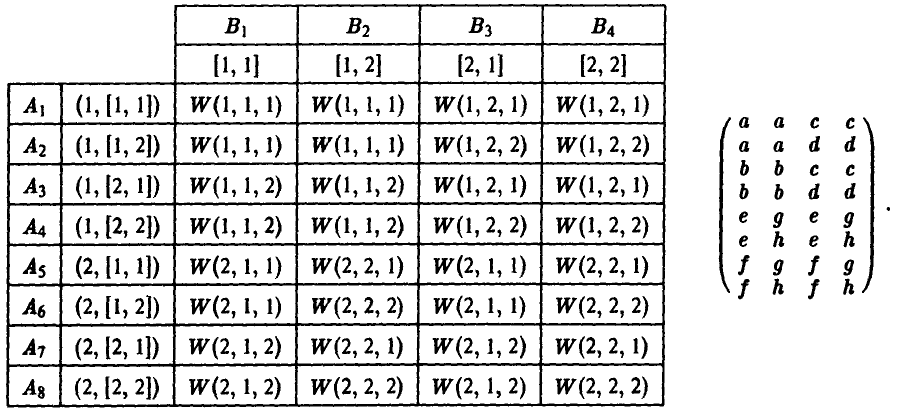
Вследствие того, что рассматриваемая позиционная игра является игрой с полной информацией, полученная матрица имеет седловую точку при любой функции выигрышей. В этом легко убедиться, произвольно выбирая значения параметров а, b, с, d, е, f, g и h.

При увеличении числа ходов стратегии в позиционной игре с полной информацией строятся по аналогичной схеме.

Рассмотрим, например, четырехходовую позиционную игру.
1- й ход делает игрок А: он выбирает число х из множества двух чисел {1,2}.
2- й ход делает игрок В: он выбирает число у из множества двух чисел {1, 2}, зная число х, выбранное игроком А на 1-м ходе.
3- й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, зная число у, выбранное игроком В на 2-м ходе, и помня свой выбор числа х на 1-м ходе.
4-й ход делает игрок В: он выбирает число и из множества двух чисел {1,2}, зная число z, выбранное игроком А на 3-м ходе, помня свой выбор числа у на 2-м ходе и зная выбор игрока А
на 1-м хода — число х.

После этого игроки А и В расплачиваются в соответствии с заданной функцией выигрышей W(x, y, z, u).

В этой игре стратегии у игрока А те же, что и в задаче, рассмотренной выше: каждая из них задается тройкой вида

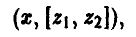
и общее их число равно восьми.

Что касается стратегий игрока В, то в этой игре их шестнадцать и каждая из них задается четверкой вида

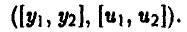
Матрица выигрышей игрока А в данной игре имеет размер 8 х 16. Покажем, как определяются ее элементы в зависимости от применяемых стратегий игроков.

Пусть, например, игрок А выбрал стратегию A’ — (2, [2,1]), а игрок В стратегию 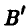— ([2,1], [1,2]). Тогда х = 1, у = 2, a z = 1. Из того, что 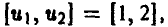получаем, что u = 1. Отсюда следует, что искомый элемент матрицы выплат равен

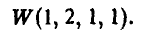
Остальные элементы матрицы вычисляются аналогично.

Так как эта позиционная игра также является игрой с полной информацией, то получаемая матрица будет иметь седловую точку.

Несколько слов в заключение

В рассмотренных примерах основное внимание было уделено описанию процесса нормализации позиционной игры — построению дерева игры и информационных множеств, выработке стратегий игроков и вычислению элементов платежной матрицы. Следующий естественный шаг — отыскание цены игры и оптимальных стратегий игроков — проводится методами, о которых рассказывалось в главе, посвященной матричным играм.

Мы достаточно подробно остановились на позиционных играх двух лиц, где были явно выражены интересы одного из игроков (игрока A). Следует, однако, иметь в виду, что в одних случаях интересы игрока В могут быть полностью противоположными интересам игрока A, в то время как в других вполне может оказаться, что то, что хорошо для одного игрока, не обязательно плохо для другого. Приведем два простых примера.

Пример:
1- й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.
2- й ход. Игрок В выбирает число у из множества двух чисел {1,2}, зная выбор числа х игроком А.

Функции выплат игрокам А и В — 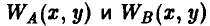соответственно — задаются так:

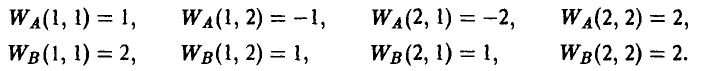
Дерево игры показано на рис. 12. Исход игры зависит от того, каковы намерения игрока В — максимизировать свой выигрыш:

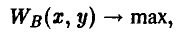
или максимизировать свой относительный выигрыш:

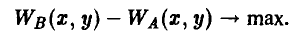
В первом случае это достигается так.

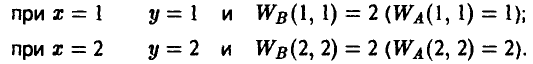
Во втором случае:

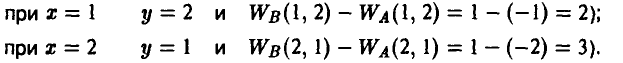
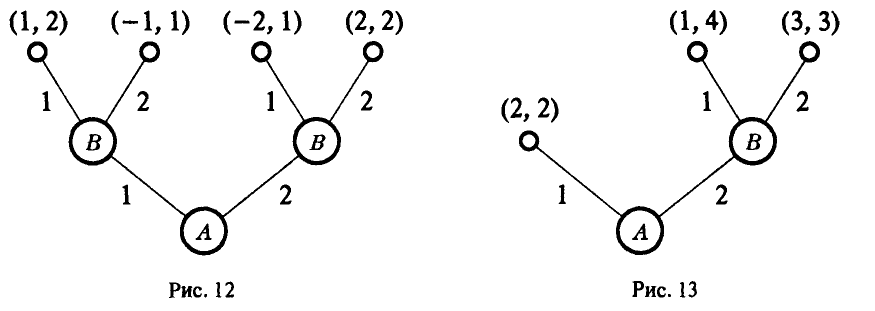
Пример:

Игра задается деревом (см. рис. 13).

1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2).

Если х = 1, то каждый из игроков получает свой выигрыш, равный 2.

Если х = 2, то право 2-го хода получает игрок В, где он и выбирает выбирает число у из множества двух чисел {1, 2}.

При у = 1 выигрыш игрока А равен 1, а игрока В — 4. При у — 2 оба игрока получают поровну — по 3.

В случае, когда каждый из игроков стремится к получению максимального выигрыша и любые виды кооперации запрещены, исход игры ясен — игрок А выбирает х = 1, и игра заканчивается. Но при х = 2 и у = 2 каждый из игроков получает по 3 (такой исход предпочтительнее простейшего (1, 1)), и, если допустить соглашение между игроками, это обстоятельство вполне может изменить исход игры.

Биматричные игры

Предыдущие рассмотрения касались игр двух лиц, в которых интересы игроков были прямо противоположны (антагонистические, или матричные игры), а также позиционных игр, сводимых к матричным. Однако ситуации, в которых интересы игроков хотя и не совпадают, но уже не обязательно являются противоположными, встречаются значительно чаще.

Рассмотрим, например, конфликтную ситуацию, в которой каждый из двух участников имеет следующие возможности для выбора своей линии поведения:

игрок А — может выбрать любую из стратегий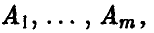

игрок В — любую из стратегий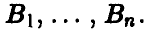

При этом всякий раз их совместный выбор оценивается вполне определенно:

если игрок А выбрал i-ю стратегию 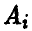, а игрок В — k-ю стратегию 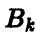, то в итоге выигрыш игрока А будет равен некоторому числу 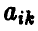, а выигрыш игрока В некоторому, вообще говоря, другому числу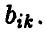

Иными словами, всякий раз каждый из игроков получает свой приз.

Последовательно перебирая все стратегии игрока А и все стратегии игрока В, мы сможем заполнить их выигрышами две таблицы

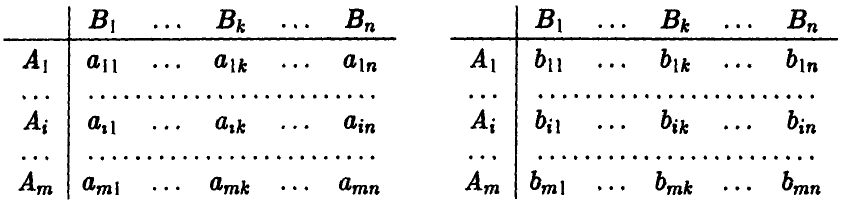
Первая из таблиц описывает выигрыши игрока А, а вторая — выигрыши игрока В. Обычно эти таблицы записывают в виде матриц

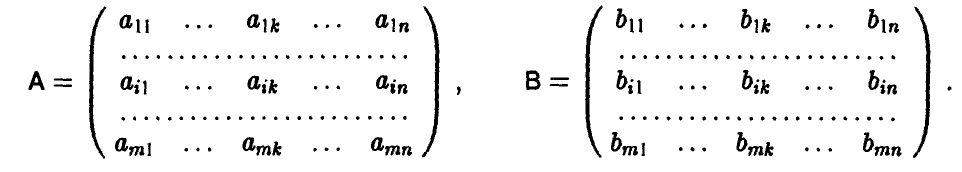
Здесь А — платежная матрица игрока А, а В — платежная матрица игрока В.

При выборе игроком А i-й стратегии, а игроком В — k-й стратегии их выигрыши находятся в матрицах выплат на пересечении i-x строк и k-х столбцов: в матрице А это элемент 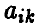, а в матрице В — элемент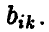

Таким образом, в случае, когда интересы игроков различны (но не обязательно противоположны), получаются две платежные матрицы: одна — матрица выплат

игроку А, другая — матрица выплат игроку В. Поэтому совершенно естественно звучит название, которое обычно присваивается подобной игре — биматричная.

Замечание:

Рассматриваемые ранее матричные игры, разумеется, можно рассматривать и как биматричные, где матрица выплат игроку В противоположна матрице выплат игроку А: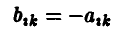

или

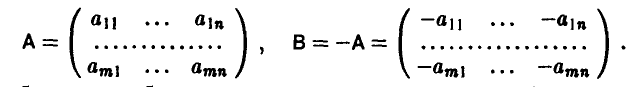
Тем не менее, в общем случае биматричная игра — это игра с ненулевой суммой.

Нам кажется вполне естественным время от времени сопоставлять наши рассмотрения с рассуждениями, проведенными ранее для матричных игр (особенно при попытках разрешения схожих проблем). Подобные сопоставления часто оказываются одновременно и удобными и полезными. Конечно, класс биматричных игр значительно шире класса матричных (разнообразие новых моделируемых конфликтных ситуаций весьма заметно), а, значит, неизбежно увеличиваются и трудности, встающие на пути их успешного разрешения. Впрочем, мы надеемся, что часть из этих трудностей мы сумеем преодолеть уже в настоящем издании.

Примеры биматричных игр

Примеры этого раздела описывают некоторые типические конфликтные ситуации, приводящие к биматричным играм. Сначала мы обсудим вопросы, связанные с формализацией рассматриваемых конфликтов (построение платежных матриц), а позднее связанные с рекомендациями по их разрешению.

Пример:

«Борьба за рынки». Небольшая фирма (игрок A) намерена сбыть партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок В). Для этого фирма А готова предпринять на одном из рынков соответствующие приготовления (например, развернуть рекламную компанию). Господствующая на рынках фирма В может попытаться воспрепятствовать этому, приняв на одном из рынков предупредительные меры (разумеется, в рaмках закона). Не встречая противодействия на рынке, фирма А захватывает его; при наличии препятствий — терпит поражение,

Будем считать для определенности, что проникновение фирмы А на первый рынок более выгодно для нее, нежели проникновение на второй. Естественно также считать, что и борьба за первый рынок потребует вложения ббльших средств. Например, победа фирмы А на первом рынке принесет ей вдвое больший выигрыш, чем победа на втором, но зато и поражение при попытке освоиться на первом рынке полностью ее разорит, а фирму В избавит от конкурента.

Что же касается второго рынка, то при поражении фирмы А ее потери будут не столь разорительны, но и победа принесет немного.

Таким образом, у фирмы А две стратегии:
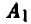— выбор первого рынка, 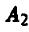— выбор второго рынка.

Такие же стратегии и у фирмы В:

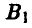— выбор первого рынка, 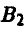— выбор второго рынка.

Для того, чтобы составить платежные матрицы игроков, нужны расчетные количественные показатели, которые мы приведем здесь в условных единицах:

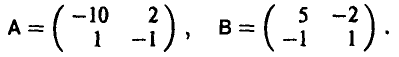
Взглянем на выписанные матрицы выплат. Из сказанного выше ясно, что если оба игрока выберут один и тот же рынок, то победа останется за более сильной фирмой В.

То, что в ситуации 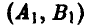выигрыш игрока В равен 5, а в ситуации 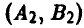— 1, подчеркивает, что первый рынок более выгоден (удобно расположен, хорошо посещаем и т. п.), чем второй. Выигрыш (—10) игрока A в ситуации 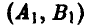(а точнее, проигрыш) в сопоставлении с его выигрышем (-1) в ситуации 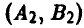выглядит, разумеется, вполне сокрушительно. Что же касается ситуации, когда фирмы уделяют основное внимание разным рынкам 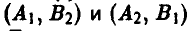, то здесь фирму А ждет настоящий выигрыш, бoльший на более выгодном рынке. Потери, которые при этом несет фирма В, оказываются прямо противоположными.

Замечание:

Ясно, что точно рассчитать выгоду и ущерб сторон в этом конфликте заранее довольно трудно. А вот в следующей конфликтной ситуации размеры выигрышей игроков известны со всей определенностью.

Пример:

«Дилемма узников». Игроками являются два узника, находящихся в предварительном заключении по подозрению в совершении преступления. При отсутствии прямых улик возможность их осуждения в большой степени зависит от того, заговорят они или будут молчать.

Если оба будут молчать, то наказанием будет лишь срок предварительного заключения (потери каждого из узников составят (—1)). Если сознаются, то получат срок, учитывающий признание как смягчающее обстоятельство (потери каждого из узников составят в этом случае (—6)). Если же заговорит только один из узников, а другой будет молчать, то в этом случае заговоривший будет выпущен на свободу (его потери равны 0), а сохраняющий молчание получит максимально возможное наказание (его потери будут равны (—9)).

Эта конфликтная ситуация приводит к би матричной игре, в которой каждый из игроков имеет по две стратегии — молчать (М) или говорить (Г).

Выигрыши игроков А и В соответственно описываются так:

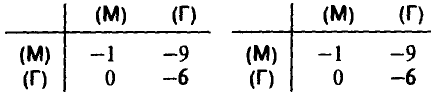
Пример:

«Семейный спор». Два партнера договариваются о совместном проведении одного из двух действий, (1) и (2), каждое из которых требует их совместного участия.

В случае осуществления первого из этих двух действий выигрыш первого партнера (игрок А) будет вдвое выше выигрыша второго партнера (игрок В). Напротив, в случае осуществления второго из этих двух действий выигрыш игрока А будет вдвое меньше выигрыша игрока В. Если же партнеры выполнят различные действия, то выигрыш каждого из них будет равен нулю.

Эта конфликтная ситуация приводит к биматричной игре, в которой каждый из игроков имеет по две стратегии. Выигрыши игроков А и В соответственно описываются таблицами следующего вида:

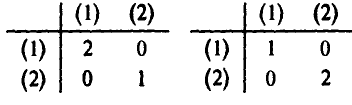
Пояснение:

Довольно понятно, что различные конфликтные ситуации могут иметь одну и ту же формализацию. В частности, рассмотренная биматричная игра частно интерпретируется, как одновременный выбор супругами совместного развлечения: посещение оперного спектакля или хоккейного матча. При этом в посещении оперного театра жена заинтересована в большей степени, чем муж, а при посещении стадиона наблюдается обратная картина. В случае же непреодоления разногласий, возникших при выборе, день оказывается вообще испорченным.

Отсюда и название, вынесенное в заголовок.

Пример:

«Студент — Преподаватель». Рассмотрим следующую ситуацию. Студент (игрок А) готовится к зачету, который принимает Преподаватель (игрок В). Можно считать, что у Студента две стратегии — подготовиться к сдаче зачета (+) и не подготовиться (-). У Преподавателя также две стратегии — поставить зачет [+] и не поставить зачета [-].

В основу значений функций выигрыша игроков положим следующие соображения:

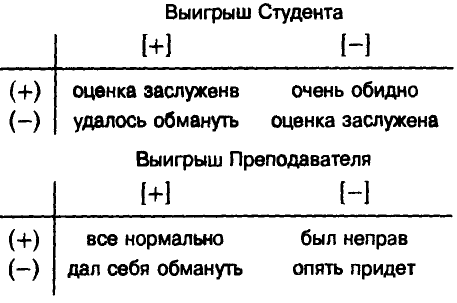
Количественно это можно выразить, например, так

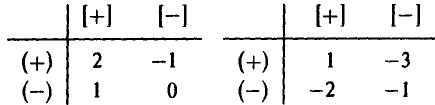
Смешанные стратегии

В приведенных примерах (позже мы вернемся к подробному рассмотрению каждого) описаны ситуации, в которых интересы игроков не совпадают. Естественно встает вопрос о том, какие рекомендации необходимо дать игрокам для того, чтобы моделируемая конфликтная ситуация разрешилась. Иными словами, что мы будем понимать под решением биматричной игры?

Попробуем ответить на это вопрос так:

вследствие того, что интересы игроков не совпадают, нам нужно построить такое (компромиссное) решение, которое бы в том или ином, но в одинаковом смысле удовлетворяло обоих игроков.

Не пытаясь сразу выражать эту мысль совсем точно, скажем — попробуем найти некую равновесную ситуацию, явное отклонение от которой одного из игроков уменьшало бы его выигрыш.

Подобный вопрос мы ставили и при рассмотрении матричных игр. Напомним, что возникающее при разработке минимаксного подхода понятие равновесной ситуации приводило нас к поиску седловой точки, которая, как оказалось, существует далеко не всегда — конечно, если ограничиваться только чистыми стратегиями игроков А и В, т. е. стратегиями

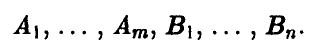
Естественно ожидать, что в более сложном случае биматричной игры дело вряд ли обстоит проще.

Однако при расширении матричной игры путем перехода к смешанным стратегиям, т. е. к такому поведению игроков, при котором они чередуют (чистые) стратегии с определенными частотами: игрок А — стратегии 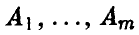с частотами

где

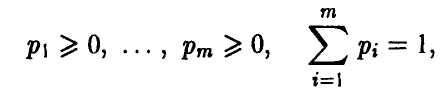
а игрок В — стратегии с частотами , где

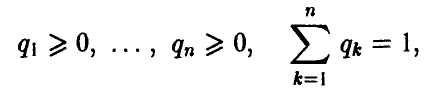
выяснилось, что в смешанных стратегиях равновесная ситуация всегда существует. Иными словами, любая матричная игра в смешанных стратегиях разрешима.

Поэтому, рассматривая здесь биматричные игры, разумно попробовать сразу же перейти к смешанным стратегиям игроков (тем самым, мы предполагаем, что каждая игра может быть многократно повторена в неизменных обстоятельствах).

В матричном случае смешивание стратегий приводило к расширению возможности выплат в том смысле, что расчет строился из вычисления средних выигрышей игроков А и В, которые определялись по элементам платежной матрицы А и вероятностям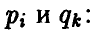

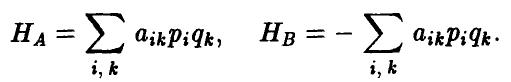
При смешанных стратегиях в биматричных играх также естественно возникают средние выигрыши игроков А и В, определяемые по правилам, в которых уже нет

никакой дискриминации игрока В:

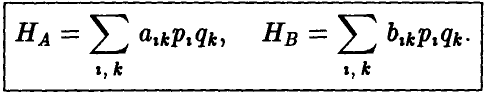
2×2 биматричные игры. Ситуация равновесия

Мы предполагаем уделить основное внимание случаю, когда у каждого из игроков имеется ровно две стратегии, т. е. случаю m = n = 2. Поэтому нам кажется уместным выписать приведенные выше формулы именно для такого случая.

В 2 х 2 биматричной игре платежные матрицы игроков имеют следующий вид

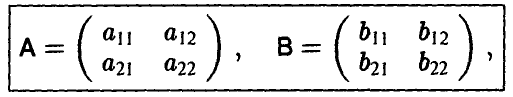
вероятности

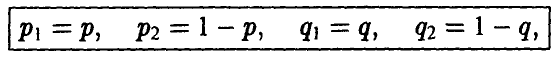
а средние выигрыши вычисляются по формулам

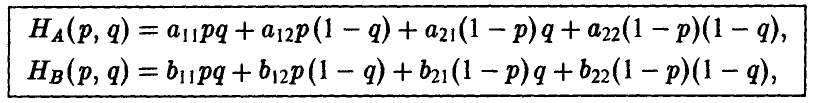
где

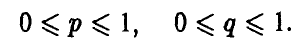
Сформулируем основное определение.

Определение:

Будем говорить, что пара чисел

определяет равновесную ситуацию, если для любых р и q, подчиненных условиям 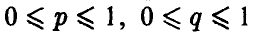, одновременно выполнены следующие неравенства

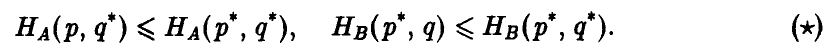
Пояснение:

Выписанные неравенства (★) означают следующее: ситуация, определяемая смешанной стратегией 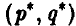, является равновесной, если отклонение от нее одного из игроков при условии, что другой сохраняет свой выбор, приводит к тому, что выигрыш отклонившегося игрока может только уменьшиться. Тем самым, получается, что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку.

Но может ли быть подобная ситуация равновесия в биматричной игре? Ответ на поставленный вопрос дает следующее утверждение.

Теорема Дж. Нэша. Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.

Заметим, что весьма похожее утверждение мы уже встречали при изучении вопроса разрешимости матричных игр. Напомним также, что в соответствующем разделе после формулировки аналогичного утверждения о существовании равновесной ситуации описывался и способ отыскания точки равновесия. Та же проблема встает перед нами и здесь.

Итак, равновесная ситуация существует. Но как ее найти?

Если некоторая пара чисел 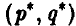претендует на то, чтобы определять ситуацию равновесия, то для того, чтобы убедиться в обоснованности этих претензий, или, наоборот, доказать их необоснованность, необходимо проверить справедливость неравенств (★) для любого р в пределах от 0 до 1 и для любого q в пределах от 0 до 1.

В общем случае число таких проверок бесконечно. И, следовательно, действенный способ определения равновесной ситуации нужно искать где-то в ином месте.

Для этого мы обопремся на следующий теоретический результат.

Теорема:

Выполнение неравенств

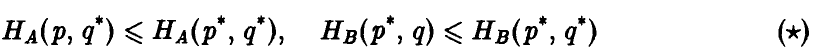
равносильно выполнению неравенств

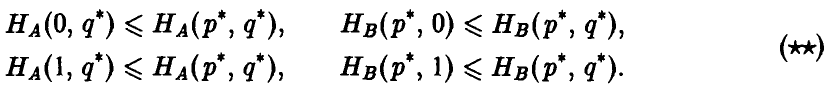
Иными словами, для того, чтобы убедиться в обоснованности претензий пары 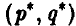на то, чтобы определять равновесную ситуацию, достаточно проверить справедливость неравенства

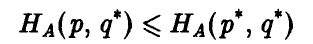
только для двух чистых стратегий игрока А (р = 0 и р= 1) и неравенства

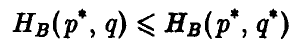
только для двух чистых стратегий игрока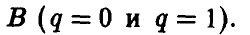

Четыре неравенства (**) позволяют провести поиск точки равновесия уже вполне конструктивно.

Запишем средние выигрыши игроков Л и В в более удобной форме. Имеем

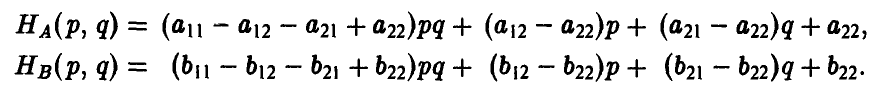
Обратимся к первой из полученных формул. Полагая в ней сначала р = 1, а потом р = 0, получаем, что

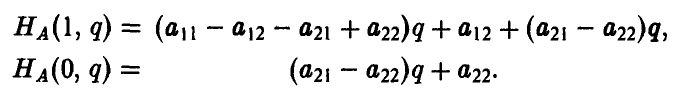
Рассмотрим разности

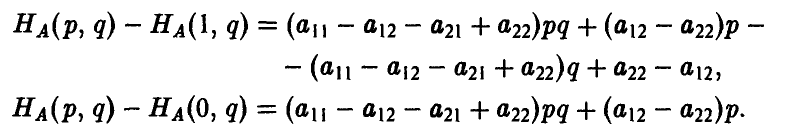
Полагая

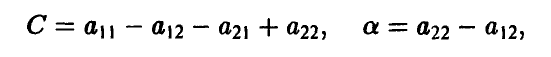
получим для них следующие выражения

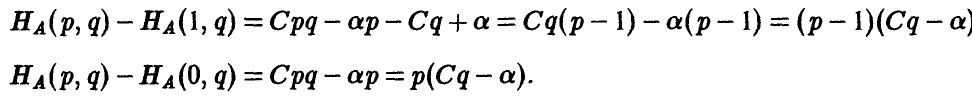
В случае, если пара (р, q) определяет точку равновесия, эти разности неотрицательны

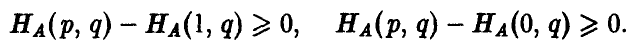
Поэтому окончательно поручаем

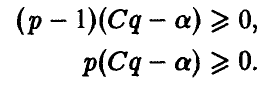
Из формул для функции 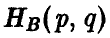при q = 1 и q — 0 соответственно имеем

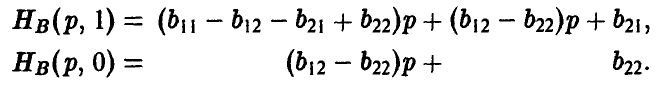
Разности

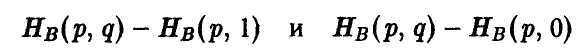
с учетом обозначений

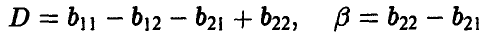
приводятся к виду

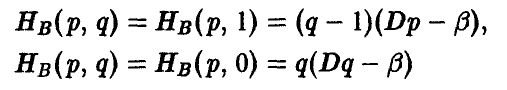
совершенно так же, как соответствующие разности для функции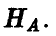

Если пара (р, q) определяет точку равновесия, то эти разности неотрицательны

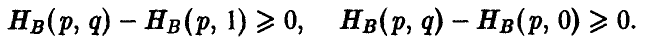
Поэтому

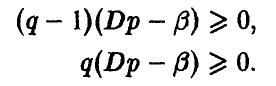
Прежде чем приступать к последующим шагам, подведем некоторые итоги.

Для того, чтобы в биматричной игре

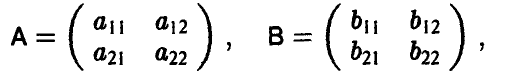
пара (р, q) определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств

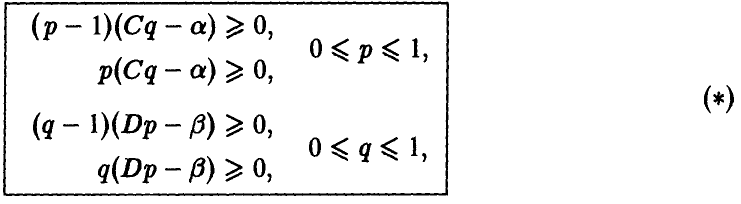
где

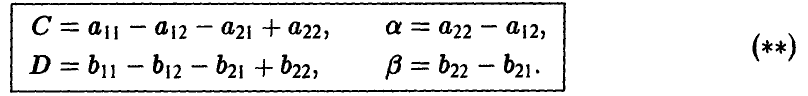
Поиск равновесных ситуаций

Геометрический смысл условий (*) рассмотрим на примерах описанных выше биматричных игр.

Пример:

«Борьба за рынки» (продолжение). Напомним, что ситуация, сложившаяся в этой задаче, задается платежными матрицами следующего вида

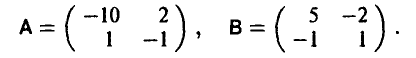
Заменяя в неравенстве (*) величины С, a, D и 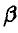их конкретными значениями

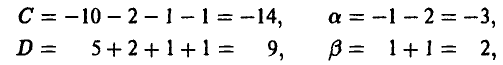
получаем

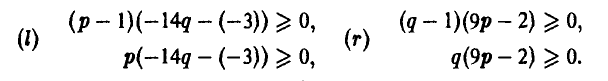
Рассмотрим сначала левую пару неравенств (l)

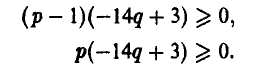
Возможны следующие три случая

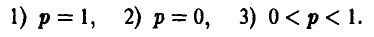
Разберем каждый из этих случаев подробно.

1. Полагая р = 1, получаем

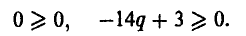
Откуда

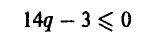
и, значит,

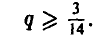
2. Полагая р = 0, получаем

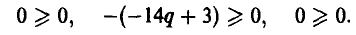
Откуда

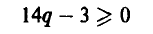
и, значит,

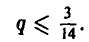
3. Наконец, положив 0 < р < 1, получим

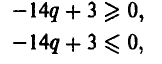
что возможно лишь в случае, если

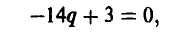
т.е.

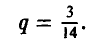
Сформулируем результат наших рассмотрений:

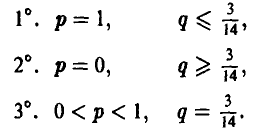
Перенесем теперь полученные сведения на чертеж.

Введем на плоскости прямоугольную систему координат (р, q) и выделим на ней единичный квадрат, соответствующий неравенствам

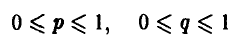
(рис.1).

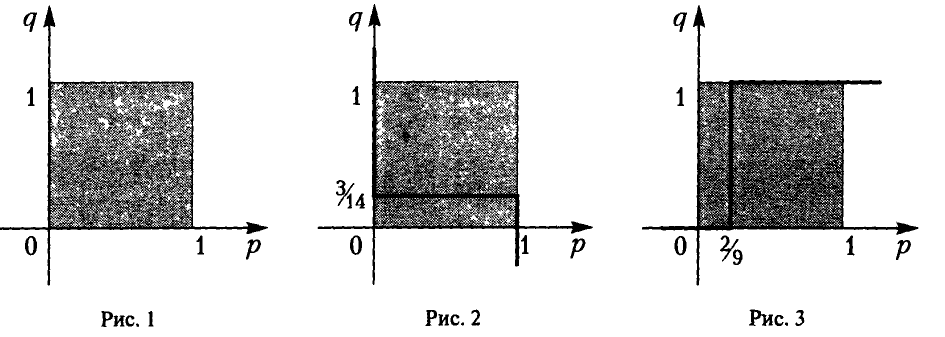
Нанесем на этот чертеж то множество точек, которое описывается условиями 1°, 2° и 3°. Это множество (на рис. 2 его точки выделены жирной линией) состоит из трех прямолинейных участков — двух вертикальных лучей и одного горизонтального отрезка — и представляет собой «зигзаг». Нас будет интересовать только та его часть, которая попала в заштрихованный на рис. 2 единичный квадрат.

Оставив на время полученные результаты в покое, обратимся к правой части неравенств (r):

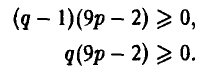
Три интересных для нас случая

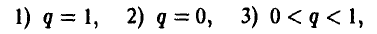
приводят нас к следующему результату

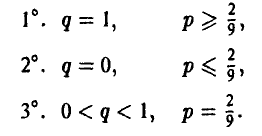
Перенося его на чертеж, получим второй «зигзаг», но уже горизонтальный (рис.З).

Теперь остается только объединить полученное на рис. 4.

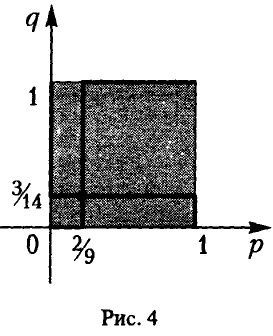
Общая точка построенных зигзагов — точка равновесия — имеет координаты

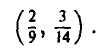
Соответствующие смешанные стратегии игроков имеют следующий вид

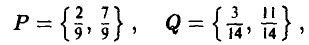
а средние выигрыши игроков таковы

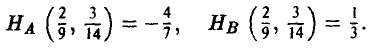
Замечание:

Попробуем разбить рассмотренную биматричную игру
на две матричные игры с нулевой суммой.

1. Игра с матрицей А.

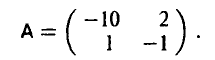
Решая эту игру графическим методом, найдем оптимальную смешанную стратегию для игрока А

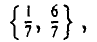
цену этой игры

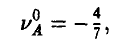
а затем и оптимальную смешанную стратегию для игрока В

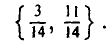
2. Игра с матрицей В

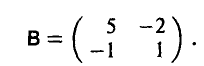
Решая эту игру графическим методом, найдем оптимальную смешанную стратегию для игрока В

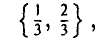
цену этой игры

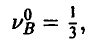
а затем и оптимальную смешанную стратегию для игрока А

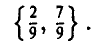
Сравнивая полученные результаты с решением биматричной игры, можно заметить следующее: если каждый игрок будет применять свои стратегии в этой игре, исходя только из матрицы своих выигрышей, то его оптимальный средний выигрыш совпадет с его выигрышем при равновесной ситуации’, кстати, по своей матрице игрок может найти и оптимальную смешанную стратегию другого игрока (но не свою!).

Пример:

«Дилемма узников» (продолжение). Выигрыши игроков А и В описываются соответствующими матрицами выплат:

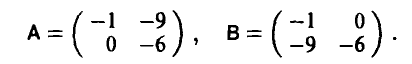
Проведем необходимые вычисления. Имеем

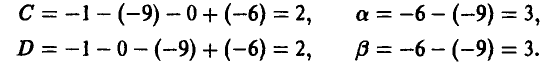
Отсюда

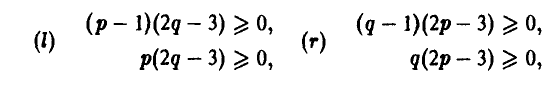
получаем, что

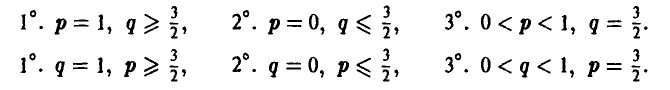
Полученные зигзаги изображены на рис. 5.

Единственная равновесная ситуация — (0, 0). Это ситуация, в которой каждый из игроков выбирает вторую чистую стратегию — сознаться — и теряет 6.

Как мы уже отмечали ранее, отклонение от ситуации равновесия одного из игроков не дает ему никаких преимуществ. Однако при одновременном отклонении обоих каждый из них может получить больший выигрыш, нежели в равновесной ситуации. Например, в ситуации (1, 1), когда оба игрока выбирают первую чистую стратегию — молчать, — каждый из них теряет лишь 1.

Напомним, что по условию задачи сговор (создание коалиции) между игроками недопустим.

Совершенно ясно однако, что в рассматриваемых обстоятельствах ситуация (0, 0) неустойчива — любой из узников, изменяя свою стратегию, увеличивает свой выигрыш (избегает наказания).

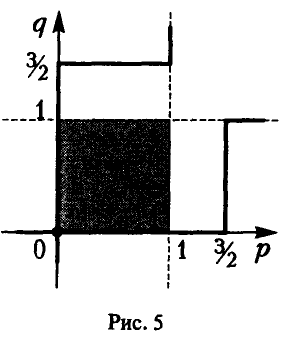
Пример:

«Семейный спор» (продолжение). Выигрыши игроков А и В в этой биматричной игре задаются так:

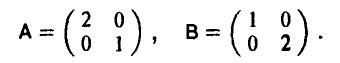
Проводя необходимые вычисления

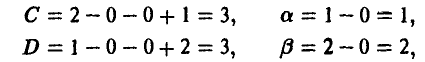
и рассуждения

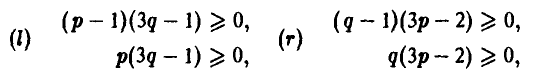
получаем, что

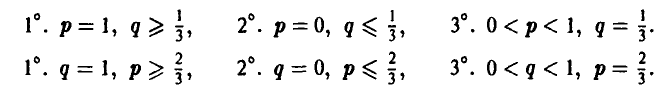
Геометрически полученный результат выглядит так (рис. 6).

Данная игра имеет три точки равновесия. Две из них отвечают чистым стратегиям игроков,

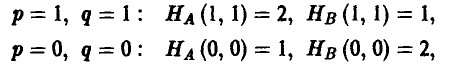
одна — смешанная,

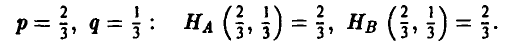
Признаться, полученные результаты ставят больше вопросов, чем дают ответов.

Ситуации (1,1) и (0,0) соответствуют одновременному выбору игроками своих первых или, соответственно, вторых стратегий, то есть определенной договоренности о совместных действиях.

Однако в данном случае есть еще одна ситуация равновесия, состоящая в выборе игроками вполне определенных смешанных стратегий. В ней оба игрока получают одинаковые выигрыши, правда, меньшие тех, которые дааали две другие равновесные ситуации.

Какой же из этих трех ситуаций равновесия следует отдать предпочтение? Какую выбрать игрокам?

Если бы игроки договорились играть оба, скажем, первую чистую стратегию, причем игрок A за получение большего выигрыша, чем игрок В, заплатил бы ему 1/2, то выигрыш каждым полутора единиц можно было бы считать и выгодным и справедливым. Однако в рамках теории бескоалиционных игр такого рода дележи не рассматриваются.

Вполне ясно, что для выбора каждым из игроков своей линии поведения (напомним, что подобная ситуация может повторяться, и повторяется, многократно) необходимы либо расширение возможностей, имеющихся у игроков, либо иные, измененные критерии.

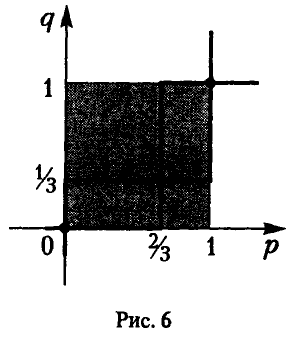
Наконец, обратимся к последнему из приведенных выше примеров биматричных игр — «Студент — Преподаватель».

Пример:

«Студент — Преподаватель» (продолжение). Впечатления у каждого из них относительно результатов общения в матричном виде выглядят следующим образом

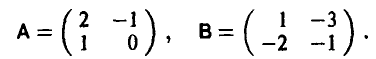
Проводя необходимые вычисления

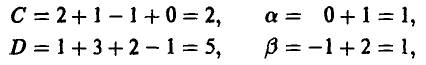
рассуждения

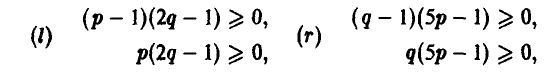
получаем, что

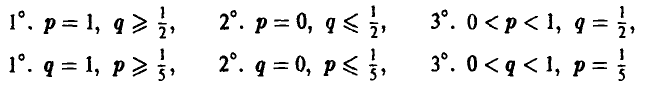
(рис. 7).

Число точек пересечения у зигзагов (равновесных ситуаций) равно трем. Две из них отвечают чистым стратегиям игроков,

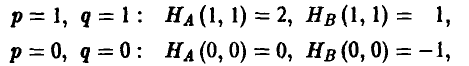
одна — смешанная,

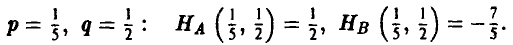
В данной задаче, а отличие от предыдущей, все довольно ясно: наилучшим является выбор каждым из игроков первой чистой стратегии — хорошо подготовиться к зачету и поставить зачет.

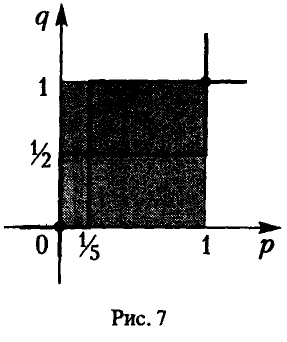
Как нетрудно заметить, тем самым в этой задаче реализуется весьма редкая возможность, когда функции выигрыша каждого из игроков достигают своих максимумов одновременно. Выгодность такой ситуации совершенно ясна. Ее устойчивость также вполне очевидна: любое отклонение от ситуации (1,1) одним из игроков или обоими игроками может привести разве что к уменьшению их выигрышей.

Оптимальность по Парето

Содержательные представления об устойчивости, выгодности и справедливости многообразны. Выше мы рассматривали проявление устойчивости через равновесие. Существует и иной вариант устойчивости ситуации, в большей степени, чем равновесность, отражающий черты ее выгодности. Это оптимальность по Парето.

Множество Парето

Рассмотрим на плоскости (U, V) множество (рис. 8). Каждая его точка обладает одним из следующих свойств: либо все точки, ближайшие к ней, принадлежат множеству (такая точка называется внутренней точкой множества ), либо сколь угодно близко от нее расположены как точки множества , так и точки, множеству не принадлежащие (такие точки называются граничными точками множества ). Граничная точка может как принадлежать множеству , так и не принадлежать. Здесь мы будем рассматривать только такие множества, которым принадлежат все точки границы. Множество всех граничных точек множества называется его границей. Обозначение:

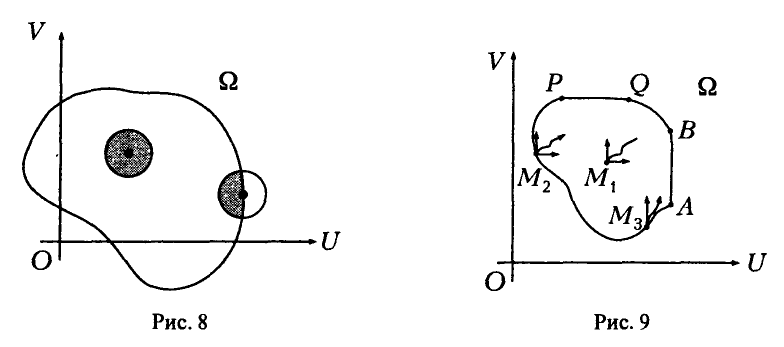
Пусть М — произвольная точка множества 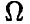, внутренняя или граничная, и (U, V) —ее координаты. Поставим следующий вопрос: можно ли, оставаясь во множестве 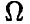, переместиться из точки М в близкую точку так, чтобы при этом увеличились обе ее координаты. Если М — внутренняя точка, то это бесспорно возможно. Если же М — граничная точка, то такое возможно не всегда (рис. 9). Из точек 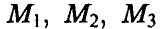это сделать можно, но уже из точек вертикального отрезка АВ можно переместиться, увеличивая лишь координату V (координата U при этом остается неизменной). Перемещая точку горизонтального отрезка PQ вправо, мы увеличиваем координату U (при этом координата V сохраняет свое значение). Что же касается дуги BQ, то перемещение вдоль нее способно увеличить лишь одну из координат при одновременном уменьшении другой.

Тем самым, точки множества 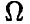можно разбить на три класса:
• в первый класс относятся точки, которые, оставаясь во множестве 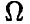, можно сдвинуть так, чтобы одновременно увеличились обе координаты (в этот класс попадают все внутренние точки множества и часть его граничных точек),
• второй класс образуют точки, перемещением которых по множеству можно увеличить только одну из координат при сохранении значения второй (вертикальный отрезок АВ и горизонтальный отрезок PQ на границе множества ),

• в третий класс попадут точки, перемещение которых по множеству способно лишь уменьшить либо одну из координат, либо обе (дуга BQ границы 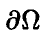) (рис. 10).

Множество точек третьего класса называется множеством Парето, или границей Парето данного множества Q (выделено на рис. 10).

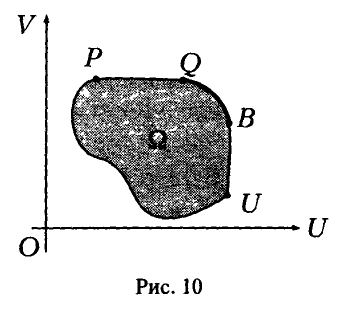
Метод идеальной точки

Пусть на плоскости (х, у) задано множество (рис. 11) и в каждой точке этого множества определены две непрерывные функции

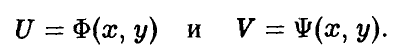
Рассмотрим следующую задачу.

Во множестве 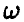найти точку 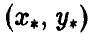, в которой

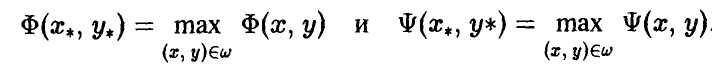
Обычно это записывается так

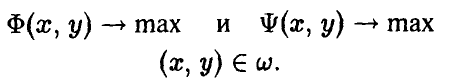
Сразу же отметим, что в общем случае поставленная задача решения не имеет.

В самом деле, нарисуем на плоскости (U, V) все точки, координаты которых вычисляются по формулам

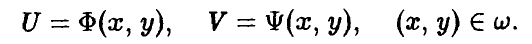
Из рис. 12 видно, что наибольшее значение 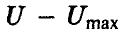— и наибольше значение 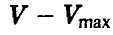— достигаются в разных точках, а точка с координатами

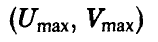
лежит вне множества .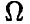

Тем самым, в исходной постановке задача, вообще говоря, неразрешима — удовлетворить обоим требованиями одновременно невозможно. И, следовательно, нужно искать какое-то компромиссное решение.

Опишем один из путей, использующий множество Парето.

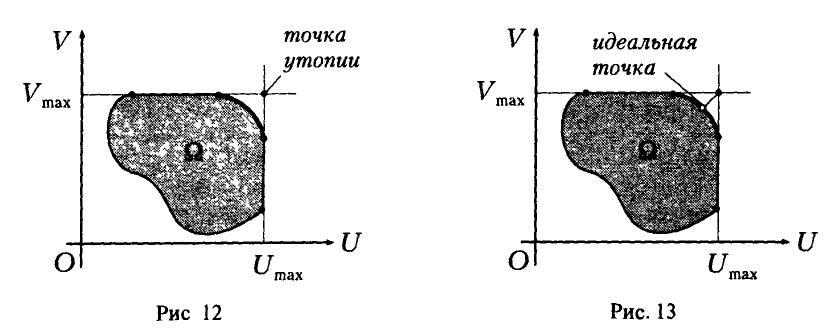
Сначала на плоскости (U, V) задается целевая точка, в качеств координат которой часто выбирается сочетание наилучших значений обоих критериев U и V.

В данном случае это точка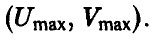

Вследствие того, что обычно такая точка при заданных ограничениях не реализуется, ее называют точкой утопии.

Затем строится множество Парето и на нем ищется точка, ближайшая к точке утопии — идеальная точка (рис. 13).

Оптимальность по Парето в биматричной игре

Рассмотрим биматричную игру с 2 х 2-матрицами

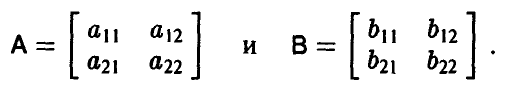
Пусть 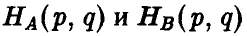— средние выигрыши игроков А и В.

Ситуация 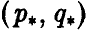в биматричной игре А и В наказывается оптимальной по Парето, если из того, что

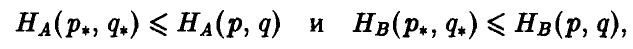
вытекают равенства

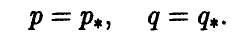
Иными словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш одного из игроков, не уменьшив при этом выигрыш другого.

Различие ситуации равновесия от ситуации, оптимальной по Парето, состоит в следующем:
• в ситуации равновесия ни один из игроков, действуя в одиночку, не может увеличить своего собственного выигрыша;
• в ситуации, оптимальной по Парето, игроки, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого.

Обратившись к игре «Дилемма узников», покажем, как практически отыскиваются оптимальные по Парето ситуации.

Напомним, что соответствующие платежные матрицы в этой игре имели следующий вид

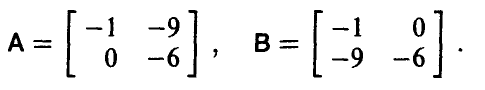
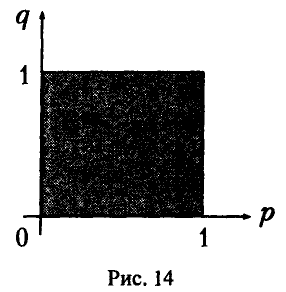
Тем самым, на единичном квадрате

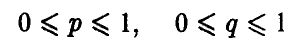
(рис. 14) возможных значений вероятностей р и q заданы две функции

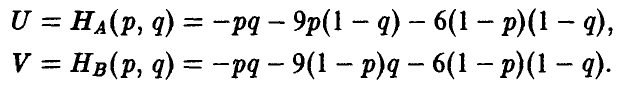
Точки с координатами (U, V), вычисленными по приведенным формулам, на плоскости (U, V) заполняют четырехугольник с вершинами К(-1, -1), L(-9, 0), М(-6, -6) и N(0, -9) (рис. 15). Граница Парето этого множества — ломаная NKL.

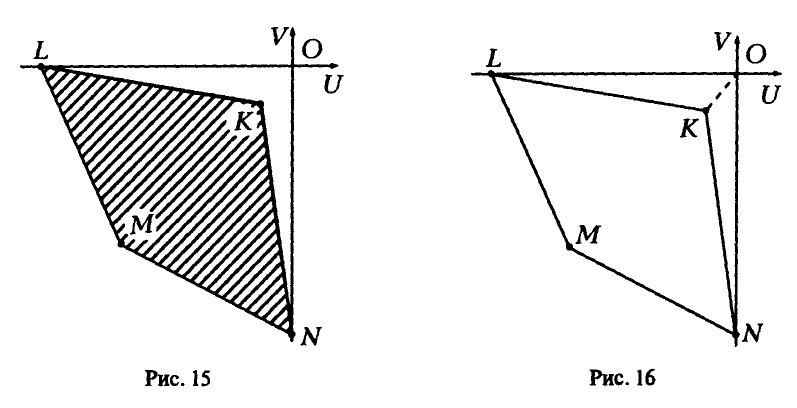
Каждый из игроков заинтересован в наибольшем значении своего среднего выигрыша

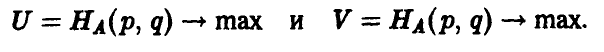
Нетрудно заметить, что в данном случае

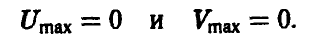
Тем самым, точкой утопии в этой задаче является начальная точка O(0, 0). Ближайшая к ней точка множества Парето — К(-1, -1) (рис. 16).

Идеальная точка К(-1, -1) — точка с наибольшими выигрышами для каждого из игроков — оказывается лучше, чем равновесная точка М(-6, -6), и ей соответствуют чистые стратегии обоих игроков

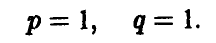
Несколько слов в заключение

На анализе полученных результатов стоит остановиться чуть подробнее.

Из приведенных примеров видно, что числа С и D из соотношений (**) на с. 273 могут быть как положительными, так и отрицательными. Они могут, в частности, даже обращаться в нуль.

Рассмотрим однако наиболее интересный в приложениях случай, когда ни С ни D нулю не равны, т. е.

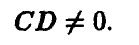
Тогда, как нетрудно видеть, точка равновесия определяется парой

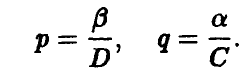
Эти формулы являются весьма примечательными: в равновесной ситуации выбор игрока А полностью определяется элементами платежной матрицы игрока В,

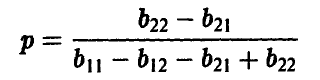
(и не зависит от элементов его собственной платежной матрицы), а выбор игрока В в равновесной ситуации полностью определяется элементами платежной матрицы

игрока А,

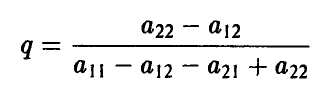
(и не зависит от элементов его собственной платежной матрицы).

Иными словами, равновесная ситуация обоих игроков определяется не столько стремлением увеличить собственный выигрыш, сколько желанием держать под контролем выигрыш другого игрока (минимизировать этот выигрыш). И если, например, заменить в биматричной игре матрицу выплат игроку А, а матрицу выплат игроку В оставить прежней, то игрок А никак не изменит своего «равновесного» поведения (просто не обратит внимания на эту замену), в то время как игрок В изменит свою стратегию на новую, равновесную.

Таким образом, в биматричной (неантагонистической) игре мы вновь встречаемся с антагонизмом. Правда, теперь это уже не антагонизм интересов (как это было в антагонистической, матричной игре), а антагонизм поведения.

Отметим, что в биматричными играх (в отличие от матричных) при наличии нескольких ситуаций равновесия средний выигрыш игрока в разных равновесных ситуациях различен (напомним, что в матричной игре выигрыш игрока один и тот же вне зависимости от количества точек равновесия).

Но если средние выигрыши разнятся, то какую равновесную ситуацию следует считать оптимальной?

Наконец, еще одно, не менее интересное. Вспомним, с какими трудностями мы столкнулись, пытаясь перевести эмоциональные оценки результатов общения студент-преподаватель в количественные показатели. В целом сохраняя основные соотношения, эти количественные оценки могут, конечно, изменяться как от студента к студенту, так и от преподавателя к преподавателю. Однако, если эти изменения будут не слишком значительными — элементы платежной матрицы пошевельнутся «слегка» — то слегка пошевелятся и зигзаги, не изменяя ни своей общей формы, ни взаимного расположения, а, значит, число равновесных ситуаций не изменится. Впрочем, сказанное относится лишь к случае, когда множество ситуаций равновесия конечно и состоит из нечетного числа точек (одной или трех). Как принято говорить в подобных случаях, это число устойчиво относительно малых шевелений.

Конечно, в некоторых биматричных играх равновесные ситуации случаются и вчистых стратегиях (в последнем из разобранных примеров таких ситуаций даже две). И (в принципе это совсем нетрудно) можно дать определение ситуации равновесия в чистых стратегиях. Найти ее (если она, конечно, существует) — дело довольно простое. Но, как показывают приведенные примеры, во-первых, чистой ситуации равновесия может вовсе не быть, а, во-вторых, даже при ее наличии не исключено существование равновесных ситуаций в смешанных стратегиях. И желая найти их все, неизбежно приходится обращаться к описанному выше подходу.

Теории игр и статистических решений

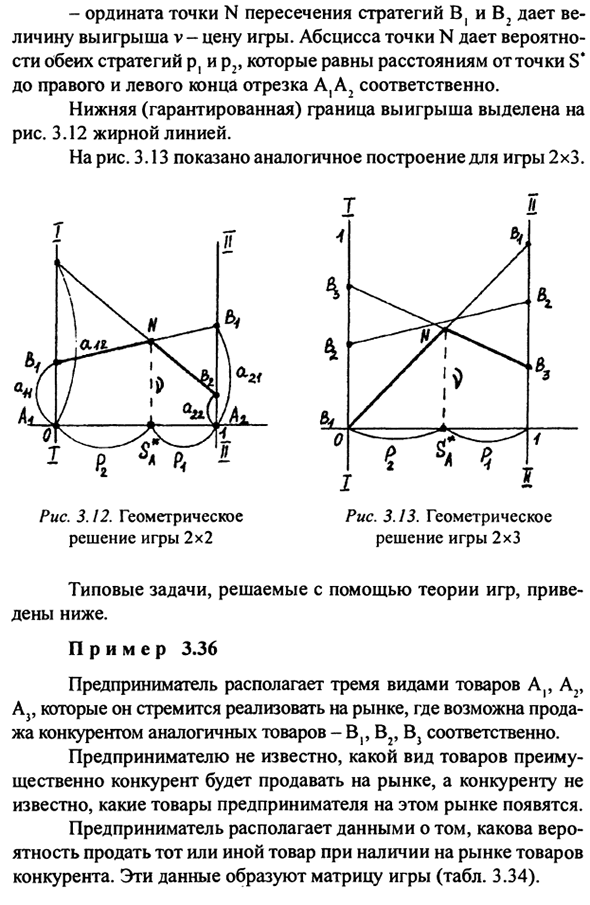
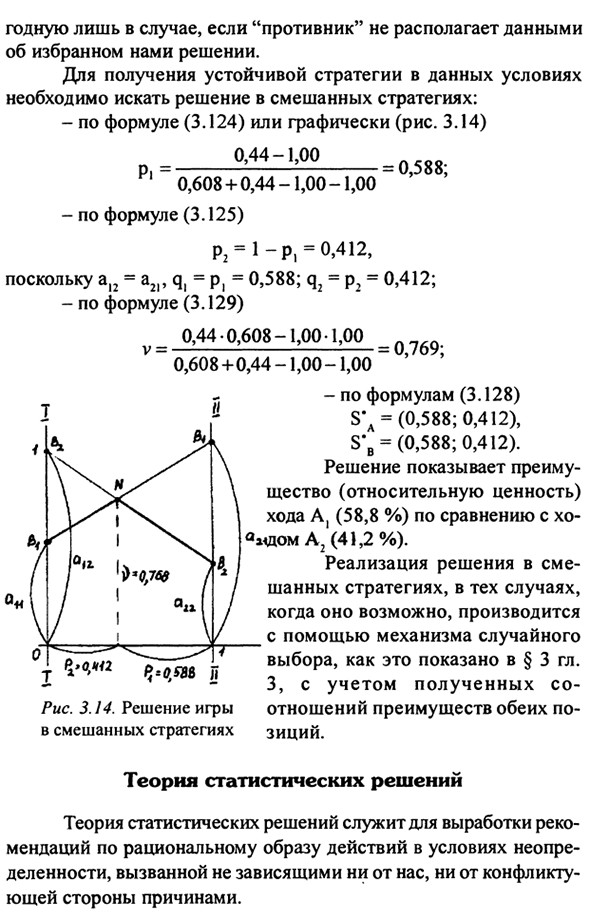
Смотрите также:

• Решение экономико математических методов

Законы распределения случайных величин	Сетевое планирование
Теория массового обслуживания (теория очередей). Метод Монте-Карло	Логические задачи и задачи на смекалку

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Вероятность события
10. Теорема умножения вероятностей
11. Формула полной вероятности
12. Теорема о повторении опытов
13. Нормальный закон распределения
14. Определение законов распределения случайных величин на основе опытных данных
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность