Вероятностное пространство с примерами решения и образцами выполнения

Взяв практически любую статью по теории вероятностей, мы увидим, что либо она начинается словами: «Пусть 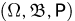— вероятностное пространство», либо в одной из первых же фраз написано: «где 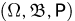— вероятностное пространство». Иногда добавляется: 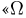— пространство элементарных исходов, 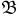— 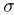-алгебра (сигма-алгебра) событий, 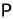— вероятностная мера (или вероятность)». Естественно, у неискушенного читателя пропадает всякое желание читать эту статью дальше. Однако понятие вероятностного пространства является весьма естественным математическим обобщением хорошо известных физических понятий: исход опыта, случайное событие, вероятность события. В настоящей главе мы попытаемся, насколько это возможно, дать читателю, знакомому только с основами высшей математики, разъяснение этого основополагающего для теории вероятностей понятия.

Пространство элементарных исходов

Рассмотрим простейший вариант случайного испытания — подбрасывание монеты. Если отвлечься от чисто гипотетических возможностей — падения монеты на ребро или вообще исчезновения монеты, то возможны только два исхода: выпадение «герба» и выпадение «цифры». Эти два исхода в рамках данного опыта уже нельзя разбить на более мелкие составляющие, т.е. они являются в некотором роде «элементарными». При бросании игральной кости такими неделимыми исходами являются: выпадение одного очка, выпадение двух очков, …, выпадение шести очков. Значит, мы имеем уже 6 элементарных исходов. Более сложный пример получим, если рассмотрим падение идеальной (т. е. не имеющей размера) частицы на плоскость. Тогда результат испытания представляет собой попадание частицы в определенную точку плоскости и его можно отождествить с двумерным вектором в некоторой системе координат на плоскости.

Аналогично, если проанализировать любое испытание со случайным исходом, можно заметить, что его результат представляет собой один из множества допустимых исходов. Поскольку в математике принято абстрагироваться от несущественных деталей, то всегда можно рассматривать все возможные в данном опыте исходы как некоторое множество 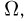которое и носит название пространства элементарных исходов или пространства элементарных событий. Сами элементарные исходы будем обозначать строчной буквой 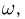снабжая ее при необходимости индексами.

Пример:

При подбрасывании монеты пространство элементарных исходов 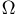состоит всего из 2 исходов: 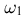— выпадение «герба» и 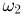— выпадение «цифры».

Пример:

При бросании игральной кости возможны 6 элементарных исходов: 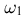— выпадение одного очка, 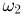— выпадение 2 очков….. 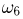— выпадение 6 очков.

Пример:

При подбрасывании двух монет пространство элементарных исходов 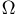содержит уже 4 исхода. Перечислим их: 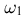— пара «герб»-«герб», 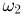— «герб»-«цифра», 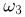— «цифра»-«герб», 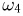— «цифра»-«цифра». При подбрасывании трех монет возможны 8 элементарных исходов типа «герб»-«цифра»-«герб» и т.д.

Пример:

При определении времени жизни элементарной частицы пространство элементарных исходов 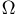представляет собой полупрямую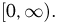

Следует отметить, что в практических исследованиях существует определенный произвол в описании пространства элементарных исходов Так, однократное подбрасывание монеты (пример 1) можно рассматривать как часть более сложного опыта, заключающегося в подбрасывании двух или более монет (пример 3). При определении времени жизни частицы (пример 4) можно также рассматривать типы получившихся после распада частиц и т. д. Очевидно, при решении практических задач разумно выбирать всегда наиболее простой вариант пространства элементарных исходов, необходимый для решения стоящей перед исследователем задачи.

События, действия над ними

Понятие «событие» лингвистически отличается от понятия «элементарное событие» только отсутствием прилагательного «элементарное». Естественно поэтому определить событие так же, как исход испытания, но только не обязательно неделимый.

Пример:

При бросании игральной кости (см. пример 2) событиями являются: выпадение четного числа очков (это событие происходит тогда и только тогда, когда появляется один из элементарных исходов 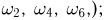выпадение нечетного числа очков (элементарные исходы 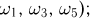выпадение не менее двух очков (элементарные исходы 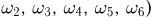и т. д.

Пример:

При подбрасывании двух монет примерами событий будут: падение обеих монет на одну и ту же сторону (появлению этого события благоприятствуют элементарные исходы 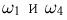из примера 3); падение монет на разные стороны (элементарные исходы 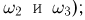выпадение, по крайней мере, одного «герба» (элементарные исходы 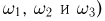и т. п.

Пример:

При определении времени безотказной работы электрической лампочки можно привести следующие примеры событий: безотказная работа лампочки до момента Т; отказ лампочки до момента Т; отказ лампочки между моментами 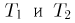и т. д. Здесь так же, как и в примере 4, пространство элементарных исходов 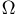представляет собой полупрямую 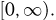Тогда первому событию соответствует множество точек на полупрямой 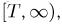второму — на интервале 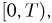третьему — на интервале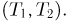

Вспоминая, что в результате опыта может произойти один и только один элементарный исход 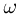из пространства элементарных исходов 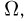мы приходим к теоретико-множественному определению события как произвольного набора элементарных исходов или, иными словами, произвольного подмножества множества элементарных исходов 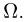События будем обозначать прописными латинскими буквами, снабженными при необходимости индексами: 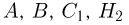и т.д.

Заметим, что приведенное выше определение события не всегда позволяет построить логически безупречную аксиоматику теории вероятностей. Поэтому в следующем параграфе мы уточним понятие «событие». Сейчас же наша цель состоит в описании теоретико-множественных операций над событиями, и нам удобно отказаться от несущественных пока деталей.

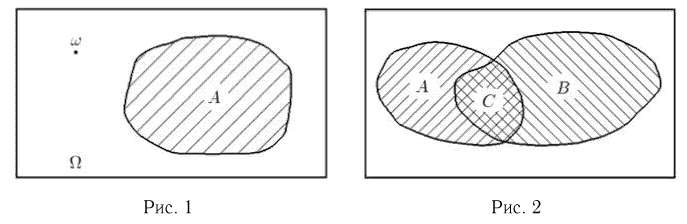
Часто бывает полезным наглядное представление событий в виде так называемой диаграммы Эйлера-Венна. Будем изображать все пространство элементарных исходов прямоугольником (рис.1). Тогда каждый элементарный исход 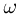соответствует точке внутри прямоугольника, а каждое событие А отождествимо с некоторой областью.

Само пространство элементарных исходов 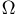представляет собой событие, состоящее из всех возможных исходов, т. е. происходящее всегда (при любом элементарном исходе 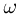), и носит название достоверного события. Таким образом, пространство элементарных исходов выступает в двух качествах: в качестве собственно множества всех элементарных исходов и в качестве достоверного события.

Для дальнейшего нам удобно ввести еще одно событие называемое невозможным. Невозможное событие не происходит никогда, т.е. не содержит ни одного элементарного исхода.

Пример:

При бросании игральной кости событие «выпадение не менее одного очка» является достоверным 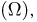событие «выпадение более 6 очков» — невозможным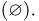

Над событиями как над подмножествами фиксированного множества можно производить действия, которые мы сейчас опишем.

Пересечением (произведением) двух событий А и В называется событие С, происходящее тогда и только тогда, когда наступают одновременно оба события А и В, или, иными словами, состоящее из тех элементарных исходов, которые принадлежат и А, и В (рис. 2).

Пересечение событий А и В записывается следующим образом:

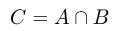
или

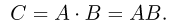
Аналогично определяется пересечение трех и более событий.

Пример:

Событие А — при подбрасывании двух монет падение их одной стороной, событие В — выпадение хотя бы одного «герба». Пересечением событий А и В является событие С, состоящее в выпадении двух «гербов».

Пример:

Событие А — выпадение четного числа очков при бросании игральной кости, событие В — выпадение не менее 3 очков. Пересечение А ий — событие С, состоящее в выпадении 4 или 6 очков. □

События А и В называются непересекающимися или несовместными, если их пересечение является невозможным событием, т.е. 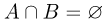(рис.3).

Для трех и более событий понятие несовместности можно определить разными способами. Мы будем, в основном, пользоваться следующим понятием несовместности n событий, которое также называется попарной несовместностью событий: события называются (попарно) несовместными, или (попарно) непересекающимися, если 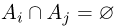для любых 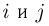при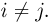

Пример:

Событие А — выпадение четного числа очков при бросании игральной кости, событие В — выпадение нечетного числа очков. События А и В несовместны.

Нетрудно видеть, что справедливы следующие простейшие формулы для пересечения двух событий, одно из которых достоверно или невозможно:

Объединением (суммой) двух событий А и В называется событие С, происходящее тогда и только тогда, когда наступает хотя бы одно из событий А или В, т. е. состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из множеств А или В (рис.4).

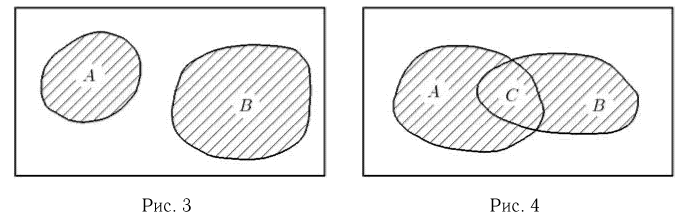
Для объединения событий А и В применяется запись

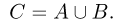
Пример:

Событие А — выпадение 1 или 3 очков при бросании игральной кости, событие В — выпадение 3 или 5 очков. Объединением событий А и В является событие С, состоящее в выпадении нечетного числа очков.

Для объединения двух событий, одно из которых достоверно или невозможно, имеют место следующие формулы:

В том случае, когда события А и В несовместны, наряду со знаком для их объединения употребляют знак «+». Обычно знак «+» применяют тогда, когда заведомо известно, что А и В несовместны, и это особо хотят подчеркнуть. В частности, поскольку невозможное событие несовместно с любым событием А, то

Аналогично определяется объединение трех и более событий. При этом знак «+» используется в случае попарной несовместности входящих в объединение событий.

Разностью двух событий А и В называется событие С, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В, т. е. состоящее из тех элементарных исходов, которые принадлежат ,4, но не принадлежат В (рис.5).

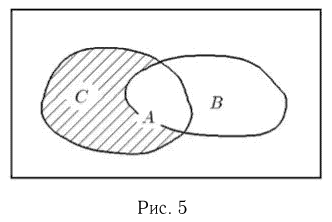
Разность событий А и В записывается в виде

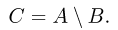
Пример:

Событие А — выпадение хотя бы одного «герба» при подбрасывании двух монет, событие В — падение обеих монет одной стороной. Разность С событий А к В представляет собой событие, заключающееся в выпадении ровно одного «герба».

Справедливы следующие формулы для разности двух событий, одно из которых достоверно или невозможно:

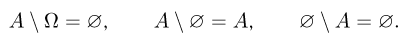
Кроме того, если А и В несовместны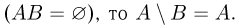

Симметрической разностью двух событий А и В (обозначается знаком или называется событие С, представляющее собой объединение событий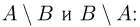

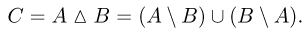
Поскольку события 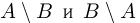несовместны (рис. 6), симметрическую разность можно записать также в виде

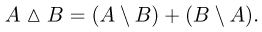
Нетрудно заметить, что симметрическая разность есть объединение событий а и в без их общей части:

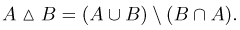
Пример:

Событие А — выпадение не менее 2 очков при бросании игральной кости, событие в — выпадение не более 4 очков. Симметрической разностью событий а и в является событие С, заключающееся в выпадении 1, 5 или 6 очков.

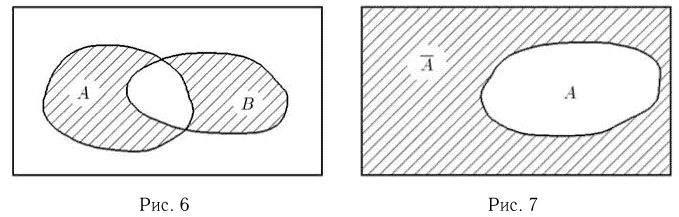
Если А и В несовместны, то

Дополнением события А (обычно обозначается 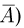называется событие, происходящее тогда и только тогда, когда не происходит событие А (рис. 7), или, иными словами,

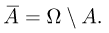
Пример:

Событие А — выпадение четного числа очков при бросании игральной кости. Дополнительное событие 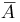— выпадение нечетного числа очков.

Справедливы формулы:

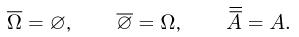
Если некоторое событие записано в виде нескольких действий над различными событиями, то сначала вычисляются дополнения, затем выполняются умножения и, наконец, сложения и вычитания событий. Так, формула

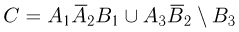
эквивалентна формуле

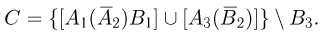
Пользуясь диаграммой Эйлера-Венна, нетрудно показать справедливость следующих формул (формулы де Моргана):

Формулы де Моргана элементарно переносятся на произвольное число событий. В частности, для n событий 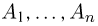они имеют вид:

Следует отметить, что все действия над событиями можно получить с помощью только двух действий — объединения и дополнения (или пересечения и дополнения). Основанием для этого утверждения служат формулы де Моргана, а также соотношение

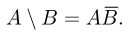
Кроме вышеперечисленных действий над событиями нам в дальнейшем понадобится понятие включения. Событие А принадлежит (содержится в, включается в) событию В (записывается 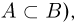если появление события А обязательно влечет за собой наступление события В (рис.8) или, иными словами, каждый элементарный исход 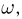принадлежащий А, обязательно принадлежит и В. Ясно, что включение 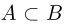эквивалентно выполнению равенства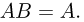

Используют и обратное понятие: событие В содержит (включает) событие 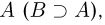если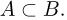

Пример:

Событие А — выпадение четного числа очков при бросании игральной кости, событие В — выпадение не менее 2 очков. Событие А принадлежит событию В, поскольку если выпало четное число очков (2, 4 или 6), то обязательно выпало не менее 2 очков.

Следующие включения очевидны:

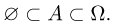
Кроме того, если 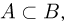то

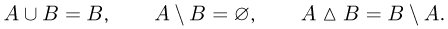
Алгебра событий

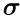-алгебра событий

Итак, мы назвали событием произвольное подмножество пространства элементарных исходов 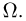Такое определение прекрасно работает, когда 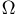конечно или даже счетно (т.е. его можно пересчитать с помощью чисел натурального ряда). Однако если 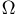более чем счетно,

то, вообще говоря, мы уже не сможем построить логически непротиворечивую теорию, называя событием произвольное подмножество 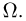Причина этого заключается в существовании так называемых неизмеримых множеств, что в свою очередь кроется в топологической структуре классических рассматриваемых пространств (прямой, плоскости, трехмерного пространства и т.д.). Поэтому приходится отказаться от, казалось бы, естественного желания назвать событием любое подмножество пространства элементарных исходов 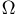и выделить среди всех подмножеств некоторый класс подмножеств 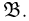Именно только подмножества из выделенного класса 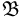и будут называться событиями. Интуитивно ясно, что описанные в предыдущем пункте теоретико-множественные операции над событиями не должны приводить к подмножествам, не являющимся событиями.

С точки зрения повседневной практики подмножества пространства элементарных исходов 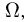не являющиеся событиями, представляют собой чистую математическую абстракцию и в реальной жизни никогда не встречаются. Даже само доказательство их существования представляет весьма сложную задачу. Поэтому читателю, не желающему вдаваться в математические тонкости, мы рекомендуем пропустить параграф, посвященный -алгебре событий, и в дальнейшем под событием понимать произвольное подмножество элементарных исходов 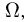а под -алгеброй — систему всех этих подмножеств. Любознательному читателю мы предоставляем возможность познакомиться со строгим определением последнего понятия, излагаемым ниже.

Алгеброй событий 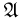назовем непустую систему подмножеств 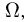удовлетворяющую следующим аксиомам:

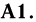Если подмножество А принадлежит 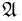(является событием), то дополнение 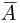также принадлежит 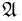(является событием).

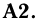Если подмножества А и В принадлежат 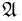(являются событиями), то и объединение 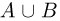принадлежит 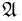(является событием).

Как мы знаем, любую из рассмотренных нами операций над подмножествами можно получить с помощью только двух операций: дополнения и объединения. Поэтому пересечение и разность двух событий также будут событиями. Поскольку 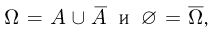то все пространство элементарных исходов 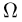и пустое подмножество 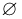обязательно являются событиями в любой алгебре событий. Очевидно также, что объединение и пересечение любого конечного числа событий снова будет событием. Иными словами, алгебру событий 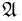можно определить как систему подмножеств пространства элементарных исходов 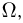замкнутую 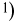относительно конечного числа теоретико-множественных операций.

Однако понятие алгебры событий также оказывается недостаточным для аксиоматического построения теории вероятностей в том случае, когда пространство элементарных исходов 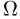не является конечным. Интересы общей теории меры требуют, чтобы аксиома А2 была заменена на более сильную, и мы приходим к новому определению:

-алгеброй событий назовем систему подмножеств из 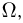удовлетворяющую аксиоме А1 и аксиоме

2′. Если подмножества принадлежат (являются событиями), то и их (счетное) объединение также принадлежит (является событием).

Основываясь на формулах де Моргана, нетрудно показать, что пересечение счетного числа событий снова будет событием. Таким образом, -алгебру событий можно определить как систему подмножеств пространства элементарных исходов 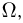замкнутую относительно счетного числа теоретико-множественных операций.

.Любая -алгебра событий является одновременно и алгеброй событий. Обратное, вообще говоря, не верно, т.е. существуют алгебры событий, не являющиеся -алгебрами. Однако если пространство элементарных исходов 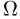конечно, то любая алгебра событий будет также и -алгеброй событий, т.е. в этом случае понятия алгебры событий и -алгебры событий эквивалентны.

-алгебра событий является второй компонентой вероятностного пространства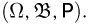

Пример:

Для любого пространства элементарных исходов 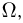содержащего хотя бы один исход, семейство подмножеств, состоящее всего из двух подмножеств 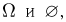является -алгеброй. Ясно, однако, что на такой ст-алгебре, состоящей всего из достоверного и невозможного событий, сколь-нибудь содержательную теорию построить невозможно, и мы ее в дальнейшем рассматривать не будем.

Пример 18. Пусть пространство элементарных исходов 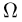содержит по крайней мере два исхода. Возьмем в 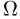некоторое подмножество А, отличное от 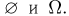Тогда система из четырех подмножеств 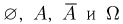будет являться -алгеброй Поскольку в дальнейшем мы будем рассматривать только события, а других событий, кроме перечисленных четырех, -алгебра не содержит, то естественно отождествить ее с -алгеброй, определенной на пространстве элементарных исходов 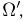состоящем всего из двух элементарных исходов: 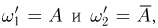и содержащей подмножества 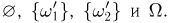Здесь мы имеем дело с тем принципом упрощения пространства элементарных исходов, о котором говорилось в параграфе 1.

В качестве иллюстрации рассмотрим время работы электрической лампочки. Первоначально пространство элементарных исходов представляет собой полупрямую 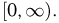Однако если наблюдателю доступна только информация, произошел отказ за фиксированное время Т (событие A) или нет (событие 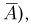то он фактически имеет дело с двумя элементарными исходам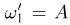и: и 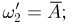соответствующая -алгебра состоит из четырех событий, описанных выше. В этом случае наблюдение за работой электрической лампочки с точки зрения числа возможных элементарных исходов ничем не отличается от наблюдения за подбрасыванием монеты.

Пример:

Пусть пространство элементарных исходов 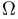содержит конечное 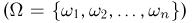или счетное 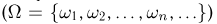число исходов. Такое пространство называется дискретным. В качестве -алгебры возьмем систему всех подмножеств. Именно эту -алгебру мы всегда будем рассматривать в дальнейшем в случае дискретного пространства элементарных исходов. Нетрудно видеть, что любое событие А можно отождествить с последовательностью из 0 и 1, причем 0 на месте означает, что элементарный исход 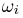не принадлежит событию А. В частности, невозможному событию 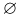соответствует последовательность 0,0…..а достоверному 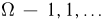Ясно, что если число исходов n конечно, то -алгебра содержит 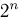событий (на каждом из n мест последовательности может стоять одно из двух чисел: 0 или 1).

В случае дискретного 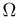-алгебру можно определить исходя и из других предпосылок. Для этого достаточно объявить событиями все элементарные исходы 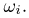Поскольку в случае дискретного 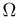любое его подмножество будет содержать не более счетного числа элементарных исходов, то в соответствии с аксиомой 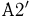оно обязательно будет событием. Таким образом, -алгебру 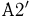можно трактовать как 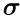-алгебру, порожденную всеми элементарными исходами.

В частности, в случае конечного 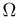-алгебра порождается конечным числом элементарных исходов и поэтому совпадает с алгеброй 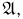порожденной всеми элементарными исходами 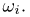Однако в случае счетного 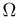алгебра 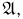порожденная всеми элементарными исходами 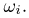, уже не будет совпадать с -алгеброй поскольку она будет содержать только подмножества, состоящие из конечного числа элементарных исходов (как объединения событий в соответствии с аксиомой А2) или подмножества, состоящие из всех элементарных исходов за исключением их конечного числа (как дополнения к подмножествам первого типа в соответствии с аксиомой А1).

Пример:

Пусть пространство элементарных исходов 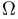представляет собой прямую 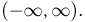И здесь система всех подмножеств будет представлять собой -алгебру. Однако оказывается, что такая «максимальная» -алгебра в наиболее интересных случаях представляет собой негодный объект для дальнейших исследований. Дело в том, что введение понятия -алгебры является вспомогательным процессом, необходимым для дальнейшего определения собственно вероятности, и, если бы только было возможно, никто не стал бы «городить огород» ради, разве что, красивого названия.

О невозможности использования «максимальной» 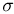-алгебры мы еще скажем несколько слов, когда будем рассматривать геометрическую вероятность. Сейчас попробуем построить другую 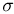-алгебру, опираясь на более умеренные запросы. Итак, что бы мы хотели от 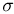-алгебры на прямой? Разумеется, основное требование к ней заключается в том, чтобы ей принадлежали всевозможные интервалы 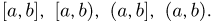Минимальная 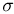-алгебра, удовлетворяющая этому требованию, носит название борелевской 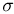—алгебры и является тем объектом, на котором без всяких логических противоречий можно построить математически строгую теорию.

Все сказанное относительно прямой в полной мере относится и к пространствам элементарных исходов, представляющим собой плоскость, трехмерное пространство и пространства более высоких размерностей, а также их невырожденные части (отрезки, многоугольники, круги, шары и т.д.). В теории вероятностей такие пространства элементарных исходов называются непрерывными. □

Определение вероятности

Приступим теперь к аксиоматическому определению последней составляющей вероятностного пространства 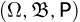— вероятности или, как иногда говорят, вероятностной меры Р.

Предположим сначала, что пространство элементарных исходов конечно. Пусть каждому событию А ( т.е. подмножеству А пространства элементарных исходов 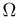принадлежащему 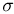-алгебре поставлено в соответствие число Р(A). Числовая функция Р(A) (заданная на 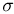-алгебре ) называется вероятностью, если она удовлетворяет следующим аксиомам:

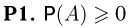(аксиома неотрицательности );

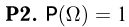(аксиома нормированности);

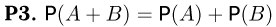(аксиома сложения), есл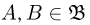и и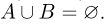

Как говорилось во введении, аксиомы вероятности представляют собой не что иное, как математическое отражение основных свойств частоты.

Из аксиом Р1-РЗ можно вывести ряд очевидных свойств вероятности.

Поскольку 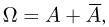то по аксиоме сложения 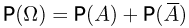или, с учетом аксиомы нормированности,

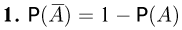(вероятность дополнительного события).

Далее, поскольку 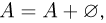то из аксиомы сложения имеем

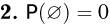(вероятность невозможного события).

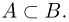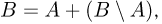Пусть Тогда по аксиоме сложения 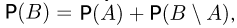и из аксиомы неотрицательности получаем

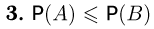(«большему» событию соответствует большая вероятность).

В частности, так как всегда 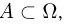то, с учетом аксиомы неотрицательности,

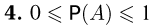(вероятность заключена между 0 и 1).

Наконец, поскольку 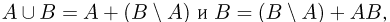то из аксиомы сложения находим: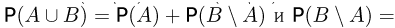 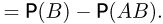Следовательно,

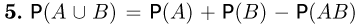(вероятность объединения двух событий).

Последнее свойство допускает очевидное, но весьма полезное обобщение на случай произвольного числа слагаемых

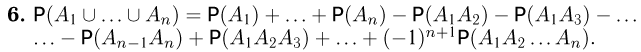
Свойство 6 доказывается индукцией по n. Так, для трех событий А, В и С

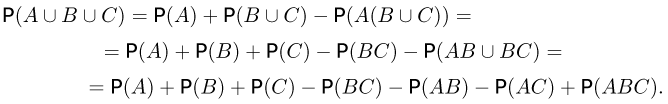
Из свойств 6 и 2 имеем для любого числа n (попарно) непересекающихся событий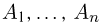

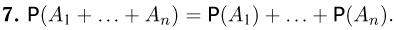
В случае, когда 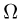содержит конечное число n элементарных исходов, вероятность можно определить конструктивно.

Действительно, с одной стороны, пусть на пространстве элементарных исходов 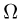задана некоторая вероятность 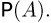Обозначим через вероятности элементарных исходов 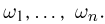Тогда по аксиоме сложения РЗ вероятность любого события А определяется формулой 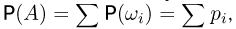где суммирование ведется по всем индексам 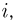соответствующим входящим в событие А элементарным исходам. В силу аксиом не отрицательности Р1 и нормированности Р2 числа являются неотрицательными и удовлетворяют свойству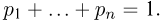

С другой стороны, пусть — любой набор неотрицательных чисел, таких, что 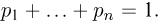Поставим в соответствие каждому элементарному исходу 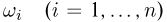число 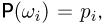а любому событию А — число 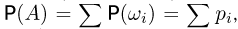где суммирование ведется по всем индексам 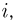соответствующим входящим в событие А элементарным исходам. Очевидно, достоверному событию 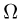мы должны сопоставить число 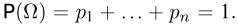Нетрудно видеть, что определенная таким образом функция Р(А) удовлетворяет аксиомам Р1-РЗ, т.е. является вероятностью.

Итак, существует взаимно однозначное соответствие между всеми вероятностями Р(А) на 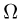наборами неотрицательных чисел, удовлетворяющими условию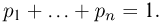

В частности, мы можем всем элементарным исходам 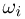приписать одну и ту же вероятность 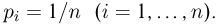В этом случае реализуется так называемый принцип классической вероятности, о котором мы подробно поговорим в следующей главе.

В случае произвольного (не обязательно конечного) пространства элементарных исходов 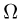аксиому РЗ необходимо заменить более сильной расширенной аксиомой сложения

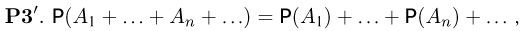
справедливой для счетного числа попарно несовместных событий.

Именно аксиомы 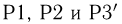и определяют аксиоматическое понятие вероятности.

Очевидно, что свойства вероятности 1-7 сохраняются и в этом случае.

Пример:

Пусть 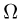состоит из счетного числа элементарных исходов 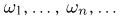И в этом случае любую вероятностную меру Р(А) можно получить, задав вероятности 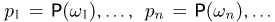элементарных исходов, причем последовательность 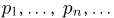должна удовлетворять только условиям неотрицательности 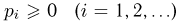и нормированности 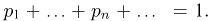По-прежнему вероятность любого события А определяется как сумма 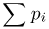вероятностей всех входящих в А элементарных исходов 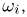однако если событие А содержит бесконечное число элементарных исходов, то и сумма будет бесконечной.

Пример:

Пусть пространство элементарных исходов 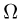представляет собой прямую 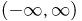с борелевской 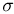-алгеброй на нем (см. пример 20). Теперь уже в наиболее интересных случаях мы не можем приписать каждому элементарному исходу 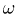иной вероятности, кроме 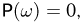и, следовательно, определить вероятность любого события на основе вероятностей входящих в него элементарных исходов. Тем не менее и сейчас вероятность можно задать конструктивно.

Для того чтобы показать это, предположим сначала, что она каким-то образом уже задана для всех событий (элементов борелевской 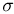-алгебры), и рассмотрим функцию 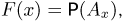равную вероятности события 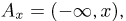состоящего из всех точек полупрямой 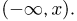Как вероятность функция F(x) обязана обладать определенными свойствами, которые мы сейчас опишем.

Во-первых, значения функции F(x) как вероятности должны лежать между 0 и 1.

Во-вторых, так как для любых 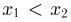событие 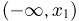содержится в событии 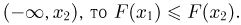Иными словами, F(x) — неубывающая функция аргумента х.

В-третьих, поскольку событие 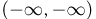невозможно, а событие 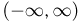достоверно, то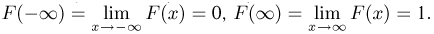

Наконец, так как событие 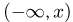представляет собой объединение счетного числа событий 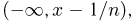то из расширенной аксиомы сложения и монотонности F(x) можно вывести (см. параграф 2 гл. 5), что F(x) — непрерывная слева функция.

Зная функцию F(a-), можно определить вероятности любых других событий. В частности, вероятность события 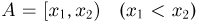определяется формулой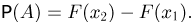

Таким образом, любая вероятность на прямой полностью определяется своей функцией F(x), которая удовлетворяет перечисленным выше свойствам.

Справедливо и обратное. Любая неубывающая непрерывная слева функция F(x), удовлетворяющая условиям 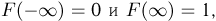задает некоторую вероятность на прямой 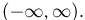Действительно, достаточно сопоставить каждому событию 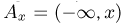число 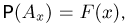а событию 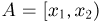— число 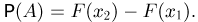Можно показать, что определенная таким образом для всех событий 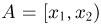числовая функция Р(А) будет удовлетворять трем аксиомам вероятности. Для любых других событий, составляющих борелевскую 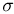-алгебру на прямой, вероятность определяется единственным образом с помощью так называемой теоремы о продолжении меры.

Вероятное пространство

Смотрите также:

Предмет теория вероятностей и математическая статистика

Предмет теории вероятностей	Конечное вероятностное пространство. Классическое определение вероятности
События	Геометрические вероятности

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Теорема о повторении опытов
14. Нормальный закон распределения
15. Определение законов распределения случайных величин на основе опытных данных
16. Системы случайных величин
17. Нормальный закон распределения для системы случайных величин
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность