Оглавление:
Сначала идёт теория, а потом готовые контрольные работы с подробным решением.
Теоретическая механика
Теоретическая механика — это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел.
Теоретическая механика – наука, которая изучает общие законы механического движения и механического взаимодействия материальных тел. Она имеет большое значение для качественной подготовки инженерных кадров в различных отраслях техники, так как является фундаментальной наукой для многих специальных технических дисциплин. Теоретическая механика построена на законах И. Ньютона, а также на ряде аксиом, справедливость которых проверена многовековой практической деятельностью человека в области механики.
Статика
Основные понятия
В теоретической механике в основном рассматриваются две модели реальных объектов: материальная точка и абсолютно твердое тело. Материальная частица, размерами которой в условиях исследуемой задачи можно пренебречь называется материальной точкой. Абсолютно твердое тело есть такое тело, в котором расстояние между его точками при всех условиях остаются неизменными, т.е. оно не деформируется.
В разделе статики рассматриваются две основные задачи:
- приведение данной системы сил к простейшему виду;
- определение условий равновесия тела, находящегося под действием данной системы сил.
Сила определяет меру взаимодействия между телами. Сила есть скользящий вектор, который
характеризуется численным значением (модулем), точкой приложения и линией действия. Системой сил называется совокупность сил, действующих на данное тело. Различают системы сходящихся сил, параллельных сил, плоскую и пространственную систему сил. Сходящейся называется система сил, линии действия которых пересекаются в одной точке; плоской — система сил, лежащих в одной плоскости. В общем случае, пространственная система сил есть совокупность сил произвольным образом расположенных в пространстве. Параллельные и сходящиеся системы сил могут быть плоскими и пространственными. Тела, объекты, ограничивающие перемещения рассматриваемого тела, называются связями. Сила, с которой связь действует на тело есть реакция связи. Эта сила направлена в сторону, противоположную той, куда связь не дает перемещаться телу.
Силы, действующие на тело со стороны других тел (не являющихся связями), называются активными. Реакции связей зависят от активных сил и, в отличие от них, вызвать перемещение данного тела не могут. Поэтому их называют пассивными силами. Единица измерения силы в системе СИ — Ньютон (Н), 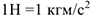 . Часто используют также
. Часто используют также 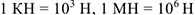 .
.
Возможно эта страница вам будет полезна:
| Предмет теоретическая механика |
Связи и их реакции
Конструктивно связи могут быть выполнены в виде различного рода опор, шарнирных соединений, тяг и др. В расчетных схемах удобно использовать идеальные связи. Идеальный характер связей понимается в том смысле, что соприкасающиеся тела абсолютно твердые, поверхности их соприкосновения гладкие, т.е. отсутствует трение, гибкие крепежные элементы (трос, цепь, веревка и т.д.) носят название «нить», нерастяжимые и невесомые. Ниже приведены часто встречающиеся на практике реакции и направления линий их действия.
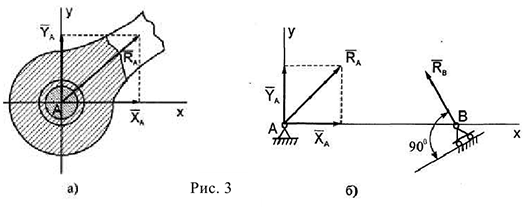
- Соприкосновение тел. Линии действия векторов реакций известны, за исключением случая, указанного на рис. 26.
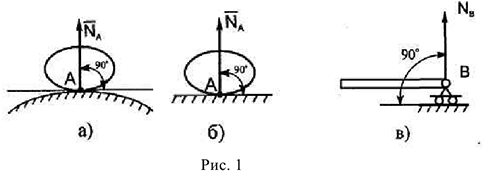
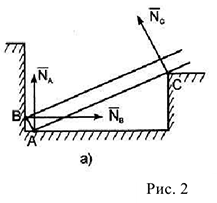
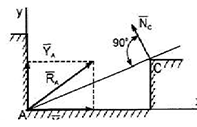
б) Линия действия 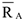 неизвестна, поэтому определяется ее составляющие
неизвестна, поэтому определяется ее составляющие 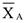 и
и 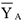 .
.
- Цилиндрический шарнир. Определяются составляющие
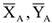 полной реакции
полной реакции 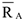 , линии действия которых параллельны соответствующим осям системы координат.
, линии действия которых параллельны соответствующим осям системы координат.
- Сферический шарнир и подпятник. Определяются составляющие реакции
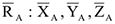

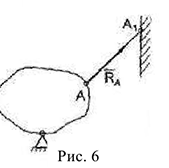
- Невесомый стержень с шарнирно-закрепленными концами.
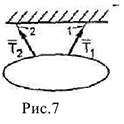
- Гибкая нить — односторонняя связь сжимающие нагрузки не воспринимает.
- Жесткое закрепление.
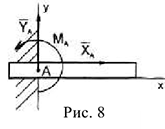
 — реакции. Здесь и выше
— реакции. Здесь и выше  препятствуют линейным перемещениям, а
препятствуют линейным перемещениям, а  — повороту тел.
— повороту тел.
Важной характеристикой вращающего действия силы на тело является момент силы. Различают алгебраический момент силы относительно полюса или просто момент силы относительно точки, векторный момент силы и момент силы относительно оси.
Момент силы относительно точки
Момент силы относительно точки используется при исследовании плоской системы сил. Моментом силы относительно точки называется принятое со знаком (+) или (-) произведение модуля силы на её плечо.
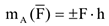
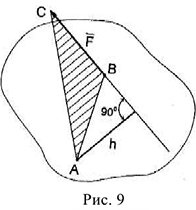
Точка  , относительно которой вычисляется, момент силы называется полюсом. В качестве полюса может быть выбрана любая точка плоскости, на которой расположена рассматриваемая система сил. Плечо силы есть перпендикуляр, опущенный из полюса на линию действия силы. Отсюда очевидно, что моменты силы относительно точек, лежащих на линии действия силы, равны нулю. В выражении (2.1) знак (+) ставится, т.е. момент силы считается положительным, в том случае, если сила стремится вращать тело вокруг полюса против хода часовой стрелки. Если же сила стремится вращать тело по ходу часовой стрелки, то момент силы относительно точки считается отрицательным, т.е. в выражении (2.1) ставится знак (-). Момент силы относительно точки геометрически определяется удвоенной площадью
, относительно которой вычисляется, момент силы называется полюсом. В качестве полюса может быть выбрана любая точка плоскости, на которой расположена рассматриваемая система сил. Плечо силы есть перпендикуляр, опущенный из полюса на линию действия силы. Отсюда очевидно, что моменты силы относительно точек, лежащих на линии действия силы, равны нулю. В выражении (2.1) знак (+) ставится, т.е. момент силы считается положительным, в том случае, если сила стремится вращать тело вокруг полюса против хода часовой стрелки. Если же сила стремится вращать тело по ходу часовой стрелки, то момент силы относительно точки считается отрицательным, т.е. в выражении (2.1) ставится знак (-). Момент силы относительно точки геометрически определяется удвоенной площадью 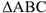 .
.
Векторный момент силы относительно центра
Векторный момент силы относительно центра и момент силы относительно оси используются при рассмотрении пространственной системы сил. Векторным моментом силы  относительно центра
относительно центра 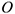 называется вектор
называется вектор 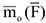 , приложенный в точке
, приложенный в точке 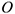 и совпадающий по модулю и направлению с векторным произведением радиуса вектора
и совпадающий по модулю и направлению с векторным произведением радиуса вектора  на вектор силы
на вектор силы  (рис.10).
(рис.10).
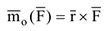
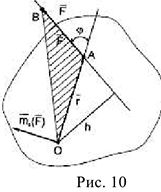
Этот вектор перпендикулярен плоскости 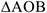 , в которой лежат векторы
, в которой лежат векторы  и
и  , и направлен в ту сторону, откуда видно, что сила стремится повернуть тело против хода часовой стрелки. Модуль этого вектора определяется формулой
, и направлен в ту сторону, откуда видно, что сила стремится повернуть тело против хода часовой стрелки. Модуль этого вектора определяется формулой
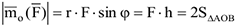
где 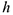 — плечо силы
— плечо силы  относительно центра
относительно центра 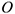 . В качестве центра может быть выбрана любая точка в пространстве.
. В качестве центра может быть выбрана любая точка в пространстве.
Таким образом, векторный момент силы относительно центра определяет и плоскость действия силы, и численное значение момента, и направление возможного вращения тела, т.е. полностью характеризует вращающий эффект силы в пространстве.
Момент силы относительно оси
Моментом силы  относительно оси
относительно оси 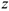 называется момент вектора проекции
называется момент вектора проекции 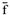 этой силы на плоскость
этой силы на плоскость 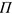 , перпендикулярную данной оси, относительно точки
, перпендикулярную данной оси, относительно точки 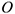 пересечения оси
пересечения оси 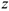 с плоскостью
с плоскостью 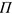 .
.
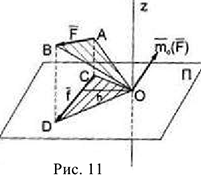

где 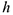 — плечо проекции силы
— плечо проекции силы 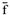 относительно точки
относительно точки 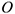 . Момент силы относительно оси есть скалярная величина. В формуле (2.5) знак (+) ставится в том случае, если сила стремится вращать тело вокруг оси (если смотреть с конца оси) против хода часовой стрелки. В противном случае принимается знак (-). Момент силы относительно оси равен нулю в двух случаях:
. Момент силы относительно оси есть скалярная величина. В формуле (2.5) знак (+) ставится в том случае, если сила стремится вращать тело вокруг оси (если смотреть с конца оси) против хода часовой стрелки. В противном случае принимается знак (-). Момент силы относительно оси равен нулю в двух случаях:
а) сила параллельна рассматриваемой оси, т.е. 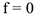 ;
;
б) сила пересекает данную ось, т.е.  .
.
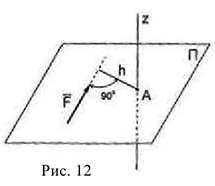
Это означает, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости. Если сила  перпендикулярна оси и её не пересекает (рис.12), то момент этой силы относительно оси равен её моменту относительно полюса
перпендикулярна оси и её не пересекает (рис.12), то момент этой силы относительно оси равен её моменту относительно полюса  . Полюс
. Полюс  есть точка пересечения оси с плоскостью
есть точка пересечения оси с плоскостью 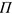 , ей перпендикулярной, на которой лежит сила
, ей перпендикулярной, на которой лежит сила  .
.
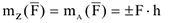
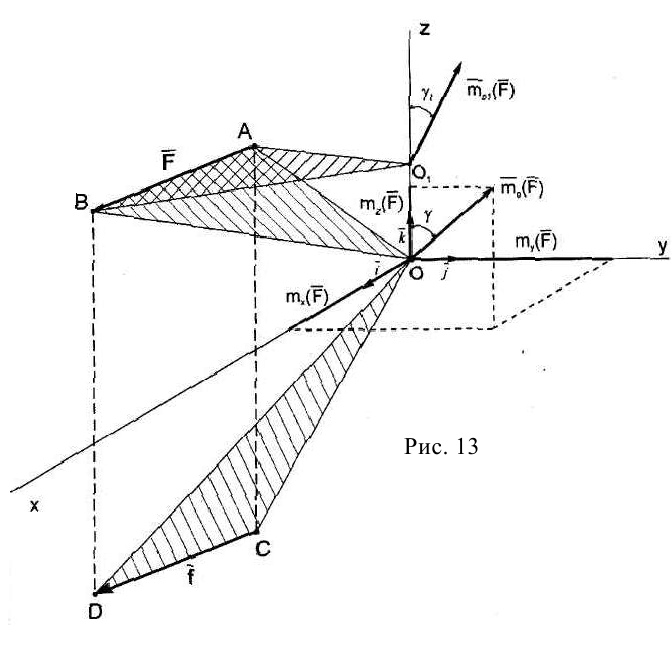
Поэтому в исследованиях плоской системы сил достаточно рассмотреть скалярную величину момента силы относительно точки. Известно, что момент силы относительно оси равен проекции на эту ось векторного момента относительно любого центра, лежащего на этой оси (рис.13).

Поэтому в декартовой системе осей векторный момент силы относительно начала координат можно представить в форме

где  — моменты силы
— моменты силы  относительно соответствующих декартовых осей.
относительно соответствующих декартовых осей.
Пара сил
Парой сил или просто парой называется система двух, равных по модулю, параллельных и направленных в противоположные стороны сил. Пара сил не имеет равнодействующей.
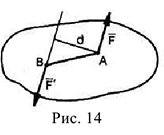
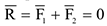
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары. Наикратчайшее расстояние 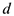 между линиями действия сил пары называется плечом пары.
между линиями действия сил пары называется плечом пары.
Пара сил оказывает на тело вращающее действие, которое оценивается моментом пары. При исследовании плоской системы сил плоскость действия пары совпадает с плоскостью, в которой лежат силы. В этом случае достаточно рассмотреть алгебраический момент или просто момент
Момент пары есть принятое со знаком (+) или (-) произведение одной из сил пары на плечо пары
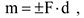
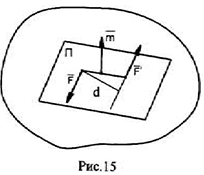
где знак (+) принимается, если пара стремится вращать тело против хода часовой стрелки. В этом случае момент пары считается положительным. В противном случае — знак (-) и момент пары считается отрицательным.
Две пары, расположенные в одной плоскости, имеющие равные моменты (т.е. равные численные значения и знаки) эквивалентны. Из этой теоремы следует, что:
1) не изменяя действия пары на тело её можно переносить в её плоскости;
2) действие пары не изменится, если изменить величину сил и плеча при условии, что величина момента, т.е. произведения силы на плечо и направление вращения остаются прежними.
При рассмотрении пространственных систем сил, особенно в их теоретических исследованиях, удобно использовать векторный момент пары 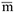 (рис. 15). Векторный момент имеет модуль
(рис. 15). Векторный момент имеет модуль
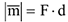
и перпендикулярен к плоскости действия пары 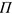 , направлен в ту сторону, откуда возможное вращение тела видно происходящим против хода часовой стрелки. Векторный момент пары, таким образом, полностью характеризует её вращающее действие в пространстве, определяя при этом и численное значение момента пары, и плоскость её действия, и направления возможного вращения тела. Векторный момент пары есть свободный вектор, т.е. его можно переносить в пространстве параллельно самому себе. Это означает, что пару в пространстве можно переносить как в плоскости её действия, так и в любую ей параллельную плоскость.
, направлен в ту сторону, откуда возможное вращение тела видно происходящим против хода часовой стрелки. Векторный момент пары, таким образом, полностью характеризует её вращающее действие в пространстве, определяя при этом и численное значение момента пары, и плоскость её действия, и направления возможного вращения тела. Векторный момент пары есть свободный вектор, т.е. его можно переносить в пространстве параллельно самому себе. Это означает, что пару в пространстве можно переносить как в плоскости её действия, так и в любую ей параллельную плоскость.
В конкретных задачах о равновесии в большинстве случаев плоскости действия пар бывают известны, поэтому при решении этих задач в основном используется алгебраический момент пар сил. Пары сил на чертежах, рисунках указываются следующим образом:
где 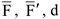 — соответственно силы и плечо пары в первом случае;
— соответственно силы и плечо пары в первом случае;  — момент пары, стрелка указывает направление вращения.
— момент пары, стрелка указывает направление вращения.
Моменты сил и пар сил в системе СИ измеряются в (Нм).
Приведение системы сил к заданному центру
Произвольная пространственная с 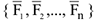 эквивалентна одной силе
эквивалентна одной силе 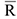 , которая равна векторной сумме всех сил и называется главным вектором системы (рис.16).
, которая равна векторной сумме всех сил и называется главным вектором системы (рис.16).
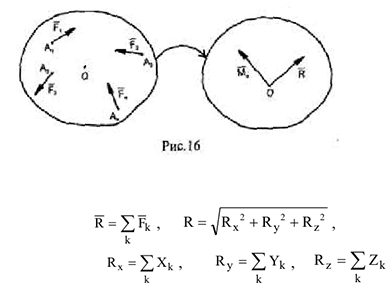
и одной паре сил с векторным моментом относительно центра приведения 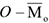 , который равен сумме векторных моментов всех сил относительно того же центра и называется главным моментом системы.
, который равен сумме векторных моментов всех сил относительно того же центра и называется главным моментом системы.
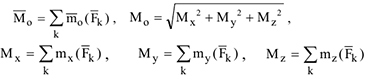
Здесь 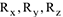 — проекции главного вектора на декартовые оси, которые соответственно равны суммам проекций входящих в эту систему сил на эти оси;
— проекции главного вектора на декартовые оси, которые соответственно равны суммам проекций входящих в эту систему сил на эти оси;
 — проекции главного момента на декартовые оси, которые равны суммам моментов этих сил относительно соответствующих осей.
— проекции главного момента на декартовые оси, которые равны суммам моментов этих сил относительно соответствующих осей.
В качестве центра приведения может быть выбрана любая точка в пространстве.
Таким образом, замена системы сил 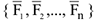 на эквивалентную систему векторов
на эквивалентную систему векторов 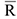 и
и 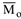 называется приведением системы сил к заданному центру.
называется приведением системы сил к заданному центру.
Частные случаи
1 Система сходящих сил эквивалентна одной равнодействующей силе 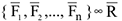 (рис.17). Причем
(рис.17). Причем
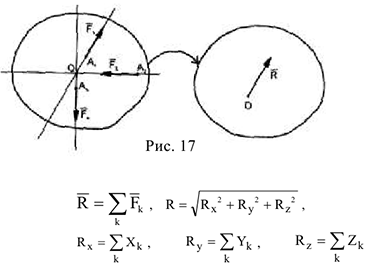
2 Плоская система приводится к главному вектору и главному моменту. Причем главный момент перпендикулярен плоскости, на которой расположена система сил, например, плоскость  (рис.18), т.е.
(рис.18), т.е.  .
.
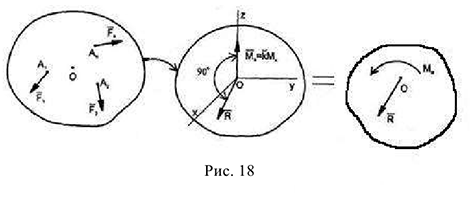
В этом случае  и
и 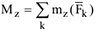 можно заменить алгебраическим моментом относительно полюса
можно заменить алгебраическим моментом относительно полюса 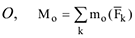 (см. рис. 12 и 13). Таким образом, в случае плоской системы сил главный момент можно рассматривать как алгебраический момент, равный сумме моментов всех сил относительно полюса
(см. рис. 12 и 13). Таким образом, в случае плоской системы сил главный момент можно рассматривать как алгебраический момент, равный сумме моментов всех сил относительно полюса 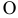 .
.

Равновесие твердого тела
Для равновесия твердого тела в пространстве, находящегося под действием произвольной системы сил, необходимо и достаточно, чтобы главный вектор и главный момент были равны нулю.

Записывая эти два векторных равенства в проекциях на оси координат, т.е. учитывая выражения (2.11) и (2.12), получим систему из шести уравнений равновесия.
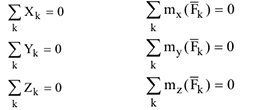
Частные случаи
1 Равновесие пространственной системы параллельных сил. Пусть эти силы параллельны оси 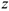 . В этом случае очевидно (рис.19), что первые два и последнее уравнения (2.16) тождественно равны нулю, поэтому исключаются из рассмотрения. Уравнения равновесия имеют вид:
. В этом случае очевидно (рис.19), что первые два и последнее уравнения (2.16) тождественно равны нулю, поэтому исключаются из рассмотрения. Уравнения равновесия имеют вид:
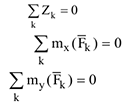
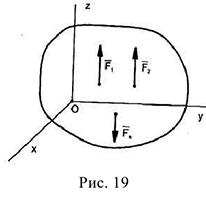
2 Сходящиеся силы. Необходимым и достаточным условием равновесия этой системы сил является равенство нулю её равнодействующей 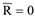 . Тогда в соответствии с формулами (2.14) уравнения равновесия приобретают форму:
. Тогда в соответствии с формулами (2.14) уравнения равновесия приобретают форму:

3 Плоская система сил. В этом случае необходимыми и достаточными условиями равновесия являются
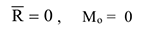
Уравнения равновесия для плоской системы сил можно записать в трех формах: а) первая формула непосредственно связана с условиями (2.19). С учетом выражений (2.14) можно записать
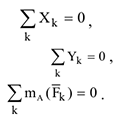
б) вторая форма уравнений равновесия получается, если одно из двух уравнений проекций в выражении (2.20) заменить уравнением моментов относительно точки, отличной от полюса  .
.
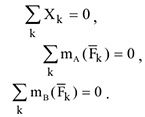
При этом на рисунках, чертежах прямая 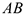 , соединяющая эти два полюса не должна быть перпендикулярна оси
, соединяющая эти два полюса не должна быть перпендикулярна оси  .
.
в) третья форма уравнений равновесия связана с заменой обоих уравнений проекций уравнениями моментов.

Точки  не должны лежать на одной прямой. Отметим ещё два простейших случая:
не должны лежать на одной прямой. Отметим ещё два простейших случая:
1) в случае плоской системы сходящихся сил уравнение равновесия имеет вид

2) в случае плоской системы параллельных сил

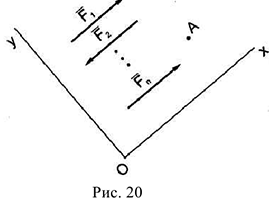
В последнем случае упрощение уравнений равновесия достигается надлежащим выбором системы координат — одну из осей координат направляют параллельно рассматриваемым силам (рис.20).
Различают статически определимые и статически неопределимые задачи. Задачи, в которых число искомых ‘ +неизвестных величин не превышает числа уравнений равновесия, называются статически определимыми. Задачи, в которых число неизвестных больше числа уравнений равновесия, называются статически неопределимыми. В статике твердого тела рассматриваются только статически определимые задачи.
Здесь же сформулируем теорему Вариньона, которая часто используется при решении задач о равновесии.
Если система сил имеет равнодействующую, то векторный момент этой равнодействующей относительно произвольно выбранного центра равен сумме векторных моментов всех сил системы относительно того же центра.
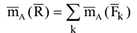
Теорема справедлива также для моментов сил относительно произвольно выбранной оси
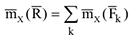
и для моментов плоской системы сил относительно произвольно выбранного полюса
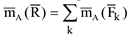
Последовательность решения задач о равновесии
Рекомендуется придерживаться следующей последовательности решения задач.
- Выделить точку или тело, равновесие которого рассматривается. Нарисовать его отдельно. Указать все необходимые размеры.
- Освободить тело от связей, заменив их действие реакциями. Показать на рисунке все действующие активные силы и реакции связей ( в том числе и пары сил).
- Классифицировать эту систему сил (сходящаяся, плоская или пространственная система сил).
- Выбрать систему координат и составить уравнения равновесия, из решения которых определить искомые величины.
- Проверочные расчеты.
В задачах о равновесии проверочные расчеты связаны с составлением лишнего (в смысле определения искомых величин) уравнения равновесия. Если задача решена верно, то это уравнение выполняется со знаком тождества. Поскольку расчеты приближенные и тождество должно выполняться в пределах принятой точности.
Готовые контрольные работы:
- Контрольная работа С1. Жесткая рама (рис.С1) закреплена в точке шарнирно, а в точке прикреплена к подвижной шарнирной опоре. Действующие нагрузки и размеры указаны на рисунке.
- Контрольная работа С2. На угольник , конец которого жестко заделан, в точке опирается стержень (рис. С2а). Стержень имеет в точке неподвижную шарнирную опору и к нему приложена сила , а к угольнику — равномерно распределенная на участке нагрузка интенсивности и пара с моментом .
- Контрольная работа СЗ. Вертикальная прямоугольная плита весом (рис. СЗ) закреплена сферическим шарниром в точке , цилиндрическим (подшипником) в точке и невесомым стержнем лежащим в плоскости, параллельной плоскости . На плиту действуют сила (в плоскости ), сила (параллельная оси ) и пара сил с моментом (в плоскости плиты).
Возможно эта страница вам будет полезна:
| Решение задач по теоретической механике |
Кинематика
Кинематика — раздел теоретической механики, в которой движение точек или тел изучается с чисто геометрической стороны, без учета их масс и вне зависимости от действующих на них сил. Движение изучается в пространстве и во времени, причем время считается абсолютным (одинаковым во всех системах отсчета).
Кинематика точки
Задачей кинематики точки является определение траектории, скорости и ускорения точки. Траекторией точки называется геометрическое место её последовательных положений в пространстве с течением времени относительно рассматриваемой системы координат. По виду траектории движения точки делятся на прямолинейные и криволинейные.
Способы задания движения
Задать движение точки — это значит указать способ, позволяющий в любой момент времени определить её положение по отношению к выбранной системе отчета.
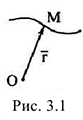
1 Векторный способ задания движения. Положение точки по отношению к выбранному центру отсчета будет определено, если для любого момента времени известен её радиус-вектор 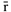 (рис. 3.1), т.е.
(рис. 3.1), т.е.

Вектор-функция (3.1) называется уравнением движения точки в векторной форме. Выражение (3.1) является также векторным уравнением траектории толчки.
2 Координатный способ задания движения. Способ задания движения, заключающийся в задании координат точки как известных функций времени, называется координатным. При рассмотрении движения в прямоугольной декартовой системе координат задаются координаты точки как функции времени (рис. 3.2).
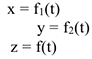

Уравнения (3.2) называются законом движения или уравнениями
У движения точки в координатной форме. Выражения (3.2) можно рассмотреть также как параметрические (параметр — 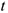 ) уравнения траектории точки. В общем случае, исключив параметр
) уравнения траектории точки. В общем случае, исключив параметр 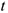 из выражений (3.2), можно получить уравнения траектории.
из выражений (3.2), можно получить уравнения траектории.

Таким образом, траекторией точки в пространстве является линия пересечения поверхностей, описываемых уравнениями (3.3).
В случае двумерного (плоского) движения точки уравнения движения и уравнения траектории соответственно имеет вид

Связь между координатным и векторным способами задания движения. Из рис. 3.3 очевидно, что
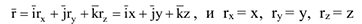
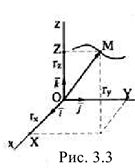
Таким образом, если движение задано координатным способом, то вектор-функцию 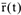 можно определить и наоборот —
можно определить и наоборот — 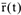 однозначно определяет функции
однозначно определяет функции 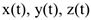 .
.
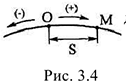
3 Естественный способ задания движения. При этом способе задания движения указывается траектория точки, начало и направление отсчета на У траектории и закон движения точки по этой траектории (рис. 3.4). Уравнение движения точки по траектории имеет вид
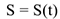
где 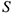 — дуговая координата, отсчитываемая от выбранного начала отсчета на траектории. Знак определяется в соответствии с выбранным направлением отсчета.
— дуговая координата, отсчитываемая от выбранного начала отсчета на траектории. Знак определяется в соответствии с выбранным направлением отсчета.
Связь между координатным и естественным способами задания движения.
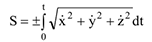
где 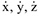 — произвольные по времени от координат точки
— произвольные по времени от координат точки 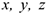 . Знак (+) или (-) перед интегралом ставится в соответствии с выбранным направлением отсчета.
. Знак (+) или (-) перед интегралом ставится в соответствии с выбранным направлением отсчета.
Скорость и ускорение точки
1 При векторном способе задания движения скорость  — вектор, направленный по касательной к траектории в сторону движения точки и приложенный в этой точке, который равен первой производной радиус-вектора по времени:
— вектор, направленный по касательной к траектории в сторону движения точки и приложенный в этой точке, который равен первой производной радиус-вектора по времени:
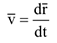
Ускорение  — вектор, направленный в вогнутую сторону траектории, равный первой производной по времени от вектора скорости или второй производной по времени от радиус-вектора точки:
— вектор, направленный в вогнутую сторону траектории, равный первой производной по времени от вектора скорости или второй производной по времени от радиус-вектора точки:
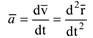
2 При координатном способе задания движения, когда, в частности, декартовые координаты 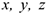 — известные функции времени, сначала определяются проекции скорости на соответствующие декартовые оси
— известные функции времени, сначала определяются проекции скорости на соответствующие декартовые оси
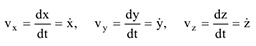
затем — модуль и направляющие косинусы вектора скорости
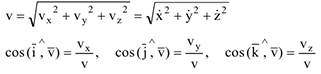
Декартовые проекции, модуль и направляющие конусы вектора ускорения определяются по формулам:
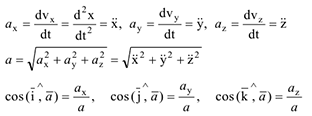
3 При естественном способе задания движения скорость и ускорение определяются по их проекциям на естественные оси, начало которых находится в движущейся точке, а 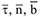 — направляющие орты (рис. 3.5). При этом скорость точки определяется как алгебраическая
— направляющие орты (рис. 3.5). При этом скорость точки определяется как алгебраическая
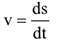
Скорость точки как векторную величину можно представить в виде
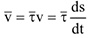
Ускорение определяется про формулам:
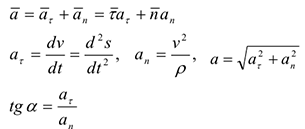
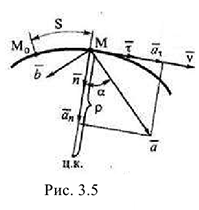
Здесь  — единичный вектор касательной,
— единичный вектор касательной,  — единичный вектор главной нормали,
— единичный вектор главной нормали, 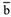 — единичный вектор бинормали,
— единичный вектор бинормали, 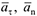 — соответственно касательное и нормальное составляющие полного ускорения, причем
— соответственно касательное и нормальное составляющие полного ускорения, причем 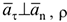 — радиус кривизны траектории для т.
— радиус кривизны траектории для т.  — направляющий угол полного ускорения. Таким образом, движение точки исследуется в подвижной ортогональной системе координат, начало которых находится в самой движущейся т.
— направляющий угол полного ускорения. Таким образом, движение точки исследуется в подвижной ортогональной системе координат, начало которых находится в самой движущейся т. 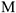 , а их направления определяются ортами
, а их направления определяются ортами 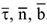 . В силу такого выбора системы координат третьей составляющей ускорения
. В силу такого выбора системы координат третьей составляющей ускорения  не будет,
не будет,
т.е. 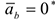 . В этом заключается существенное отличие естественного способа задания движения точки от задания её движения в декартовой системе координат. Естественный способ задания движения часто используется при исследовании криволинейного движения точки и особенно — движений точек вращающихся тел.
. В этом заключается существенное отличие естественного способа задания движения точки от задания её движения в декартовой системе координат. Естественный способ задания движения часто используется при исследовании криволинейного движения точки и особенно — движений точек вращающихся тел.
Частные случаи движения точки
1 Равномерное прямолинейное движение. При этом 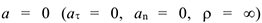 и закон движения определяется по формуле:
и закон движения определяется по формуле:

где  .
.
2 Равномерное криволинейное движение. При этом 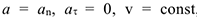 , уравнение движения описывается выражением (3.16).
, уравнение движения описывается выражением (3.16).
3 Равномерное движение по окружности. При этом 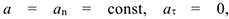
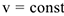 . Отсюда следует, что
. Отсюда следует, что 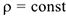 . Траекторией движения точки является дуга окружности, так как радиус кривизны только окружности есть
. Траекторией движения точки является дуга окружности, так как радиус кривизны только окружности есть 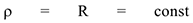 (
( — радиус окружности). Закон движения имеет также вид (3.16).
— радиус окружности). Закон движения имеет также вид (3.16).
4 Переменное прямолинейное движение. При этом 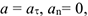 , так как
, так как 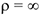 . Тогда
. Тогда
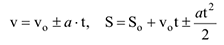
5 Переменное криволинейное движение,
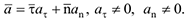
В этом случае
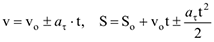
В выражениях (3.17) и (3.18) знак (+) принимается в случае равноускоренного движения, знак (-) — равнозамедленного движения точки.
Последовательность решения задач по кинематике точки
При решении задач по кинематике точки рекомендуется придерживаться следующей последовательности:
- По заданным уравнениям движения точки определяем уравнение её траектории и указываем на этой кривой действительную траекторию точки. Для заданного момента времени находим положение точки на траектории.
- Определяем скорость точки.
- Определяем полное ускорение точки.
- Определяем касательное и нормальное ускорения.
- Определяем радиус кривизны траектории точки.
- Вычислим указанные выше кинематические характеристики в заданный момент времени. Изображаем схематично векторы скорости, касательного, нормального, полного ускорений и радиус кривизны траектории, соответствующий для положения точки в данный момент времени.
Готовые контрольные работы:
- Контрольная работа К1а. Даны уравнения движения точки в плоскости : Определить уравнение траектории точки для момента времени . Найти скорость и ускорение точки, а также её нормальное и касательное ускорения и радиус кривизны в соответствующей точке траектории.
- Контрольная работа К1б. Точка движется по дуге окружности радиуса по закону ( — в метрах, — в секундах), где (рис. К16). Определить скорость и ускорение в момент времени .
Поступательное и вращательное движения твердого тела
Поступательное движение твердого тела
Поступательным называется такое движение твердого тела, при котором любая прямая, поведенная в этом теле, перемещается, оставаясь параллельно самой себе.
Таким образом, при движении тела (рис. 3.6) из положения I в положение II прямая 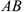 в любой момент времени остаётся параллельно самой себе, т.е.
в любой момент времени остаётся параллельно самой себе, т.е. 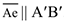 .
.
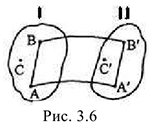
При поступательном движении твердого тела все его точки описывают конгруэнтные (совпадающие при наложении) траектории и имеют в каждый момент времени равные по модулю и направлению скорости и ускорения.

Вращение твердого тела вокруг неподвижной оси Угловая скорость и угловое ускорение
Вращательным называется такое движение твердого тела, при котором две точки остаются всё время неподвижными.
В силу определения абсолютно твердого тела все его точки, лежащие на оси вращения, остаются неподвижными. Уравнение вращательного движения имеет вид:
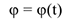
где  — угол поворота тела.
— угол поворота тела.
Угловая скорость вращательного движения определятся по формуле:
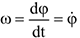
Угловое ускорение:
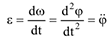
Размерности угловой скорости —  или
или 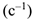 , углового ускорения —
, углового ускорения — 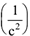 или
или 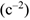 . В технике часто используется другая размерность угловой скорости —
. В технике часто используется другая размерность угловой скорости —  . Если известно число оборотов в минуту
. Если известно число оборотов в минуту  , то угловую скорость
, то угловую скорость 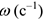 можно определить по формуле:
можно определить по формуле:
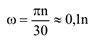
Частные случаи вращения твердого тела
1 Равномерное вращение —
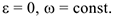

2 Переменное вращение —
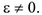

где 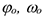 — начальные (при
— начальные (при 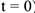 ) значения угла поворота и угловой скорости. В выражениях (3.25) знак (+) принимается в случае ускоренного вращения и знак (-) — в случае замедленного вращения.
) значения угла поворота и угловой скорости. В выражениях (3.25) знак (+) принимается в случае ускоренного вращения и знак (-) — в случае замедленного вращения.
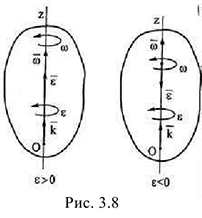
Угловая скорость и угловое ускорение часто рассматриваются как векторные величины. При этом вектор  по оси вращения направляется в ту сторону, откуда вращение твердого тела видно происходящим против хода часовой стрелки (рис. 3.8). Вектор
по оси вращения направляется в ту сторону, откуда вращение твердого тела видно происходящим против хода часовой стрелки (рис. 3.8). Вектор 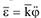 также направляется по оси ращения. Причем, если вращение равноускоренное, то векторы
также направляется по оси ращения. Причем, если вращение равноускоренное, то векторы 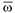 и
и 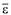 совпадают по направлению, в случае равнозамедленного вращения эти векторы направляются по оси вращения в противоположные стороны.
совпадают по направлению, в случае равнозамедленного вращения эти векторы направляются по оси вращения в противоположные стороны.
Траектории, скорости и ускорения точек вращающегося тела
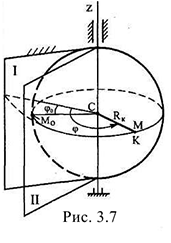
При вращении твердого тела вокруг неподвижной оси точки (частицы) тела двигаются по окружностям радиуса 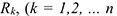 — номера частиц тела) (рис. 3.7, 3.9) в параллельных плоскостях, перпендикулярных оси вращения. Если закон вращательного движения твердого тела
— номера частиц тела) (рис. 3.7, 3.9) в параллельных плоскостях, перпендикулярных оси вращения. Если закон вращательного движения твердого тела 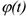 и направление его вращения известны, то движение точек этого тела можно считать заданными естественным способом, так как траектории известны — окружности, направления их движения и начало отсчета движения определяются вращением твердого тела, а закон движения точек можно определить по формуле:
и направление его вращения известны, то движение точек этого тела можно считать заданными естественным способом, так как траектории известны — окружности, направления их движения и начало отсчета движения определяются вращением твердого тела, а закон движения точек можно определить по формуле:
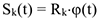
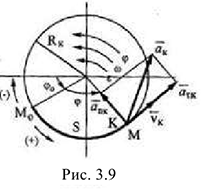
Тогда скорость, касательное, нормальное и полное ускорения точек определяются по формулам (3.13), (3.14), (3.15).
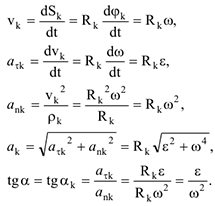
где 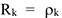 постоянен по определению абсолютно твердого тела, векторы скорости
постоянен по определению абсолютно твердого тела, векторы скорости 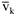 и касательного ускорения
и касательного ускорения 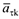 направлены по касательной к окружности (траектории), а нормальное ускорение
направлены по касательной к окружности (траектории), а нормальное ускорение 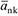 — к центру окружности (к центру кривизны траектории), лежащей на оси вращения тела. Причем, если вращение тела ускоренное, векторы
— к центру окружности (к центру кривизны траектории), лежащей на оси вращения тела. Причем, если вращение тела ускоренное, векторы  совпадают по направлению, в случае замедленного вращения тела эти векторы имеют противоположные направления.
совпадают по направлению, в случае замедленного вращения тела эти векторы имеют противоположные направления.
Векторные формулы для скоростей и ускорений точек тела
Скорость точки по модулю и направлению можно определить по формуле Эйлера векторным произведением:
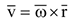
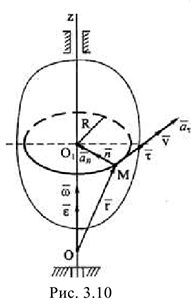
где 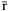 — радиус-вектор точки
— радиус-вектор точки 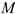 , проведенной из произвольной точки оси вращения
, проведенной из произвольной точки оси вращения 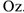 , например точки
, например точки 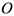 (рис. 3.10). В справедливости формулы (3.28) можно убедится определив по ней модуль скорости.
(рис. 3.10). В справедливости формулы (3.28) можно убедится определив по ней модуль скорости.
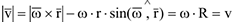
Из определения ускорения и векторной формулы Эйлера имеем:
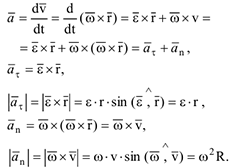
Касательное и нормальное ускорения также можно записать в виде:
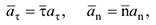
где 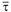 и
и  — соответственно ортогональные единичные векторы (см. выше 3.1.2). Рассмотрим конкретные задачи.
— соответственно ортогональные единичные векторы (см. выше 3.1.2). Рассмотрим конкретные задачи.
Готовые контрольные работы:
- Контрольная работа 3.1 Ротор мотора в период пуска имеет угловое ускорение . Определить скорость, касательное, нормальное и полное ускорения точки (рис. 3.11), лежащей на ободе ротора в момент . Диаметр ротора .
- Контрольная работа 3.2 В период разгона маховика закон его вращения характеризуется Определить скорость и ускорение точки, находящейся на расстоянии от оси вращения в тот момент, когда касательное и нормальное ускорения точки равны.
- Контрольная работа 3.3 Шестерня 1 радиуса приводится во вращение рукояткой . Эта шестерня сцеплена зубчатым колесом 2 радиуса , которое наглухо насажено на вал диаметра . На вал намотан нерастяжимый канат, к которому прикреплен груз . Определить скорость и ускорение груза , если рукоятка , вращаясь равноускоренно из состояния покоя совершает 16 оборотов за 2 с после начала движения (рис. 3.12).
Сложное движение точки
В ряде случаев приходится рассматривать движение точки по отношению к системе координат 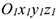 , которая в свою очередь движется по отношению системы координат
, которая в свою очередь движется по отношению системы координат 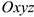 , условно принятой в качестве неподвижной. При этом:
, условно принятой в качестве неподвижной. При этом:
- движение точки относительно системы координат
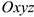 называется абсолютным;
называется абсолютным; - движение точки относительно подвижной системы осей
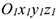 называется относительным;
называется относительным; - движение той точки подвижного пространства, с которой неизменно связана подвижная система отсчета
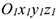 и с которой в данный момент времени совпадает рассматриваемая точка по отношению к неподвижной системе отсчета
и с которой в данный момент времени совпадает рассматриваемая точка по отношению к неподвижной системе отсчета 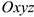 называется переносным.
называется переносным.
Различают также абсолютные, относительные и переносные траектории, скорости и ускорения точки как кинематические характеристики соответствующие указанным выше её движениям.
Разложение сложного (абсолютного) движения точки на относительные, переносные часто дает возможность привести сложное движение к простейшим движениям и этим самым облегчить решение конкретной задачи. Из определения абсолютного движения очевидно (рис. 3.13), что


Теорема о сложении скоростей
При сложном движении точки абсолютная скорость равна геометрической (векторной) сумме относительной и переносной скоростей (рис. 3.13).
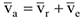
Модуль абсолютной скорости определяется по формуле:
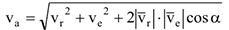
В разных учебниках можно встретить следующие обозначения скоростей:
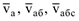 — абсолютная скорость;
— абсолютная скорость; 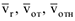 — относительная скорость;
— относительная скорость; 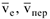 — переносная скорость.
— переносная скорость.
Ускорение точки в сложном движении
При определении ускорений точки в сложном движении пользуются теоремой Кориолиса, по которой абсолютное ускорение точки равно сумме трех ускорений: переносного, относительного и поворотного или Кориолисова.
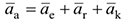
В общем случае, когда и переносное и относительное движения точки криволинейные, формула (3.33) приобретает вид:
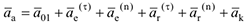
где  — соответственно ускорения начала подвижной системы координат, касательные и нормальные составляющие переносного и относительного ускорений. В случаях, когда переносное движение представляет собой вращение вокруг неподвижной оси начало подвижной системы осей удобно поместить на оси вращения и поэтому
— соответственно ускорения начала подвижной системы координат, касательные и нормальные составляющие переносного и относительного ускорений. В случаях, когда переносное движение представляет собой вращение вокруг неподвижной оси начало подвижной системы осей удобно поместить на оси вращения и поэтому 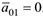 . Вектор ускорения Кориолиса определяется по формуле:
. Вектор ускорения Кориолиса определяется по формуле:
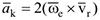
модуль которого вычисляется:
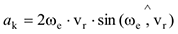
где  — угловая скорость переносного движения,
— угловая скорость переносного движения, 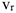 — относительная скорость точки. Ускорение Кориолиса равно нулю в следующих случаях:
— относительная скорость точки. Ускорение Кориолиса равно нулю в следующих случаях:
1) если  , т.е. в случаях поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступательного переносного движения;
, т.е. в случаях поступательного переносного движения или в моменты обращения в нуль угловой скорости непоступательного переносного движения;
2) если 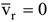 т.е. в случаях относительного покоя точки или в моменты обращения в нуль относительной скорости точки;
т.е. в случаях относительного покоя точки или в моменты обращения в нуль относительной скорости точки;
3) если 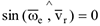 , т.е. в случаях
, т.е. в случаях  относительная скорость параллельна оси переносного вращения.
относительная скорость параллельна оси переносного вращения.
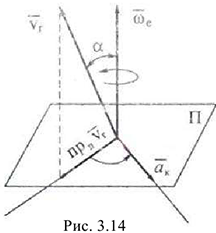
Направление ускорения Кориолиса определяем по правилу векторного произведения. Векторы  составляют правую систему ортогональных векторов. Для определения направления ускорения Кориолиса удобно пользоваться правилом Жуковского: чтобы найти направление ускорения Кориолиса следует спроектировать вектор скорости относительного движения точки на плоскость, перпендикулярную к оси переносного вращения и повернуть эту проекцию в той же плоскости на 90° в сторону переносного вращения (рис. 3.14).
составляют правую систему ортогональных векторов. Для определения направления ускорения Кориолиса удобно пользоваться правилом Жуковского: чтобы найти направление ускорения Кориолиса следует спроектировать вектор скорости относительного движения точки на плоскость, перпендикулярную к оси переносного вращения и повернуть эту проекцию в той же плоскости на 90° в сторону переносного вращения (рис. 3.14).
При решении каждой конкретной задачи рекомендуется соблюдать следующий порядок.
- Разложить сложное (абсолютное) движение точки на относительное и переносное движения.
- Выбрать неподвижную и подвижную системы координат.
- Мысленно остановить переносное движение и определить скорость и ускорение точки в относительном движении.
- Мысленно отвлекаясь от относительного движения, найти скорость и ускорение переносного движения точки.
- По угловой скорости переносного движения и скорости точки в относительном движении определить Кориолисово ускорение.
- Изобразить на рисунке векторы относительной и переносной скоростей, относительного, переносного и Кориолисова ускорений или их составляющих.
- Спроектировать векторы ускорений или их составляющих на оси координат.
- По найденным проекциям определить искомые скорости и ускорения (модули этих векторов и их направляющие косинусы).
В случаях, когда число рассматриваемых векторов не превышает трех, что имеет место при определении скоростей и в некоторых частных случаях определения ускорений, можно использовать формулы теоремы синусов и теоремы косинусов, т.е. непосредственно рассмотреть треугольники векторов скоростей и ускорений.

Готовая контрольная работа:
Плоскопараллельное движение твердого тела
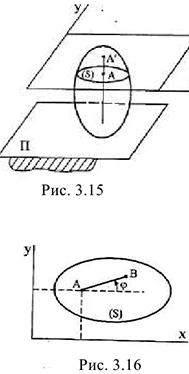
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости (плоскости  , рис. 3.15).
, рис. 3.15).
Плоскопараллельное движение — основа кинематики плоских механизмов.
Уравнение плоскопараллельного движения
Рассмотрим сечение  тела плоскостью
тела плоскостью  , параллельной неподвижной плоскости
, параллельной неподвижной плоскости  (рис. 3.15).
(рис. 3.15).
При плоском движении все точки тела, лежащие на прямой 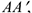 перпендикулярной к сечение
перпендикулярной к сечение  и, следовательно, к плоскости
и, следовательно, к плоскости  , движутся тождественно. Поэтому исследование плоскопараллельного движения твердого тела сводится к изучению движения сечения
, движутся тождественно. Поэтому исследование плоскопараллельного движения твердого тела сводится к изучению движения сечения  в плоскости
в плоскости  . Плоскость
. Плоскость  совмещают с плоскостью рисунка, а вместо всего твердого тела изображают его сечение
совмещают с плоскостью рисунка, а вместо всего твердого тела изображают его сечение  , которое называют плоской фигурой. Положение плоской фигуры
, которое называют плоской фигурой. Положение плоской фигуры  в плоскости
в плоскости  можно определить положением лежащего на ней некоторого отрезка
можно определить положением лежащего на ней некоторого отрезка 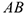 (рис. 3.16).
(рис. 3.16).
Положение же отрезка 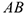 определяется координатами
определяется координатами 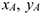 точки
точки  и углом
и углом 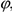 , который отрезок
, который отрезок 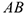 образует с осью
образует с осью 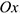 . Точку
. Точку  называют полюсом. В качестве полюса можно выбрать любую точку плоской фигуры. При движении тела величины
называют полюсом. В качестве полюса можно выбрать любую точку плоской фигуры. При движении тела величины  будут изменяться. Выражения
будут изменяться. Выражения
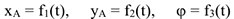
в любой момент времени определяют положение тела в пространстве при его плоском движении.
Зависимости (3.35), определяющие закон происходящего движения, называются уравнениями плоскопараллельного движения твердого тела. Плоское движение тела есть результат сложения двух его движений: поступательного и вращательного. Поступательная часть движения описывается первыми двумя уравнениями (3.35), т.е. уравнениями движения точки, выбранной в качестве полюса, а вращение вокруг полюса — третьим уравнением. Причем вращательная часть плоского движения инвариантна относительно выбора полюса, т.е. не зависит от выбора полюса, а поступательная часть — зависит.
Основными кинематическими характеристиками плоского движения являются скорость и ускорение поступательного движения, равные скорости и ускорения полюса 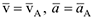 , а также угловая скорость
, а также угловая скорость 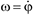 и угловое ускорение
и угловое ускорение 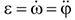 вращения вокруг полюса, которые в любой момент времени можно определить по уравнениям (3.35).
вращения вокруг полюса, которые в любой момент времени можно определить по уравнениям (3.35).
Существуют три метода кинематического исследования плоского движения твердого тела.
1 Аналитический метод базируется на составлении и исследовании уравнений плоскопараллельного движения (3.35).
2 Графический метод или метод диаграмм основан на графическом дифференцировании.
3 Графоаналитические методы, которые широко используются при решении конкретных задач.
Ниже более подробно рассмотрим графоаналитические методы.
Возможно эта страница вам будет полезна:
| Помощь по теоретической механике |
Графоаналитические методы определения скоростей точек плоской фигуры
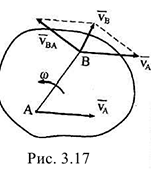
Графоаналитический метод определения скоростей основан на теореме, определяющий закон распределения скоростей: при плоскопараллельном движении твердого тела скорость любой его точки равна векторной сумме скорости полюса и скорости во вращательном движении вокруг полюса (рис. 3.17).
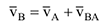
где 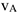 — скорость полюса,
— скорость полюса,  ;
;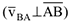 — скорость точки
— скорость точки 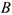 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса  . Формула (3.36) отражает отмеченный выше факт о том, что плоскопараллельное движение тела слагается из поступательного — движения, при котором все точки тела движутся со скоростью полюса
. Формула (3.36) отражает отмеченный выше факт о том, что плоскопараллельное движение тела слагается из поступательного — движения, при котором все точки тела движутся со скоростью полюса  ,и из вращательного движения вокруг этого полюса со скоростью
,и из вращательного движения вокруг этого полюса со скоростью 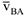 .
.
При плоском движении тела движение любой его точки 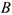 относительно принятой системы отсчета можно рассмотреть как сложное движение с абсолютной скоростью
относительно принятой системы отсчета можно рассмотреть как сложное движение с абсолютной скоростью 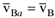 . Поступательную часть плоского движения можно рассмотреть как переносное движение со скоростью
. Поступательную часть плоского движения можно рассмотреть как переносное движение со скоростью 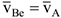 ,a вращательное движение вокруг полюса -как относительное движение со скоростью
,a вращательное движение вокруг полюса -как относительное движение со скоростью 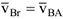 . Тогда формула (3.36) приобретает вид
. Тогда формула (3.36) приобретает вид
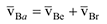
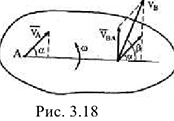
Полезной для решения практических задач является теорема о проекциях скоростей двух точек тела: проекции векторов скоростей двух точек твердого тела на прямую, соединяющую эти точки равны (рис. 3.18).
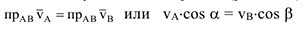

Мгновенный центр скоростей (МЦС)
При исследовании плоского движения объектов наряду с выше изложенными теоремами часто используется понятие мгновенного центра скоростей. При плоскопараллельном движении плоской фигуры в каждый данный момент времени существует точка, скорость которой в этот момент равна нулю. Эта точка  называется мгновенным центром скоростей. МЦС удобно использовать в качестве полюса. При этом скорости любых других точек тела определяются как вращательные вокруг МЦС (рис. 3.19).
называется мгновенным центром скоростей. МЦС удобно использовать в качестве полюса. При этом скорости любых других точек тела определяются как вращательные вокруг МЦС (рис. 3.19).

Из равенств (3.38) следует, что
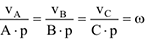

Необходимо особо подчеркнуть, что указанное в выражениях (3.38) распределение скоростей имеет место только в данный момент времени, т.е. только для данного положения плоской фигуры. В другой момент времени МЦС будет другая точка плоской фигуры и радиусы вращения 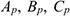 … будут другими. Ось вращения, проходящая через МЦС, перпендикулярна к плоской фигуре является мгновенной.
… будут другими. Ось вращения, проходящая через МЦС, перпендикулярна к плоской фигуре является мгновенной.
Положение МЦС определяется одним из следующих способов.
1 Известна скорость одной из точек тела, например, точки  (рис.3.20), а также угловая скорость плоской фигуры в данный момент. МЦС находится на перпендикуляре к
(рис.3.20), а также угловая скорость плоской фигуры в данный момент. МЦС находится на перпендикуляре к  , восстановленного из точки
, восстановленного из точки  на расстоянии
на расстоянии
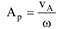
2 Известны линии действия векторов скоростей двух точек  и
и 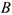 плоской фигуры. МЦС находится в точке пересечения перпендикуляров, восстановленных в точках
плоской фигуры. МЦС находится в точке пересечения перпендикуляров, восстановленных в точках  и
и 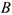 , к этим линиям (рис. 3.19).
, к этим линиям (рис. 3.19).
3 Известны скорости двух точек плоской фигуры 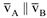 . Причем эти скорости могут иметь противоположные направления, в частности,
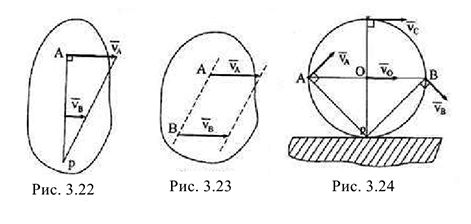
. Причем эти скорости могут иметь противоположные направления, в частности, 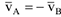 (рис. 3.21) и могут быть направлены в одну сторону (рис. 3.22) перпендикулярно к отрезку, соединяющему начала этих векторов. МЦС находится в точке пересечения этого отрезка и прямой, соединяющей концы векторов скоростей.
(рис. 3.21) и могут быть направлены в одну сторону (рис. 3.22) перпендикулярно к отрезку, соединяющему начала этих векторов. МЦС находится в точке пересечения этого отрезка и прямой, соединяющей концы векторов скоростей.
4 В случае 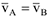 (рис. 3.23) МЦС отсутствует и тело совершает мгновенное поступательное движение.
(рис. 3.23) МЦС отсутствует и тело совершает мгновенное поступательное движение.
5 Плоская фигура катится без скольжения по неподвижной поверхности; МЦС находится в точке соприкосновения (рис. 3.24).
Определение угловой скорости при плоском движении
Угловую скорость плоской фигуры при плоском движении можно вычислить согласно её определению, как
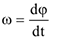
Ее можно вычислить по формуле (3.39), предварительно определив МЦС
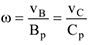
где 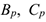 — расстояния точек
— расстояния точек 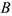 и
и 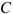 до МЦС. Направление
до МЦС. Направление 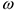 определяется направлением скоростей точек относительно МЦС.
определяется направлением скоростей точек относительно МЦС.
Угловую скорость можно также вычислить по формуле (3.36) путем предварительного нахождения скорости какой-либо точки (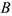 ) плоской фигуры при известной скорости другой её точки, принятой за полюс, например, точки
) плоской фигуры при известной скорости другой её точки, принятой за полюс, например, точки 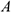
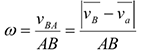
Графоаналитические методы определения ускорений точек плоской фигуры
Ускорения какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки во вращательном движении плоской фигуры вокруг полюса.
где 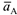 — ускорение точки
— ускорение точки 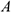 , принятой за полюс;
, принятой за полюс;  — ускорение т.
— ускорение т. 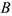 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса 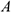 ;
; 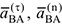 — соответственно касательная и нормальная составляющая
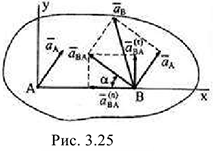
— соответственно касательная и нормальная составляющая 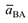 (рис. 3.25). Причем
(рис. 3.25). Причем

где 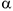 — угол наклона относительного ускорения
— угол наклона относительного ускорения 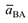 к отрезку
к отрезку 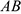 .
.
В случаях, когда 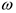 и
и 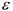 известны, формула (3.44) непосредственно используется для определения ускорений точек плоской фигуры. Однако во многих случаях зависимость угловой скорости от времени неизвестно, поэтому и угловое ускорение неизвестно. Кроме того, линия действия вектора ускорения одной из точек плоской фигуры известно. В этих случаях задача решается проектированием выражения (3.44) на соответствующим образом выбранные оси. Третий подход к определению ускорений точек плоской фигуры основан на использовании мгновенного центра ускорений (МЦУ).
известны, формула (3.44) непосредственно используется для определения ускорений точек плоской фигуры. Однако во многих случаях зависимость угловой скорости от времени неизвестно, поэтому и угловое ускорение неизвестно. Кроме того, линия действия вектора ускорения одной из точек плоской фигуры известно. В этих случаях задача решается проектированием выражения (3.44) на соответствующим образом выбранные оси. Третий подход к определению ускорений точек плоской фигуры основан на использовании мгновенного центра ускорений (МЦУ).
В каждый момент времени движения плоской фигуры в своей плоскости, если 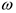 и
и 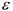 не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. МЦУ лежит на прямой, проведенной под углом
не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. МЦУ лежит на прямой, проведенной под углом 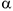 к ускорению точки, выбранной в качестве полюса, на расстоянии от которого
к ускорению точки, выбранной в качестве полюса, на расстоянии от которого
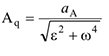
При этом угол 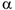 надо отложить от ускорения полюса
надо отложить от ускорения полюса  в направлении дуговой стрелки углового ускорения
в направлении дуговой стрелки углового ускорения  (рис. 3.26). В различные моменты времени МЦУ лежит в разных точках плоской фигуры. В общем случае МЦУ не совпадает с МЦС. При определении ускорений точек плоской фигуры МЦУ используется в качестве полюса. Тогда по формуле (3.44)
(рис. 3.26). В различные моменты времени МЦУ лежит в разных точках плоской фигуры. В общем случае МЦУ не совпадает с МЦС. При определении ускорений точек плоской фигуры МЦУ используется в качестве полюса. Тогда по формуле (3.44)
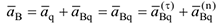
так как 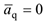 и следовательно
и следовательно
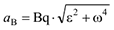
Ускорение 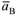 направлено под углом
направлено под углом 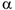 к отрезку
к отрезку 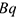 , соединяющему точку
, соединяющему точку  с МЦУ в сторону дуговой стрелки углового ускорения
с МЦУ в сторону дуговой стрелки углового ускорения  (рис. 3.26). Для точки
(рис. 3.26). Для точки 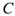 аналогично.
аналогично.
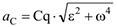
Из формулы (3.48), (3.49) имеем
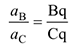
Таким образом, ускорение точек фигуры при плоском движении можно определить так же как при чистом её вращении вокруг МЦУ. Определение МЦУ.
1 В общем случае, когда 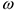 и
и  известны и не равны нулю, для угла а имеем
известны и не равны нулю, для угла а имеем
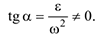
МЦУ лежит на пересечении прямых линий, проведенных к ускорениям точек фигуры под одним и тем же углом 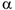 , причем угол
, причем угол 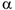 нужно откладывать от ускорений точек в направлении дуговой стрелки углового ускорения (рис. 3.26).
нужно откладывать от ускорений точек в направлении дуговой стрелки углового ускорения (рис. 3.26).

2 В случае
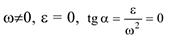
и, следовательно, 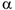 =0. МЦУ лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры (рис. 3.27)
=0. МЦУ лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры (рис. 3.27)
3 В случае

МЦУ лежит в точке пересечения перпендикуляров, восстановленных в точках 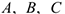 к соответствующим векторам ускорений
к соответствующим векторам ускорений 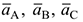 (рис. 3.28).
(рис. 3.28).
Определение углового ускорения при плоском движении
1 Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение определяется по известной формуле
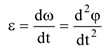
2 Если в указанной выше формуле 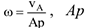 — расстояние от точки
— расстояние от точки 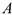 плоской фигуры до МЦС, величина постоянная, то угловое ускорение определяется путем дифференцирования угловой скорости по времени
плоской фигуры до МЦС, величина постоянная, то угловое ускорение определяется путем дифференцирования угловой скорости по времени

где  — касательно ускорение точки
— касательно ускорение точки 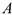 .
.
3 Иногда угловое ускорение удастся найти путем проектирования соотношения типа (3.44) на соответствующим образом выбранные оси координат. При этом ускорение т. 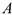 , выбранной в качестве полюса, известно, известна также линия действия ускорения другой т.
, выбранной в качестве полюса, известно, известна также линия действия ускорения другой т.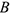 фигуры. Из таким образом полученной системы уравнений определяется касательное ускорение
фигуры. Из таким образом полученной системы уравнений определяется касательное ускорение  . Тогда
. Тогда  вычисляется по известной формуле
вычисляется по известной формуле 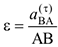 .
.
Готовая контрольная работа:
Возможно эта страница вам будет полезна:
| Заказать работу по теоретической механике |
Динамика
Динамика является важнейшим разделом теоретической механики, в котором изучается движение материальных тел в зависимости от действующих на них сил. В динамике на основании объективных законов и процессов устанавливаются количественные соотношения между мерами действия на материальные объекты и мерами их движения. Мерами действия между объектами являются силы, момент силы, импульс силы и работа силы, а мерами механического движения -количество движения, момент количества движения (кинетический момент) и кинетическая энергия.
Законы Ньютона — Галилея
В основе динамики лежат законы Ньютона — Галилея и принцип независимости действия сил. В соответствии с первым законом постулируется существование такой системы отсчета, в которой изолированная материальная точка движется равномерно и прямолинейно или покоится. Такая система координат называется инерциальной и является основной.
В соответствии со вторым законом Ньютона для свободной материальной точки можно записать:
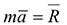
Здесь 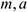 — соответственно масса и ускорение точки,
— соответственно масса и ускорение точки, 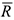 — действующая на неё сила. Если на точку действует несколько сил, то под
— действующая на неё сила. Если на точку действует несколько сил, то под 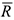 — понимают их равнодействующую. Выражение (4.1) называется основным уравнением динамики.
— понимают их равнодействующую. Выражение (4.1) называется основным уравнением динамики.
Дифференциальные уравнения движения материальной точки. Первая и вторая задачи динамики
Принимая во внимание то, что ускорение точки есть вторая производная по времени от её радиуса — вектора, а сила может зависеть от времени, положения и скорости точки, равенство (4.1) можно записать в виде:

Это выражение называют дифференциальным уравнением движения свободной точки в векторной форме.
Записывая его в проекциях на декартовые оси, получаем дифференциальные уравнения точки в скалярной форме.

а в проекциях на оси естественного трехгранника имеем:
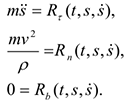
Из уравнений (4.4) следует, что равнодействующая 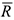 (так же как и ускорение точки
(так же как и ускорение точки 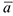 ) лежит в соприкасающейся плоскости.
) лежит в соприкасающейся плоскости.
Если точка несвободная, то силу целесообразно записывать в виде:
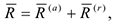
где  — соответственно равнодействующие активных сил и реакций связи.
— соответственно равнодействующие активных сил и реакций связи.
Как видно из дифференциальных уравнений движения, в динамике материальной точки можно решить две задачи.
Первая (прямая) задача динамики.
Даны уравнения движения точки, например в координатной форме:

Требуется найти действующие на неё силы. Решение этой задачи сводится дифференцированию выражений (4.5) по времени.
Вторая (обратная) задача динамики.
Даны силы, действующие на точку

требуется найти закон движения точки. Решение этой задачи значительно сложнее. Оно сводится к интегрированию системы дифференциальных уравнений при соответствующих начальных условиях. Число начальных условий равно порядку системы дифференциальных уравнений, в общем случае (4.6) — шести:
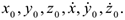
Контрольная работа 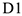 посвящена второй задаче динамики.
посвящена второй задаче динамики.
Готовая контрольная работа:
Механическая система. Основные понятия
Механической системой называется совокупность материальных точек или тел, в которой движение каждой из них зависит от движения остальных.
При рассмотрении механических систем различают внешние и внутренние силы. Силы действующие на точку механической системы со стороны точек (или тел) не входящих в систему, называются внешними и обозначаются 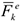 , где
, где 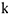 — индекс соответствующей точки системы. Силы, характеризующие взаимодействие точек (или тел) самой системы называются внутренними и обозначаются
— индекс соответствующей точки системы. Силы, характеризующие взаимодействие точек (или тел) самой системы называются внутренними и обозначаются  . В динамике системы активные силы, силы инерции и реакции связей соответственно обозначаются:
. В динамике системы активные силы, силы инерции и реакции связей соответственно обозначаются:
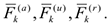
В соответствии с третьим законом Ньютона, внутренние силы удовлетворяют следующим условиям.
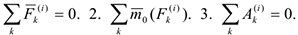
работа внутренних сил неизменяемой системы равно нулю.
Массой механической системы называется сумма масс материальных точек системы
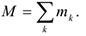
Центром масс механической системы называется геометрическая точка, радиус — вектор которой определяется формулой.

Отсюда следует и скалярные выражения для координат центра масс.
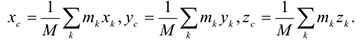
При изучении движения твердого тела, важную роль играют моменты инерции.
Моментом инерции относительно оси называется сумма произведений масс точек тела на квадраты их расстояний до этой оси.
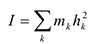
Обычно ось, относительно которой вычисляется осевой момент инерции, указывается соответствующим индексом, например:
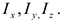
Момент инерции относительно центральной оси, проходящей через центр масс тела, часто обозначают  .
.
Для определения закона движения точек механической системы на основании второго закона Ньютона можно записать.

Здесь 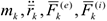 — соответственно масса ускорение
— соответственно масса ускорение 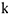 — ой точки системы, результирующая внешних и внутренних сил, приложенных в этой точке. Решение этих уравнений в общем случае оказывается трудным и громоздким, а иногда и невозможным.
— ой точки системы, результирующая внешних и внутренних сил, приложенных в этой точке. Решение этих уравнений в общем случае оказывается трудным и громоздким, а иногда и невозможным.
Вмсстс с тем во многих задачах в этом нет необходимости. Для описания движения достаточно знать поведение с течением времени интегральных кинетических характеристик системы, которые определяются общими теориями динамики системы.
Кинетические характеристики движения механической системы
1. Количество движения.
Количеством движения механической системы называется векторная величина 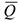 , равная геометрической сумме количеств движений всех точек системы:
, равная геометрической сумме количеств движений всех точек системы:
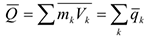
Где 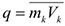 — количество движения
— количество движения 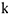 — ой точки. Количество движения можно представить также в следующей форме
— ой точки. Количество движения можно представить также в следующей форме

Здесь 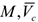 — масса системы и скорость её центра масс соответственно.
— масса системы и скорость её центра масс соответственно.
- Главный момент количества движения или кинетический момент механической системы.
Кинетическим моментом механической системы относительно которого центра 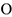 называется векторная величина
называется векторная величина 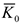 , равная геометрической сумме моментов количеств движения точек системы относительно центра
, равная геометрической сумме моментов количеств движения точек системы относительно центра 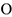 .
.
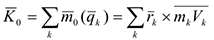
где 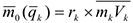 — момент количества движения
— момент количества движения 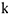 -ой точки относительно центра
-ой точки относительно центра 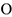 . Момент количества движения системы относительно оси, проходящей через точку
. Момент количества движения системы относительно оси, проходящей через точку 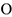 — есть проекция вектора
— есть проекция вектора 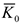 на эту ось. В случае твердого тела.
на эту ось. В случае твердого тела.
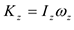
Где 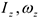 — соответственно момент инерции тела относительно оси
— соответственно момент инерции тела относительно оси 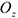 и проекция угловой скорости на эту ось. Если система состоит из нескольких тел, вращающихся вокруг одной оси, то
и проекция угловой скорости на эту ось. Если система состоит из нескольких тел, вращающихся вокруг одной оси, то
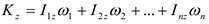
3.Кинетическая энергия.
Кинетическая энергия механической системы есть величина равная сумме кинетических энергий соответствующих её точек.

При вычислении кинетической энергии механической системы удобно пользоваться формулой

которая следует из теоремы Кёнига. Кинетическая энергия системы складывается из кинетической энергии центра масс и кинетической энергии системы в её движении относительно центра масс. В зависимости от характера движения тела рассмотрим следующие простейшие частные случаи: 1) Кинетическая энергия при поступательном движении, которое характеризуется 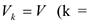
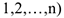
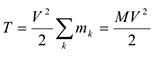
 — масса системы;
— масса системы;
2) При вращении вокруг неподвижной оси 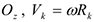 и поэтому
и поэтому
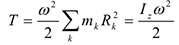
где 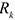 — радиус вращения (расстояние до оси вращения) точки;
— радиус вращения (расстояние до оси вращения) точки;
3) В случае плоскопараллельного движения
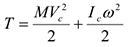
где  — скорость центра масс,
— скорость центра масс, 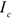 — момент инерции тела относительно центральной оси. Структура формула (3.20) отражает тот факт, что плоскопараллельное движение является результатом сложения поступательного и вращательного его движения.
— момент инерции тела относительно центральной оси. Структура формула (3.20) отражает тот факт, что плоскопараллельное движение является результатом сложения поступательного и вращательного его движения.
Общие теоремы динамики точки и механической системы. Теорема о движении центра масс системы
Центр масс механической системы движется как материальная точка, масса которой равна массе системы и к которой приложены все внешние силы, действующие на систему.
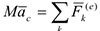
уравнение движения центра масс системы в векторной форме и в скалярной форме:
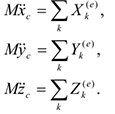
Закон сохранения движения центра масс.
Если 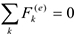 , то из выражения (4.21) следует, что
, то из выражения (4.21) следует, что  или
или 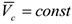 .
.
Следовательно, если сумма внешних сил равна нулю, то центр масс системы движется с постоянной скоростью (равномерно и прямолинейно). Таким образом, действие внутренних сил движения центра масс изменить не может.
Если в уравнениях (4.22) имеет место 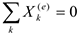 , то первое из этих уравнений дает
, то первое из этих уравнений дает 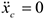 или
или  . При этом порядок системы дифференциальных уравнений снижается на единицу. Если в начальный момент
. При этом порядок системы дифференциальных уравнений снижается на единицу. Если в начальный момент  , то и в любой другой момент вращения
, то и в любой другой момент вращения 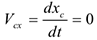 или
или 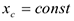 . В этом случае механическая система совершает плоскопараллельное движение. Порядок системы уравнений (4.22) снижается на две единицы.
. В этом случае механическая система совершает плоскопараллельное движение. Порядок системы уравнений (4.22) снижается на две единицы.
Теорема об изменении количества движения материальной точки и механической системы
Для характеристики действия силы, оказываемого на тело за некоторый промежуток времени, вводится понятие об импульсе силы:
 — элементарный импульс силы;
— элементарный импульс силы;
 — импульс силы за конечный промежуток времени, причем
— импульс силы за конечный промежуток времени, причем
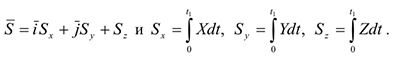
Запишем основное уравнение динамики для материальной точки с постоянной массой в форме.
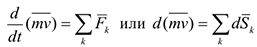
Уравнение (4.23) выражает теорему об изменении количества движения точки. Интегрируя выражение (4.23) по  от 0 до
от 0 до  , и
, и 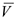 от
от  до
до  , получим
, получим
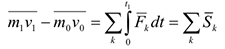
Уравнение (4.24) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на неё сил за тот же промежуток времени. Проектируя равенство (4.24) на координатные оси получим скалярные уравнения
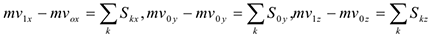
которые используются при решении задач.
Теорема об изменении количества движения механической системы
Количество движения системы, как векторная величина, определяется формулами (4.12) и (4.13). Теорема. Производная от количества движения системы по времени равна геометрической сумме всех действующих на нее внешних сил.
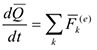
В проекциях декартовые оси получим скалярные уравнения.
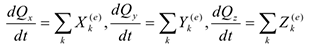
Можно записать векторное
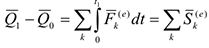
и скалярные уравнения
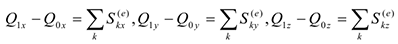
Которые выражают теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов за тот же промежуток времени. При решении задач чаще используются уравнения (4.27)
Закон сохранения количества движения
- Если в уравнении (4.26)
 . Следовательно, если сумма внешних сил равна нулю, то вектор количества движения будет постоянен (постоянны и модуль и направление).
. Следовательно, если сумма внешних сил равна нулю, то вектор количества движения будет постоянен (постоянны и модуль и направление). - Если сумма проекций внешних сил на какую-нибудь ось равна нулю, то проекция количества движения на эту ось есть величина постоянная, т.е. из равенств (4.27) при
 следует
следует  . При этом порядок системы дифференциальных уравнений снижается на единицу. Отмстим, что теоремы о движении центра масс системы и об изменении количества движения удобно использовать при исследовании поступательных движениях механических систем, в частности твердых тел.
. При этом порядок системы дифференциальных уравнений снижается на единицу. Отмстим, что теоремы о движении центра масс системы и об изменении количества движения удобно использовать при исследовании поступательных движениях механических систем, в частности твердых тел.
Теорема об изменении кинетического момента
Теорема об изменении момента количества движения точки относительно центра: производная по времени от момента количества движения точки относительно неподвижного центра равна векторному моменту, действующей на точку силы относительно того же центра.
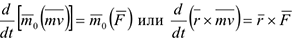
Сравнивая (4.23) и (4.30), видим, что моменты векторов 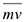 и
и 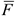 связаны такой же зависимостью, какой связаны сами векторы
связаны такой же зависимостью, какой связаны сами векторы 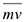 и
и 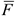 (рис. 4.1). Если спроектировать равенство на ось
(рис. 4.1). Если спроектировать равенство на ось  , проходящую через центр
, проходящую через центр 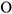 , то получим
, то получим
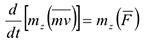

Это равенство выражает теорему момента количества движения точки относительно оси.
Теорема об изменении главного момента количества движения или кинетического момента механической системы относительно центра: производная по времени от кинетического момента системы относительно некоторого неподвижного центра равно сумме моментов всех внешних сил относительно того же центра.
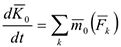
Если спроектировать выражение (4.32) на ось 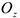 , проходящей через центр
, проходящей через центр 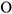 , то получим равенство, характеризующее теорему об изменении кинетического момента относительно оси.
, то получим равенство, характеризующее теорему об изменении кинетического момента относительно оси.
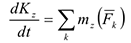
Подставляя (4.10) в равенство (4.33) можно записать дифференциальное уравнение вращающегося твердого тела (колес, осей, валов, роторов и т.д.) в трех формах.
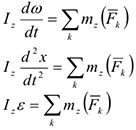
Таким образом, теорему об изменении кинетического момента целесообразно использовать для исследования весьма распространенного в технике движения твердого тела, его вращения вокруг неподвижной оси.
Закон сохранения кинетического момента системы
- Пусть в выражении (4.32)

Тогда из уравнения (4.32) следует, что 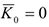 , т.е. если сумма моментов всех приложенных к системе вешних сил относительно данного центра равно нулю, то кинетический момент системы относительно этого центра будет численно и по направлению будет постоянен.
, т.е. если сумма моментов всех приложенных к системе вешних сил относительно данного центра равно нулю, то кинетический момент системы относительно этого центра будет численно и по направлению будет постоянен.
- Если
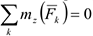 , то
, то 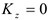 . Таким образом, если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то кинетический момент системы относительно этой оси будет величиной постоянной.
. Таким образом, если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то кинетический момент системы относительно этой оси будет величиной постоянной.
Эти результаты выражают собой закон сохранения кинетического момента.
В случае вращающегося твердого тела из равенства (4.34) следует, что, если 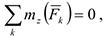 то
то 
Отсюда приходим к следующим выводам:
Если система неизменяема (абсолютно твердое тело), то 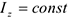 , следовательно, и
, следовательно, и 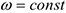 и твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью.
и твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью.
Если система изменяема, то  . При увеличении
. При увеличении  (тогда отдельные элементы системы удаляются от оси вращения) угловая скорость
(тогда отдельные элементы системы удаляются от оси вращения) угловая скорость  уменьшается, т.к.
уменьшается, т.к. 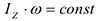 , а при уменьшении
, а при уменьшении 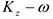 увеличивается, таким образом, в случае изменяемой системы с помощью внутренних сил можно изменить угловую скорость.
увеличивается, таким образом, в случае изменяемой системы с помощью внутренних сил можно изменить угловую скорость.
Вторая задача Д2 контрольной работы посвящена теореме об изменении кинетического момента системы относительно оси.
Готовая контрольная работа:
Теорема об изменении кинетической энергии
Теорема об изменении кинетической энергии точки.
В основе этой теоремы, как и рассмотренных выше теорем, лежит второй закон Ньютона. Проектируя равенство 4.1 на касательную ось получим:
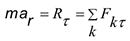
Касательное ускорение запишем в формуле:
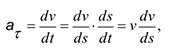
где  — элементарное перемещение точки (рис. 4.2). В результате найдем, что
— элементарное перемещение точки (рис. 4.2). В результате найдем, что
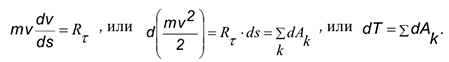
Здесь  — кинетическая энергия,
— кинетическая энергия, 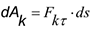 — элементарная работа силы
— элементарная работа силы 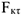 (рис. 4.2.) Элементарная работа
(рис. 4.2.) Элементарная работа 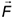 также может быть представлена в виде
также может быть представлена в виде

где 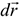 — дифференциал радиуса-вектора точки,
— дифференциал радиуса-вектора точки, 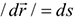 .
.
Работа на конечном перемещении точки 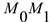 может быть вычислена как предел интегральной суммы.
может быть вычислена как предел интегральной суммы.
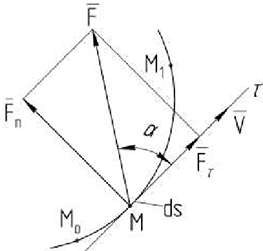
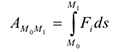
или
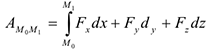
Единицей измерения работы в СИ является — 1 джоуль (1 дж.= 1 кН). Величина
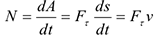
есть мощность силы 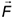 . Единица измерения мощности в СИ — ватт (1 Вт= 1 дж/с).
. Единица измерения мощности в СИ — ватт (1 Вт= 1 дж/с).
Равенство (4.37) есть выражения теоремы об изменении кинетической энергии в дифференциальной форме. Можно записать выражение теоремы в конечном виде.

Теорема. Изменения кинетической энергии точки на некотором перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
Возможно эта страница вам будет полезна:
| Курсовая работа по теоретической механике |
Теорема об изменении кинетической энергии системы
Для 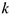 -ой точки системы можно записать
-ой точки системы можно записать
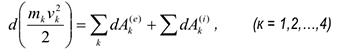
Где 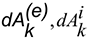 — элементарные работы приложенных к точке внешних и внутренних сил. Суммируя это выражения по
— элементарные работы приложенных к точке внешних и внутренних сил. Суммируя это выражения по

найдем, что
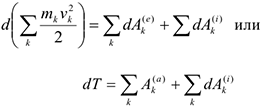
Равенство (4.43.) выражает теорему об изменении кинетической энергии в дифференциальной форме. Проинтегрировав это равенство в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна  в положение, где
в положение, где 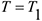 получим
получим
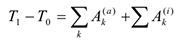
Это уравнение выражает теорему об изменении кинетической энергии в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных в системе внешних и внутренних сил. Частные случаи.
1.Неизменяемая система. В случае неизменяемой системы сумма работ всех внутренних сил равно нулю

или

Система с идеальными связями. В этом случае
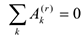
и поскольку

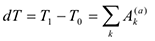
Здесь
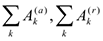
суммы работ активных сил и реакций связей. Примеры вычисления работы.
Работа силы тяжести
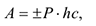
где  — вес системы,
— вес системы, 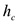 — вертикальное перемещение центра масс системы.
— вертикальное перемещение центра масс системы.
- Работа силы упругости пружины
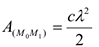
где  — коэффициент жесткости пружины,
— коэффициент жесткости пружины, 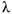 — удлинение пружины.
— удлинение пружины.
- Работа силы трения

где 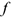 — коэффициент трения,
— коэффициент трения,  — нормальная реакция поверхности.
— нормальная реакция поверхности.
- Работа сил и пар сил, приложенных к вращающемуся телу. Элементарная работа момента силы или момента пары относительно оси вращения равна

где 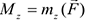 — вращающий момент. При повороте на конечный угол
— вращающий момент. При повороте на конечный угол

и в случае постоянного момента
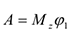
В этом случае мощность определяется по формуле
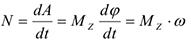
В задаче ДЗ используется теорема об изменении кинетической энергии системы.
Готовая контрольная работа:
Принцип Даламбера
Наряду с общими теоремами динамики позволяют найти эффективные методы решения задач принципы механики, которые также базируются на законах Ньютона-Галилея. Рассмотрим основное уравнение динамики (4.1.) для несвободной материальной точки в форме.
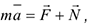
где  — активная сила и реакция связи соответственно. Запишем выражение (4.47.) в виде
— активная сила и реакция связи соответственно. Запишем выражение (4.47.) в виде

при этом введем в рассмотрение величину 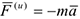 , которую назовем силой инерции. Она направлена противоположно ускорению точки. На что указывает знак (-) Тогда
, которую назовем силой инерции. Она направлена противоположно ускорению точки. На что указывает знак (-) Тогда
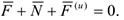
В этом заключается принцип Даламбера: если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной.
Принцип Даламбера для механической системы
Для которой точки системы запишем

Принцип. Если в любой момент времени к каждой из точек системы кроме действующих на нее внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной. Таким образом, принцип Даламбера математически задачи динамики сводит к задачам статики о равновесии, часто упрощая соответствующие расчеты.
Выражение (4.49.) суммируем по 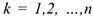 и умножив его слева векторно на радиусы-векторы соответствующих точек, снова суммируем по
и умножив его слева векторно на радиусы-векторы соответствующих точек, снова суммируем по 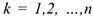

Здесь

на основании свойств внутренних. Введем обозначения
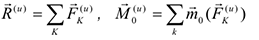
Тогда из равенства (4.32) получим
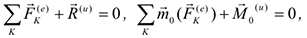
где  — соответственно главный вектор и главный момент относительно центра
— соответственно главный вектор и главный момент относительно центра 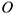 системы сил инерции.
системы сил инерции.
На основании ранее рассмотренных теорем можно записать
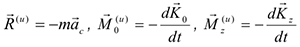
Следовательно, главный вектор сил инерции механической системы равен произведению массы системы на ускорение центра масс и направлен противоположно этому ускорению; главный момент сил инерции механической системы относительно центра 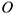 или оси
или оси 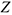 равен взятой со знаком минус производной по времени кинетического момента системы относительно того центра или той же оси.
равен взятой со знаком минус производной по времени кинетического момента системы относительно того центра или той же оси.
Частные случаи.
- Поступательное движение. В этом случае
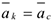 . Тогда все силы
. Тогда все силы 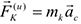 образуют систему направленных сил и имеют равнодействующую, проходящую через центр, точку масс, точку
образуют систему направленных сил и имеют равнодействующую, проходящую через центр, точку масс, точку 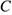 .
. - Вращательное движение. Пусть твердое тело имеет плоскость симметрии
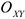 и вращается вокруг оси
и вращается вокруг оси 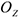 . Тогда
. Тогда 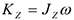 .
.
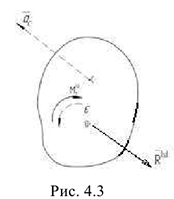
Таким образом, система сил инерции вращающегося тела, приводится к силе 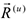 , определяемой формулой (4.52) и приложенной к точке
, определяемой формулой (4.52) и приложенной к точке 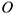 (рис.4.3.) и паре с моментом
(рис.4.3.) и паре с моментом 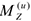 определяемым формулой (4.53.)
определяемым формулой (4.53.)
Если тело вращается вокруг центральной оси  , проходящей через центр масс
, проходящей через центр масс 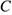 тела, то
тела, то 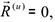 т.к.
т.к.  . Следовательно, в этом случае система сил инерции тела приводится к паре с моментом
. Следовательно, в этом случае система сил инерции тела приводится к паре с моментом 
Плоскопараллельное движение. Если тело имеет плоскость симметрии и движется параллельно этой плоскости, то система сил инерции тела приводится к лежащим в плоскости симметрии силе 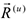 , приложенной к центру масс тела
, приложенной к центру масс тела 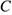 , и паре с моментом
, и паре с моментом

Готовая контрольная работа:
Принцип возможных перемещений и общее уравнение динамики. Принцип возможных перемещений
Эффект связей можно учитывать не только вводя их реакции, но и рассматривая те перемещения, которые точки механической системы могут иметь при наложенных на нее связях . Такой метод позволяет сразу получить уравнение равновесия или движения системы, не содержащие наперед неизвестных реакций связей, что существенно облегчает решение многих задач механики. Эти перемещения называют возможными или виртуальными перемещениями. Они должны быть малыми (элементарными), так как при конечном перемещении система может прийти в положение, где эффект наложенных связей будет другим; быть такими, чтобы все наложенные в данный момент времени на систему связи сохранились, иначе может измениться вид рассматриваемой механической системы.
Следует различать действительное элементарное перемещение 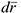 от виртуальных перемещений. Поэтому возможное перемещение принято обозначать
от виртуальных перемещений. Поэтому возможное перемещение принято обозначать 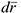 , при этом
, при этом  будет обозначать его модуль
будет обозначать его модуль  — проекции
— проекции 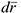 на координатные оси.
на координатные оси.
Следует отметить также, что число независимых между собой возможных перемещений системы равно ее числу степеней свободы.
Обозначим равнодействующие всех(внешних и внутренних) активных сил и реакции связей действующих на некоторую точку системы  соответственно через
соответственно через 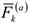 и
и 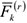 . В случае равновесия механической системы, когда каждая ее точка находится в равновесии, имеет место равенств
. В случае равновесия механической системы, когда каждая ее точка находится в равновесии, имеет место равенств
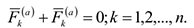
Умножаем это равенство скалярно на 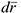 и получим
и получим
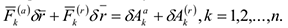
Сложив эти равенства по индексу к получим
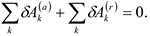
В случае идеальных связей сумма работ их реакций на любом возможном перемещений равна нулю, т.е. 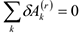 . Тогда окончательно приходим к соотношению
. Тогда окончательно приходим к соотношению
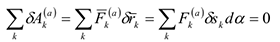
которое характеризует принцип возможных перемещений: для равновесия механической системы с иральными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.
Уравнение (4.54) можно записать в аналитической форме
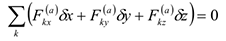
Равенства (4.54) и (4.55) часто называют общим уравнением статики.
Принцип Даламбера — Лагранжа
Принцип возможных перемещений дает общий метод решения задач статики, а принцип Даламбера позволяет использовать методы статики для решения задач динамики. Следовательно, применяя эти два принципа одновременно мы можем получить общий метод решения задачи динамики. Согласно принципу Даламбера система активных сил 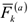 реакций связей
реакций связей 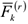 и сил инерции
и сил инерции 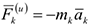 образуют уравновешенную систему сил. Тогда, применяя к этим силам принцип возможных перемещений, получим
образуют уравновешенную систему сил. Тогда, применяя к этим силам принцип возможных перемещений, получим
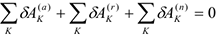
Но поскольку связи идеальные и
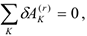
окончательно запишем
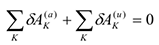
Равенство (4.56) выражает принцип Даламбера — Лагранжа, при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещений системы будет равна нулю. В аналитической форме уравнение (4.56) имеет вид

Уравнение (4.56) и (4.57) называют общим уравнением динамики.
