Оглавление:
Под графом понимают систему объектов произвольной природы (вершин) и связок (ребер, соединяющих некоторые пары этих объектов).
Определение графа
Строгое определение графа: графом G называется пара множеств 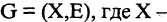 непустое множество вершин
непустое множество вершин 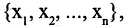 а элементами множества Е являются некоторые двухэлементные подмножества
а элементами множества Е являются некоторые двухэлементные подмножества 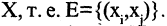 Эти двухэлементные подмножества называются ребрами. Например,
Эти двухэлементные подмножества называются ребрами. Например,
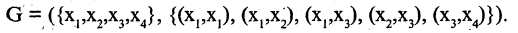
Несложные графы изображают в виде графических схем, где вершины — точки, а ребра — соединяющие их линии. В этих схемах длина линий, их толщина и форма, а также взаиморасположение вершин не имеют никакого значения. Таким образом, граф — свободная конструкция, для которой имеет значение факт наличия связей между двумя вершинами и, в некоторых случаях, характер этих связей.
Если вершины 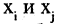 принадлежат некоторому ребру
принадлежат некоторому ребру 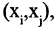 то говорят, что это ребро инцидентно вершинам
то говорят, что это ребро инцидентно вершинам 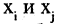 которые в свою очередь называются смежными. Если ребро инцидентно одной и той же вершине, то оно называется петлей. Вершина, не инцидентная никакому ребру, называется изолированной. Если в графе есть вершины, соединенные двумя или большим числом вершин, то такой граф называют мультиграфом (см. рис. 1.18).
которые в свою очередь называются смежными. Если ребро инцидентно одной и той же вершине, то оно называется петлей. Вершина, не инцидентная никакому ребру, называется изолированной. Если в графе есть вершины, соединенные двумя или большим числом вершин, то такой граф называют мультиграфом (см. рис. 1.18).
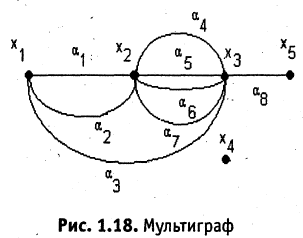
Число ребер, инцидентных данной вершине, называется степенью (кратностью) данной вершины. В графе, изображенном на рис. 1.18, вершина 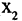 имеет степень 6, т.к. ей инцидентны ребра
имеет степень 6, т.к. ей инцидентны ребра 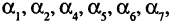 а вершина
а вершина 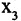 имеет степень 5. Вершина
имеет степень 5. Вершина 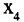 имеет степень 0, т. е. это изолированная вершина. Граф без петель и кратных ребер называется простым или обыкновенным. Граф может быть задан и в виде квадратной таблицы — матрицы смежности графа.
имеет степень 0, т. е. это изолированная вершина. Граф без петель и кратных ребер называется простым или обыкновенным. Граф может быть задан и в виде квадратной таблицы — матрицы смежности графа.
Номера строк и столбцов этой матрицы совпадают с номерами вершин графа, а ее элемент 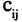 есть число ребер, соединяющих вершины
есть число ребер, соединяющих вершины 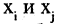 . Для графа, изображенного на рис. 1.18, матрица смежности имеет вид
. Для графа, изображенного на рис. 1.18, матрица смежности имеет вид
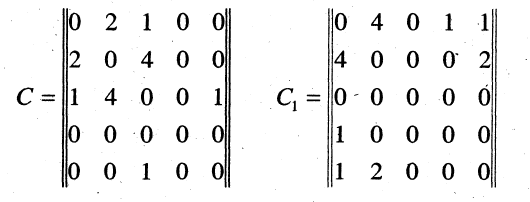
Нумеровать вершины графа можно произвольным образом. Например, в графе, изображенном на рис. 1.18, перенумеруем вершины следующим образом: 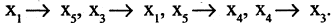 При этом матрица смежности
При этом матрица смежности 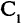 изменится (сравните матрицы С и
изменится (сравните матрицы С и 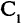 ).
).
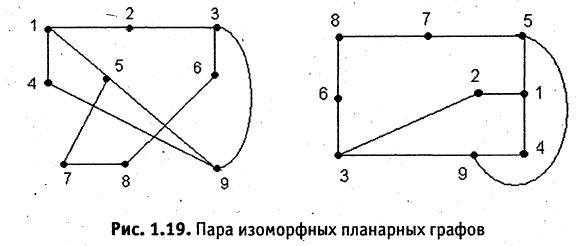
Для графов существенно лишь число вершин и ребер, а также отношения инцидентности вершин и ребер. Следовательно, графы, отличающиеся только нумерацией вершин и сохраняющие отношения их инцидентности, отличаются лишь начертанием. Поэтому говорят, что матрица определяет графы с точностью до изоморфизма, а такие графы называются изоморфными. В подавляющем большинстве приложений изоморфные графы не различаются, и решения задач на изоморфных графах по существу совпадают. Граф называется планарным (плоским), если существует изоморфный ему граф, который может быть изображен на плоскости без пересечения ребер. На рис. 1.19 представлена пара изоморфных графов 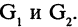 В первом из них ребра пересекаются, но поскольку в изоморфном ему графе ребра не пересекаются, то оба они являются планарными.
В первом из них ребра пересекаются, но поскольку в изоморфном ему графе ребра не пересекаются, то оба они являются планарными.
Ориентированным, или орграфом D, называется пара 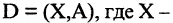 произвольное множество вершин и А — множество упорядоченных пар вершин, называемых дугами
произвольное множество вершин и А — множество упорядоченных пар вершин, называемых дугами 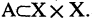 В паре
В паре 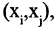 первая вершина
первая вершина 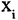 называется началом дуги, а вторая
называется началом дуги, а вторая 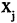 — концом дуги. На рисунках дуги изображаются стрелками (см. рис. 1.20).
— концом дуги. На рисунках дуги изображаются стрелками (см. рис. 1.20).
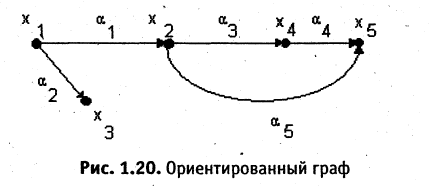
Ориентированные графы задают в виде таблиц — матриц ин-циденций. Номера строк матрицы инциденций равны номерам вершин, а номера столбцов — номерам дуг. Если дуга выходит из вершины 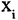 , то соответствующий элемент матрицы инциденций
, то соответствующий элемент матрицы инциденций 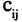 равен -1. Если же дуга
равен -1. Если же дуга 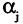 входит в вершину
входит в вершину 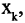 то элемент
то элемент 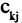 равен +1. Все другие элементы столбца j равны нулю. Для ориентированного графа, изображенного на рис. 1.18, матрица инциденций имеет вид
равен +1. Все другие элементы столбца j равны нулю. Для ориентированного графа, изображенного на рис. 1.18, матрица инциденций имеет вид
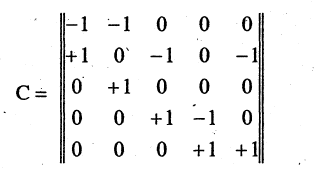
Матрицы часто используются для задания графов в памяти компьютеров.
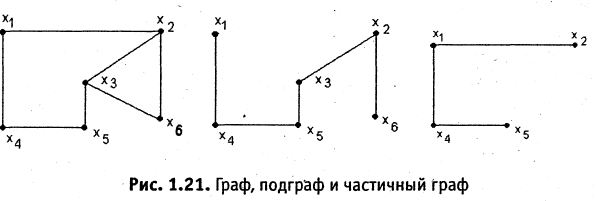
Граф 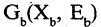 называется частичным графом (суграфом) графа
называется частичным графом (суграфом) графа 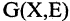 , если он содержит все вершины исходного графа и лишь часть ребер исходного графа, т.е.
, если он содержит все вершины исходного графа и лишь часть ребер исходного графа, т.е. 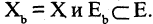 Подграфом
Подграфом 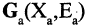 графа
графа 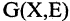 называется граф, в который входит подмножество вершин исходного графа
называется граф, в который входит подмножество вершин исходного графа 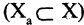 и все ребра, соединяющие вершины
и все ребра, соединяющие вершины 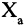 этого графа
этого графа 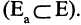 На рис. 1.21 представлены: подграф и частичный граф для данного исходного графа
На рис. 1.21 представлены: подграф и частичный граф для данного исходного графа 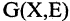 .
.
Маршруты на графах
Возьмем неориентированный граф 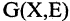 . Маршрутом длины m называется последовательность m ребер графа
. Маршрутом длины m называется последовательность m ребер графа 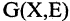 , такая, что вершины двух соседних ребер последовательности совпадают. Примерами маршрутов на графе, изображенном на рис. 1.18, могут служить следующие последовательности ребер
, такая, что вершины двух соседних ребер последовательности совпадают. Примерами маршрутов на графе, изображенном на рис. 1.18, могут служить следующие последовательности ребер 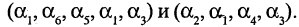 Первый из них проходит последовательно через вершины
Первый из них проходит последовательно через вершины 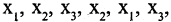 соединяя
соединяя 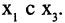 Второй,, проходя через вершины
Второй,, проходя через вершины 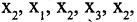 образует замкнутый маршрут, т.к. приводит в ту же вершину, из которой и начался.
образует замкнутый маршрут, т.к. приводит в ту же вершину, из которой и начался.
Две вершины графа называются связанными, если существует маршрут, соединяющий эти вершины. Граф, любая пара вершин которого связана, называют связным графом. Представленный на рис. 1.18 граф не является связным, поскольку, например, отсутствует маршрут из 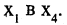
Маршрут, все ребра которого различны, называется цепью. Цепь, проходящая через различные вершины, называется простой (элементарной) цепью. Замкнутая цепь называется циклом, а цикл, проходящий через различные вершины, — простым циклом. Так в графе, изображенном на рис. 1.18, маршрут 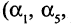
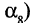 является простой цепью, маршрут
является простой цепью, маршрут 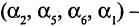 циклом.
циклом.
Для практики большое значение имеют задачи о нахождении различного рода маршрутов. Наиболее известные из них два: эйлеров цикл и гамильтонов цикл. Простой цикл, содержащий все ребра графа, называется эйлеровым, а граф, имеющий эйлеров цикл, называется эйлеровым графом. Если эйлеров граф — плоский, то его можно изобразить одним росчерком пера (не отрывая пера от бумаги), причем начальная и конечная вершины совпадут. На рис. 1.22 изображен граф, обход всех ребер которого ровно один раз возможен по маршруту: 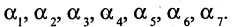
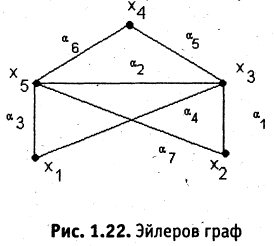
Конечный неориентированный граф — эйлеров тогда и
только тогда, когда он связан и степени всех его вершин четны. Граф изображенный на рис 1.22 — эйлеров, т.к. степени его вершин 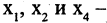 2, вершин
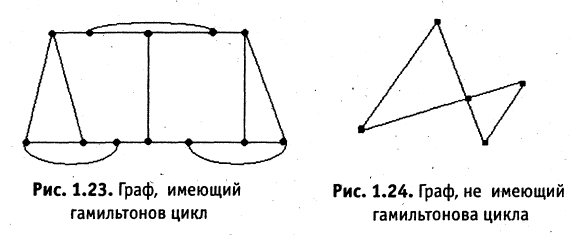
2, вершин 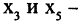 4. Простой цикл, который проходит через все вершины графа, называется гамильтоновым. На рис. 1.23 и 1.24 представлены граф, имеющий гамильтонов цикл и не имеющий такового.
4. Простой цикл, который проходит через все вершины графа, называется гамильтоновым. На рис. 1.23 и 1.24 представлены граф, имеющий гамильтонов цикл и не имеющий такового.
В ориентированном графе маршруты называются ориентированными: начальная вершина каждой последующей дуги маршрута должна совпадать с конечной вершиной предыдущей дуги. Если рассматривать изображение ориентированного графа, то движение по маршрутам на нем должно осуществляться только в направлениях, указанных стрелками. Маршрут, не содержащий повторяющихся дуг, называется путем. Путь, не содержащий повторяющихся вершин, называется простым путем. Замкнутый путь называется контуром. Простой контур — контур, не имеющий повторяющихся вершин. Если в графе содержится хотя бы один контур, то это контурный граф.
При помощи ориентированного графа можно задавать бинарные отношения, например, отношения порядка. Говорят, что на ориентированном графе 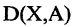 задано отношение порядка, если для любых двух вершин
задано отношение порядка, если для любых двух вершин 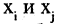 , удовлетворяющих условию
, удовлетворяющих условию 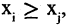 существует путь из
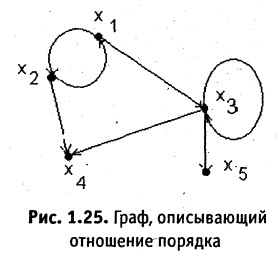
существует путь из 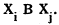 На рисунке 1.25 представлено изображение графа, на котором определено отношение порядка «
На рисунке 1.25 представлено изображение графа, на котором определено отношение порядка «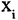 не больше
не больше 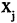 » Для отношения порядка характерны три свойства: рефлексивность, антисимметричность и транзитивность. Рефлексивность означает истинность условия
» Для отношения порядка характерны три свойства: рефлексивность, антисимметричность и транзитивность. Рефлексивность означает истинность условия 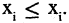 Следовательно, вершина
Следовательно, вершина 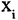 не больше самой себя, т. е. имеется путь из
не больше самой себя, т. е. имеется путь из 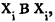 что обусловливает допустимость петли для вершины
что обусловливает допустимость петли для вершины 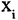 . Антисимметричность
. Антисимметричность 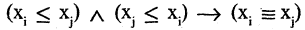 показывает, что если на графе имеется путь из
показывает, что если на графе имеется путь из 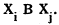 , то имеется и путь из
, то имеется и путь из 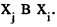 Таким образом, в графе имеется контур.
Таким образом, в графе имеется контур.
Транзитивность отношения «быть не больше» означает истинность выражения 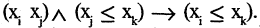 Транзитивность эквивалентна тому, что вершины
Транзитивность эквивалентна тому, что вершины 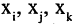 последовательно встречаются на одном и том же пути. Отношение строгого порядка антирефлексивно и асимметрично, поэтому его можно задать на графе без петель и без контуров.
последовательно встречаются на одном и том же пути. Отношение строгого порядка антирефлексивно и асимметрично, поэтому его можно задать на графе без петель и без контуров.
Деревья и графы
Связный граф, не имеющий циклов, называется деревом, а ребра дерева называются ветвями. У дерева с n вершинами есть ровно 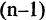 ветка (ребро) (рис. 1.26 а).
ветка (ребро) (рис. 1.26 а).
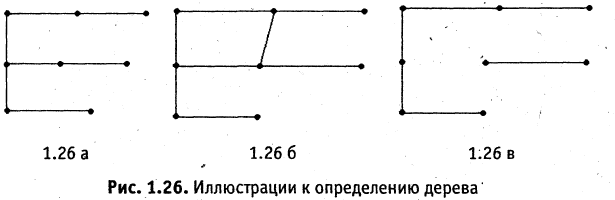
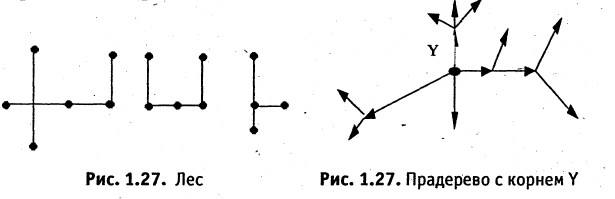
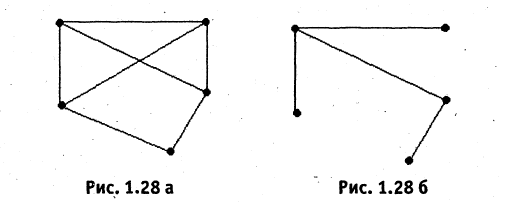
Несвязный граф без циклов называется лесом. При этом любая связная часть леса является деревом (см. рис.1.27). Могут рассматриваться и деревья с ориентированными ребрами. Ориентированное дерево называется прадеревом с корнем y, если существует путь между вершиной y и любой другой его вершиной (см. рис. 1.28).
Пара 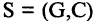 называется сетью, если
называется сетью, если 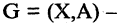 произвольный ориентированный граф,
произвольный ориентированный граф, 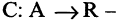 функция, ставящая каждой дуге графа в соответствие неотрицательное вещественное число
функция, ставящая каждой дуге графа в соответствие неотрицательное вещественное число 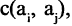 которое, в зависимости от решаемой задачи, называют по-разному: весом дуги, пропускной способностью, длиной дуги и т.п. Сеть иногда называют взвешенным графом, а сумму весов всех дуг — весом графа.
которое, в зависимости от решаемой задачи, называют по-разному: весом дуги, пропускной способностью, длиной дуги и т.п. Сеть иногда называют взвешенным графом, а сумму весов всех дуг — весом графа.
Задачи о покрывающих деревьях
Пусть задан неориентированный граф 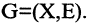 Дерево
Дерево 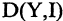 называется покрывающим деревом графа
называется покрывающим деревом графа 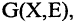 если
если 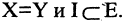 Таким образом, покрывающее дерево связывает все вершины данного графа, но не обязательно при этом включает все его ребра. На рис. 1.28 а показан граф, для которого на рис. 1.28 б построено покрывающее дерево. Любой связанный граф содержит хотя бы одно покрывающее дерево.
Таким образом, покрывающее дерево связывает все вершины данного графа, но не обязательно при этом включает все его ребра. На рис. 1.28 а показан граф, для которого на рис. 1.28 б построено покрывающее дерево. Любой связанный граф содержит хотя бы одно покрывающее дерево.
Существует ряд задач, к которым сводятся многие приложения графов.
Задача:
Для связного графа 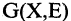 без петель построить покрывающее дерево.
без петель построить покрывающее дерево.
При решении предварительно строят так называемые связки. Связка представляет собой некоторое поддерево искомого покрывающего дерева. Для построения связки последовательно выделяются отдельные вершины, объединенные некоторыми ребрами. По мере рассмотрения все новых и новых ребер исходного графа связки постепенно нарастают и объединяются до тех пор, пока не будет получена одна единая связка, включающая в себя все вершины графа — искомое покрывающее дерево. При образовании связок следует следить за тем, чтобы не образовывались циклы. Процедуры выделения вершин и ребер во время выполнения алгоритма называют окрашиванием.
Алгоритм построения покрывающего дерева.
Шаг 0. Все ребра исходного графа 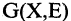 не окрашены и множество связок пусто.
не окрашены и множество связок пусто.
Шаг 1. Произвольным образом выбирается ребро. Окрашиваем это ребро. Формируем из этого ребра и инцидентных ему вершин первую связку.
Шаг 2. Произвольным образом выбираем следующее неокрашенное ребро. При этом возможно возникновение одной из четырех ситуаций:
2.1. Обе вершины выбранного нового ребра принадлежат выбранной ранее связке (в дальнейшем — одной из рассмотренных ранее связок). Исключаем выбранное ребро из дальнейшего рассмотрения. Переходим к шагу 3.
2.2. Одна вершина выбранного ребра принадлежит одной из связок, а другая не принадлежит ни одной из связок. Окрашиваем ребро и включаем его вторую концевую вершину в ту связку, в которую входит первая концевая, вершина (наращиваем связку). Переходим к шагу 3.
2.3. Ни одна из вершин, инцидентных выбранному ребру, не принадлежит ни одной из связок. Окрашиваем это ребро и формируем новую связку из выбранного ребра и инцидентных ему вершин. Переходим к шагу 3.
2.4. Концевые вершины выбранного ребра принадлежат различным связкам. Окрашиваем это ребро. Обе связки, которые связывают рассматриваемое ребро, сливаем в одну связку и переходим к шагу 3.
Шаг 3. Если все ребра графа рассмотрены, то переходим к шагу 4, иначе переходим к шагу 2.
Шаг 4. Если получилась единственная связка, то она и является искомым покрывающим деревом, иначе задача не имеет решения. Конец алгоритма.
Замечание 1. Описанный алгоритм относится к так называемым «поедающим» алгоритмам, в которых судьба рассматриваемых элементов решается только один раз на протяжении всей процедуры. Поэтому, если число вершин графа конечно, то алгоритм заканчивается за конечное число шагов. Поедающие алгоритмы считаются самыми «быстрыми» из комбинаторных алгоритмов.
Замечание 2. Если алгоритм не заканчивается построением покрывающего дерева, то это означает, что граф 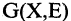 несвязный и поставленная задача не имеет решения. Признаком такой ситуации является наличие более чем одной связки при рассмотрении всех ребер графа.
несвязный и поставленная задача не имеет решения. Признаком такой ситуации является наличие более чем одной связки при рассмотрении всех ребер графа.
Замечание 3. Изложенный алгоритм позволяет построить одно из возможных покрывающих для исходного графа деревьев, поскольку очередное ребро выбирается произвольные образом. Необходимость выбора наиболее подходящего дерева приводит к задаче о построении покрывающего дерева минимального веса.
Задача:
Для заданной сети 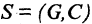 построить покрывающее дерево минимального веса.
построить покрывающее дерево минимального веса.
Пример:
Построить покрывающее дерево для графа, изображенного на рис. 1.29.
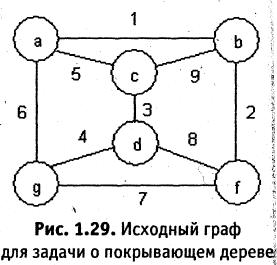
Решение:
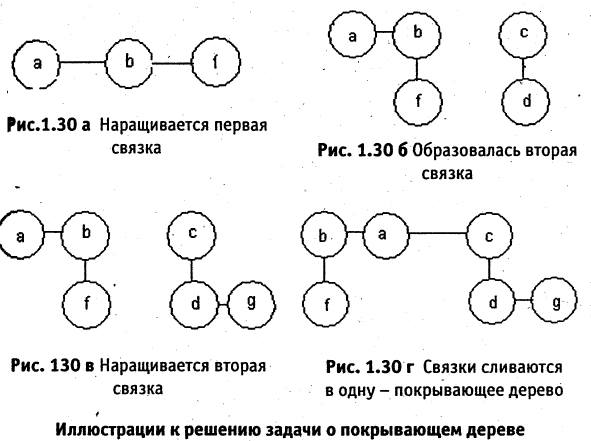
Произвольным образом пронумеруем ребра графа, например, так, как показано на рисунке. Согласно изложенному алгоритму, первое выбранное ребро (а, в) образует первую связку 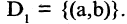 Второе ребро (b, f) окрашивается (реализуется ситуация 2.2), а связка
Второе ребро (b, f) окрашивается (реализуется ситуация 2.2), а связка 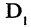 уже включает вершины а, b и f (см. рис. 1.30 а). Выбор третьего ребра (c, d) реализует случай 2.3. Поэтому образовывается вторая связка
уже включает вершины а, b и f (см. рис. 1.30 а). Выбор третьего ребра (c, d) реализует случай 2.3. Поэтому образовывается вторая связка 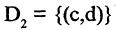 (см. рис. 1.30 б).; Четвертое выбранное ребро (d,g), как показано на рис. 1.30 в, наращивает вторую связку
(см. рис. 1.30 б).; Четвертое выбранное ребро (d,g), как показано на рис. 1.30 в, наращивает вторую связку 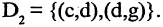 Рассматривая следующее ребро (а, с), видим, что реализуется случай 2.4. Это требует объединения обеих связок в одну, а именно,
Рассматривая следующее ребро (а, с), видим, что реализуется случай 2.4. Это требует объединения обеих связок в одну, а именно, 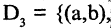
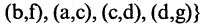 (см. рис. 1.30 г). Шестое ребро в дерево не включается так же, как и все остальные ребра (случай). В итоге получаем покрывающее исходный граф дерево (рис. 1.30 г.). Из приведенного выше алгоритма видно, что граф в общем случае может иметь более одного покрывающего дерева.
(см. рис. 1.30 г). Шестое ребро в дерево не включается так же, как и все остальные ребра (случай). В итоге получаем покрывающее исходный граф дерево (рис. 1.30 г.). Из приведенного выше алгоритма видно, что граф в общем случае может иметь более одного покрывающего дерева.
Необходимость выбора наиболее подходящего дерева и приводит к задаче 2 — построения покрывающего дерева минимального веса. В таком случае можно поступить следующим: образом. В целом сохранить алгоритм решения задачи 1, но выбирать очередное ребро не произвольным образом, а строго в
порядке возрастания весов. В качестве примера построим минимальное покрывающее дерево для графа, изображенного на рис. 1.31а, цифры при ребрах в скобках означают вес соответствующего ребра. Первым выбирается ребро (d, f), так как оно имеет наименьший вес, равный единице. Второе ребро (a, g) об-
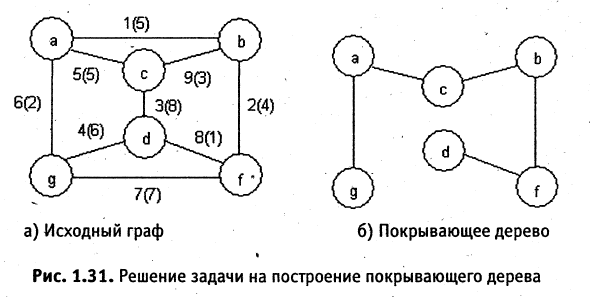
разует вторую связку {а, g}. Следующим должно быть выбрано ребро (с, b), которое образует третью связку {с, b}. В итоге имеем дерево, изображенное на рис. 1.316 и имеющее вес 15. Сравните этот вес с весом дерева, изображенного на рис. 1.32 г, вес которого составляет 27 единиц.
Описанный алгоритм обеспечивает построение дерева минимального веса.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
