Оглавление:
Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются её координатами.
Предмет геометрии
Предметом аналитической геометрии служит изучение свойств геометрических образов (линий, фигур, тел, поверхностей и т. п.) с помощью особого метода, называемого методом координат. При этом широко используется алгебра.
В элементарной геометрии также прибегают иногда к методам алгебры, например, при определении площади треугольника по трем сторонам или при вычислении стороны вписанного в окружность правильного многоугольника и т. п. Однако область приложения методов алгебры к геометрии стала наиболее широкой со времени введения метода координат, который позволил изучать не только форму и размеры геометрических образов, но и их положение на плоскости и в пространстве.
Аналитическая геометрия состоит из двух частей. Первая часть — аналитическая геометрия на плоскости, вторая часть — аналитическая геометрия в пространстве.
Здесь мы дадим элементарное изложение только аналитической геометрии на плоскости.
Декартова прямоугольная система координат на плоскости
Возьмем на плоскости две взаимно перпендикулярные прямые Ох и Оу (рис. 1) и произвольную точку М. Опустим из нее перпендикуляры МN и МР на Оу и Ох. Выбрав какую-нибудь единицу масштаба и измерив ею отрезки NМ и РМ, получим числа: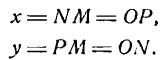
Эти числа х и у, определяющие положение точки М по отношению к заданным прямым Оу и Ох, называются координатами точки М. Их обычно записывают в скобках рядом с обозначением точки: М(х; у), причем сначала выписывают координату х, а потом координату у.
Пусть, например,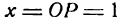 единице выбранного масштаба, а
единице выбранного масштаба, а 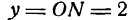 единицам того же масштаба. Тогда говорят, что точка М имеет координаты М( 1; 2).
единицам того же масштаба. Тогда говорят, что точка М имеет координаты М( 1; 2).
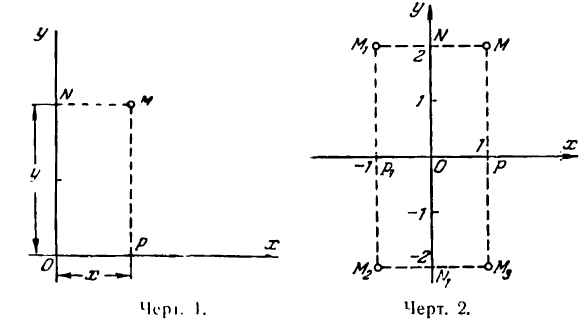
Возникает, однако, вопрос, нет ли на плоскости еще точек, имеющих те же координаты, что и точка М. На рис. 2 показано, что каждая из точек М, М1, М2 и М3 удалена на 1 единицу масштаба от прямой Оу и на 2 единицы масштаба от прямой Ох. Получается неопределенность: четыре точки имеют одинаковые координаты (1; 2). Чтобы устранить этот недостаток, уточним определение прямоугольных координат точек на плоскости.
Координатой х точки М называется число, измеряющее расстояние точки М от прямой Оу и взятое со знаком + если М удалена вправо от Оу, и со знаком — , если М удалена влево от Оу.
Координатой у точки М называется число, измеряющее расстояние точки М от прямой Ох и взятое со знаком если М удалена вверх от Ох, и со знаком — , если М удалена вниз от Ох.
Теперь точки М, М1, М2 и М3 на рис. 2 имеют уже различные и вполне определенные координаты: М( 1; 2), М1(— 1; 2), М2(— 1; —2), М3(1; —2).
Таким образом, чтобы определить положение любой точки на плоскости координатами х и у, нужно задать:
1) две взаимно перпендикулярные прямые Ох и Оу, называемые осями координат, точку О пересечения которых принято называть началом координат;
2) единицу масштаба;
3) направление на каждой из осей координат, принимаемое за положительное (на рисеже принятое положительное направление на осях отмечается стрелками).
Все эти данные называются декартовой системой прямоугольных координат на плоскости |по имени французского математика Декарта (1596—1650)—создателя аналитической геометрии).
Координату х называют абсциссой, а координату у — ординатой.
Как выше показано, в декартовой системе прямоугольных координат на плоскости каждой точке плоскости соответствует пара действительных чисел х и у (ее координат), определяющих положение точки на плоскости, и наоборот, каждой паре действительных чисел х и у соответствует одна точка плоскости. Вследствие указанного соответствия между точками и координатами этих точек принято говорить: «дана точка М(а; b)» вместо «даны координаты точки М», «найти точку М(х; у)» вместо «найти координаты точки М».
Расстояние между двумя точками
Пусть даны дне точки А(х1;у1) и В(х2; у2) (рис. 3); требуется найти расстояние между ними.
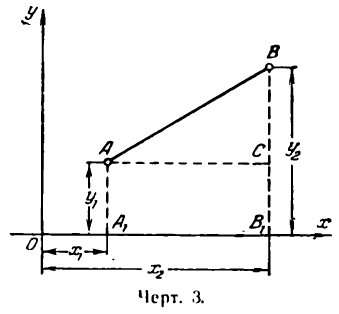
Опустим из А и В перпендикуляры АА1 и ВВ1 на ось Ох и проведем 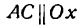 . Из
. Из 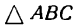 по теореме Пифагора найдем:
по теореме Пифагора найдем:
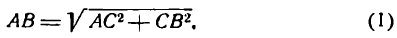
Но, как видно из рисежа,
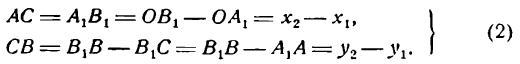
Подставив значение АС и СВ из равенств (2) в выражение (1)
и обозначив АВ через d, получим:
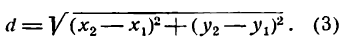
Можно показать, что формула (3) верна для любого положения точек А и В на плоскости. Пусть, например, точки А и В расположены, как указано на рисеже 4, тогда по-прежнему напишем равенство (1), в котором
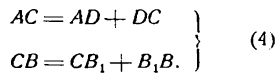
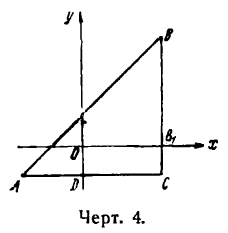
Так как АС и СВ, как длины сторон треугольника, положительны, то и слагаемые правых частей равенств (4) должны быть положительными. Но координаты точки А
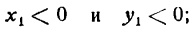
следовательно,
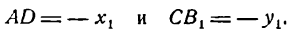
Отрезки же
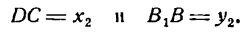
Итак,
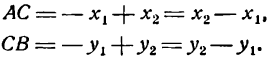
После замены АС и СВ в равенстве (1) их (значениями получим ту же формулу (3).
Пример:
Найти расстояние между точками А(—3; 5) и В( 1; 2).
Решение:
По условию х1 = — 3, у1 = 5, х2 = 1, у2 = 2. Подставив эти координаты в формулу (3), получим:
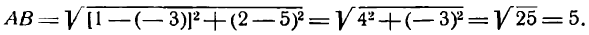
Решим тот же пример графически. Для этого построим данные точки А и В (рис. 5) и, измерив отрезок АВ, найдем АВ = 5.
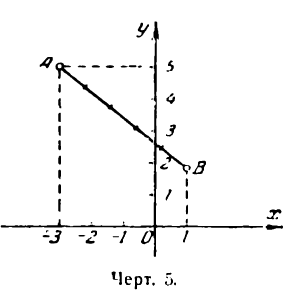
Если одной из точек будет начало координат 0(0; 0), а другой М (х ; у), то формула (3) примет вид

Деление отрезка в данном отношении
Пусть даны точки А(х1; у1) и В(х2; у2) (рис. 6). Требуется найти точку М(х; у), делящую отрезок АВ в отношении:
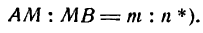
Опустим из точек А, М и В перпендикуляры АА1, ММ1 и ВВ1 на ось Ох и проведем прямые 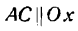 и
и 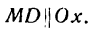 Из подобия треугольников АМС и МВО найдем:
Из подобия треугольников АМС и МВО найдем:
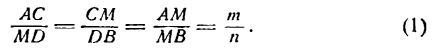
*) Отношение 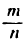 имеет положительное значение, так как
имеет положительное значение, так как
точка М находится внутри отрезка АВ. В случае, если точка М
расположена на продолжении отрезка АВ, величина 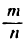 имеет
имеет
отрицательное значение
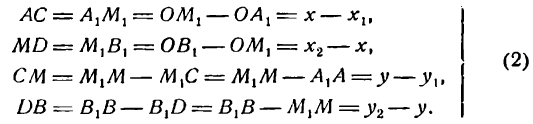
Подставив (2) в (1) получим:
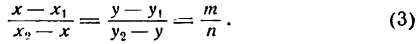
Для краткости положим 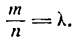 Тогда из равенств (3) получим два уравнения:
Тогда из равенств (3) получим два уравнения:

Решив уравнения (4) и (5) относительно х и у, получим:
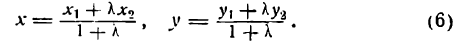
Формулы (6) служат для определения координат точки М(х; у), делящей отрезок между точками А(х1 ; у1) и В(х2; у2) в отношении 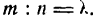
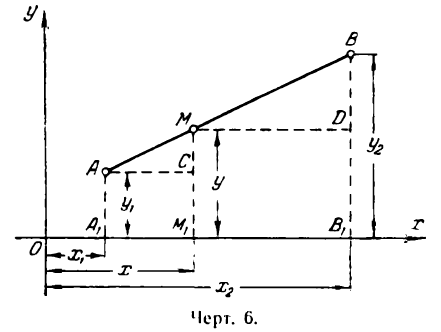
Можно показать, что формулы (6) справедливы для любого положения точек А и В на плоскости.
В частном случае, при делении отрезка АВ пополам, т. е. в отношении 1:1, получим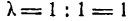 , и поэтому
, и поэтому
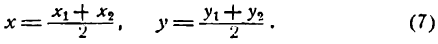
Если в формулах (6) заменить 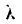 отношением
отношением 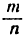 , то получим:
, то получим:
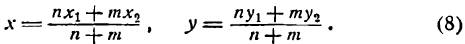
Формулы (8) часто применяются в механике для определения положения центра тяжести однородного тела или отыскания центра параллельных сил.
Пример:
Даны точки А (7; 4) и В(10; — 2). Точка М делит отрезок АВ в отношении АМ : МВ=0,2. Найти точку М.
Решение:
По условию х1 = 7, у1 = 4, х2= 10, у2 = — 2, 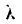 = 0,2. Подставив эти данные в формулы (6), получим:
= 0,2. Подставив эти данные в формулы (6), получим:
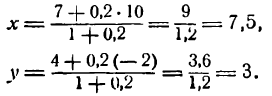
Итак, искомая точка будет М(7,5; 3).
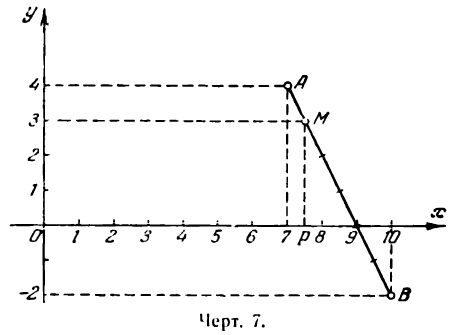
Решим тот же пример графически. Для этого построим точки А и В (рис. 7) и разделим отрезок АВ на шесть равных частей. Отложив одну такую часть от точки А, получим точку М, которая и разделит АВ в отношении 1 : 5 = 0,2. Измерив отрезки ОР и РМ, найдем координаты точки М:
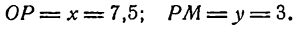
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
