Интегральное исчисление с примерами решения и образцами выполнения

Основной задачей дифференциального исчисления является отыскание производной заданной функции. В этой главе рассматривается обратная задача: восстановить функцию по известной производной. Указанная задача является основной для интегрального исчисления.

Неопределенный интеграл и первообразная

Как и выше, через D будет обозначаться промежуток на числовой оси 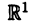, т. е. D — это множество вида [а,b], [а,b), (a,b] или (а,b), причем промежуток может быть и бесконечным.

Функция F(x) называется первообразной для функции 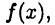заданной на промежутке D, если для 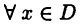выполнено равенство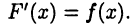

Например, для функции 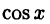первообразной на всей числовой оси служит функция 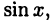так как 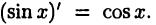Отметим, что для функции 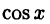первообразной будет и любая функция вида 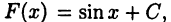где С — произвольная постоянная. Действительно, 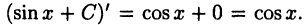Этот факт носит общий характер. А именно, верна очевидная

Теорема:

Ecли 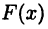—первообразны для 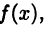то функция 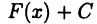при любом значении постоянной С также является первообразной для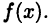

Таким образом, если функция 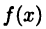имеет первообразную 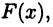то она имеет семейство первообразных вида 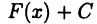.Оказывается, кроме функций из этого семейства, других первообразных функция 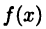иметь не может. Для установления этого важного факта понадобится

Лемма:

Если 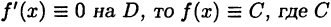— некоторая постоянная.

► Лемма будет доказана, если показать, что для 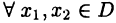выполнено равенство 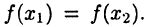Пусть 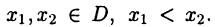По теореме Лагранжа (см. с. 82) 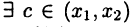такое, что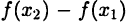 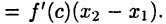Но так как 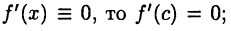следовательно,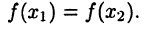

Теорема:

Если 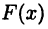— первообразная для 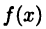, то любая другая ее первообразная представляется в виде 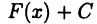при некотором значении постоянной С.

► Пусть 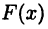и 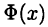— две первообразные для функции 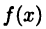. Теорема будет доказана, если показать, что при некотором постоянном С выполнено тождество 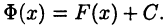Положим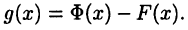

Имеем

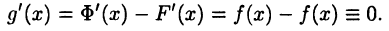
Тогда в силу леммы 21.1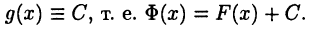

Понятие неопределенного интеграла

Пусть 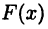— некоторая первообразная для функции 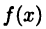. Тогда в силу теоремы 21.2 множество всех ее первообразных — это семейство функций вида 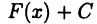. Это семейство функций называют неопределенным интегралом 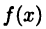и обозначают символом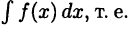

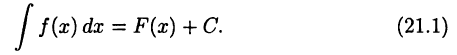
При этом произведение 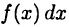называют подынтегральным выражением, функцию 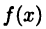— подынтегральной функцией, а переменную х — переменной интегрирования. Отыскание неопределенного интеграла функции называют интегрированием функции.

Отметим, что из равенства 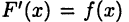следует, что выражение 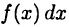под знаком интеграла в (21.1) представляет собой дифференциал первообразной функции :

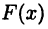Пример:

Пусть 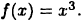Ее неопределенный интеграл равен

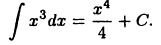
Ответ проверяется просто: достаточно найти производную функции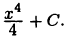

Закономерен вопрос: какие функции имеют неопределенный интеграл? В дальнейшем будет установлено: если 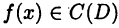(т. е. функция 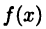непрерывна на D), то она имеет неопределенный интеграл. Пока же будет предполагаться, что существуют все рассматриваемые неопределенные интегралы.

Свойства первообразных

Теорема:

Имеют место равенства

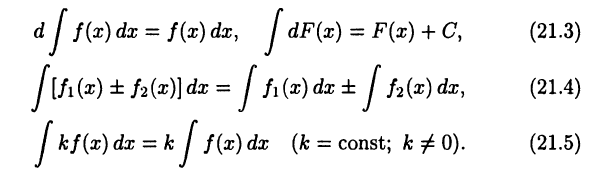
► Равенства (21.3) непосредственно следуют из соотношений (21.1) и (21.2). Равенства (21.4) и (21.5) устанавливаются однотипными рассуждениями, поэтому ограничимся доказательством равенства (21.5). Пусть 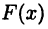— первообразная для 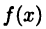, тогда 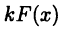— первообразная для 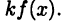Следовательно,

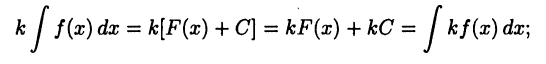
здесь использован тот факт, что если 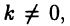то выражение 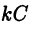так же, как и само С, означает произвольную постоянную.

Из приведенных в теореме 21.3 свойств неопределенных интегралов особо отметим равенства (21.3), означающие, что знаки d и 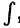стоящие рядом, уничтожают друг друга. Это легко объяснимо, если вспомнить, что дифференцирование и интегрирование — взаимно обратные операции.

Таблица интегралов

Пользуясь таблицей производных основных элементарных функций (см. стр. 74), несложно составить аналогичную таблицу неопределенных интегралов (табл. 4).

Методы интегрирования

При вычислении производных обычно пользуются стандартным набором правил и формул, что превращает дифференцирование в единообразную, выполняемую по одним и тем же схемам, работу. Иначе обстоит дело с интегрированием функций. Не существует единого рецепта вычисления неопределенного интеграла, пригодного для произвольных элементарных функций. Поэтому приходится рассматривать отдельные классы функций и для них разрабатывать правила или хотя бы рекомендации по вычислению интегралов.

Очень многое зависит от опыта и фантазии человека. И то, и другое приходит лишь в результате самостоятельных вычислений, начиная с самых простых и переходя к все более и более сложным.

Непосредственное интегрирование

Пользуясь свойствами неопределенных интегралов, изложенными в теореме 21.3, а также таблицей неопределенных интегралов, можно вычислять простейшие интегралы.

Пример:

Вычислить 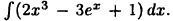Учитывая равенства (21.4) и (21.5), по таблице интегралов получим

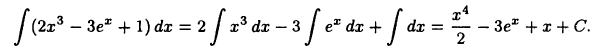
Метод замены переменной

Одним из основных при интегрировании функций является метод замены переменной (или метод подстановки), определяемый соотношением

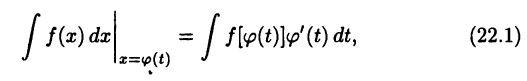
в котором 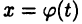— дифференцируемая функция, определение на некотором промежутке так, что существует сложная функция 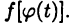Равенство (22.1) понимается в том смысле, что результат вычисления интеграла 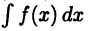и подстановки в полученное выражение функции 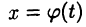совпадает с результатом непосредственного вычисления интеграла в правой части равенства (22.1).

► Докажем равенство (22.1). Пусть 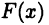— некоторая первообразная для 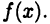Так как существует сложная функция 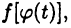то определена и функция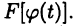

Тогда

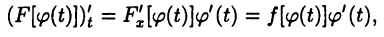
т. е. функция 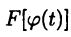является первообразной для 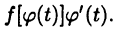Следовательно,

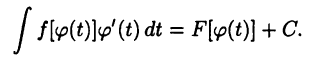
Но

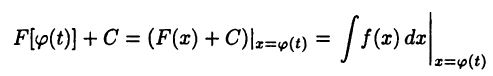
Поэтому верно равенство (22.1).

Формула (22.1) обычно применяется в тех случаях, когда непосредственное вычисление интеграла 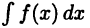затруднительно, однако подстановкой 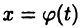можно перейти к интегралу, более удобному для исследования.

Одним из вариантов метода замены переменной является способ подведения под знак дифференциала, заключающийся в преобразовании:

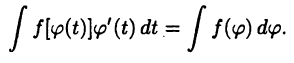
Пример:

Вычислить 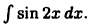Это не табличный интеграл (мешает число 2). Произведем замену 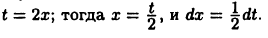Поэтому

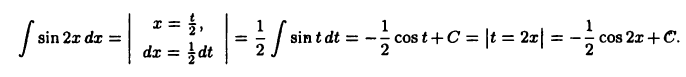
Пример:

Вычислить 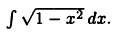Подынтегральная функция определена при 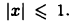Выполним замену 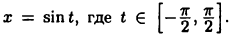Тогда 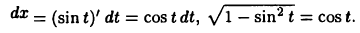Следовательно,

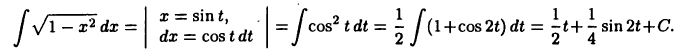
Возвращаясь к переменной 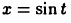посредством равенства 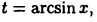получим:

Пример:

Вычислить 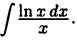Так как 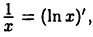то можно воспользоваться способом подведения под знак дифференциала. Имеем

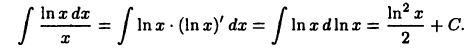
Общих рекомендаций по разыскиванию нужной подстановки не существует. Умение здесь создается упражнениями.

Интегрирование по частям

Метод интегрирования по частям основан на равенстве

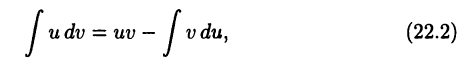
в котором 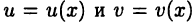— две дифференцируемые на промежутке D функции.

► Докажем равенство (22.2). По правилу дифференцирования произведения получим 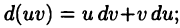следовательно,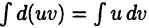 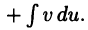Отсюда и из второго из равенств (21.3) получим (22.2).

Формула (22.2) позволяет свести задачу вычисления интеграла 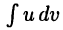к вычислению интеграла 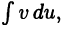что в ряде случаев проще.

Пример:

Вычислить 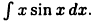Положим 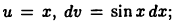тогда 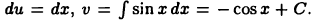Так как в качестве 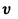можно брать любую функцию вида 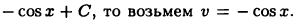Отсюда и из формулы (22.2) получим

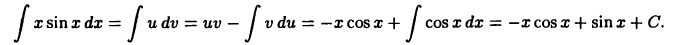
Пример:

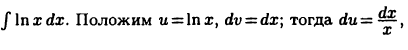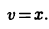Вычислить тогда Отсюда

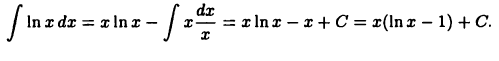
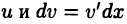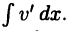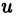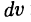Применяя формулу (22.2), следует разбить подынтегральное выражение на два множителя таким образом, чтобы вычислялся или хотя бы упрощался интеграл Нельзя выбирать и произвольно, иначе можно получить еще более сложный интеграл. Метод интегрирования по частям позволяет вычислять, например, интегралы типа

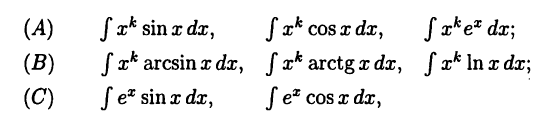
а также подобные им. В случае (А) следует полагать 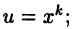в случае 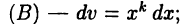в случае 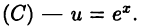При этом для интегралов вида (А) и (В) требуется ровно к раз применять формулу (22.2), а для интегралов вида (С) требуется двукратное интегрирование.

Пример:

Вычислить 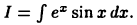Положим 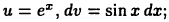тогда 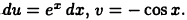Отсюда 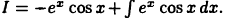Применяя для вычисления интеграла снова формулу (22.2) при 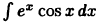снова формулу (22.2) при 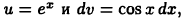имеем

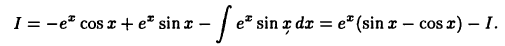
Перенося интеграл I из правой части равенства в левую, получим 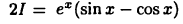и, следовательно,

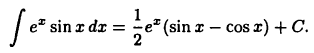
Пример:

Применим метод интегрирования по частям для вычисления интеграла

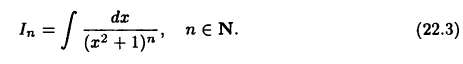
Полагая 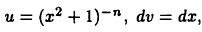получим

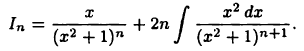
Но

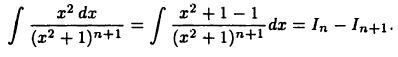
Поэтому

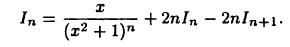
Отсюда

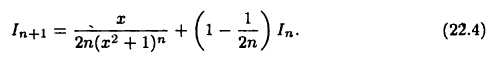
Полученная формула сводит вычисление интеграла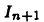 к вычислению интеграла 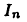с меньшим на единицу показателем степени. Формулы такого типа называют рекуррентными. Применим, например, формулу (22.4) к вычислению интеграла 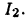Так как при 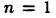интеграл (22.3) является табличным, а именно, 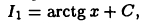то из (22.4) получим (при ):

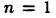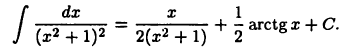
Интегрирование некоторых классов функций

Изложенные выше методы интегрирования носили общий характер и не указывали алгоритма вычисления интеграла, предоставляя многое фантазии вычислителя. В этом разделе будут указаны некоторые классы функций, для которых можно указать правила интегрирования.

Рациональные функции

Напомним, что многочленом 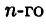порядка называется функция вида

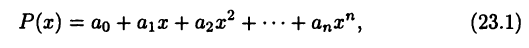
в которой 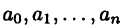— вещественные или комплексные числа, причем 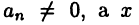— вещественная или комплексная переменная. Для обозначения степени 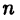многочлена (23.1) используют символ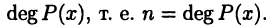

Рациональной функцией или рациональной дробью называется функция вида

где 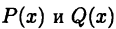— многочлены. Функция (23.2) называется правильной дробью, если 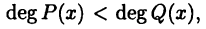и неправильной дробью в противном случае.

Если функция (23.2) является неправильной дробью, то, выполнив деление, получим равенство

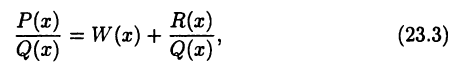
в котором 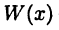— некоторый многочлен, а выражение 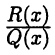является

правильной дробью. Например,

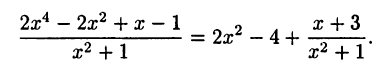
Таким образом, если требуется вычислить интеграл от неправильной дроби 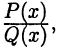то из (23.3) получим

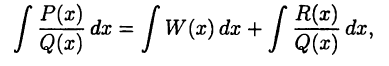
и так как 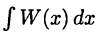легко вычисляется, то дело сводится к интегрированию правильной дроби 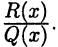Поэтому достаточно изучить интегрирование правильных дробей. Ниже будут рассматриваться только вещественные рациональные функции, т. е. функции вида (23.2) с вещественными коэффициентами.

Простые дроби

Рассмотрим сначала простейшие рациональные функции — так называемые простые дроби:

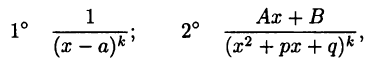
где 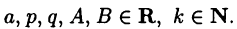Предполагается, что числа 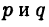связаны неравенством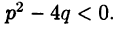

Дробь вида 1° легко интегрируется. Действительно, при 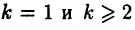получим

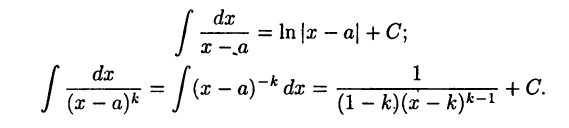
Для интегрирования дроби вида 2° выделим из выражения 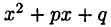полный квадрат:

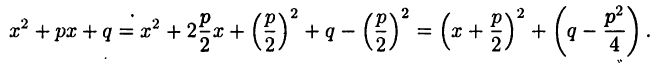
Так как 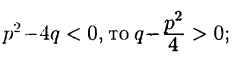и, следовательно, число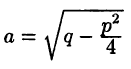

является вещественным. Положим 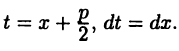Тогда

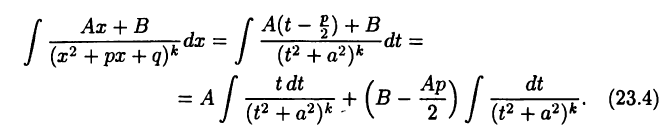
В случае 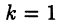; каждый из полученных интегралов нетрудно вычисляется подстановкой 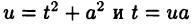соответственно:

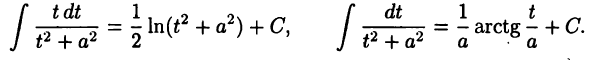
В случае 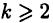для первого интеграла в правой части равенства (23.4) вновь применим подстановку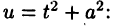

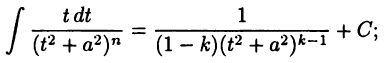
что касается второго интеграла, то замена 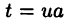сводит его к интегралу типа (22.3) и, следовательно, для его вычисления можно воспользоваться рекуррентной формулой (22.4).

Разложение правильных дробей на простые

Рассмотрим теперь произвольную правильную дробь вида (23.2). Ее интегрирование основано на теореме из алгебры, гласящей, что каждая правильная дробь может быть представлена в виде суммы конечного числа простых дробей.

Указанное представление тесным образом связано с приведенным на с. 23 разложением (4.12) знаменателя 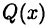дроби (23.2) на простые множители вида 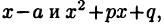где квадратичное выражение имеет отрицательный дискриминант, т. е. 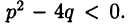Пусть разложение 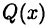имеет вид

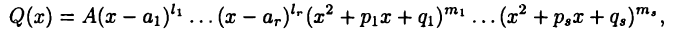
где 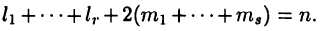Тогда дробь (23.2) представитсяв виде

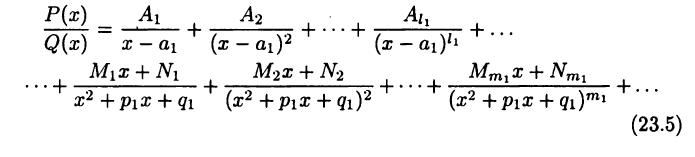
с некоторыми вещественными коэффициентами

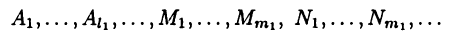
Так как равенство (23.5) должно выполняться при всех х (за исключением корней многочлена 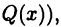то, умножая (23.5) на 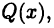придем к тому, что многочлен 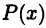должен быть равен полученному в правой части (23.5) многочлену. Это означает, что коэффициенты, стоящие при равных степенях 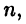равны между собой. Таким образом, получим систему уравнений, из которой определим значения коэффициентов в числителях дробей в правой части равенства (23.5). Изложенный метод называют методом неопределенных коэффициентов. После разложения дроби (23.2) на простые дроби (23.5) ее интегрирование сводится к сумме интегралов от простых дробей, приемы вычисления которых изложены выше.

Пример:

Вычислить

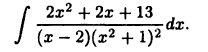
Разложим подынтегральную функцию в виде (23.5):

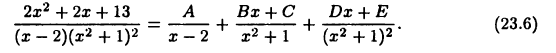
Отсюда

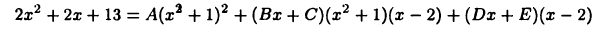
или

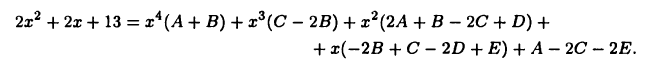
Следовательно,

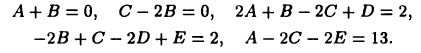
Решая полученную систему, найдем А = 1, В = -1, С= -2, D= -З, Е = -4. Подставляя эти числа в (23.6) и применяя формулы предыдущего пункта, получим

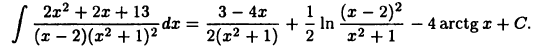
Иррациональные функции

Рассмотрим предварительно рациональную функцию 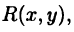зависящую от двух аргументов х и у, т. е. функцию

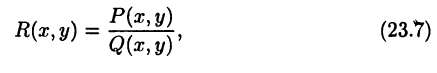
где 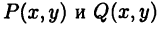— многочлены вида

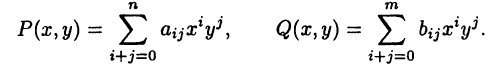
При каждом фиксированном х (или у) функция (23.7) является рациональной функцией типа (23.2). Пример 23.2. Функция

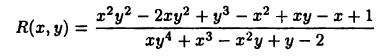
является рациональной функцией переменных х и у. При этом степень числителя равна 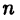= 4, а степень знаменателя — т= 5.

Читатель может задать вопрос: при чем здесь функции двух аргументов? До сих пор же шла речь об интегрировании функции одной переменной. Мы, конечно, не собираемся сейчас интегрировать функции двух переменных (до них очередь дойдет ближе к концу пособия). Просто рациональные функции вида (23.7) мы используем для получения функций одной переменной t , подставляя вместо x и у функции 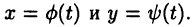Получаемая таким образом функция одной переменной во многих случаях интегрируется.

В этом пункте рассмотрим интеграл вида

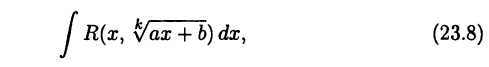
т. е. вопрос об интегрировании функции (23.7), когда в ней положено 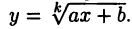Интегралы вида (23.8) переходят в рассмотренные выше интегралы от рациональных функций путем подстановки

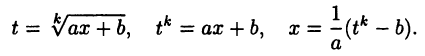
Действительно, в результате преобразований интеграл (23.8) примет вид:

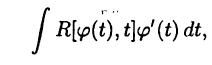
где 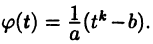Ясно, что подынтегральная функция в последнем интеграле является рациональной функцией и, следовательно, для его вычисления можно привлекать изложенные в предыдущем пункте методы.

Пример:

Вычислить интеграл

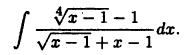
Полагая 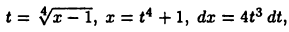перейдем к интегралу

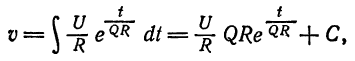
для вычисления которого можно использовать изложенные выше приемы.

Интегрирование тригонометрических выражений

Отметим еще один класс функций, интегрирование которых может быть осуществлено по вполне определенным правилам. Рассмотрим интеграл вида

в котором 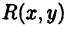— функция вида (23.7). Интеграл (23.9) может быть вычислен с помощью универсальной подстановки

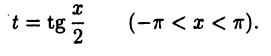
Действительно, во-первых, 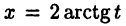и, следовательно, 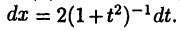Во-вторых, применяя известные формулы тригонометрии, получим

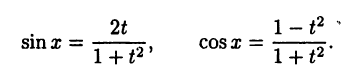
Тогда интеграл (23.9) преобразуется к виду

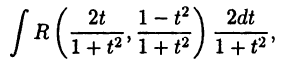
в котором подынтегральное выражение является рациональной дробью и, следовательно, интеграл может быть вычислен в соответствии с изложенными выше схемами.

Пример:

Вычислить интеграл

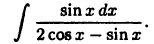
Применяя универсальную тригонометрическую подстановку, получим интеграл

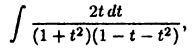
для вычисления которого можно воспользоваться методом неопределенных коэффициентов.

В ряде случаев вычисление интегралов вида (23.9) осуществляется проще, используя другие подстановки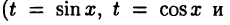

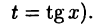
Пример:

Вычислить интегралы

Решение:

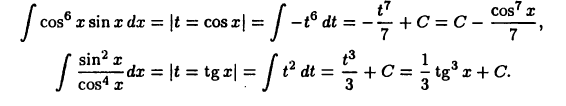
О «неберу щихся» интегралах

Рассмотренными классами функций, конечно, не исчерпываются все виды функций, интеграл от которых можно вычислить за конечное число действий. Возникает вопрос о возможности вычисления интеграла от любой элементарной функции. В главе IV отмечалось, что все элементарные функции дифференцируемы и их производные снова являются элементарными функциями. Об интегрировании функций это сказать нельзя. Существует немало элементарных функций, интегралы от которых не являются элементарными функциями. Например,

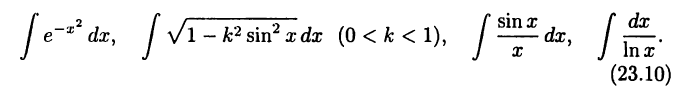
Подчеркнем, что эти интегралы существуют, но они определяют функции, не являющиеся элементарными. Такие интегралы назовем «неберущимися».

Было бы ошибочным считать, что «неберущиеся» интегралы являются экзотикой, придуманной математиками. На самом деле, именно «берущиеся» интегралы следует считать экзотикой; они представляют собой редкое исключение в многообразии «неберущихся» интегралов. К «неберущимся» интегралам приводят многие теоретические и практические задачи. Например, первый из интегралов (23.10) возникает в задачах теории вероятностей и статистики, второй (относящийся к так называемым эллиптическим интегралам) — в задачах механики. Подробную информацию о «неберущихся» интегралах можно получить в специальной литературе.

Определенный интеграл

Рассмотренное выше понятие неопределенного интеграла в естественном смысле является обратным к понятию производной функции. Можно ли к понятию интегрирования функций прийти независимым путем, не ограничивал себя рамками требования существования первообразной? Такие пути возможны, они позволяют с новых позиций взглянуть на задачу интегрирования и провести глубокий анализ теории интегрирования функций.

Задача о площади

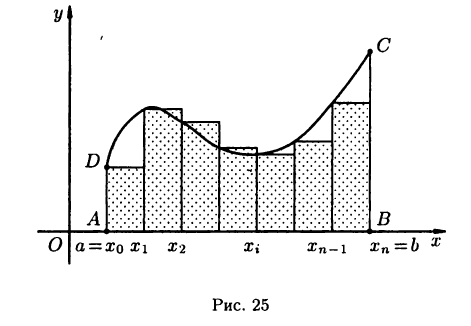
Пусть Требуется вычислить площадь криволинейной трапеции АВСD, изображенной на рис. 25.

Сначала искомую площадь вычислим приближенно. С этой целью разделим отрезок [a, b] на 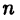частей (не обязательно равных) точками деления

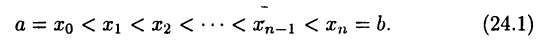
Число

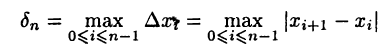
назовем мелкостью разбиения отрезка [а,b].

Ясно, что соотношение 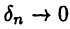означает, что 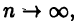но не наоборот: из того, что 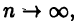еще не следует 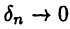(приведите пример!).

Каждую точку деления соединим вертикальным отрезком с кривой 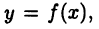в результате чего получим 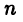прямоугольников. Основание і-го прямоугольника обозначим 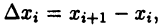а высота его, очевидно, равна 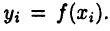Поэтому площадь і-го прямоугольника будет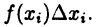

Просуммировав площади всех прямоугольников, получим приближенное значение площади S криволинейной трапеции ABCD:

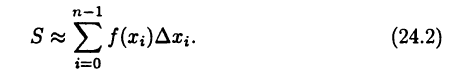
При уменьшении значения 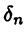формула (24.2) будет становиться все более точной. Точное значение S получится как предел

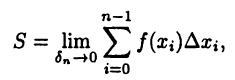
если он, конечно, существует.

Понятие определенного интеграла

Пусть функция 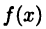определена на конечном промежутке [а,b]. Разобьем отрезок [а, b] каким-либо образом на 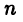частей точками деления (24.1) и пусть 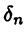означает мелкость этого разбиения.

Выберем произвольные точки 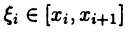и составим интегральную сумму

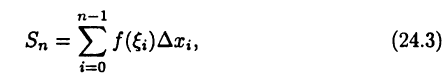
функции 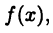отвечающую разбиению (24.1) и выбору точек 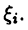Если последовательность интегральных сумм 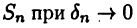имеет конечный предел I, не зависящий ни от способа разбиения отрезка [а, b], ни от выбора точек 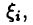то этот предел называют определенным интегралом функции 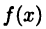в промежутке от а до b и обозначают символом

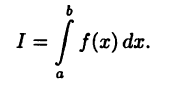
В этом случае функция 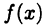называется интегрируемой или суммируемой на [а, b]. Числа а и b называют нижним и верхним пределами интегрирования, 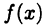— подынтегральной функцией, а х — переменной интегрирования.

Таким образом, в отличие от неопределенного интеграла, определенный интеграл представляет собой число, а не функцию. Сразу же отметим, что вычисление определенного интеграла в соответствии с приведенным определением связано с трудностями и громоздкими подсчетами. Поэтому чаще используют другие подходы, о которых будет говориться ниже.

Пусть функция 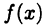является интегрируемой на отрезке [a, b] функцией. В этом случае будем писать 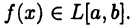Здесь L[a, b] обозначает множество всех интегрируемых на [а, b] функций (вспомните, что представляют из себя множества С[а,b] и [а, b]).

Свойства определенного интеграла

Откладывая на время вопрос об условиях, при которых функция 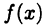является интегрируемой, изучим основные свойства определенных интегралов.

Сначала расширим понятие определенного интеграла, полагая, что

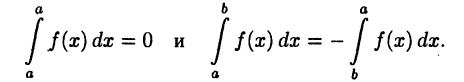
Линейность операции интегрирования

Теорема:

Если 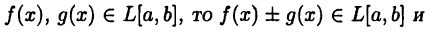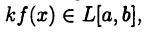причем

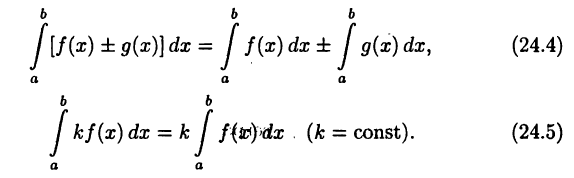
► Ограничимся доказательством лишь первого утверждения теоремы для суммы; остальные утверждения устанавливаются аналогич-

Пусть отрезок [а, b] разбит на 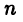частей точками деления (24.1).

Тогда, очевидно,

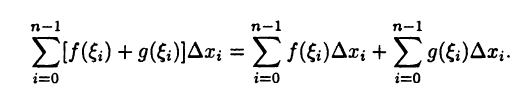
Так как 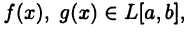то слагаемые в правой части последнего равенства при 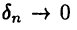стремятся к интегралам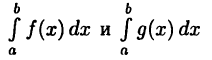

соответственно. Поэтому и левая часть указанного равенства имеет предел при 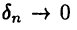. Отсюда следует, что, во-первых, 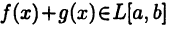и, во-вторых, равенство (24.4) для суммы. ^

Ограниченность интегрируемой функции

Теорема:

Если 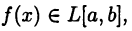то она ограничена на [а, b].

► Допустим противное, т. е. функция 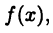неограничена на [a, b]. Тогда при любом разбиении отрезка [а, b] на части точками деления (24.1), по крайней мере, на одном из отрезков 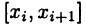функции 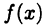будет неограничена. Пусть для определенности она неограничена на отрезке 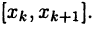Интегральную сумму (24.3) представим в виде

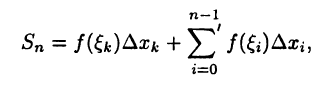
где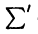 означает, что в указанной сумме отсутствует слагаемое с номером i = k. Числа 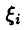во втором слагаемом последнего равенства выберем произвольным образом, а число подберем так, чтобы 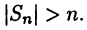Это возможно, так как 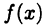неограничена на 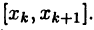При указанном выборе чисел 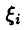очевидно, получим 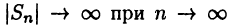и, следовательно, функция 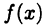не интегрируема на [а, b], что противоречит условию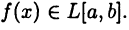

Таким образом, при изучении интегрируемых функций достаточно рассматривать только ограниченные функции.

Аддитивность операции интегрирования

Теорема:

Пусть 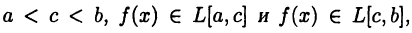тогда 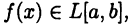причем

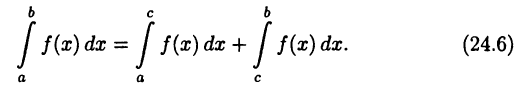
► Теорема будет доказана, если показать, что при любом разбиении (24.1) отрезка [а, b] и любом выборе точек 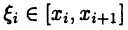последовательность интегральных сумм (24.3) сходится к числу А + В, где

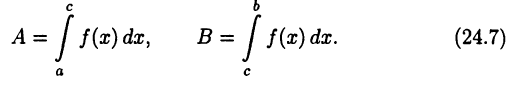
Пусть (24.1) — некоторое разбиение отрезка [a, b] и точки 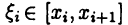выбраны произвольным образом. Тогда либо число с совпадает c одной из точек деления 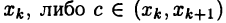при некотором k. В первом случае интегральную сумму (24.3) представим в ви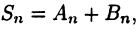де где

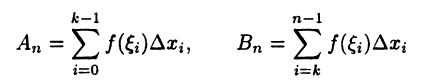
суть интегральные суммы функции 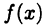отвечающие разбиению отрезков [а, с] и [с, b] соответственно. Во втором случае возможны две ситуации: 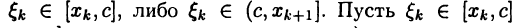(случай 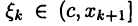рассматривается аналогично); тогда, задаваясь произвольным числом 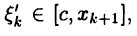интегральную сумму (24.3) представим в виде

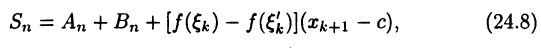
где

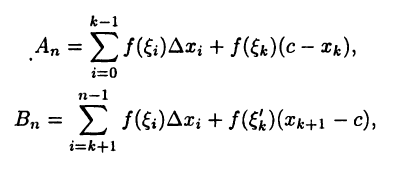
суть интегральные суммы функции 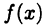отвечающие разбиению отрезков [а, с] и [с,b ] соответственно. Последнее слагаемое в правой части равенства (24.8) стремится к нулю при 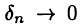(и, следовательно, при 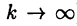). Действительно, в силу теоремы 24.2 функция 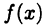ограничена на отрезках [а, с] и [с, b]; тогда и последовательность 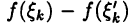также ограничена. Отсюда и из условия, что 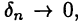получим нужный результат (см. лемму 7.1).

Таким образом, интегральные суммы (24.3) представимы в виде 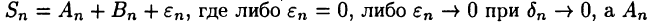и и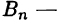нтегральные суммы функции 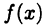соответствующие разбиению отрезков [а, с] и [с, b]. В силу условий 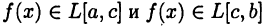получим, что 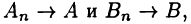где А и В — интегралы (24.7). Отсюда следует, что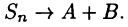

Будет установлено, что теорема 24.3 обратима, т. е. формула (24.6) верна для 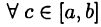в предположении, что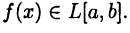

Оценки интегралов

Отметим теперь полезные оценки для интегралов, справедливость которых непосредственно следует из приведенных выше утверждений.

Теорема:

Если 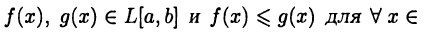то

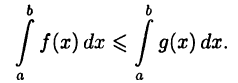
Теорема 24.5. Если 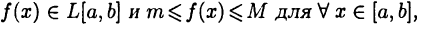то

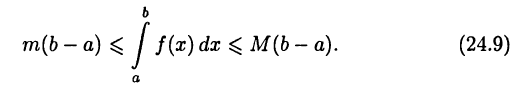
Теорема о среднем

Последнее утверждение позволяет установить теорему о среднем значении.

Теорема:

Если 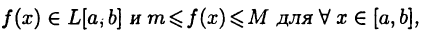то 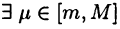такое, что

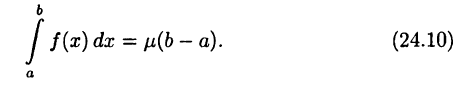
Положим

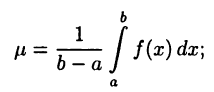
тогда равенство (24.10) очевидно. Включение 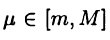следует из оценок (24.9).

В следующем параграфе будет установлено включение 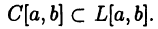С учетом этого факта в случае 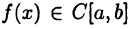теореме 24.6 можно придать другую форму.

Теорема:

Если 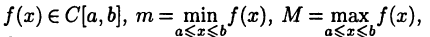тогда 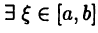такое, что

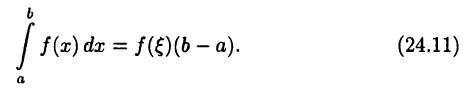
► Из теоремы Больцано-Коши (см. с. 64) следует, что для 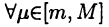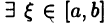такое, что 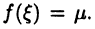Отсюда и из теоремы 24.6 получим равенство (24.11).

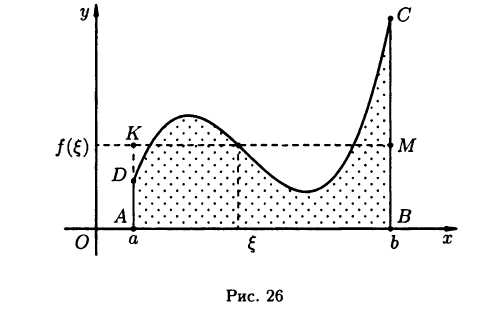
Теорема о среднем имеет простой геометрический смысл: площадь криволинейной трапеции ABCD равна площади прямоугольника АВМК, имеющего высоту 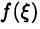и основание b-а (см. рис. 26).

Классы интегрируемых функций

В этом параграфе обсуждается вопрос об условиях, при которых функция будет интегрируемой. Устанавливается, что такими условиями могут, например, быть непрерывность или монотонность функции.

Критерий существования интеграла

Выше было отмечено (теорема 24.2), что интегрируемая функция обязательно ограничена. Верно ли обратное, т. е. достаточно ли для интегрируемости 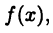ее ограниченности? Нет, не достаточно.

Пример:

Функция Дирихле, определенная равенством (10.1), очевидно, ограничена. Покажем, что она не интегрируема, например, на отрезке [0,1]. Действительно, каким бы ни было разбиение отрезка [0,1], на каждом из интервалов 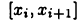разбиения в качестве 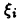можно брать как рациональное, так и иррациональное число. В первом случае получим 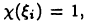а во втором — 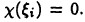Поэтому интегральную сумму 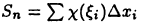за счет выбора 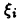можно сделать нулевой или равной 1; последовательность таких интегральных сумм не может иметь предела.

Хотя условие ограниченности функции еще недостаточно для интегрируемости, однако искать интегрируемые функции следует лишь среди ограниченных.

Пусть 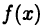— ограниченная на [а, b] функция, т. е. 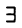М и m такие, что 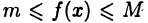для 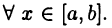Пусть (24.1) — некоторое разбиение отрезка [а, b]. Функция 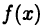будет ограниченной на каждом из отрезков 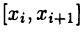и, следовательно, в силу теоремы 2.1 существуют числа

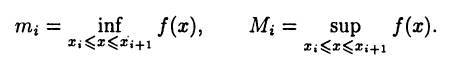
Числа

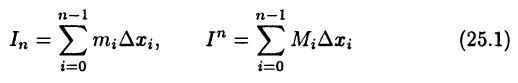
называют нижней и верхней суммами функции 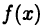отвечающими разбиению (24.1) отрезка [а, b].

Отметим следующие свойства нижних и верхних сумм.

Свойство 1. Если 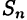— произвольнее интегральная сумм а функции 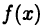, то 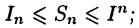здесь отвечают одному и тому же разбиению отрезка [а, b].

Свойство:

Если к имеющимся точкам деления (24.1) добавить новые точки деления, то нижняя сумма 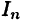может только увеличиться, а верхняя сумма 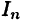только уменьшится.

Свойство:

Каждая нижняя сумма не превосходит каждой верхней суммы, хотя бы отвечающей и другому разбиению отрезка [а, b].

Первые два свойства очевидны: они следуют непосредственно из определений соответствующих сумм, а также из того факта, что если отрезок разбить на две части, то инфимум (супремум) функции на всем отрезке не больше (не меньше) инфимума (супремума) функции на каждой из частей. Что касается свойства 3, то оно следует из свойства 2, если предварительно объединить точки деления отрезка [а,b], отвечающие двум разбиениям.

Множество всех нижних и верхних сумм (25.1) обозначим через 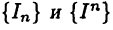соответственно. Из свойства 3 следует

Свойство:

Множества 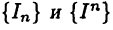ограничены сверху и снизу соответственно.

В силу этого свойства и теоремы 2.1 множества 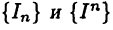имеют супремум и инфимум; положим 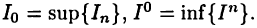Тогда для любой нижней 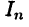и верхней 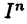суммы верны неравенства

Укажем, наконец, критерий существования определенного интеграла.

Теорема:

Для того чтобы 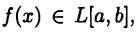необходимо и достаточно выполнения равенства

независимо от способа разбиения отрезка [а, b].

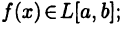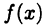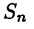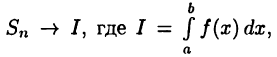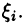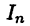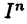► Необходимость. Пусть покажем, что выполнено (25.3). Так как интегрируема, то для любой последовательности ее интегральных сумм имеем независимо от способа разбиения отрезка [a, b] и выбора точек Так как и являются, при заданном разбиении отрезка [а, b], для множества интегральных сумм 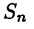инфимумом и супремумом соответственно, то, например, для 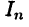найдется интегральная сумма 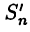такая, что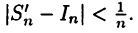

Тогда

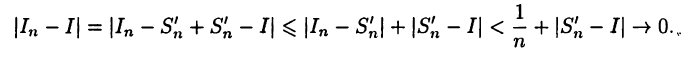
Поэтому 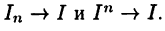Следовательно, выполнено (25.3).

Достаточность. Пусть выполнено (25.3). Покажем, что 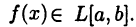Из (25.2) и (25.3) следует равенство 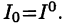Если обозначить 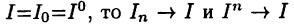независимо от способа разбиения отрезка [а, b]. Но тогда из свойства 1 и леммы 8.2 («леммы о двух милиционерах») следует, что и 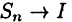независимо от способа разбиения отрезка [а, b] и выбора точек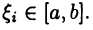

Теорема 25.1 имеет фундаментальное значение при описании классов интегрируемых функций. Прежде, чем указать некоторые из них, перепишем равенство (25.3) с учетом (25.1) в более удобной для дальнейшего изложения форме

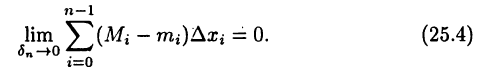
Основные классы интегрируемых функций

Прежде всего отметим, что верно включение 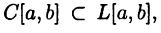a именно, верна

Теорема:

Если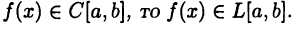

► Пусть (24.1) — произвольное разбиение отрезка [а, b]. Теорема будет доказана, если установить равенство (25.4). Последнее, в свою очередь, будет установлено, если показать, что для 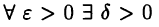такое, что каким бы ни было разбиение отрезка [а, b] на 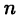частей при условии, что 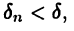выполняется неравенство

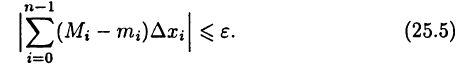
Так как 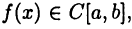то по теореме Кантора (см. с. 66) для 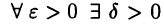такое, что если 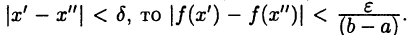В частности, если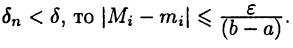

Отсюда

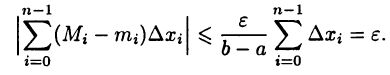
Из теорем 24.3 и 25.2 немедленно следует

Теорема:

Если функция 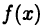имеет на отрезке [а,b ] лишь конечное число точек разрыва первого рода, то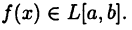

Укажем наконец еще один класс интегрируемых функций.

Теорема:

Если функция 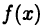является ограниченной и монотонной на [а, b], то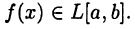

► Так же, как и при доказательстве теоремы 25.2, достаточно установить (25.5). Для монотонной функции, очевидно, имеем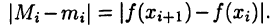 Поэтому для данного 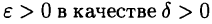можно взять число 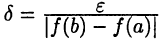(покажите это!).

Таким образом, интегрируемыми являются все непрерывные, кусочно-непрерывные (т. е. с конечным числом точек разрыва первого рода) и монотонные ограниченные функции. Класс этих функций можно существенно расширить на основе следующего утверждения.

Теорема:

Если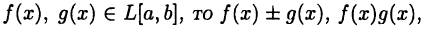

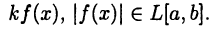
Часть этих утверждений была установлена выше (см. теорему 24.1), остальные доказываются с использованием теоремы 25.1 по схеме, близкой к доказательству теоремы 25.2.

В заключение этого пункта укажем еще два утверждения, имеющие как самостоятельное значение, так и необходимые в дальнейших построениях.

Теорема:

Пусть 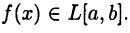Тогда 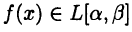для любого отрезка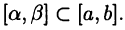

Справедливость этого утверждения устанавливается с использованием теоремы 25.1.

Из теоремы 25.6, в частности, следует, что если 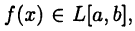то формула (24.6) верна для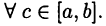

Теорема:

Пусть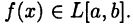

Тогда

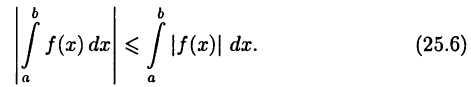
Включение 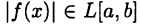следует из теоремы 25.5. Оценка (25.6) следует из аналогичной оценки для интегральных сумм.

Формула Ньютона-Лейбница и приложения

В этом параграфе доказывается основная формула интегрального исчисления — формула Ньютона-Лейбница. Приводятся приложения определенного интеграла в задачах геометрии и механики.

Интеграл с переменным верхним пределом

Пусть 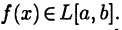Тогда в силу теоремы 25.6 имеем 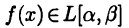для любого отрезка 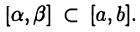Следовательно, для 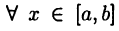определен интеграл

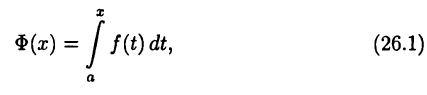
называемый интегралом с переменным верхним пределом. Отметим свойства функции (26.1).

Теорема:

Если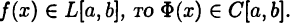

► По определению непрерывности функции достаточно показать, что если 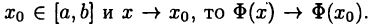Имеем (см. теоремы 24.3 и 24.6)

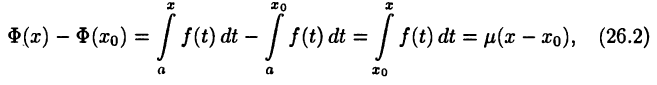
где 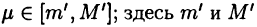— наименьшее и наибольшее значения функции 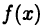на отрезке 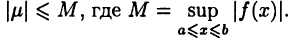Но по теореме 24.2 функция 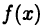ограничена, т. е.

Переходя теперь в (26.2) к пределу при 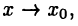получим требуемый результат.

Теорема:

Если 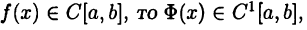причем

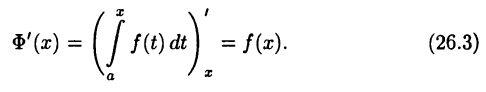
► Пусть 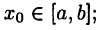тогда, так же как и в (26.2), получим равенство

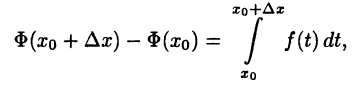
в котором для определенности будем считать, что 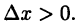Применяя к правой части этого равенства теорему 24.7, придем к существованию 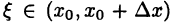такого, что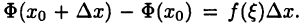

Разделив это равенство на 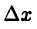и переходя к пределу при 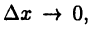получим

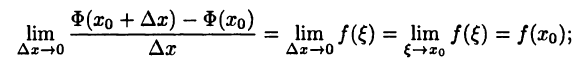
последнее равенство следует из условия непрерывности функции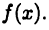

Теорема 26.2 означает, что любая непрерывная функция 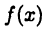имеет первообразную и, следовательно, неопределенный интеграл 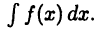Другими словами, верно

Следствие:

Если 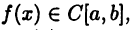то функция (26.1) является первообразной для функции 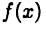на отрезке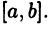

Формула Ньютона-Лейбница

Теорема 26.2 и следствие 26.1 указывают на тесную связь между понятиями неопределенного и определенного интегралов. Более того, они указывают практический способ вычисления определенных интегралов в случае, когда подынтегральная функция непрерывна.

Пусть 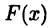является какой-нибудь первообразной для 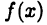на отрезке [a,b]. Так как функция (26.1) также является первообразной, то (см. теорему 21.2) 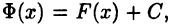где С — некоторая постоянная. Эту постоянную можно найти, если положить х = а и учесть, что 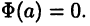Тогда 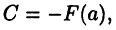или

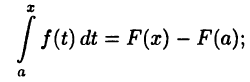
в частности, при х = b получим

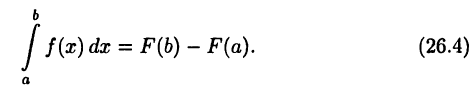
Разность 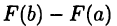часто обозначают в виде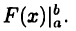

Равенство (26.4) является основным в интегральном исчислении и называется формулой Ньютона-Лейбница. Она дает простой способ вычисления определенных интегралов от непрерывной функции: достаточно найти какую-нибудь первообразную 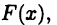а затем вычислить разность ее значений для верхнего и нижнего пределов интегрирования.

Пример:

Находим:

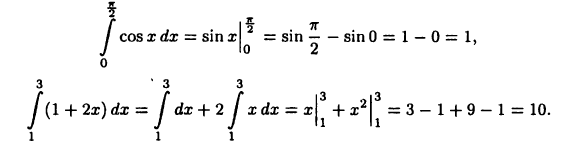
Методы вычисления определенных интегралов

Так как формула Ньютона-Лейбница (26.4) сводит задачу вычисления определенного интеграла от непрерывной функции к нахождению первообразной, то все основные методы вычисления неопределенных интегралов (см. § 22) переносятся и на задачу вычисления определенных интегралов. Сформулируем эти методы с учетом специфики определенных интегралов.

Теорема:

Замена переменной в определенном интеграле.

Пусть:

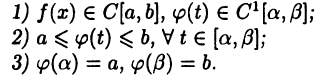
Тогда

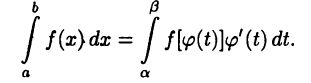
Для доказательства этого равенства достаточно применить к обеим его частям формулу (26.4), учитывая при этом, что если 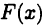будет первообразной для 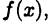то функция 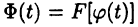будет первообразной для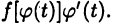

Пример:

Находим

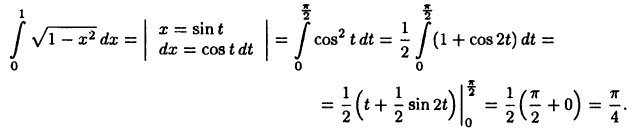
Теорема:

Интегрирование по частям в определенном интеграле. Пусть 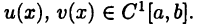Тогда

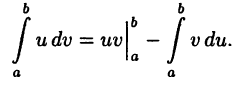
Справедливость этой формулы следует из равенства 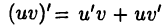и применения формулы (26.4) к интегралу от функции 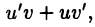для которой первообразной будет функция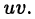

Пример:

Находим

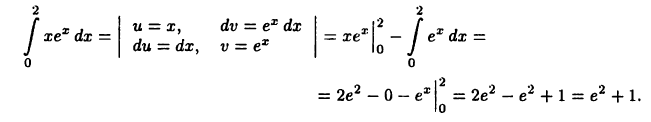
Приложения определенных интегралов

Определенные интегралы имеют многочисленные приложения в самых разнообразных задачах. Здесь мы ограничимся рассмотрением лишь некоторых геометрических и механических приложений.

Вычисление площадей

Площадь криволинейной трапеции, ограниченной сверху функцией 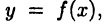снизу — отрезком [а, b] оси х, а по бокам — прямыми х = a и х = b, вычисляется по формуле

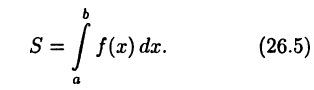
Обоснование этой формулы было дано выше в п. 24.1. Легко модифицировать равенство (26.5) для вычисления площадей плоских фигур самых различных конфигураций.

Пример:

Вычислить площадь фигуры, образованной пересечением графиков функций 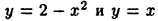(рис. 27). Найдем сначала координаты точек пересечения графиков указанных функций, для чего решим систему уравнений 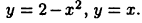Отсюда находим 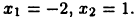Тогда искомая площадь равна

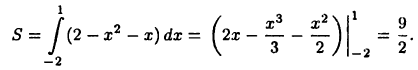
Отметим, что если верхняя граница криволинейной трапеции за-, дана уравнениями в параметрической форме 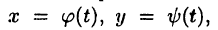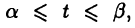то, произведя в формуле (26.5) замену переменной,

получим

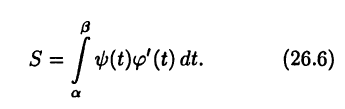
Пример:

Найти площадь фигуры, oграниченной одной аркой циклоиды (см. рис. 9 б на с. 47) 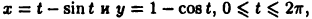и осью х. По формуле (26.6) получим

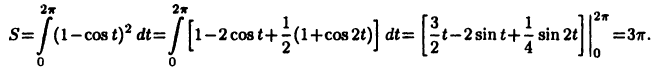
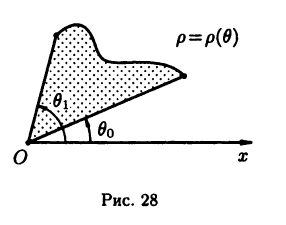
В полярных координатах 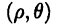площадь фигуры (см. рис. 28), ограниченной графиком непрерывной функции 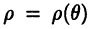и лучами 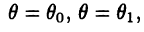находят по формуле:

Длина дуги кривой

Пусть требуется определить длину дуги АВ кривой 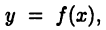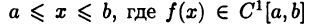(см. рис. 29). Разобьем отрезок [а, b].

на 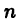частей точками деления 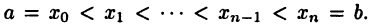Тогда длина L дуги АВ приближенно равна

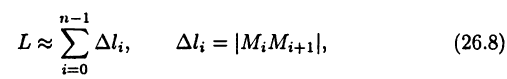
где 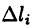— длина отрезка, соединяющего точки 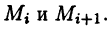Естественно, длиной L дуги AB считать предел

если, конечно, этот предел существует.

По теореме Пифагора имеем 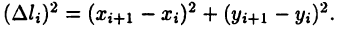Но в силу теоремы Лагранжа (см. с. 82) получим

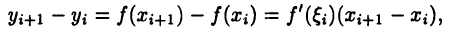
где 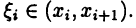Тогда

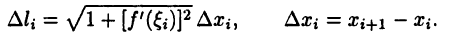
Если подставить эти равенства в правую часть соотношения (26.8), то получим интегральную сумму функции 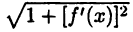на отрезке [а,b]. Поэтому из (26.9) получим искомое значение длины дуги

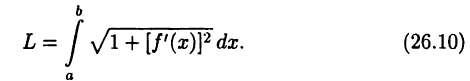
Пример 26.6. Вычислить длину дуги кривой 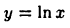на участке от 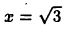до 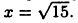По формуле (26.10) получим

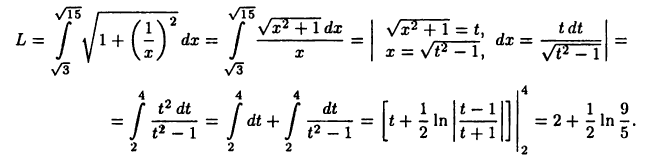
Формулы вычисления длины дуги кривой, заданной параметрическими уравнениями 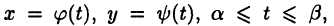и в полярных координатах 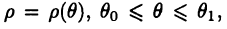соответственно, имеют вид (доказать!):

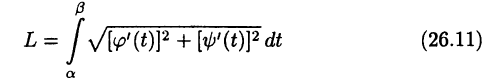
и

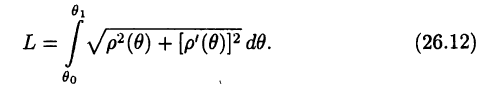
Объем тела вращения

Пусть требуется найти объем тела, образованного вращением криволинейной трапеции, ограниченной кривой осью х и вертикальными прямыми х = а и х = b вокруг оси х (см. рис. 30).

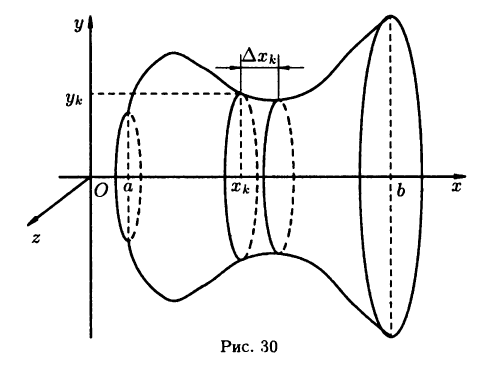
Разбивая отрезок [а,b ] на n частей точками деления 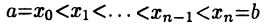и проведя через каждую точку деления плоскость, параллельную плоскости получим разбиение тела на п частей, объем каждой из которых приближенно равен объему цилиндра радиуса 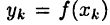и имеющего высоту 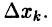Поэтому искомый объем V приближенно равен

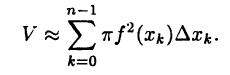
Переходя теперь в этом соотношении к пределу при 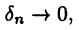получим искомую формулу для объема

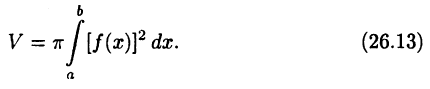
Аналогично может быть получена формула для объема тела, образованного вращением криволинейной трапеции 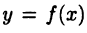вокруг оси у. Эта формула имеет вид

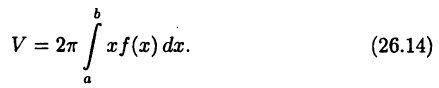
Пример:

Вычислить объем тела, образованного вращением кривой 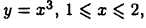вокруг оси х. По формуле (26.13) получим

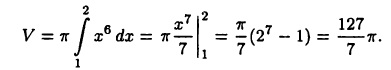
Несложно получить аналоги формул (26.13) и (26.14) для кривой, заданной параметрическими уравнениями или в полярных координатах.

Механические приложения

Пусть на дуге кривой, описываемой уравнением 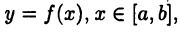распределены массы с плотностью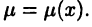

• Статические моменты дуги относительно осей х и у имеют вид:

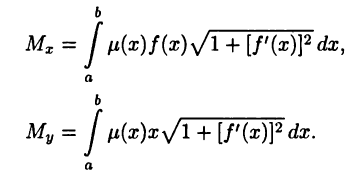
• Моменты инерции дуги относительно тех же осей имеют вид:

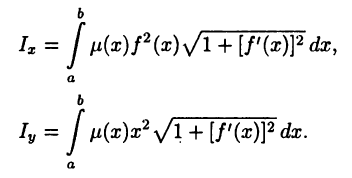
• Координаты центра масс дуги вычисляются по формулам:

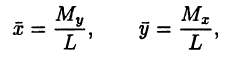
где L — длина дуги кривой.

Несобственные интегралы

Понятие определенного интеграла вводилось и изучалось, во-первых, в предположении, что интегрируемая функция должна быть ограниченной на отрезке интегрирования, во-вторых, сам отрезок должен быть конечным. Если хотя бы одно из этих необходимых требований не выполнено, то определенный интеграл не существует.

Оказывается, существуют классы функций, для которых, хотя и нарушены указанные требования, можно говорить о существовании определенного интеграла. Естественно, при этом определенный интеграл понимается не в смысле введенного в п. 24.2 определения, а некоторого его обобщения. Укажем два основных класса таких функций.

Несобственные интегралы первого рода

Пусть 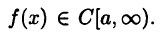Тогда 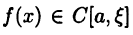и, следовательно,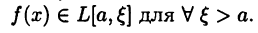

Несобственным интегралом первого рода функции 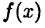в промежутке 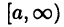называют предел

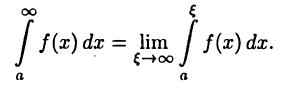
Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае — расходящимся.

Пример:

Рассмотрим несобственный интеграл первого рода функции 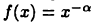на промежутке 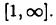Имеем при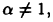

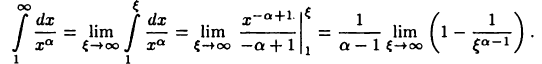
Отсюда следует, что при а < 1 несобственный интеграл расходится, а при а > 1 он сходится, причем

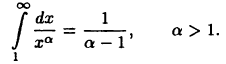
Легко убедиться, что рассматриваемый несобственный интеграл расходится и при a= 1 (проверьте!).

Несобственный интеграл вида

вводится аналогичным образом.

Несобственные интегралы второго рода

Пусть 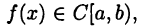где а и b — некоторые числа, причем 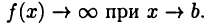Ясно, что тогда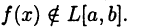

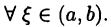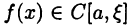Возьмем Тогда и, следовательно, в силу теоремы 25.2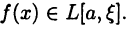

Несобственным интегралом второго рода функции 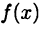в промежутке [а, b] называют предел

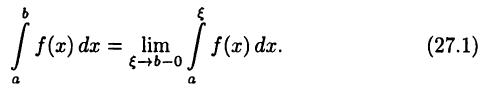
Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае — расходящимся.

Так же, как и выше, определяют интеграл от функции, неограниченной в окрестности точки х = а.

Пример:

Исследовать на сходимость несобственный интеграл второго рода функции 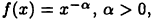на промежутке [0,1]. Имеем при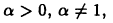

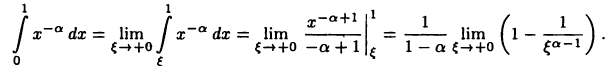
Из полученных соотношений следует, что если а> 1, то несобственный интеграл расходится, если же а < 1, то сходится, причем

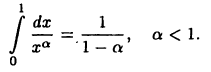
Рассматриваемый несобственный интеграл расходится и при а = 1 (проверьте!). Наконец, если 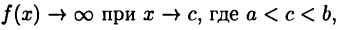то полагают:

Приближенное интегрирование

Рассмотренные выше методы вычисления определенных интегралов эффективны в задачах интегрирования функций, имеющих относительно просто подсчитываемую первообразную. Но не все функции такие хорошие. Многие задачи приводят к необходимости интегрирования функций, найти первообразную которых либо крайне

сложно, либо просто невозможно (вспомним о «неберущихся» интегралах: см. с. 108). Более того, нередко функция может задаваться не формулой, а таблично или вычисляться по какой-либо программе лишь в отдельных точках. Проблемы интегрирования таких функций в совокупности с широким распространением компьютерной техники стимулировали развитие методов приближенного вычисления интегралов.

Мы ограничимся рассмотрением самых простых методов приближенного интегрирования. Пусть 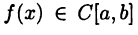и требуется приближенно вычислить интеграл Имеют место приближенные равенства:

• простая формула прямоугольников

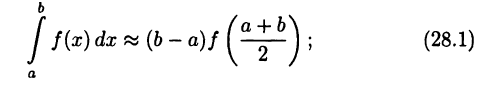
• простая формула трапеций

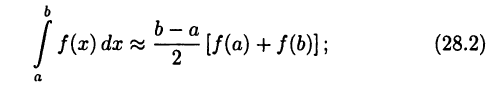
• простая формула Симпсона (формула парабол)

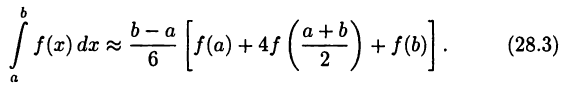
Название этих формул легко объяснить. Пусть для простоты 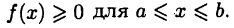В этом случае, согласно геометрическому смыслу интеграла (см. с. 109), значение 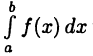равно площади криволинейной трапеции, ограниченной сверху функцией 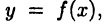снизу — отрезком [а, b] оси х, а по бокам — прямыми х = а и х = b. Тогда, например, формула (28.1) означает ни что иное, как замену площади названной криволинейной трапеции площадью прямоугольника, основанием которого служит отрезок [а,b], а высотой — ордината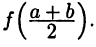

Аналогично формулы (28.2) и (28.3) означают, соответственно, переход к площади обычной трапеции и к площади другой криволинейной трапеции, когда кривая 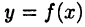заменяется параболой, проходящей через три точки этой кривой (читатель без труда может дать более детальное объяснение).

Формулы (28.1)—(28.3) обладают важным свойством: они превращаются в точные равенства, если в качестве рассматривать многочлены первого или второго порядка. А именно, формулы (28.1) и (28.2) точны для многочленов первого порядка 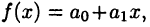а формула (28.3) — для многочленов второго порядка 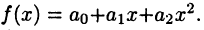Это несложно установить простым подсчетом (в чем рекомендуем убедиться читателю).

При переходе к более сложным функциям формулы (28.1)-(28.3) становятся все менее точными и уж Совсем неважными, если функция имеет участки в виде пиков, колебаний и т.п. Поэтому на практике чаще используют модификации указанных формул. Для этого отрезок [а, b] делят на n частей точками

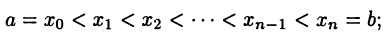
множество 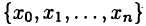называют сеткой, а сами точки 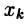— узлами или узловыми точками.

Хотя неравномерное разбиение отрезка [а, b] не ведет к каким-то особым трудностям, для простоты будем рассматривать сетки, узловые точки которых делят отрезок [а, b] на равные части. Тогда если обозначить через h расстояние между соседними узловыми точками, то получим

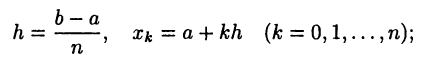
Число h называют шагом сетки.

К каждой части 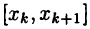отрезка [а,b] применим одну из формул (28.1)-(28.3) и полученные результаты просуммируем. В результате получим приближенные равенства:

• общая формула прямоугольников

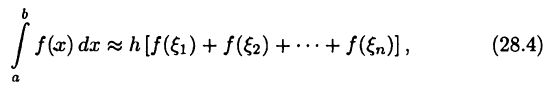
где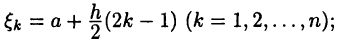

• общая формула трапеций

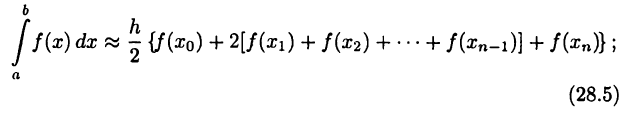
• общая формула Симпсона (формула парабол)

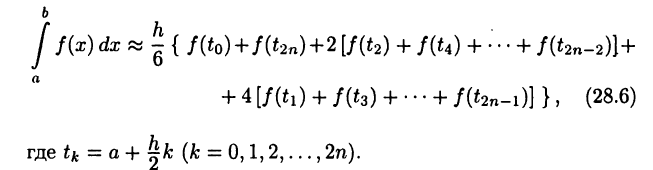
Пусть дана функция 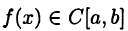и требуется приближенно найти значение интеграла 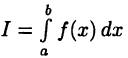по одной из формул (28.4)-(28.6).

Через 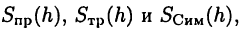соответственно, обозначим значения, полученные по этим формулам, а через

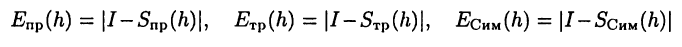
погрешности этих формул. При разных значениях шага h естественно будут получаться и различные результаты. Конечно, при уменьшении шага h погрешности также должны уменьшаться так, чтобы 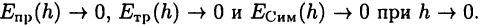Другими словами, функции 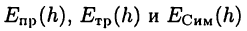должны быть бесконечно малыми при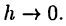

Оказывается погрешности формул (28.4)-(28.6) удовлетворяют соотношениям (вспомните соответствующие обозначения, введенные при изучении б.м.ф. и их классификации)

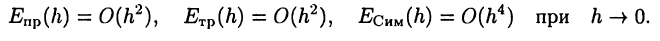
Другими словами, формулы прямоугольников и трапеций имеют второй порядок точности (т.е. при уменьшении шага вдвое, погрешность уменьшается примерно в четыре раза), а формула Симпсона имеет четвертый порядок точности.

Пример:

Вычислим интеграл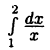 — по формулам (28.4)-(28.6) при h= 0,2. После соответствующего подсчета (оставляя 4 цифры после запятой) получим 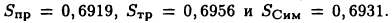Сравнение полученных результатов с точным значением интеграла 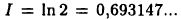подтверждает тот факт, что формула Симпсона имеет существенно меньшую погрешность, чем формулы прямоугольников и трапеций.

Пространства

Выше неоднократно рассматривались множества, элементами которых являются функции. Были определены функциональные множества 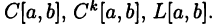В этом разделе эти и подобные множества рассматриваются с общих позиций.

Линейные пространства

Основными объектами математического анализа являются числа, функции и действия над ними. Изучение тех или иных задач приводит к возникновению различных числовых и функциональных множеств. Так появились множества R и С вещественных и комплексных чисел, пространство векторов 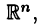функциональные множества 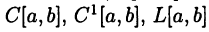и т. п.

Указанные множества обладают общим свойством: если через Е обозначить одно из них, то в нем определены две операции — сложения х+у элементов 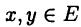и умножения ах на число а из некоторого множества К (обычно К = R или К = С). Эти операции обладают свойствами:

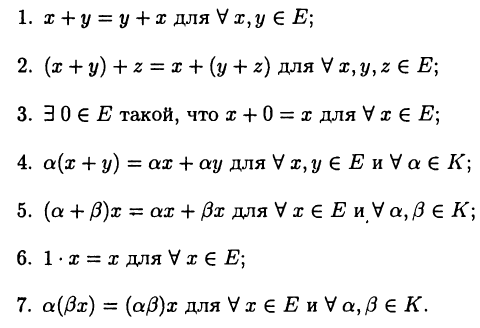
Совокупность объектов, для которых установлены такие операции, называют линейным пространством. Если при этом К=R (К = С), то говорят о вещественном (комплексном) линейном пространстве.

Таким образом, множества 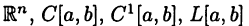и т. п. являются линейными пространствами с естественными операциями сложения элементов и умножения их на число. При этом пространство 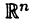является вещественным, а пространства 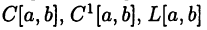могут быть как вещественными, так и комплексными. Аналогом вещественного пространства 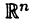является комплексное пространство

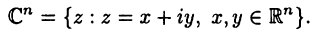
Нормированные пространства

Линейное пространство можно снабдить также понятием расстояния 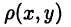между любыми его элементами х и у. Это позволяет не только придать смысл степени близости между элементами данного пространства Е, но и, что особенно важно, определить понятие сходимости 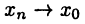как соотношение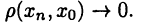

В линейных пространствах понятие расстояния часто связывают с понятием нормы элемента х, т. е. вещественного числа, обозначаемого 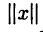и удовлетворяющего условиям:

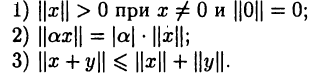
В этом случае пространство называют нормированным, а расстояние между элементами х и у определяют равенством 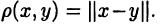Понятие нормы для числовых множеств R и С совпадает с понятием модуля числа, а для векторного пространства 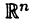— с понятием длины вектора х. В пространствах 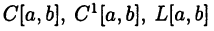норма обычно вводится следующим образом.

• Пространство С[а,b] непрерывных на отрезке [а, b] функций с нормой

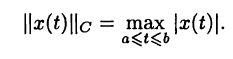
• Пространство 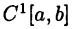функций, имеющих на отрезке [а, b] непрерывную производную с нормой

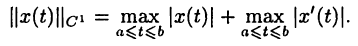
• Пространство L[a, b] интегрируемых на отрезке (а, b] функций с нормой

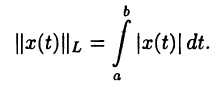
Ниже будет рассматриваться еще один вид функциональных пространств.

• Пространство P[а, b] ограниченных на отрезке [а, b] функций с нормой

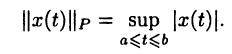
Обратим внимание читателя на тот факт, что в главе 4 функциональное множество 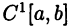описывалось как совокупность функций 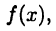имеющих для 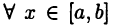производную 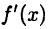без требования непрерывности этой производной. В последующем изложении под 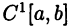будем понимать нормированное пространство с указанной выше нормой.

Евклидовы пространства

В нормированном пространстве определено понятие расстояния, но отсутствует понятие угла, что сужает возможности геометрического толкования пространства. Этот недостаток устраняется введением понятия скалярного произведения векторов х и у, т. е. комплексного числа (х,у), удовлетворяющего условиям:

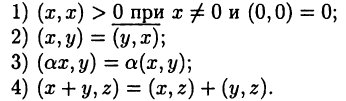
Если пространство является вещественным, то скалярное произведение также вещественное, а условие 2) превращается в условие (х,у) = (у,х).

Линейное пространство со скалярным произведением называют евклидовым пространством. Евклидово пространство становится нормированным, если положить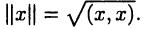

Пример:

В векторных пространствах 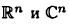скалярное произведение определяется по формулам

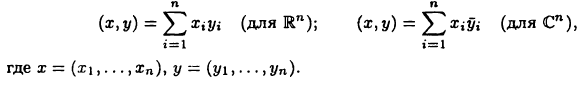
Пример:

В вещественных пространствах L[а,b] или С[а,b] скалярное произведение можно определить равенством

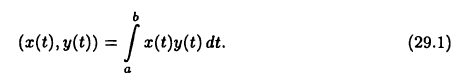
Соответствующая норма 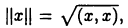конечно, будет отличаться от вышеприведенных норм (покажите это!).

Пусть H — вещественное нормированное евклидово пространство. Угол 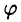между его элементами х и у определяется по формуле

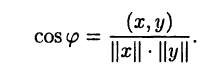
Векторы х и у называют ортогональными, если (х,у) = 0. Вектор х называют нормированным, если 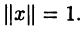Систему (последовательность) векторов

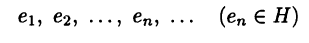
называют ортогональной, если 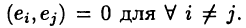Если к тому же все векторы 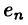нормированы, то система векторов называется ортонормированной.

Пример:

Рассмотрим вещественное пространство 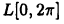со скалярным произведением (29.1). Функции

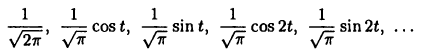
образуют в нем ортонормированную систему (покажите это!).

Пример:

Рассмотрим теперь пространство 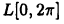комплекснозначных функций со скалярным произведением

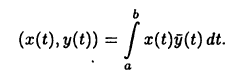
Функции

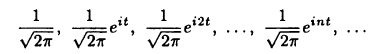
образуют в нем ортонормированную систему (покажите это!).

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические функции числового аргумента
101. Тригонометрические выражения и их преобразования
102. Преобразование тригонометрических выражений
103. Комбинаторика
104. Вычислительная математика
105. Прямая линия на плоскости и ее уравнения
106. Прямая и плоскость
107. Линии и уравнения
108. Прямая линия
109. Уравнения прямой и плоскости в пространстве
110. Кривые второго порядка
111. Кривые и поверхности второго порядка
112. Числовые ряды
113. Степенные ряды
114. Ряды Фурье
115. Преобразование Фурье
116. Функциональные ряды
117. Функции многих переменных
118. Метод координат
119. Гармонический анализ
120. Вещественные числа
121. Предел последовательности
122. Аналитическая геометрия
123. Аналитическая геометрия на плоскости
124. Аналитическая геометрия в пространстве
125. Функции одной переменной
126. Высшая алгебра
127. Векторная алгебра
128. Векторный анализ
129. Векторы
130. Скалярное произведение векторов
131. Векторное произведение векторов
132. Смешанное произведение векторов
133. Операции над векторами
134. Непрерывность функций
135. Предел и непрерывность функций нескольких переменных
136. Предел и непрерывность функции одной переменной
137. Производные и дифференциалы функции одной переменной
138. Частные производные и дифференцируемость функций нескольких переменных
139. Дифференциальное исчисление функции одной переменной
140. Матрицы
141. Линейные и евклидовы пространства
142. Линейные отображения
143. Дифференциальные теоремы о среднем
144. Теория устойчивости дифференциальных уравнений
145. Функции комплексного переменного
146. Преобразование Лапласа
147. Теории поля
148. Операционное исчисление
149. Системы координат
150. Рациональная функция
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат