Оглавление:
Непрерывная дробь (или цепная дробь) — это конечное или бесконечное математическое выражение вида. где. есть целое число, а все остальные. — натуральные числа (положительные целые). При этом числа. называются неполными частными или элементами цепной дроби.
Конечные цепные дроби
В арифметике часто приходится искать наибольший общий делитель двух натуральных чисел. В младших классах эту задачу решают с помощью разложения чисел на простые множители. Однако этот способ в школе не получает теоретического обоснования, так как он опирается на не доказываемую (а часто и не формулируемую ) довольно трудную теорему о существовании и единственности разложения натуральных чисел на простые множители.
Другой метод решения этой задачи, свободный от указанного недостатка, изложен еще в книге Евклида «Начала» (III век до н. э.); его называют алгоритмом Евклида или способом последовательного деления. Изложим этот способ.
Напомним сначала некоторые свойства деления с остатком. Пусть а — целое число и b — натуральное число. Существуют такие целые числа q (частное) и r (остаток), что 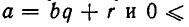
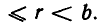 Эти числа однозначно определены.
Эти числа однозначно определены.
Справедливо следующее утверждение: если а = bq + r, то наибольший общий делитель чисел а и b совпадает с наибольшим общим делителем чисел b и r.
В самом деле, обозначим наибольший общий делитель чисел а и b через d, а наибольший общий делитель чисел b и r — через 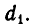 Из соотношения r = а — bq получаем, что d является делителем и числа r, то есть d будет общим (но не обязательно наибольшим) делителем чисел b и r. Отсюда следует, что
Из соотношения r = а — bq получаем, что d является делителем и числа r, то есть d будет общим (но не обязательно наибольшим) делителем чисел b и r. Отсюда следует, что 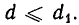 Обратно, из соотношения а = bq + r следует, что наибольший общий делитель чисел b и r является делителем числа а, а значит,
Обратно, из соотношения а = bq + r следует, что наибольший общий делитель чисел b и r является делителем числа а, а значит, 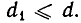 Из двух соотношений
Из двух соотношений 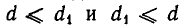 получаем
получаем 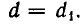
Теперь опишем алгоритм Евклида. Он заключается в том, что для целого числа а и натурального числа b последовательно находят две конечные последовательности чисел 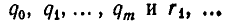
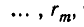 такие, что
такие, что 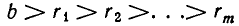 и
и
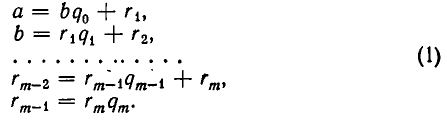
Тогда 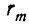 — наибольший общий делитель чисел а и b. Это следует из того, что по доказанному наибольшие общие делители пар чисел
— наибольший общий делитель чисел а и b. Это следует из того, что по доказанному наибольшие общие делители пар чисел 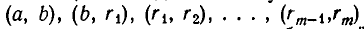
совпадают друг с другом. Но 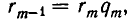 и потому наибольший общий делитель чисел
и потому наибольший общий делитель чисел 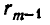 и
и 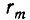 равен
равен 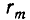 .
.
Заметим, что цепь равенств (1), выражающая алгоритм Евклида, не может быть бесконечной, так как из 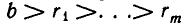
вытекает, что в (1) не более чем b равенств.
Пример цепной дроби
В некоторых приложениях математики встречаются очень громоздкие дроби. Возникает вопрос, нельзя ли подобрать дробь со сравнительно небольшим знаменателем, достаточно близкую к данной громоздкой дроби. Аппаратом для решения этой задачи являются дроби особого вида, называемые цепными или непрерывными дробями.
Прежде чем излагать общую теорию цепных дробей, рассмотрим следующий пример. Отношение экваториального радиуса Земли к ее полярному радиусу выражается дробью 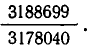
Попробуем упростить эту дробь. Для этого сначала выделим из нее целую часть: 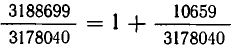 . Оставшуюся дробную часть
. Оставшуюся дробную часть 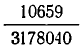 преобразуем так:
преобразуем так: 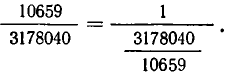
В знаменателе получившейся дроби снова выделим целую часть:
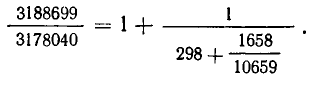
Это выражение позволяет получить хорошее приближение для рассматриваемой дроби. Ясно, что при отбрасывании в знаменателе дробной части 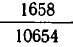 мы получим число
мы получим число 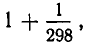 которое
которое
больше, чем наша дробь. Если же округлить знаменатель в сторону увеличения, то мы получим дробь 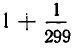 , которая меньше рассматриваемой. Таким образом,
, которая меньше рассматриваемой. Таким образом,
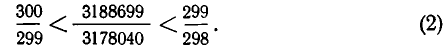
Разность полученных приближений 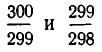 мала:
мала:
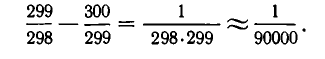
Значит, как 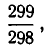 так и
так и 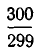 дают приближенное значение для дроби
дают приближенное значение для дроби 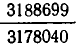 с точностью не меньшей, чем
с точностью не меньшей, чем 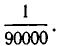
Если мы хотим получить еще лучшее приближение, надо аналогичным образом преобразовать отброшенную дробную часть 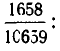
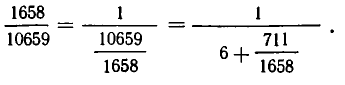
Подставляя это выражение в (1), получаем:
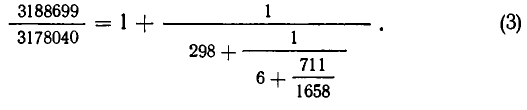
Ясно, что дробь 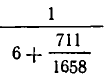 заключена между
заключена между 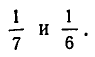
Поэтому получаем для  границы:
границы:

или, преобразуя дроби,

Получились оценки с большими знаменателями, чем в (2). Но их точность существенно выше — погрешность полученных приближений не больше, чем 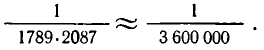
Продолжая описанный процесс, мы получим в конце концов точное выражение для 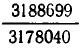 в виде «многоэтажной» дроби:
в виде «многоэтажной» дроби:
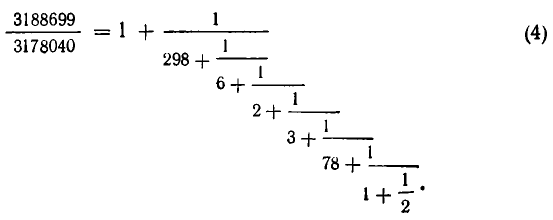
Разумеется, полученная дробь менее удобна, чем  . Но она позволяет получать приближенные значения заданной дроби, имеющие небольшие знаменатели. Чтобы получить такие приближенные значения, надо оборвать процесс на каком-то шагу, заменив смешанное число его целой частью, и превратить полученное выражение в обыкновенную дробь. Дроби вида (4) и называют цепными или, иначе, непрерывными дробями.
. Но она позволяет получать приближенные значения заданной дроби, имеющие небольшие знаменатели. Чтобы получить такие приближенные значения, надо оборвать процесс на каком-то шагу, заменив смешанное число его целой частью, и превратить полученное выражение в обыкновенную дробь. Дроби вида (4) и называют цепными или, иначе, непрерывными дробями.
Определение цепной дроби
Введем следующее общее определение:
Всякое выражение вида
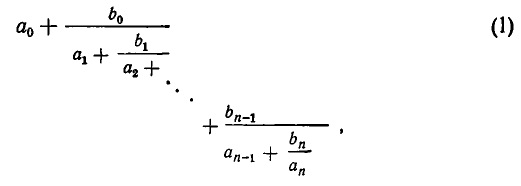
где 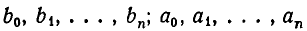 могут быть любыми действительными или комплексными числами, а также функциями от одной или нескольких переменных, называется конечной цепной (или непрерывной) дробью.
могут быть любыми действительными или комплексными числами, а также функциями от одной или нескольких переменных, называется конечной цепной (или непрерывной) дробью. 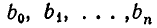 называются частными числителями,
называются частными числителями, 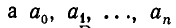 — частными знаменателями или неполными частными. В записи (1), естественно, предполагается, что
— частными знаменателями или неполными частными. В записи (1), естественно, предполагается, что 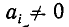
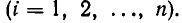 Это условие не касается а0, которое может быть равным нулю.
Это условие не касается а0, которое может быть равным нулю.
Для получения приближенных значений дробей используют частный вид цепных дробей, у которых все числители равны 1  а знаменатели — натуральные числа
а знаменатели — натуральные числа 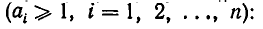
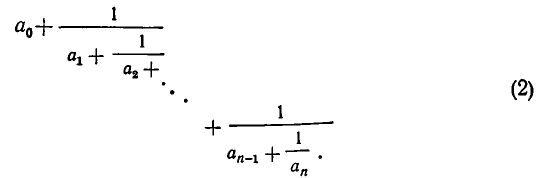
Форма записи (2), как и форма (1), очень громоздка; поэтому вместо (2) часто употребляются упрощенные записи, например
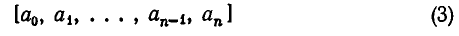
или
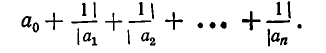
Все же часто мы будем пользоваться развернутой записью (2).
Ясно, что всякая цепная дробь вида (2) выражает некоторое рациональное число. Чтобы получить выражение этого числа в виде обыкновенной дроби, надо «свернуть» цепную дробь, выполняя (начиная «с конца») все указанные операции.
Пример:
Вычислить значение цепной дроби 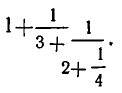 Здесь
Здесь 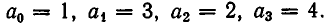 Вычисление будет состоять из следующих шагов:
Вычисление будет состоять из следующих шагов:
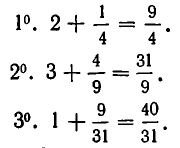
Ответ: 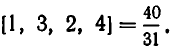
Обращение конечной цепной дроби в обыкновенную — всегда выполнимая задача. На это потребуется не более чем n шагов, каждый из которых состоит в сложении двух чисел: целого числа и правильной дроби.
Представление рациональных чисел в виде конечной цепной дроби
В предыдущем параграфе было показано, что любую конечную цепную дробь можно обратить в рациональное число. Покажем теперь, что и обратно — любое рациональное число r можно обратить в цепную дробь.
Теорема:
Всякое рациональное число можно представить в виде конечной цепной дроби.
Доказательство:
Всякое рациональное число r можно представить в виде отношения двух целых чисел 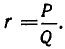 При этом, не теряя общности, можно считать
При этом, не теряя общности, можно считать  (в противном случае изменим знаки у Р и Q). Применим к числам Р и Q алгоритм Евклида (см. § 1):
(в противном случае изменим знаки у Р и Q). Применим к числам Р и Q алгоритм Евклида (см. § 1):
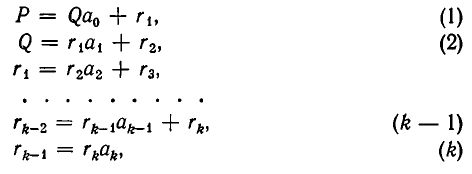
где  (если
(если 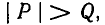 то
то 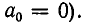 Каждое из полученных равенств можно переписать по-другому:
Каждое из полученных равенств можно переписать по-другому:
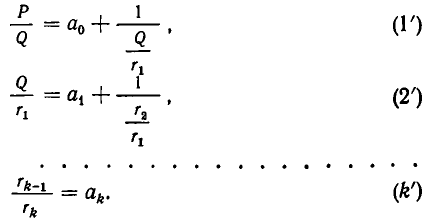
Нетрудно заметить, что каждое из этих равенств можно понимать как нахождение целой части неправильной дроби; каждое из неполных частных 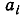 представляет собой целую часть соответствующей дроби:
представляет собой целую часть соответствующей дроби:
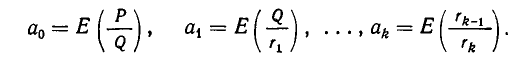
Подставив значение дроби 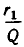 из (2′) в знаменатель дроби равенства
из (2′) в знаменатель дроби равенства 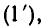 получим:
получим:
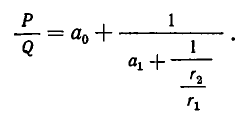
Затем значение дроби 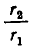 , взятое из равенства (3), подставим в знаменатель дроби
, взятое из равенства (3), подставим в знаменатель дроби 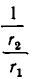 . Продолжая процесс подстановки до конца, получим:
. Продолжая процесс подстановки до конца, получим:
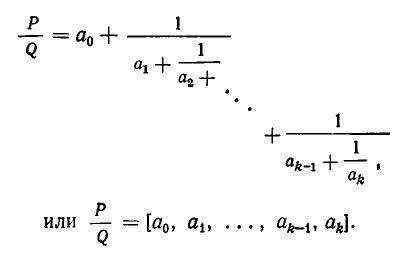
Число частных знаменателей, которое получится при разложении заданного рационального числа в цепную дробь, заранее узнать невозможно. Оно зависит от «природы» числа. Так, мало отличающиеся «на вид» числa 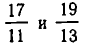 .
.
разлагаются в цепные Дроби, имеющие разное число частных знаменателей:
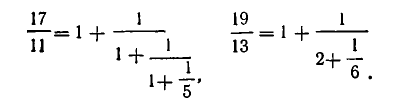
Обратите внимание на характер доказательства теоремы 1. По существу получено больше, чем требовалось. Ведь надо было лишь доказать, что любое рациональное число можно представить в виде конечной цепной дроби. Мы же не только доказали этот факт, но и указали способ построения искомой цепной дроби.
Покажем теперь, что разложение любого рационального числа в цепную дробь однозначно определено. При этом рассматриваются лишь разложения, удовлетворяющие следующему условию: последний частный знаменатель должен быть больше 1. В противном случае могут существовать и различные разложения в цепную дробь одного и того же рационального числа.
Пример:
Разложим в цепную дробь число 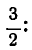
—:
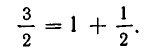
Последний частный знаменатель можно представить в виде 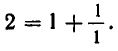 В таком случае число
В таком случае число 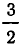 можно записать в виде цепной дроби по-иному:
можно записать в виде цепной дроби по-иному: 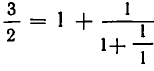 . Получилось, что одну и ту же дробь
. Получилось, что одну и ту же дробь 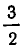 мы разложили в цепную дробь двумя различными способами: [1, 2] и [1, 1, 1]. Так можно поступить с любым рациональным числом. Например, для числа
мы разложили в цепную дробь двумя различными способами: [1, 2] и [1, 1, 1]. Так можно поступить с любым рациональным числом. Например, для числа 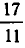 можно получить две цепные дроби:
можно получить две цепные дроби:
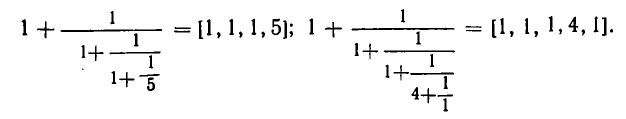
Чтобы исключить двузначность в разложении рационального числа в цепную дробь, связанную с такими искусственными «удлинениями», как раз и приходится предполагать последний частный знаменатель большим 1.
Однозначность разложения мы докажем от противного. Допустим, что число 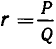 удалось разложить в две разные цепные дроби:
удалось разложить в две разные цепные дроби:
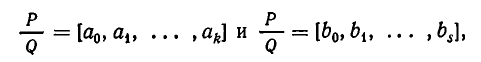
где
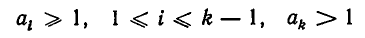
и
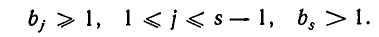
При этом допускается, что различны не только сами частные знаменатели, но и их количество 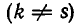 .
.
Мы имеем равенства:
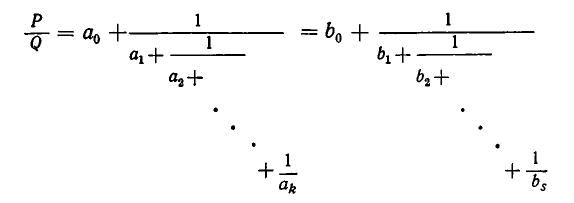
Так как  — натуральные числа, то
— натуральные числа, то 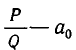 лежит между 0 и 1,
лежит между 0 и 1, 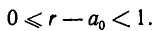 Иными словами,
Иными словами, 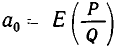 . Точно так же
. Точно так же 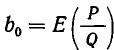 . Значит,
. Значит, 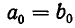 и
и
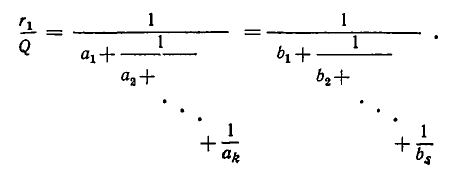
Отсюда следует, что
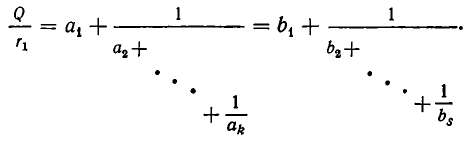
Но точно так же 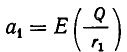 и
и 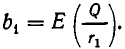 Отсюда следует
Отсюда следует 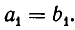 Продолжая процесс сравнения соответствующих частных знаменателей, получим для всех
Продолжая процесс сравнения соответствующих частных знаменателей, получим для всех 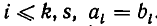 Если теперь допустить, например, что k<5, то после k-го шага мы придем к равенству
Если теперь допустить, например, что k<5, то после k-го шага мы придем к равенству
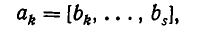
которое невозможно, поскольку 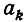 — целое число, а
— целое число, а 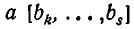 — дробное. Точно так же доказывается, что невозможно неравенство k > s. Итак, k = s и
— дробное. Точно так же доказывается, что невозможно неравенство k > s. Итак, k = s и 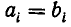 для всех i. Однозначность разложения доказана.
для всех i. Однозначность разложения доказана.
Подходящие дроби
Как уже говорилось, цепные дроби служат для получения приближенных значений, имеющих малые знаменатели. Эти приближенные значения получаются так: число разлагают в цепную дробь и обрывают процесс разложения на некотором шагу, заменяя смешанную дробь ее целой частью. Получающиеся таким образом дроби называются подходящими дробями для данной цепной дроби. Иными словами, подходящими дробями для заданной цепной дроби

называются дроби
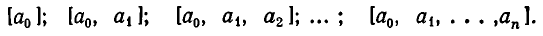
У цепной дроби с n частными знаменателями имеется ровно n подходящих дробей; последняя подходящая дробь равна данной цепной дроби.
Пример:
Вычислим подходящие дроби цепной дроби [1, 2, 3, 4,]:

Чем больше номер подходящей дроби, тем утомительнее ее непосредственное обращение в обыкновенную дробь. При этом все предыдущие вычисления оказываются бесполезными для дальнейшего, все приходится выполнять вновь.
Естественно искать путь вычисления подходящих дробей данной цепной дроби, при котором использовались бы значения предыдущих дробей. Оказывается, для этого можно использовать так называемые рекуррентные соотношения между тремя последовательными подходящими дробями.
Вернемся к предыдущему примеру. Запишем подходящие дроби следующим образом:
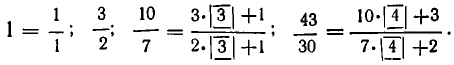
Правило, по которому записаны третья и четвертая подходящие дроби, таково: в числителе записываются два слагаемых — числители двух предыдущих подходящих дробей, а в знаменателе — знаменатели предыдущих подходящих дробей, как показано ниже. И тут и там делается пропуск для множителя:
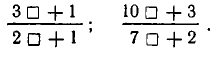
Оставленное место для множителя заполняется соответствующим частным знаменателем.
Докажем это правило в общем виде. Обозначим числитель и знаменатель i-й подходящей дроби через 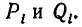 В этих обозначениях правило записывается так:
В этих обозначениях правило записывается так:
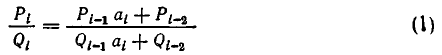
(здесь I = 2, 3, . . . , n).
Доказательство ведется с помощью математической индукции по индексу i.
Проверим сперва правило для i = 2; первые три подходящие дроби имеют вид:
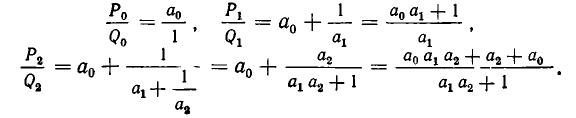
Отсюда следует, что
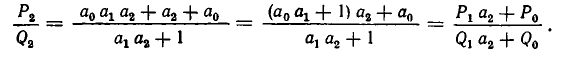
Таким образом, правило верно при i = 2.
Допустим теперь, что правило верно для i = k — 1, то есть что
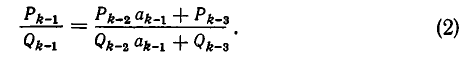
Докажем, что это же правило верно и при i=k, а именно, что имеет место равенство:
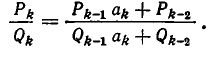
Чтобы получить k-ю подходящую дробь, надо в (k — 1)-й подходящей дроби (k — 1)-й частный знаменатель 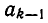 заменить на выражение
заменить на выражение 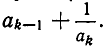 Сделаем эту замену и преобразуем числитель и знаменатель:
Сделаем эту замену и преобразуем числитель и знаменатель:
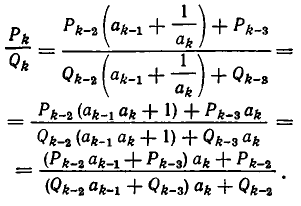
По предположению индукции имеем:
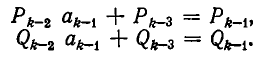
Поэтому
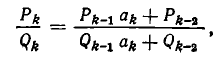
Итак, наша формула верна и при i=k. Значит, она верна при всех Иными словами, мы доказали, что
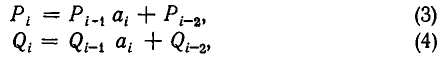
где i — 2, 3, …. n, … .
Для того чтобы формулы (3) и (4) не теряли смысла при i = 1, вводят определения 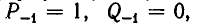 которые носят чисто формальный характер, но делают правила (3) —(4) верными и при i = 1.
которые носят чисто формальный характер, но делают правила (3) —(4) верными и при i = 1.
Покажем, как проводится вычисление, на примере цепной дроби [2, 3, 2, 7, 4]. Вычисление удобно располагать в табличку, которую заполняют последовательно. Первые два столбика заполняют компонентами первых двух подходящих дробей (нулевой и первой подходящей дроби), которые вычисляются непосредственно; третий столбик заполняется компонентами второй подходящей дроби, которые находятся по правилу: числитель первой подходящей дроби умножается на второй частный знаменатель, к полученному произведению прибавляется числитель нулевой подходящей дроби: так же находится и знаменатель второй подходящей дроби. Точно так же определяются числители и знаменатели последующих подходящих дробей. Вот последовательные шаги заполнения таблички:
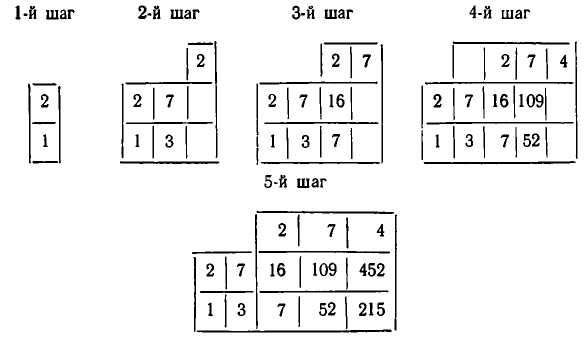
Значит, 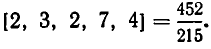
Свойства подходящих дробей
Полученное выше правило вычисления подходящих дробей имеет фундаментальное значение для всей теории цепных дробей. Кроме способа непосредственного вычисления последовательности подходящих дробей, из него получается ряд важных свойств частных числителей и частных знаменателей и подходящих дробей цепной дроби.
Рассмотрим некоторые из этих свойств.
1) Докажем, что для i =1, 2, 3, . . . , n имеет место равенство:
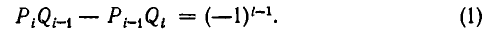
Доказательство проведем индукцией по индексу i.
Покажем прежде всего справедливость формулы (1) при i=1. Заметим, что 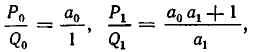 откуда
откуда 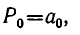
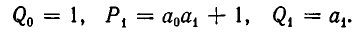
Значит,
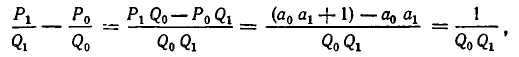
откуда следует, что
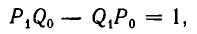
то есть формула (1) справедлива при i = 1.
Предположим, что формула (1) справедлива при i = m — 1:
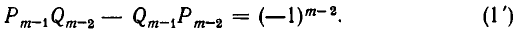
Докажем, что она справедлива и при i = m, то есть что
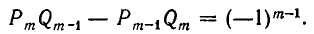
Для этого выразим 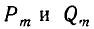 по формулам (3) и (4) из п. 5 и сделаем соответствующие подстановки:
по формулам (3) и (4) из п. 5 и сделаем соответствующие подстановки:
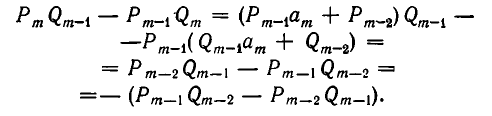
В силу формулы (1′) получаем:
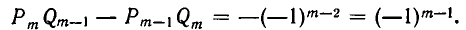
Итак, из справедливости формулы (1) при i = m — 1 следует ее справедливость при i = m. Значит, она верна при всех значениях i.
2) Докажем, что при i = 1,2,3,… имеет место равенство:
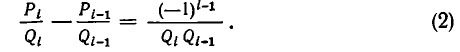
Доказательство:
Преобразуем левую часть равенства (2) и применим свойство (1):
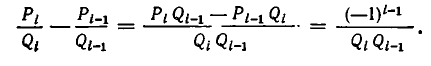
Из последних двух свойств вытекает важное следствие.
3) Пoдходящие дроби цепной дроби несократимы.
Будем доказывать это утверждение от противного. Предположим, что какая-то дробь 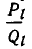 сократима. Это значит, что числитель и знаменатель дроби имеют общий множитель. Обозначим его через с; тогда
сократима. Это значит, что числитель и знаменатель дроби имеют общий множитель. Обозначим его через с; тогда 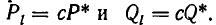 Подставив эти значения
Подставив эти значения 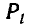 и
и 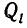 в равенство (1), мы получим:
в равенство (1), мы получим:
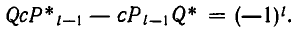
Но последнее равенство неверно, так как левая часть делится на с, а правая — нет. Следовательно, наше предположение, что частные числитель и знаменатель 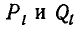 имеют общий множитель, неверно.
имеют общий множитель, неверно.
Диофантовы уравнения первой степени
Мы знаем, что одно уравнение с двумя неизвестными, вообще говоря, имеет бесчисленное множество решений. Однако если рассматривать такие уравнения лишь в множестве целых чисел, то может оказаться, что уравнение имеет лишь конечное множество решений.
Например, уравнение 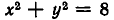 имеет бесчисленное множество действительных решений. Целыми же решениями уравнения являются лишь (2, 2); (— 2, 2); (2, — 2); ( — 2, — 2).
имеет бесчисленное множество действительных решений. Целыми же решениями уравнения являются лишь (2, 2); (— 2, 2); (2, — 2); ( — 2, — 2).
Уравнения, для которых ищутся лишь целые решения, обычно называют диофантовыми.
Вопрос о решении уравнений в целых числах довольно сложен. Мы рассмотрим сейчас самый простой вид таких уравнений, а именно уравнения вида

где а, b и с — целые числа.
Такие уравнения можно решать с помощью цепных дробей. Для примера рассмотрим
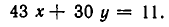
Разложим 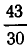 в цепную дробь:
в цепную дробь: 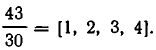 Рассмотрим разность между предпоследней и последней подходящими дробями:
Рассмотрим разность между предпоследней и последней подходящими дробями:
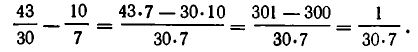
Значит,

Умножим обе части равенства (2) на 11:
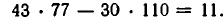
Получилось, что х = 77 и у = — 110 являются решениями заданного уравнения.
Нетрудно заметить, что решением того же уравнения будет любая пара чисел (х, у), следующим образом выражающихся через целый параметр t:
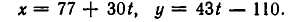
Этот метод всегда применим, если с делится на наибольший общий делитель чисел а и b. В противном случае уравнение не имеет целых решений.
Иногда ставится задача решений диофантовых уравнений в множестве натуральных чисел. Для этого нужно сначала решить его в целых числах, а потом найти значения t, при которых х и у положительны.
В разобранном выше примере для этого нужно решить в целых числах систему неравенств:
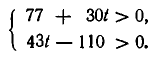
Решая ее, находим t = 3, 4, 5, . . .
Подходящие дроби и календарь
Астрономы подсчитали, что время полного оборота Земли вокруг Солнца приближенно равно 365 суткам 5 часам 48 минутам 46 секундам. Если это время выразить в сутках, то получим приближенно 365,2422 суток.
Обратим дробную часть в цепную дробь:
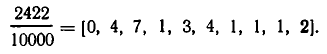
Первые три подходящие дроби: 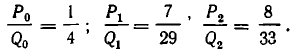
Первая подходящая дробь 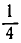 показывает, что, считая год равным 365 дням, мы делаем ошибку на четверть суток. За четыре года получается отставание на одни сутки. Чтобы устранить это отставание, Юлий Цезарь в 45 году до нашей эры ввел новый («юлианский») календарь, в котором каждый четвертый год считался високосным — в феврале прибавляют один день.
показывает, что, считая год равным 365 дням, мы делаем ошибку на четверть суток. За четыре года получается отставание на одни сутки. Чтобы устранить это отставание, Юлий Цезарь в 45 году до нашей эры ввел новый («юлианский») календарь, в котором каждый четвертый год считался високосным — в феврале прибавляют один день.
Однако через столетия снова начала накопляться ошибка. Чтобы ее оценить, рассмотрим разность
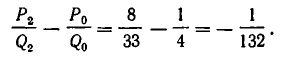
Таким образом, за каждые 132 года прибавляется лишний день (за 396 лет — 3 лишних дня).
Более точный календарь был введен папой Григорием XXII в 1582 году.
Во-первых, он выкинул в этом году 10 дней (следующий день после четверга 4 октября 1582 года именовался пятницей 15 октября), во-вторых, постановил в каждые четыреста лет три високосных года обращать в простые, а один оставить високосным. При переходе нашей страны на григорианский календарь в 1918 году разница во времени уже возросла до 13 суток, что и составляет разницу между старым и новым стилем.
Приближение цепной дроби подходящими дробями
Выясним теперь характер приближения подходящих дробей к рациональному числу, разложенному в данную цепную дробь. Для этого нам понадобится следующее утверждение.
Теорема:
Пусть дана цепная дробь длины т:

При увеличении последнего знаменателя 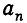 дробь увеличивается, если ее длина п четная, и уменьшается, если п нечетно.
дробь увеличивается, если ее длина п четная, и уменьшается, если п нечетно.
Доказательство:
Проведем доказательство с помощью индукции по n. При n = 0 утверждение очевидно. В этом случае «дробь» имеет вид 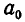 и увеличивается при увеличении
и увеличивается при увеличении 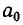 (при этом
(при этом 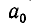 может, увеличиваясь, принимать не только целые, а любые значения).
может, увеличиваясь, принимать не только целые, а любые значения).
Пусть теорема уже доказана для дробей длины k. Рассмотрим дробь длины 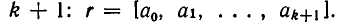 Ее можно представить в виде
Ее можно представить в виде
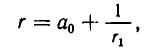
где
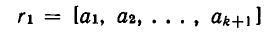
— цепная дробь длины k.
Пусть k + 1 — четное число. Тогда — дробь нечетной длины k. Поэтому по предположению индукции она уменьшается при увеличении 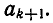 Но при уменьшении
Но при уменьшении 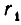 выражение
выражение 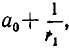 то есть
то есть 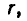 увеличивается.
увеличивается.
Если же k + 1 — нечетное число, то 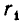 — дробь четной длины k и по предположению индукции увеличивается при увеличении
— дробь четной длины k и по предположению индукции увеличивается при увеличении 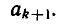 Но тогда
Но тогда 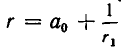 уменьшается при увеличении
уменьшается при увеличении 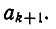
Итак, предположив, что теорема верна для n = k мы доказали ее справедливость при n = k + 1. Так как при n = 0 она верна, то она справедлива для всех значений n.
Из теоремы 2 вытекает важное
Следствие:
Всякая четная подходящая дробь не больше значения цепной дроби у а всякая нечетная подходящая дробь не меньше этого значения.
Доказательство:
Пусть дана дробь
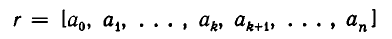
и
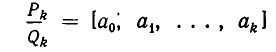
— ее k-я подходящая дробь. Дробь r можно записать в виде
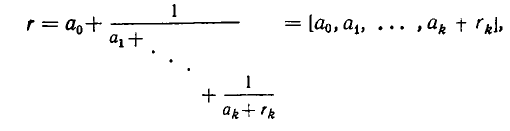
где положено
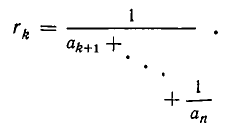
Таким образом, цепная дробь r получается из подходящей дроби 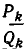 увеличением последнего знаменателя
увеличением последнего знаменателя 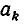 до значения
до значения 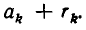 Из теоремы 2 следует, что если k— четное число, то дробь при этом увеличивается, а если k — нечетно, то она уменьшается. Значит, при четном
Из теоремы 2 следует, что если k— четное число, то дробь при этом увеличивается, а если k — нечетно, то она уменьшается. Значит, при четном 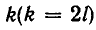 имеем:
имеем: 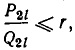 а при нечетном
а при нечетном 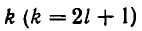 имеет место
имеет место 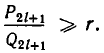 Следствие доказано.
Следствие доказано.
Из этого следствия вытекает, что если 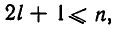 то справедливо неравенство
то справедливо неравенство
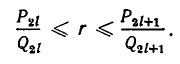
Более точную информацию о характере приближения подходящих дробей 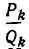 к числу r дает следующая
к числу r дает следующая
Теорема:
Имеют место неравенства

Доказательство:
Подходящая дробь 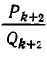 получается из подходящей дроби
получается из подходящей дроби 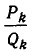 заменой частного знаменателя
заменой частного знаменателя 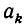 выражением
выражением 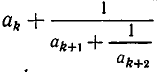 . Так как это выражение больше
. Так как это выражение больше 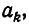 то при четном k подходящая дробь увеличивается, а при нечетном уменьшается. Отсюда и вытекает теорема 3.
то при четном k подходящая дробь увеличивается, а при нечетном уменьшается. Отсюда и вытекает теорема 3.
Из теоремы 3 и следствия из теоремы 2 вытекает, что четные подходящие дроби приближаются к числу 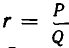 , монотонно возрастая и оставаясь все время не больше, чем
, монотонно возрастая и оставаясь все время не больше, чем 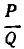 . Нечетные подходящие дроби приближаются к
. Нечетные подходящие дроби приближаются к 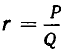 , монотонно убывая и оставаясь все время не меньше, чем
, монотонно убывая и оставаясь все время не меньше, чем 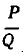 . При этом равняться
. При этом равняться 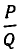 — может лишь последняя подходящая дробь. Итак, мы имеем:
— может лишь последняя подходящая дробь. Итак, мы имеем:
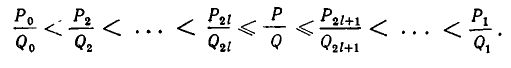
Знак равенства имеет место слева, если n = 2l, и справа, если n = 2l + 1.
Оценим теперь отклонение подходящей дроби 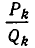 от числа
от числа 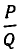 .<3′ Для этого воспользуемся доказанным выше утверждением: при любом k число
.<3′ Для этого воспользуемся доказанным выше утверждением: при любом k число 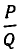 лежит между подходящими дробями
лежит между подходящими дробями 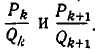
Из него вытекает, что
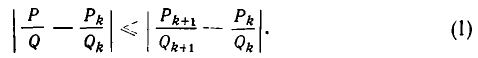
Но
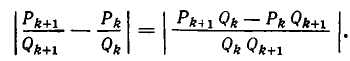
По формуле (1) из п. 6 имеем:
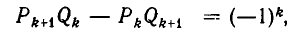
а потому
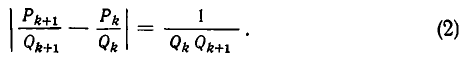
Из формул (1) и (2) следует, что
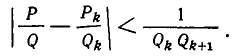
Так как 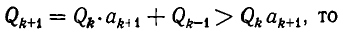
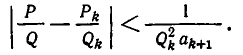
Бесконечные цепные дроби
Разложение иррациональных чисел в цепные дроби: До сих пор мы разлагали в цепные дроби рациональные числа. При этом процесс нахождения частных знаменателей сводился на каждом шагу к выделению целой части неправильной обыкновенной дроби.
Возьмем теперь какое-нибудь иррациональное число, например 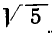 Алгоритм Евклида здесь неприменим. Однако выделение целой части этого числа — вполне реальная задача. В самом деле, ясно, что
Алгоритм Евклида здесь неприменим. Однако выделение целой части этого числа — вполне реальная задача. В самом деле, ясно, что 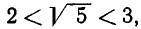 так что
так что 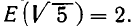 Значит, число
Значит, число 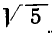 представимо в виде
представимо в виде 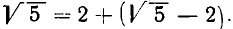 Во втором слагаемом уничтожим иррациональность в числителе:
Во втором слагаемом уничтожим иррациональность в числителе:
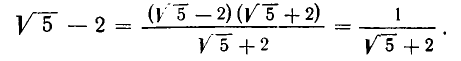
Таким образом, 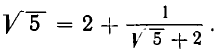
Выделим целую часть числа 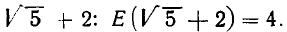 Значит
Значит 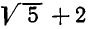 можно представить в виде
можно представить в виде 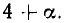 Ясно, что
Ясно, что 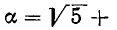
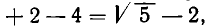 поэтому
поэтому 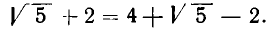 Снова уничтожим иррациональность в числителе второго слагаемого:
Снова уничтожим иррациональность в числителе второго слагаемого:
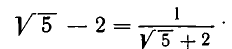
В итоге получилось:
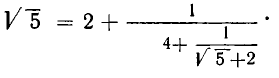
Проделаем еще один аналогичный шаг:
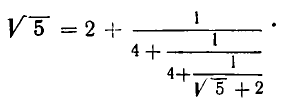
Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться 4 и слагаемое 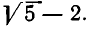 Поэтому ясно, что
Поэтому ясно, что 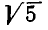 представляется в виде бесконечной цепной дроби:
представляется в виде бесконечной цепной дроби:
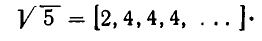
Мы видим, что цепные дроби являются хорошим аппаратом для вычисления квадратных корней.
Проверим, насколько полезен этот способ — как точно находится значение 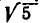 с помощью цепных дробей.
с помощью цепных дробей.
Для сравнения будем брать подходящие дроби и обращать их в обыкновенные, а затем полученные обыкновенные — в десятичные. Десятичные приближения, получаемые из подходящих дробей, будем сравнивать со значением 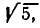 взятым из таблиц Брадиса
взятым из таблиц Брадиса 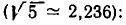
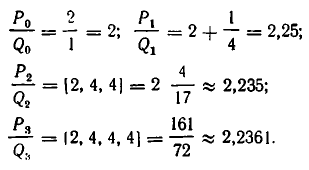
Получилось, что уже для четвертой подходящей дроби результат приближения 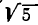 по точности не уступает значению, указанному в четырехзначной таблице значений квадратных корней. Больше того, значение той же подходящей дроби
по точности не уступает значению, указанному в четырехзначной таблице значений квадратных корней. Больше того, значение той же подходящей дроби 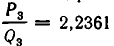 равно значению
равно значению 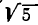 , указанному в пятизначной таблице. Вообще, нахождение приближений с помощью цепных дробей — мощный вычислительный аппарат.
, указанному в пятизначной таблице. Вообще, нахождение приближений с помощью цепных дробей — мощный вычислительный аппарат.
Возьмем произвольное иррациональное число а. Выделим его целую часть и обозначим ее через 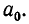
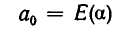
или
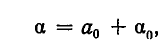
где 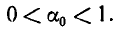 Далее, пусть
Далее, пусть 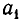 — целая часть
— целая часть 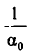 , то есть
, то есть 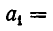
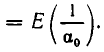 Тогда
Тогда
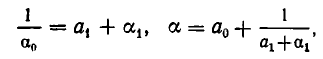
гдe 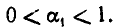
Пусть 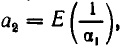 тогда
тогда
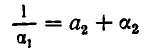
и
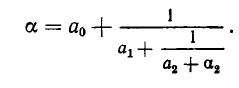
Через n шагов получим:
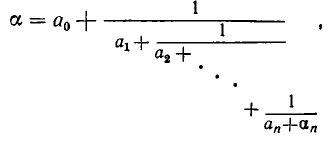
где 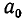 — целое число,
— целое число,  — натуральные числа и 0 <
— натуральные числа и 0 < 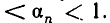 Этот процесс бесконечен. В самом деле, ни одно
Этот процесс бесконечен. В самом деле, ни одно 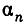 не может оказаться равным нулю. Ведь если какое-то
не может оказаться равным нулю. Ведь если какое-то 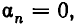 то цепная дробь окажется конечной, а такие дроби являются рациональными числами. Мы же взяли для разложения иррациональное число.
то цепная дробь окажется конечной, а такие дроби являются рациональными числами. Мы же взяли для разложения иррациональное число.
Таким образом, каждому иррациональному числу соответствует бесконечная цепная дробь
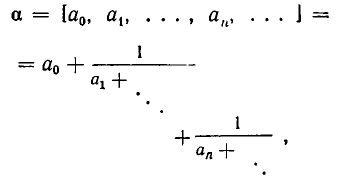
для которой  — натуральные числа (
— натуральные числа (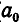 может быть целым числом любого знака).
может быть целым числом любого знака).
Построим для полученной дроби последовательность ее подходящих дробей (в отличие от случая разложения рациональных чисел эта последовательность бесконечна). Можно доказать, что последовательность
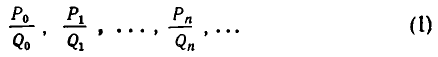
подходящих дробей сходится к разлагаемому числу а. Мы опускаем здесь это доказательство.
Подходящие дроби и наилучшие приближения иррациональных чисел рациональными
Мы научились изображать любые числа, как рациональные, так и иррациональные, в виде цепных дробей. Выясним теперь, в чем заключаются преимущества и недостатки такого изображения.
Основное преимущество записи чисел в виде цепных дробей по сравнению с их записью в виде систематических (например, десятичных) дробей состоит в том, что эта запись не зависит от выбора системы счисления. Ведь неполные знаменатели получались путем выделения целой части из неправильных дробей, а эта операция при любой системе счисления приводит к одному и тому же результату (конечно, с точностью до записи в разных системах счисления самих неполных знаменателей). Поэтому запись числа в виде цепной дроби отражает его «существенные» арифметические свойства, а не свойства, связанные с выбором той или иной системы счисления.
Например, при записи рационального числа в виде систематической дроби может получиться либо конечная дробь, либо бесконечная периодическая или смешанная) дробь. При записи же рационального числа в виде цепной дроби всегда получается конечная дробь, причем это характерно только для рациональных чисел. Можно доказать, что квадратичные иррациональности, и. только они, представляются в виде периодических цепных дробей. Выразить же условие того, что данное число является квадратичной иррациональностью, в терминах систематических дробей невозможно.
Но самое важное преимущество цепных дробей по сравнению с систематическими заключается в том, что они дают наилучшие приближения данного числа с помощью дробей, имеющих не слишком большие знаменатели. Уточним это утверждение.
Пусть даны число 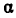 и несократимая дробь
и несократимая дробь 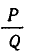 . Естественной мерой отклонения
. Естественной мерой отклонения 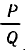 от
от 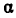 является
является 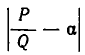 . Однако в теоретических вопросах оказалось удобнее рассматривать в качестве меры отклонения число
. Однако в теоретических вопросах оказалось удобнее рассматривать в качестве меры отклонения число 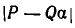 . Ясно, что если
. Ясно, что если 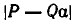 мало, то тем более мало число
мало, то тем более мало число 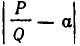 . Обратное верно не всегда, так как знаменатель Q может оказаться большим числом.
. Обратное верно не всегда, так как знаменатель Q может оказаться большим числом.
Пусть число 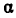 разложено в цепную дробь. Легко оценить отклонение подходящей дроби
разложено в цепную дробь. Легко оценить отклонение подходящей дроби 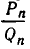 от
от 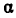 . Так как
. Так как 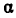 лежит между
лежит между 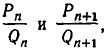 то имеем:
то имеем:
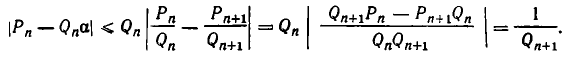
Оказывается, для любой дроби, знаменатель которой не превосходит 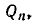 отклонение больше, чем
отклонение больше, чем 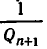 . Иными словами, справедлива следующая
. Иными словами, справедлива следующая
Теорема:
Если 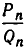 — подходящая дробь для разложения числа
— подходящая дробь для разложения числа 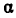 в цепную дробь, то для любой дроби
в цепную дробь, то для любой дроби 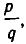 такой, что
такой, что 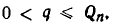 выполняется неравенство
выполняется неравенство
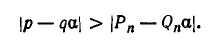
Единственным исключением является подходящая дробь 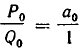 для числа вида
для числа вида 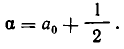
Доказательство этой теоремы мы опускаем.
Теорема 4 показывает, что подходящие дроби являются наилучшими приближениями для числа 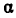 по сравнению со всеми дробями, знаменатель которых не превосходит знаменателя подходящей дроби. Именно это свойство послужило причиной введения цепных дробей в математику и детального изучения их теории. В конце XVII века голландский математик и физик Гюйгенс хотел построить модель Солнечной системы с помощью зубчатых колес. При этом возникла задача определить число зубцов так, чтобы отношение этих чисел для двух связанных между собой колес было по возможности близко к отношению времен
по сравнению со всеми дробями, знаменатель которых не превосходит знаменателя подходящей дроби. Именно это свойство послужило причиной введения цепных дробей в математику и детального изучения их теории. В конце XVII века голландский математик и физик Гюйгенс хотел построить модель Солнечной системы с помощью зубчатых колес. При этом возникла задача определить число зубцов так, чтобы отношение этих чисел для двух связанных между собой колес было по возможности близко к отношению времен 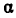 обращения соответствующих планет, причем число зубцов не должно быть слишком большим. Таким образом, встал вопрос об отыскании рациональной дроби, числитель и знаменатель которой были бы не слишком большими числами и которая наилучшим образом приближала число
обращения соответствующих планет, причем число зубцов не должно быть слишком большим. Таким образом, встал вопрос об отыскании рациональной дроби, числитель и знаменатель которой были бы не слишком большими числами и которая наилучшим образом приближала число 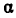 . С помощью теории цепных дробей задача была решена.
. С помощью теории цепных дробей задача была решена.
Отметим, что цепные дроби как аппарат для изображения действительных чисел имеют и недостатки: дело в том, что над действительными числа ми, изображенными в виде цепных дробей, практически трудно выполнять арифметические операции — сложение, вычитание, умножение и деление. (Попробуйте, например, сложить или перемножить дроби
[2, 1, 3, 1, 4] и [3, 2, 4, 6, 8 ],
не переводя их в обыкновенные.)
Цепные дроби как вычислительный инструмент
Рассмотрим некоторые примеры приближения иррациональных чисел подходящими дробями.
Начнем с числа 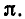 Разлагая число
Разлагая число 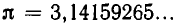 в цепную дробь, получаем:
в цепную дробь, получаем: 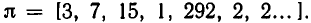 Найдем подходящие дроби для этой цепной дроби:
Найдем подходящие дроби для этой цепной дроби:
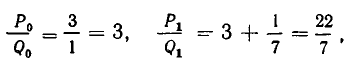
а затем составим таблицу для вычисления последующих дробей с помощью рекуррентного правила:
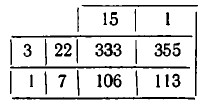
Получаем подходящие дроби 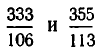 . Приближение
. Приближение 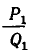 , равное
, равное 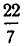 , было известно еще Архимеду, а приближением
, было известно еще Архимеду, а приближением 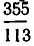 пользовался Андриан Меций еще в конце XVI столетия. Первое приближение очень удобно тем, что знаменатель 7 очень невелик. Во второй дроби при сравнительно небольшом знаменателе 113 получается приближенное значение
пользовался Андриан Меций еще в конце XVI столетия. Первое приближение очень удобно тем, что знаменатель 7 очень невелик. Во второй дроби при сравнительно небольшом знаменателе 113 получается приближенное значение 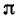 с высокой точностью.
с высокой точностью.
Чтобы оценить эту точность, используем формулу
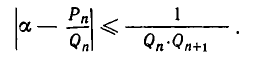
В нашем случае 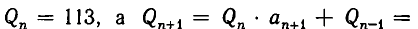
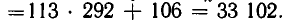
Значит,
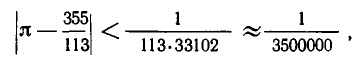
то есть точность полученного ответа превышает 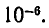 Обращая дробь
Обращая дробь 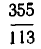 в десятичную, получаем:
в десятичную, получаем:
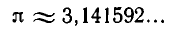
С помощью цепных дробей можно выполнять вычисление логарифмов при любом основании. Вычислим, например, 1g 20. Полученный результат будем сравнивать со значением 1g 20, взятым из таблицы Брадиса:
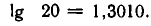
Обозначим искомое число через х; 1g 20 = х. Значит,

Ясно, что 1 < х < 2; поэтому
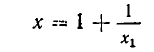
и
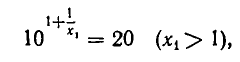
откуда

Последнее равенство возведем в степень 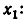

Значит,
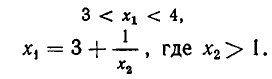
Подставим значение 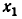 в равенство (2):
в равенство (2):
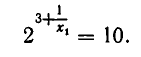
Отсюда 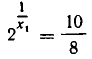 и потому
и потому 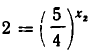 . Но тогда
. Но тогда
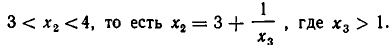
Получаем:
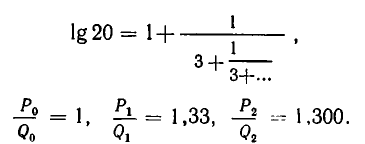
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
