Оглавление:
Задачи, приводящие к возникновению понятия ряда:
Понятие ряда возникает при рассмотрении очень многих важных вопросов.
Примеры:
1. Выяснение смысла бесконечной периодической десятичной дроби, например,
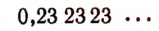
сводится к выяснению смысла следующего выражения:
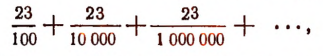
имеющего вид бесконечной последовательности слагаемых.
2. Число 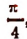 , как это доказывается в курсе высшей математики, может быть изображено выражением
, как это доказывается в курсе высшей математики, может быть изображено выражением
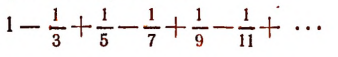
3. Если пересечь плоскостью поверхность прямого круглого конуса так, чтобы образовалась замкнутая линия, то получим кривую линию, называемую эллипсом (рис. 142).
Пусть имеется эллипс с размерами, указанными на рисунке 143.
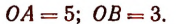
Точная длина l этого эллипса изобразится, как это доказывается в высшей математике, так:
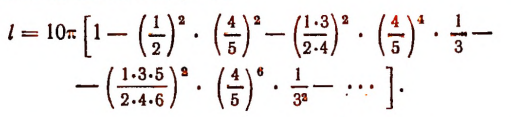
В квадратных скобках содержится опять же выражение, имеющее вид бесконечной последовательности слагаемых.
Чем больше членов мы будем брать внутри квадратных скобок, тем точнее будем находить значение l, т. е. значение длины эллипса.
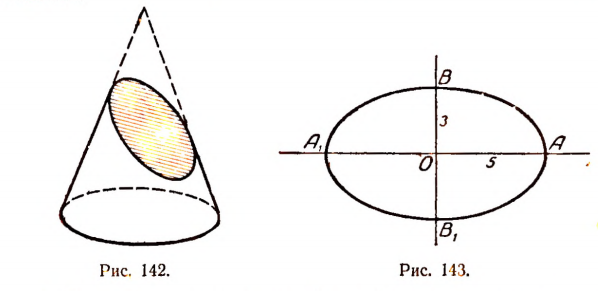
4. Если считать х радианной мерой угла, то, как доказывается в курсе высшей математики, точное выражение sin x может быть представлено так:
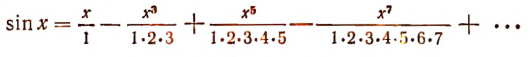
Эти примеры показывают, что изучение выражений, имеющих вид суммы бесконечной последовательности слагаемых, необходимо и полезно.
Понятие ряда
Определение:
Выражение
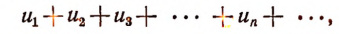
в котором  являются членами последовательности, называется рядом.
являются членами последовательности, называется рядом.

n-й член ряда, т. е. 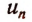 , называется общим членом ряда.
, называется общим членом ряда.
Ряд содержит бесконечно много членов. Поэтому в нем не может быть члена, который можно было бы назвать последним.
Сумма первых n членов ряда называется его частной суммой порядка n и обозначается символом 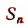 . Эту сумму
. Эту сумму 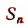 будем называть для краткости усеченной суммой ряда. Значит,
будем называть для краткости усеченной суммой ряда. Значит,
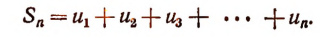
Если 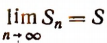 , где S — определенное число, то ряд называется сходящимся, а число S называется суммой этого ряда.
, где S — определенное число, то ряд называется сходящимся, а число S называется суммой этого ряда.
Если 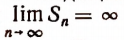 или
или 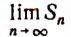 не существует, то ряд называется расходящимся. В этом случае говорят, что ряд не имеет суммы.
не существует, то ряд называется расходящимся. В этом случае говорят, что ряд не имеет суммы.
Итак, суммой сходящегося рядя называется предел суммы первых n его членов при n стремящемся к бесконечности.
Было бы неправильно называть суммой ряда сумму всех его членов, так как этих членов имеется бесконечно много. Подсчитать же сумму, в которой бесконечно много слагаемых, невозможно. Поэтому фраза «сумма всех членов ряда» является бессмысленной.
Примеры вычисления сумм сходящихся рядов
1. Найти сумму ряда:
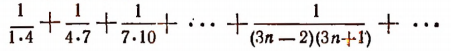
Сначала найдем усеченную сумму этого ряда:
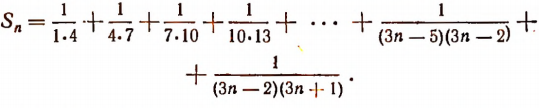
Каждое слагаемое данной суммы можно представить в новой форме:
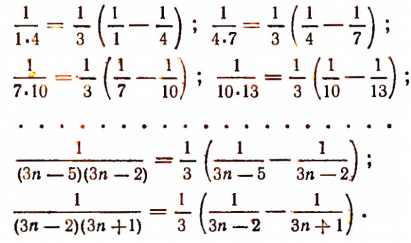
Благодаря этому наша усеченная сумма примет вид:
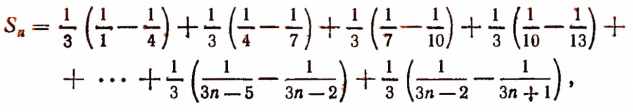
или
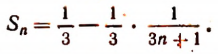
Сумма S данного ряда определяется так:
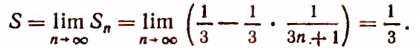
Итак, данный ряд является сходящимся и имеет сумму, равную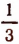 .
.
2. Найти сумму ряда
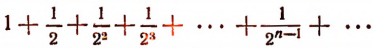
Сначала найдем усеченную сумму этого ряда:
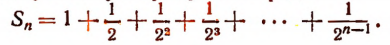
Пользуясь формулой суммы членов конечной геометрической прогрессии, получим:
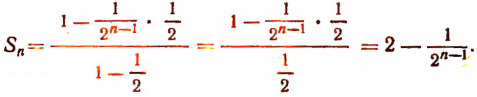
Сумма S данного ряда определяется формулой
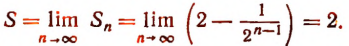
Итак, данный ряд является сходящимся и имеет сумму, равную 2.
Бесконечно убывающая геометрическая прогрессия и ее сумма
Определение:
Бесконечную геометрическую прогрессию мы называем бесконечно убывающей, если ее знаменатель по абсолютной величине меньше 1.
Рассмотрим ряд
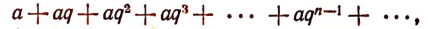
в котором |q| < 1.
В этом ряду члены идут по закону геометрической прогрессии со знаменателем q.
Докажем, что такой ряд всегда сходится и имеет сумму S, определяемую формулой
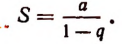
Сначала найдем усеченную сумму данного ряда:
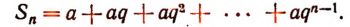
Пользуясь формулой суммы членов конечной геометрической прогрессии, получим:
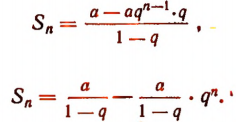
Сумма S данного ряда определяется так:
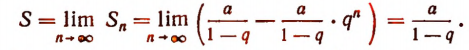
Здесь мы воспользовались тем, что при |q| < 1
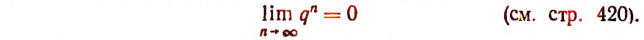
Итак, данный ряд сходится и имеет сумму, равную 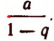
Сумму ряда

в котором |q| < 1 называют ради краткости «суммой бесконечно убывающей геометрической прогрессии».
Обратите внимание на то, что было бы неправильно сказать: «сумма членов бесконечно убывающей прогрессии».
Итак, сумма бесконечно убывающей геометрической прогрессии равна первому члену, деленному на разность между единицей и знаменателем прогрессии, т. е.
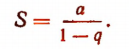
Пример:
Найти сумму ряда:
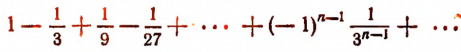
Здесь
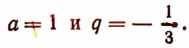
Поэтому
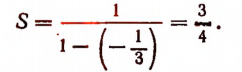
Пример:
Чистую периодическую дробь 0,(13) обратить в обыкновенную.
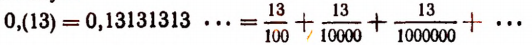
Здесь 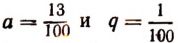 . Поэтому
. Поэтому
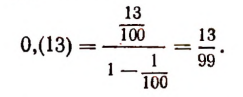
Пример:
Смешанную периодическую дробь 0,3(8) обратить в обыкновенную.
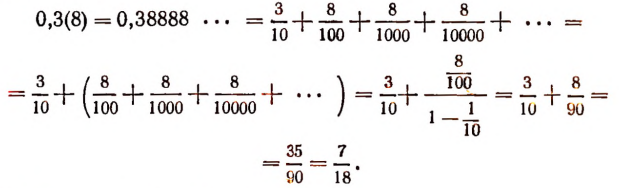
Пример:
Найти сумму ряда:
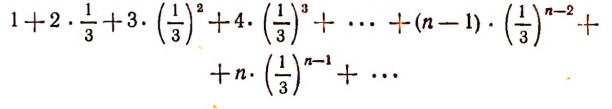
Найдем усеченную сумму 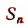 , т. е. сумму n первых членов этого ряда:
, т. е. сумму n первых членов этого ряда:
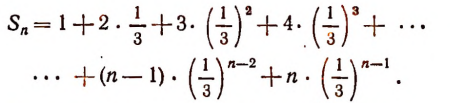
Умножив обе части этого равенства на 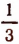 , получим:
, получим:
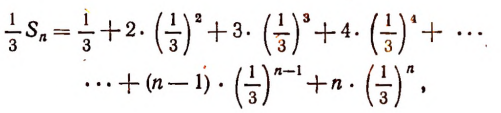
или
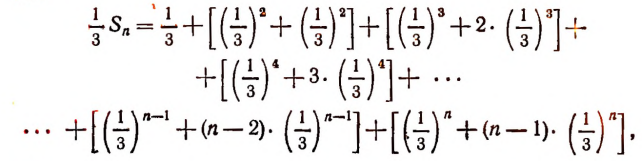
или
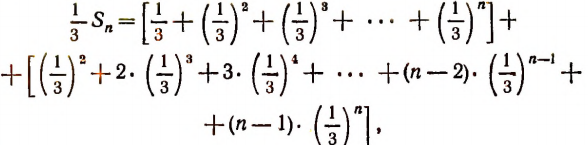
или
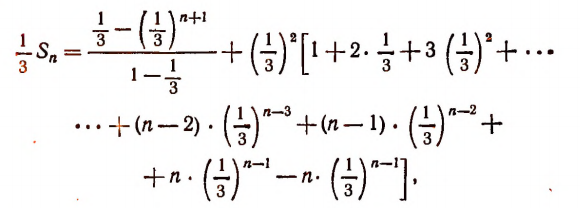
или
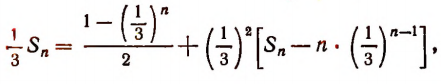
или
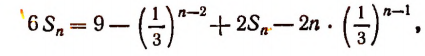
или
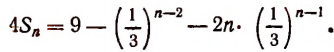
Отсюда
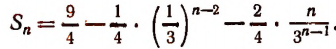
Теперь сумма S данного ряда определится так: 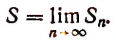
Но
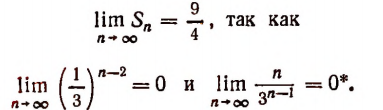
Итак, сумма данного ряда равна 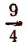 , т. е. 2,25.
, т. е. 2,25.
То что
мы принимаем к сведению здесь без доказательства.
Примеры расходящихся рядов
- Ряд

расходящийся, так как 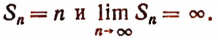
2. Ряд
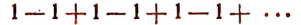
расходящийся, так как 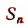 равно 1 при нечетных значениях n и равно нулю при четных значениях n. Поэтому величина
равно 1 при нечетных значениях n и равно нулю при четных значениях n. Поэтому величина 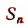 при неограниченном возрастании натурального числа n попеременно принимает значения, равные то единице, то нулю, а потому ни к какому пределу не стремится. Значит, данный ряд является расходящимся.
при неограниченном возрастании натурального числа n попеременно принимает значения, равные то единице, то нулю, а потому ни к какому пределу не стремится. Значит, данный ряд является расходящимся.
3. Ряд
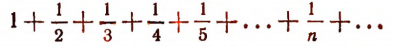
является расходящимся.
Доказательство:
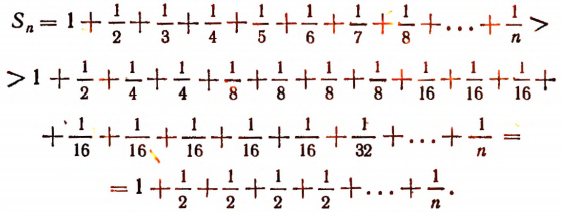
Если n взять достаточно большим, то число слагаемых, равных 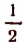 , может стать сколь угодно большим. Поэтому при неограниченном возрастании числа n величина
, может стать сколь угодно большим. Поэтому при неограниченном возрастании числа n величина 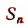 также будет неограниченно возрастать, т. е.
также будет неограниченно возрастать, т. е. 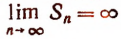 . Значит, данный ряд является расходящимся.
. Значит, данный ряд является расходящимся.
Парадокс. Рассмотрим ряд 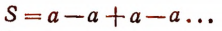 Сгруппировав члены по два, получим, что
Сгруппировав члены по два, получим, что
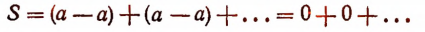
Оказалось, что S=0.
Теперь, оставляя первый член в отдельности, сгруппируем по 2 остальные. Тогда получим:
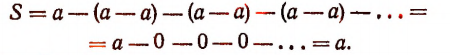
Оказалось, что S=а.
Перепишем наш ряд еще так:
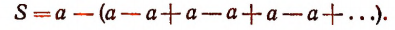
Тогда окажется, что S = a — S. Тогда 2S = a, или
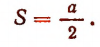
Итак, оказалось, что одна и таже сумма S имеет различные значения .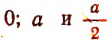 .
.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
