Оглавление:
Мы рассмотрели задачи на доказательство и решение неравенств, содержащих одно неизвестное. В случае многих неизвестных задачи становятся значительно сложнее. Не которые из них будут рассмотрены здесь. Неравенства, которые будут установлены тут, играют важную роль в самых различных вопросах математики. В частности, мы покажем ниже, как с помощью этих неравенств решать задачи на отыскание наибольших и наименьших значений.
Среднее арифметическое и среднее геометрическое двух чисел
Возьмем два числа 2 и 8. Среднее арифметическое этих чисел равно 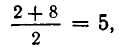 а среднее геометрическое
а среднее геометрическое 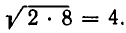 Мы видим, что для этих чисел среднее геометрическое меньше среднего арифметического. То же самое получится, если взять числа 1 и 9: их среднее арифметическое равно 4, 5, а среднее геометрическое равно 3. Для чисел 1 и 2 среднее арифметическое равно 1,5, а среднее геометрическое равно
Мы видим, что для этих чисел среднее геометрическое меньше среднего арифметического. То же самое получится, если взять числа 1 и 9: их среднее арифметическое равно 4, 5, а среднее геометрическое равно 3. Для чисел 1 и 2 среднее арифметическое равно 1,5, а среднее геометрическое равно 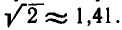 Во всех разобранных примерах подмеченная нами закономерность имеет место. Это дает основание предположить, что вообще для любых двух неотрицательных чисел х и у их среднее геометрическое ху не больше среднего арифметического
Во всех разобранных примерах подмеченная нами закономерность имеет место. Это дает основание предположить, что вообще для любых двух неотрицательных чисел х и у их среднее геометрическое ху не больше среднего арифметического 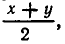 то есть что
то есть что

Мы докажем сейчас это утверждение. Так как числа х и у по условию неотрицательны, то мы можем положить 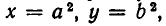 где
где 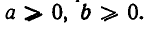 Тогда неравенство (1) примет вид:
Тогда неравенство (1) примет вид:
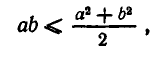
или, что то же самое,  Но это неравенство очевидно, поскольку равносильно заведомо верному неравенству
Но это неравенство очевидно, поскольку равносильно заведомо верному неравенству 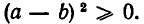
Итак, неравенство (1) доказано. Отметим, что оно верно лишь при условии 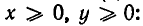 если числа х и у имеют различные знаки, то левая часть неравенства не имеет смысла; если же х и у отрицательны, то
если числа х и у имеют различные знаки, то левая часть неравенства не имеет смысла; если же х и у отрицательны, то 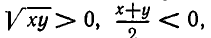 а потому неравенство (1) не имеет места.
а потому неравенство (1) не имеет места.
Отметим еще, что 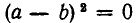 тогда и только тогда, когда а=b. Отсюда сразу следует, что
тогда и только тогда, когда а=b. Отсюда сразу следует, что 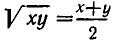 тогда и только тогда, когда х = у.
тогда и только тогда, когда х = у.
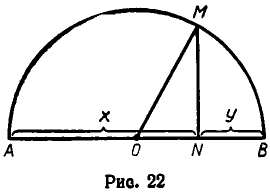
Мы доказали неравенство (1) чисто алгебраически. Но его можно доказать и геометрически. Д ля этого отложим отрезки х и у и примем сумму этих отрезков за диаметр полуокружности (см. рис. 22). Тогда среднее геометрическое отрезков х и у равно отрезку МN, а их среднее арифметическое — радиусу окружности. Ясно, что МN не превосходит ОМ, причем МN = ОМ тогда и только тогда, когда х = у.
Среднее арифметическое и среднее геометрическое трех чисел
Попробуем теперь обобщить выведенное в п. 1 неравенство. Для положительных чисел  их средним арифметическим называют
их средним арифметическим называют
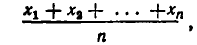
а средним геометрическим —
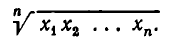
В п. 1 мы доказали, что при n = 2 выполняется неравенство
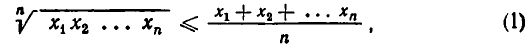
причем знак равенства имеет место тогда и только тогда, когда
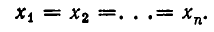
Это неравенство верно для всех натуральных значений л. Мы ограничимся доказательством этого неравенства при n = 3.
В математике часто, прежде чем доказывать гипотезу в общем виде, пытаются доказать какой-нибудь частный случай сделанного предположения. Если оказывается, что частный случай неверен, то тем более неверна и гипотеза в общем виде; если же удается доказать гипотезу в частном случае, то возрастают шансы на то, что и в общем случае предположение верно.
Итак, попытаемся доказать, что при 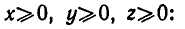
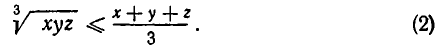
Так как по условию 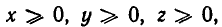 то мы можем положить
то мы можем положить 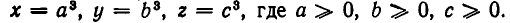 Неравенство (2) принимает вид:
Неравенство (2) принимает вид:
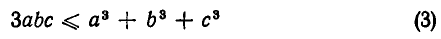
или
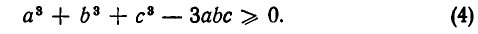
Чтобы доказать неравенство (3), используем разложение на множители
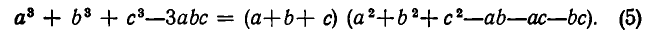
(Формулу (5) можно проверить непосредственно, перемножив многочлены в правой части равенства.)
Так как по условию 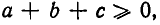 то все свелось к доказательству неравенства
то все свелось к доказательству неравенства
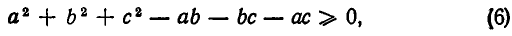
а оно справедливо, так как
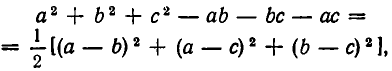
тем самым соотношение (4), а с ним и (2) доказано. Это, как мы говорили, повышает шансы на то, что неравенство (1) справедливо при всех n.
Заметим, что 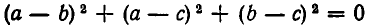 тогда и только тогда, когда а = b = с. Поэтому в соотношении (2) знак равенства имеет место лишь при х = у = z.
тогда и только тогда, когда а = b = с. Поэтому в соотношении (2) знак равенства имеет место лишь при х = у = z.
Неравенство Коши (двумерный вариант)
Выведем теперь новое неравенство. Для этого рассмотрим произведение 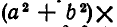
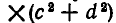 и раскроем в нем скобки. Мы получим многочлен
и раскроем в нем скобки. Мы получим многочлен 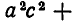
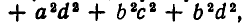 который совпадает с многочленом, получающимся после раскрытия скобок в выражении
который совпадает с многочленом, получающимся после раскрытия скобок в выражении
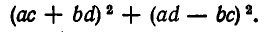
Таким образом, справедливо тождество
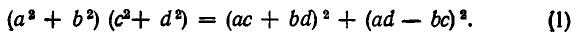
Так как 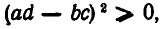 то из этого тождества следует неравенство
то из этого тождества следует неравенство
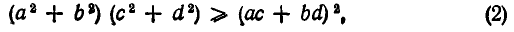
справедливое для любых действительных чисел а, b, с, d Это неравенство, а особенно его обобщения, имеет большое значение для многих вопросов математического анализа. Оно называется неравенством Коши или, точнее, двумерным случаем неравенства Коши.
Из соотношения (1) вытекает, что знак равенства имеет место в (2) тогда и только тогда, когда ad = bс. Мы будем называть в этом случае числа а, b, с, d пропорциональными. Это связано с тем, что если 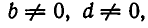 то соотношение аd = bс можно записать так:
то соотношение аd = bс можно записать так:
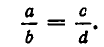
Приведенный выше вывод неравенства (2) кажется на первый взгляд очень вычурным и искусственным. В отличие от неравенства 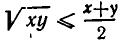 основанного на простом и очевидном тождестве
основанного на простом и очевидном тождестве 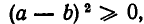 неравенство (2) основано на далеко не очевидном с первого взгляда тождестве (1). Естественно поэтому желание найти другой подход к этому неравенству, при котором оно стало бы очевидным. Американские математики Э. Беккенбах и Р. Беллман пишут по этому поводу следующее (см. их книгу «Введение в неравенства». 1965): «Нерушимым принципом математики является то, что в ней нет случайных фактов и положений. Каждый результат, какое бы место он не занимал, находит свое истолкование, благодаря которому этот результат становится прозрачным, само собой разумеющимся. Это истолкование может не сразу броситься в глаза, и оно может быть найдено не сразу. Часто подлинный смысл математической теоремы проясняется только тогда, когда мы посмотрим на нее, так сказать, «сверху», то есть с точки зрения более общей теории. Однако истолкование, поясняющее смысл теоремы, имеется всегда — и это исключительно важно. Если бы дело обстояло не так, то математика выродилась бы в набор несвязных формальных трюков и схоластических выкрутасов».
неравенство (2) основано на далеко не очевидном с первого взгляда тождестве (1). Естественно поэтому желание найти другой подход к этому неравенству, при котором оно стало бы очевидным. Американские математики Э. Беккенбах и Р. Беллман пишут по этому поводу следующее (см. их книгу «Введение в неравенства». 1965): «Нерушимым принципом математики является то, что в ней нет случайных фактов и положений. Каждый результат, какое бы место он не занимал, находит свое истолкование, благодаря которому этот результат становится прозрачным, само собой разумеющимся. Это истолкование может не сразу броситься в глаза, и оно может быть найдено не сразу. Часто подлинный смысл математической теоремы проясняется только тогда, когда мы посмотрим на нее, так сказать, «сверху», то есть с точки зрения более общей теории. Однако истолкование, поясняющее смысл теоремы, имеется всегда — и это исключительно важно. Если бы дело обстояло не так, то математика выродилась бы в набор несвязных формальных трюков и схоластических выкрутасов».
Часто наиболее простое истолкование алгебраического результата имеет геометрический характер. Формулы, которые кажутся совершенно непонятными и сложными, становятся очевидными, когда раскрывается их геометрическое содержание.
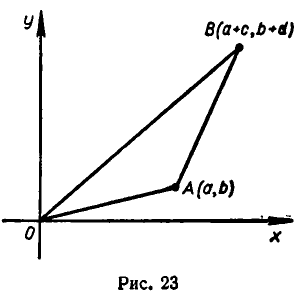
Не составляет исключение и неравенство (2). Пусть числа а, b, с, d неотрицательны. Возьмем треугольник, изображенный на рис. 23. С помощью теоремы Пифагора легко подсчитать, что длины отрезков ОА, АВ и ОВ определяются равенствами
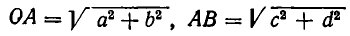
и
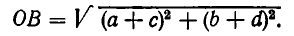
Но длина стороны ОВ не превосходит суммы длин двух других сторон. Поэтому имеем 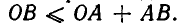 Подставляя в это неравенство выражения для длин отрезков ОВ, ОА и АВ, получаем, что
Подставляя в это неравенство выражения для длин отрезков ОВ, ОА и АВ, получаем, что
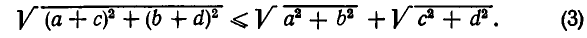
Возведем обе части этого неравенства в квадрат. Так как обе части неравенства (3) положительны, то после этого получим равносильное неравенство:
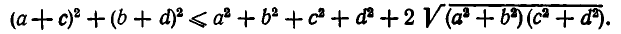
Раскроем скобки в левой части и приведем подобные члены. Мы получаем:
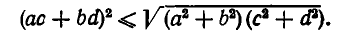
Еще раз возведя обе части неравенства в квадрат, приходим к не равенству Коши:
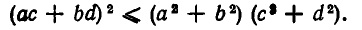
Тем самым неравенство Коши доказано при неотрицательных значениях а, b, с, d.
Чтобы доказать его для любых значений а, b, с, d, достаточно заметить, что 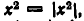 и потому
и потому
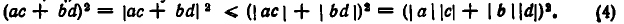
Но по доказанному
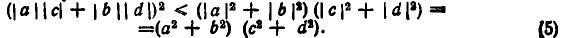
Из неравенств (4) и (5) вытекает:
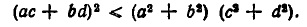
Итак, мы доказали, что неравенство Коши вытекает из элементарной теоремы геометрии: длина стороны треугольника не больше суммы длин двух других сторон. Нетрудно показать, что эти два утверждения эквивалентны друг другу — из неравенства Коши следует неравенство (3).
Неравенство (2) является частным случаем более общего не равенства
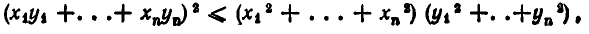
которое справедливо для любых действительных чисел 
 Это неравенство вытекает из тождества
Это неравенство вытекает из тождества
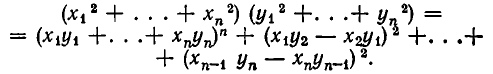
Задачи на наибольшие и наименьшие значения
Великий русский математик П. Л. Чебышев писал в одной из своих работ, что особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать средствами своими для достижения по возможности большей выгоды. Так, рабочий-металлист старается из куска металла получить как можно больше деталей; раскройщик на обувной фабрике старается из куска кожи выкроить как можно больше заготовок; строитель хочет сделать из бревна балку наибольшей прочности и т. д.
Во многих случаях задачи такого характера допускают математическую формулировку. Их называют задачами на наибольшие и наименьшие значения. Общий метод решения таких задач дает математический анализ. Однако много таких задач решается с помощью неравенств.
Рассмотрим следующую задачу.
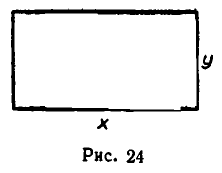
Имеется 200 м проволоки. Огородить ею прямоугольный участок земли наибольшей площади.
Обозначим стороны прямоугольника через х и у (см. рис. 24). Из условия задачи следует, что 2х + 2у =200, а потому х+у = 100. Площадь прямоугольника s =ху. Но из неравенства между средним геометрическим и средним арифметическим следует, что
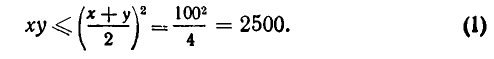
Значит, огородить участок, площадь которого была бы больше 2500 м 2, невозможно. В то же время мы знаем, что квадратный участок земли с периметром 200 м имеет площадь 2500 м 2. Задача решена: чтобы получить прямоугольный участок наибольшей площади, имеющий периметр 200 м, надо взять квадрат со стороной 50м.
Эту же задачу можно решить иначе. Из условия следует, что у = 100 — х, а потому s =x(100—х). Ясно, что сторона меняется в пределах 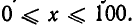 Таким образом, нам надо найти наибольшее значение функции s = х(100 — х) на отрезке
Таким образом, нам надо найти наибольшее значение функции s = х(100 — х) на отрезке 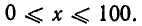 Для этого преобразуем выражение следующим образом:
Для этого преобразуем выражение следующим образом:
Ясно, что 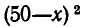 неотрицательно при всех значениях х и равно нулю лишь при х = 50. Но если уменьшаемое постоянно, то разность имеет наибольшее значение, когда вычитаемое принимает наименьшее значение. Этим наименьшим значением вычитаемого является в данном случае нуль. Поэтому мы снова приходим к выводу, что площадь максимальна, если х = 50.
неотрицательно при всех значениях х и равно нулю лишь при х = 50. Но если уменьшаемое постоянно, то разность имеет наибольшее значение, когда вычитаемое принимает наименьшее значение. Этим наименьшим значением вычитаемого является в данном случае нуль. Поэтому мы снова приходим к выводу, что площадь максимальна, если х = 50.
Рассмотрим теперь задачу, «двойственную» рассмотренной.
Требуется огородить проволокой прямоугольный участок земли площадью 2500 м. Какую форму он должен иметь, чтобы количество проволоки, пошедшей на ограду, было наименьшим?
Здесь нам задана площадь s = ху= 2500. Снова применяя неравенство между средними, получаем, что

Так как х+у>0, то из (2) получаем: 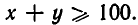 Так как на ограду надо 2х +2у проволоки, количество необходимой проволоки не может быть меньше, чем 200 м. А именно 200 м надо на ограду квадратного участка земли.
Так как на ограду надо 2х +2у проволоки, количество необходимой проволоки не может быть меньше, чем 200 м. А именно 200 м надо на ограду квадратного участка земли.
В обеих задачах мы получили одно и то же решение — участок земли должен быть квадратным. Это не случайно. Многие задачи на наибольшие и наименьшие значения распадаются на «пары» двойственных задач. В одной из них надо найти наибольшее значение некоторой величины (в нашем случае — площади) при условии, что другая величина сохраняет постоянное значение (в нашем случае — периметр). А в двойственной задаче надо найти наименьшее значение второй величины при условии, что первая сохраняет постоянное значение. Эти две задачи имеют общее решение.
Метод, применяемый нами к решению рассмотренных задач, приводит к следующему общему результату.
Из всех прямоугольников с данным периметром наибольшую площадь имеет квадрат.
На самом деле условие, что четырехугольник является прямоугольником, здесь излишне — из всех четырехугольников с данным периметром квадрат имеет наибольшую площадь.
Мы не будем сейчас доказывать это утверждение для четырехугольников, а докажем аналогичную теорему для треугольников: из всех треугольников, имеющих данный периметр 2р, наибольшая площадь у правильного треугольника.
Для доказательства воспользуемся формулой Герона, выражающей площадь треугольника S через стороны х, у , z:
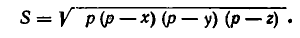
Ясно, что площадь принимает наибольшее значение одновременно с выражением (р — х) (р — у) (р — z).
Применим к числам р — х, р — р, р — z неравенство между средними. Так как х + у + z = 2р, то
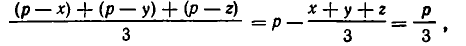
и мы получаем, что
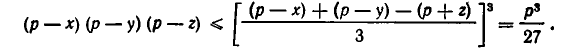
Это неравенство показывает, что площадь S треугольника с периметром 2р не превосходит 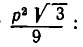
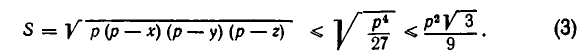
При этом знак равенства в соотношении (3) достигается, если р — х = р — y= p — z, то есть если треугольник равносторонний.
Можно доказать, что вообще из всех л-угольников с данным периметром наибольшую площадь имеет правильный многоугольник. А из всех фигур с данным периметром наибольшую площадь имеет круг. Но доказательство этого утверждения требует привлечения неэлементарных методов.
В некоторых случаях приходится прибегать к преобразованию изучаемого выражения — с таким примером мы столкнулись выше, когда заменили 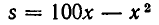 на
на 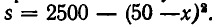 Чаще всего применяют следующие преобразования:
Чаще всего применяют следующие преобразования:
а) отбрасывание постоянных слагаемых (ясно, что они не влияют на наибольшие и наименьшие значения функции);
б) отбрасывание постоянных сомножителей (при этом если сомножитель отрицателен, то при его отбрасывании наибольшие значения становятся наименьшими и наоборот);
в) замена изучаемого выражения его квадратом. Если выражение неотрицательно, то оно принимает наибольшие и наименьшие значения одновременно со своим квадратом;
г) замена выражения А на 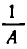 (при этом наибольшие значения переходят в наименьшие и обратно).
(при этом наибольшие значения переходят в наименьшие и обратно).
Приведем примеры, когда такие преобразования упрощают решение задачи.
Инженерные расчеты показывают, что прочность балки с прямо угольным сечением пропорциональна ширине балки а и квадрату ее высоты h. Иными словами, прочность такой балки (измеренная в некоторых единицах) равна 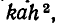 где k — коэффициент, зависящий от длины балки, материала, из которого она сделана, и т. д.
где k — коэффициент, зависящий от длины балки, материала, из которого она сделана, и т. д.
Деревянные балки обычно вытесывают из круглых бревен.
Задача:
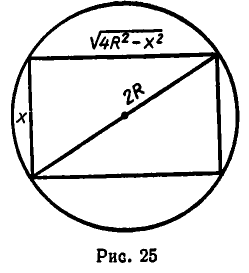
Как сделать из бревна, имеющего радиус К, балку наибольшей прочности?
Решение:
Обозначим высоту вырезанной балки через х. Тогда из рис. 25 ясно, что ее ширина равна 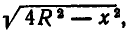 а, значит, прочность балки выражается формулой:
а, значит, прочность балки выражается формулой:

Здесь непосредственно неравенство между средними неприменимо. Однако если разделить выражение (4) на k и возвести результат в квадрат, то получим:
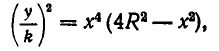
или
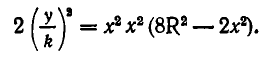
А теперь мы представили 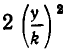 в виде произведения трех множителей, сумма которых постоянна:
в виде произведения трех множителей, сумма которых постоянна:
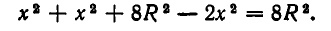
Следовательно, в силу неравенства между средними имеем:
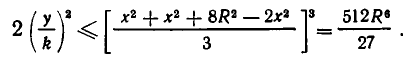
Знак равенства достигается здесь, если все три сомножителя равны друг другу. А это будет, если 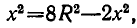 то есть если
то есть если 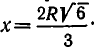
При 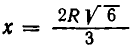 ширина балки равна:
ширина балки равна:
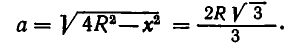
Отношение 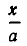 равно
равно 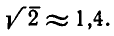 Именно такое отношение высоты балки к ее ширине и предписывается правилами производства строительных работ.
Именно такое отношение высоты балки к ее ширине и предписывается правилами производства строительных работ.
Решение неравенств
Перейдем теперь к решению неравенств. Пусть дано неравенство
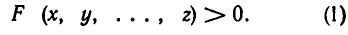
Решением этого неравенства называется любой набор чисел а, b, . . . , с такой, что F (а, b, … , с) > 0. Обычно ставится вопрос об отыскании всех решений данного неравенства, то есть о нахождении множества всех значений х= а, у = b….. z = с, при которых неравенство выполняется. Это множество называют множеством решений неравенства.
Если неравенство содержит два неизвестных, то есть имеет вид F (х, у) > 0, то множеством его решений является некоторое множество числовых пар (а, b). Каждая такая пара изображается точкой плоскости. Поэтому множество решений неравенства с двумя неизвестными геометрически изображается множеством точек плоскости.
Мы будем рассматривать также системы и совокупности неравенств. Пусть задано несколько неравенств (мы пишем неравенства с двумя неизвестными, но, вообще говоря, их число может быть любым):

Говорят, что они образуют систему неравенств, если требуется найти значения х = а, у = b, при которых выполняются все неравенства (2), то есть такие а и b, что 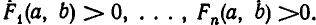
Пусть 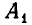 — множество решений неравенства
— множество решений неравенства 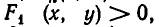
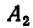 — множество решений неравенства
— множество решений неравенства 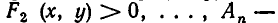 множество решений неравенства
множество решений неравенства 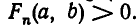 Очевидно, что множеством решений системы (2) является множество В — пересечение указанных множеств:
Очевидно, что множеством решений системы (2) является множество В — пересечение указанных множеств:
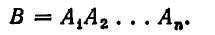
Наряду с системами неравенств мы будем рассматривать их совокупности. Говорят, что неравенства

образуют совокупность, если требуется найти значения, удовлетворяющие хотя бы одно из этих неравенств.
Ясно, что множество С всех решений совокупности (3) является суммой множеств решений каждого неравенства:
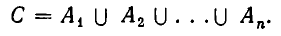
Неравенства с двумя переменными
Рассмотрим теперь неравенства с двумя переменными. Все такие неравенства равносильны неравенствам вида
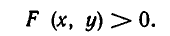
Например, неравенство
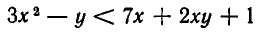
равносильно неравенству

Чаще всего встречается случай, когда уравнение F(х, у) =0 задает линию, разбивающую плоскость на две или несколько частей. В одних из этих частей выполняется неравенство F(х, у) < 0, а в других — неравенство F (х, у) > 0. Иными словами, линия F(х, у)= 0 отделяет часть плоскости, где F (х, у) > 0 , от части плоскости, где
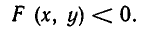
Рассмотрим, например, неравенство
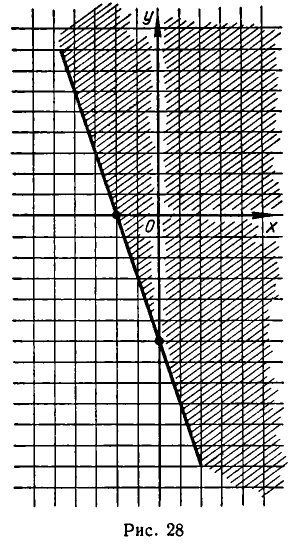
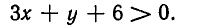
Уравнение Зх + у +6 =0 задает прямую линию (см. рис. 28). Эта прямая разбивает всю плоскость на
две полуплоскости. Ясно, что при уменьшении у величина Зх+y+6 уменьшается. Поэтому ниже прямой Зх +у+6=0 располагаются точки, в которых Зх+y +6 <0, а выше этой прямой — точки, где Зх + у+6 < 0 .
Совершенно так же решается общее линейное неравенство

Прямая Ах + Ву+С=0 разбивает плоскость на две полуплоскости. Если В > 0, то при увеличении у величина Ах+Ву+С увеличивается, а при уменьшении у — уменьшается. Поэтому при В > 0 выше прямой Ах+Ву+С<0 лежат точки, где Ах + Ву +С > 0, а ниже этой прямой — точки, где Ах+Ву+ С< 0. В случае В < 0 роли полуплоскостей меняются.
На практике для выяснения того, в какой полуплоскости мы имеем Ах + Ву+С < 0, а в какой Ах+Ву+С > 0, применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой Ах+Ву+С =0) и проверяют, какой знак имеет в этой точке выражение Ах+Ву+ С. Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости Ах + Ву + С имеет противоположный знак.
Точно так же решаются и нелинейные неравенства с двумя не известными. Например, решим неравенство:
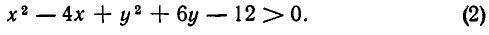
Уравнение
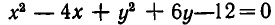
можно записать в виде
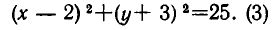
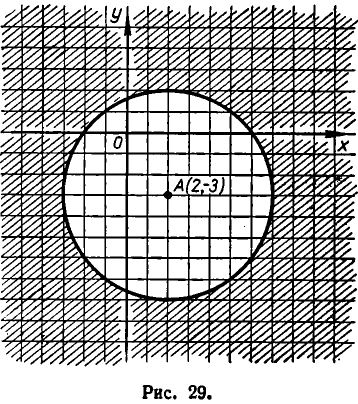
Это уравнение окружности с центром в точке А (2, —3) и радиусом 5 (рис. 29). Окружность (3) разбивает плоскость на две части — внутреннюю и внешнюю области. Чтобы узнать, в какой из них имеет место неравенство (2), возьмем контрольную точку во внутренней области. В качестве такой точки удобно взять центр А (2, —3) нашей окружности. Подставляя координаты точки А (2, —3) в левую часть неравенства (2), получаем отрицательное число—25. Значит, и во всех точках, лежащих внутри окружности, выполняется неравенство
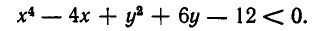
Отсюда вытекает, что неравенство (2) имеет место во внешней для окружности области (3).
Задание областей неравенствами и системами неравенств
Разобранные примеры показывают, что области на плоскости можно задавать неравенствами. Иногда вместо одного неравенства приходится брать системы или совокупности неравенств.
Рассмотрим некоторые примеры.
Пусть задана система неравенств:

Мы уже знаем, что неравенство х+у+1>0 задает полуплоскость, лежащую над прямой х +у+1 =0. Неравенство же
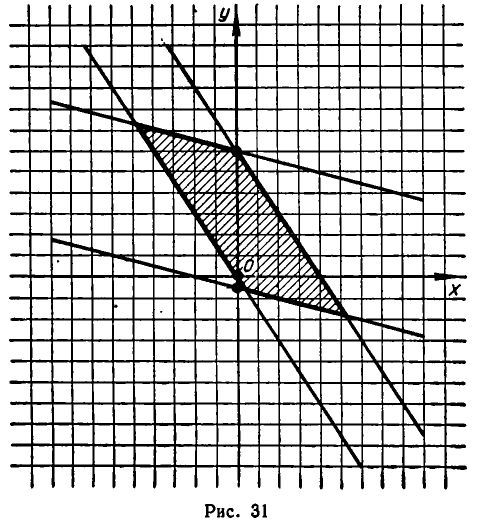
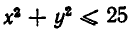 задает область, ограниченную окружностью
задает область, ограниченную окружностью 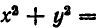
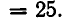 Множеством решений системы неравенств (1) является пересечение этих двух областей, изображенное на рис. 30, то есть круговой сегмент.
Множеством решений системы неравенств (1) является пересечение этих двух областей, изображенное на рис. 30, то есть круговой сегмент.
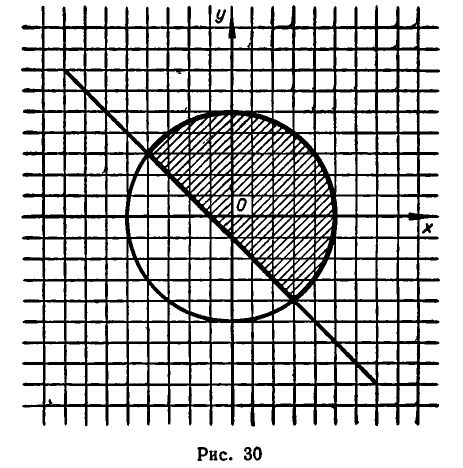
Далее, рассмотрим систему неравенств:
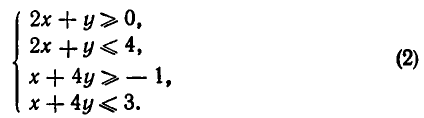
Множеством решений этой системы является параллелограмм, изображенный на рис. 31.
Во многих случаях удобнее всего задавать области системой неравенств вида:
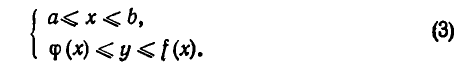
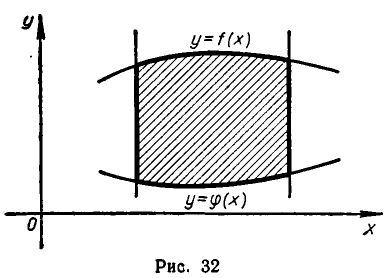
Эта система указывает границы изменения х, а для каждого х, лежащего между а и b, — границы изменения у (см. рис. 32). Иногда приходится предварительно разбивать область на части и каждую часть задавать системой вида (3) или, что то же самое, задавать область совокупностью систем (3).
Пример:
Пусть область D задана системой неравенств:
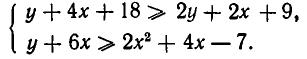
Эту систему неравенств можно переписать в виде:
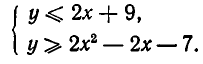
Множеством ее решений является область, изображенная на рис. 33 и ограниченная прямой у =2х+9 и параболой 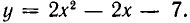 Найдем точки пересечения прямой и параболы. Для этого надо решить систему уравнений:
Найдем точки пересечения прямой и параболы. Для этого надо решить систему уравнений:
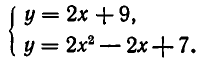
Система приводит к уравнению 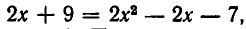 корнями которого являются
корнями которого являются 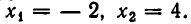 Поэтому точки пересечения прямой и параболы имеют координаты:
Поэтому точки пересечения прямой и параболы имеют координаты:
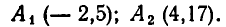
Отсюда следует, что рассматриваемая область задается неравенствами:
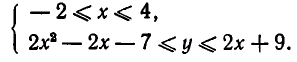
Задача:
Расстояние между двумя небесными телами A и В равно а, а масса первого 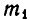 больше массы второго
больше массы второго 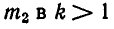 раз.
раз.
Найти область, в которой сила притяжения ко второму телу больше, чем к первому.
Решение:
Проведем плоскость через прямую АВ и выберем на этой плоскости систему координат следующим образом. В качестве начала координат выберем точку А, а ось абсцисс проведем через точку В. Координаты точки В имеют вид В (а, 0). Выберем любую точку плоскости М (.х, у). Расстояние этой точки до А равно
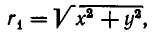
а до В равно
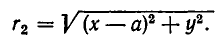
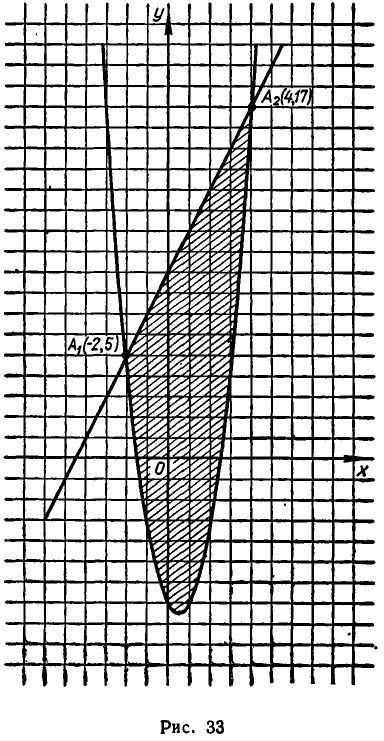
По закону всемирного тяготения сила притяжения между телами с массами 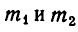 равна
равна 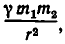 где
где 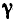 —гравитационная постонная, а r — расстояние между этими телами. По этому если в точке N находится тело с массой m , то оно притягивается к первому небесному телу с силой
—гравитационная постонная, а r — расстояние между этими телами. По этому если в точке N находится тело с массой m , то оно притягивается к первому небесному телу с силой
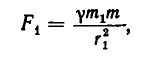
а ко второму — с силой
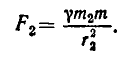
По условию задачи нам надо найти точки, в которых выполняется неравенство  то есть
то есть
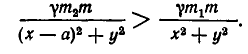
Учитывая, что по условию 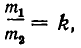 получаем равносильное неравенство
получаем равносильное неравенство
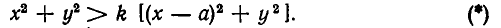
Раскрывая скобки и преобразуя полученное выражение, получаем:
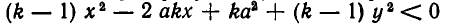
или
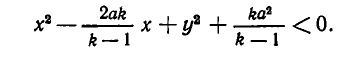
Выделяя полный квадрат, перепишем это неравенство в виде
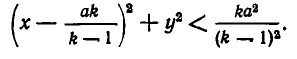
Уравнение
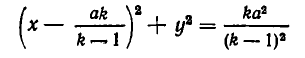
является уравнением окружности с центром в точке 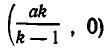 и радиусом
и радиусом 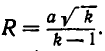 Внутри этой окружности притяжение ко второму телу больше, чем к первому. Чтобы получить область в пространстве, внутри которой притяжение ко второму телу больше, чем к первому, надо повернуть эту окружность вокруг прямой АВ. Мы получим сферу, ограничивающую область с искомым свойством.
Внутри этой окружности притяжение ко второму телу больше, чем к первому. Чтобы получить область в пространстве, внутри которой притяжение ко второму телу больше, чем к первому, надо повернуть эту окружность вокруг прямой АВ. Мы получим сферу, ограничивающую область с искомым свойством.
В решенном примере мы получили неравенство (*), определяющее искомую область на плоскости.
Понятие о линейном программировании
Решение систем не равенств находит многочисленные практические приложения. Наиболее важные из них связаны с задачами экономики и планирования. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств. Поэтому приходится искать наибольшее или наименьшее значение, принимаемое некоторой функцией в области, за данной системой неравенств.
Приведем пример такой задачи:
Имеются два пункта производства А и В некоторого вида продукции и три пункта I, И, III его потребления. В пункте А производится 250 единиц продукции, а в пункте В — 350 единиц. В пункте I требуется 150 единиц, в пункте II — 240 единиц и в пункте III — 210 единиц. Стоимость перевозки одной единицы продукции из пункта производства в пункт потребления дается следующей таблицей.
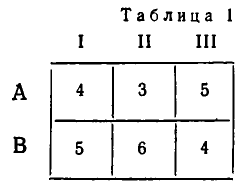
Требуется оставить план перевозки продукции, при котором сумма расходов на перевозку будет наименьшей.
Обозначим количество продукции, перевозимой из пункта А в пункт I, через х, а из пункта А в пункт II— через у. Так как полная потребность в пункте I равна 150 единиц, то из пункта В надо еще завезти (150 — х) единиц. Точно так же из пункта В в пункт II надо завезти (240 — у) единиц. Далее, производительность пункта А равна 250 единиц, а мы уже распределили (х + у) единиц. Значит, в пункт III идет из пункта А (250 — х — у) единиц. Чтобы полностью обеспечить потребность пункта III, осталось завезти 210 — (250 — х — у) = х + у — 40 единиц из пункта В.
Итак, план перевозок задается следующей таблицей.
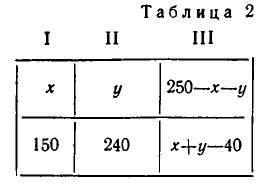
Чтобы найти полную стоимость перевозки, надо умножить каждое число этой единицы на соответствующее число таблицы 1 (там указана стоимость перевозки одной единицы продукции) и сложить полученные произведения. Мы получим выражение:
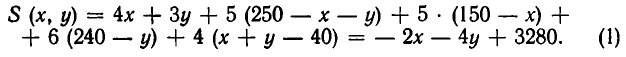
По условию задачи требуется найти минимум этого выражения. Но величины х и у не могут принимать произвольных значений.
Ведь количество перевозимой продукции не может быть отрицательным числом. Поэтому все числа таблицы II неотрицательны:
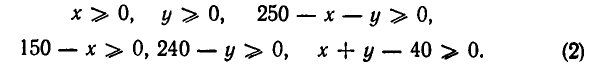
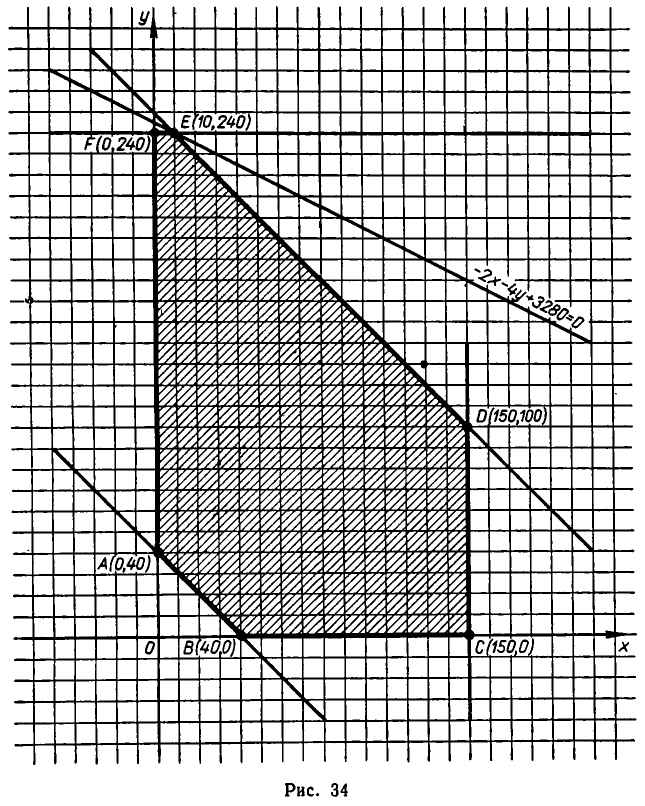
Итак, нам надо найти минимум функции 5 (л;, у) в области, задаваемой системой неравенств (2). Эта область изображена на рис. 34— она является многоугольником, ограниченным прямыми
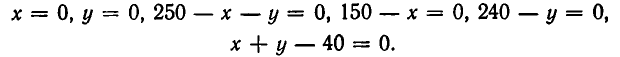
Решая совместно уравнение этих прямых, находим координаты вершин многоугольника:
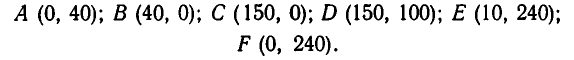
Функция S (х, у) принимает наименьшее значение в одной из вершин многоугольника АВСDЕF.
В самом деле, выясним, где располагаются точки, в которых значения этой функции одинаковы (так называемые линии уровня функции S (x, у) = —2 х — 4у+3280). Если значение функции S (x, у) равно с, то — 2х — 4у+3280=с. Но это уравнение прямой линии. Значит, для функции линиями уровня являются прямые линии —2х — 4у +3280= с. Все эти прямые параллельны друг другу.
Если линия уровня пересекает многоугольник, то соответствующее значение с не является ни наименьшим, ни наибольшим. Ведь немного изменив с, мы получим прямую, которая также пересекает многоугольник. Если же линия уровня проходит через одну из вершин многоугольника, причем весь многоугольник остается на одну сторону от этой линии, то соответствующее значение с является наименьшим или наибольшим. Когда с меняется в одну сторону, то получается линия, пересекающая многоугольник, а когда меняется в противоположную сторону, получается линия, не имеющая с многоугольником общих точек.
Итак, функция S(х, у)= — 2х — 4у+3280 принимает наименьшее значение на многоугольнике в одной из его вершин. Поскольку мы уже знаем эти вершины, то подставим соответствующие значения координат и найдем, что
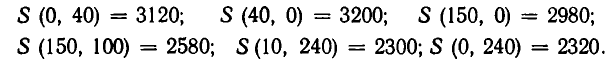
Наименьшим из этих значений является 2300. Это значение функция принимает в точке Е (10, 240). Значит, х = 10, у = 240. Подставляя эти значения в план перевозок (см. таблицу II), получаем:

Таким образом, из пункта А в пункт I надо перевезти 10 единиц продукции, из пункта А в пункт II — 240 единиц и т. д. Стоимость намеченного плана равна 2300.
Рассмотренная задача относится к большому классу задач, возникающих не только в экономике, но и в других областях человеческой деятельности. В этих задачах требуется найти наибольшее или наименьшее значение некоторой линейной функции от переменных 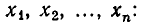
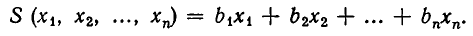
При этом область изменения переменных задается системой линейных неравенств
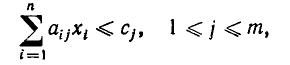
и линейных уравнений
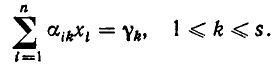
Задачи такого типа называются задачами линейного программирования.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
