Оглавление:
Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Понятие о системе двух уравнений первой степени с двумя неизвестными
Задача:
В 7а и 1б классах школы 75 учеников. Сколько
учеников в каждом классе, если в 7а на 5 учеников больше, чем в 1б?
Решение:
Обозначим буквой х число учеников в 7б классе. Тогда в 7а классе (х + 5) учеников. В 7а и 7б классах вместе [х +(х + 5) ] учеников. По условию, в 7а и 7б классах 75 учеников. Значит,
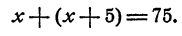
Уравнение составлено. Решая его, имеем
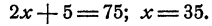
Выходит, что в 7б классе 35 учеников, а в 7а классе 40
учеников.
Ответ. 35 и 40 учеников.
В приведенной задаче требовалось найти две величины: число учеников в 7а классе и число учеников в 7б классе. Для решения задачи мы ввели только одну букву х, через нее выразили обе неизвестные величины и составили уравнение.
Так мы поступали и раньше. Так и надо стараться поступать всегда. Встречаются, однако, такие задачи, где трудно бывает составить уравнение, если ввести только одну букву для обозначения неизвестной величины, и гораздо легче это сделать при помощи введения двух букв для обозначения двух неизвестных величин.
Вот, например, задача.
Задача:
За 2 м сукна и 3 м ткани заплачено 165 руб. В
другой раз за 5 м того же сукна и 2 м той же ткани заплачено 330 руб. Сколько стоит 1 м сукна и сколько стоит 1 м ткани?
Решение:
Решим эту задачу посредством введения только одной буквы для обозначения неизвестной величины. Обозначим буквой х стоимость 1 м сукна (в рублях), Тогда 2 м сукна стоят 2х руб., 3 м ткани стоят (165 — 2х) руб., 1 м ткани стоит 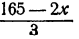 руб.
руб.
Мы использовали первую часть условия задачи. Используем теперь вторую часть условия. 5 м сукна стоят 5х руб., 2 м ткани стоят 330 — 5х руб., 1 м ткани стоит 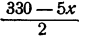 руб.
руб.
Мы получили два различных выражения для стоимости 1 м ткани. Приравняв их, имеем

Уравнение составлено. Решая его, имеем
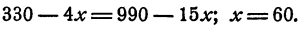
Значит, метр сукна стоит 60 руб. Для определения стоимости метра ткани подставим 60 вместо х в выражение 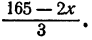 Получим
Получим
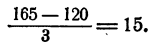
Значит, метр ткани стоит 15 руб.
Проверка. 2 м сукна стоят 120 руб., 3 м ткани стоят 45 руб. За 2 м сукна и 3 м ткани надо заплатить 165 руб. Далее, 5 м сукна стоят 300 руб., 2 м ткани стоят 30 руб. За 5 м сукна и 2 м ткани надо заплатить 330 py6. Проверка показала, что задача решена правильно.
Ответ. 60 руб. и 15 руб.
Посмотрим теперь, как решается последняя задача, если ввести две буквы для обозначения неизвестных.
Обозначим буквой х стоимость 1 м сукна (в рублях), а буквой у стоимость 1 м ткани (в рублях). Тогда

Мы составили два уравнения. Уравнение (а) составлено по первой части условия задачи, уравнение (б) составлено по второй части условия.
Для того чтобы решить задачу, надо найти такие значения х и у, которые удовлетворяли бы одновременно и уравнению (а) и уравнению (б).
В таких случаях говорят, что уравнения (а) и (б) надо решить совместно, или говорят, что надо решить систему уравнений (а) и (б). Для того чтобы показать, что уравнения надо решать совместно, ставят скобку }, т. е. систему уравнений записывают- так;

Такая система называется системой двух уравнений первой степени с двумя неизвестными. Что же оказалось легче составить: одно уравнение с одним неизвестным или систему двух уравнений с двумя неизвестными? Бесспорно, систему (2) легче составить, чем уравнение (1).
Мы пока нe умеем решать системы. Однако мы можем проверить решение, которое мы нашли другим приемом.
Сделаем это, чтобы знать, как проверяется решение системы уравнений. Подставим в систему (2) число 60 вместо x; и 15 вместо у, получим два тождества:
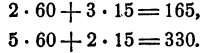
Эти тождества и показывают, что x = 60, y = 15— решение системы (2) или, как говорят, значения x = 60, у =15 удовлетворяют системе (2).
Определения:
Два или несколько уравнений образуют
систему уравнений, если одноименные неизвестные в них обозначают одну и ту же величину. Решить систему уравнений—это значит найти такие значения неизвестных, при которых каждое из уравнений системы превращается в тождество. Решением системы двух уравнений с двумя неизвестными называется пара таких чисел; которые, будучи подставлены в систему вместо неизвестных, превращает каждое из уравнений системы в тождество.
Одно уравнение первой степени с двумя неизвестными
Для того чтобы научиться решать системы двух уравнений первой степени с двумя неизвестными, ознакомимся сначала с основными свойствами одного уравнения первой степени с двумя неизвестными. Рассмотрим такую задачу:
Задача:
За 2 м сукна и 3 м ткани заплатили 165 руб.
Сколько стоит 1 м сукна и 1 м ткани?
(При составлении этой, задачи мы взяли известную нам задачу и исключили из ее условия вторую часть.)
Решение:
Обозначим, как и раньше, буквой х стоимость 1 м сукна (в рублях), буквой у — стоимость 1 м ткани (в рублях). Тогда

Мы получили одно уравнение первой степени с двумя
неизвестными. Уравнение это имеет бесконечное множество решений. Их можно находить так. Дадим х какое-нибудь значение, например 10. Тогда уравнение (1) примет вид
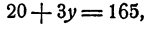
откуда 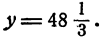 Мы получили решение x=10;
Мы получили решение x=10;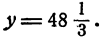 Теперь дадим х какое-нибудь другое значение, например 20. Тогда уравнение (1) примет вид
Теперь дадим х какое-нибудь другое значение, например 20. Тогда уравнение (1) примет вид
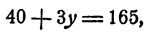
откуда
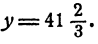
Так можно поступать и дальше. Давая х произвольные значения, мы будем получать все новые и новые решения уравнения (1). Разумеется, мы могли бы давать произвольные значения у и вычислять соответствующие значения другого неизвестного х.
Чтобы упростить отыскание решений уравнения (1), поступим так. Решим уравнение (1) относительно какой-нибудь неизвестной, например у т. е. выразим у через х. Получим
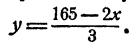
Теперь удобнее вычислять значения у при произвольных значениях х. Вычислим несколько решений уравнения (1) и запишем их в таблицу:
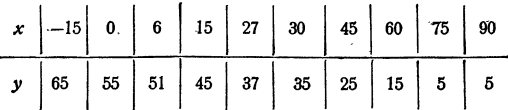
По таблице, как известно, можно построить график (рис. 20). Назовем его графиком решений уравнения (1). Каждая точка этого
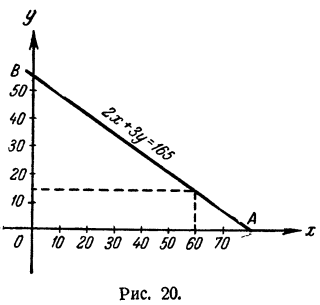
графика соответствует столбцу таблицы и служит, таким образом, изображением одного решения уравнения (1). С другой стороны каждое решение уравнения (1) изображается определенной точкой графика.
Так как по смыслу задачи х и у положительны, условию
задачи удовлетворяют только те решения уравнения (1), которые изображаются точками, лежащими между А и В (рис. 20).
Ответ. Решение представлено таблицей и графиком (рис. 20).
Из сказанного вытекает, что одно уравнение первой степени с двумя неизвестными имеет бесконечное множество решений *). Для получения решений такого уравнения достаточно одной из неизвестных давать произвольные значения и вычислять соответствующие значения другой неизвестной. Чтобы удобнее было вычислять эти решения, следует разрешить уравнение относительно какой-нибудь неизвестной. Решения уравнения можно представить таблицей и графиком.
Рассмотрим теперь такую задачу:
Задача:
За 5 м сукна и 2 м ткани заплатили 330 руб. Сколько стоит 1 м сукна и 1 м ткани?
(При составлении этой задачи мы взяли известную нам задачу и исключили из ее условия первую часть.)
Решение:
Все, что было сказано по поводу задачи, рассмотренной в начале параграфа, можно повторить здесь по поводу этой задачи.
Обозначим опять буквой х стоимость 1 м сукна (в рублях), а буквой у — стоимость 1 м ткани (в рублях). Наша задача приводит к уравнению
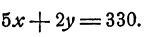
Разрешив это уравнение относительно у, имеем
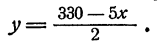
Составим таблицу некоторых решений этого уравнения:

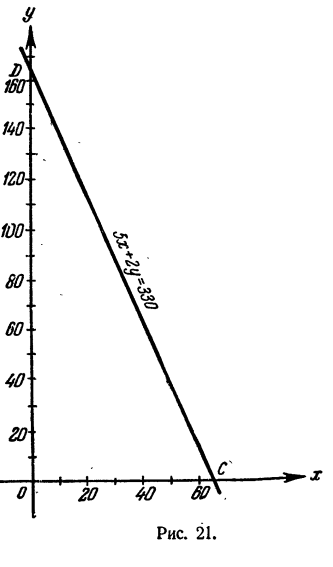
Построим график решений уравнения (рис. 21). Условию задачи удовлетворяют только те решения уравнения, которые изображаются точками, лежащими между С и D).
Ответ. Решение представлено таблицей и графиком (рис. 21).
*) За исключением уравнения О х + О у = m, где m отлично от нуля. Такое уравнение не имеет решения.
Графики, которые мы здесь строили, все оказались прямыми линиями. Это не случайно. Можно доказать, что график решений любого уравнения первой степени с двумя неизвестными — прямая линия.
Для доказательства этого утверждения нужны некоторые сведения по геометрии, которые излагаются в курсе VIII класса.
Поэтому
сейчас мы доказать это
утверждение не можем и примем его
без доказательства.
Для построения прямой
линии достаточно определить две
точки, через которые она
проходит. Поэтому для
построения графика решений
уравнения первой степени с двумя
неизвестными достаточно
вычислить какие-нибудь два
решения этого уравнения.
Решение систем уравнений при помощи графиков
Вернемся еще раз к задаче, которую мы рассматривали раньше.
За 2 м сукна и 3 м ткани заплачено 165 руб. В другой раз за 5 м того же сукна и 2 м той же ткани заплачено 330 руб. Сколько стоит 1 м сукна и 1 м ткани?
Мы обозначили буквой х стоимость 1 м сукна (в рублях), а буквой у — стоимость 1 м ткани (в рублях). Нами была составлена система уравнений
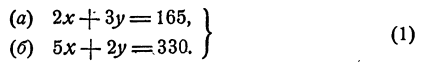
Каждое из этих уравнений имеет бесконечное множество решений. У нас составлены таблицы этих решений, составлены и их графики. Сравнивая эти две таблицы, можно заметить, что у них имеется одинаковый столбец:
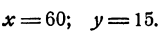
Это решение является общим для обоих уравнений (а) и (б) и вместе с тем, как мы знаем, является решением нашей задачи. Кроме этого общего решения, у каждого уравнения системы имеется сколько угодно решений, которые не удовлетворяют другому уравнению системы. Так, например, уравнение (а) имеет решение х = 30; у = 35, но это решение не удовлетворяет уравнению (б) и не является решением задачи.
Почему же общее решение уравнений (а) и (б) является решением нашей задачи, а всякая пара чисел, удовлетворяющих только одному уравнению системы, не является решением задачи?
Дело в том, что условие
задачи состоит из двух частей:
1) 2м сукна и 3 ж ткани
стоят 165 руб.,
2) 5м сукна и 2 м ткани
стоят 330 руб.
Если бы в условии задачи была только первая часть, а второй не было, всякое решение уравнения (а), подходящее по смыслу, было бы и решением задачи. Если бы в условии задачи была только вторая часть, а первой бы не было, всякое решение уравнения (б), подходящее по смыслу, было бы и решением задачи. Но в том то и дело, что в условии задачи две части, два требования, и потому искомые числа должны удовлетворять не только уравнению (а) или уравнению (б), а обоим этим уравнениям или, как говорят, удовлетворять системе этих двух уравнений.
Для того чтобы при помощи графиков решить систему двух уравнений первой степени с двумя неизвестными, поступают так: графики уравнений (а) и (б), выполненные в одинаковом масштабе, наносят на один чертеж, как бы накладывая один на другой. Тогда всякая
общая точка этих графиков изображает общее решение уравнений (а) и (б) и, таким образом, изображает решение системы этих уравнений.
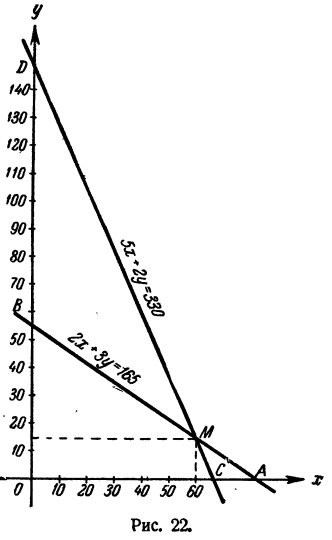
Построим графики решений уравнений (а) и (б) на одном чертеже (рис. 22).
По чертежу видно, что точка М пересечения прямых имеет координаты x = 60; у =15.
Надо сказать, что способ решения систем при помощи графиков имеет тот недостаток, что он не дает точного значения для неизвестных, так как значения эти приходится брать с чертежа. Но решение систем этим способом очень наглядно.
О числе решений системы двух уравнений первой степени с двумя неизвестными
Из геометрии известно, что две прямые линии или пересекаются (т, е. имеют одну общую точку), или параллельны (т. е. не имеют ни одной общей точки), или совпадают (т. е. у них все точки общие).
Отсюда можно сделать вывод, что система двух уравнений первой степени с двумя неизвестными либо имеет одно решение, либо не имеет ни одного решения, либо имеет бесконечное множество решений.
Пример:
Решить систему

Решение:
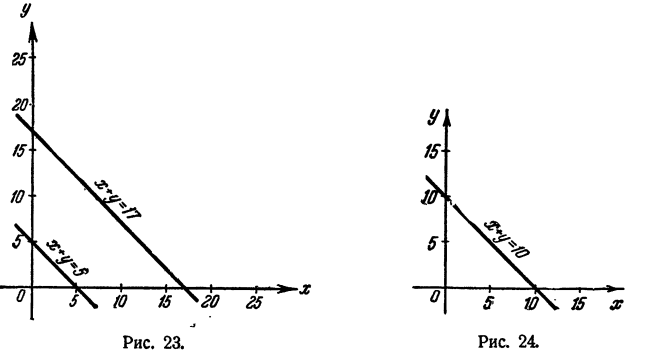
Первое уравнение требует от нас, чтобы мы нашли два числа, сумма которых 5, а второе уравнение требует, чтобы сумма этих же чисел равнялась 17. Такие числа найти нельзя (рис. 23), следовательно, система (1) не имеет решения.
Пример:
Решить систему

Решение:
Сразу видно, что второе уравнение системы (2) получается из первого посредством умножения обеих частей на 2. Поэтому каждое решение первого уравнения является также решением второго, а каждое решение второго уравнения является также решением первого. Таким образом, каждое решение любого из уравнений является решением системы (2).
Таблица решений одного из этих уравнений служит также и таблицей решений другого, а графики решений обоих уравнений совпадают всеми своими точками.
Все это означает, что одно из уравнений можно совсем не принимать во внимание, а решить только другое уравнение. Выходит, что система (2) имеет бесконечное множество решений. Эти решения получаются из уравнения y = 10 — х, где х— любое (рис. 24).
Способ сравнения
Кроме графического способа, существуют и другие способы решения систем. Мы рассмотрим три способа: способ сравнения, способ сложения и вычитания, способ подстановки. Каждый из них, в отличие от графического способа, дает точное решение системы.
Способ сравнения основан на следующих соображениях: для того чтобы решить систему, достаточно отыскать в таблицах решений уравнений системы одинаковые решения.
Спрашивается, нельзя ли найти эти одинаковые решения не вычисляя при этом других, ненужных нам решений? Оказывается, можно. Покажем на примере, как это делается, и попутно дадим все необходимые пояснения.
Рассмотрим систему
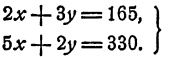
Подготовим каждое «из уравнений системы так, как будто мы собираемся вычислять таблицы решений, т. е. из каждого уравнения выразим у через х (можно выразить и х через у). Получим:

Предположим теперь, что мы одновременно вычисляем обе таблицы:

Мы вычислили две строчки, которые нам не нужны, так как значения для у получились разные. Чтобы сразу получить строчки, которые нам нужны, достаточно найти такие значения x, при которых выражения
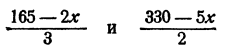
имеют одинаковые значения. Такие задачи мы решали и знаем, что для этого следует решить уравнение
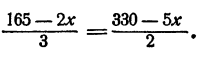
Решая его по известным правилам, находим, что x = 60.
(Сравните это уравнение с уравнением (1) на стр. 170.) Итак, одинаковые решения в таблицах получаются при х = 60 и только при этом значении х. Вычисляя y по формулам (1) или (2), находим: что y=15.
Ответ. x = 60;y = 15. Решение единственное.
Приведем второй, прием решения той же системы. Выразим из каждого уравнения у через ху приравняем полученные выражения и, решив уравнения с одним неизвестным, найдем, что #==60. (Все это точно так же, как и раньше.)
Выразим теперь из каждого уравнения системы х через у и приравняем полученные выражения
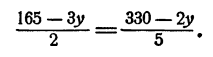
Решая это уравнение, получим y = 15. Итак, x = 60; у =15.
Этот прием отличается от предыдущего тем, что, найдя значение x = 60, мы не стали подставлять его в условие, а искали у тем же путем, как и х.
Правило. Для того чтобы решить систему двух уравнений первой степени с двумя неизвестными, достаточно:
1) из каждого уравнения системы выразить какую-нибудь из неизвестных через другую (например, х через у),
2) приравнять полученные выражения и решить уравнение с одним неизвестным (у),
3) тем же способом или при помощи найденного неизвестного (у) определить значение другого неизвестного (х).
Пример:
Решить систему уравнений
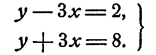
Решение:
Выразим из каждого уравнения системы у через х, получим
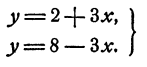
Приравняем правые части, получим
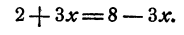
Отсюда
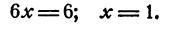
Подставим х= 1 в первое уравнение системы, получим
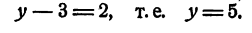
Проверка.
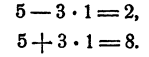
Каждое из уравнений системы превратилось в тождество.
Ответ. x = 1; у = 5. Других решений нет.
Пример:
Решить систему уравнений
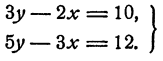
Решение:
Выразим из каждого уравнения системы у через х. Получим

Приравняем правые части, получим
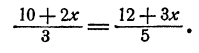
Отсюда
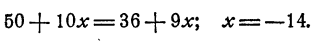
Подставим х = —14 в первое уравнение системы, получим З у + 28=10; у = — 6.
Проверка.
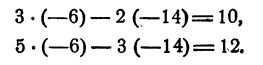
Каждое из уравнений системы превратилось в тождество.
Ответ. х = —14; у = —6. Других решений нет.
Пример:
Решить систему уравнений
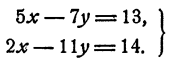
Решение:
Выразим х через у из каждого уравнения системы и приравняем результаты. Получим
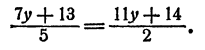
Отсюда
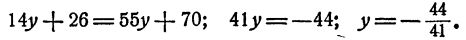
Выразим теперь у через х из каждого уравнения системы и приравняем результаты. Получим
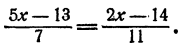
Отсюда
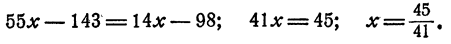
Проверка.
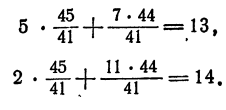
Каждое из уравнений системы превратилось в тождество.
Ответ .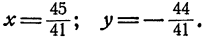 Решение единственное.
Решение единственное.
Возникает вопрос, является ли проверка решения в таких примерах логически необходимой или она производится только потому, что в процессе решения могли вкрасться ошибки.
Следующий, пример показывает, что рассуждения, подобные тем, которые проводятся при решении систем методом сравнения, могут привести к неверным выводам. Вот этот пример.
Даны два уравнения

и

Из первого уравнения

Из второго уравнения

Приравняем правые части, получим

Отсюда
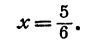
Нетрудно, однако, видеть, что 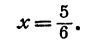 не удовлетворяет ни одному из данных уравнений.
не удовлетворяет ни одному из данных уравнений.
Объясняется это тем, что значения х, при которых 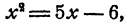 , не совпадают со значениями х, при которых
, не совпадают со значениями х, при которых 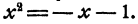 Подробнее, равенство (5) справедливо не при всех, а лишь при некоторых значениях х скажем при х = а. Равенство (6) справедливо тоже лишь при некоторых значениях х скажем при х = b. Тогда
Подробнее, равенство (5) справедливо не при всех, а лишь при некоторых значениях х скажем при х = а. Равенство (6) справедливо тоже лишь при некоторых значениях х скажем при х = b. Тогда
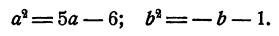
Приравнивая правые части равенств (3) и (4) и во всем дальнейшем, мы поступаем так, как будто а — b.
Эти рассуждения надо было излагать так. Допустим, что существует такое значение x, которое удовлетворяет как уравнению (3), так и уравнению (4). При таком значении х имеют место равенства (5) и (6). Следовательно, при таком значении х имеет место равенство (7) и
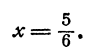
Отсюда следует условный вывод: если существует такое значение х при котором удовлетворяются оба уравнения (3) и (4), то 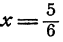 , и никакому другому числу х равняться не может. Это, однако, не означает, что
, и никакому другому числу х равняться не может. Это, однако, не означает, что 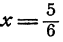 безусловно удовлетворяет обоим уравнениям. Проверка обнаруживает, что
безусловно удовлетворяет обоим уравнениям. Проверка обнаруживает, что 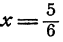 не удовлетворяет ни уравнению (3), ни уравнению (4). Окончательный вывод: уравнения (3) и (4) не имеют
не удовлетворяет ни уравнению (3), ни уравнению (4). Окончательный вывод: уравнения (3) и (4) не имеют
общих решений.
Соответственно с этим решение систем методом сравнения следует излагать так:
Допустим, что система
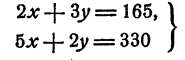
имеет решение. Тогда
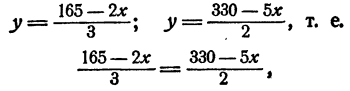
откуда
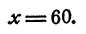
Из первого уравнения системы находим, что при x = 60 у =15.
Вывод: если система имеет решение, то #=60;^= 15. Никакая другая пара чисел не может удовлетворять этой системе. Остается доказать, что x = 60; y = 15 удовлетворяют системе. Это делается подстановкой в систему числа 60 вместо х и числа 15 вместо у.
Свойство выводных уравнений
Прежде чем приступить к изложению другого способа решения систем уравнений, рассмотрим вопрос о почленном сложении равенств. С этой целью рассмотрим несколько примеров, которые помогут нам
установить некоторые новые свойства равенств. Рассмотрим равенства

Нетрудно проверить, что равенства (1) и (2) являются справедливыми (т. е. верными) равенствами. Составим теперь новое равенство (3) так, чтобы левая часть равенства (3) была суммой левых частей равенств
(1) и (2), а правая — суммой правых частей, т. е., как говорят, сложим равенства (1) и (2) почленно. Получим
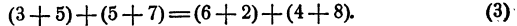
Нетрудно проверить, что равенство (3) тоже справедливо. Объясняется это тем, что суммы, находящиеся в левой и правой частях равенства (3), состоят из двух соответственно равных слагаемых.
При почленном сложении справедливых равенств в результате получается опять справедливое равенство. В частности, при почленном сложении двух тождеств в результате получается опять тождество. Рассмотрим равенства

Мы написали справедливое равенство (4) и несправедливое равенство (5). Сложим (4) и (5) почленно, получим
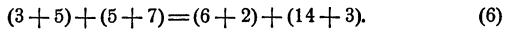
Равенство (6) несправедливо. Первые слагаемые в левой и правой частях его равны, а вторые неравны. Ясно, что и суммы в этом случае неравны.
При почленном сложении справедливого равенства с
несправедливым в результате получается несправедливое равенство. Рассмотрим равенства

Здесь оба равенства несправедливы. Сложим их почленно, получим
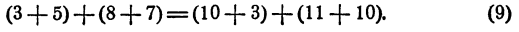
Равенство (9) тоже несправедливо. Рассмотрим равенства

Равенства (10) и (11) несправедливы. Сложим их почленно, получим
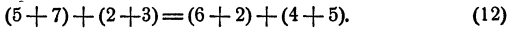
Нетрудно проверить, что равенство (12) справедливо. Последние два примера позволяют сделать такой вывод:
При почленном сложении двух несправедливых равенств может получиться как справедливое, так и несправедливое равенство. Рассмотрим теперь два равенства, содержащие буквы:

Мы взяли два уравнения, которые были хорошо изучены раньше. Нам известны и таблицы решений этих уравнений, и графики этих решений.
Сложим теперь уравнения (13) и (14) почленно. Получим уравнение

Рассмотрим график решений уравнения (15) совместно с графиками решений уравнений (13) и (14) (рис. 25).
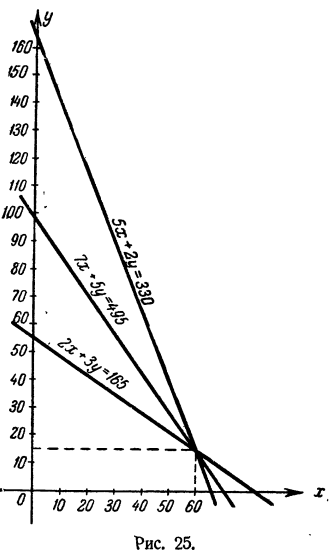
Мы видим, что прямая, соответствующая уравнению (15), проходит
через точку пересечения прямых, соответствующих уравнениям (13)
х = 60; у = 15 являются также решением
уравнения (15). В то же
время остальные решения уравнения (15) не удовлетворяют ни уравнению (13), ни уравнению (14). Почему общее решение . уравнений (13) и (14) является также решением и уравнения (1.5)? Почему уравнение (15). имеет решения, которые не удовлетворяют ни уравнению (13), ни уравнению (14)?
Все это объясняется тем, что при сложении уравнений мы складываем равенства, которые при одних
значениях неизвестных справедливы, а при других
несправедливы. В самом деле, при
x = 60; у = 15 оба равенства (13) и (14) справедливы. Значит, при этих значениях неизвестных должно быть справедливо и равенство (15).
При всех других значениях х и у хоть одно из равенств (13) или (14) несправедливо. Ясно поэтому, что при этих значениях хну равенство (15) может оказаться и справедливым и несправедливым.
Уравнение (15), полученное сложением уравнений (13) и (14), называется уравнением, выводным из системы уравнений (13) и (14) (оно выведено из уравнений (13) и (14)). Таким образом, мы пришли к следующему результату:
Всякое решение системы уравнений является решением и уравнения, выводного из этой системы. Однако не всякое решение выводного уравнения является решением системы.
Точно так же можно убедиться, что все свойства равенств, выведенных почленным сложением, справедливы и для равенств, выведенных почленным вычитанием.
Приведем теперь два примера, в которых используется свойство выводных уравнений.
Задача:
Доказать, что уравнения 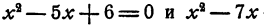
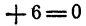 не имеют общих решений.
не имеют общих решений.
Решение:
Допустим, что эти уравнения имеют общее решение. Тогда это решение должно удовлетворять уравнению 2x = 0, полученному почленным вычитанием второго уравнения из первого. Таким образом, если бы рассматриваемые уравнения имели общее решение, то этим решением было бы x=0. Однако х = 0 этим уравнениям не удовлетворяет.
Задача:
Найти общее решение уравнений
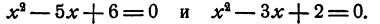
Решение:
Общее решение этих уравнений должно удовлетворять уравнению 2х — 4 = 0, полученному почленным вычитанием первого уравнения из второго. Следовательно, общим решением рассматриваемых уравнений может быть только х = 2.
Так как при х = 2 каждое из уравнений превращается в тождество, эти уравнения имеют единственное общее решение x = 2.
Ответ. Единственное общее решение x = 2.
Задачи, которые мы только что решили, можно решить и не опираясь на свойство выводных уравнений. Для этого достаточно уметь решать уравнения второй степени.
Способ сложения и вычитания
Рассмотрим систему

Сложим уравнения почленно, получим
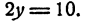
Это уравнение не содержит х, значит, его решения имеют такой вид: у = 5; х — любое. Среди полученных решений выводного уравнения надо искать и решение системы. Значит, решение системы должно быть такое: х пока неизвестно; у = 5.
Чтобы узнать, какое значение может иметь х, подставим в какое-нибудь уравнение системы вместо у число 5. Первое уравнение дает 5 — 3x = 2; x = l. Теперь ясно, что решением системы только и может быть x = 1; у = 5.
Подставим в систему вместо х и у найденные значения, получим тождества
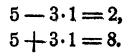
Теперь доказано, что x = 1; y = 5 — решение системы. Других, решений система не имеет.
Ответ. х = 1; у = 5— единственное решение.
Замечание:
Подстановка в систему вместо неизвестных их значений нужна была для доказательства, что. х = 1; у = 5 — действительно решение системы. Из рассуждений, которые мы провели, вытекает только, что если решение существует, то x = 1; у = 5. Другого решения не может быть. Однако это еще не означает, что х = 1; у = 5 есть решение системы.
Приведем второй прием решения той же системы.
Предположим, что система (1) имеет решение. Складывая уравнения почленно, имеем 2у = 10; x = 5. Вычитая из второго уравнения первое почленно, имеем
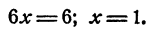
Получили тот же ответ: х = 1; у = 5.
Заметим, что при отыскании х мы здесь не пользовались тем, что у = 5. Мы искали х так же, как раньше искали у, т. е. исключением у из системы посредством вычитания.
Проверка решения и в этом случае необходима, так как из свойства выводных уравнений вытекает только, что система не может иметь других решений, кроме x = 1; y= 5, но не вытекает, что x = 1; у = 5 есть на самом деле решение системы. Рассмотрим систему

Если бы мы сложили уравнения почленно, мы получили бы 8у — 5x = 22 — уравнение с двумя неизвестными, которое нисколько не помогает найти какое-нибудь из неизвестных.
Почленное вычитание тоже приведет к уравнению с двумя неизвестными.
Выходит, что способ сложения и вычитания здесь не помогает. Почему же систему (1) удалось решить этим способом, а систему (2) решить не удается? Дело в том, что при сложении уравнений системы (1) х исчезал и получалось уравнение с одним неизвестным. При вычитании уравнений системы (1) исчезал^ и получалось уравнение с одним неизвестным х. В системе (1) коэффициенты при х равны по абсолютной величине и противоположны по знаку, поэтому х и исчезал при сложении уравнений. В системе (1) коэффициенты при у равны, поэтому у и исчезал при вычитании.
Отсюда видно, что систему-(2) надо раньше подготовить к сложению или вычитанию с таким расчетом, чтобы коэффициенты при каком-нибудь неизвестном слали равными по абсолютной величине.
Делается это так: умножим обе части первого из уравнений системы на 3, а обе части второго из уравнений системы на 2; получим новую систему

Ни одно решение системы при этом не потеряется и ни одно не будет приобретено, т. е. система (3) равносильна системе (2). Это вытекает из общих свойств уравнений, которые нам известны (см. § 1 и 2 гл. VII). Вычитая из второго уравнения системы (3) первое, получим
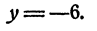
Подставляя в первое уравнение системы (2) у =—6, получим
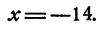
Таким образом, если система (2) имеет решение, то х =—14; у ——6, и никаких других решений быть не может. Остается показать, что х =—14, у = —6 удовлетворяет системе. Это было сделано раньше.
Правило. Для того чтобы решить систему двух уравнений первой степени с двумя неизвестными, достаточно
1) умножить обе части уравнений системы на такие числа, чтобы коэффициенты при одном из неизвестных стали равными по абсолютной величине,
2) почленно сложить или вычесть уравнения системы, чтобы получить уравнение с одним неизвестным,
3) решить это уравнение с одним неизвестным,
4) тем же способом или при помощи найденного неизвестного определить значение другого неизвестного.
Пример:
Решить систему

Решение:
Умножим почленно первое уравнение системы на 3, второе на 5, получим

Сложим почленно уравнения системы (5), получим
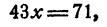
откуда
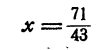
Умножим теперь первое уравнение системы (4) на 2, а второе на 11, получим

Вычитая из второго уравнения системы (6) почленно первое, имеем
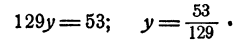
Итак, если Система (4) имеет решение, то
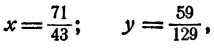
и никаких других решений быть не может.
Замечание:
При отыскании у мы не стали пользоваться тем, что 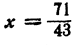 , а подготовили систему к исключению х й тогда нашли значение у.
, а подготовили систему к исключению х й тогда нашли значение у.
Проверка. Равенства
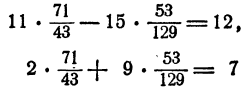
являются тождествами.
Значит,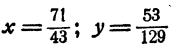 —решение системы.
—решение системы.
Ответ. 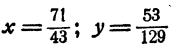
Способ подстановки
Рассмотрим опять систему

Предположим, что мы ее решили, нашли значения х и у и подставили их в (1). Тогда равенства (1) должны быть тождествами. Из первого тождества выразим у через х, получим новое тождество
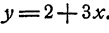
Полученное выражение для у подставим вместо^ во второе тождество, получим новое тождество
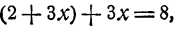
или
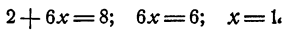
Зная, что x = 1, подставим 1 вместо х в какое-либо из тождеств (1), например в первое. Получим
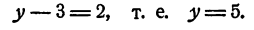
Таким образом, если предположить, что система (1) имеет решение, то выходит, что х=1; y = 5, и никаких других решений нет. Остается доказaть, что x = 1; y = 5 есть решение системы (1). Это решение получалось и другими способами и было в свое время показано, что оно удовлетворяет системе.
Приведем второй прием решения той же системы. Допустим, что система
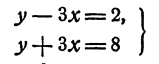
имеет решение.
Из первого уравнения имеем у = 2 + Зx. Подставим 2 +Зx; вместо у во второе уравнение, находим
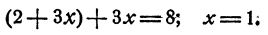
Теперь из первого уравнения выразим х через у. Получим
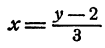
Подставим 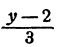 вместо х во второе уравнение, получим
вместо х во второе уравнение, получим
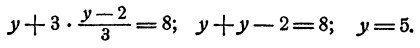
Заметим, что при отыскании у мы не стали пользоваться тем, что х нам известен, а искали у тем же путем, как раньше искали х.
Правило. Для того чтобы решить систему двух уравнений первой степени с двумя неизвестными, достаточно
1) из одного уравнения системы выразить одно неизвестное через другое (например, у через х),
2) полученное выражение подставить вместо этого
неизвестного (у) в другое уравнение системы и решить получающееся при этом уравнение с одним неизвестным (х),
3) тем же способом или при помощи найденного неизвестного (х) найти значение другого неизвестного (у).
Рассмотрим систему
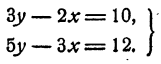
Допустим, что она имеет решение. Тогда из первого уравнения имеем
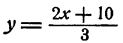
Подставим полученное для у выражение во второе уравнение системы. Получим
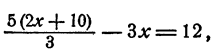
или 10x + 50 — 9x = 36; x = —14. Зная х, как всегда, находим у =—6. Таким образом, если допустить, что система имеет решение, то х =—14; у =—6. Других решений нет.
Остается доказать, что х =—14; у = — 6 —решение системы.
Для этого достаточно подставить это решение в систему и убедиться, что каждое из уравнений системы превращается в тождество. Это было уже сделано. Рассмотрим более сложный пример
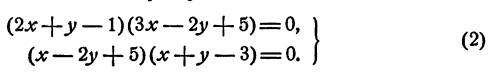
Предложенная система является системой двух уравнений второй степени с двумя неизвестными. В этом легко убедиться, раскрыв скобки.
Однако скобки здесь раскрывать невыгодно. Рассуждаем так. Левая часть каждого из уравнений представляет собой произведение двух сомножителей. Для того чтобы произведение равнялось нулю, необходимо и достаточно, чтобы хоть один из сомножителей равнялся нулю.
Поэтому система разбивается на четыре системы двух уравнений первой Степени с двумя неизвестными:
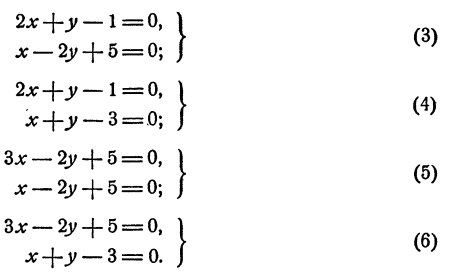
Система (3) имеет решение: 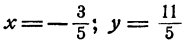
Система (4) имеет решение: 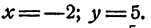
Система (5) имеет решение: 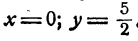
Система (6) имеет решение: 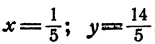
Ответ. Система (1) имеет четыре решения:
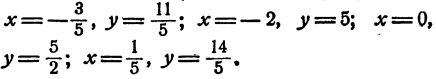
Решение систем уравнений первой степени с двумя неизвестными с буквенными коэффициентами
Так как буквы означают у нас числа, все сказанное о решении систем уравнений с числовыми коэффициентами относится также и к системам уравнений с буквенными коэффициентами. Нужно лишь, как всегда в таких случаях, следить за тем, чтобы незаметно для себя не допустить деления на нуль.
Пример:
Решить систему уравнений

Решение:
Вычитая из второго уравнения первое, имеем
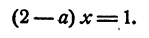
Сейчас нам предстоит делить обе части уравнения на 2— а. Но выражение 2 — а при а = 2 равно нулю, при всех других значениях а оно отлично от нуля. Итак, возможны два случая.
Случай 1. 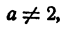 тогда
тогда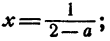 отсюда
отсюда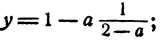
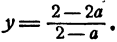
Случай 2. а = 2. Система имеет вид

Система (2) решений не имеет.
Ответ. Если 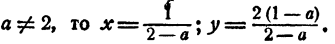 Если а = 2, система решений не имеет.
Если а = 2, система решений не имеет.
Пример:
Решить систему уравнений

Решение:
Вычитая из второго уравнения первое, имеем
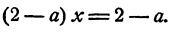
Если 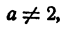 то x = 1; y = 0. Если а = 2, система примет такой вид:
то x = 1; y = 0. Если а = 2, система примет такой вид:

Эта система имеет бесконечное множество решений. Именно, у = 2 — 2x, где х — любое число.
Ответ. Если 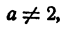 то х = 1; у = 0. Если а = 2, то у = 2 — 2х, х — любое число.
то х = 1; у = 0. Если а = 2, то у = 2 — 2х, х — любое число.
Решение задач при помощи системы двух уравнений первой степени с двумя неизвестными
Задача:
Отправлены два груза. Известно, что 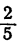 веса первого груза на 96 кг меньше, чем
веса первого груза на 96 кг меньше, чем 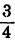 веса второго, а
веса второго, а 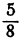 веса второго груза содержат столько же килограмм, сколько
веса второго груза содержат столько же килограмм, сколько 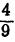 веса первого. Найти вес того и другого груза.
веса первого. Найти вес того и другого груза.
Решение:
Обозначим буквой х вес первого груза (в килограммах), буквой у — вес второго груза (в килограммах). Тогда
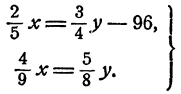
Из второго уравнения имеем

Подставляя в первое уравнение вместо х его выражение через у, получим
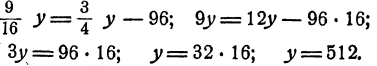
Пользуясь равенством (1), находим, что x = 720.
Проверка. 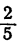 веса первого груза составляют 288 кг;
веса первого груза составляют 288 кг;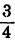 веса
веса
второго груза составляют 384 кг; 288 кг на 96 кг меньше, чем 384 кг;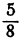 веса второго груза составляют 320 кг;
веса второго груза составляют 320 кг;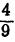 веса первого составляют тоже 320 кг. Задача решена правильно.
веса первого составляют тоже 320 кг. Задача решена правильно.
Ответ. 720 кг и 512 кг.
Задача:
Двое рабочих могли выполнить некоторую работу за 8 часов. Случилось так, что первый рабочий работал 6 час, а второй 9 час, и в результате они выполнили 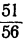 всей работы. Во сколько часов мог бы выполнить эту работу каждый рабочий в отдельности?
всей работы. Во сколько часов мог бы выполнить эту работу каждый рабочий в отдельности?
Решение:
Обозначим буквой х число часов, в течение которых первый рабочий, работая один, мог бы выполнить всю работу. Буквой у обозначим число часов, в течение которых эту работу мог бы выполнить второй рабочий, если бы работал один. Тогда
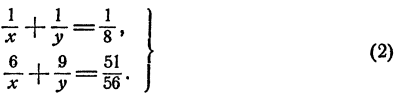
Разделим обе части второго уравнения на 3, умножив одновременно обе части первого уравнения на 2. Получим

Вычитая из второго уравнения первое, имеем
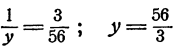
Подставим найденное значение у в первое из уравнений системы (2), получим
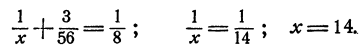
Проверка.
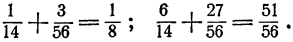
Задача решена верно.
Ответ. 14 час и 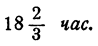
Системы трех уравнений первой степени с тремя неизвестными
Задача:
Периметр треугольника ABC равен 43 см, АВ больше АС на 8 см, АС больше ВС на 1 см. Определить стороны этого треугольника.
Решение:
Обозначим длину ВС буквой х (в см). Тогда длина АС составляет (x + 1) см, длина АВ составляет (х + 9) см. По условию, периметр треугольника равен 43 см. Значит,
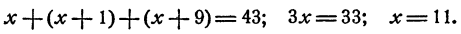
Ответ: ВС =11 см; АС = 12 см; АВ = 20 см.
В этой задаче требовалось найти три величины. Мы решили задачу при помощи уравнения с одним неизвестным. Так мы поступали и раньше, так и следует поступать всегда, если это возможно.
Эту же задачу можно решить и при помощи системы двух, уравнений первой степени с двумя неизвестными.
Обозначим буквой х длину стороны ВС (в см), буквой у длину стороны АС (в см). Тогда длина стороны АВ составляет (у + 8) см. По условию,
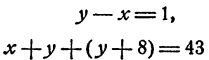
или
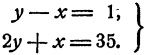
Значит,
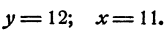
Ответ. ВС = 11 см; АС =12 см; АВ = 20 см.
Если бы мы пожелали ввести три буквы для обозначения неизвестных, условие задачи позволило бы составить три уравнения первой степени с тремя неизвестными.
Действительно, обозначим буквой х{ длину стороны ВС (в см), буквой у длину стороны АС (в см), буквой z длину стороны АВ (в см). Тогда
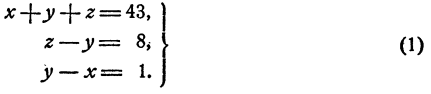
Нам нужно найти такие значения х, у, z, которые удовлетворяли бы всем трем уравнениям, а не одному или двум из них, т. е. нам нужно решить систему трех уравнений первой степени с тремя неизвестными. Мы еще не знаем,- как решаются такие системы, однако решение системы (1) нам известно, эту задачу мы решили другим способом. Именно,
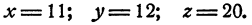
Подставив в систему (1) вместо неизвестных эти значения, убедимся, что в результате каждое из уравнений системы превращается в тождество. Действительно,
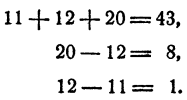
Эта задача. легко решается и при помощи уравнения с , одним неизвестным, и при помощи системы двух уравнений с двумя неизвестными.
Встречаются, однако, такие задачи, которые легче привести к системе трех уравнений с тремя неизвестными, чем к уравнению с одним неизвестным или к системе уравнений с двумя неизвестными. Вот, например, такая задача.
Задача:
За 5 открытых писем, 3 одинаковые почтовые марки и 3 конверта надо заплатить 2 руб. 60 коп. За 2 открытых письма и 6 таких же марок надо уплатить на 2 руб. 75 коп. больше, чем за 3 конверта. За 8 открытых писем и 2 конверта надо заплатить на 90 коп. больше, чем за 3 марки. Сколько стоит открытое письмо, марка и конверт (в отдельности)?
Решение:
Обозначим стоимость открытого письма буквой х (в коп.), стоимость марки буквой y (в коп.), стоимость конверта буквой z (в коп.). Тогда
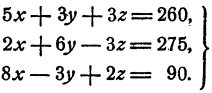
Задача без особого труда привела к системе трех уравнений первой степени с тремя неизвестными. Всякое другое ее решение было бы гораздо сложнее.
Решение системы трех уравнений первой степени с тремя неизвестными
Решение системы трех уравнений первой степени с тремя неизвестными основано на тех же соображениях, что и решение системы двух уравнений первой степени с двумя неизвестными.
Основные свойства уравнений, которые мы установили для уравнений с одним неизвестным, уравнений с двумя неизвестными и систем уравнений с двумя неизвестными, полностью справедливы, и для уравнения с тремя неизвестными и для систем таких уравнений (см. гл. VII, § 1, 2, 3, 4 и гл. VIII, § 6).
Изложим основные способы решения систем трех уравнений первой степени с тремя неизвестными: способ сравнения, способ сложениями вычитания, способ подстановки.
Способ сравнения. Разъясним этот способ на системе
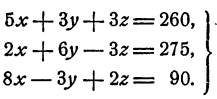
Выразим из каждого уравнения х через у и z. Получим
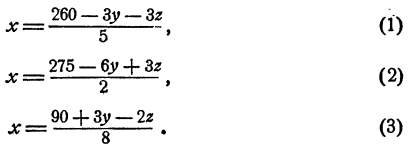
Приравнивая друг другу три различных выражения для х, получаем систему
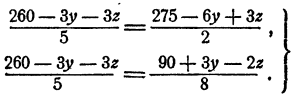
Решая эту систему по известным правилам, найдем, что у = 40; z = 5. Пользуясь любым из уравнений (1), (2) или (3), найдем x = 25. Итак,
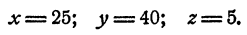
Других решений система не может иметь. Проверка решения и здесь логически необходима. Из сказанного можно вывести такое правило:
Для того чтобы решить систему трех уравнений первой степени с тремя неизвестными, достаточно:
1) из каждого уравнения системы выразить какое-нибудь неизвестное (например, х) через другие неизвестные (у и z),
2) одно из этих выражений приравнять двум другим и решить полученную систему двух уравнений первой степени с двумя неизвестными (у и z),
3) из любого уравнения системы найти значение третьего неизвестного (х).
Пример:
Решить систему
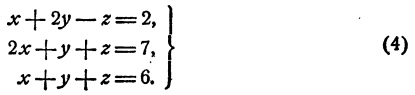
Решение:
Выразим z через х и у. Получим

Сравнивая (5) и (6), затем (5) и (7), получим систему
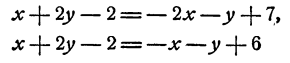
или
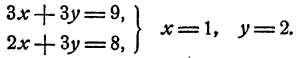
Из уравнения (5) находим, что z = 3. Других решений система не может иметь.
Для проверки подставим в систему (4) вместо х, у ,z числа 1, 2 и 3 соответственно. Получим тождества
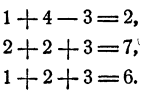
Ответ. х = 1; у = 2; z = 3.
Способ сложения и вычитания. Разъясним этот способ
решения на примере

Сложим почленно первые два уравнения. Получим первое выводное уравнение

Сложим теперь почленно первое уравнение с третьим. Получим второе выводное уравнение

Всякое решение системы (8) должно быть и решением каждого из выводных уравнений (9) и (10), следовательно, должно удовлетворять системе

Система (11) имеет единственное решение х = 1; у = 2. Значит, решение системы (8) имеет такой вид: x = 1; у = 2; z пока неизвестно. Из первого уравнения системы (8) находим, что при x = 1; у = 2 неизвестное z имеет единственное значение z = 3. Выходит, что системе (8) могут удовлетворять только х = 1; y = 2; z = 3; других решений система (8) иметь не может.
Остается убедиться,чтоx = 1; y = 2; z = 3 — решение системы(8). Это сделано выше. Заметим, что проверка здесь необходима, так как не всякое решение выводного уравнения является решением исходной системы.
Ответ. x =1; y = 2; z = 3.
Пример:
Решить систему
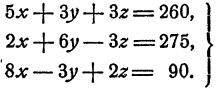
Решение:
Сложив первое уравнение почленно со вторым, имеем
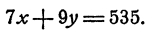
Чтобы уравнять (по абсолютной величине) коэффициенты при 2, умножим теперь обе части второго уравнения на 2, а обе части третьего уравнения на 3; получим
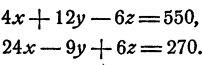
Сложив последние два уравнения почленно, получим
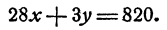
Теперь имеем систему
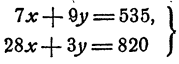
или
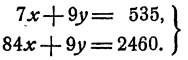
Отсюда

Из последнего уравнения системы имеем
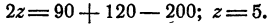
Проверка этого решения производилась ранее.
Ответ. x = 25; y = 40; z = 5.
Способ подстановки. Поясним этот способ на примере. Решить систему
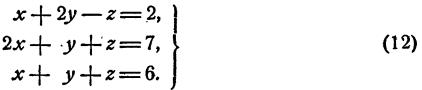
Предположим, что система решена и каждое из уравнений (12) есть тождество. Из первого уравнения имеем
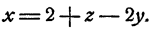
Подставим во второе и третье уравнения системы вместо х полученное для него выражение. Имеем
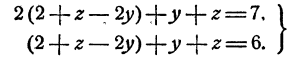
Откуда
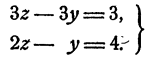
Значит,
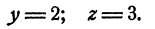
Теперь из уравнения (12) найдем, что x = 1.
Проверка и здесь необходима, так как в основе решения лежит предположение, что система имеет решение; иначе мы не могли бы с уравнениями системы обращаться как с тождествами. Проверку производить не станем, так как мы ее производили раньше.
Ответ. x = 1; y = 2; z = 3.
Иногда для упрощения вычислений следует отступить от общего правила и строить выводные уравнения, удобные для данного частного случая.
Пример:
Решить систему
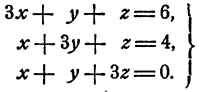
Решение:
Сложив почленно все три уравнения системы, имеем

Вычитая уравнение (13) почленно из каждого уравнения системы, найдем
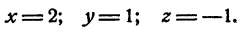
Других решений система не может иметь.
Подставив в условие найденные значения вместо неизвестных, имеем
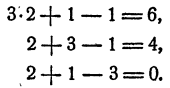
Ответ. x = 2; у = 1 z =—1.
Обычно уравнения надо приводить к целому виду. Вот пример, когда от этого общего правила следует отступить.
Пример:
Решить систему
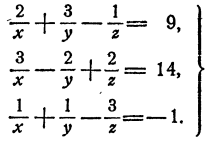
Решение:
Положим 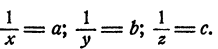 Тогда система примет такой вид:
Тогда система примет такой вид:
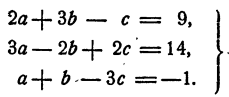
Исключим b сначала из первого и третьего, а затем из второго и третьего уравнений системы. Получим
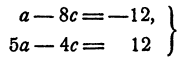
или
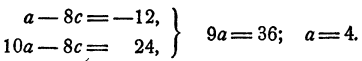
Далее: с = 2; b = 1. Наконец, 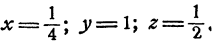
Проверка.
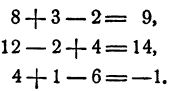
Ответ. 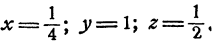
О числе решений системы трех уравнений первой степени с тремя неизвестными
Мы встречались с системами, которые имели единственное решение. Сейчас мы приведем пример системы, имеющей бесконечное множество решений, а также системы, совсем не имеющей решений.
Пример:
Система
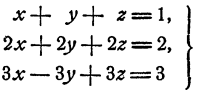
имеет бесконечное множество решений, так как всякое решение первого уравнения системы удовлетворяет второму и третьему уравнениям.
Пример:
Система
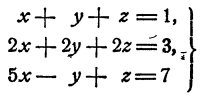
не имеет решения.
Действительно, первое уравнение требует, чтобы мы отыскали такие х, у, z, сумма которых равна единице, а второе уравнение требует, чтобы сумма тех же чисел равнялась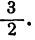 Такие числа найти нельзя.
Такие числа найти нельзя.
Замечание:
Рассуждения, которые мы применяли для решения системы трех уравнений с тремя неизвестными, могут быть применены и для решения системы четырех уравнений с четырьмя неизвестными и т. д.
Системы уравнений и их решение
Пусть задано равенство, содержащее две неизвестные буквы, например, 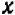 и
и 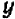 , Рассматривая его как уравнение относительно обеих букв, мы называем пару значений букв
, Рассматривая его как уравнение относительно обеих букв, мы называем пару значений букв 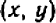 решением этого уравнения, если при подстановке этих значений равенство оказывается верным, или, как говорят, «уравнение удовлетворяется».
решением этого уравнения, если при подстановке этих значений равенство оказывается верным, или, как говорят, «уравнение удовлетворяется».
Так, уравнение 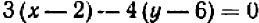 имеет решение
имеет решение 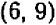 ,
, 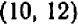 и другие.
и другие.
Подобным же образом, если дано равенство, содержащее три неизвестные буквы, например, 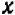 ,
, 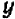 и
и 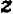 , то, рассматривая его как уравнение относительно этих трех букв, мы его решением назовем тройку чисел
, то, рассматривая его как уравнение относительно этих трех букв, мы его решением назовем тройку чисел 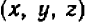 , если при подстановке этих значений равенство оказывается верным («уравнение удовлетворяется»).
, если при подстановке этих значений равенство оказывается верным («уравнение удовлетворяется»).
Так, уравнение  имеет решения
имеет решения 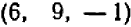 ,
, 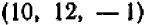 ,
, 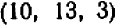 и многие другие.
и многие другие.
Если даны два уравнения, содержащих две неизвестные буквы, и требуется найти такую пару значений этих букв, которая была бы решением обоих уравнений, то говорят, что задана система двух уравнений с двумя неизвестными. Всякая пара значений, удовлетворяющая поставленному требованию, называется решением системы. Так, например, система уравнений 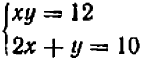 имеет решение
имеет решение 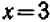 ,
, 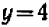 ; она имеет также и другое решение
; она имеет также и другое решение 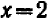 ,
, 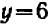 .
.
Найти какое-нибудь решение системы — еще не значит решить систему: решить систему — значит найти все ее решения. Систему в предыдущем примере нельзя считать решенной, так как, хотя найдено даже не одно, а два ее решения, однако, остается невыясненным, не существует ли еще иных решений. Можно идти таким образом дальше и рассматривать системы трех уравнений с тремя неизвестными и т. п.
Число уравнений в системе не должно обязательно совпадать с числом неизвестных: возможны, например, системы двух уравнений с тремя неизвестными и системы трех уравнений с двумя неизвестными.
Если речь идет о системе уравнений с тем или иным числом неизвестных букв, то при подсчете степени каждого уравнения все буквы, являющиеся неизвестны ми, считаются главными. Так, в приведенном выше примере первое уравнение — второй степени, второе — первой.
В курсе начальной алгебры изучаются только системы уравнений с двумя неизвестными, притом преимущественно такие системы, в состав которых входят уравнения только первой степени (линейные системы).
Линейные системы. Способ подстановки
Пусть дано одно линейное уравнение с двумя не известными, например, уравнение 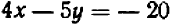 (1). Оно имеет, очевидно, сколько угодно решений; в самом деле, чтобы получить решение, достаточно, дав одной из букв совершенно произвольное значение, подобрать значение другой буквы таким образом, чтобы уравнение удовлетворялось.
(1). Оно имеет, очевидно, сколько угодно решений; в самом деле, чтобы получить решение, достаточно, дав одной из букв совершенно произвольное значение, подобрать значение другой буквы таким образом, чтобы уравнение удовлетворялось.
Предположим, что дано другое линейное уравнение с двумя неизвестными, скажем 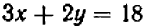 . (2) Оно также имеет бесчисленное множество решений.
. (2) Оно также имеет бесчисленное множество решений.
Рассмотрим теперь систему, составленную из этих двух уравнений 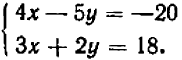 (1)(2). Допустим, что решение системы существует; значит, существует такая пара чисел
(1)(2). Допустим, что решение системы существует; значит, существует такая пара чисел 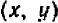 , которая одновременно удовлетворяет обоим уравнениям (1) и (2).
, которая одновременно удовлетворяет обоим уравнениям (1) и (2).
Посмотрим, какие следствия можно вывести из такого допущения. Решим одно из уравнений, например (2), относительно одной из букв, хотя бы относительно 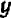 , для этого вычтем из обеих частей (2) по
, для этого вычтем из обеих частей (2) по 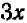 (прибавим по
(прибавим по 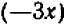 ) и затем полученное равенство разделим на
) и затем полученное равенство разделим на 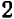 ; получаем равенство
; получаем равенство 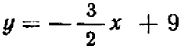 (3).
(3).
Если верны одновременно равенства (1) и (2), то верно и равенство (3). Это последнее равенство удобно в том отношении, что оно решено относительно 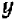 , и потому значение
, и потому значение 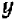 может быть немедленно получено с его помощью, если только известно значение
может быть немедленно получено с его помощью, если только известно значение 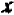 . Теперь «подставим» выражение (3), полученное для
. Теперь «подставим» выражение (3), полученное для 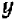 , в уравнение (1). Это значит, что из равенств (1), (2) и (3) мы выводим дальнейшее следствие:
, в уравнение (1). Это значит, что из равенств (1), (2) и (3) мы выводим дальнейшее следствие: 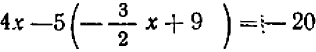 .
.
При выполнении указанной подстановки нет надобности ссылаться на какие-либо иные свойства равенства, кроме тех, которые нам уже известны. Именно, мы сначала умножаем обе часта равенства (3) на 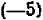 :
: 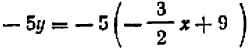 затем прибавляя к обеим частям выражение
затем прибавляя к обеим частям выражение 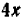 , получаем
, получаем 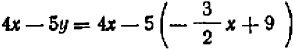 (4).
(4).
Согласно (1), левая часть этого равенства равна 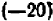 ; значит, и правая равна тому же; отсюда следует равенство (4).
; значит, и правая равна тому же; отсюда следует равенство (4).
Уравнение (4), являющееся следствием уравнений (1) и (2), уже не содержит буквы у (мы ее «исключили»).
Умножая, дальше, (4) на 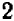 , чтобы освободиться от дроби, и совершая тождественные преобразования в левой части, получим
, чтобы освободиться от дроби, и совершая тождественные преобразования в левой части, получим
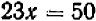 , откуда, наконец, следует
, откуда, наконец, следует 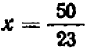 (5′).
(5′).
Но в таком случае, «подставляя» значение 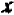 в формулу (3), мы приходим к равенству
в формулу (3), мы приходим к равенству 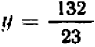 (5»).
(5»).
Таким образом, иных решений нашей системы (1 — 2), кроме решения 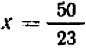 ,
, 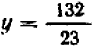 (5) быть не может.
(5) быть не может.
Подставляя значения 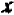 и
и 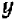 в уравнения (1—2)
в уравнения (1—2) 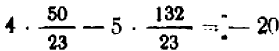 ,
, 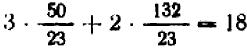 мы убеждаемся, что данная система имеет единственное решение, определяемое формулами (5).
мы убеждаемся, что данная система имеет единственное решение, определяемое формулами (5).
Следует ясно понимать, что, получив формулы (5), мы вовсе не имели права заключить из приведенных рассуждений, что система (1—2) имеет решение, определяемое этими формулами: заключить можно было бы только то, что никакая пара чисел, кроме указанных формулами (5), не представляет собой решения системы. То же, что пара чисел (5) есть решение, вытекает не иначе, как из последней подстановки.
Таким образом, подстановку полученных значений 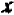 ,
, 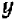 в уравнениях (1—2) следует рассматривать не только как проверку правильности проделанных вычислений.
в уравнениях (1—2) следует рассматривать не только как проверку правильности проделанных вычислений.
Способ уравнивания коэффициентов
Этот способ основывается на следующем свойстве равенств (которое не было упомянуто раньше): если  и
и 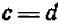 , то
, то 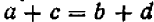 .
.
Доказательство вытекает из свойств равенств. Прибавив к обеим частям равенства  по
по 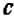 , получим
, получим 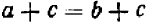 .
.
Прибавив таким же образом к обеим частям равенства 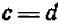 по
по 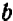 , получим
, получим 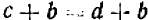 или
или  .
.
В таком случае из двух полученных равенств вытекает равенство 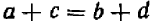 .
.
Кратко говорят: «равенства можно складывать почленно» , понимая под этим, что если сложить два (или больше) верных равенства (левую часть с левой, правую — с правой), то новое равенство также будет верным.
Таким же образом можно почленно выполнять следующие операции над равенствами: «одно равенство можно вычесть из другого», «равенства можно перемножать» , «одно равенство можно разделить на другое (если только левая и правая части второго равенства не равны нулю)».
Рассмотрим в качестве примера прежнюю систему уравнений: 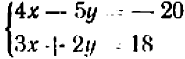 (1)(2).
(1)(2).
Предположим, как п раньше, что система имеет решение, т. е. что существует пара чисел 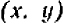 , удовлетворяющая одновременно обоим уравнениям (1) и (2).
, удовлетворяющая одновременно обоим уравнениям (1) и (2).
Пользуясь способом подстановки, мы «исключали» букву 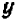 таким образом: определяли у из уравнений (2) и результат подставляли в уравнение (1).
таким образом: определяли у из уравнений (2) и результат подставляли в уравнение (1).
Попробуем теперь «исключить» букву 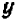 из уравнений (1—2) сразу. С этой целью, посмотрев, каковы коэффициенты при
из уравнений (1—2) сразу. С этой целью, посмотрев, каковы коэффициенты при 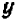 в уравнениях (1) и (2), умножим уравнение (1) на
в уравнениях (1) и (2), умножим уравнение (1) на 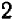 :
: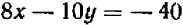 (1′), а уравнение (2) на
(1′), а уравнение (2) на 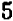 :
: 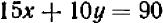 (2′), затем, складывая между собою полученные равенства, мы придем к заключению, что
(2′), затем, складывая между собою полученные равенства, мы придем к заключению, что 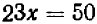 ,
,
и, значит,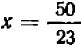 (3′)
(3′)
С другой стороны, заметив, каковы коэффициенты в данных уравнениях при 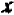 , мы можем «исключить» букву
, мы можем «исключить» букву 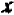 . Для этого умножим уравнение (1) на
. Для этого умножим уравнение (1) на 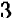 :
: 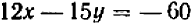 , (1») а уравнение (2) на
, (1») а уравнение (2) на 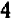 :
: 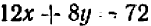 (2») и затем вычтем хотя бы (1′) из (2′), тогда получится
(2») и затем вычтем хотя бы (1′) из (2′), тогда получится 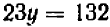 , или
, или 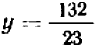 ( 3»)
( 3»)
Этот способ, как и способ подстановки, приводит нас к следующему заключению. Если система (1—2) имеет решение, то этим решением может быть только пара чисел 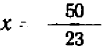 ,
, 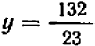 .
.
Остается подставить эти числа в уравнения (1—2), чтобы убедиться, что они действительно дают нам решение.
Можно порекомендовать научиться решать линейные системы вида (1—2) указанным здесь способом, не выписывая при этом промежуточных результатов(1’—2′), (1″- 2″) и вместе с тем действуя с помощью отрицательных чисел таким образом, чтобы избегать вычитаний.
Желая исключить 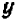 , справа за вертикальной чертой пишут множители
, справа за вертикальной чертой пишут множители 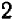 и
и 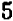 и подчеркивают запись
и подчеркивают запись 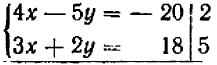 . Затем говорят: коэффициент при
. Затем говорят: коэффициент при 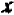 (после умножения уравнения (1) на
(после умножения уравнения (1) на 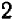 , уравнения (2) на
, уравнения (2) на 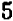 и последующего сложения, равен
и последующего сложения, равен 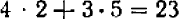 ; коэффициент при
; коэффициент при 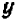 (это — контроль) равен
(это — контроль) равен 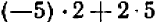 , т. е. обращается в нуль; свободный член (справа) равен
, т. е. обращается в нуль; свободный член (справа) равен 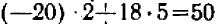 . Результат записывается под чертой.
. Результат записывается под чертой.
Далее добавляют еще вертикальную черту и за нею пишут, намереваясь исключить 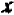 , множители
, множители 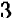 и
и 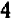 .
.
Чтобы избежать вычитания, при одном из этих множителей ставят знак минус, именно в данном случае перед первым множителем 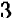 , с таким расчетом, чтобы после сложения сразу получить положительный коэффициент при
, с таким расчетом, чтобы после сложения сразу получить положительный коэффициент при 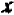 . Проверяют, что при сложении коэффициент при
. Проверяют, что при сложении коэффициент при 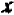 обращается в нуль, и подсчитывают коэффициент при
обращается в нуль, и подсчитывают коэффициент при 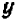 и свободный член.
и свободный член.
Итак, запись в целом имеет вид:
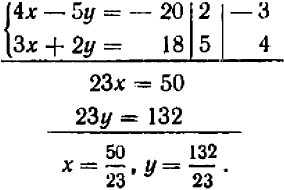
Примечание. В качестве множителей (в случае целых или буквенных коэффициентов при неизвестных) целесообразно брать, ради упрощения вычислений, дополнительные множители до НОК коэффициентов при исключаемом неизвестном.
Так, и следующем примере вместо схемы множителей 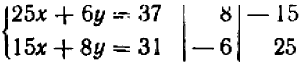 следует взять более простую схему
следует взять более простую схему 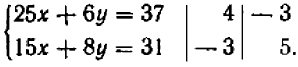 . (НОК
. (НОК  и
и 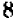 равно
равно 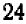 ;
; 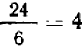 ;
; 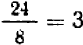 . НОК
. НОК 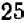 и
и 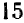 равно
равно 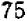 ;
; 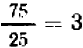 ,
,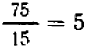 ).
).
Действуя способом уравнивания коэффициентов, решим линейную систему двух уравнений с двумя не известными общего вида , т. е, с буквенными коэффициентами: 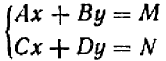 (*).
(*).
Приписывая множители за вертикальной чертой, как было указано раньше, мы наметим схему 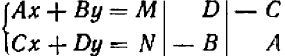
Умножение на множители 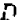 ,
, 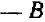 и последующее сложение дают:
и последующее сложение дают: 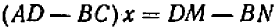 .
.
Умножение на множители 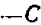 ,
, 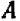 и последующее сложение дают:
и последующее сложение дают: 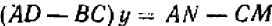 .
.
Если только коэффициенты 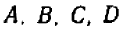 удовлетворяют условию
удовлетворяют условию 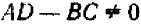 (**), то отсюда сейчас же следует, что иного решения системы быть не может, кроме
(**), то отсюда сейчас же следует, что иного решения системы быть не может, кроме 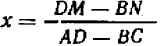 ,
, 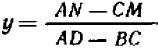 .
.
Чтобы убедиться в том, что эта пара значений 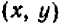 в самом деле есть решение системы, нужно сделать подстановку этих значений в данные уравнения.
в самом деле есть решение системы, нужно сделать подстановку этих значений в данные уравнения.
Подставим эти значения 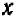 и
и 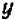 в левую часть первого уравнения и сделаем упрощения; получим:
в левую часть первого уравнения и сделаем упрощения; получим:
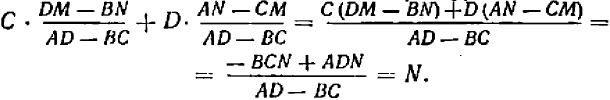
Точно так же подстановка во второе уравнение дает:
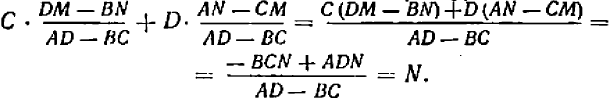
Мы приходим, таким образом, к следующему важному результату, который нужно твердо помнить: каковы бы ни были коэффициенты в данной системе (*), лишь бы только выражение 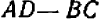 не равнялось нулю, система имеет одно и только одно решение. Этот результат имеет общий характер — и именно по той причине, что все коэффициенты в уравнениях (*) были взяты в буквенной форме. Полезно как-нибудь назвать те системы вида (*), для которых выполняется условие (**). Их называют регулярными.
не равнялось нулю, система имеет одно и только одно решение. Этот результат имеет общий характер — и именно по той причине, что все коэффициенты в уравнениях (*) были взяты в буквенной форме. Полезно как-нибудь назвать те системы вида (*), для которых выполняется условие (**). Их называют регулярными.
Из сказанного следует практический вывод: в случае, если линейная система — регулярная, проверка посредством подстановки полученных значений неизвестных 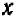 и
и 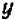 в уравнения данной системы необходима лишь постольку, поскольку имеются сомнения в правильности проделанных вычислений.
в уравнения данной системы необходима лишь постольку, поскольку имеются сомнения в правильности проделанных вычислений.
Что касается систем, не являющихся регулярными, то мы ограничимся рассмотрением отдельных примеров,
Особенные случаи
Пример:
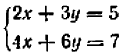 (1)(2)
(1)(2)
Действуя способом подстановки, определим 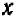 из уравнения (1):
из уравнения (1): 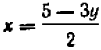 подставим найденное выражение в уравнение (2):
подставим найденное выражение в уравнение (2): 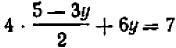 отсюда, после тождественных преобразований, получается:
отсюда, после тождественных преобразований, получается: 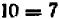 .
.
Далее остается провести следующее рассуждение: допустив, что данная система имеет решение, мы пришли к нелепому заключению, что 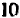 равно
равно 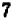 , так как
, так как 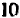 на самом деле не равно, то, значит, наше допущение было ошибочно. Итак, данная система не имеет ни одного решения.
на самом деле не равно, то, значит, наше допущение было ошибочно. Итак, данная система не имеет ни одного решения.
Действуя способом уравнивания коэффициентов исключая, например, 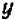 по схеме
по схеме 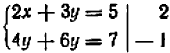 , мы сталкиваемся с тем фактом, что одновременно с
, мы сталкиваемся с тем фактом, что одновременно с 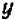 исключается также и
исключается также и 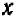 , и мы получаем
, и мы получаем 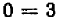 .
.
Следует рассуждение, подобное приведенному выше.
Пример:
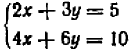 (1)(2).
(1)(2).
Действуя способом подстановки, мы получаем: 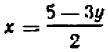 , далее
, далее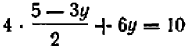 , и после преобразований
, и после преобразований 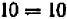 .
.
Действуя способом уравнивания коэффициентов, мы пришли бы к подобному же неоспоримому заключению.
Разберемся, в чем здесь дело. Рассматривая данную систему внимательнее, мы видим, что равенство (2) есть следствие равенства (1) : оно получается из него посредством умножения на 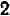 . Поэтому всякое решение уравнения (1) есть вместе с тем и решение системы (1—2); и уравнение (1) имеет бесчисленное множество решений; значит, то же можно сказать и о системе (1—2).
. Поэтому всякое решение уравнения (1) есть вместе с тем и решение системы (1—2); и уравнение (1) имеет бесчисленное множество решений; значит, то же можно сказать и о системе (1—2).
Легко заметить, что в примерах 1 и 2 мы имеем дело как раз с системами, которые не являются регулярными: в самом деле, 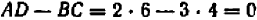 .
.
Из этих примеров можно сделать следующий вывод: существуют нерегулярные системы, не имеющие ни одного решения (несовместные системы), и существуют нерегулярные системы, имеющие бесчисленное множество решений (неопределенные системы) .
В примере 1 мы встретились с несовместной системой, в примере 2 — с неопределенной.
Геометрическое представление решения системы двух линейных уравнений с двумя неизвестными
Мы решили систему уравнений 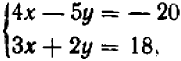 (1)(2) и оказалось, что система имеет единственное решение
(1)(2) и оказалось, что система имеет единственное решение  (3).
(3).
Что это значит геометрически?
Посмотрим, каковы графики уравнений (1) и (2).
Геометрическое место точек координатной плоскости  , координаты которых удовлетворяют уравнению (1), представляет собою прямую линию; построить ее по точкам не представляет труда: достаточно, впрочем, отметить две точки пересечения с осями
, координаты которых удовлетворяют уравнению (1), представляет собою прямую линию; построить ее по точкам не представляет труда: достаточно, впрочем, отметить две точки пересечения с осями  и
и  , именно точки
, именно точки 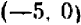 и
и 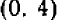 , и затем провести через них прямую.
, и затем провести через них прямую.
Точно так же геометрическое место точек, координаты которых удовлетворяют уравнению (2), есть другая прямая: она пересекается с осями в точках 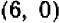 и
и 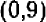 .
.
Оба графика изображены на черт. 47.
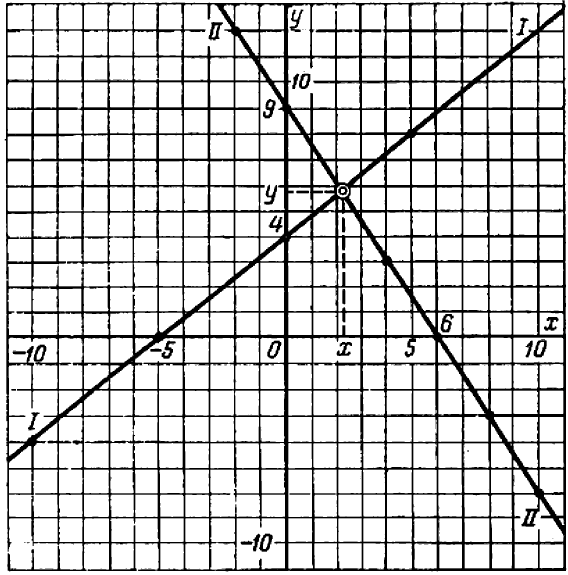
Решив систему (1—2), мы установили, что существует единственная пара чисел 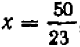 ,
, 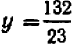 , удовлетворяющая обоим уравнениям сразу: эти числа — координаты единственной точки, принадлежащей одно временно как графику (1), так и графику (2).
, удовлетворяющая обоим уравнениям сразу: эти числа — координаты единственной точки, принадлежащей одно временно как графику (1), так и графику (2).
Записав эти числа в виде десятичных дробей (с округлением хотя бы в десятых) 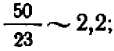
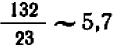 и взглянув па чертеж, мы видим, что таковы (при мерно) в самом деле координаты точки пересечения прямых (1) и (2).
и взглянув па чертеж, мы видим, что таковы (при мерно) в самом деле координаты точки пересечения прямых (1) и (2).
Итак, каждому из данных линейных уравнений системы геометрически соответствует его график — прямая линия; решению системы — точка пересечения этих графиков.
Геометрическое представление решения системы позволяет проконтролировать правильность решения посредством несложных построений на координатной сетке (клетчатой бумаге).
В тех случаях, когда достаточно найти приближенное решение системы, но нужно сделать это по возможности скорее и без вычислений, на геометрическое построение можно смотреть и как на метод решения системы (графическое решение системы).
Прямая, являющаяся графиком уравнения 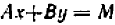 , имеет наклон, равный —
, имеет наклон, равный — 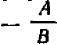 при условии
при условии 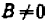 ; прямая, являющаяся графиком уравнения
; прямая, являющаяся графиком уравнения 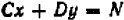 , имеет таким же образом наклон—
, имеет таким же образом наклон— 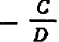 (при условии
(при условии 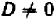 ). Равенству
). Равенству 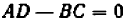 , разделив на
, разделив на 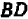 , можно придать вид
, можно придать вид 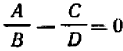
или 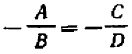 .
.
Но это значит, что наклоны двух прямых равны, т. е. прямые параллельны.
Если 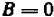 , то из условия
, то из условия 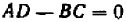 следует, что и
следует, что и 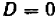 (так как
(так как 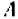 и
и 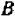 не могут обращаться в пуль одновременно); прямые параллельны и в этом случае.
не могут обращаться в пуль одновременно); прямые параллельны и в этом случае.
Итак, невыполнение условия регулярности свидетельствует о том, что прямые, являющиеся графиками данных уравнений, параллельны. В таком случае очевидно геометрически, что у них или вовсе нет общих точек (если они различны), или имеется их бесконечное множество (если они совпадают).
Общие соображения по поводу решения систем уравнений
Было бы ошибочно, основываясь на рассмотрении систем линейных уравнений, сделать общее заключение о том, что система двух уравнений с двумя неизвестными всегда имеет единственное решение. Такое утверждение, как мы видели, справедливо даже не для всех линейных систем. В случае, если уравнения данной системы — оба или хотя бы одно — степени выше первой, возможно существование нескольких решений или же их может не быть вовсе.
Почему это так — в этом легко отдать себе отчет, если рассмотреть вопрос с геометрической точки зрения. Решая систему двух уравнений, мы ставим своей задачей найти все точки пересечения двух графиков, соответствующих данным уравнениям. Если оба уравнения линейные, то графики — прямые линии, и две прямые, при условии, что они не параллельны, имеют только одну точку пересечения. Но если хотя бы одно из уравнений системы — не линейное, то уже нельзя сказать, что его график — прямая линия, а в та ком случае графики могут пересекаться в нескольких точках, а могут и совсем не иметь общих точек.
В подтверждение высказанных соображений мы рассмотрим несколько примеров.
Решая системы, в дальнейшем мы будем пользоваться методом подстановки: именно, определяем одно из неизвестных (выражаем его через другое) какого-ни будь уравнения и затем подставляем то, что получится, в другое уравнение; вновь получаемое уравнение есть следствие данных, но содержит уже только одну неизвестную букву.. «Исключив», таким образом, одну из букв, находят, решая уравнение, значение другой, а затем не представляет труда найти и значение первой буквы.
Пример:
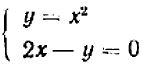 (1)(2)
(1)(2)
Уравнение (1) — второй степени, уравнение (2) — линейное и легко решается относительно 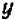 :
: 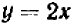 .
.
Подставляя полученное значение в уравнение (1), мы получаем: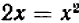 или
или 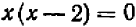 . (3) Произведение равно нулю в том, и только в том случае, если один из множителей равен нулю: значит, или
. (3) Произведение равно нулю в том, и только в том случае, если один из множителей равен нулю: значит, или 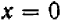 , или
, или  , т. е.
, т. е.  .
.
Уравнение второй степени (3) имеет два корня х — 0 и х — 2. Из уравнения (2) затем видно, что если 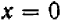 , то непременно
, то непременно 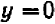 ; и если
; и если  , то непременно
, то непременно 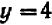 .
.
Итак, решениями системы (1—2) могут быть только пары чисел 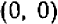 и
и 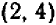 ;непосредственная подстановка показывает, что эти пары, действительно, дают решения.
;непосредственная подстановка показывает, что эти пары, действительно, дают решения.
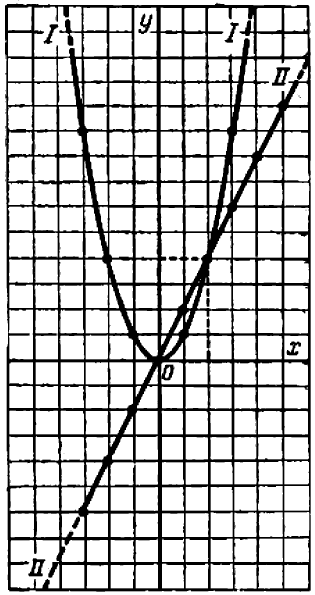
Пример иллюстрируется чертежом 48: парабола 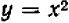 (1) и прямая
(1) и прямая 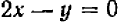 (2) пересекаются в двух точках с координатами
(2) пересекаются в двух точках с координатами 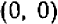 и
и 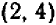 .
.
Пример:
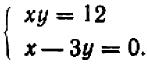 (1)(2)
(1)(2)
Подставляя выражение для 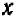 , взятое из уравнения (2), в уравнение (1), мы получаем после сокращений:
, взятое из уравнения (2), в уравнение (1), мы получаем после сокращений: 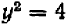 (3).
(3).
Уравнение второй степени (3) имеет два корня: 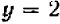 и
и 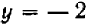 .
.
Из уравнения (2) видно, что если 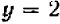 , то
, то 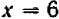 , и если
, и если 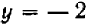 , то
, то 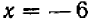 .
.
Итак, решениями системы (1—2) могут быть только пары чисел 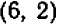 и
и 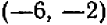 .
.
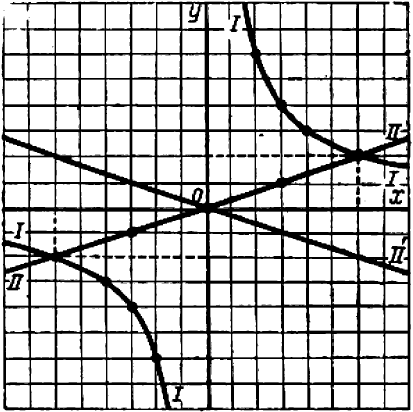
Черт. 49 показывает, что мы имеем здесь дело с пересечением гиперболы 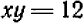 (1) и прямой
(1) и прямой 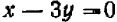 (2).
(2).
Если бы вместо системы (1—2) была задана система 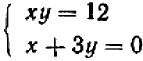 ,то вместо уравнения (3) у нас получилось бы уравнение
,то вместо уравнения (3) у нас получилось бы уравнение
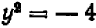 (3′) которое, очевидно, не имеет ни одного корня (так как правая часть отрицательна, а левая не может быть отрицательной).
(3′) которое, очевидно, не имеет ни одного корня (так как правая часть отрицательна, а левая не может быть отрицательной).
Отсюда следует, что система ( 1 — 2′) не имеет решений. Прямая (2′) на черт. 49 не пересекается с гиперболой (1).
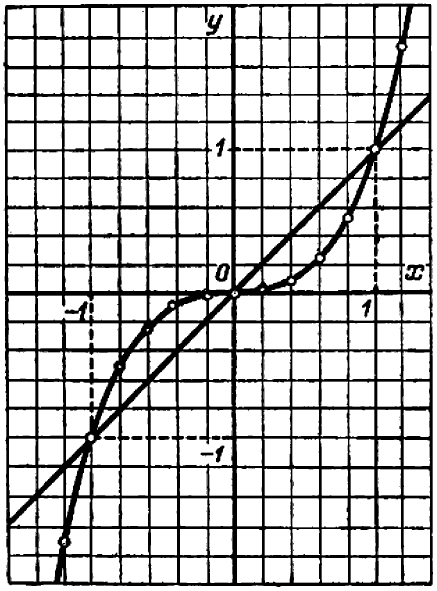
Пример:
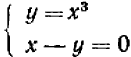 (1)(2).
(1)(2).
После исключения у мы получаем, перенося все члены в одну сторону и разлагая на множители: 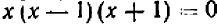 (3). Из этого уравнения вытекает одно из трех: или
(3). Из этого уравнения вытекает одно из трех: или 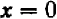 , или
, или  , или
, или 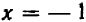 . Соответствующие значения
. Соответствующие значения 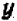 также равны
также равны 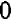 ;
; 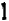 или
или 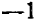 . Итак, возможны только три решения:
. Итак, возможны только три решения: 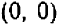 ,
, 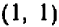 и
и 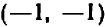 , и легко проверить, что их действительно три.
, и легко проверить, что их действительно три.
На черт. 50 видны три точки пересечения кривой 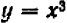 (1) с прямой линией
(1) с прямой линией 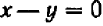 (2).
(2).
Пример:
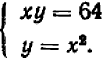 (1)(2).
(1)(2).
Исключая 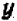 , мы получаем:
, мы получаем: 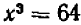 (3) и, значит
(3) и, значит 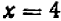 . Отсюда следует, что система (1—2) имеет единственное решение:
. Отсюда следует, что система (1—2) имеет единственное решение: 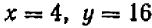 .
.
Гипербола (1) и парабола (2) пересекаются только в одной точке 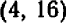 — см. черт. 51.
— см. черт. 51.
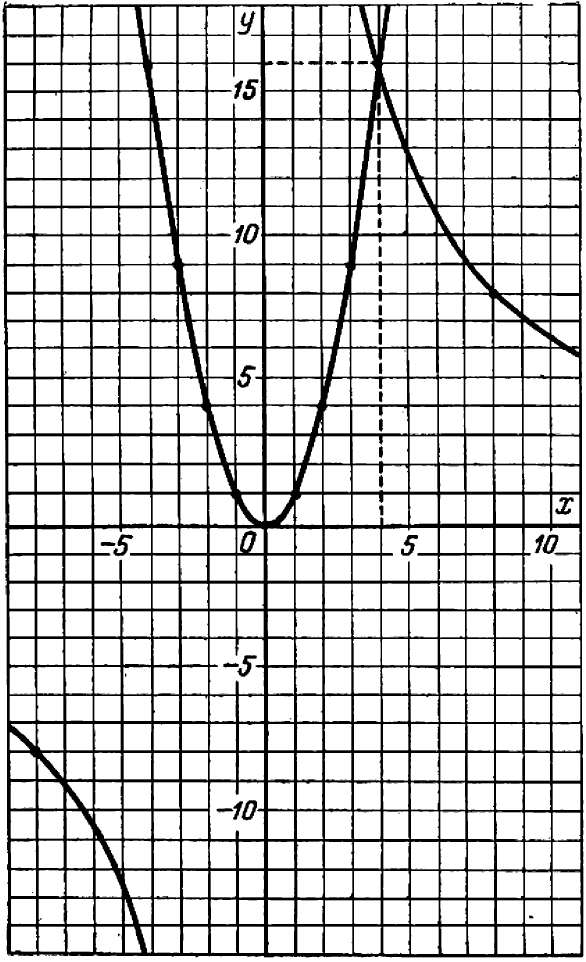
Исключение буквы из двух уравнений
Мы уже несколько раз пользовались выражением «исключить такую-то букву из двух данных уравнений».
Очень важно не только понимать смысл этих слов, но и уметь правильно ответить на вопрос: «Что значит исключить букву из двух уравнений?» Точный ответ таков:
Исключить названную букву из двух равенств (которые могут содержать также и другие буквы) — значит составить новое равенство, не являющееся тождеством и, кроме того, обладающее двумя свойствами: 1) оно есть следствие данных равенств, 2) оно не содержит названной буквы.
На вопрос же: «Как исключить букву из двух уравнений?»— нужно ответить: это можно сделать разными способами. Мы видели, например, в случае линейных уравнений, что для этого можно определить букву из одного уравнения и полученное выражение подставить вместо этой буквы в другое уравнение.
Но можно, наоборот, определить букву из второго уравнения и подставить в первое. Уравнивание коэффициентов представляет собой еще один, боль шей частью самый удобный, способ исключения буквы из линейных уравнений.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
