Тригонометрические функции произвольного угла с примерами решения

Тригонометрические функции произвольного угла

Что такое угол и угловой градус, мы предполагаем известными читателю из курса геометрии.

.В теории тригонометрических функций угол рассматривается как величина, могущая принимать любые положительные и отрицательные значения, а также и значение, равное нулю.

Например, если луч OA (или вектор 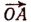), оставаясь в данной плоскости, совершит 10 полных оборотов вокруг точки О против движения часовой стрелки и еще ‘ повернется в том же направлении на угол 120°, то говорят, что этим движением луча OA образован угол, содержащий 360° • 10 + 120°, т. е. 3720°.

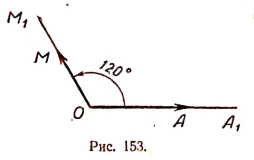
Допустим, что на рисунке 153 луч ОМ (или вектор 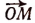) изображает положение луча OA после указанного выше его вращения вокруг точки О. Тогда мы скажем что луч ОМ составляет с лучом 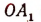(или вектор 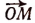с вектором 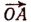) угол, содержащий 3720°.

Вращение луча OA в данной плоскости вокруг точки О может происходить в двух противоположных направлениях (против движения часовой стрелки и по ее движению).

Поэтому величину угла, полученного при вращении против движения часовой стрелки, принято выражать положительным числом, а образованного вращением по движению часовой стрелки — отрицательным числом.

Например, если луч 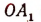совершит 10 полных оборотов по движению часовой стрелки и повернется в том же направлении еще на 120°, то мы скажем, что этим движением образован угол, равный — 3720° (минус 3720°).

Если луч 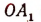совершит один полный оборот против движения часовой стрелки, то его положение совпадет с первоначальным, а угол, образованный этим движением, будет равен 360°. Если бы такое же вращение произошло по движению часовой стрелки, то угол был бы равен —360°.

Если луч 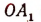совершит пол-оборота против движения часовой стрелки, то он займет положение, противоположное первоначальному, а угол, образованный этим движением, будет равен 180°. Если бы такое же вращение произошло по движению часовой стрелки, то угол был бы равен — 180°.

Если луч 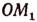не совершив никакого движения, находится в положении, совпадающем с лучом 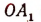то и в этом случае принято считать, что совпадающие луч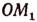и и также составляют угол, причем такой угол считается равным нулю.

Углы, по абсолютной величине большие 360°, мы можем наблюдать, например, при завертывании или отвертывании гайки ключом, при вращении воздушного винта и т. п.

Угол, описанный минутной стрелкой часов за 6,25 часа, содержит — 360° • 6 + (— 90°), т. е. — 2250°. Секундная же стрелка за это время опишет угол— 135000°.

Синус

В круге произвольного радиуса r (рис. 154) проведем два взаимно перпендикулярных диаметра. Один из них, например , назовем первым диаметром, а другой — вторым.

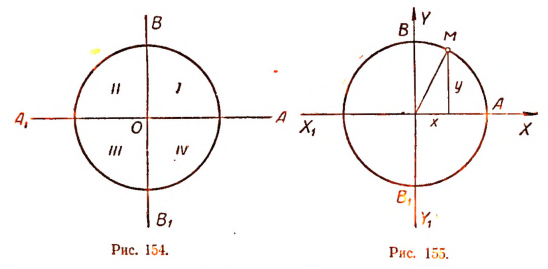
Первый диаметр независимо от его положения называют иначе начальным или горизонтальным. Второй диаметр называют вертикальным. Эти диаметры делят круг на четыре четверти (квадранта):

первая четверть —.АОВ, вторая — третья — 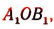четвертая —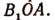

Для удобства обозначений и формулировок примем продолженный первый диаметр за ось абсцисс 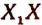, а продолженный второй диаметр — за ось ординат 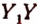(рис. 155).

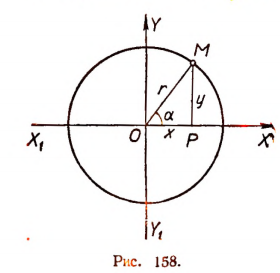
Вектор 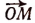, соединяющий начало координат О с произвольной точкой М окружности, называется радиусом-вектором точки М. Координаты точки М как текущей точки обозначим буквами х и у.

Радиус-вектор 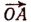называется начальным положением вращающегося радиуса-вектора .

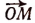Пусть текущий (подвижный) радиус-вектор совершил в плоскости координат вокруг точки О некоторое вращение в ту или другую сторону, начиная со своего начального положения 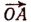, и, наконец, занял положение ОМ. Каков бы ни был угол поворота положительный или отрицательный, больший или меньший по абсолютной величине 360°), т. е. где бы ни расположился вектор 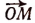, отношение 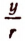называют синусом угла и обозначают символом sin . 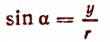Таким образом, (у — ордината конца текущего радиуса-вектора 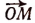, а r — его длина).

Длина r радиуса-вектора 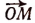является всегда положительным числом. Ордината же у положительна лишь для точек, лежащих в четвертях I и II; для точек же, лежащих в четвертях III и IV, она отрицательна. Для точек, лежащих на границе между верхней и нижней плоскостями, т. е. на оси 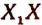, ордината у равна нулю.

Теорема:

Величина sin , т. е. отношения 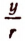, не зависит от величины радиуса окружности.

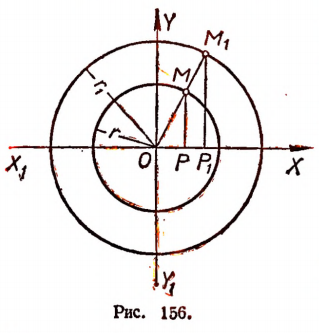
Доказательство.

Возьмем две окружности с радиусами 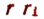(рис. 156) и пусть

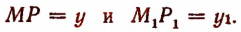
Пользуясь подобием треугольников и учитывая знаки ординат 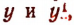получим

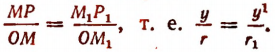
Это равенство справедливо, где бы ни оказался расположенным радиус-вектор 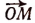. Теорема доказана.

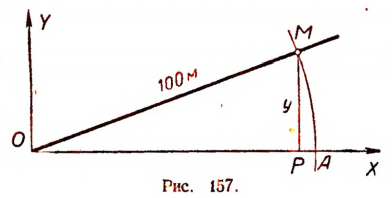
Графический способ нахождения приближен-ного значения отношения 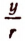. Построим на миллиметровой бумаге с помощью транспортира угол 20° (рис. 157) и опишем из его вершины как из центра окружность радиусом 100 мм.

На рисунке 157 оказалось, что у = MP = 34 мм. Следовательно, для угла 20° отношение 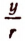(т. е. значение синуса угла в 20°) равно 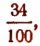т. е. 0,34 с точностью до 0,01. Итак, sin 20° = 0,34. Таким же способом можно находить значение отношения 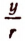и для любых других углов.

С помощью других (более совершенных) способов можно находить значение отношения 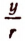с любой степенью точности. Например, для угла 20° отношение 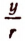с точностью до 0,00001 равно 0,34202, т. е. sin 20° = 0,34202.

Обратим внимание на то, что синусы углов, очень близких к нулю, являются числами, также очень близкими к нулю. Например,
sin 2° = 0,0349; sin 1° = 0,0175;
sin 30′ = 0,0087; sin 10′ = 0,0029.

Синусы углов, близких к 90°, близки к единице. Например,
sin 88° = 0,9994; sin 89° = 0,9998; sin 89°30′ = 0,9999.

Изменение синуса. Характер происходящих изменений синуса угла (т. е. отношения 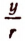) при изменениях угла можно записать в виде следующей таблицы:

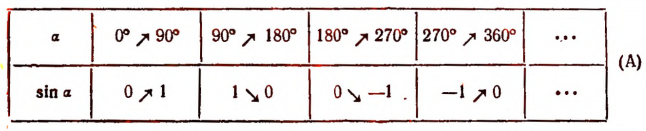
Таблица значений sin а с точностью до 0,001 для углов от 1 до 89°

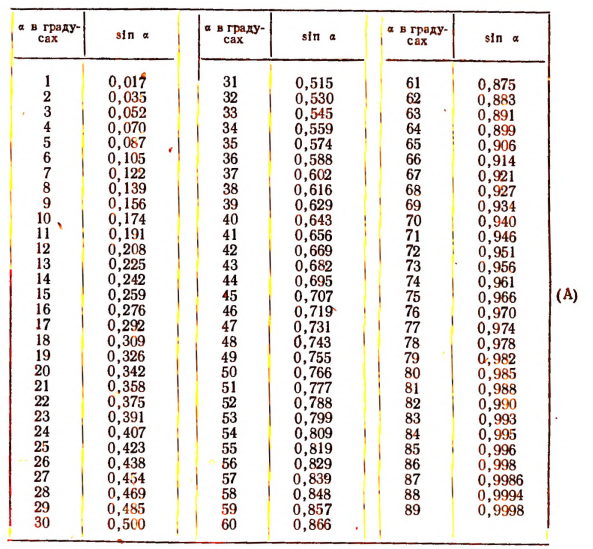
Таблицу (А) нужно читать и понимать так: если угол возрастает от 0 до 90°, то sin возрастает от 0 до 1; если угол возрастает от 90 до 180°, то sin убывает от 1 до 0 и т. д. Если угол станет возрастать от 360 до 450°, то sin снова станет возрастать от О до 1, т. е. процесс изменения sin станет повторяться после каждого полного оборота радиуса-вектора 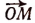. Поэтому

sin (360° n + а) = sin а,

где n — любое целое число (положительное, отрицательное или нуль).

Обратим внимание на то, что

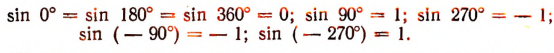
Каждому значению соответствует единственное определенное значение sin , т. е. sin есть однозначная функция аргумента .

Значения функции sin а суть числа отвлеченные.

С изменением угла изменяется и sin . Однако могут быть случаи, когда неодинаковые углы имеют одинаковые синусы. Например,

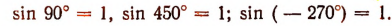
Синус по своему абсолютному значению никогда не может быть больше единицы, т. е.

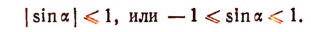
Примечание:

Символ sin не является синусом, а является лишь знаком синуса. Выражение же sin уже является синусом, а именно синусом угла .

Синус острого угла. В прямоугольном треугольнике ОМР (рис. 158) с острым углом отрезок MP есть катет, противолежащий углу , а отрезок ОМ есть гипотенуза. Поэтому синус острого угла прямоугольного треугольника есть отношение катета, противолежащего углу , к гипотенузе.

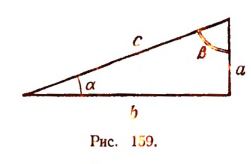
Пусть в прямоугольном треугольнике катеты равны а и b, гипотенуза равна с и острые углы обозначены и (рис. 159). Тогда

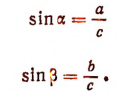
Задача:

Найти сторону вписанного в круг правильного девятиугольника по данному радиусу круга.

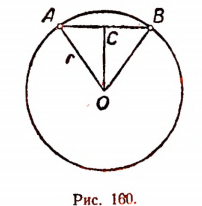
Пусть радиус круга равен r, а хорда АВ есть сторона правильного девятиугольника. Пусть 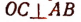(рис. 160). Тогда

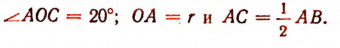
Из прямоугольного треугольника АОС следует, что sin 20° =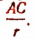
Отсюда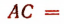

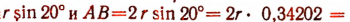
С грубым приближением сторона правильного вписанного в круг девятиугольника равна .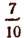

Косинус

Все вопросы, изложенные в предыдущем параграфе, относительно отношения 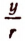т. е. синуса угла, распространяются соответствующим образом и на отношение 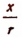. Отношение 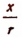(рис. 158) называется косинусом угла и обозначается символом cos .

Итак,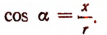

Абсцисса х конца радиуса-вектора 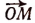положительна лишь для точек, расположенных в четвертях I и IV; для точек же, лежащих в четвертях II и III, она отрицательна. Для точек, лежащих на границе между левой и правой полуплоскостями, т. е. на оси 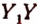, абсцисса х равна нулю.

Обратим внимание на то, что отношение 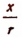для угла, близкого к нулю, т. е. косинус угла, близкого к нулю, близок к единице. Например,

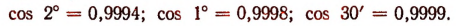
Косинусы углов, близких к 90°, близки к нулю. Например,

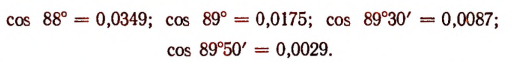
Изменение косинуса. Характер происходящих изменений косинуса угла (т. е. отношения при изменении угла можно записать в виде следующей таблицы:

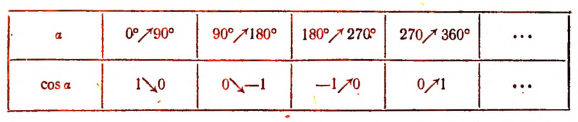
Эту таблицу нужно читать и понимать так: если угол возрастает от 0 до 90°, то косинус убывает от 1 до 0; если угол возрастает от 90 до 180°, то cos убывает от 0 до — 1 и т. д.

Если угол станет возрастать от 360 до 450°, то cos снова станет убывать от 1 до 0, т. е. процесс изменения cos станет повторяться после каждого полного оборота радиуса-вектора 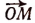. Поэтому

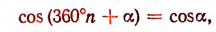
где n — любое целое число.

Обратим внимание на то, что

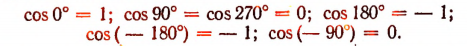
Каждому значению соответствует единственное определенное значение cos , т. е. cos есть однозначная функция аргумента .

Значения функции cos суть числа отвлеченные.

С изменением угла а изменяется и cos . Однако могут быть случаи, когда неодинаковые углы имеют одинаковые косинусы. Например,

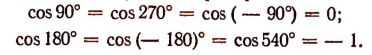
Косинус по своему абсолютному значению не может быть больше единицы, т. е. |cos < 1 , или — 1 cos < 1.

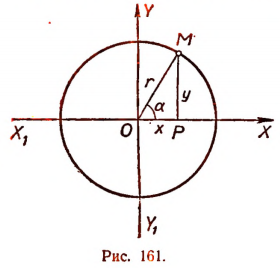
Косинус острого угла прямоугольного треугольника. В прямоугольном треугольнике ОМР (рис. 161) с острым углом отрезок ОР есть катет, прилежащий к углу , а отрезок ОМ есть гипотенуза. Поэтому косинус острого угла прямоугольного треугольника есть отношение прилежащего катета к гипотенузе.

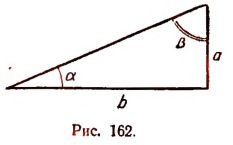
Пусть в прямоугольном треугольнике имеются катеты а и b гипотенуза с, а острые углы обозначены и (рис. 162), тогда

Тангенс

Отношение 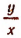(см. рис. 161) называется тангенсом угла и обозначается символом tg . Итак, tg = .

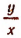Отношение 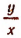для угла, близкого к нулю, т. е. тангенс угла, близкого к нулю, является числом, близким к нулю. Например, tg 2° = 0,035;
tg 1° = 0,017.

Если угол близок к 90°, но меньше, чем 90°, то его тангенс будет положительным числом, которое тем больше, чем ближе угол к 90°.

Когда радиус-вектор 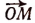окажется расположенным в четверти I, то и ордината у и абсцисса x будут положительными, а потому будет положительным и отношение 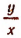, т. е. tg .

Если радиус-вектор окажется в четверти II, то tg < 0.
Для четверти III tg > 0 и для четверти IV tg < 0.

Если угол близок к 90°, но больше, чем 90°, то отношение 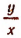, т. е. tg , будет числом отрицательным, которое по своей абсолютной величине тем больше, чем ближе угол к 90°.

Изменение тангенса. Изменения тангенса даны на следующей таблице:

Читается так: если угол возрастает от 0 до 90°, то tg возрастает от нуля до плюс бесконечности; если угол возрастает от 90 до 180° , то tg возрастает от минус бесконечности до нуля и т. д.

Процесс изменения tg повторяется после каждого пол-оборота радиуса-вектора 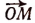. Поэтому

tg(180° n + ) = tga,

где n — любое целое число.

Обратим внимание на то, что tg 0° = tg 180° = tg 360° = =tg (—180°)=
= tg (— 360°)=0. Тангенс угла 90° не существует, так как при = 90° абсцисса x обращается в нуль и отношение 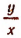теряет смысл.

По такой же причине не существует и тангенса угла 270°.

Наряду с этим принято писать, что 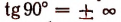(читается так: тангенс угла 90° равен плюс или минус бесконечности).

Также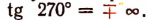

Мы сказали, что tg 90° не существует и что 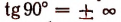. Но в этих двух утверждениях нет противоречия. Когда мы говорим, что тангенс равен бесконечности, то это и значит, что он не существует.

Запись 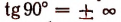характеризует картину изменения тангенса вблизи угла 90° слева и справа от него. Когда угол приближается к 90°, оставаясь меньше 90°, тангенс принимает положительные неограниченно возрастающие значения. Когда же угол , приближаясь к 90°, остается больше 90°, то тангенс принимает отрицательные значения, также неограниченно возрастающие по своей абсолютной величине.

Каждому значению , взятому на промежутке (0°; 90°) или (90°; 180°) и т. д., соответствует единственное определенное значение tg, т. е. tg есть на каждом из указанных промежутков однозначная функция аргумента .

Значения функции tg есть числа отвлеченные.

С изменением угла изменяется и tg . Однако могут быть случаи, когда неодинаковые углы имеют одинаковые тангенсы. Например,
tg 225° = tg 45° = 1.

Функция tg, изменяясь, может принимать любое действительное значение.

Тангенс острого угла прямоугольного треугольника. В прямоугольном треугольника ОМР (см. рис. 161) с острым углом отрезок MP есть катет, противолежащий углу , а ОР прилежащий. Поэтому тангенс острого угла прямоугольного треугольника есть отношение противолежащего катета к прилежащему.

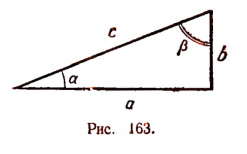
Возьмем прямоугольный треугольник с катетами a и b, гипотенузой с и острыми углами и (рис. 163); тогда

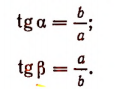
Замечание:

Функции sin, cos , tg возникли исторически из таких задач, в которых надо было находить одни элементы треугольника в зависимости от других. Поэтому эти функции получили название тригонометрических функций. Слово «тригонометрия» составлено из греческих слов: «тригоном» — треугольник и «метрезис» — измерение. Но тригонометрические функции оказались необычайно мощным средством для решения не только геометрических вопросов, а но и многочисленных весьма важных вопросов математического анализа, естествознания и техники.

Замечание:

Знак sin называется не синусом, а лишь знаком синуса и сам по себе никакой величины не изображает. Он является знаком нового математического действия. Это относится и к знакам cos или tg.

Значения всех тригонометрических функций суть числа отвлеченные.

Замечание:

Выражение 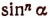надо понимать как 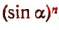. Например,

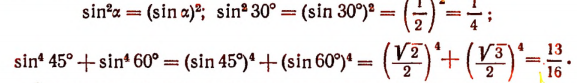
Сказанное распространяется и на остальные тригонометрические функции.

Функции углов 30, 60 и 45°

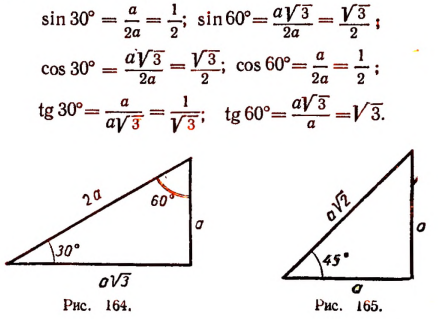
Возьмем прямоугольный треугольник с острым углом 30° (рис. 164). Обозначим катет, лежащий против угла в 30°, буквой . Тогда гипотенуза будет равна 2а; другой катет будет равен (по теореме Пифагора) 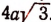. Поэтому

Возьмем прямоугольный треугольник с острым углом 45° (рис. 165). Обозначим каждый из равных катетов буквой а. Тогда гипотенуза будет равна 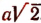. Поэтому

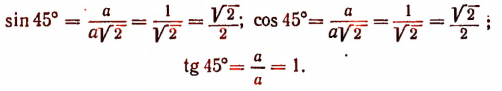
Радианное измерение углов

Для измерения углов употребляются две основные единицы: градус и радиан.

Градус есть 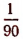часть прямого угла.

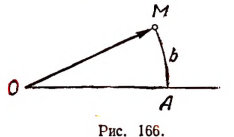
Радианом называется такой центральный угол, которому соответствует дуга, по длине равная радиусу. Угол АОМ будет радианом, если длина дуги АвМ равна длине радиуса OA (рис. 166). Если длина дуги в два раза больше длины радиуса, то центральный угол будет содержать два радиана. Если точка М пройдет по окружности путь, равный, например, 40 радиусам, то угол, описанный радиусом-вектором 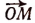, будет содержать 40 радианов и т. д.

Если длина дуги равна l, а длина радиуса R, то число радианов w, содержащихся в соответствующем угле, будет равно отношению ,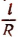
т. е.

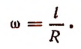
Предполагается, что длина дуги и длина радиуса выражаются в одной и той же единице длины.

При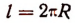

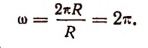
Следовательно, полный угол, т. е. угол в 360°, содержит 2 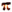радианов.

Развернутый угол содержит 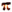радианов. Так как в развернутом угле содержится 180°, то 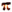радианов содержат 180°, а один радиан 180° равен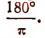

Взяв 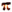= 3,14159, получим, что 1 радиан = 57°17’44». Нельзя говорить, что 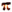равно 180°, а следует говорить 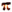радианов равны 180°.

Если же взять, скажем, 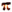рублей, то получится нечто другое, а именно получится приблизительно 3 рубля 14 копеек.

Чтобы перевести градусное измерение в радианное, надо исходить из равенства

180° = 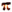радианам.

Найдем, например, радианное измерение угла 75°.

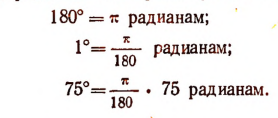
Чтобы перевести радианное измерение в градусное, надо исходить из равенства

Найдем, например, градусное измерение угла, содержащего 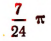радианов.

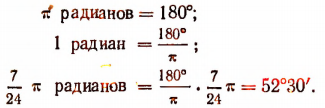
Полезно запомнить значения простейших углов в радианном измерении, приводимые в нижеследующей таблице:

2* я/2 я/4 я/6 | я/8 2*/3 5д/6 Зя/2

Тригонометрические функции отвлеченного числа

Выражение, например, sin 2° означает синус угла, содержащего 2°.

Общепринято считать, что по определению выражение sin 2, т. е. синус отвлеченного числа 2, есть синус угла, содержащего два радиана. Выражение sin 3 есть синус угла, содержащего три радиана; sin 0,184 есть синус угла, содержащего 0,184 радиана; sin (cos 60°) есть синус угла, содержащего 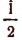радиана; sin 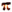есть синус угла, cодержащего 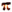радианов, т. е. угла, содержащего 180°, и т. д. Очевидно, что

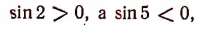
так как угол, содержащий 2 радиана, оканчивается в четверти II, а угол, содержащий 5 радианов, — в четверти IV. Очевидно также, что

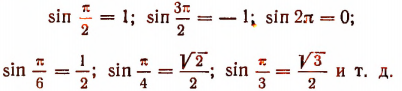
Запись sin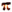 = sin 180° является правильной; запись же 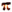= 180° будет неправильной, так как не 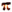равняется 180°, а 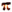радианов равняются 180°.

Все сказанное о синусе отвлеченного числа распространяется соответствующим образом и на остальные тригонометрические функции.

Определение:

Тригонометрической функцией отвлеченного числа х (числового аргумента х) называется функция угла, содержащего х радианов.

В дальнейшем мы будем употреблять на равных правах выражения: «тригонометрическая функция угла» или «тригонометрическая функция числа». Например, говорить «синус угла» или «синус числа» и т. д.

Таблица
значений синуса числового аргумента х (с точностью до 0,0001) для значений от х= 0 до х= 1,5, взятых через 0,1

Таблица
значений некоторых углов в радианной и градусной мере

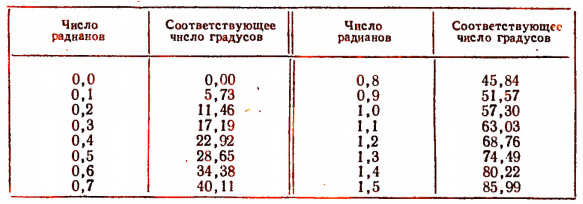
Более полные таблицы значений тригонометрических функций числового аргумента и значений углов в радианной и градусной мере имеются, например, в книге «Математические таблицы» (пособие для учителей, Учпедгиз, 1952 г.).

Первые три группы формул

Выражения функций угла — через функции угла
(первая группа формул)

Концы радиусов-векторов, соответствующих углам — и , имеют одну и ту же абсциссу х (рис. 167). Поэтому cos(— ) = cos . Например,

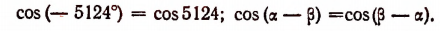
Это означает, что косинус является четной функцией (см. стр. 347).

Концы радиусов-векторов, соответствующих углам — и , имеют одинаковые по абсолютной величине и противоположные по знаку ординаты (см. рис. 167). Поэтому sin (—) =— sin . Например, ‘

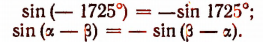
Это означает, что синус является нечетной функцией (см. стр. 347).

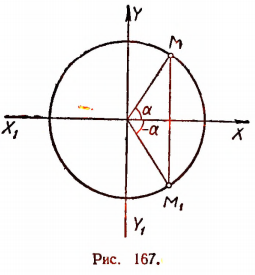
Концы радиусов-векторов, соответствующих углам — и , имеют одну и ту же абсциссу х и ординаты, одинаковые по абсолютной величине, но противоположные по знаку (см. рис. 167). Поэтому

tg (- ) = — tg.

Например.

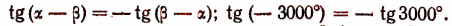
Это означает, что тангенс является также нечетной функцией. Итак, мы получили первую группу формул:

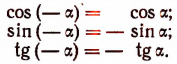
Формулы приведения (вторая группа формул)

Формулами приведения называются следующие формулы:

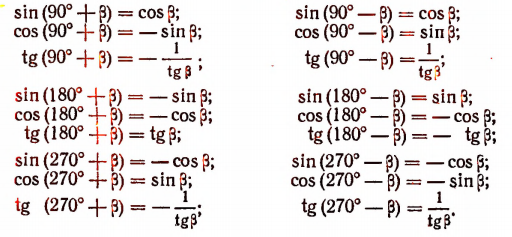
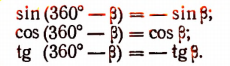
Заучивать эти формулы не нужно. Нужно лишь усвоить правило, по которому они записываются. Разъясним это правило.

Перед правой частью формулы ставится знак минус лишь в тех случаях, когда левая часть (в предположении, что — острый положительный угол) является числом отрицательным.

Примеры:

sin (180° + ) является отрицательным числом, так как
180° < 180° + < 270°. Поэтому в формуле

sin (180° + ) = — sin

в правой части поставлен знак минус.

sin (180° — ) является положительным числом, так как
90° < 180° — < 180°. Поэтому в формуле

sin (180° — ) = sin

знака минус в правой части нет.

Продолжим разъяснения дальше. В тех формулах, в которых фигурирует угол 180° или 360°, название функции в правой части берется то же, что и в левой части.

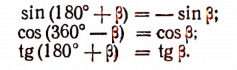
В тех же формулах, в которых фигурируют углы 90° или 270°, название сиНус изменяется на косинус, название косинус — на синус, вместо тангенса появляется единица, деленная на тангенс.

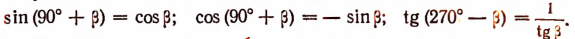
Приведем примеры на изменение правила в целом.

Пусть требуется написать формулу для cos (180° + ). Так как
180° < 180° + < 270°, значит, cos (180° + ) есть число отрицательное. Поэтому перед правой частью ставится знак минус. Далее, в выражении cos (180° + ) фигурирует угол 180°. Поэтому название функции берется то же, что и в левой части. Получим:

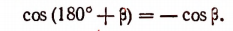
Пусть требуется написать формулу для tg (90° + ). Так как
90° < 90° + < 180°, значит, tg (90° + ) — число отрицательное. Поэтому в правой части ставится знак минус. Далее, в выражении
tg (90° + ) фигурирует угол 90°. Поэтому тангенс заменяется на единицу, деленную на тангенс. Получаем:

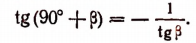
Примечание:

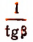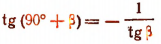Выражение можно записать в виде Тогда формулу можно записать в виде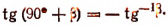

Теперь в качестве примера докажем справедливость каких-нибудь двух формул, например формул для sin (180° + ) и tg (270° +).

Рассмотрим положение радиуса-вектора для углов и 180° + (рис. 168).

Ординаты концов этих радиусов-векторов одинаковы по абсолютной величине и -противоположны по знаку. Поэтому sin (180° + ) =
= — sin .

Рассмотрим положение радиусов-векторов для углов и 270° + (рис. 169). .

Ордината конца второго радиуса-вектора равна минус абсциссе первого. Абсцисса же конца второго радиуса-вектора равна ординате конца первого. Поэтому

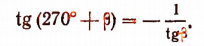
Записывая и доказывая формулы приведения, мы предполагали, что 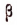есть острый положительный угол. Однако все эти формулы справедливы в общем случае, т. е. для любых значений 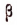. Например,

sin(180° + 3726°) = — sin 3726°.

На доказательстве общности формул приведения мы останавливаться не будем.

С помощью формул, выражающих функции угла — через функции угла , и формул приведения можно функцию любого угла выразить через функцию угла, находящегося в границах от 0 до 45° включительно.

Примеры:

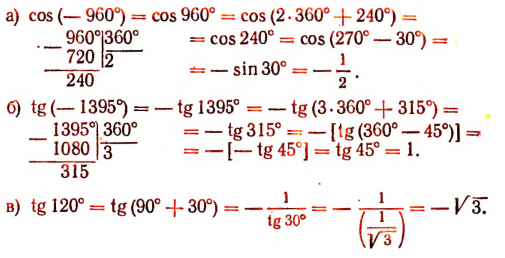
Дополнительные углы. Два угла 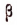и 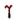называются дополнительными, если их сумма равна 90°. Например, дополнительными будут следующие пары углов:

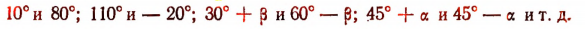
Чтобы получить угол, дополнительный данному углу w, достаточно из 90° вычесть w. Например, если данный угол равен 1°, то ему дополнительный угол будет равен 90°—1°, т. е. 89°. Если данный угол 120°, то ему дополнительный угол будет равен 90° — 120°, т. е. — 30°.

Если данный угол 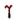+ 40°, то дополнительный угол будет равен
90 —(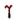 + 40°), или 50° —.

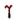Формулы приведения 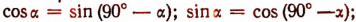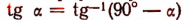можно сформулировать так:

Косинус любого угла равен синусу дополнительного.
Синус любого угла равен косинусу дополнительного.
Тангенс любого угла равен минус первой степени тангенса дополнительного угла.

Формулы приведения для тригонометрических функций числового аргумента

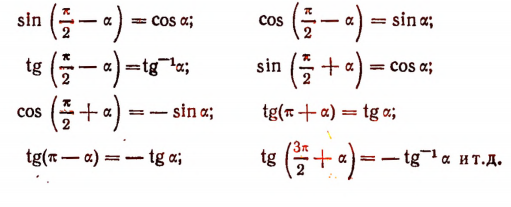
Формулы, связывающие функции одного и того же угла
(третья группа формул)

Первая формула: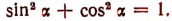

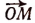Вывод. Пусть — какой угодно угол и — соответствующий ему радиус-вектор.Где бы ни оказался расположенным радиус-вектор ,

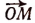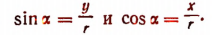
Отсюда

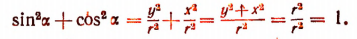
Вторая формула: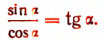

Вывод. По определению

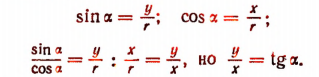
Следовательно,

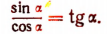
Эта группа формул позволяет выражать все тригонометрические функции в зависимости от любой одной из них.

Примеры:

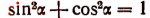1. Выразить cos и tg в зависимости от sin . Из формулы следует, что

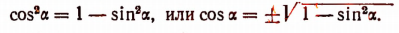
Из формулы 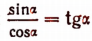следует, что

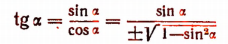
(Аналогично можно sin и tg выразить в зависимости от соs.)

Мы здесь получили для cos и для tg по два значения (положительное и отрицательное). Чем это объяснить? Это объясняется так. Если sin есть положительное число, то радиус-вектор , соответствующий углу , расположится либо в четверти I, либо в четверги II. В первом случае соs и tg окажутся положительными числами, а во втором — отрицательными.

Если sin есть отрицательное число, то расположится либо в четверти III, либо в IV. В первом случае cos окажется отрицательным числом, а во втором — положительным, т. е. опять может иметь два значения. В первом случае tg окажется положительным, а во втором — отрицательным, т. е. tg может иметь два значения.

Выразить cos и tg в зависимости от sin , зная, что 90° < < 180°.

При данных условиях cos и tg должны быть числами отрицательными. Поэтому

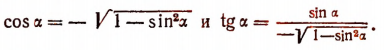
Здесь мы получим только по одному ответу, так как знали, что радиус-вектор 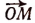расположен в четверти II.

2. Выразить cos и sin в зависимости от tg :

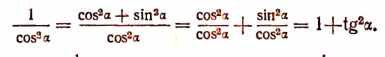
Отсюда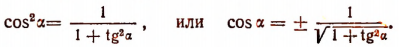

Далее,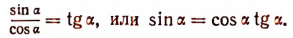

Отсюда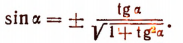

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат