Действительные числа в математике с примерами решения и образцами выполнения

Оглавление:

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби.

Натуральные числа

Натуральные числа выражают количество подлежащих счету однотипных или неоднотипных предметов; таковы, например, числа один, два, десять, двадцать, его, двести пятьдесят шесть, тысяча и т. д.

Понятие натурального числа относится к простейшим, первоначальным понятиям математики и не подлежит определению через другие, более простые понятия.

Натуральные числа могут быть естественным образом расположены по их возрастанию: каждое следующее натуральное число получается из предыдущего прибавлением единицы. Записанные в порядке возрастания:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … ,

натуральные числа образуют натуральный ряд. Многоточие показывает возможность неограниченного продолжения этого ряда. В этом смысле говорят, что имеется бесконечное множество натуральных чисел. Единица — наименьшее натуральное число; наибольшего числа натуральный ряд не имеет.

Напомним принцип записи натуральных чисел в десятичной системе счисления при помощи десяти цифр

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Цифры, участвующие в записи числа, при чтении их справа налево указывают последовательно, сколько в данном числе содержится единиц, затем десятков, сотен, тысяч и т. д. Вообще, цифра, стоящая на k-м месте, считая справа, покажет, сколько данное число содержит единиц разряда 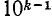Действительные числа . Так, например,

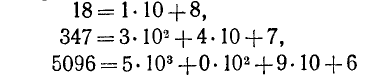
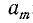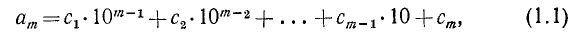
и, в общей форме, для m-значного числа Действительные числа :

где 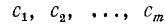Действительные числа —цифры, при помощи которых число 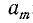записывается в виде 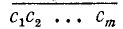(здесь черта сверху ставится, чтобы не смешивать число 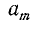с произведением чисел ).

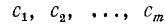Замечание:

Десятичная система счисления —не единственно возможная. В древности (в Вавилоне) использовалась система счисления, в которой, наряду с десяткой, в основу было положено число 60 (шестидесятеричная система счисления). Ее влияние сохранилось до сих пор в делении часа на 60 минут, окружности на 360 градусов и т. д. В настоящее время при использовании электронных вычислительных машин, в процессе программирования применяются двоичная и восьмеричная системы счисления. Приведем для примера запись нескольких чисел в троичной системе. В этом случае используем только три цифры 0, 1, 2 в их обычном смысле. Число 3 в троичной системе играет роль десятки в десятичной системе счисления и должно обозначаться как 10. Вместо 32 = 9 будем писать 100 и т. д. Вот запись нескольких чисел в десятичной и троичной системах счисления:

Десятичная система Троичная система

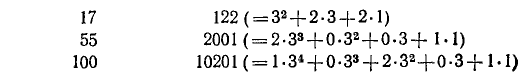
В дальнейшем мы будем пользоваться исключительно десятичной системой счисления.

В арифметике и алгебре рассматривают различные действия над числами: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня и т. д. Первые четыре из этих действий называют арифметическими или рациональными. Но только два из них—сложение и умножение—безусловно выполнимы в области натуральных чисел: сумма и произведение натуральных чисел суть снова натуральные числа.

Сформулируем законы, которым подчиняются действия сложения и умножения; строгие определения этих действий и обоснование их свойств (выводимых из небольшого числа аксиом) рассматриваются в теоретической арифметике и здесь опускаются.

Переместительный (или коммутативный) закон сложения:

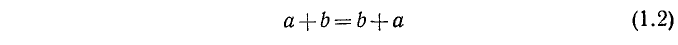
— от перестановки слагаемых сумма не изменяется.

Переместительный (или коммутативный) закон умножения:

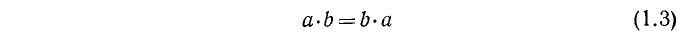
— от перестановки сомножителей произведение не изменяется. В дальнейшем, по большей части, в записи произведения 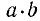Действительные числа точку опускаем и пишем просто ab.

Сочетательный (или ассоциативный) закон сложения:

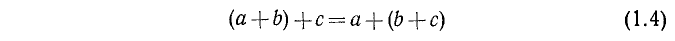
— сумма не зависит от группировки слагаемых.

Этот закон позволяет записывать сумму нескольких слагаемых без скобок. Например:

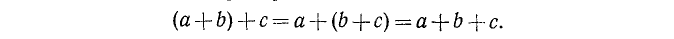
Сочетательный (или ассоциативный) закон умножения:

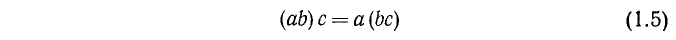
— произведение не зависит от группировки сомножителей.

Этот закон позволяет писать произведение нескольких сомножителей без скобок. Например:

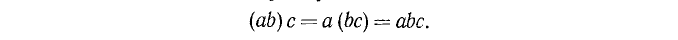
Распределительный (или дистрибутивный) закон умножения относительно сложения:

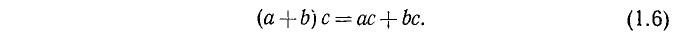
Этот закон лежит в основе правила раскрытия скобок, которым часто пользуются в вычислениях и преобразованиях.

Простые и составные числа и признаки делимости

Если а и b — натуральные числа, причем

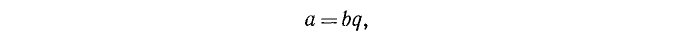
где q — также натуральное число, то говорят, что q — частное от деления числа а на число b, и пишут: q — a/b. Также говорят, что а делится на b нацело или без остатка. Всякое число b, на которое а делится без остатка, называется делителем числа а. Само число а по отношению к своему делителю называется кратным. Таким образом, числа, кратные b, суть числа b, 2b , 3b, …

Числа, кратные числу 2 (т. е. делящиеся на 2 без остатка), называются четными. Числа, не делящиеся на 2 нацело, называются нечетными. Каждое натуральное число либо четно, либо нечетно.

Если каждое из двух чисел 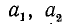Действительные числа является кратным числа b, то и сумма 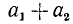— кратное числа b. Это видно из записи

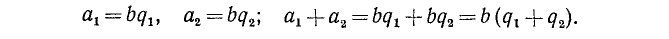
Обратно, если 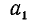Действительные числа и 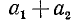— кратные числа b, то 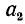— также кратное числа b.

Всякое отличное от единицы натуральное число имеет по меньшей мере два делителя: единицу и самоё себя. Если число не имеет никаких других делителей, кроме себя и единицы, оно называется простым. Число, имеющее какой-нибудь делитель, отличный от себя и единицы, называют составным числом. Единицу принято не относить ни к простым, ни к составным числам. Вот несколько первых простых чисел, записанных в порядке возрастания:

2, 3, 5, 7, 11, 13, 17, …

Число 2—единственное четное простое число; все остальные простые числа — нечетные.

То, что простых чисел имеется бесконечное множество, было установлено еще в древности (Евклид, III век до нашей эры).

Идея доказательства Евклида бесконечности множества простых чисел весьма проста. Допустим, что простых чисел — конечное число; перечислим их все, например, расположив в порядке возрастания:

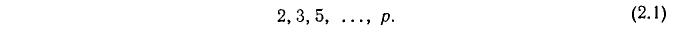
Составим число, равное их произведению плюс единица:

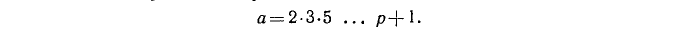
Очевидно, что это число не делится ни на одно из чисел (2.1). Следовательно, либо оно само является простым, либо, если оно составное, то имеет простой делитель, отличный от чисел (2.1), что противоречит допущению о том, что в записи (2.1) перечислены все простые числа.

Это доказательство представляет большой интерес, так как дает пример доказательства теоремы существования (бесконечного множества простых чисел), не связанного с фактическим отысканием объектов, существование которых доказывается.

Можно доказать, что всякое составное число представимо в виде произведения простых чисел. Так, например,

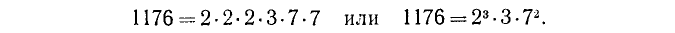
Как видно нз этого примера, в разложении данного числа на простые множители некоторые из них могут повторяться несколько раз.

В общем случае в записи разложения числа а на простые множители

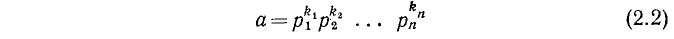
подразумевается, что все простые числа 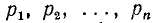Действительные числа различны между собой (причем 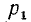повторяется множителем 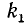раз, 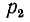повторяется множителем 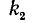раз и т. д.). При этом условии можно доказать, что разложение единственно с точностью до порядка записи сомножителей.

При разложении числа на простые множители полезно бывает использовать признаки делимости, позволяющие выяснить, делится ли данное число на некоторое другое число без остатка, не производя самого деления. Мы выведем признаки делимости на числа 2, 3, 4, 5, 9

Признак делимости на 2. На 2 делятся те и только те числа, в записи которых последняя цифра выражает четное число (0, 2, 4, 6 или 8).

Доказательство:

Представим число 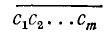Действительные числа в виде

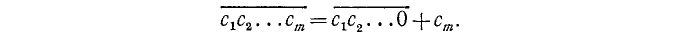
Первое слагаемое в правой части делится на 10 и потому — четное; сумма будет четной тогда и только тогда, когда ст— четное число.

2. Признак делимости на 4. Число 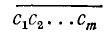Действительные числа делится на 4 тогда и только тогда, когда двузначное число, выражаемое его последними двумя цифрами, делится на 4.

Доказательство:

Представим число 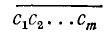Действительные числа в виде

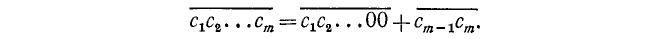
Первое слагаемое делится на 100 и тем более на 4. Сумма будет делиться на 4 в том и только в том случае, если 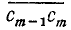Действительные числа делится на 4.

3. При знак делимости на 5. На 5 делятся те и только те числа, запись которых заканчивается цифрой 0 или цифрой 5.

Рекомендуем читателю доказать этот признак самостоятельно.

4. Признаки делимости на 3 и на 9. Число делится на 3 (соответственно на 9) в том и только в том случае, когда сумма его цифр делится на 3 (соответственно на 9).

Доказательство:

Запишем очевидные равенства

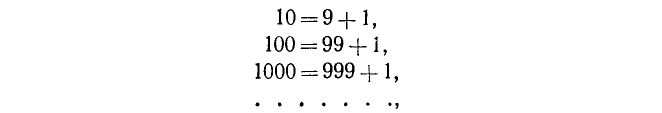
в силу которых можно число 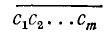Действительные числа представить в виде

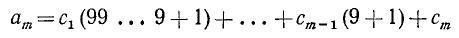
или

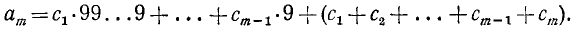
Видно, что все слагаемые, кроме, быть может, последней скобки, делятся на 9 (и тем более на 3). Поэтому данное число делится на 3 или на 9 тогда и только тогда, когда делится на 3 или на 9 сумма его цифр 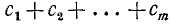Действительные числа .

Наибольший общий делитель и наименьшее общее кратное

Если каждое из натуральных чисел а, b, …, f делится нацело на натуральное число k, то говорят, что число k является их общим делителем. Так, числа 108 и 144 имеют ббщие делители 1, 2, 3, 6, 9, 12, 18, 36. Если два или несколько чисел не имеют общих делителей, отличных от единицы, то эти числа называются взаимно простыми. Так, числа 49 и 121 взаимно простые.

Так как данные числа а, b, …, f могут иметь лишь конечное число общих делителей, то среди их общих делителей имеется наибольший; в случае взаимно простых чисел он равен единице.

Для наибольшего общего делителя (н.о.д.) применяется обозначение

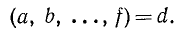
Например:

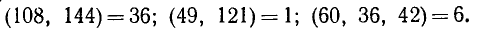
Наибольший общий делитель двух чисел можно находить, пользуясь их разложением на простые множители. Пусть требуется, например, найти н.о.д. чисел 504 и 540. Разложим каждое из них на простые множители:

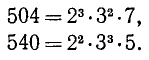
Мы видим, что, кроме единицы, общими делителями данных чисел являются

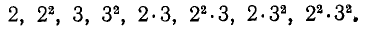
Таким образом,

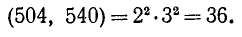
В общей форме процесс отыскания н.о.д. можно описать на примере двух чисел следующим образом. Запишем разложение данных чисел а и b на попарно различные простые множители:

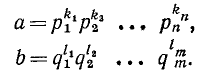
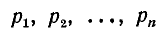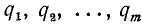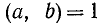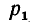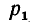Может случиться, что среди чисел Действительные числа нет ни одного, равного кому-либо из чисел . Тогда а и b—взаимно простые, . Если, например, совпадает с одним из чисел , то оба числа а и b делятся на Действительные числа взятое в степени, меньшей из двух степеней, с которыми это число 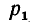входит в разложение каждого из чисел а и b. Поэтому для получения н.о.д. чисел а и b следует: 1) выбрать все одинаковые простые множители, входящие в разложения а и b 2) каждый из них взять в степени, меньшей из двух степеней, с которыми этот множитель входит в указанные разложения; 3) взять произведение найденных таким путем общих множителей—оно и будет н.о.д. чисел а и b.

Подобным же образом находится и н.о.д. нескольких чисел.

Имеется и иной метод отыскания н.о.д. двух чисел; о нем рассказывается в п. 4.

Если число m является кратным для каждого из чисел а, b, …, f (т. е. делится на любое из этих чисел нацело), то m называется общим кратным чисел а, b, …, f. В частности, произведение нескольких натуральных чисел всегда является их общим кратным. Среди всех общих кратных данных чисел а, b, …, f имеется наименьшее; оно называется наименьшим общим кратным (и.о.к.) данных чисел и обозначается так:

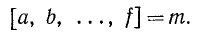
Н.о.к. двух или нескольких чисел также удобно находить, используя разложение этих чисел на простые множители. Так, для чисел

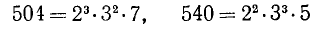
мы найдем н.о.к., взяв каждый из простых множителей в их разложениях в большей из двух степеней, в которых он входит в эти разложения:

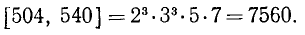
Аналогично,

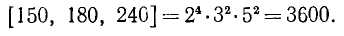
Итак, для отыскания н.о.к. нескольких чисел следует: 1) выписать все простые множители, входящие в разложение хотя бы одного из этих чисел; 2) взять каждый из этих простых множителей в наибольшей из степеней, в которых он входит в разложения данных чисел; 3) взять произведение найденных степеней простых сомножителей—оно и будет н.о.к. данных чисел.

Нетрудно заметить, что для двух взаимно простых чисел а и b

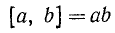
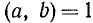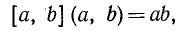
— н.о.к. двух взаимно простых чисел равно произведению этих чисел. Отметим, без доказательства, более общее соотношение (оно сводится к предыдущему в случае, если Действительные числа ):

имеющее место для любых двух чисел: произведение наибольшего общего делителя на наименьшее общее кратное двух чисел равно произведению этих чисел.

Целые числа. Рациональные числа

Если сложение и умножение натуральных чисел всегда приводят вновь к натуральному числу, то уже вычитание не всегда выполнимо, если оставаться в области арифметики натуральных чисел. Для возможности образования разности любых двух натуральных чисел возникает необходимость расширить совокупность чисел, вводя нуль и целые отрицательные числа —1, —2, —3, …, —п, … Натуральные числа называются также целыми положительными числами. Если хотят подчеркнуть, что данное число положительное, то перед ним ставится знак «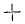 Действительные числа », но, как правило, пишут не +4, а просто 4 и т. д., перед отрицательными же числами знак «—» ставится обязательно. Число нуль не относят ни к отрицательным, ни к положительным числам. Числа n и —n называют противоположными.

Вся совокупность целых чисел

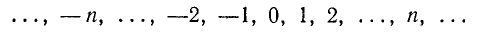
состоит из целых положительных (натуральных) чисел, целых отрицательных чисел и нуля.

Теперь уже, во множестве всех целых чисел, действие вычитания (так же как и сложения) всегда выполнимо. При этом, действие вычитания может быть сведено к сложению с числом, противоположным вычитаемому:

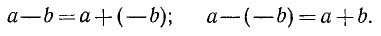
Мы предполагаем известными правила действий с целыми (положительными и отрицательными) числами.

Для умножения целых чисел вводится известное правило знаков: если a, b положительные, то

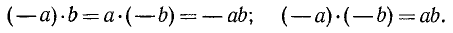
В частности, 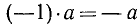Действительные числа .

Таким образом, произведение двух чисел одного знака есть положительное число, двух чисел противоположного знака — отрицательное число. Число, противоположное данному, равно произведению данного числа на минус единицу.

Произведение любого числа на нуль равно нулю.

Множество чисел, обладающее тем свойством, что сумма, разность и произведение двух любых чисел этого множества снова ему принадлежат, называется числовым кольцом. В числовом кольце неограниченно выполнимы целые рациональные действия, т. е. рациональные действия, кроме, быть может, деления. Натуральные числа не образовали числового кольца, так как действие вычитания не всегда приводило вновь к натуральному числу. Целые числа образуют числовое кольцо, кольцо целых чисел.

Множество чисел, в котором выполнимы все рациональные действия, включая и деление (кроме деления на нуль, которое невозможно), называется числовым полем. Целые числа не образуют поля, так как в области целых чисел деление не всегда выполнимо.

В связи с этим множество целых чисел вновь расширяют до множества рациональных чисел. Рациональным числом называется число, представимое в виде a/b, где числитель а—целое, а знаменатель b—натуральное число. Если а делится на b нацело, то рациональное число — целое; в противном случае рациональное число называется дробным. Оно считается положительным, если а—положительное, и отрицательным, если а—отрицательное.

Дробь a/b можно сократить, разделив числитель и знаменатель на н.о.д. чисел а и b. В дальнейшем, как правило, при записи рационального числа в виде а/b дробь а/b считается несократимой, т. е. а и b полагаются взаимно простыми числами.

В области рациональных чисел неограниченно выполнимы все рациональные действия (кроме деления на нуль): сумма, разность, произведение и частное рациональных чисел также являются рациональными числами. Поэтому рациональные числа образуют числовое поле—поле рациональных чисел.

Практически правила действий над рациональными числами хорошо известны из арифметики. Для сложения и умножения справедливы те же основные законы, что и для натуральных чисел (п. 1).

Каждое рациональное число х, если оно само не является целым, заключено между двумя соседними целыми числами: 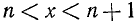Действительные числа . Так, например, 7/2 лежит между 3 и 4, 13/54 — между 0 и 1, —8/3 — между —3 и —2.

Введем следующее определение: целой частью числа называется наибольшее целое число, не превосходящее данного.

Целая часть числа х обозначается так: [х]. Например:

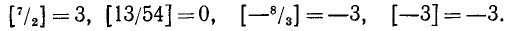
Разность между данным числом и его целой частью называется дробной частью числа. Дробная часть числа х равна х — [х] и иногда обозначается через (х). В наших примерах дробная часть чисел 7/2, 13/54, —8/3, —3 равна соответственно 1/2, 13/54, 1/3, 0. Дробная часть целого числа равна нулю, так как целое число совпадает со своей целой частью. Для любого числа его дробная часть неотрицательна и строго меньше единицы:

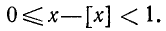
Всякое рациональное число однозначно разлагается на сумму целой и дробной частей, например:

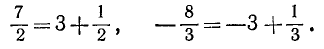
С разложением рационального числа на целую и дробную части связано понятие деления (натуральных чисел) с остатком. Число a/b однозначно представляется в виде суммы своей целой части [ a/b ] = q и дробной части h (не исключено, что целая или дробная часть равна нулю):

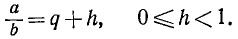
Обозначим bh = r (ясно, что Действительные числа ). Тогда

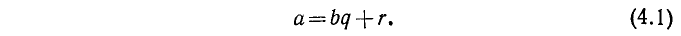
Здесь q называется частным, а r —остатком при делении а на b. При этом остаток удовлетворяет неравенствам 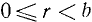Действительные числа .

Равенство (4.1) можно использовать для такого более формального определения понятий частного и остатка. Пусть a, b—натуральные числа. Два целых неотрицательных числа q, г называются соответственно частным и остатком от деления а на b, если выполняется равенство (4.1) и неравенство 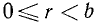Действительные числа .

На процессе деления с остатком основывается способ отыскания н.о.д. двух чисел; исторически он связан с теорией измерения отрезков у Евклида (см. п. 163) и носит название алгоритма Евклида.

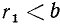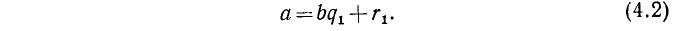
Пусть даны два натуральных числа а и b < а. Произведем деление а на b; если а разделится на b нацело, то b—н.о.д. чисел а, b В противном случае получится некоторый остаток Действительные числа :

Теперь будем делить b на 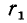Действительные числа , если b разделится на 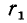нацело, то 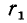окажется общим делителем чисел а и b; действительно, в этом случае оба слагаемых правой части равенства (4.2) делятся на 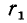Действительные числа нацело, значит, делится на 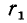нацело и его левая часть а. 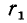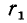То, что явится именно наибольшим общим делителем а и b, также видно из (4.2): если d—какой-нибудь общий делитель чисел а, b, то он будет также делителем числа Действительные числа .

Если b делится на 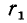Действительные числа с остатком, то придем к равенству вида

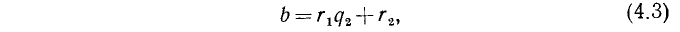
где уже 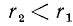Действительные числа . После этого разделим 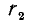на 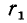. Снова представляются две возможности: 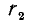делится на 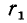нацело, или 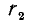делится на 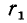с остатком. Если осуществится первая из этих возможностей, то 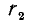Действительные числа будет н.о.д. чисел а и b (это легко доказать, пользуясь равенствами (4.2), (4.3); рекомендуем читателю провести это докательство). Если же осуществляется вторая возможность, то получим результат деления

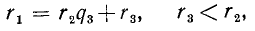
и вновь будем делить 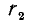Действительные числа на 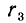. Процесс обязательно закончится на некотором шаге: числа 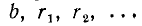последовательно уменьшаются, и либо одно из них, не равное единице, окажется делителем предыдущего (оно и будет н.о.д. чисел а, b), либо цепочка чисел 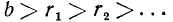Действительные числа закончится единицей. В этом случае н.о.д. чисел a, b равен единице, числа a, b взаимно простые.

Пример:

Найти н.о.д. чисел 162 и 42, пользуясь алгоритмом Евклида.

Решение:

Делим 162 на 42:

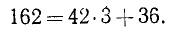
Остаток 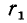Действительные числа = 36; делим b = 42 на 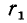= 36:

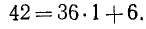
Второй остаток 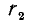Действительные числа = 6. Делим 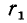= 36 на 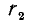= 6:

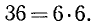
Деление выполняется без остатка; поэтому 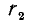Действительные числа = 6 — н.о.д. чисел 162 и 42.

Десятичные дроби. Представление рациональных чисел десятичными дробями

Десятичной дробью называется дробь, у которой знаменатель представляет собой натуральную степень числа 10. Такой, например, является дробь 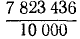Действительные числа . Эту дробь можно записать в следующей форме: выписать в строку цифры числителя и отделить запятой справа столько из них, сколько нулей содержится в знаменателе, а именно:

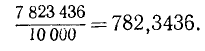
В такой записи цифры, стоящие слева от запятой, образуют целую часть, а цифры, стоящие справа от запятой,— дробную часть данной десятичной дроби.

Пусть p/q — какое-либо положительное рациональное число. Из арифметики хорошо известен процесс деления, позволяющий представлять число p/q в виде десятичной дроби. Сущность процесса деления состоит в том, что сначала находят, какое наибольшее целое число раз q содержится в р; если р — кратное q, то на этом процесс деления и заканчивается. В противном случае, появляется остаток. Далее находят, сколько в этом остатке содержится десятых долей q, и на этом шаге процесс может закончиться, либо появится новый остаток. В последнем случае находят, сколько в нем содержится сотых долей q, и т. д.

Если знаменатель q не имеет никаких других простых делителей, кроме 2 или 5, то через конечное число шагов остаток окажется равным нулю, процесс деления закончится и данная обыкновенная дробь обратится в конечную десятичную дробь. В самом деле, в указанном случае всегда можно подобрать такое целое число, что после умножения на него числителя и знаменателя данной дроби получится равная ей дробь, у которой знаменатель будет представлять натуральную степень десяти. Такой, например, является дробь

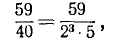
которую можно представить так:

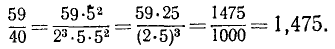
Однако, не производя этих преобразований, разделив числитель на знаменатель, читатель получит тот же результат: 59/40= 1,475.

Если знаменатель несократимой дроби имеет по меньшей мере один простой делитель, отличный от 2 или 5, то процесс деления р на q не закончится никогда (никакой из очередных остатков в нуль не обратится).

Пример:

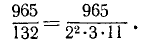
Выполнив деление, найдем

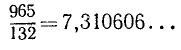
Для записи результата, получаемого в этом примере, периодически повторяющиеся цифры 0 и 6 заключают в круглые скобки и пишут:

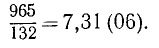
В этом примере и в других подобных случаях действие деления не приводит к окончательному результату в виде десятичной дроби. Можно, обобщая понятие десятичной дроби, все же говорить, что частное 965/132 представлено бесконечной периодической дробью 7,31(06). Повторяющиеся цифры 06 называют периодом этой дроби, а их число, равное в нашем примере 2,—длиной периода.

Чтобы уяснить причину явления периодичности дроби, разберем, например, процесс деления на 7. Если деление нацело не выполняется, то появляется остаток, который может иметь только одно из следующих значений: 1, 2, 3, 4, 5, 6. И на каждом из следующих шагов остаток будет иметь снова одно из этих шести значений. Поэтому не позднее чем на седьмом шаге мы неизбежно нстретимся с одним из значений остатка, которые раньше уже появлялись, Начиная с этого места, процесс деления приобретет периодический характер. Периодически будут повторяться и значения остатков, и цифры частного. Такое рассуждение применимо и в случае любого другого делителя.

Таким образом, всякая обыкновенная дробь p/q представляется конечной или бесконечной периодической десятичной дробью. Замечательно, что и, обратно, всякая периодическая десятичная дробь представима в виде обыкновенной дроби. Покажем, как выполняется это действие. При этом используется формула суммы бесконечно убывающей геометрической прогрессии (п. 92).

Запись

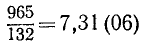
можно понимать так:

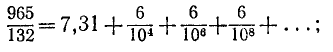
здесь члены правой части, начиная со второго, образуют бесконечную геометрическую прогрессию со знаменателем 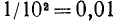Действительные числа и первым членом 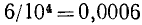. Пользуясь формулой (92.2):

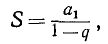
найдем

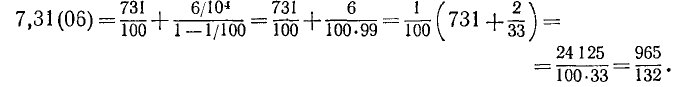
Ясно, что этот же процесс позволит любую заданную бесконечную периодическую дробь представить в виде обыкновенной дроби (и, как можно показать, именно той, из которой в процессе деления в свою очередь получается данная бесконечная периодическая дробь). Впрочем, здесь имеется одно исключение. Рассмотрим дробь

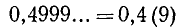
и применим к ней процесс преобразования в обыкновенную дробь:

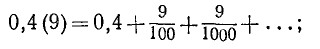
находим

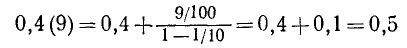
— мы пришли к числу 1/2, которое представляется конечной десятичной дробью 1/2 = 0,5.

Сходный результат получится всякий раз, когда период данной бесконечной дроби имеет вид (9). Поэтому мы отождествляем такие пары чисел, как, например,

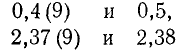
и т. д.

Иногда полезно еще допускать записи вида

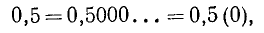
представляя формально конечные десятичные дроби как бесконечные с периодом (0).

Все сказанное об обращении обыкновенной дроби в десятичную периодическую дробь и обратно относилось к положительным рациональным числам. В случае отрицательного числа можно поступить двояким образом.

1) Взять положительное число, противоположное данному отрицательному, обратить его в десятичную дробь, а затем поставить перед ней знак минус. Например, для — 5/3 получим

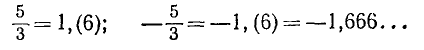
2) Данное отрицательное рациональное число представить в виде суммы его целой части (отрицательной) и его дробной части (неотрицательной), а затем обратить в десятичную дробь только эту дробную часть числа. Например:

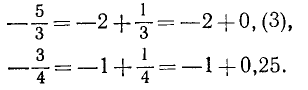
Для записи чисел, представленных в виде суммы своей отрицательной целой части и конечной или бесконечной десятичной дроби, принято такое обозначение (искусственная форма записи отрицательного числа):

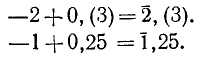
Здесь знак минус ставится не перед всей дробью, а над ее целой частью, чтобы подчеркнуть, что только целая часть отрицательна, а следующая за запятой дробная часть положительна.

Такая запись создает единообразие в записи положительных и отрицательных десятичных дробей и будет использована в будущем в теории десятичных логарифмов (п. 28). Предлагаем читателю для практики проверить переход от одной записи к другой в примерах:

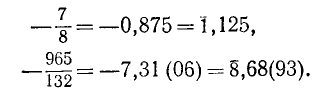
Теперь уже можно сформулировать окончательный вывод: всякое рациональное число может быть представлено бесконечной десятичной периодической дробью, и, обратно, всякая такая дробь задает рациональное число. Конечная десятичная дробь допускает также две формы записи в виде бесконечной десятичной дроби: с периодом (0) и с периодом (9).

Иррациональные числа. Действительные числа

Не все действия, рассматриваемые в алгебре, выполнимы в поле рациональных чисел. Примером может служить операция извлечения квадратного корня. Так, если равенство 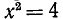Действительные числа выполняется при значениях 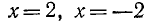, то равенство 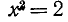не имеет места ни при каком рациональном значении х. Докажем это. Сначала заметим, что целое х не может иметь квадрата, равного 2: при 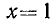Действительные числа имеем 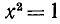, а при 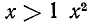заведомо больше 2. Предположим теперь, что х дробное: x — p/q (дробь считается несократимой) и .

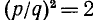Отсюда имеем 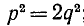Действительные числа ; должно быть четным числом (иначе кзадрат р не был бы четным). Положим 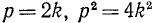. Теперь 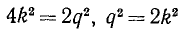; получается, что и q—четное, что противоречит допущению о несократимости дроби p/q.

Это показывает, что в области рациональных чисел из числа 2 нельзя извлечь квадратный корень, символ 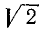Действительные числа не имеет смысла в области рациональных чисел. Между тем задача: «найти сторону х квадрата, зная, что площадь его равна S» — столь же естественна при S = 2, как и при S = 4. Выход из этого и других подобных затруднений состоит в дальнейшем расширении понятия числа, во введении нового вида чисел — иррациональных чисел.

Покажем, как вводятся иррациональные числа на примере задачи извлечения квадратного корня из числа 2; для простоты ограничимся положительным значением корня.

Для каждого положительного рационального числа х будет иметь место одно из неравенств Действительные числа или 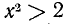. Очевидно, что 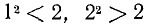. Рассматриваем затем числа 1,0; 1,1; 1,2; …, 1,9; 2,0 и находим два соседних среди них с тем свойством, что первое имеет квадрат, меньший двух, а второе—больший двух. Именно, 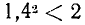Действительные числа и 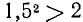. Аналогично, продолжая этот процесс, получим ряд неравенств (для получения десятичных дробей, написанных здесь, можно также использовать известный алгоритм приближенного извлечения квадратного корня, п. 13):

Сопоставляя сначала целые части, а затем первые, вторые, третьи и т. д. цифры после запятой у рациональных чисел, между квадратами которых лежит 2, мы можем последовательно выписать эти десятичные знаки:

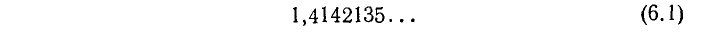
Процесс отыскания пар рациональных чисел (выраженных конечными десятичными дробями), отличающихся друг от друга на 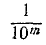Действительные числа , со все большим m может быть продолжен неограниченно. Поэтому можно рассматривать дробь (6.1) как бесконечную десятичную дробь (непериодическую, так как в случае периодичности она представляла бы рациональное число). Эта бесконечная непериодическая дробь, любое число десятичных знаков которой мы можем выписать, но для которой нельзя осуществить записи одновременно всех знаков, и принимается за число, равное 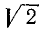Действительные числа (т. е. за число, квадрат которого равен 2). Отрицательное значение корня квадратного из двух мы представим в виде

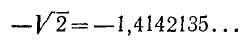
или, пользуясь искусственной формой записи чисел, в виде

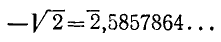
Введем теперь следующее определение: иррациональным числом называется всякая бесконечная непериодическая десятичная дробь

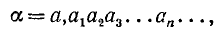
где а—целая часть числа (она может быть положительной, равной нулю или отрицательной), a Действительные числа —десятичные знаки (цифры) его дробной части.

Заданное бесконечной непериодической дробью иррациональное число определяет две последовательности конечных десятичных дробей, называемых десятичными приближениями а по недостатку и по избытку:

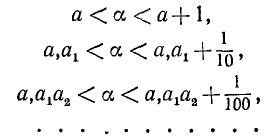
Например, для 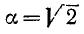Действительные числа запишем

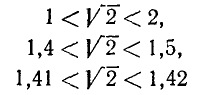
и т. д. Здесь, например, 1,41—десятичное приближение 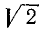Действительные числа с точностью до 0,01 по недостатку, а 1,42—по избытку.

Запись неравенств между иррациональным числом и его десятичными приближениями входит в самое определение понятия иррационального числа и может быть положена в основу определения соотношений «больше» и «меньше» для иррациональных чисел.

Возможность представления иррациональных чисел их все более и более точными десятичными приближениями лежит также в основе опрелеленгя арифметических действий над иррациональными числами, которые фактически производятся над их иррациональными приближениями по недостатку или по избытку.

К иррациональным числам приводят многие действия, как, например, действие извлечения корня степени п из рационального числа (если оно не представляет собой n-ю степень другого рационального числа), логарифмирование и т. д. Иррациональным является число 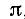Действительные числа , равное отношению длины окружности к ее диаметру (п. 229).

Все рациональные и иррациональные числа образуют в совокупности множество действительных (или вещественных) чисел. Таким образом, всякая десятичная дробь, конечная или бесконечная (периодическая или непериодическая), всегда определяет действительное число.

Всякое отличное от нуля действительное число либо положительно, либо отрицательно.

Напомним в связи с этим следующее определение. Абсолютной величиной или модулем действительного числа а называется число |а|, определяемое равенствами

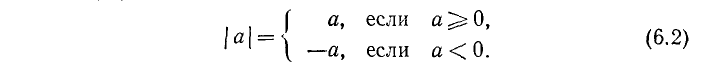
Таким образом, модуль неотрицательного числа равен самому этому числу (верхняя строка равенства); модуль отрицательного числа равен этому числу, взятому с противоположным знаком (нижняя строка). Так, например,

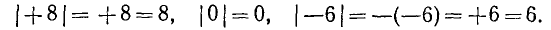
Из определения модуля следует, что модуль любого числа есть число неотрицательное; если модуль числа равен нулю, то и само число равно нулю, в остальных случаях модуль положителен.

Действительные числа образуют числовое поле — поле действительных чисел: результат рациональных действий над действительными числами снова выражается действительным числом. Заметим, что взятые в отдельности иррациональные числа не образуют ни поля, ни_даже кольца: например, сумма двух иррациональных чисел 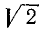Действительные числа и 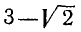равна рациональному числу 3.

Наш краткий очерк развития понятия о числе, построенный по схеме

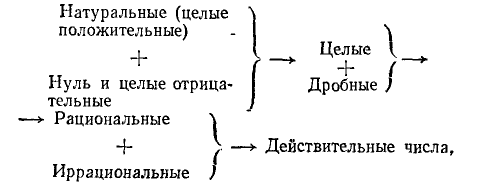
мы заключим указанием на наиболее важные свойства совокупности действительных чисел.

Действительные числа образуют поле.
Действия над действительными числами подчинены обычным законам (например, сложение и умножение—законам коммутативности, ассоциативности, дистрибутивности, п. 1).
Для любых двух действительных чисел а и b имеет место одно и только одно из трех соотношений: а больше b (a>b), а меньше b (a<b), а равно b (a = b). Говорят поэтому, что множество действительных чисел упорядочено.
Принято, наконец, говорить, что множество действительных чисел обладает свойством непрерывности. Смысл, который придается этому выражению, пояснен в п. 8. Именно это свойство существенно отличает поле действительных чисел от поля рациональных чисел.

Действия с приближенными числами

Имеется целый ряд причин, в силу которых практически приходится использовать не точные, а приближенные числовые значения различных величин (условно называемые приближенными числами). Вот некоторые из этих причин. 1) Числа, полученные в результате измерения (эксперимента), естественно представляют собой приближенные значения измеряемых величин по причине несовершенства инструментов, применяемых для измерения. 2) Числа, значения которых определены точно, все же приходится заменять их приближенными значениями. Это очевидно, когда речь идет об иррациональных числах, например 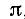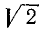Действительные числа , и т. д. Но и такое, например, число, как 73/254, при проведении вычислений придется использовать в виде десятичной дроби, сохранив лишь некоторое число ее десятичных знаков после запятой. 3) Часто нет необходимости в получении точного результата и есть смысл провести расчет приближенно, чтобы сократить время, затрачиваемое на вычисление.

При выполнении приближенных вычислений приходится руководствоваться некоторыми правилами, позволяющими получить результат с требуемой степенью точности и без чрезмерных усилий на проведение вычислений. Эти правила основаны на некоторых понятиях и определениях, которые мы здесь кратко приведем.

А. Абсолютная погрешность числа. Если 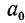Действительные числа — некоторое число (известное точно или нет), а а—число, принимаемое за приближенное значение числа 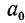, то абсолютной погрешностью приближенного числа а называют любое число 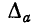Действительные числа такое, что

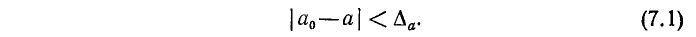
Заметим, что абсолютная погрешность здесь не определяется однозначно (то, что мы назвали абсолютной погрешностью, часто называют предельной абсолютной погрешностью). Так, если 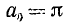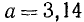Действительные числа , , то, учитывая, что 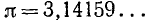, можно записать

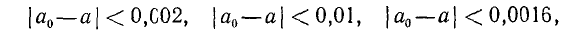
и каждое из чисел 0,002, 0,01, 0,0016 будет абсолютной погрешностью.

Ясно, что при производстве вычислений в качестве 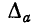Действительные числа берут по возможности наименьшее из чисел, удовлетворяющих неравенству (7.1).

Величина 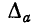Действительные числа обычно характеризуется не более чем двумя значащими цифрами (чаще всего даже одной), причем принято величину 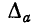округлять в сторону увеличения.

Пример:

Определить абсолютную погрешность, возникающую при замене иррационального числа 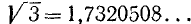Действительные числа его приближенным значением 1,73.

Решение:

Имеем 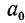Действительные числа = 1,7320508… , a = 1,73. Заменяя точное число 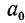его приближенным значением а, мы допускаем следующую ошибку: 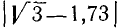= 0,0020508…

Ясно, что в рассматриваемом случае можно положить 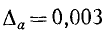Действительные числа (число 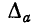в соответствии с принятым условием записано с помощью одной цифры и получено путем округления ошибки 0,0020508… в сторону увеличения).

Пример:

Известно, что для некоторого числа его приближенное значение 647,35 найдено с абсолютной погрешностью, равной 0,17. Что можно сказать о точном значении этого числа?

Решение:

Неравенство (7.1) равносильно неравенствам

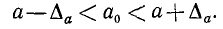
В нашем случае эти неравенства запишутся так:

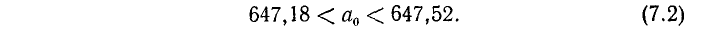
По исходным данным точное значение Действительные числа искомого числа найти нельзя—можно только указать границы, между которыми оно находится.

Б. Относительная погрешность числа. Абсолютная погрешность числа а, принимаемого за приближенное значение числа Действительные числа не всегда является удобной характеристикой степени точности а в качестве приближения к . Так, погрешность в один метр будет очень грубой ошибкой при измерении длины помещения, но будет рассматриваться как малая ошибка при измерении расстояния между двумя удаленными точками земной поверхности. Дело в том, что обычно важна не сама величина погрешности, а ее отношение к измеряемой (или вычисляемой) величине, часто выражаемое в процентах. 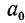В связи с этим дадим определение: относительной погрешностью называется отношение абсолютной погрешности к модулю числа Действительные числа ; относительная погрешность обозначается через :

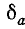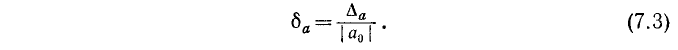
На практике точное значение 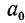Действительные числа обычно неизвестно, и, учитывая, что, как правило, абсолютная погрешность бывает мала, находят 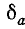по формуле

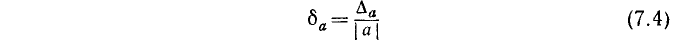
(заменяя в знаменателе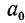 Действительные числа его приближенным значением а).

Пример:

За приближенное значение числа 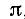Действительные числа иногда принимают 22/7. Какова относительная погрешность этого значения?

Решение:

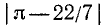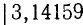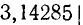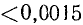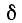Находим Действительные числа = — = ; приняв за число 0,0015, найдем = 0,0015/3,14 и, снова округляя 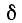в сторону увеличения, 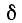= 0,0005, или 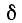= 0,05% Число 22/7 дает приближенное значение 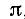Действительные числа с точностью до 0,05%.

В. Значащие цифры числа. Верные и сомнительные цифры. Напомним определение значащей цифры: значащей цифрой приближенного числа называется всякая его цифра, начиная с первой ненулевой цифры (считая слева направо). Например, в числе 0,00030900 первые четыре нуля не являются значащими цифрами (они служат только для указания десятичных разрядов других цифр). Остальные три нуля являются значащими цифрами.

При записи приближенных чисел важно договориться о том, какие цифры (знаки) в этой записи следует считать верными, а какие — сомнительными. В связи с этим примем следующее определение: пусть а есть приближенное число с абсолютной погрешностью 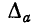Действительные числа ; тогда любая из значащих цифр числа а называется «верной», если 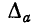не превосходит пяти единиц разряда, следующего за этой цифрой; остальные значащие цифры числа а называются «сомнительными». Так, например, пусть для приближенного числа а = 647,35 будет 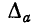Действительные числа = 0,17 (см. пример 2). Замечаем, что здесь 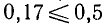, и поэтому цифры 6, 4 и 7 являются верными, а цифры 3 и 5—сомнительными. Этот ответ приобретет большую наглядность, если его сопоставить с неравенствами (7.2).

При расчетах, в которых участвуют приближенные числа, принято сохранять в промежуточных выкладках одну (или две) сомнительную цифру. В конечном результате сомнительные цифры могут быть округлены.

Г. Округление чисел. При замене числа, выражаемого десятичной дробью, дробью с меньшим числом десятичных знаков допускается погрешность, называемая погрешностью округления. Приняты следующие правила округления: если первый из отбрасываемых знаков дроби меньше пяти, то остальные знаки просто отбрасывают, а стоящие перед ними сохраняют. Если первый из отбрасываемых знаков больше пяти, то предшествующий знак увеличивают на единицу. Если первый из отбрасываемых знаков равен пяти, то пригодно любое из указанных правил, но обычно округление производят так, чтобы последний сохраненный знак стал четным. Примеры округления десятичных дробей:

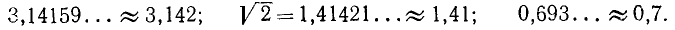
Такие же правила округления применяются и к целым числам. Если, например, число жителей города равно в данный момент 23 542, то спустя месяц уже бессмысленно указывать единицы и даже десятки в этом числе. Можно написать число жителей округленно как 23 500, но принято записывать 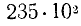Действительные числа , чтобы подчеркнуть, что число единиц и десятков неизвестно (а не именно равно нулю, как может показаться при первой записи).

При округлении приближенного числа вносится дополнительная погрешность (погрешность округления), которая складывается с его абсолютной погрешностью. Для того чтобы уменьшить накопление погрешностей округления, в промежуточных результатах обычно сохраняют одну-две сомнительные цифры.

Пример:

Округлить приближенное число а = 967,358, взятое с абсолютной погрешностью 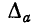Действительные числа = 0,137, сохранив в результате одну сомнительную цифру.

Решение:

В числе а верными являются цифры 9, 6 и 7, а следующая цифра 3 уже сомнительна. Округляем число а по правилу дополнения и получаем новое приближенное число 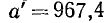Действительные числа . Чтобы определить его абсолютную погрешность, мы находим, что погрешность округления составляет 967,4 — 967,358 = 0,042, складываем эту последнюю с абсолютной погрешностью 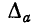Действительные числа = 0,137 числа а и получаем 0,179. В полученном числе, округляя его в большую сторону, сохраняем одну значащую цифру и находим для новой абсолютной погрешности 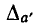Действительные числа , т. е. для абсолютной погрешности числа 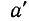, следующий результат: 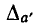= 0,2. Итак, вернувшись к обычным обозначениям, заключаем, что приближенное число а = 967,4, полученное при округлении числа 967,358, найдено с абсолютной погрешностью 0,2, причем оно содержит одну (последнюю) сомнительную цифру 4.

Пример:

Округлить приближенное число а = 967,358, взятое с абсолютной погрешностью 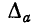Действительные числа = 0,137, сохранив только верные цифры (сравнить с примером 3).

Решение:

Число а округляем до числа 967. После сложения погрешности округления 0,358 с данной абсолютной погрешностью 0,137 находим число 0,495. Замечаем, что 0,495 < 0,5, а это и означает, что в приближенном числе 967 все цифры верные. Поэтому здесь и в подобных случаях абсолютную погрешность можно явно вообще не указывать.

Д. Погрешность результата арифметических действий. Пусть даны два числа а, b, рассматриваемые как приближенные значения чисел 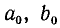Действительные числа с абсолютными погрешностями 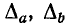соответственно. В этом случае выполняются неравенства

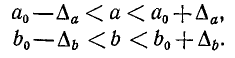
Складывая эти неравенства почленно, получим

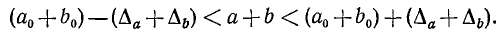
Отсюда видно, что 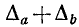Действительные числа является абсолютной погрешностью для суммы чисел а и b: абсолютная погрешность суммы равна сумме абсолютных погрешностей. Это правило верно для алгебраической суммы любого числа слагаемых.

Для умножения и деления принято следующее правило: относительная погрешность произведения (частного) равна сумме относительных погрешностей сомножителей (делимого и делителя). Это правило мы оставим без обоснования.

Пример:

Стороны треугольника измерены с точностью до 1 мм и оказались равны 17,8 см, 23,6 см, 14,2 см. Найти периметр (т. е. сумму сторон) треугольника.

Решение:

Находим 17,8 + 23,6+ 14,2 = 55,6 см. Так как абсолютная погрешность каждого слагаемого была равна 0,1 см, то погрешность результата может составить 0,3 см. Поэтому периметр Р удовлетворяет неравенствам 55,3 < Р < 55,9. Ответ в таких случаях часто записывают в виде Р = 55,6 ±0,3, указывая тем самым возможные границы ошибки.

Пример:

Ребра прямоугольного параллелепипеда известны с абсолютной погрешностью в 1 см: а = 43 см, b = 16 см, с = 25 см. С какой относительной и абсолютной погрешностью может быть найден объем параллелепипеда?

Решение:

Объем прямоугольного параллелепипеда находится по формуле (п. 168)

Относительные погрешности ребер составляют соответственно (с округлением) 2,5%; 7%; 4%. При умножении относительные погрешности суммируются: 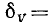Действительные числа 2,5 + 7 + 4 13,5%. Объем может быть найден с относительной погрешностью 13%. Читателю предоставляется найти абсолютную погрешность объема.

Приведенные здесь правила позволяют, в принципе, контролировать точность производимых вычислений и предсказать относительную и абсолютную погрешности их результата; при значительном объеме производимых вычислений такой контроль точности становится практически слишком трудоемким и дает, как правило, завышенные значения погрешностей.

Числовая ось. Координаты точки на плоскости

Осью называется прямая, на которой одно из двух возможных направлений выделено как положительное (противоположное направление считается отрицательным). Положительное направление обозначается обычно стрелкой. Числовой (или координатной) осью называется ось, на которой выбрана начальная точка (или начало) О и единица масштаба или масштабный отрезок ОЕ (рис. 1).

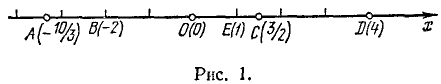
Таким образом, числовая ось задается указанием на прямой направления, начала и масштаба.

С помощью точек числовой оси изображают действительные числа. Целые числа изображаются точками, которые получаются откладыванием масштабного отрезка нужное число раз вправо от начала О в случае положительного целого числа и влево в случае отрицательного. Нуль изображается начальной точкой О (сама буква О напоминает о нуле; она является первой буквой слова origo, означающего «начало»). Дробные (рациональные) числа также просто изображаются точками оси; например, чтобы построить точку, соответствующую числу —10/3= — З 1/3, следует отложить влево от О три масштабных отрезка и еще одну третью часть масштабного отрезка (точка А на рис. 1).

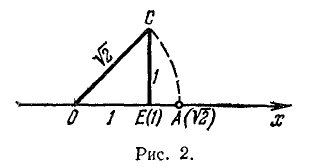
Кроме точки А на рис. 1 показаны еще точки В, С, D, изображающие соответственно числа —2; 3/2; 4.

Целых чисел имеется бесконечное множество, но на числовой оси целые числа изображаются точками, расположенными «редко», целочисленные точки оси отстоят от соседних на единицу масштаба. Рациональные точки расположены на оси весьма «густо» — нетрудно показать, что на любом сколь угодно малом участке оси имеется бесконечно много точек, изображающих рациональные числа. Тем не менее на числовой оси имеются точки, которые не являются изображениями рациональных чисел. Так, если на числовой оси построить отрезок OA, равный гипотенузе OC прямоугольного треугольника ОЕС с катетами OE = ЕС = 1 (рис. 2), то длина этого отрезка (по теореме Пифагора, п. 216) окажется равной 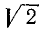Действительные числа и точка А не будет изображением рационального числа.

Исторически именно факт существования отрезков, длины которых не могут быть выражены числом (рациональным числом!), привел к введению иррациональных чисел. В связи с этим рекомендуем прочитать п. 163.

Введение иррациональных чисел, которые в совокупности с рациональными образуют множество всех действительных чисел, приводит к тому, что каждой точке числовой оси соответствует единственное действительное число, изображением которого она служит. Напротив, каждое действительное число изображается вполне определенной точкой числовой оси. Между действительными числами и точками числовой оси устанавливается взаимно однозначное соответствие.

Поскольку мы числовую ось мыслим как непрерывную линию, а точки ее находятся во взаимно однозначном соответствии с действительными числами, то мы говорим о свойстве непрерывности множества действительных чисел (п. 6).

Заметим еще, что в некотором смысле (мы его не уточняем) иррациональных чисел несравненно больше, чем рациональных.

Число, изображением которого служит данная точка А числовой оси, называется координатой этой точки; тот факт, что а—координата точки А, записывают так: А (а). Координата любой точки А выражается как отношение ОА/ОЕ отрезка OA к масштабному отрезку ОЕ, которому для точек, лежащих от начала О в отрицательном направлении, приписывают знак минус.

Введем теперь прямоугольные декартовы координаты на плоскости. Возьмем две взаимно перпендикулярные числовые оси Ох и Оу, имеющие общее начало О и равные масштабные отрезки (на практике часто применяют и координатные оси с различными масштабными единицами). Скажем, что эти оси (рис. 3) образуют декартову прямоугольную систему координат на плоскости. Точка О называется началом координат, оси Ох и Оу — осями координат (ось Ох называют осью абсцисс, ось Оу—осью ординат).

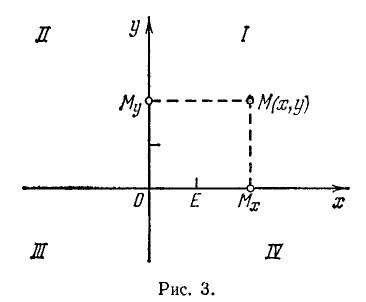
На рис. 3, как обычно, ось абсцисс расположена горизонтально, ось ординат —вертикально. Плоскость, на которой задана система координат, называют координатной плоскостью.

Каждой точке плоскости ставится в соответствие пара чисел— координат этой точки относительно данной координатной системы. Именно, возьмем прямоугольные проекции точки М на оси Ох и Оу; соответствующие точки на осях Ох, Оу обозначены на рис. 3 через 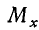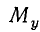Действительные числа , . Точка 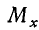имеет, как точка числовой оси Ох, координату (абсциссу) х, точка 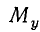, как точка числовой оси Оу,—координату (ординату) у. Эти два числа х, у (записанные в указанном порядке) и называются координатами точки М.

При этом пишут: М (х, у).

Итак, каждой точке плоскости ставится в соответствие упорядоченная пара действительных чисел (х, у)—декартовы прямоугольные координаты этой точки. Термин «упорядоченная пара» указывает на то, что следует различать первое число пары — абсциссу и второе—ординату. Напротив, каждая пара чисел ( х, у ) определяет единственную точку М, для которой х служит абсциссой, а у — ординатой.

Задание в плоскости прямоугольной декартовой системы координат устанавливает взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел.

Координатные оси делят координатную плоскость на четыре части, четыре квадранта. Квадранты нумеруются, как показано на рис. 3, римскими цифрами. Знаки координат точки зависят от того, в каком квадранте она лежит, как указано в следующей таблице:

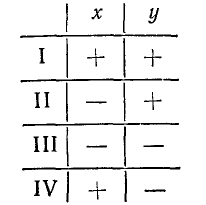
Точки, лежащие на оси Ох, имеют ординату у, равную нулю, точки на оси Оу — абсциссу х, равную нулю. Обе координаты начала О равны нулю: О (0, 0).

Пример:

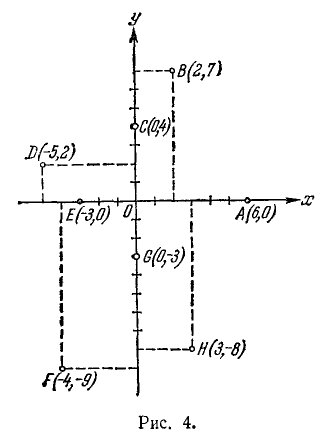
Построить на плоскости точки

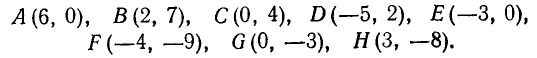
Решение дается на рис. 4.

Если известны координаты некоторой точки М (х, у), то легко указать координаты точек, симметричных с ней относительно осей Ох, Оу и начала координат: точка, симметричная с М относительно оси Ох, будет иметь координаты (х, —у); точка, симметричная с М относительно Оу,— координаты (—х, у); наконец, у точки, симметричной с М относительно начала, координаты будут (—х, —у).

Можно также указать связь между координатами пары точек, симметричных относительно биссектрисы I — III координатных углов (рис. 5); если одна из этих точек М имеет координаты х и у, то у второй абсцисса равна ординате первой

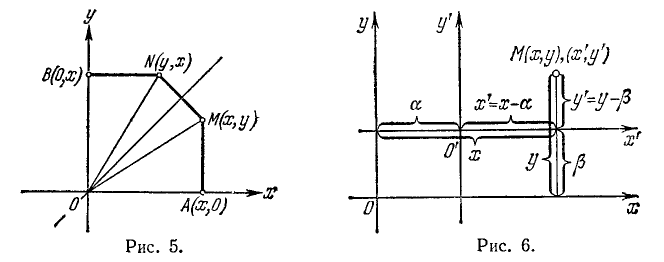
точки, а ордината — абсциссе первой точки. Иначе говоря, координаты точки N, симметричной с М относительно биссектрисы I — III координатных углов, будут (у, х). Для доказательства этого положения рассмотрим прямоугольные треугольники ОAM и OBN. Они расположены симметрично относительно биссектрисы координатного угла и потому равны. Сравнивая их соответственные катеты, убедимся в правильности нашего утверждения.

Систему декартовых прямоугольных координат можно преобразовать с помощью переноса ее начала О в новую точку О’ без изменения направления осей и величины масштабного отрезка. На рис. 6 показаны одновременно две системы координат: «старая» с началом О и «новая» с началом О’. Произвольная точка М имеет теперь две пары координат, одну относительно старой координатной системы, другую относительно новой. Если координаты нового начала в старой системе обозначены через (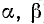 Действительные числа ), то связь между старыми координатами (х, у) точки М и ее новыми координатами (х’, у’) выразится формулами

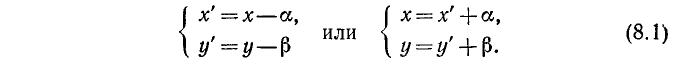
Эти формулы называют формулами переноса системы координат, при их выводе по рис. 6 выбрано самое удобное положение точки М, лежащей в первом квадранте как старой, так и новой системы. Можно убедиться, что формулы (8.1) остаются верны при любом расположении точки М.

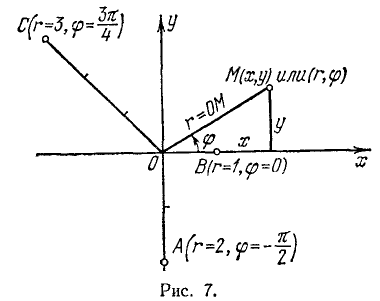
Положение точки М на плоскости может быть задано не только ее декартовыми прямоугольными координатами х, у, но и другими способами. Соединим, например, точку М с началом О (рис. 7) и рассмотрим следующие два числа: длину отрезка ОМ = r и угол 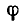Действительные числа наклона этого отрезка к положительному направлению оси Ох (этот угол определяется как угол, на который надо повернуть ось Ох до ее совмещения с ОМ, и считается положительным, если поворот совершается против часовой стрелки, и отрицательным в противном случае, как это принято в тригонометрии (п. 96)). Отрезок r = ОМ называется полярным радиусом точки М, угол Действительные числа — ее полярным углом, пара чисел — полярными координатами точки М.

Как видно, для определения полярных координат точки требуется задание только одной координатной оси Ох (называемой в этом случае полярной осью). Удобно, однако, рассматривать одновременно и полярные и декартовы прямоугольные координаты, как это сделано на рис. 7.

Полярный угол точки определяется заданием точки неоднозначно: если Действительные числа — один из полярных углов точки, то и всякий угол

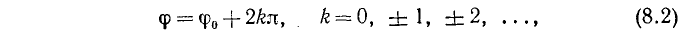
будет ее полярным углом. Задание полярного радиуса и угла определяет положение точки единственным образом. Начало О (называемое полюсом полярной системы координат) имеет радиус, равный нулю, никакого определенного полярного угла точке О не приписывается.

Между декартовыми и полярными координатами точки имеются следующие соотношения:

непосредственно вытекающие из определения тригонометрических функций (п. 97). Эти соотношения позволяют находить декартовы координаты по заданным полярным. Следующие формулы:

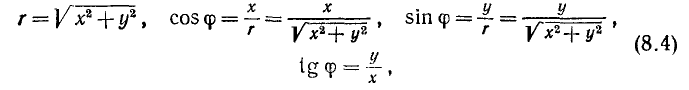
позволяют решать обратную задачу: по данным декартовым координатам точки находить ее полярные координаты. При этом по значению 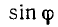Действительные числа (или 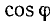) можно найти два возможных значения угла 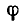в пределах первого круга; по знаку 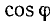(или 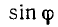) выбирается одно из них. Можно также определять угол 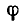по его тангенсу: 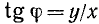Действительные числа , но и в этом случае четверть, в которой лежит 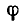уточняется по знаку 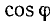или .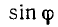

Точка, заданная своими полярными координатами, строится (без вычисления декартовых координат) по своему полярному углу и радиусу.

Пример:

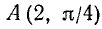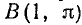Найти декартовы координаты точек Действительные числа ; .

Решение:

По формулам (8.3) находим:

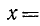
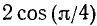
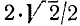
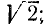
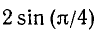
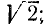
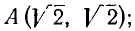
1) для точки А находим Действительные числа

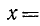
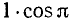
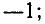
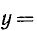
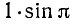
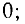
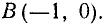
2) для точки В: Действительные числа

Пример:

Найти полярные координаты точек (заданных декартовыми координатами)

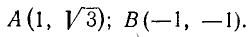
Решение:

Находим по формулам (8.4):

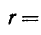
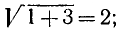
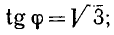
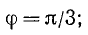
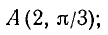
1) для точки А: Действительные числа

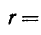
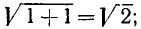
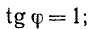
2) для точки В: 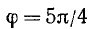Действительные числа (с учетом знаков х и у);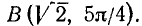

Пример:

Построить точки по их полярным координатам:

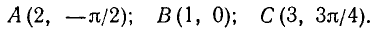
Решение показано на рис. 7.

Дополнение к действительным числам

Смотрите также:

Действительные переменные	Соотношения величины между действительными числами
Иррациональные числа	Алгебраические действия над действительными числами

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: