Несобственные интегралы в математике с примерами решения и образцами выполнения

Определённый интеграл называется несобственным, если выполняется по крайней мере одно из следующих условий.

• Область интегрирования является бесконечной. Например, является бесконечным промежутком
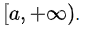
• Функция 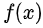является неограниченной в окрестности некоторых точек области интегрирования.

Если интервал 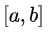конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.

Интегралы с бесконечными пределами интегрирования

Понятие определенного интеграла связано с функцией, рассматриваемой на некотором конечном отрезке 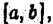так что область интегрирования в определенном интеграле всегда ограничена. Однако часто приходится иметь дело с функциями в неограниченных областях: в бесконечных полуинтервалах вида 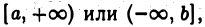или же в интервале 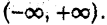С подобной ситуацией мы встречаемся, например, при вычислении потенциала гравитационной или электростатической силы.

Чтобы распространить понятие определенного интеграла на случай неограниченных областей интегрирования, нужны новые определения, устанавливающие, что следует понимать под символами

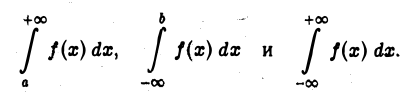
Пусть функция 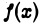определена для всех 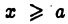и интегрируема (например, непрерывна) на каждом конечном отрезке 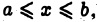где a — фиксировано, a 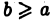— произвольно. Определим, что мы будем понимать под символом

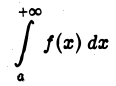
(несобственный интеграл 1-го рода). Рассмотрим функцию аргумента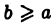

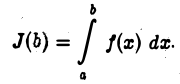
Определение:

Если при 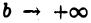функция 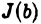имеет конечный предел L, то мы называем несобственный интеграл (1) сходящимся и полагаем по определению

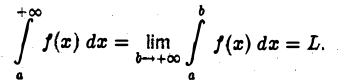
Если при 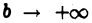функция 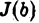не имеет (конечного) предела, то мы называем интеграл (1) расходящимся и не приписываем ему никакого числового значения.

Пример:

Рассмотрим несобственный интеграл

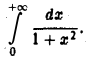
По определению:

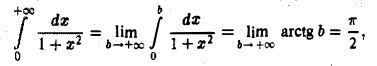
так что интеграл

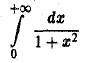
сходится и равен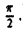

Пример:

Рассмотрим несобственный интеграл

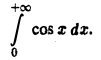
Так как интеграл

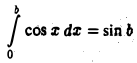
не имеет предела при 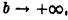то данный несобственный интеграл расходится.

Пример:

Пусть точечные электрические заряды 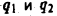имеют одинаковые знаки, например, 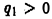и 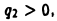так что заряд 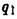будет отталкивать заряд 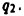По закону Кулона сила F электростатического взаимодействия в вакууме двух точечных электрических зарядов равна

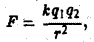
где r — расстояние между зарядами, k — постоянная.

Пусть заряд 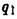помещен в точке 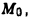которая принимается за начало отсчета. Требуется найти работу А по перемещению заряде 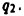из точки М, отстоящей от точки 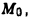на расстоянии 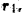в бесконечность. Искомая работа А выражается несобственным интегралом

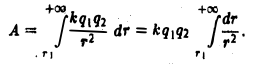
По определению

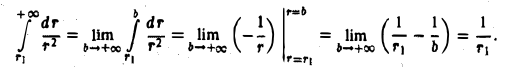
Таким образом, 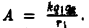Если 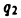— единичный заряд, то 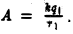Эта величина называется потенциалом поля, создаваемого зарядом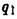

Пример:

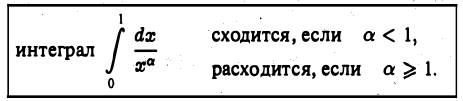
Рассмотрим интеграл

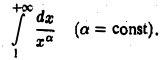
Установим, при каких значениях а интеграл (3) сходится и при каких расходится. По определению имеем

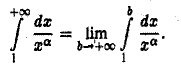
Пусть 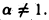Тогда

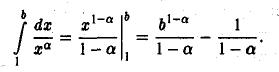
Поэтому, если a> 1, то

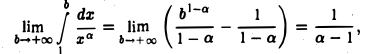
так что при а > 1 интеграл (3) сходится; если же а < 1, то при 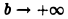интеграл

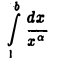
не имеет конечного предела, так что при а < 1 интеграл (3) расходится. Пусть а=1. Тогда

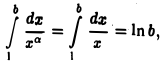
откуда видно, что при а = 1 интеграл

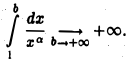
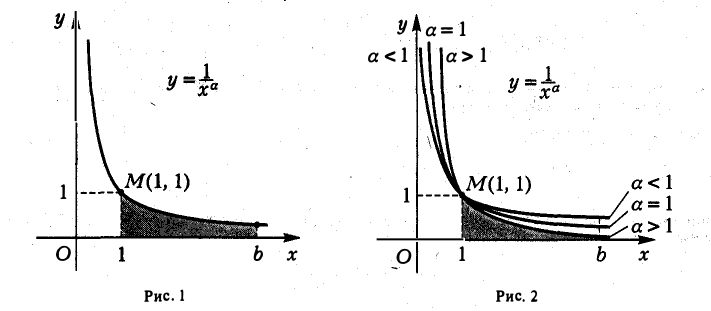
Полученные результаты имеют простой геометрический смысл. Рассмотрим область D, ограниченную слева прямой х =1, снизу — осью Ох, а сверху — кривой 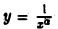(рис. 1). Вправо эта область простирается безгранично. Условимся под площадью всей бесконечной области D понимать предел площади конечной ее части до прямой х=b (рис. 2) при 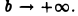Тогда полученные выше результаты будут означать, что если область D сверху ограничена кривой 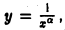где а > 1, то она имеет конечную площадь, если же верхняя граница области D есть гипербола 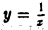или кривая 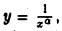где а < 1, то говорить о площади области D не имеет смысла.

Замечание:

Нетрудно видеть, что для любого 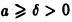интеграл

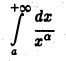
также сходится при а > 1 и расходится при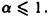

Пользуясь определением несобственного интеграла

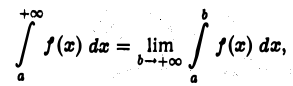
можно доказать справедливость следующих утверждений.

1. Если интеграл

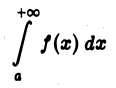
сходится и 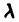— любое действительное число, то интеграл

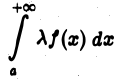
также сходится, причем

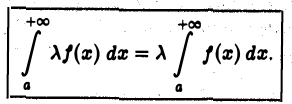
2.Если интегралы

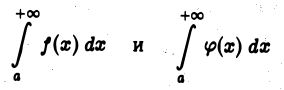
сходятся, то интеграл

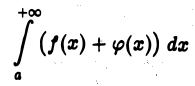
также сходится, причем

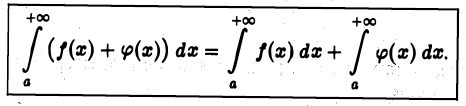
Действительно, для любого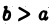

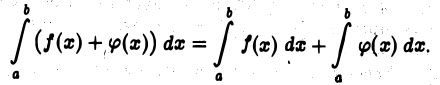
Каждое слагаемое в правой части (5) имеет предел при 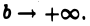Значит, существует предел левой части (5) при 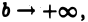т. е. интеграл

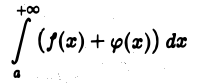
сходится. Переходя в равенстве (5) к пределу при 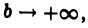получаем равенство (4).

Задача:

Пусть интеграл

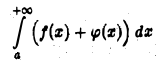
сходится. Что можно сказать о сходимости интегралов

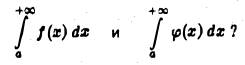
Можно показать, что если функции 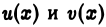непрерывно дифференцируемы на полупрямой 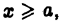то

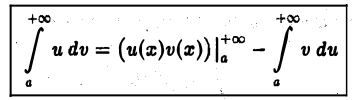
(формула интегрирования по частям). При этом предполагается, что из трех входящих в равенство (6) выражений (два интеграла и двойная подстановка) имеют смысл по крайней мере два; существование третьего отсюда уже вытекает.

Пример:

Рассмотрим интеграл

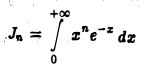
(n — натуральное число или нуль).

Интегрируя по частям, находим

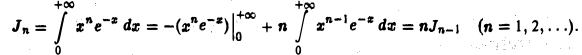
Замечая, что

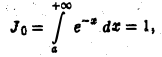
получаем

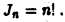
Несобственные интегралы 1-го рода от неотрицательных функций. Теоремы сравнения

Во многих задачах вычислять несобственный интеграл не требуется, а нужно лишь установить, сходится ли этот интеграл или расходится. Вопрос о сходимости или расходимости несобственногоинтеграла часто решается с помощью теорем сравнения.

Теорема:

Пусть на отрезке 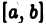при любом 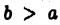функции 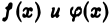интегрируемы и

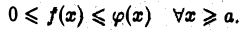
Тогда

1) если интеграл

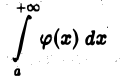
сходится, то сходится и интеграл

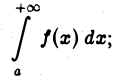
2) если интеграл

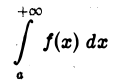
расходится, то расходится и интеграл

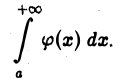
1) Пусть интеграл

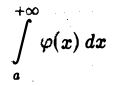
сходится. Докажем, что сходится и интеграл

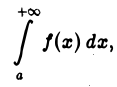
т. е. 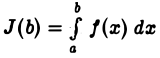имеет конечный предел при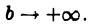

Прежде всего из неотрицательности функции 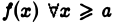следует, что 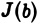есть неубывающая функция от Ь. Действительно, если 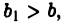то

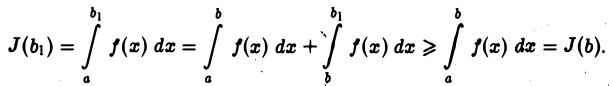
Далее, т. к. 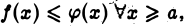то при любо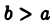м имеем

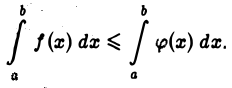
Интеграл 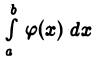не превосходит несобственного интеграла 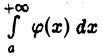который по условию сходится. Следовательно, при любом b> а имеем

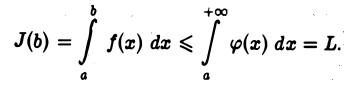
Итак, интеграл 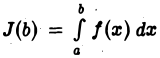представляет собой функцию от b, неубывающую и ограниченную сверху (при 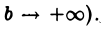Поэтому 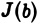имеет конечный предел при 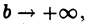а это, согласно определению, означает, что интеграл 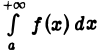сходится.

Первое утверждение теоремы доказано.

2) Докажем второе ее утверждение. Пусть интеграл

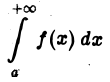
расходится. Применяя метод рассуждения от противного, допустим, что интеграл

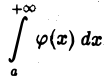
сходится. Тогда, согласно уже доказанной первой части теоремы, будет сходящимся интеграл 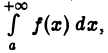что противоречит условию. Следовательно, наше допущение неверно, т. е. интеграл 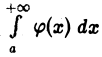расходится.

Пример:

Рассмотрим несобственный интеграл

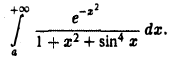
Исследовать его на сходимость при помощи определения не представляется возможным. Воспользуемся тем, что для всех 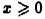функция

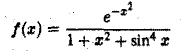
удовлетворяет условию

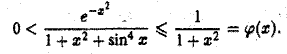
Так как интеграл

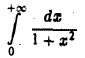
сходится, то в силу теоремы 1 сходится и рассматриваемый интеграл.

Теорема:

Пусть функции 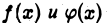непрерывны и неотрицательны для всех 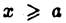и пусть 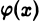отлична от нуля для всех достаточно больших х. Тогда, если существует конечный предел

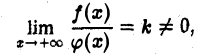
то интегралы

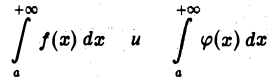
сходятся или расходятся одновременно.

Пусть

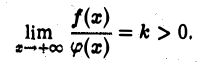
Это означает, согласно определению предела, что для всякого числа 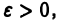например, 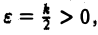существует такое число N, что для всех 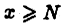выполняется неравенство

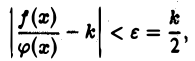
или, что то же,

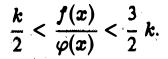
Отсюда, в силу того, что 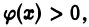получаем двойное неравенство

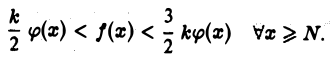
Пользуясь теоремой 1, из неравенства 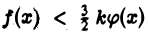заключаем: если интеграл 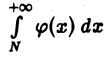сходится, то сходится и интеграл 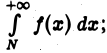из неравенства 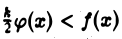усматриваем: если интеграл 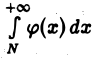расходится, то расходится и интеграл 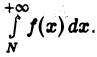Аналогично устанавливаем, что если интеграл 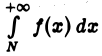сходится (расходится), то интеграл 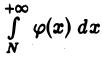будет также сходящимся (расходящимся).

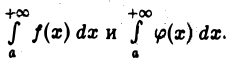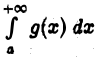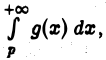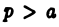Полученные выводы остаются в силе и для интегралов Это следует из того, что интеграл будет сходящимся или нет одновременно с интегралом где — сколь угодно большое фиксированное число, поскольку разность этих интегралов является собственным интегралом.

Пример:

Исследовать на сходимость интеграл

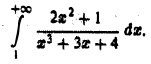
На полупрямой 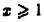подынтегральная функция 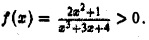Запишем ее так:

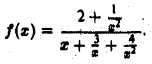
Отсюда видно, что для больших х функция 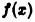ведет себя как 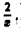Выберем а качестве функции сравнения 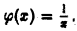Будем иметь

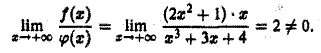
Интеграл

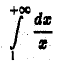
расходится. В силу теоремы 2 расходится и данный интеграл.

Используя теорему 1, а также результаты, касающиеся интеграла 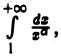приходим к следующим признакам сходимости и расходимости интеграла 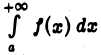от неотрицательной функции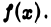

Теорема 3. Если существует такое число а > 1, что для всех достаточно больших х

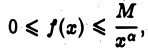
где М > 0 и не зависит от х, то интеграл

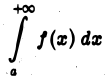
сходится.

Если для всех достаточно больших х

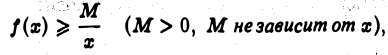
то интеграл

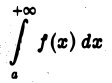
расходится.

Пусть условие

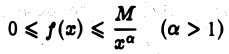
выполнено для всех 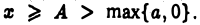Так как интеграл 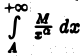для 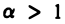сходится, то, взяв в качестве 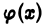функцию 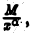по теореме 1 получим, что сходится и интеграл 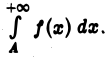Отсюда, в свою очередь, вытекает сходимость интеграла 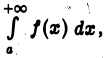так как

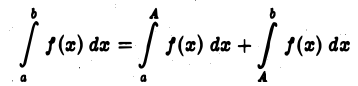
и при 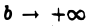интегралы 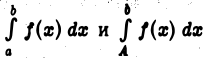имеют конечные пределы только одновременно.

Пусть теперь для всех 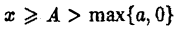выполнено условие 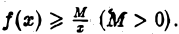Так как интеграл 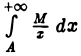расходится, то по теореме 1 расходится и интеграл 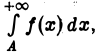а вместе с ним и интеграл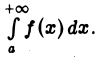

Пример:

Исследовать на сходимость интеграл

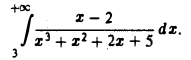
Для 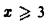имеем

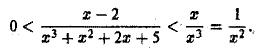
Интеграл

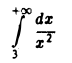
сходится 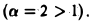Следовательно, сходится и данный интеграл.

Абсолютно сходящиеся интегралы 1-го рода

Пусть функция 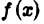определена для 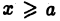и интегрируема на любом отрезк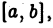е где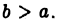

Определение:

Интеграл

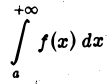
называется абсолютно сходящимся, если сходится интеграл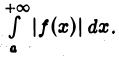

Если интеграл 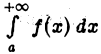сходится, 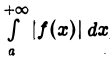расходится, то

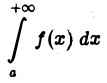
называют (условно) сходящимся интегралом.

Теорема:

Если интеграл

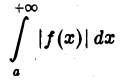
сходится, то сходится и интеграл

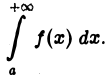
Пусть интеграл 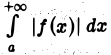сходится,

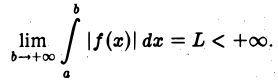
Так как для всякого х из области определения функции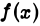

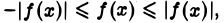
то

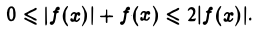
Вместе с интегралом 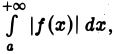который сходится по условию, сходится и интеграл 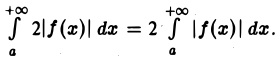Поэтому, согласно 1-й теореме сравнения, из (1) следует, что сходится также и интеграл 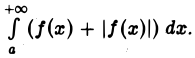Последнее означает, что интеграл 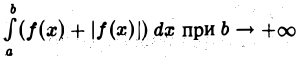имеет конечный предел.

Имеем, очевидно,

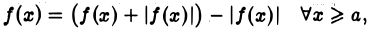
откуда для всякого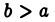

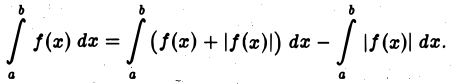
Каждое слагаемое правой части (2) имеет конечный предел при 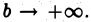Следовательно, интеграл 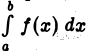при 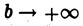также имеет конечный предел, т. е. интеграл 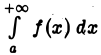сходится.

Теорема 1 и результаты касающиеся интегралов 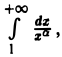позволяют сформулировать следующий признак абсолютной сходимости интеграла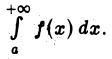

Теорема:

Если существует такое число а > 1, что для всех достаточно больших х функция 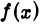удовлетворяет условию

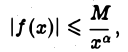
где М > 0 и не зависит от х, то интеграл

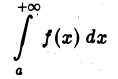
сходится абсолютно.

В самом деле, пусть условие (3) выполнено для всех 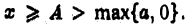Так как интеграл 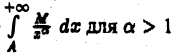сходится, то по теореме 1 сходится интеграл 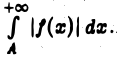А тогда сходится и интеграл 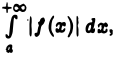и, значит, интеграл 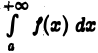сходится абсолютно.

Пример:

Рассмотрим интеграл

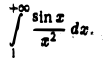
Имеем, очевидно, 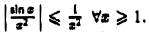Интеграл

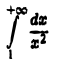
сходится, следовательно, данный интеграл сходится абсолютно.

Итак, если интеграл

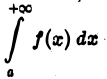
сходится абсолютно, то он сходится. Обратное неверно: интеграл

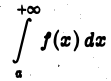
может быть сходящимся, но не быть абсолютно сходящимся.

Пример:

Рассмотрим интеграл

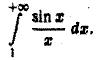
Для исследования его сходимости применим формально интегрирование по частям:

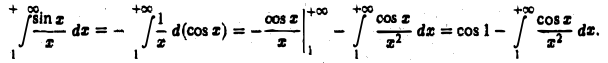
Интеграл 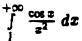сходится абсолютно и, значит, сходится. Таким образом, оба выражения в правой части (5) конечны. Поэтому, во-первых, проделанное интегрирование по частям законно, а во-вторых, левая часть конечна, т.е. интеграл 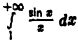сходится.

Покажем теперь, что интеграл (4) не сходится абсолютно, т. е, что интеграл

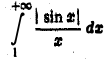
ресходится. Действительно, из неравенства

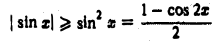
при любо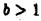м имеем

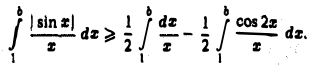
Интеграл 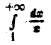расходится:

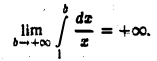
Интеграл 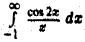сходится. Чтобы а этом убедиться, достаточно проинтегрировать его по частям (см. (5)). Перехода в неравенстве (7) к пределу при 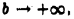получим, что правая, а следовательно, и левая часть этого неравенства стремитьса к бесконечности и поэтому интеграл (S) расходится. Таким образом, интеграл (4) не сходится абсолютно.

Приведем один достаточной критерий сходимости интегралов, называемый признаком Абеля—Дирихле.

Теорема:

Пусть

1)функция 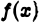непрерывна и имеет ограниченную первообразную 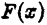при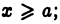

2) функция 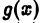непрерывно дифференцируема при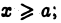

3) функция 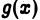монотонно убывает при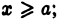

4)

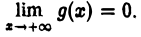
Тогда интеграл

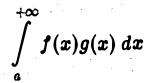
сходится.

Пример:

Применим признак Абеля—Дирихле к исследованию сходимости интеграла

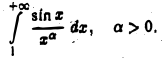
Функция 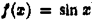имеет всюду ограниченную первообразную 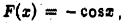а непрерывно дифференцируемая при 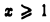функция 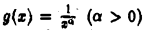монотонно убывает и стремится к нулю, когда 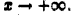Все условия теоремы Абеля—Дирихле выполнены, так что интеграл (8) сходится.

Задача:

Доказать сходимость интеграла Френеля

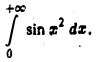
(Указание: сделать замену переменной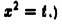

Главное значение интеграла 1-го рода

Несобственный интеграл

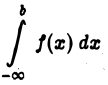
определяется следующим образом:

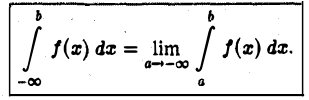
Интеграл 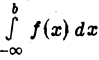называется сходящимся, если указанный предел существует,и расходящимся в противном случае.

Если оба предела интегрирования бесконечны, то по определению полагают

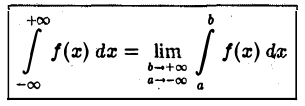
или

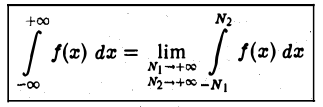
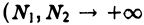независимо друг от друга). Может оказаться, что определенный таким образом несобственный интеграл не существует, но существует главное значение интеграла по Коши, определяемое по формуле

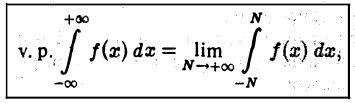
т. е. когда 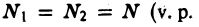— начальные буквы слов valeur principal — главное значение). Тогда говорят, что несобственный интеграл

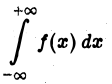
сходится в смысле главного значения по Коши.

Пример:

Рассмотрим интеграл

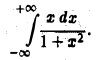
Имеем

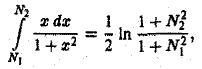
откуда видно, что при произвольном стремлении 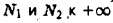интеграл 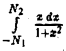предела не имеет, т.е. интеграл 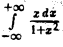расходится. В то же время

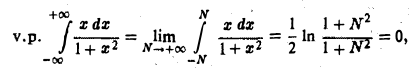
т.е. рассматриваемый интеграл сходится в смысле главного значения по Коши.

Интегралы от неограниченных функций

Необходимым условием существования определенного интеграла

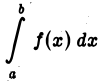
является ограниченность функции 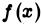на отрезке 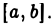Так что, если, например, функция 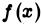интегрируема на отрезке 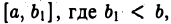и неограничен в окрестности точки х =b, то интеграл от 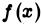на 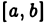в обычном смысле (в смысле Римана) не может существовать. Однако при помощи новых определений понятие интеграла можно распространить и на такие случаи, когда подынтегральная функция оказывается неограниченной на отрезке интегрирования.

Пусть функция 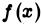интегрируема на отрезке 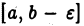при любом как угодно малом 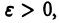но не ограничена в интервале 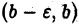(см. рис. 3). Определим, что мы будем понимать под символом

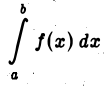
(несобственный интеграл 2-го рода). Для этого рассмотрим функцию от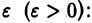

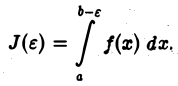
Определение:

Если при 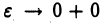функция 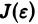имеет конечный предел L, то мы говорим, что несобственный интеграл 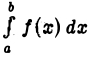сходится, и полагаем по определению

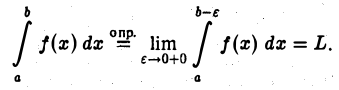
Если при 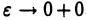функция 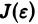не имеет предела, то говорят, что несобственный интеграл (1) расходится и не приписывают ему никакого числового значения.

Пример:

Рассмотрим интеграл

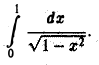
Здесь функция 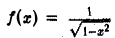непрерывна и, значит, интегрируема на любом отрезке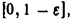 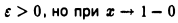функция 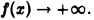Имеем

так что рассматриваемый несобственный интеграл сходится.

Аналогично, если функция 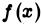неограничена только в интервале 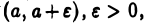несобственный интеграл

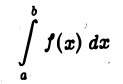
определяется так:

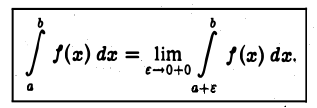
Несобственный интеграл

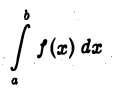
называется сходящимся, если указанный предел существует, и расходящимся — в противном случае.

Пример:

Исследовать на сходимость интеграл

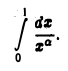
По определению

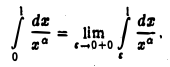
Так как при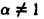

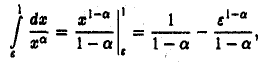
то

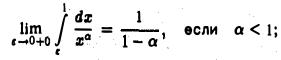
если же 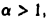то интеграл 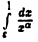не имеет конечного предела при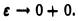

При 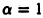имеем

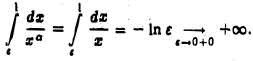
Следовательно,

Если функция 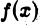на отрезке 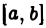не ограничена только в окрестности точки с, где 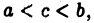то полагаем

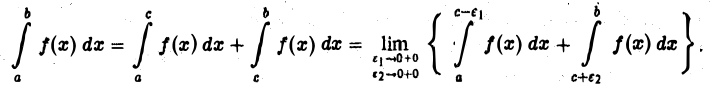
Рассмотрение других вариантов распределения особенностей функции 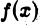предоставляем читателю.

Несобственные интегралы 2-го рода от неотрицательных функций. Теоремы сравнения

Теорема:

Пусть функции 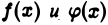интегрируемы на отрезке 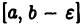при любом сколь угодно малом 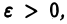неограничены в интервале 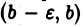и связаны условием

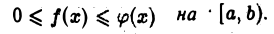
Тогда

1)если интеграл 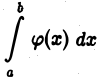сходится, то сходится интеграл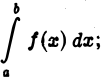

2) если интеграл 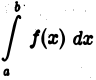расходится, то расходится интеграл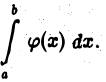

Пусть интеграл

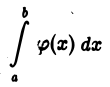
сходится, т. е. существует

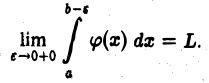
Докажем, что интеграл

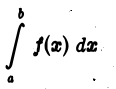
также сходится, т. е. что функция 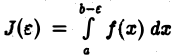имеет конечный предел при 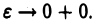В самом деле, так как 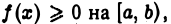то для любого 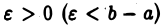функция 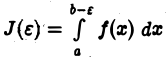неотрицательна и не убывает при убывании 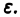Кроме того, из условия 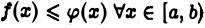при любо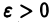м имеем

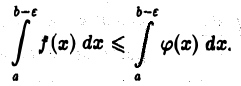
Интеграл 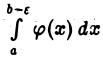не превосходит интеграла 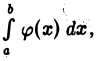который по условию сходится. Следовательно, для любого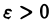

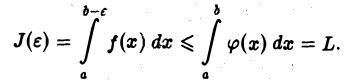
Таким образом, 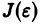есть неубывающая при 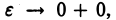ограниченная сверху функция. Поэтому существует конечный предел 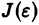при 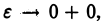что означает, согласно определению, сходимость несобственного интеграла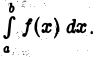

Справедливость второго утверждения теоремы легко доказывается методом рассуждения от противного.

Теорема:

Пусть положительные на 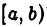функции 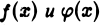неограничены только в окрестности точки х =b, и пусть существует предел

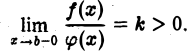
Тогда интегралы

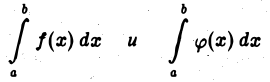
сходятся или расходятся одновременно.

Пример:

Исследовать на сходимость интеграл

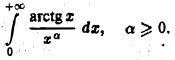
Интеграл 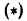является объединением несобственных интегралов 1-го и 2-го рода. Действительно, во-первых, это интеграл с бесконечным верхним пределом, в во-вторых, подынтегральная функция 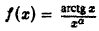не определена в точке х = 0 и становится неограниченной при 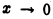для достаточно большого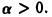

Для исследования сходимости интеграла 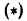разобьем промежуток интегрирования на два так, чтобы первый промежуток учитывал особенность функции 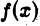в точке х = 0, а второй — поведение функци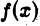и при 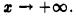Выберем, например, полуинтервалы 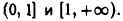Тогда будем иметь

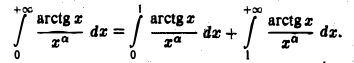
Рассмотрим интеграл

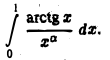
Для исследования его сходимости воспользуемся теоремой 6. Известно, что 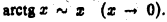Положив 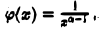будем иметь

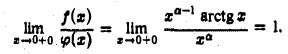
Интеграл 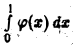сходится при 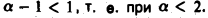В силу теоремы 8 интеграл 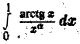также сходится при а < 2.

Рассмотрим теперь интеграл

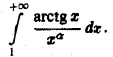
Воспользуемся теоремой 2, положив 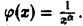Имеем

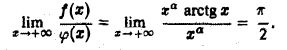
Интеграл 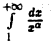сходится при a > 1. а поэтому при a > 1 сходится и рассматриваемый интеграл.

Значит, оба интеграла в правой части равенства (**) будут сходиться лишь когда 1 < а < 2. Это и есть условие сходимости интеграла (*).

Абсолютно сходящиеся интегралы 2-го рода

Определение:

Интеграл 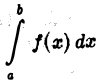называется абсолютно сходящимися, если сходится интеграл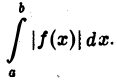

Теорема:

Если сходится интеграл 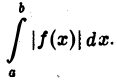то сходится и интеграл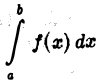

Пользуясь теоремой 7, нетрудно доказать следующий признак абсолютной сходимости интеграла.

Теорема:

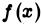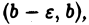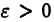Пусть функция неограничена только в интервале где сколь угодно мало. Если существует такое положительное число а < 1, что для всех х, достаточно близких к b,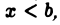

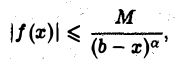
где М > 0 и не зависит от х, то интеграл

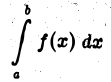
сходится абсолютно.

Задача:

Показать, что если для всех х, достаточно близких к b, х <b

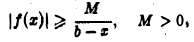
то интеграл

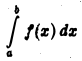
абсолютно сходиться не может.

Замечание:

Интегралы второго рода приводятся к интегралам первого рода с помощью подстановок Поэтому элементарную теорию несобственных интегралов 2-го рода можно вывести из теории интегралов 1-го рода.

Главное значение интеграла 2-го рода

Пусть функция 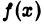интегрируема на отрезках 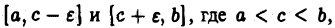при любом 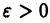и не ограничена в окрестности точки с. Тогда,

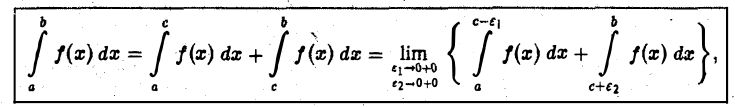
причем для сходимости интеграла предел должен существовать при независимом стремлении 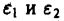к нулю.

Говорят, что несобственный интеграл сходится в смысле главного значения по Коши, если существует предел

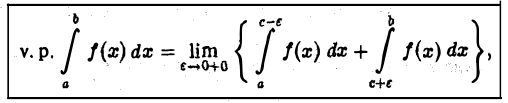
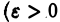одно в обоих интегралах). Величину

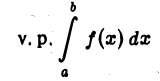
называют главным значением интеграла по Коши. Очевидно, что интеграл может быть сходящимся в смысле главного значения, но не быть сходящимся.

Пример:

Пусть 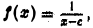где 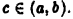Тогда

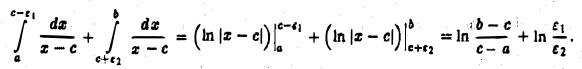
Предел правой части (1) при произвольном стремлении 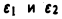к нулю не существует. Положим 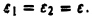Тогда при 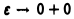предел правой части существует и есть главное значение рассматриваемого интеграла

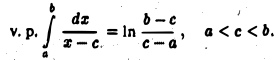
Задача:

Пусть функция 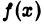определена а окрестности 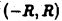точки х = 0, кроме, выть может, самой этой точки, и не ограничена при 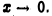Известно, что всякую функцию 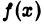а окрестности точки х=0 можно однозначно представить в виде суммы четной и нечетной функций

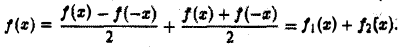
Показать, что

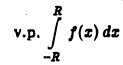
существует, если существует интеграл 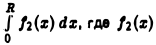— четная составляющая функции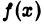

Дополнение к несобственным интегралам

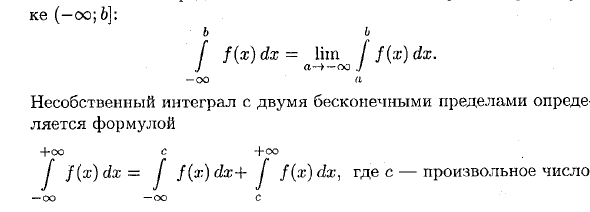
Смотрите также:

Вычисление определенного интеграла	Схемы применения определенного интеграла к нахождению геометрических и физических величин
Интегрирование четных и нечетных функций в симметричных пределах	Вычисление площадей плоских фигур

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Кратные интегралы
36. Интегралы, зависящие от параметра
37. Квадратный трехчлен
38. Производная
39. Применение производной к исследованию функций
40. Приложения производной
41. Дифференциал функции
42. Дифференцирование в математике
43. Формулы и правила дифференцирования
44. Дифференциальное исчисление
45. Дифференциальные уравнения
46. Дифференциальные уравнения первого порядка
47. Дифференциальные уравнения высших порядков
48. Дифференциальные уравнения в частных производных
49. Тригонометрические функции
50. Тригонометрические уравнения и неравенства
51. Показательная функция
52. Показательные уравнения
53. Обобщенная степень
54. Взаимно обратные функции
55. Логарифмическая функция
56. Уравнения и неравенства
57. Положительные и отрицательные числа
58. Алгебраические выражения
59. Иррациональные алгебраические выражения
60. Преобразование алгебраических выражений
61. Преобразование дробных алгебраических выражений
62. Разложение многочленов на множители
63. Многочлены от одного переменного
64. Алгебраические дроби
65. Пропорции
66. Уравнения
67. Системы уравнений
68. Системы уравнений высших степеней
69. Системы алгебраических уравнений
70. Системы линейных уравнений
71. Системы дифференциальных уравнений
72. Арифметический квадратный корень
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат