Оглавление:
Степень с рациональным показателем — это степень в показателе которой находится конечная обыкновенная или десятичная дробь.
Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.
Степенная функция
Четные и нечетные функции:
Сравним значения функции 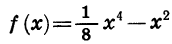 при двух противоположных значениях аргумента, например при х = 3 и х= — 3:
при двух противоположных значениях аргумента, например при х = 3 и х= — 3:
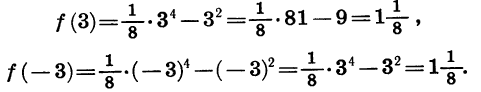
Мы видим, что f (- 3) = f(3). Значения этой функции равны и при любых других противоположных значениях аргумента. Действительно,
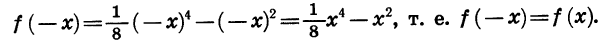
При этом рассматриваемая функция такова, что для каждого значения аргумента х противоположное ему число — х также принадлежит ее области определения. В таких случаях говорят, что область определения функции симметрична относительно нуля.
Функции, обладающие такими свойствами, называют четными функциями.
Определение:
Функция y = f(х) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство
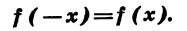
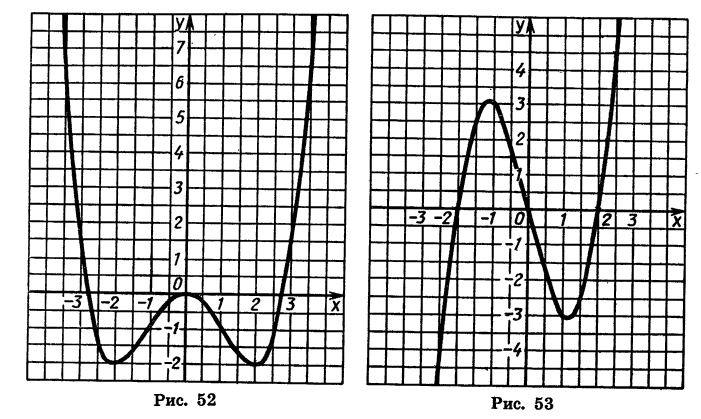
На рисунке 52 построен график функции 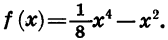
График этой функции симметричен относительно оси у.
Вообще график любой четной функции симметричен относительно оси ординат. Это следует из того, что если y=f(x) — четная функция, то любым противоположным значениям аргумента х и -х соответствует одно и то же значение функции у, а точки (x; у) и ( -х; у) симметричны относительно оси ординат.
Рассмотрим теперь функцию 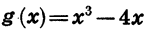 и сравним ее значения при двух противоположных значениях аргумента, например при x = 5 и х= -5:
и сравним ее значения при двух противоположных значениях аргумента, например при x = 5 и х= -5:
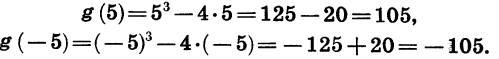
Мы видим, что g( -5) = — g(5). Эта функция принимает противоположные значения и при любых других противоположных значениях аргумента. Действительно,
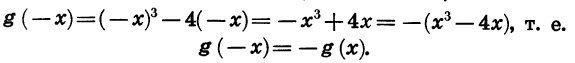
При этом область определения функции g симметрична относительно нуля.
Функции, обладающие такими свойствами, называют нечетными функциями.
Определение:
Функция y = g (х) называется нечетной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство
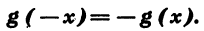
На рисунке 53 построен график функции 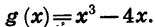 Ее график симметричен относительно начала координат.
Ее график симметричен относительно начала координат.
График любой нечетной функции симметричен относительно начала координат. Это следует из того, что если y = g (х) — нечетная функция, то любым противоположным значениям аргумента х и -х соответствуют противоположные значения функции у и -у, а точки (х; у) и ( -х; -у) симметричны относительно начала координат.
С примерами четных и нечетных функций мы уже встречались. Так, функции, заданные формулами  являются четными, а функции
являются четными, а функции 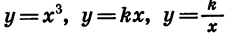 — нечетными.
— нечетными.
Заметим, что не всякая функция является четной или нечетной. Например, каждая из функций 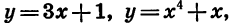
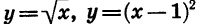 не является ни четной, ни нечетной.
не является ни четной, ни нечетной.
Функция 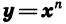
Рассмотрим функцию, заданную формулой 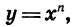 где х — независимая переменная, а n — натуральное число. Такую функцию называют степенной функцией с натуральным показателем.
где х — независимая переменная, а n — натуральное число. Такую функцию называют степенной функцией с натуральным показателем.
Степенные функции при я = 1, 2 и 3, т. е. функции у = х, 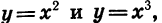 мы уже рассматривали. Их свойства и графики нам известны.
мы уже рассматривали. Их свойства и графики нам известны.
Выясним теперь свойства степенной функции и особенности ее графика при любом натуральном n.
Выражение 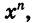 где n — натуральное число, имеет смысл при любом х. Поэтому областью определения степенной функции с натуральным показателем является множество всех действительных чисел.
где n — натуральное число, имеет смысл при любом х. Поэтому областью определения степенной функции с натуральным показателем является множество всех действительных чисел.
Сначала рассмотрим случай, когда показатель п — четное число. Свойства функции 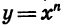 при четном п аналогичны свойствам функции
при четном п аналогичны свойствам функции 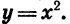
- Если х = 0, то у = 0. График функции проходит через начало координат.
- Если
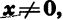 то у > 0. Это следует из того, что четная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях.
то у > 0. Это следует из того, что четная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях. - Функция является четной. Это следует из того, что при четном n равенство
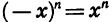 верно для любого х. График функции симметричен относительно оси ординат.
верно для любого х. График функции симметричен относительно оси ординат. - Функция возрастает в промежутке
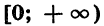 и убывает в промежутке
и убывает в промежутке 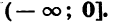
Действительно, пусть 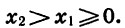 Если X1 = 0, то очевидно, что
Если X1 = 0, то очевидно, что 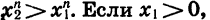 то, перемножив почленно п одинаковых неравенств
то, перемножив почленно п одинаковых неравенств  получим верное неравенство
получим верное неравенство  Значит, в промежутке
Значит, в промежутке 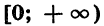 функция возрастает. Пусть теперь
функция возрастает. Пусть теперь 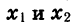 принадлежат промежутку
принадлежат промежутку 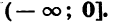 и
и 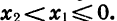 Тогда
Тогда 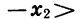
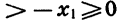 и по доказанному выше
и по доказанному выше  Отсюда в силу четности n следует, что
Отсюда в силу четности n следует, что  Значит, в промежутке
Значит, в промежутке 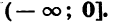 функция убывает. С возрастанием х график функции слева от начала координат опускается вниз, а справа поднимается вверх.
функция убывает. С возрастанием х график функции слева от начала координат опускается вниз, а справа поднимается вверх.
5. Область значений функции есть множество неотрицательных чисел.
Мы установили, что при любом х и четном n функция принимает неотрицательные значения. Можно доказать, что любое неотрицательное число является значением степенной функции с натуральным показателем при некотором  Значит, область значений функции — промежуток
Значит, область значений функции — промежуток 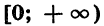 . График функции пересекает любая прямая у = а, если
. График функции пересекает любая прямая у = а, если  Если же а< 0, то прямая у = а не пересекает график.
Если же а< 0, то прямая у = а не пересекает график.
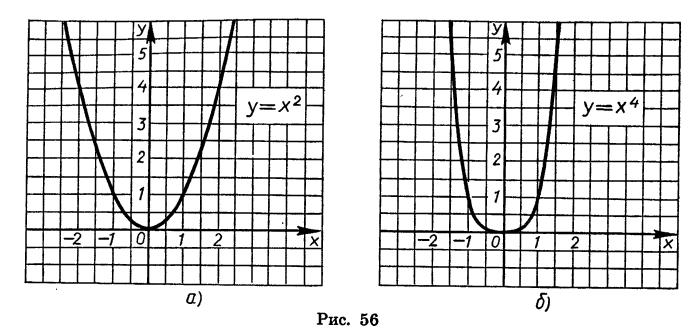
На рисунке 56 изображены графики функций 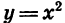 и
и 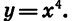 На рисунке 57 показано, как выглядит график функции
На рисунке 57 показано, как выглядит график функции 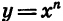 с четным показателем n.
с четным показателем n.
Рассмотрим теперь свойства степенной функции 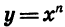 при
при
нечетном n. Эти свойства аналогичны свойствам функции 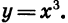
- Если х = 0, то у = 0. График функции проходит через начало координат.
- Если x > 0, то у > 0; если x < 0 то у < 0. График функции расположен в первой и третьей координатных четвертях.
- Функция является нечетной. Это следует из того, что при нечетном n для любого х верно равенство
 График функции симметричен относительно начала координат.
График функции симметричен относительно начала координат. - Функция возрастает на всей области определения.
Доказательство того, что функция возрастает в промежутке 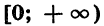 , такое же, как для степенной функции с четным показателем.
, такое же, как для степенной функции с четным показателем.
Докажем, что функция возрастает также и в промежутке 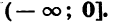 Пусть
Пусть 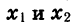 принадлежат этому промежутку и
принадлежат этому промежутку и  Тогда
Тогда 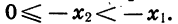 Так как
Так как 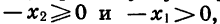 то
то  В силу нечетности числа n заключаем, что
В силу нечетности числа n заключаем, что 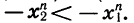 Отсюда
Отсюда  Значит, функция возрастает и в промежутке
Значит, функция возрастает и в промежутке 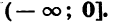 Если же
Если же 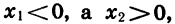 то очевидно, что
то очевидно, что  Значит, функция возрастает на всей области определения. График функции с возрастанием х поднимается вверх.
Значит, функция возрастает на всей области определения. График функции с возрастанием х поднимается вверх.
5. Область значений функции есть множество всех действительных чисел.
Это следует из свойств 1 — 3 и из того, что любое неотрицательное
число является значением степенной функции с натуральным показателем при некотором 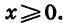 График функции пересекает любая прямая у = а.
График функции пересекает любая прямая у = а.
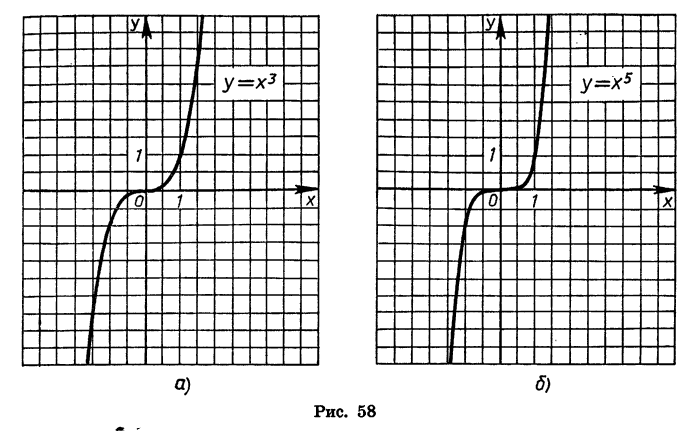
На рисунке 58 изображены графики функций 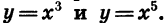 На рисунке 59 показано, как выглядит график функции
На рисунке 59 показано, как выглядит график функции 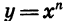 с нечетным показателем п, большим 1.
с нечетным показателем п, большим 1.
Корень n -й степени
Определение корня n-й степени:
Напомним, что квадратным корнем из числа о называется такое число, квадрат которого равен а. Аналогично определяется корень любой натуральной степени n.
Корнем n-й степени из числа а называется такое число, n-я степень которого равна а.
Например, корнем пятой степени из 32 является число 2, так как 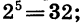 корнем четвертой степени из 81 является каждое из чисел 3 и -3, так как
корнем четвертой степени из 81 является каждое из чисел 3 и -3, так как 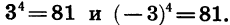 Корень второй степени принято называть квадратным корнем, а корень третьей степени — кубическим корнем. Корень второй степени принято называть квадратным корнем, а корень третьей степени — кубическим корнем.
Корень второй степени принято называть квадратным корнем, а корень третьей степени — кубическим корнем. Корень второй степени принято называть квадратным корнем, а корень третьей степени — кубическим корнем.
Рассмотрим степенную функцию 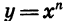 с нечетным показателем n (рис. 61). Для любого числа с существует единственное значение х, n-я степень которого равна а. Это значение является корнем n-й степени из а. Для записи корня нечетной степени n из числа а используют обозначение
с нечетным показателем n (рис. 61). Для любого числа с существует единственное значение х, n-я степень которого равна а. Это значение является корнем n-й степени из а. Для записи корня нечетной степени n из числа а используют обозначение 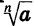 (читают: «Корень n-й степени из а»). Число n называют показателем корня, выражение, стоящее под знаком корня,— подкоренным выражением.
(читают: «Корень n-й степени из а»). Число n называют показателем корня, выражение, стоящее под знаком корня,— подкоренным выражением.
Приведем примеры.
Запись 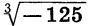 означает кубический корень из —125. Из определения корня следует, что
означает кубический корень из —125. Из определения корня следует, что 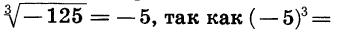 —125. Запись
—125. Запись 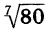 означает корень седьмой степени из 80. Число
означает корень седьмой степени из 80. Число 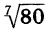 иррациональное. Его значение с точностью до 0,01 равно 1,87.
иррациональное. Его значение с точностью до 0,01 равно 1,87.
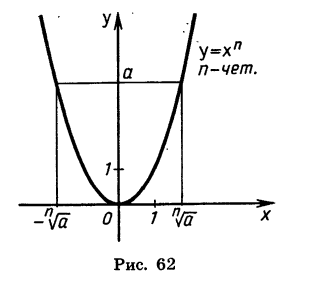
Рассмотрим теперь степенную функцию 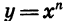 с четным показателем n (рис. 62). При любом а > 0 существуют два противоположных значения х, n-я степень которых равна а. При a = 0 такое число одно (число 0), при а < 0 таких чисел нет.
с четным показателем n (рис. 62). При любом а > 0 существуют два противоположных значения х, n-я степень которых равна а. При a = 0 такое число одно (число 0), при а < 0 таких чисел нет.
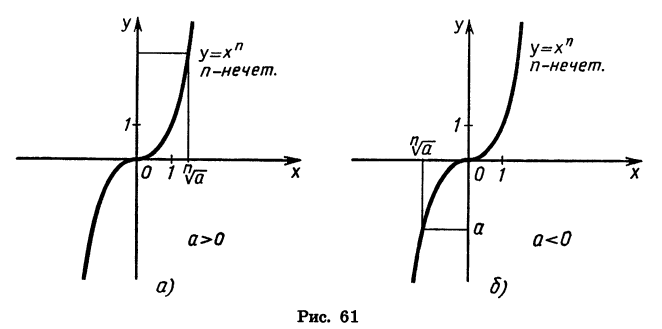
Другими словами, если n — четное число и а > 0, то существуют два корня n-й степени из а. Эти корни являются противоположными числами. Если а = 0, то корень n-й степени из а равен нулю. Если а < 0 и n — четное число, то корень n-й степени из а не существует.
В случае четного n знаком 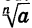 обозначают неотрицательный корень n-й степени из а. Отрицательный корень n-й степени из а (при a > 0) записывают так:
обозначают неотрицательный корень n-й степени из а. Отрицательный корень n-й степени из а (при a > 0) записывают так: 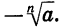 Выражение
Выражение 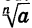 при четном n и а < 0 не имеет смысла.
при четном n и а < 0 не имеет смысла.
Например, запись 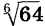 означает неотрицательный корень шестой степени из 64. Имеем
означает неотрицательный корень шестой степени из 64. Имеем 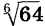 = 2, так как 2 — неотрицательное число и
= 2, так как 2 — неотрицательное число и 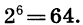
Если n = 2, то показатель корня не пишется.
Итак, если n — нечетное число, то выражение 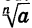 имеет смысл при любом а; если n — четное число, то выражение
имеет смысл при любом а; если n — четное число, то выражение 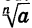 имеет смысл лишь при
имеет смысл лишь при 
Из определения корня n-й степени следует, что при всех значениях а, при которых выражение 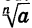 имеет смысл, верно равенство
имеет смысл, верно равенство 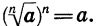
Выражение 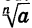 при
при  имеет смысл как при четном, так и при нечетном n, и значение этого выражения является неотрицательным числом. Его называют арифметическим корнем n-й степени из а.
имеет смысл как при четном, так и при нечетном n, и значение этого выражения является неотрицательным числом. Его называют арифметическим корнем n-й степени из а.
Определение:
Арифметическим корнем n-й степени из неотрицательного числа а называется неотрицательное число, n-я степень которого равна а.
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень. Например, 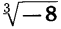 =
= 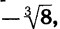 так как
так как 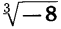 = -2 и
= -2 и 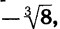 = -2.
= -2.
Вообще при любом положительном а и нечетном n
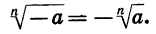
С помощью знака корня n-й степени записываются решения уравнений вида 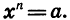 Приведем примеры.
Приведем примеры.
Пример:
Решим уравнение 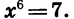
Корнями уравнения служат числа, шестая степень которых равна 7. Таких чисел два: 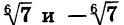 (см. рис. 62).
(см. рис. 62).
Пример:
Решим уравнение 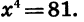
Уравнение имеет два корня:
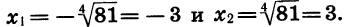
Пример:
Решим уравнение 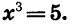
Уравнение имеет единственный корень (см. рис. 61). Этот корень есть число, третья степень которого равна 5, т. е. 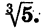
Пример:
Решим уравнение 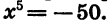
Уравнение имеет единственный корень (см. рис. 61). Этот корень есть число, пятая степень которого равна —50, т. е. 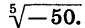 Выразив
Выразив 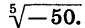 через арифметический корень, получим
через арифметический корень, получим 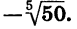
Свойства арифметического корня n-й степени
Нам известны следующие свойства арифметического квадратного корня:
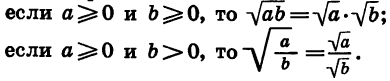
Аналогичными свойствами обладает арифметический корень n-й степени и при n > 2.
Теорема:
Если 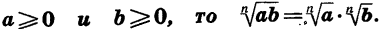 Пусть
Пусть  Тогда каждое из выражений
Тогда каждое из выражений 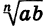 и
и 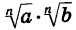 имеет смысл. Докажем, что выполняются условия:
имеет смысл. Докажем, что выполняются условия: 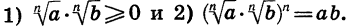
Значение выражения 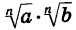 неотрицательно, так как по определению арифметического корня
неотрицательно, так как по определению арифметического корня 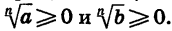 Кроме того, по свойству степени произведения
Кроме того, по свойству степени произведения
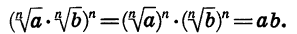
Значит, по определению арифметического корня n-й степени верно равенство 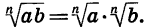
Доказанная теорема распространяется на случай, когда число множителей под знаком корня больше двух. Например, если 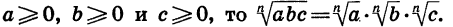 Действительно,
Действительно,
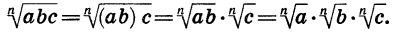
Таким образом, арифметический корень п-й степени обладает свойством: корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Теорема:
Если 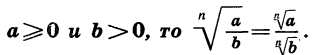
Доказательство проводится аналогично доказательству теоремы 1.
Итак, справедливо еще одно свойство арифметического корня n-й степени: корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Поменяв местами в каждом равенстве 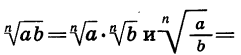
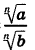 их левые и правые части, получим равенства, выражающие правила умножения и деления арифметических корней n-й степени:
их левые и правые части, получим равенства, выражающие правила умножения и деления арифметических корней n-й степени:
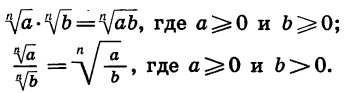
Приведем примеры применения доказанных свойств.
Пример:
Найдем значение выражения 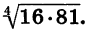 По теореме о корне из произведения имеем:
По теореме о корне из произведения имеем:
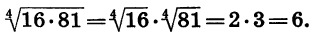
Пример:
Перемножим корни 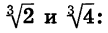
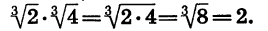
Пример:
Найдем значение выражения 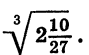
Пользуясь теоремой о корне из дроби, получаем:
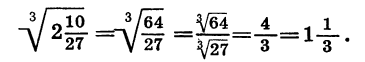
Рассмотрим другие свойства корня n-й степени. Начнем с примера. Сравним значения выражений 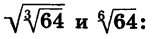
Мы видим, что значения этих выражений равны, т. е.
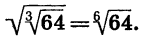
Теорема:
Если п и к — натуральные числа и 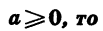
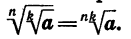
Так как 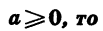 выражения
выражения 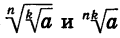 имеют смысл и неотрицательны. Кроме того,
имеют смысл и неотрицательны. Кроме того,
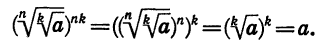
Следовательно, по определению арифметического корня верно равенство 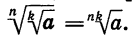
Теорема:
Если n, k и m — натуральные числа и 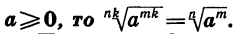
По теореме 3 имеем:
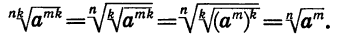
Мы доказали, что арифметический корень n-й степени обладает свойством: если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
Это свойство иногда называют основным свойством корня. Приведем пример применения теорем 3 и 4.
Пример:
Упростим выражение
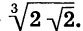
Внесем множитель 2 под знак квадратного корня. Получим:
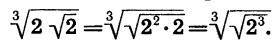
По теореме о корне из корня имеем:
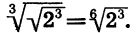
Применив основное свойство корня, получим:
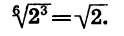
Итак,
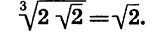
Степень с рациональным показателем и ее свойства
Определение степени с дробным показателем
Мы знаем, какой смысл имеет выражение 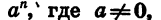 если показатель n — целое число. Например,
если показатель n — целое число. Например, 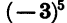 означает произведение пяти множителей, каждый из которых равен — 3. Число
означает произведение пяти множителей, каждый из которых равен — 3. Число 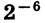 означает число, обратное степени
означает число, обратное степени 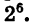 Введем теперь понятие степени, у которой показатель не целое, а дробное число.
Введем теперь понятие степени, у которой показатель не целое, а дробное число.
Из определения арифметического корня следует, что если m — целое число, n — натуральное и m делится на n, то при а > 0 верно равенство 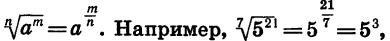
Так как 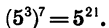 Если принять, что равенство
Если принять, что равенство 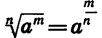 имеет место и в том случае, когда
имеет место и в том случае, когда 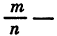 дробное число, то все свойства, верные для целого показателя степени, будут выполняться и для дробного показателя с положительным основанием (это будет доказано в следующем пункте).
дробное число, то все свойства, верные для целого показателя степени, будут выполняться и для дробного показателя с положительным основанием (это будет доказано в следующем пункте).
Определение:
Если а — положительное число, 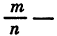 дробное число (m — целое, n — натуральное), то
дробное число (m — целое, n — натуральное), то
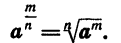
По определению имеем:
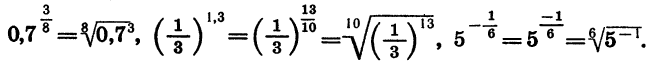
Степень с основанием, равным нулю, определяется только для положительного дробного показателя: если 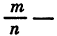 дробное положительное число (тип — натуральные), то
дробное положительное число (тип — натуральные), то 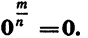 Для отрицательных оснований степень с дробным показателем не рассматривается. Такие выражения, как
Для отрицательных оснований степень с дробным показателем не рассматривается. Такие выражения, как 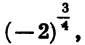
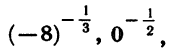 не имеют смысла.
не имеют смысла.
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,76 можно представить в виде дроби так:
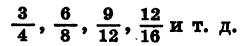
Значение степени с дробным показателем r не зависит от способа записи числа r в виде дроби: представляя r в виде отношения целого числа к натуральному разными способами, всегда будем получать один и тот же результат. Например:
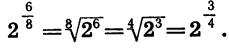
Покажем это в общем случае.
Пусть а > 0, m — целое, n и k — натуральные числа. Пользуясь определением степени с дробным показателем и основным свойством корня, получим:
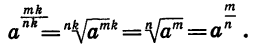
Значения степеней с дробным показателем и положительным основанием можно находить приближенно с помощью инженерного микрокалькулятора, например, «Электроника БЗ-Зб». Микрокалькулятор «Электроника Б3-36» имеет 25 клавиш, из них 22 клавиши можно использовать для выполнения двух операций. Одна операция обозначена на самой клавише, а другая написана над ней. При выполнении операций, обозначенных на клавишах, микрокалькулятор работает в нормальном режиме, а когда производят операции, обозначенные над клавишами, то микрокалькулятор работает в совмещенном режиме. Чтобы перейти к этому режиму, надо нажать клавишу  После того как операция произведена, микрокалькулятор возвращается в нормальный режим работы. Вычисление значений степеней производится в совмещенном режиме, для чего используется клавиша
После того как операция произведена, микрокалькулятор возвращается в нормальный режим работы. Вычисление значений степеней производится в совмещенном режиме, для чего используется клавиша 
Пример:
Найдем значение степени 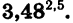
Вводим основание степени у, равное 3,48, нажимаем клавишу  (микрокалькулятор начинает работать в совмещенном режиме) и клавишу
(микрокалькулятор начинает работать в совмещенном режиме) и клавишу 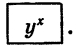 , затем показатель степени х,
, затем показатель степени х,
равный 2,5, и клавишу 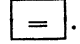 На экране высветится результат. Программа вычислений выглядит так:
На экране высветится результат. Программа вычислений выглядит так:
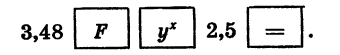
Выполнив вычисления, найдем, что приближенное значение степени 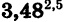 равно 22,591658.
равно 22,591658.
Пример:
Вычислим значение степени 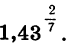
Этот пример отличается от примера 1 тем, что показатель степени представлен не в виде десятичной дроби, а в виде обыкновенной дроби. Поэтому после введения основания степени 1,43 надо и нажатия клавиш 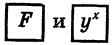 надо представить
надо представить 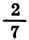 в виде десятичной дроби, выполнив деление 2 на 7. Для таких случаев в микрокалькуляторе предусмотрены клавиши
в виде десятичной дроби, выполнив деление 2 на 7. Для таких случаев в микрокалькуляторе предусмотрены клавиши  (открывающая скобки) и
(открывающая скобки) и  (закрывающая скобки), которые позволяют получить промежуточный результат. Программа вычислений будет выглядеть так:
(закрывающая скобки), которые позволяют получить промежуточный результат. Программа вычислений будет выглядеть так:
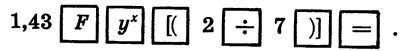
Выполнив вычисление, получим 1,1075969.
Заметим, что в тех случаях, когда результат вычислений по модулю оказывается меньше 0,0000001 или больше 99 999 999, микрокалькулятор дает ответ в виде 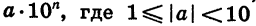
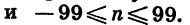 Знак числа а высвечивается в 1-м разряде слева (положительный знак не высвечивается), цифры числа а — в разрядах от 2-го до 9-го включительно, знак порядка — в 10-м разряде и цифры порядка — в 11-м и 12-м разрядах.
Знак числа а высвечивается в 1-м разряде слева (положительный знак не высвечивается), цифры числа а — в разрядах от 2-го до 9-го включительно, знак порядка — в 10-м разряде и цифры порядка — в 11-м и 12-м разрядах.
Свойства степени с рациональным показателем
Известные нам свойства степени с целым показателем справедливы и для степени с любым рациональным показателем. Перечислим их.
Для любого а > 0 и любых рациональных чисел р и q:

Для любых а >0 и b > 0 и любого рационального числа р:

Докажем свойство (1). Сначала покажем на частном примере способ доказательства этого свойства.
Пусть, например, 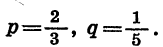 Докажем, что
Докажем, что
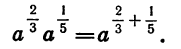
Приведем дроби 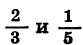 к общему знаменателю:
к общему знаменателю:
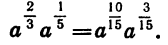
Так как 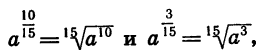 то по свойству арифметического корня имеем:
то по свойству арифметического корня имеем:
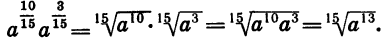
Переходя к степени с дробным показателем, получим:
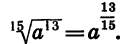
Следовательно, 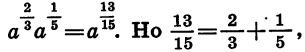 поэтому
поэтому
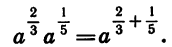
Проведем теперь доказательство свойства (1) в общем виде. Представим рациональные числа р и q в виде дробей с одинаковыми знаменателями: 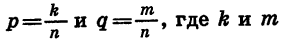 — целые числа, а n — натуральное число. Тогда
— целые числа, а n — натуральное число. Тогда
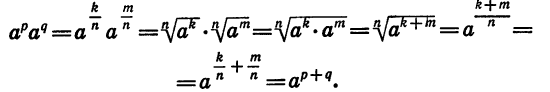
Значит, 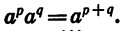
Из свойства (1) следует, что для любого положительного а и любого рационального числа р
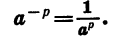
Действительно, 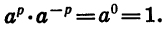
Свойство (2) следует из свойства (1) и определения частного. Докажем свойство (3), т. е. докажем, что при а > 0 и любых рациональных р и q
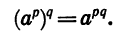
Пусть 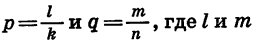 — целые, а k и n — натуральные числа. Тогда
— целые, а k и n — натуральные числа. Тогда
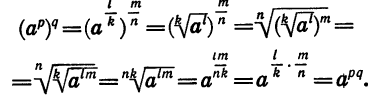
Значит, 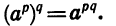
Покажем, что при любом рациональном р и любом натуральном n
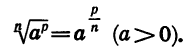
Действительно, по определению степени с дробным показателем и свойству (3) имеем:
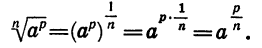
Докажем свойство (4), т. е. докажем, что при а > 0 и b > 0 и любом рациональном р
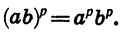
Пусть 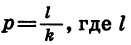 — целое число и к — натуральное число. Тогда
— целое число и к — натуральное число. Тогда
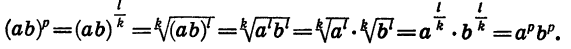
Значит, 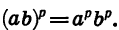
Свойство (5) можно доказать, представив дробь 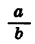 в виде произведения
в виде произведения 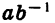 и применив затем свойство (4).
и применив затем свойство (4).
Преобразование выражении, содержащих степени с дробными показателями
Рассмотрим примеры, в которых используются тождественные преобразования выражений, содержащих степени с дробными показателями.
Пример:
Найдем значение выражения
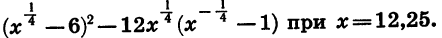
Предварительно упростим это выражение:
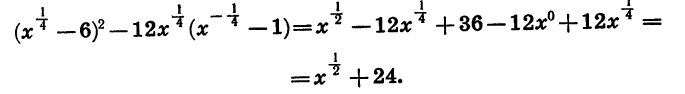
Подставим в выражение 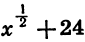 данное значение х и выполним вычисления:
данное значение х и выполним вычисления:
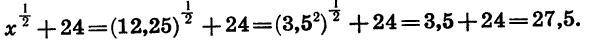
Пример:
Упростим выражение
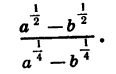
Представим числитель 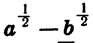 в виде разности квадратов и разложим ее на множители. Получим:
в виде разности квадратов и разложим ее на множители. Получим:
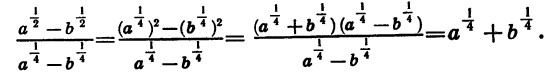
Пример:
Сократим дробь
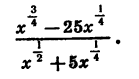
Разложим на множители числитель и знаменатель дроби. Получим
Степени с рациональными показателями
Теперь, когда введено понятие арифметического корня n -й степени, можно определить степень с рациональным показателем.
Пусть а — положительное действительное число, x — произвольное рациональное число, т.е. число, представимое в виде несократимой обыкновенной дроби 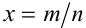 , где
, где 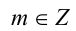 ,
, 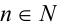 . В частности, при n = 1 рациональное число x является целым, а понятие степени с целым показателем было введено ранее. При
. В частности, при n = 1 рациональное число x является целым, а понятие степени с целым показателем было введено ранее. При 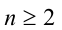 под рациональной степенью x числа а понимают положительное число, равное арифметическому корню степени n из числа
под рациональной степенью x числа а понимают положительное число, равное арифметическому корню степени n из числа 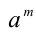 , т.е.
, т.е. 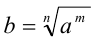 , и обозначают
, и обозначают 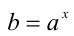 (или
(или 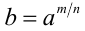 ). Например, под
). Например, под 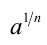 понимают
понимают 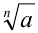 . При а = 1 и любом рациональном x имеем
. При а = 1 и любом рациональном x имеем 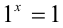 .
.
Если основание а = 0, то рациональная степень определена только при положительном показателе 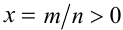 , при этом полагают
, при этом полагают 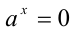 .
.
Степень с рациональным показателем можно определить и для отрицательного основания. Пусть 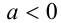 и показатель степени имеет в знаменателе нечётное число
и показатель степени имеет в знаменателе нечётное число 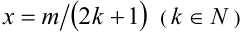 . В этом случае под
. В этом случае под 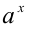 понимают алгебраический (при нечётном m) или арифметический (при чётном m) корень степени
понимают алгебраический (при нечётном m) или арифметический (при чётном m) корень степени 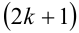 из числа
из числа 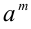 , т.е.
, т.е.
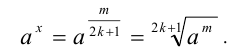
В этом случае справедливы все перечисленные ниже свойства степеней с рациональными показателями, которые доказываются аналогично.
Большинство свойств степеней с рациональными показателями выглядят аналогично (хотя являются обобщением) соответствующим свойствам степеней с целыми показателями. Доказательство свойств степеней с рациональными показателями проведём для случая положительного основания. В выполнении свойств степеней для случаев нулевого и отрицательного оснований убедитесь самостоятельно.
Свойства степеней с рациональными показателями
Пусть а и b — положительные действительные числа, а x и у — рациональные числа. Тогда верны следующие равенства:
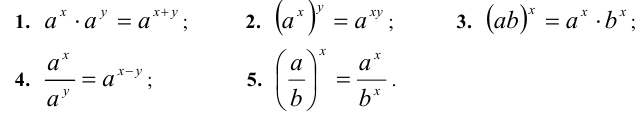
6.Пусть 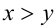 . Если
. Если 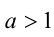 , то
, то 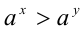 , а если
, а если 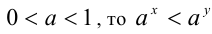 .
.
7.Если 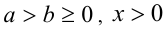 , то
, то 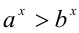 ; если
; если 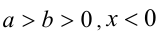 ,то
,то 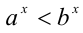 .
.
Доказательство:
Рассмотрим два рациональных числа 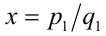 и
и 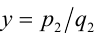 , их всегда можно привести к общему знаменателю:
, их всегда можно привести к общему знаменателю:
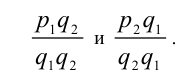
Поэтому будем считать при доказательстве этого свойства, что рациональные числа x и у уже представлены в виде двух дробей с одинаковыми знаменателями: 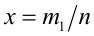 и
и 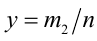 . Тогда, используя определение степени с рациональным показателем, а также свойство 2 арифметических корней и свойство 1 степеней с целым показателем, получаем
. Тогда, используя определение степени с рациональным показателем, а также свойство 2 арифметических корней и свойство 1 степеней с целым показателем, получаем
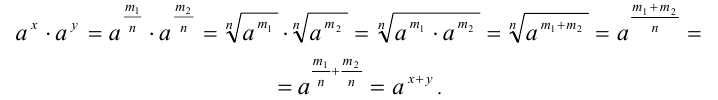
Пусть 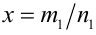 и
и 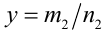 . Тогда, используя определение степени с рациональным показателем и свойства 4, 5 арифметических корней, получаем
. Тогда, используя определение степени с рациональным показателем и свойства 4, 5 арифметических корней, получаем
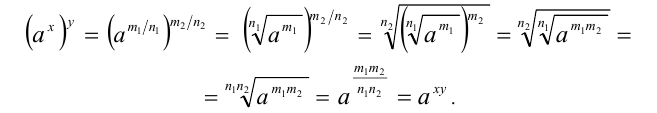
Пусть 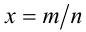 , тогда, используя определение степени с рациональным показателем, а также свойство 4 степеней с целым показателем и свойство 2 арифметических корней, получим
, тогда, используя определение степени с рациональным показателем, а также свойство 4 степеней с целым показателем и свойство 2 арифметических корней, получим
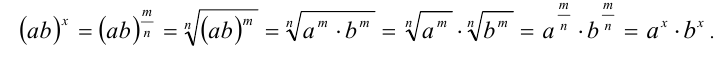
Докажем вначале, что 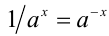 . Для этого достаточно показать, что произведение
. Для этого достаточно показать, что произведение 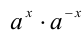 равно единице. В самом деле,
равно единице. В самом деле, 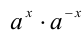
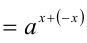
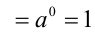 . Но это и означает, что числа
. Но это и означает, что числа 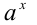 и
и 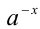 взаимнообратны , т.е. Теперь докажем свойство:
взаимнообратны , т.е. Теперь докажем свойство: 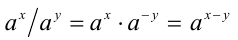 (здесь использовалось доказанное выше свойство 1 степеней с рациональным показателем).
(здесь использовалось доказанное выше свойство 1 степеней с рациональным показателем).
Воспользуемся доказанными свойствами 3 и 2 степеней с рациональным показателем:
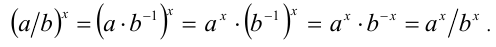
Докажем вначале два вспомогательных свойства:
1) если 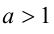 и
и 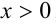 , то
, то 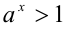 ; 2) если
; 2) если 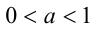 и
и 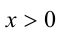 , то
, то 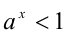 .
.
1) Пусть 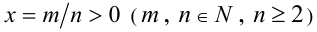 и
и 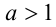 . Воспользуемся дважды
. Воспользуемся дважды
свойством 8 числовых неравенств и определением степени с рациональным показателем:
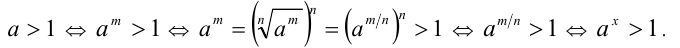
2) Пусть теперь 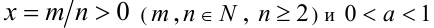 . Обозначим
. Обозначим 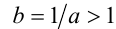 , и тогда по только что доказанному свойству имеем
, и тогда по только что доказанному свойству имеем 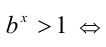
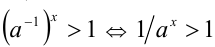
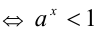 . Тогда доказательство свойства 6 вытекает непосредственно из доказанных выше свойств 1) и 2), поскольку тогда
. Тогда доказательство свойства 6 вытекает непосредственно из доказанных выше свойств 1) и 2), поскольку тогда 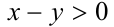 , следовательно, при
, следовательно, при 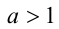 получаем
получаем
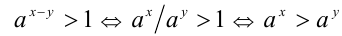
Доказательство в случае 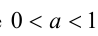 проводится аналогично.
проводится аналогично.
7.Пусть 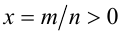 . Тогда
. Тогда 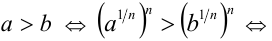 (по свойству 8 числовых неравенств)
(по свойству 8 числовых неравенств)
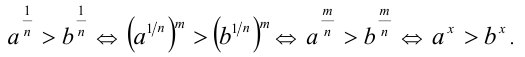
Замечание. Мы доказали более сильное утверждение, а именно: если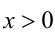 , то
, то 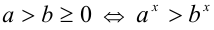 . В случае
. В случае 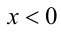 учтём, что
учтём, что 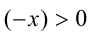 , и применим полученный выше результат:
, и применим полученный выше результат: 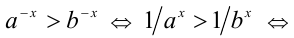 (по свойству 7б числовых неравенств)
(по свойству 7б числовых неравенств) 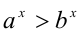 .
.
Пример:
Решить уравнения: 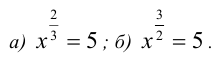
Решение:
а) ОДЗ: 
б) ОДЗ: 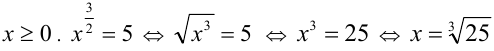
Пример:
Доказать, что если 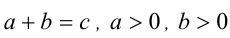 , то
, то
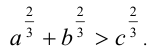
Доказательство. Рассмотрим положительные числа a/c и b/с . По условию, (а/с) + (b/с) = 1, отсюда получаем оценки 0<а/с<1, 0< b/c < 1. По свойству 6 степеней с рациональными показателями имеем:
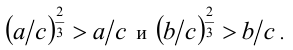
Складывая почленно два последних неравенства, получаем, что 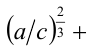
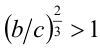 , а это равносильно доказываемому неравенству.
, а это равносильно доказываемому неравенству.
Пример:
Решить неравенство 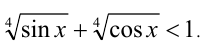
Решение:
Так как на ОДЗ 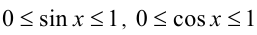 , то по свойству 6 степеней с рациональными показателями имеем:
, то по свойству 6 степеней с рациональными показателями имеем:
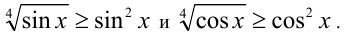
Складывая эти неравенства, получаем, что на ОДЗ 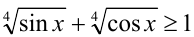 . Таким образом, исходное неравенство не имеет решений.
. Таким образом, исходное неравенство не имеет решений.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
