Оглавление:
Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линиии только они. Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные — параметрами.
Постоянные и переменные величины
В практической деятельности, в технике, при исследовании какого-либо процесса мы встречаемся с величинами двух родов: постоянными и переменными.
Постоянной величиной называется такая, которая при изучении какого-либо процесса не меняет своего значения. Например, длина радиуса одной и той же окружности, температура кипения чистой воды при постоянном давлении — величины постоянные.
Постоянные величины принято обозначать первыми буквами латинского алфавита: а, b, с, d, и т. д.
Переменной величиной называется такая, которая в условиях изучаемого процесса меняет свое значение. Например, периметр правильного вписанного в окружность многоугольника при увеличении числа его сторон, длина металлического стержня при его нагревании — величины переменные.
Переменные величины принято обозначать последними буквами латинского алфавита: х, у, z также t, u, v, w).
Часто бывает, что одна и та же величина при одних условиях является постоянной, при других — переменной. Например, в правильном вписанном в окружность многоугольнике апофема — величина постоянная; при неограниченном удвоении числа сторон этого многоугольника апофема становится величиной переменной.
Среди постоянных величин имеются, однако, и такие, которые сохраняют свое значение при любых условиях; они называются абсолютными постоянными. Например, сумма внутренних углов треугольника, отношение длины окружности к диаметру.
Функциональная зависимость между переменными величинами
Переменные величины в математике играют важную роль: они служат средством изучения явлений природы и технических процессов. При этом используются переменные величины не в отрыве друг от друга, а в их взаимной связи, в определенной зависимости между ними. Рассмотрим случай зависимости двух переменных величин между собой.
Две переменные величины могут быть взаимосвязаны так, что каждому данному значению одной из них соответствует вполне определенное значение другой. Возьмем, например, уравнение

в котором S означает расстояние, пройденное падающим телом, а t — время падения. Дадим времени t какое-либо числовое значение, тогда величина пройденного расстояния S получит соответствующее значение; например,
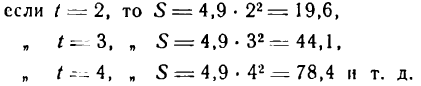
Переменная величина t которой мы давали произвольные значения, называется независимой переменной или аргументом; другая же переменная S , изменяющаяся в зависимости от изменения t, называется зависимой переменной или функцией. Связь между этими переменными носит название функциональной зависимости.
Следует отметить, что хотя аргументу мы даем произвольные значения, однако эти значения выбираются только такими, которые допускаются условиями задачи. Так, в разобранном примере время t может принимать только положительные значения или нуль, ибо время, выраженное отрицательным числом, здесь смысла не имеет.
Заметим также, что выбор независимой переменной диктуется условиями задачи. Если, например, нас интересует время, в течение которого тело прошло то или иное расстояние, то в уравнении (1) мы должны давать S числовые значения, которым будут соответствовать определенные значения t; при этом условии S явится уже аргументом, а t — функцией. В таком случае для удобства вычисления функции t уравнение (1) следует переписать так:
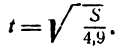
Определение:
Переменная величина у называется функцией переменной х, если каждому допустимому значению х соответствует определенное значение у.
Функция, определяемая таким образом, называется однозначной.
В математике рассматриваются и такие функции, которые имеют несколько значений, соответствующих одному значению аргумента, например
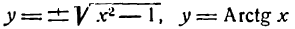
и таму подобное. Такого рода функции, называемые многозначными, в нашем курсе рассматриваться не будут.
Пример:
Площадь круга
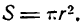
Каждому значению r в этом равенстве соответствует определенное значение S; следовательно, площадь круга есть функция радиуса, а само равенство выражает функциональную зависимость между этими переменными.
Пример:
Путь, пройденный телом в прямолинейном движении с постоянной скоростью v ,
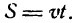
Здесь путь S получает определенное значение, соответствующее значению t; поэтому S — функция времени t .
Пример:
Согласно закону Бойля — Мариотта давление р и объем v газа связаны формулой:
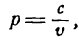
где с — постоянная величина для данной массы и температуры газа. С изменением объема v изменяется и давление р; следовательно, давление р газа есть функция его объема v.
Линии и их уравнения
Из курса алгебры известно, что по уравнению, определяющему функцию, можно построить линию, называемую графиком функции.
Пусть, например, дано уравнение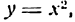 определяющее у как функцию х.
определяющее у как функцию х.
Составим таблицу значений х и соответствующих значений у:
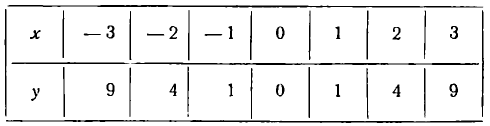
Каждой полученной в этой таблице паре значений х и у соответствует точка плоскости. Построив эти точки (рис.8) и соединив их плавной линией, мы получим график функции 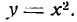
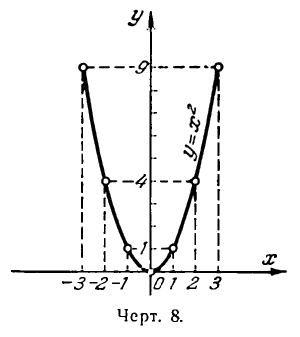
Этот график, как видно, представляет линию, все точки которой обладают одинаковым свойством, а именно: ордината каждой из них равна квадрату соответствующей абсциссы. Линия, все точки которой обладают одним и тем же свойством, называется геометрическим местом таких точек.
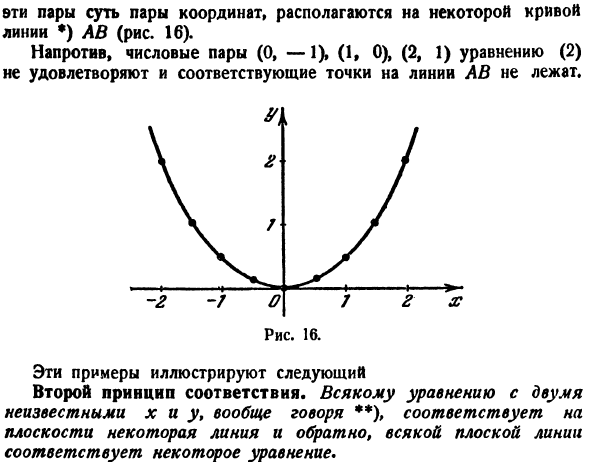
Наш пример показывает, что уравнению с переменными х и у соответствует на плоскости некоторая линия как геометрическое место точек, координаты которых удовлетворяют этому уравнению.
Обратно, линии на плоскости, представляющей геометрическое место точек, соответствует некоторое уравнение с переменными х и у.
Покажем это на примере.
Пусть дана на плоскости окружность с центром в начале координат и радиусом, равным 5 (рис. 9). Из элементарного курса геометрии известно, что эта окружность есть геометрическое место точек, удаленных от центра па 5 единиц. Возьмем на окружности произвольную точку М(х; у). По условию, ОМ = 5; с другой стороны, по формуле (5)
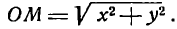
Следовательно, для любой точки нашей окружности должно быть
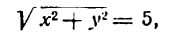
или

Итак, окружности с радиусом, равным 5, и с центром в начале координат соответствует уравнение (1).
Уравнение (1) вполне определяет данную окружность, а потом она называется уравнением этой окружности.
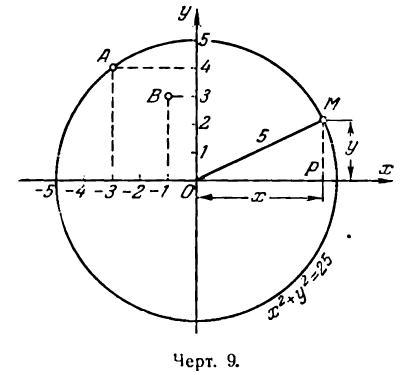
Имея уравнение (1) окружности, можно узнать, лежат ли на ней какие-нибудь данные точки, например А(- 3; 4) и В (- 1; 3). Для этого нужно проверить, удовлетворяют ли координаты точек А и В уравнению (1). Подставив их в уравнение (1) на место х и у, получим: для точки А:
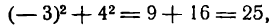
для точки В:
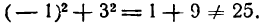
Координаты точки А удовлетворяют уравнению (1), значит, точка А лежит на данной окружности; координаты же точки В не удовлетворяют этому уравнению, значит, точка В на этой окружности не лежит (рис. 9).
Определение:
Уравнением линии называется уравнение с переменными х и у, которому удовлетворяют координаты любой точки этой линии и не удовлетворяют координаты любой точки у не лежащей на линии.
Переменные х и у входящие в уравнение линии, называются текущими координатами.
Таким образом мы установили, что между линиями, и их уравнениями существует связь, поэтому принято говорить:
«дана линия» вместо «дано уравнение линии»,
«найти линию» вместо «найти уравнение линии».
Установленная выше связь между линиями и их уравнениями позволяет изучать свойства линий путем анализа уравнений, соответствующих этим линиям. Отсюда и название изучаемого нами предмета — аналитическая геометрия.
Пример:
Лежит ли точка А (- 2; 4) на линии 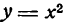 ?
?
Решение:
Подставив вместо х и у в данное уравнение координаты точки А( — 2; 4), получим тождество:
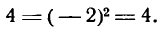
Следовательно, точка А лежит на данной линии.
Пример:
Дана линия у = — Зх + 1 и точка А на ней с абсциссой, равной — 1. Определить ординату точки А.
Решение:
Так как точка А лежит на данной линии, то ее координаты должны удовлетворять данному уравнению. Одна координата х = — 1. Чтобы найти вторую, т. е. у, мы подставим в уравнение вместо х его значение. Получим:
у = -3( — 1) + 1 = 4.
Итак, ордината точки А равна 4.









Смотрите также:
| Точки и координаты | Прямая линия |
| Решение систем линейных уравнений. теорема Кронекера-Капелли | Эллипс |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
