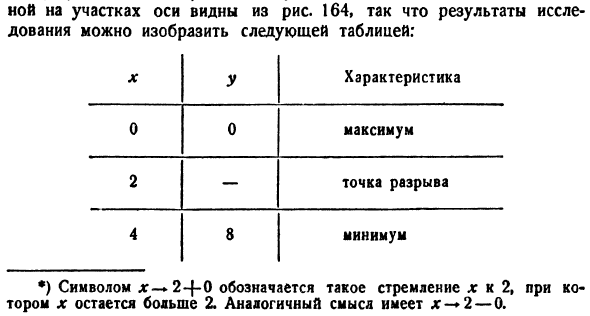
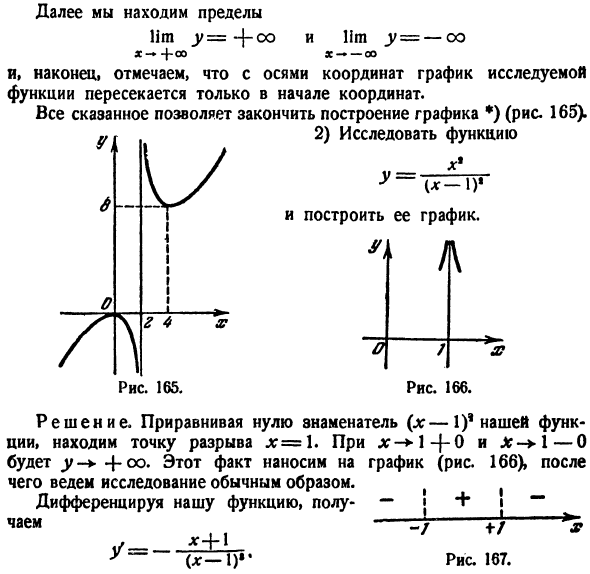
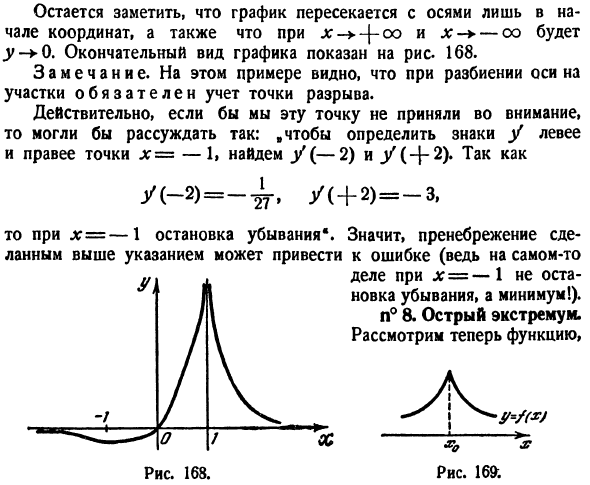
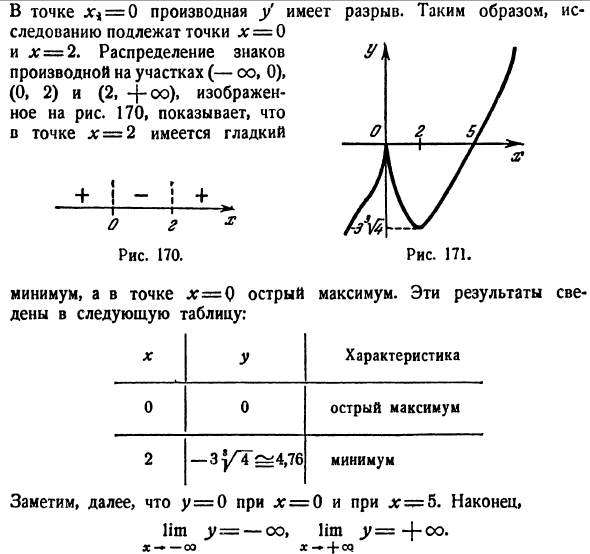
Оглавление:
Исследование функции — задача, заключающаяся в определении основных параметров заданной функции. Одной из целей исследования является построение графика функции.
Точки экстремума
Максимумом или минимумом функции y = f(x) называется
такое ее значение 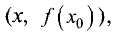 для которого имеют место
для которого имеют место
неравенства при любых малых положительных и отрицательных значениях 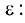
■ 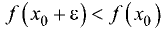 — для случая максимума;
— для случая максимума;
■ 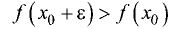 — для случая минимума.
— для случая минимума.
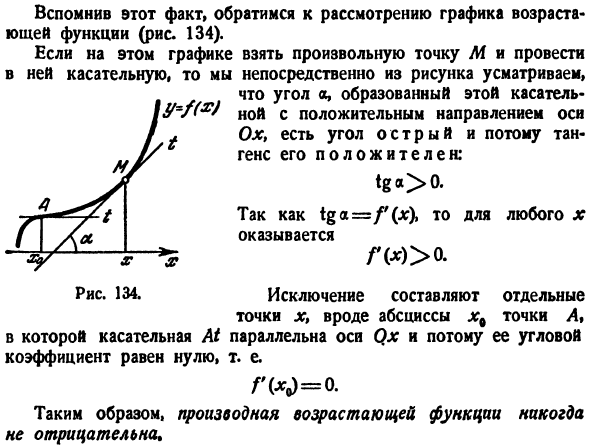
Таким образом, в точках максимума (минимума) значение 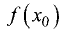 больше (соответственно меньше) всех соседних значений функции (рис. 7.1).
больше (соответственно меньше) всех соседних значений функции (рис. 7.1).
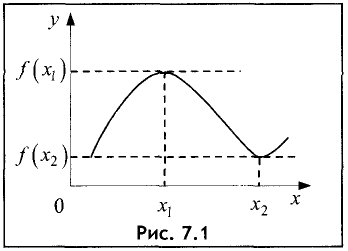
Функция, представленная на рис. 7.1, в точке 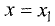 имеет
имеет
максимум, а в точке 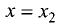 минимум.
минимум.
Точки, в которых функция принимает максимальное или минимальное значения, называются точками экстремума.
Необходимое условие максимума и минимума функции
Теорема Ферма:
Если функция определена и дифференцируема
в некотором промежутке X и во внутренней точке этого промежутка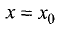 имеет наибольшее (наименьшее) значение, то
имеет наибольшее (наименьшее) значение, то
производная функции в этой точке равна нулю, т.е. 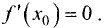
Доказательство:
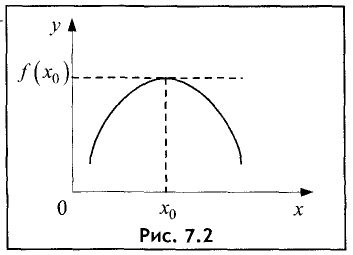
Пусть функция y = f(x) в точке 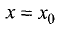
промежутка X имеет наибольшее значение (рис. 7.2).
Тогда 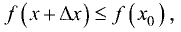 если
если 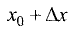 принадлежит Х. Отсюда
принадлежит Х. Отсюда 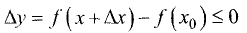 при достаточно малых
при достаточно малых 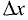 независимо от его знака.
независимо от его знака.
Если 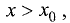 то
то 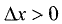 и
и 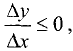 а если
а если 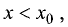 то
то 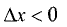 и
и 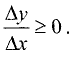
Переходя к пределам справа при 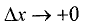 и слева при
и слева при 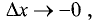
получим
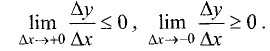
Так как по условию функция y=f(x) дифференцируема в
точке 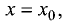 то ее предел при
то ее предел при 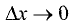 не зависит от способа
не зависит от способа
стремления (слева или справа).
Поэтому
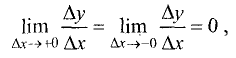
т.е. 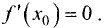 Аналогично доказывается случай для наименьшего значения функции.
Аналогично доказывается случай для наименьшего значения функции.
Необходимым условием максимума (минимума) непрерывной функции является равенство нулю первой производной.
Это условие является следствием теоремы Ферма. Действительно, если в точке 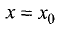 дифференцируемая функция имеет экстремум, то в некоторой окрестности этой точки выполняются условия теоремы Ферма и, следовательно, производная функции в этой точке равна нулю, т.е.
дифференцируемая функция имеет экстремум, то в некоторой окрестности этой точки выполняются условия теоремы Ферма и, следовательно, производная функции в этой точке равна нулю, т.е. 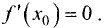
Необходимое условие максимума или минимума непрерывной функции имеет простой геометрический смысл. Так как в экстремальных точках касательная параллельна оси Ох (см. рис. 7.1 и 7.2), т.е. угол наклона касательной к оси Ох равен нулю, то тангенс данного угла, который равен производной, также равен нулю.
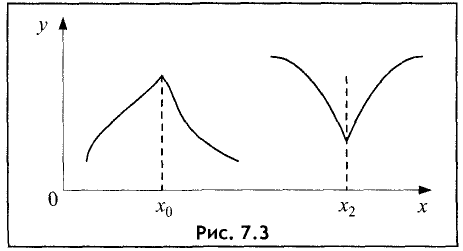
Максимум или минимум может иметь место также в тех точках, где производная не существует вовсе (рис. 7.3).
Приведенное условие существования экстремумов является необходимым, но не достаточным. На рис. 7.4 приведен случай, когда необходимое условие выполняется в точке 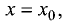 но ни максимума, ни минимума нет.
но ни максимума, ни минимума нет.
Достаточные условия существования экстремума
Первое условие. Если при переходе через точку 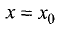 производная дифференцируемой функции y = f(x) меняет свой знак с плюса на минус, то точка
производная дифференцируемой функции y = f(x) меняет свой знак с плюса на минус, то точка 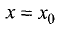 является точкой максимума, а если с минуса на плюс, то точкой минимума.
является точкой максимума, а если с минуса на плюс, то точкой минимума.
Действительно, если 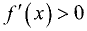 при
при 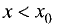 и
и 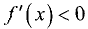 при
при 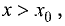 то в промежутке
то в промежутке 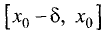 функция f(x) возрастает, а в
функция f(x) возрастает, а в
промежутке 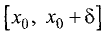 убывает, так что значение
убывает, так что значение 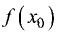 будет
будет
наибольшим в промежутке 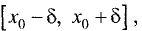 т.е. в точке
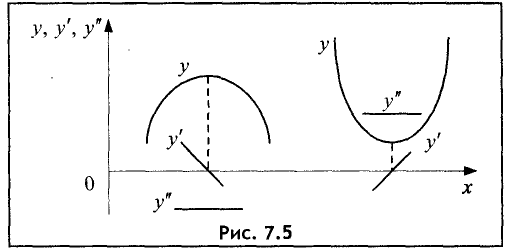
т.е. в точке 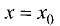 функция имеет максимум. Аналогично доказывается случай для минимума функции. Графически сказанное поясняется на рис. 7.5.
функция имеет максимум. Аналогично доказывается случай для минимума функции. Графически сказанное поясняется на рис. 7.5.
Если при переходе через точку 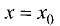 производная не меняет
производная не меняет
своего знака, то в точке 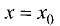 нет ни максимума, ни минимума
нет ни максимума, ни минимума
(см. рис. 7.4).
Второе условие. Если функция y = f(x) дважды дифференцируема в точке 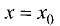 , и ее первая производная в данной точке равна
, и ее первая производная в данной точке равна
нулю, а вторая производная в этой точке положительна, то точка
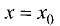 является точкой минимума. Если вторая производная
является точкой минимума. Если вторая производная
функции y = f(x) отрицательна в точке 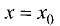 , то она является точкой максимума.
, то она является точкой максимума.
Действительно, вторая производная вычисляется по формуле:
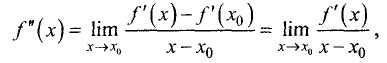
так как 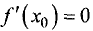 по условию.
по условию.
Пусть 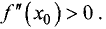 Тогда дробь
Тогда дробь 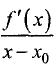 положительна для всех х
положительна для всех х
из окрестности точки 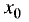 . Для
. Для 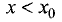 знаменатель этой дроби
знаменатель этой дроби 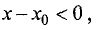 поэтому
поэтому 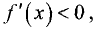 а для
а для 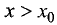 знаменатель дроби
знаменатель дроби
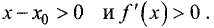 Таким образом, производная при переходе
Таким образом, производная при переходе
точки 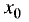 меняет знак с минуса на плюс. Согласно первому условию
меняет знак с минуса на плюс. Согласно первому условию
в такой точке имеет место минимум. Аналогично можно показать,
что при 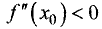 в точке
в точке 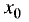 имеет место максимум. Сказанное
имеет место максимум. Сказанное
поясняется на рис. 7.5.
Если вторая производная в некоторой точке равна нулю, то эта
точка также может быть экстремальной. Например, для функции
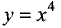 в точке х = 0 имеет место минимум, хотя вторая производная в этой точке равна нулю. Действительно,
в точке х = 0 имеет место минимум, хотя вторая производная в этой точке равна нулю. Действительно, 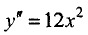 и
и 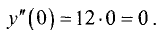
Алгоритм исследования функции на экстремум
1.Найти производную функции и приравнять ее нулю.
2.Решив это уравнение, определить подозрительные точки.
3.Исследовать знак производной слева и справа от каждой
подозрительной точки и принять решение о наличии
минимума или максимума.
4.Найти значения функции в экстремальных точках.
Пример:
Найти максимумы и минимумы функции
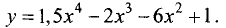
Решение:
Область определения функции — вся числовая ось.
Определяем производную:
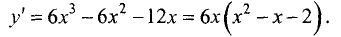
Подозрительные точки находим, решая уравнение 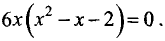
Отсюда 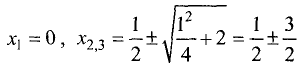 или
или 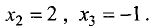
Определяем вторую производную: 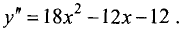
Для точки 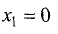 имеем у» = 18*0 —12*0 —12 = -12, т.е. в этой точке
имеем у» = 18*0 —12*0 —12 = -12, т.е. в этой точке
имеет место максимум. Его значение равно
у = 1,5*0-2*0-6*0 + 1 = 1.
Для точки 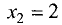 имеем
имеем 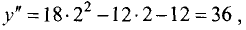 т.е. в этой точке
т.е. в этой точке
имеет место минимум. Его значение равно
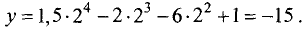
Для точки  имеем
имеем 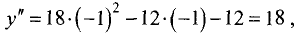 т.е. в этой
т.е. в этой
точке имеет место минимум. Его значение равно 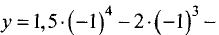
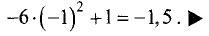
Пример:
Производитель реализует свою продукцию по цене
60 ден. ед. за единицу продукции. Издержки производителя
определяются кубической зависимостью 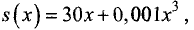 где х —
где х —
количество изготовленной и реализованной продукции. Найти оптимальный объем выпуска и соответствующий ему доход.
Решение:
Доход определяется разностью между выручкой за
проданную продукцию 60х и ее себестоимостью, т.е.
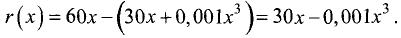
Для определения оптимального объема выпуска найдем производную
этой функции, приравняем ее нулю и решим полученное уравнение
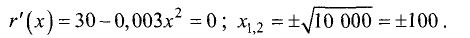
Отрицательный корень не имеет экономического смысла, поэтому
для дальнейших исследований принимаем 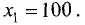 Вторая
Вторая
производная в исследуемой точке r»(х) = -0,006х = -0,006 • 100 = -0,6 является отрицательной, т.е. в этой точке имеет место максимум функции. Таким образом, оптимальный объем выпуска равен 100 единицам продукции.
Доход, соответствующий оптимальному выпуску,
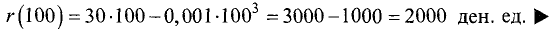
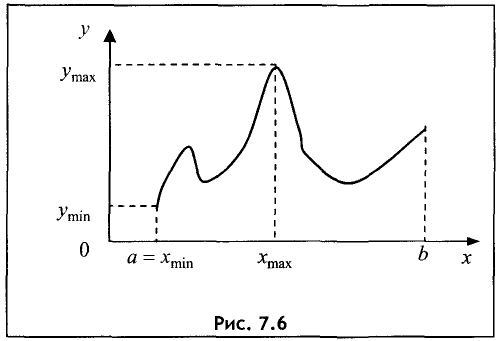
Для определения наибольшего и наименьшего значений на
отрезке, помимо указанного алгоритма, находят значения функции на концах отрезка. Затем выбирают наибольшее и наименьшее
значения из этих двух и всех экстремальных значений. Смысл
сказанного поясняется на рис. 7.6.
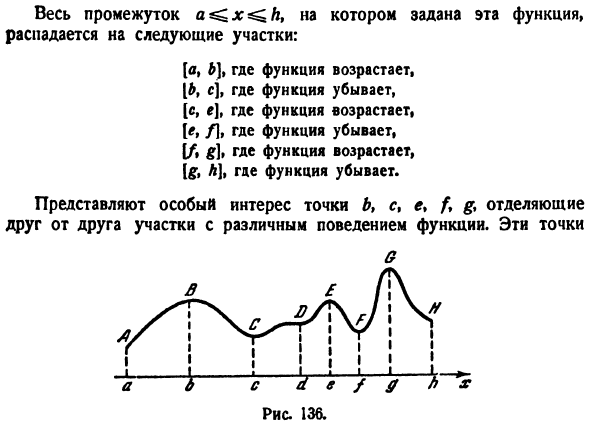
Монотонность и выпуклость функций
Функция y = f(x) не убывает (не возрастает) на промежутке X, если для любых 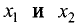 из этого промежутка при условии
из этого промежутка при условии 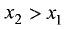 следует неравенство
следует неравенство
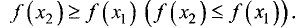
Если меньшему значению неравенства аргумента соответствует меньшее значение функции, то функция называется возрастающей (рис. 7.7). Если меньшему значению аргумента соответствует большее значение функции, то функция называется убывающей (рис.7.8).
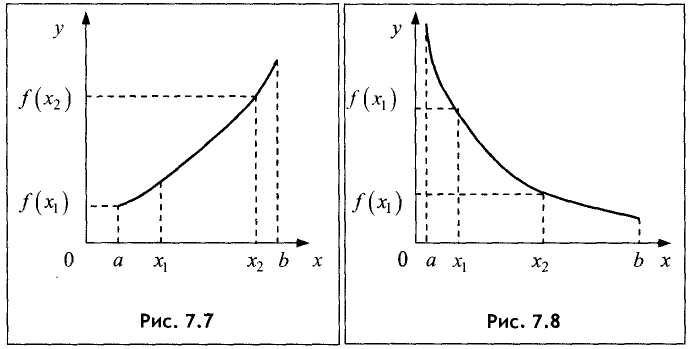
Функции возрастающие и убывающие называются монотонными.
Функция называется ограниченной на промежутке X, если существует такое положительное число М > 0, что 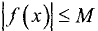 для любого х из промежутка X. Например, функция у = cos х ограничена на всей числовой оси, так как
для любого х из промежутка X. Например, функция у = cos х ограничена на всей числовой оси, так как 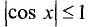 для любого х числовой оси.
для любого х числовой оси.
Функция y = f(x) на интервале (а,b) имеет выпуклость вниз (вверх), если в пределах данного интервала график лежит не ниже (не выше) любой касательной к графику функции. На рис. 7.9 изображен график функции, имеющей выпуклость вниз, а на рис. 7.10 — график функции, имеющей выпуклость вверх.
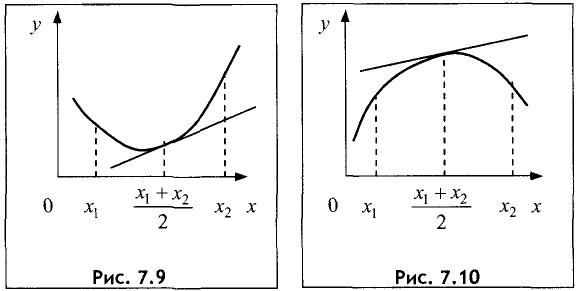
Функция y = f(x) на интервале (а, b) называется выпуклой вниз, если для любых двух значений 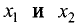 из данного интервала выполняется неравенство (рис. 7.9)
из данного интервала выполняется неравенство (рис. 7.9)
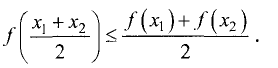
Функция y = f(x) на интервале (а, b) называется выпуклой вверх, если для любых двух значений 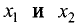 из данного интервала выполняется неравенство (рис. 7.10)
из данного интервала выполняется неравенство (рис. 7.10)
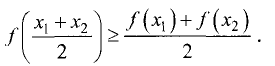
При исследовании функций бывают полезны две следующие
теоремы.
Теорема:
Функция выпукла вниз (вверх) тогда и только тогда,
когда ее первая производная на этом промежутке монотонно
возрастает (убывает).
Теорема:
Если вторая производная дважды дифференцируемой
функции положительна (отрицательна) внутри интервала (a, b), то
функция выпукла вниз (вверх) внутри этого интервала (достаточное
условие).
Однако, данное условие справедливо не всегда. Например,
функция 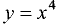 выпукла вниз на всей числовой оси, хотя вторая
выпукла вниз на всей числовой оси, хотя вторая
производная 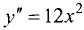 не всюду положительна (при х = 0 у» = 0).
не всюду положительна (при х = 0 у» = 0).
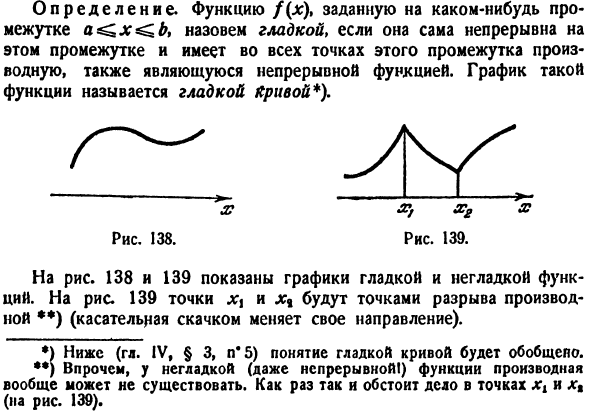
Точка 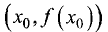 называется точкой перегиба графика функции
называется точкой перегиба графика функции
y = f(x), если в этой точке график имеет касательную и существует
такая окрестность точки 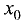 , в пределах которой график функции слева и справа от точки
, в пределах которой график функции слева и справа от точки 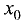 имеет разные направления выпуклости.
имеет разные направления выпуклости.
На рис. 7.4 точка 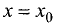 является точкой перегиба.
является точкой перегиба.
Необходимое условие перегиба. Вторая производная дважды
дифференцируемой функции в точке перегиба 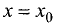 равна нулю:
равна нулю:
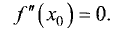
Достаточное условие перегиба. Вторая производная дважды
дифференцируемой функции при переходе точки перегиба 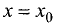
меняет свой знак.
Алгоритм исследования функции на выпуклость и точки перегиба
1.Найти вторую производную функции и приравнять ее нулю.
2.Решив это уравнение, определить подозрительные точки.
3.Исследовать знак второй производной слева и справа от
каждой подозрительной точки и принять решение об интервалах
выпуклости и наличии точек перегиба.
4.Найти значения функции в точках перегиба.
Пример:
Найти экстремальные точки, интервалы выпуклости
и точки перегиба функции 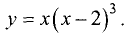
Решение:
Находим первую и вторую производные исследуемой
функции:
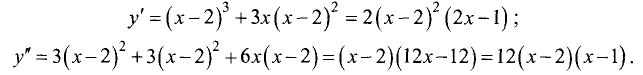
Приравняем нулю первую производную и решим полученное
уравнение:
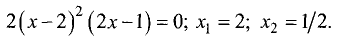
Подставив полученные значения в формулу для второй
производной, найдем
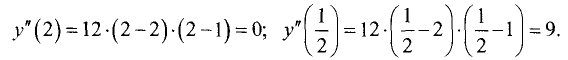
Таким образом, точка  является точкой минимума.
является точкой минимума.
Значение исследуемой функции в этой точке
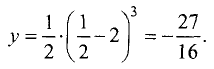
Точку 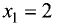 необходимо исследовать дополнительно. Первая
необходимо исследовать дополнительно. Первая
производная определена на всей числовой оси, так как точек, в которых производная отсутствует, не существует. Исследуем знак производной на интервале 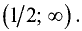 Для этого рассчитаем значения производной в точках х = 1 и х = 3:
Для этого рассчитаем значения производной в точках х = 1 и х = 3:
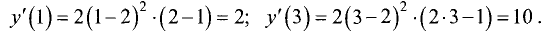
Так как слева и справа от точки 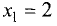 знак производной
знак производной
положительный, то в этой точке экстремума нет.
Приравняем нулю вторую производную и решим полученное
уравнение:
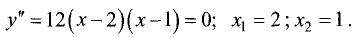
Вторая производная также определена на всей числовой оси. В
точке х = 0 значение второй производной
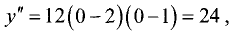
в точке 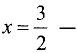
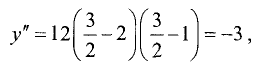
в точке х = 3 —
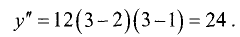
Поэтому:
■ на интервале 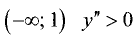 — функция выпукла вниз;
— функция выпукла вниз;
■ на интервале (1; 2) у» < 0 — функция выпукла вверх;
■ на интервале 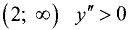 — функция выпукла вниз.
— функция выпукла вниз.
Таким образом, точки 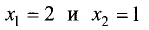 являются точками перегиба.
являются точками перегиба.
Значение исследуемой функции в этих точках:
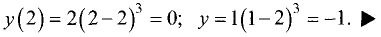
Асимптоты функций
Прямая называется асимптотой функции y = f(x), если расстояние от
точки (х, f(x)) , лежащей на графике функции, до этой прямой
стремится к нулю при движении точки по графику в бесконечность.
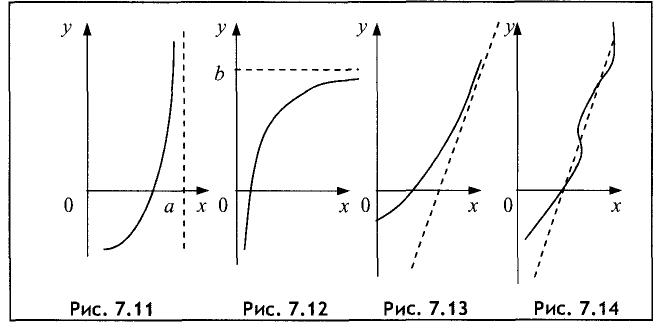
Существуют три вида асимптот: вертикальные (рис. 7.11),
горизонтальные (рис. 7.12) и наклонные (рис. 7.13, 7.14).
На рис. 7.14 кривая приближается к асимптоте, все время пересекая ее.
Прямая х = а называется вертикальной асимптотой графика
функции у = f(x), если хотя бы одно из предельных значений 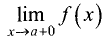 или
или 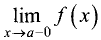 равно
равно 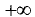 или
или 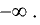
Прямая у = b называется горизонтальной асимптотой графика
функции y = f (х), если 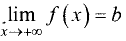 или
или 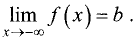
Прямая y = kx + b 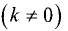 называется наклонной асимптотой
называется наклонной асимптотой
графика функции у = f(x), если существуют конечные пределы 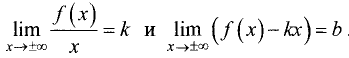
Действительно, если у = kх + b — наклонная асимптота, то 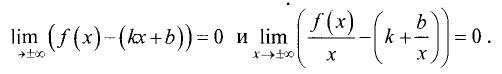
Из последнего выражения следует
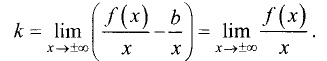
При известном k из равенства 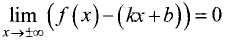 находим
находим 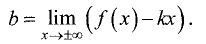
Если для горизонтальной и наклонной асимптот конечен только
предел при 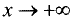 или при
или при 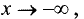 то эти асимптоты называются соответственно правосторонней или левосторонней.
то эти асимптоты называются соответственно правосторонней или левосторонней.
Пример:
Найти асимптоты графика функции 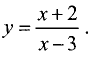
Решение:
Областью определения является вся числовая ось,
кроме точки х = 3 . Причем
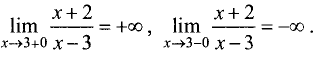
Поэтому прямая х = 3 — вертикальная асимптота. Так как 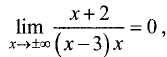 то график функции наклонных асимптот не имеет. ►
то график функции наклонных асимптот не имеет. ►
Пример:
Найти асимптоты графика функции у = х + arctg х.
Решение. Функция непрерывна на всей числовой оси, поэтому
вертикальные асимптоты отсутствуют. Так как
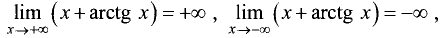
то отсутствуют и горизонтальные асимптоты.
Для правосторонней наклонной асимптоты 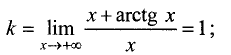
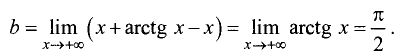
Уравнение правосторонней асимптоты имеет вид 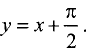
Для левосторонней наклонной асимптоты 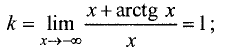
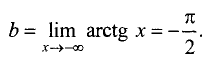
Уравнение правосторонней асимптоты имеет вид 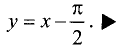
Правило Лопиталя
При отыскании предела часто сталкиваются с
неопределенностями 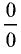 или
или 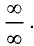 Для решения задачи применяют правило Лопиталя.
Для решения задачи применяют правило Лопиталя.
Прежде чем переходить к доказательству правила Лопиталя,
рассмотрим две теоремы.
Теорема Ролля:
Пусть функция y = f(x) удовлетворяет
следующим условиям:
■ непрерывна на промежутке [а,b];
■ дифференцируема на промежутке (а,b);
■ на концах промежутка принимает равные значения, т.е.
f(a) = f(b).
Тогда внутри промежутка существует по крайней мере одна точка
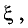 производная функции в которой равна нулю, т.е.
производная функции в которой равна нулю, т.е. 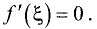
Доказательство. Действительно, если внутри промежутка функция имеет хотя бы одну точку, в которой она принимает наибольшее или наименьшее значение, то в соответствии с теоремой Ферма производная в этой точке равна нулю. Если же таких точек нет, то функция тождественно постоянна на всем интервале. Тогда производная равна нулю во всех точках указанного интервала.
Теорема Лагранжа:
Пусть функция y = f(x) удовлетворяет
следующим условиям:
■ непрерывна на промежутке [а, b];
■ дифференцируема на промежутке (а, b).
Тогда внутри промежутка существует по крайней мере одна точка
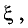 в которой производная функции равна частному от деления
в которой производная функции равна частному от деления
приращения функции на приращение аргумента на данном промежутке:
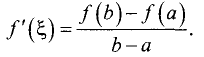
Доказательство:
Введем функцию
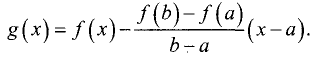
Эта функция удовлетворяет условиям теоремы Ролля, поскольку она:
■ непрерывна на промежутке [а, b];
■ дифференцируема на промежутке (а, b) и
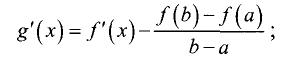
■ на концах промежутка принимает равные значения:
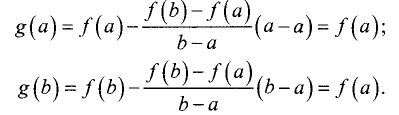
Следовательно, внутри промежутка существует по крайней мере одна точка 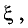 производная функции g(x) в которой равна нулю:
производная функции g(x) в которой равна нулю:
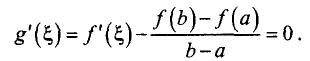
Отсюда находим 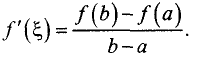
Правило Лопиталя
Пусть 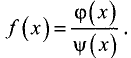 Причем функции
Причем функции 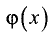 и
и 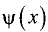 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
■ непрерывны на промежутке [х, а];
■ дифференцируемы на промежутке (х, а) и 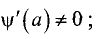
■ 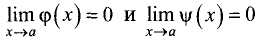 (неопределенность
(неопределенность 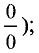
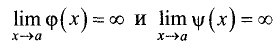 (неопределенность
(неопределенность 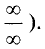
Тогда 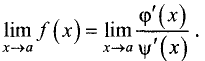
Доказательство:
Доказательство проведем для неопределенности 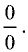 Применяя теорему Лагранжа для функций
Применяя теорему Лагранжа для функций 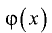 и
и 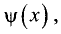 получим
получим 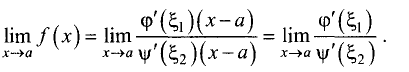
Так как при 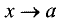 имеем
имеем 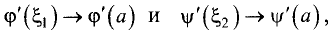 то, используя теорему о пределе частного двух функций, получим
то, используя теорему о пределе частного двух функций, получим
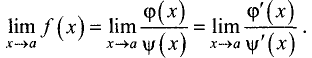
В случае, если 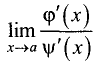 снова представляет собой неопределенность вида
снова представляет собой неопределенность вида 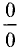 или
или 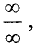 то применяют это правило вторично, и т.д.
то применяют это правило вторично, и т.д.
Пример:
Используя правило Лопиталя, найти пределы:
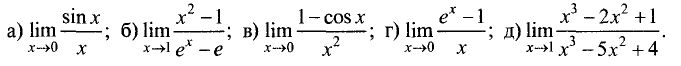
Решение:
Во всех примерах имеем неопределенность 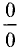 . Используя правило Лопиталя, получим
. Используя правило Лопиталя, получим
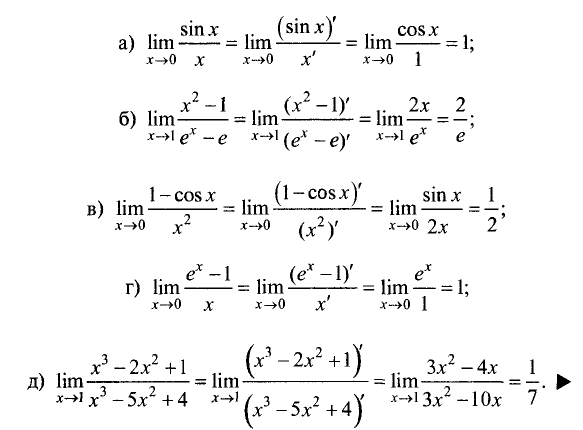
Пример:
Используя правило Лопиталя, найти предел 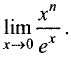
Решение:
Имеем неопределенность 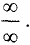 Применяя правило Лопиталя n раз, получим:
Применяя правило Лопиталя n раз, получим:
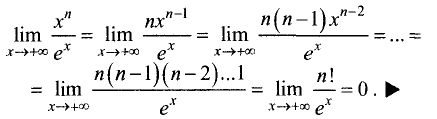
Пример:
Используя правило Лопиталя, найти предел 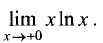
Решение:
Имеем неопределенность 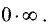 Разделив числитель и
Разделив числитель и
знаменатель на х , получим 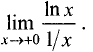 Неопределенность этого предела
Неопределенность этого предела 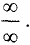 Используя правило Лопиталя, найдем:
Используя правило Лопиталя, найдем:
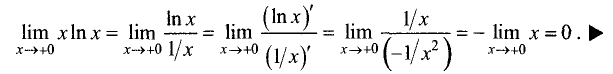
Построение графиков функций
Изучение функции и построение ее графика целесообразно
проводить по следующей схеме:
1.Найти область существования функции, точки разрыва и
определить их характер.
2.Определить поведение функции в бесконечности, вычислив
пределы
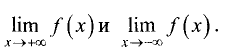
3.Найти асимптоты.
4.Найти пересечение кривой с осью Ох, решая уравнение
f(x) = 0, и с осью Оу , вычисляя у = f(0).
5.Найти экстремумы и интервалы монотонности функции.
6.Найти интервалы выпуклости функции и точки перегиба.
7.По полученным данным постепенно делают набросок
кривой, уточняя его по отдельным точкам.
Пример:
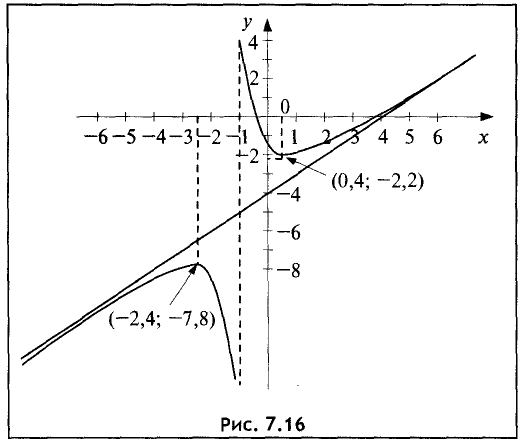
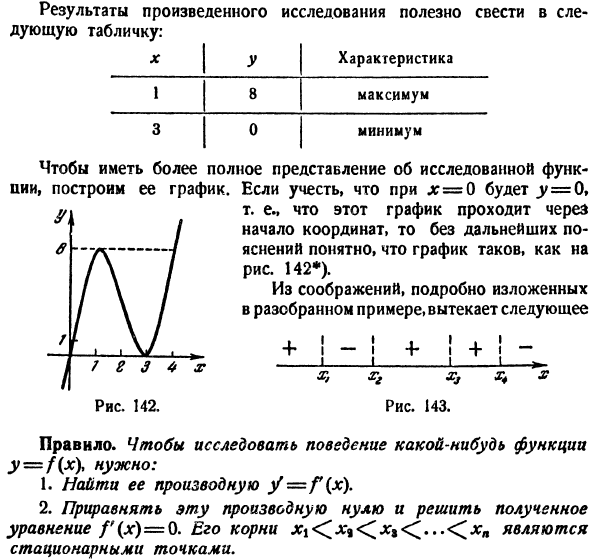
Построить график функции
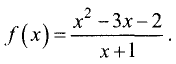
Решение:
1. Эта функция определена и непрерывна для всех 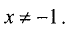 При приближении к точке
При приближении к точке 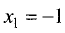 слева
слева 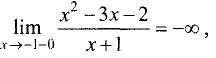
а справа — 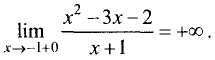 Таким образом, прямая х = -1 является вертикальной асимптотой.
Таким образом, прямая х = -1 является вертикальной асимптотой.
2.Пределы функции в бесконечности:
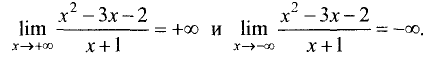
3.Определим параметры наклонных асимптот. Угловой
коэффициент справа
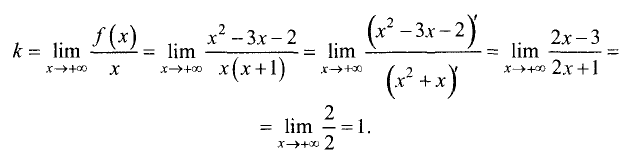
Угловой коэффициент слева
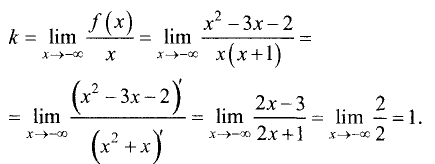
Точка пересечения асимптоты с осью Оу справа
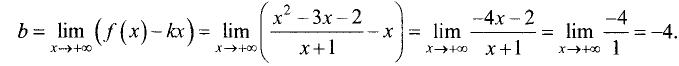
Точка пересечения асимптоты с осью Оу слева
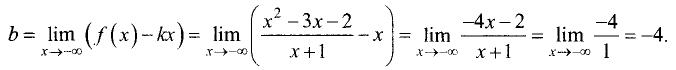
Таким образом, параметры правой и левой асимптот совпали,
т.е. имеет место одна асимптота, определенная уравнением прямой
у = х-4.
4.Точка пересечения кривой с осью Оу находится из
соотношения
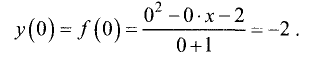
Точка пересечения кривой с осью Ох находится из уравнения
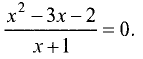
Дробь равна нулю, если числитель равен нулю, т.е.
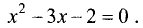
Решение данного квадратного уравнения имеет вид
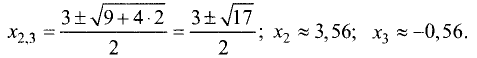
5.Для определения экстремумов и интервалов монотонности
функции найдем первую и вторую производные:
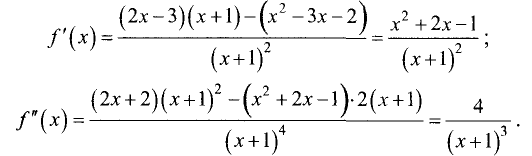
Приравняв нулю первую производную, получим:
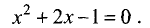
Решив данное уравнение, найдем подозрительные точки:
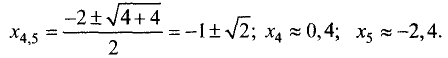
Значения функции в этих точках:
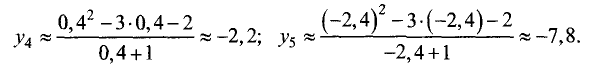
Подставив полученные координаты экстремальных точек в формулу
второй производной, найдем: 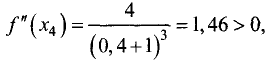
т.е. в точке (0,4; -2,2) имеет место минимум,
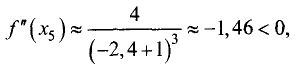
т.е. в точке (-2,4; -7,8) имеет место максимум.
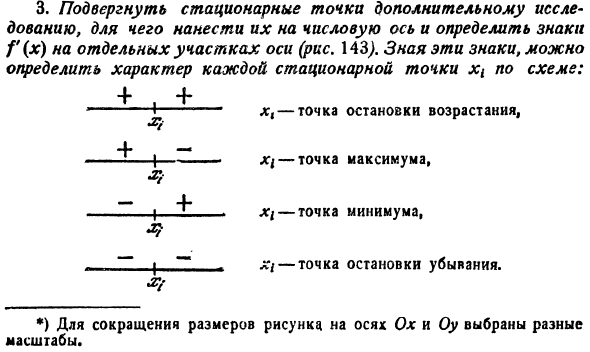
Для исследования функции на монотонность проследим поведение производных внутри полученных интервалов (рис. 7.15). Знаками плюс и минус показан знак производной на данном интервале.
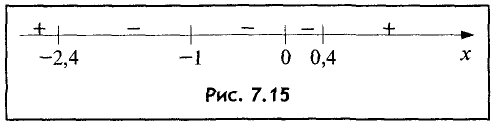
В точке  имеет место максимум, поэтому на промежутке
имеет место максимум, поэтому на промежутке 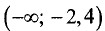 функция возрастает, а на промежутке (-2,4; -1) убывает и при
функция возрастает, а на промежутке (-2,4; -1) убывает и при 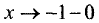 слева стремится к
слева стремится к  В точке
В точке 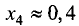 имеет
имеет
место минимум, поэтому на промежутке (-1; 0,4) функция
убывает, а на промежутке 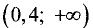 — возрастает.
— возрастает.
6.Для нахождения точек перегиба приравняем нулю вторую производную: 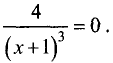 Это уравнение не имеет корней, т.е. точек перегиба нет.
Это уравнение не имеет корней, т.е. точек перегиба нет.
По полученным данным строим график функции (рис. 7.16). ►
Производные и дифференциалы функций нескольких переменных
Пусть задана функция n переменных 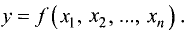
Первой частной производной функции 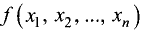 по переменной
по переменной 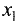 называется производная данной функции по
называется производная данной функции по 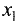 при фиксированных остальных переменных:
при фиксированных остальных переменных:
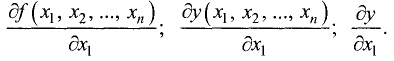
Аналогично определяется первая частная производная по любой другой переменной. Например, первую частную производную по 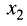 записывают в виде
записывают в виде
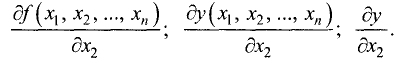
Второй частной производной функции 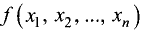 называется первая частная производная от первой частной производной данной функции.
называется первая частная производная от первой частной производной данной функции.
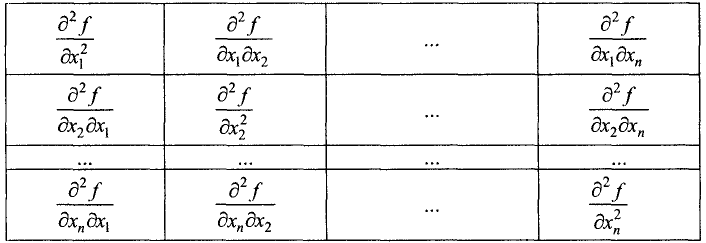
Функция n переменных имеет 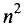 вторых частных производных. Действительно, количество частных производных от частной производной по переменной
вторых частных производных. Действительно, количество частных производных от частной производной по переменной 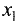 равно n (см. первую строку табл. 7.1). Количество строк в табл. 7.1 также равно n.
равно n (см. первую строку табл. 7.1). Количество строк в табл. 7.1 также равно n.
Таблица 7.1
Для функции двух переменных имеем четыре вторые частные производные:
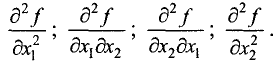
Вторая частная производная по двум различным переменным, например 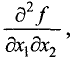 называется смешанной. Величина смешанной производной, непрерывной при данных значениях переменных
называется смешанной. Величина смешанной производной, непрерывной при данных значениях переменных 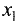 и
и 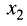 , не зависит от порядка переменных, по которым берутся производные, т.е.
, не зависит от порядка переменных, по которым берутся производные, т.е.
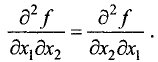
Аналогично определяются производные более высоких порядков, например третья частная производная, четвертая частная производная и т.д.
Частный дифференциал функции n переменных 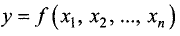 по одной из переменных, например по
по одной из переменных, например по 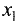 , определяется равенством
, определяется равенством
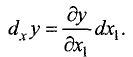
Полный дифференциал функции n переменных 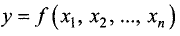 определяется по формуле
определяется по формуле
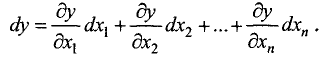
Полный дифференциал второго порядка функции двух переменных 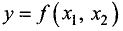 задается соотношением
задается соотношением
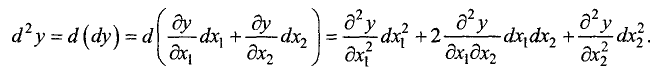
Пример:
Найти частные производные первого и второго порядка от функции 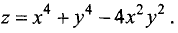
Решение:
Находим первую и вторую частные производные по х:
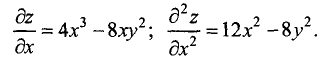
Находим первую и вторую частные производные по у :
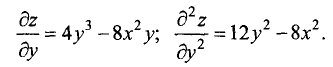
Находим смешанные вторые частные производные:
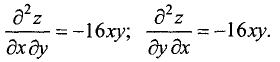
Как и следовало ожидать, смешанные частные производные равны. ►
Пример:
Найти дифференциалы первого и второго порядков от функции 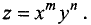
Решение. Частные производные первого и второго порядков исследуемой функции равны:
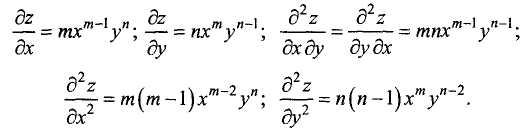
Дифференциал первого порядка
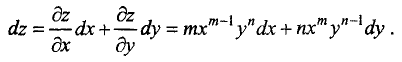
Дифференциал второго порядка
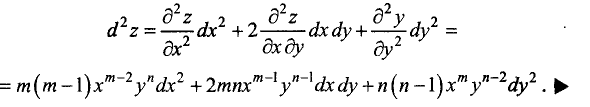
Градиент
Градиентом функции n переменных  называется вектор с координатами
называется вектор с координатами
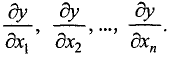
При этом пишут grad y, 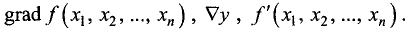
Известно, что вектор 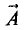 в n-мерной системе координат можно представить в виде
в n-мерной системе координат можно представить в виде
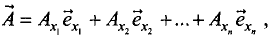
где 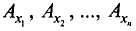 — проекции вектора
— проекции вектора 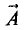 на оси координат;
на оси координат;
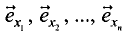 — орты или векторы единичной длины, совпадающие по направлению с координатными осями
— орты или векторы единичной длины, совпадающие по направлению с координатными осями 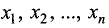 соответственно.
соответственно.
Градиент функции трех переменных u = f(x, у, z) можно представить в виде
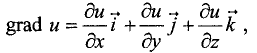
где 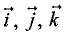 — орты координатных осей х, у, z соответственно.
— орты координатных осей х, у, z соответственно.
Градиент функции в заданной точке показывает направление самого быстрого роста функции в этой точке.
В экономике достаточно часто используются функции двух переменных. Градиент функции двух переменных u = f(х, у) можно представить в виде
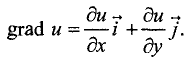
Существует четкая связь между линиями уровня таких функций и направлением градиента.
Теорема:
Пусть задана дифференцируемая функция u = f(x,у) и величина градиента данной функции, отличная от нуля, в точке  . Тогда градиент в точке
. Тогда градиент в точке  перпендикулярен линии уровня, проходящей через эту точку.
перпендикулярен линии уровня, проходящей через эту точку.
Доказательство. Линия уровня, представленная на рис. 7.17, задана уравнением L = f(x, у).
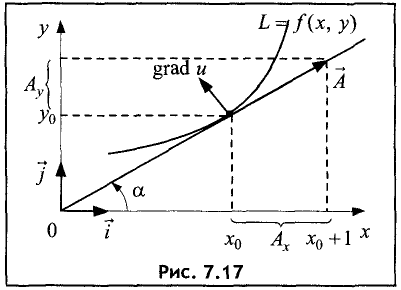
В точке  линии уровня проведем касательную и построим вектор
линии уровня проведем касательную и построим вектор  , совпадающий по направлению с касательной, с началом в этой точке.
, совпадающий по направлению с касательной, с началом в этой точке.
Пусть проекция вектора  на ось Ох будет равна единице. Отношение проекций
на ось Ох будет равна единице. Отношение проекций 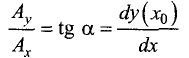 или
или 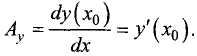
Таким образом, вектор 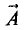 можно представить в виде:
можно представить в виде:
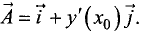
Умножив данный вектор на dx , получим
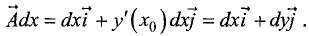
Найдем скалярное произведение градиента функции u = f(x,y)
в точке 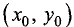 и вектора
и вектора 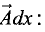
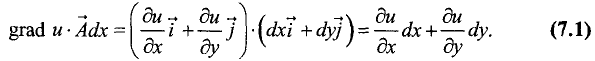
С другой стороны, полный дифференциал функции u = f(x, у)
в точке 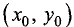
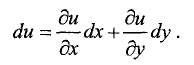
На линии уровня функция u = f(x, у) не изменяется по определению, поэтому полный дифференциал по направлению вектора 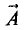 равен нулю:
равен нулю:
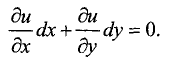
Сопоставив это выражение с (7.1), можно сделать вывод о
перпендикулярности векторов 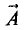 и grad u.
и grad u.
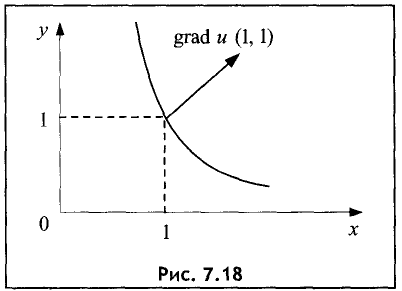
Пример:
Для функции u = ху построить линию уровня, проходящую через точку 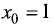 и
и 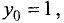 и найти градиент в данной
и найти градиент в данной
точке.
Решение:
Уровень в исследуемой точке равен с = 1 • 1 = 1. Линия уровня определяется формулой
1 = ху или 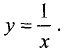
Таким образом, линией уровня является гипербола.
Для отыскания градиента найдем частные производные функции в
исследуемой точке:
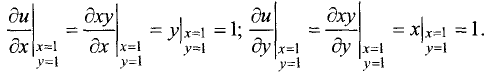
Отсюда следует выражение для градиента функции в исследуемой
точке:
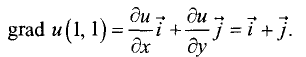
Из полученной формулы видно, что градиент в исследуемой точке
направлен вправо вверх под углом 45° к осям Ох и Оу (рис. 7.18).
Его модуль равен
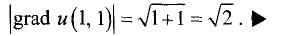
Однородные функции
Пусть задана функция и переменных 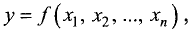 определенная при
определенная при 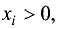 где i = 1, 2,…, n, и имеющая в области определения непрерывные первые частные производные.
где i = 1, 2,…, n, и имеющая в области определения непрерывные первые частные производные.
Функция 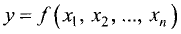 называется однородной функцией степени р, если для любого числа t > 0 выполняется равенство
называется однородной функцией степени р, если для любого числа t > 0 выполняется равенство
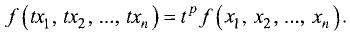
Заметим, что условие определения функции 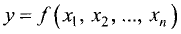 при
при 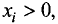 где i = 1, 2,…, n, широко используется в экономическом анализе.
где i = 1, 2,…, n, широко используется в экономическом анализе.
Для однородных функций п переменных 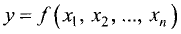 степени р справедлива формула
степени р справедлива формула
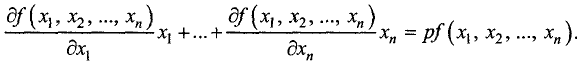
Для однородной функции двух переменных u=f(x, у) степени р имеем
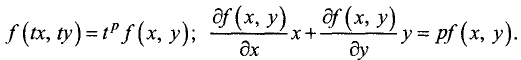
Приведенные формулы называются формулами Эйлера.
Пример:
Определить степень однородных функций:
а) u = ах + by;
б) 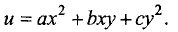
Решение:
a) a(tx) + b(ty) = t(ax + by) = tu , т.е. функция u = ax + by имеет первую степень однородности;
б) 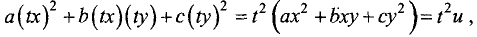 т.е. функция
т.е. функция 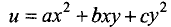 имеет вторую степень однородности. ►
имеет вторую степень однородности. ►
Экстремумы функции двух переменных
Пусть задана функция двух переменных u = f(x, у).
Точка  называется точкой локального максимума (минимума), если для всех точек (х, у) из области определения функции u = f(x, у), близких к точке
называется точкой локального максимума (минимума), если для всех точек (х, у) из области определения функции u = f(x, у), близких к точке  — лежащих в двумерной
— лежащих в двумерной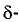 окрестности точки
окрестности точки  , справедливо неравенство
, справедливо неравенство 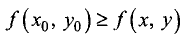 (соответственно для точки локального минимума
(соответственно для точки локального минимума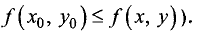
Двумерной 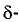 окрестностью точки
окрестностью точки  называется множество точек (х,у), принадлежащих открытому кругу сколь угодно малого радиуса
называется множество точек (х,у), принадлежащих открытому кругу сколь угодно малого радиуса 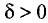 с центром в точке
с центром в точке  . Если при фиксированном числе
. Если при фиксированном числе 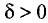 точка (х, у) принадлежит
точка (х, у) принадлежит 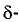 окрестности точки
окрестности точки  , то говорят, что точка (х, у) близка к точке
, то говорят, что точка (х, у) близка к точке  , в противном случае — далека от точки
, в противном случае — далека от точки  (рис. 7.19).
(рис. 7.19).
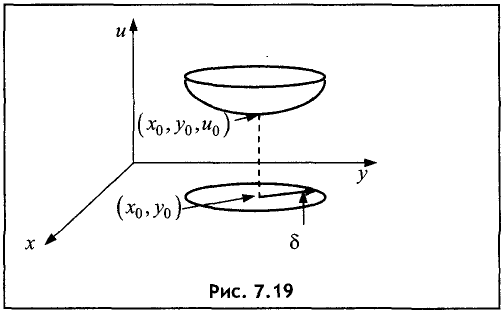
Если  — точка локального экстремума функции u = f(x,y). то около точки
— точка локального экстремума функции u = f(x,y). то около точки 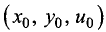 где
где 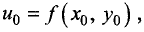 функция
функция
u = f(х,у) имеет вид шапочки, повернутой выпуклостью вверх
(максимум) или вниз (минимум).
Точка  называется точкой глобального (абсолютного)
называется точкой глобального (абсолютного)
максимума (глобального (абсолютного) минимума) функции u = f(x,у), если для всех точек (х, у), для которых функция u = f(х, у) определена, справедливо неравенство 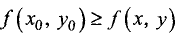 (соответственно для точки глобального минимума
(соответственно для точки глобального минимума 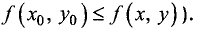
Пусть функция u = f(x, у) определена в окрестности точки
 и имеет в ней первые частные производные. Необходимым
и имеет в ней первые частные производные. Необходимым
условием локального экстремума данной функции в точке 
является равенство нулю первых частных производных:
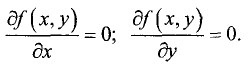
Эти точки являются подозрительными и среди них следует
искать точки локального экстремума. Подозрительные точки не
обязаны быть точками локального экстремума.
Достаточное условие локального экстремума функции u = f(x, у)
дважды дифференцируемой в точке  состоит в следующем.
состоит в следующем.
Пусть функция u = f(x, у) в точке  имеет первые частные
имеет первые частные
производные, равные нулю:
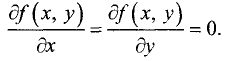
1.Если 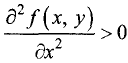 или
или 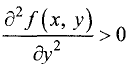 и выполняется неравенство
и выполняется неравенство 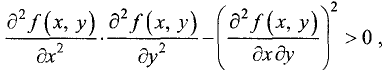 то точка
то точка  является точкой локального минимума.
является точкой локального минимума.
2. Если 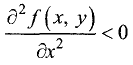 или
или 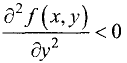 и выполняется неравенство
и выполняется неравенство 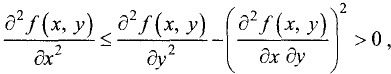 то точка
то точка  является точкой локального максимума.
является точкой локального максимума.
3.Если 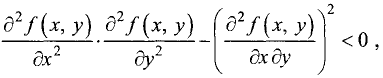 то точка
то точка  не является экстремальной.
не является экстремальной.
Пример:
Исследовать на экстремум следующие функции
нескольких переменных: 1) 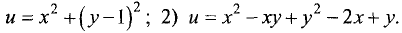
Решение:
1.Находим первые частные производные и приравниваем их к нулю:
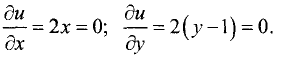
Решив полученные уравнения, находим подозрительные точки:
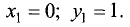
Находим в подозрительной точке вторые частные производные:
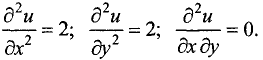
Так как 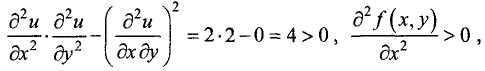 то точка (0, 1) является точкой локального минимума. Значение функции в этой точке
то точка (0, 1) является точкой локального минимума. Значение функции в этой точке 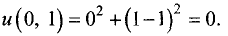
2.Находим первые частные производные и приравниваем их к нулю:
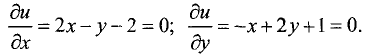
Решив систему из двух уравнений, находим подозрительные точки:
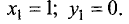
Находим в подозрительной точке вторые частные производные:
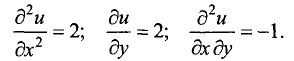
Так как 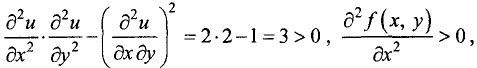 то точка (1, 0) является точкой локального минимума. Значение функции в этой точке
то точка (1, 0) является точкой локального минимума. Значение функции в этой точке 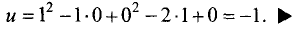
Условный экстремум
При определении безусловного экстремума функции п
независимых переменных 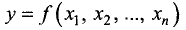 (см. §7.11) на независимые переменные
(см. §7.11) на независимые переменные 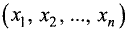 не накладывается никаких
не накладывается никаких
дополнительных условий. В задачах на условный экстремум поведение независимых переменных ограничено определенными условиями. Рассмотрим эту задачу для n независимых переменных в следующей формулировке.
Найти локальный экстремум функции n независимых
переменных 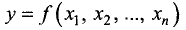 при условии, что независимые переменные удовлетворяют ограничению
при условии, что независимые переменные удовлетворяют ограничению
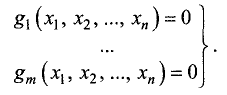
Задача на условный экстремум записывается следующим образом:
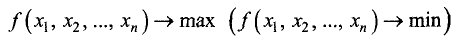
при условиях
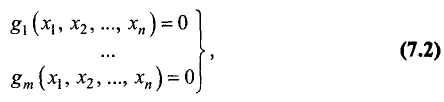
где m<n.
В задаче на условный экстремум функцию 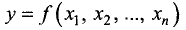 называют целевой, а функции
называют целевой, а функции 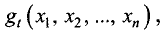 где
где 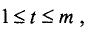 — функциями связи. При решении задач на условный экстремум обычно используется метод Лагранжа.
— функциями связи. При решении задач на условный экстремум обычно используется метод Лагранжа.
Пусть функция n независимых переменных 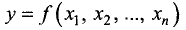 и функции, определяющие условия (7.2), непрерывны и имеют непрерывные частные первые производные в точке локального экстремума
и функции, определяющие условия (7.2), непрерывны и имеют непрерывные частные первые производные в точке локального экстремума 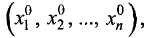 a
a 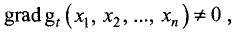 где
где 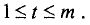 При выполнении этих условий строят функцию Лагранжа, которая имеет вид
При выполнении этих условий строят функцию Лагранжа, которая имеет вид
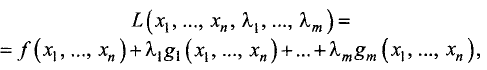
где 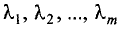 — множители Лагранжа.
— множители Лагранжа.
Затем функцию Лагранжа от n + m переменных исследуют на
абсолютный экстремум. Для этих целей определяют подозрительную точку путем решения n + m уравнений:
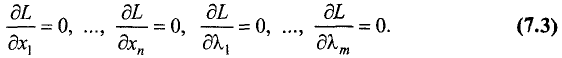
Система имеет n + m решений: 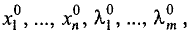 которые являются координатами абсолютного экстремума функции Лагранжа. Точка
которые являются координатами абсолютного экстремума функции Лагранжа. Точка 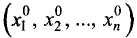 является укороченной (так как из нее удалены координаты
является укороченной (так как из нее удалены координаты 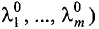 подозрительной точкой локального условного экстремума функции
подозрительной точкой локального условного экстремума функции 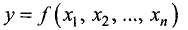 при условиях (7.2). Укороченную точку анализируют и выясняют, является ли она точкой условного экстремума при наличии ограничений (7.2) или не является.
при условиях (7.2). Укороченную точку анализируют и выясняют, является ли она точкой условного экстремума при наличии ограничений (7.2) или не является.
Условия (7.3) являются необходимыми для существования локального условного экстремума.
Для функции двух независимых переменных задача на условный экстремум формулируется следующим образом: найти локальный экстремум функции u = f(x, у) при условии, что независимые переменные удовлетворяют ограничению g(x, у) = 0 , т.е.
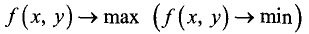
при условии
g(x,y) = 0.
Функция Лагранжа для этого случая имеет вид
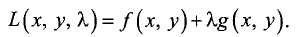
Подозрительная точка определяется путем решения трех
уравнений:
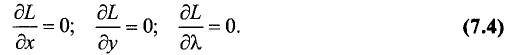
Пример:
Отыскать условный экстремум функции u = ху при
условии у = 1-х (g(x, у) = у + х-1 = 0).
Решение:
Функция Лагранжа имеет вид
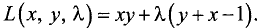
Подозрительная точка определяется путем решения трех уравнений:
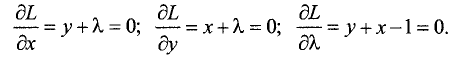
Вычитая из первого уравнения второе, находим 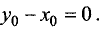 Из
Из
третьего уравнения определяем 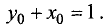 Подставив
Подставив 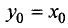 в
в
последнюю формулу, окончательно получим 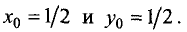 С учетом полученных значений из первого или второго уравнения находим
С учетом полученных значений из первого или второго уравнения находим 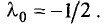 Значение функции в точке экстремума
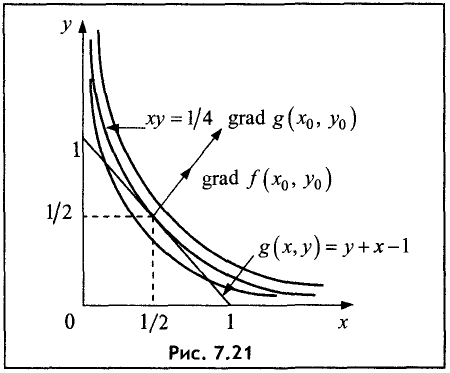
Значение функции в точке экстремума 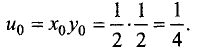 Геометрия условий данного примера в координатах хОу представлена на рис. 7.20.
Геометрия условий данного примера в координатах хОу представлена на рис. 7.20.
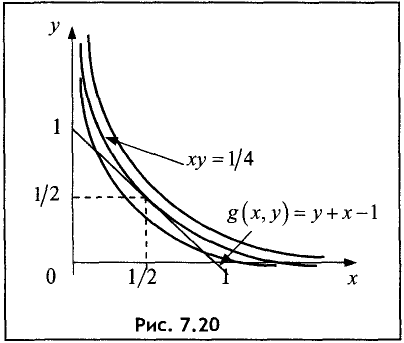
Линия уровня, проходящая через подозрительную точку,
описывается уравнением ху = 1/4. Все линии уровня, лежащие ниже линии уровня ху = 1/4 , имеют уровень меньше 1/4 , а лежащие выше линии уровня ху = 1/4 — больше 1/4 . Это следует из уравнения линий уровней 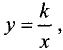 где k — значение уровня. Ясно, что чем больше k, тем
где k — значение уровня. Ясно, что чем больше k, тем
правее проходит кривая.
Функция, определяющая условие g (х, у) = у + х -1 = 0 , является
прямой линией (см. рис. 7.20). Из-за симметрии задачи функции
ху = 1/4 и g(x, у) = у + х-1 = 0 касаются друг друга в подозрительной
точке (1/4,1/4). Из сказанного следует, что на прямой g(x, у) = у + х-1 = 0 значение функции u = ху меньше 1/4, т.е. в подозрительной точке имеет место максимум. ►
Геометрический смысл локального условного экстремума
функции u = f(x, у) в точке 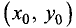 состоит в том, что градиенты
состоит в том, что градиенты
целевой функции grad 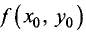 и функции связи
и функции связи 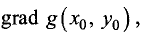
выходящие из точки 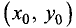 , обязательно расположены на одной
, обязательно расположены на одной
прямой. Отсюда следует, что линии уровней функций f(x, у)
и g(x, у), содержащие точку 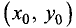 , касаются в этой точке.
, касаются в этой точке.
Действительно, пусть функции f(х, у) и g(x, у) непрерывны и
имеют непрерывные частные производные первого порядка по переменным х и у , 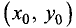 — точка условного локального
— точка условного локального
экстремума функции u = f(x, у) при наличии ограничения g(x, у) = 0, а

Перепишем условия (7.4) в виде
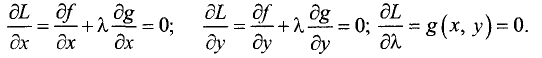
Так как grad 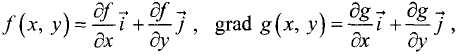 то, умножив первое уравнение системы на орт
то, умножив первое уравнение системы на орт 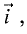 а второе — на орт
а второе — на орт 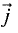 и сложив их, получим
и сложив их, получим
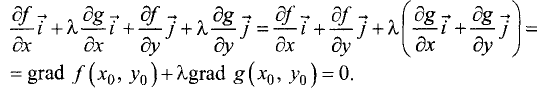
Отсюда следует, что
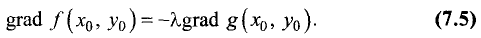
Таким образом, если два вектора равны, то они лежат на одной
прямой и противоположно направлены.
Пример:
Для условий примера 7.15 определить градиенты
целевой функции 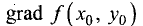 и функции связи
и функции связи 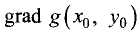 в точке экстремума и построить их на графике.
в точке экстремума и построить их на графике.
Решение. Первые частные производные целевой функции
u = ху и функции связи g(х, у) = у + х-1 = 0 имеют вид
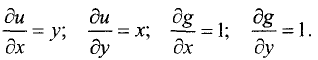
Градиенты целевой функции и функции связи в экстремальной
точке
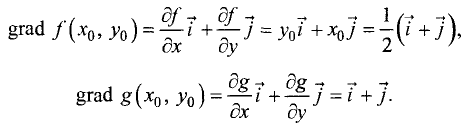
Так как 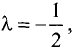 то равенство (7.5) имеет место:
то равенство (7.5) имеет место:
Полученные градиенты представлены на рис. 7.21. ►
Дополнение к исследованию функции

























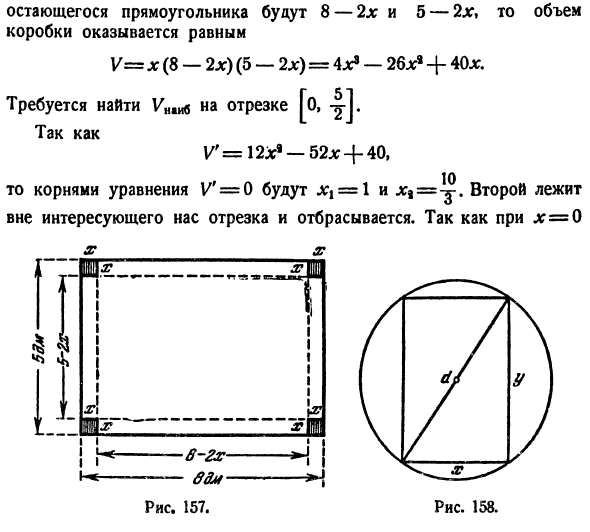







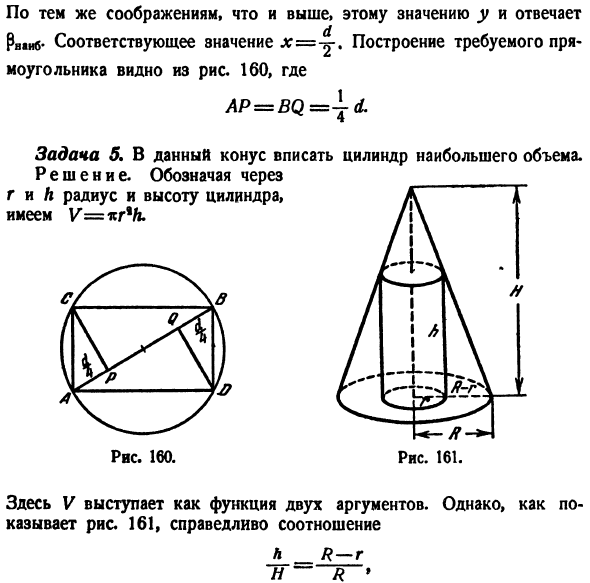
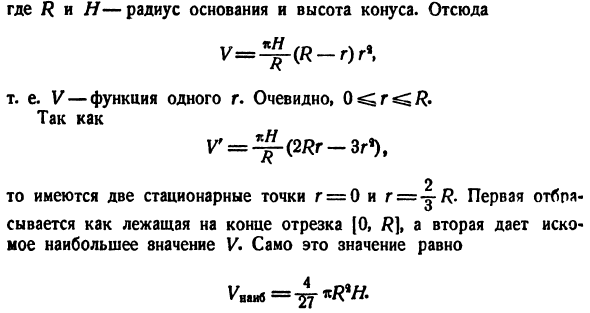
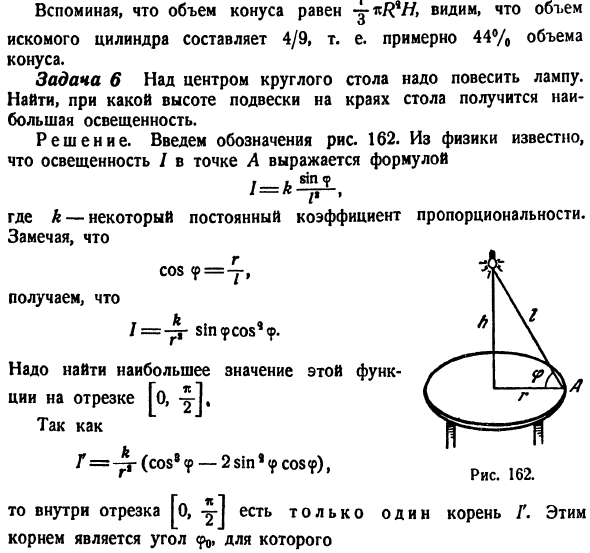




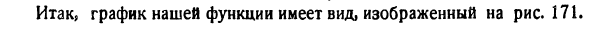
Смотрите также:
| Дифференциал | Основные теоремы дифференциального исчисления |
| Производные и дифференциалы высших порядков | Формула Тейлора |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
