Оглавление:
Предел и непрерывность функции одной переменной является одним из важнейших понятий математического анализа. Основные понятия математического анализа, такие как производная, интеграл, связаны с предельным переходом Предел и непрерывность функции одной переменной
Понятие функции. Способы задания функции
Понятие функции является основным и первоначальным, как и понятие множества.
Пусть X — некоторое множество действительных чисел х. Если каждому х ∈ X по некоторому закону поставлено в соответствие определенное действительное число у, то говорят, что на множестве X задана функция и пишут
у = f(х) или у = у(х), х ∈ x.
Введенную таким образом функцию называют числовой. При этом множество X называют областью определения функции, а независимую переменную х — аргументом.
Для указания функции иногда используют только символ, которым обозначен закон соответствия, т. е. вместо f(х) пишут просто f. Таким образом, функция задана, если указаны
1)область определения X;
2) правило f, которое каждому значению х ∈ X ставит в соответствие определенное число у = f(х) — значение функции, отвечающее этому значению аргумента х.
Функции f и g называют равными, если их области определения совпадают и равенство f(х) = g(х) верно для любого значения аргумента х из их обшей области определения. Так, функции
не являются равными; они равны только на отрезке [0, I]. Примеры функций.
- Последовательность {аn} есть функция целочисленного аргумента, определенная на множестве натуральных чисел, такая, что f(n) = аn (n = 1, 2,… ).
- Функция у = п! (читается «эн-факториал»). Задана на множестве натуральных чисел: каждому натуральному числу п ставится в соответствие произведение всех натуральных чисел от I до п включительно:
n! = 1 • 2 • 3 … n,
причем условно полагают 0! = 1.
3.
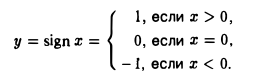
Обозначение sign происходит от латинского слова signum — знак. Эта функция определена на всей числовой прямой — ∞ < х < + ∞; множество ее значений состоит из трех чисел -1,0, 1 (рис.1).
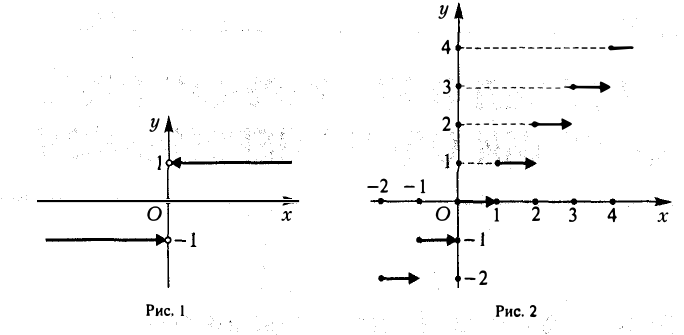
4. у = [z], где [z] обозначает целую часть действительного числа х, т. е. [z| — наибольшее целое число, не превосходящее z: [z] = п для п ≤ х<п + 1, п = 0, ±1, ±2…..Читается: «игрек равно антье икс (фр. entier). Эта функция задана на всей числовой оси, а множество всех ее значений состоит из целых чисел (рис. 2).
Способы задания функции
Аналитическое задание функции
Функция у = f(x) называется заданной аналитически, если она определяется с помощью формулы, указывающей, какие действия надо произвести над каждым значением х, чтобы получить соответствующее значение у. Например, функция
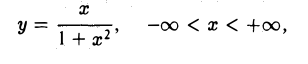
задана аналитически.
При этом под областью определения функции (если она заранее не указана) понимается множество всех действительных значений аргумента х, при которых аналитическое выражение, определяющее функцию, принимает лишь действительные и конечные значения. В этом смысле область определения функции называют также ее областью существования.
Для функции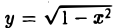 
областью определения является отрезок -1 ≤ х ≤ 1. Для функции у = sin х область определения — вся числовая ось — ∞ < х < + ∞. Заметим, что не всякая формула определяет функцию. Например, формула
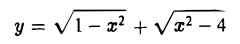
никакую функцию не определяет, так как нет ни одного действительного значения х, при котором имели бы действительные значения оба написанных выше корня.
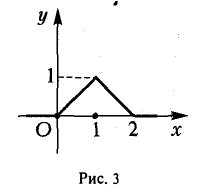
Аналитическое задание функции может выглядеть достаточно сложно. В частности, функция может быть задана различными формулами на различных частях своей области определения. Например, функция может быть определена так:
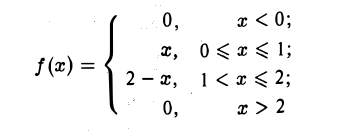
(рис.3).
Графический способ задания функции
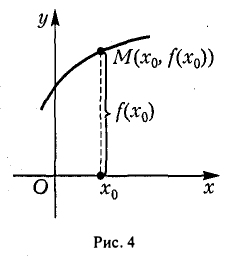
Функция у = f(x) называется заданной графически, если задан ее график, т.е. множество точек (х, f(x)) на плоскости хОу, абсциссы которых принадлежат области определения функции, а ординаты равны соответствующим значениям функции (рис. 4).
Не для каждой функции ее график можно изобразить на рисунке. Например, функция Дирихле
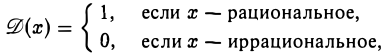
не допускает такого изображения. Функция D(х) задана на всей числовой оси, а множество ее значений состоит из двух чисел 0 и 1.
Табличный способ задания функции
Функция называется заданной таблично, если приведена таблица, в которой указаны численные значения функции для некоторых значений аргумента. При табличном задании функции ее область определения состоит только из значений х1, x2,…, хn, перечисленных в таблице.
Предел функции в точке
Понятие предела функции является центральным в математическом анализе.
Пусть функция f(х) определена в некоторой окрестности Q точки хо, кроме, быть может, самой точки хо.
Определение Коши:
Число А называется пределом функции f(х) в точке х0, если для любого числа ε > 0, которое может быть как угодно малым, существует число δ > 0, такое, что для всех х ∈ Ω , х ≠ хо, удовлетворяющих условию
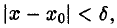
верно неравенство
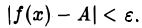
Обозначение: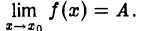 
помошью логических символов это определение выражается следующим образом
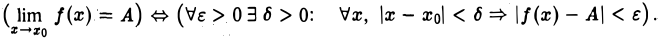
Примеры:
- Пользуясь определением предела функции в точке, показать, что
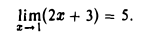
Функция f(x) = 2х + 3 определена всюду, включая точку хо = 1: f(1) = 5. Возьмем любое ε > 0. Для того, чтобы неравенство (2х + 3) — 5| < ε имело место, необходимо выполнение следующих неравенств
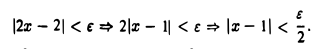
Следовательно, если взять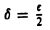 
, то при |х — 1| < 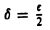будем иметь |f(х) — 5| < ε. Это означает, что число 5 есть предел функции , f(x) = 2х + 3 в точке хо = 1.
2. Пользуясь определением предела функции, показать, что
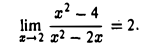
Функция
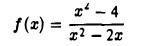
не определена в точке хо = 2. Рассмотрим f(х) в некоторой окрестности точки x0 = 2, например, на интервале (1,5). не содержащем точку х = 0, в которой функция f(x) также не определена. Возьмем произвольное число ε > 0 и преобразуем выражение |f(x) — 2| при x ≠ 2 следующим образом
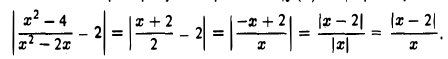
Для х ∈ (1,5) получаем неравенство
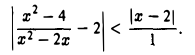
Отсюда видно, что если взять δ = с, то для всех х ∈ (1, 5), подчиненных условию
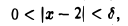
будет верно неравенство
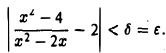
Это означает, что число А = 2 является пределом данной функции в точке хо = 2.
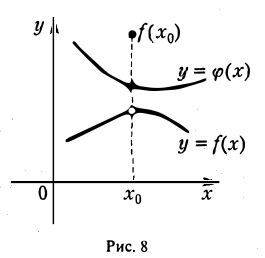
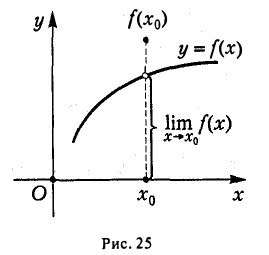
Дадим геометрическое пояснение понятия предела функции в точке, обратившись к ее графику (рис. 5). При х < х0 значения функции f(x) определяются ординатами точек кривой М1М, при х > хо — ординатами точек кривой MM2. Значение f(x0) определяется ординатой точки N. График данной функции получается, если взять «хорошую» кривую М1ММ2 и точку М(хо, А) на кривой заменить точкой N.
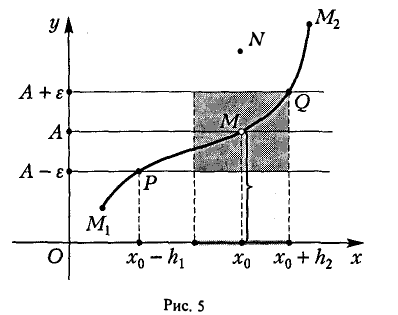
Покажем, что в точке хо функция f(х) имеет предел, равный числу А (ординате точки М). Возьмем любое (как угодно малое) число ε > 0. Отметим на оси Оу точки с ординатами А, А — ε, А + ε. Обозначим через Р и Q точки пересечения графика функции у = f(х) с прямыми у = А- ε и у = А + ε. Пусть абсциссы этих точек есть xo — h1, х0 + h2 соответственно (h1 > 0, h2 > 0). Из рисунка видно, что для любого х ≠ хо из интервала (хо — h1, хо + h2) значение функции f(х) заключено между А — ε и А + ε ,т. е. для всех х ≠ хо, удовлетворяющих условию
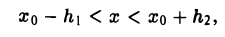
верно неравенство
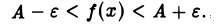
Положим δ — min {h1, h2}. Тогда интервал (хо — δ, хо + δ) будет содержаться в интервале (х0 — h1), Хо + h2) и, следовательно, неравенство А — ε < f(x) < А + ε или, что тоже,
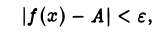
будет выполнено для всех х, удовлетворяющих условию
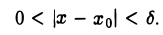
Это доказывает, что .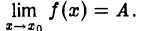
Таким образом, функция у = f(х) имеет предел А в точке хо, если, какой бы узкой ни была ε -полоска между прямыми у = А- ε и у = А + ε, найдется такое δ > 0, что для всех х из проколотой δ -окрестности точки х0 точки графика функции у= f(х) оказываются внутри указанной ε -полоски.
Замечание:
Величина δ зависит от ε: δ = δ( ε ).
Замечание:
В определении предела функции в точке Хо сама точка xo из рассмотрения исключается. Таким образом, значение функции в точке Xo не влияет на предел функции в этой точке. Более того, функция может быть даже не определена в точке Хо. Поэтому две функции, равные в окрестности точки Хо, исключая, быть может, саму точку хо (в ней они могут иметь разные значения, одна из них или обе вместе могут быть не определены), имеют при х → Хо один и тот же предел или обе не имеют предела. Отсюда, в частности, следует, что для отыскания в точке х0 предела дроби законно сокращать эту дробь на равные выражения, обращающиеся в нуль при х = Хо.
Пример:
Найти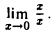 
Функция f(x) =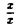
для всех х ≠ 0 равна единице, а в точке х = 0 не определена. Заменив f(х) на равную ей при х ≠ 0 функцию
g(х) = 1, получаем
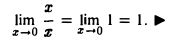
Пример:
Найти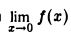 
, где
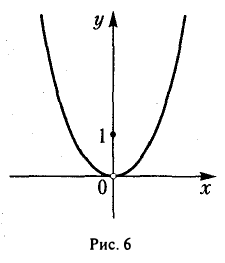
(рис.6).
Функция g(х) = х2, — ∞ < х < + ∞, совпадает с функцией f(х) всюду, исключая точку х = 0, и имеет в точке х = 0 предел, равный нулю: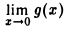 
= 0 (покажите это!). Поэтому 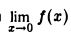= 0.
Задача:
Сформулировать с помощью неравенств (на языке ε — δ), что означает
Пусть функция f(х) определена в некоторой окрестности Ω точки х0, кроме, быть может, самой точки х0.
Определение Гейне:
Число А называется пределом функции f(х) в точке х0, если для любой последовательности {хn} значений аргумента х (fn ∈ Ω, хп ≠ х0), сходящейся к точке хо, соответствующая последовательность значений функции {f(хп)} сходится к числу А.
Приведенным определением удобно пользоваться, когда надо установить, что функция f(х) не имеет предела в точке х0. Для этого достаточно найти какую-нибудь последовательность {f(хп)}, не имеющую предела, или же указать две последовательности {f(хn)} и {f(х’n)}, имеющие различные пределы.
Покажем, например, что функция f(х) = sin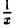
(рис.7), определенная всюду, кроме точки x = 0, не имеет предела в точке х = 0.
Рассмотрим две последовательност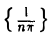и 
и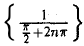 
сходящиеся к точке х = 0. Соответствующие последовательности значений функции f(х) сходятся к разным пределам: последовательность 
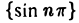сходится к нулю, а последовательность 
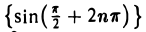— к единице. Это означает, что функция f(х) = sin 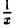в точке х = 0 предела не имеет.
Замечание:
Оба определения предела функции в точке (определение Коши и определение Гейне) равносильны.
Теоремы о пределах
Теорема:
Единственность предела. Если функция f(х) имеет предел в точке хо, то этот предел единственный.
Пусть 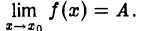. Покажем, что никакое число В ≠ А не может быть пределом функции f(х) в точке х0. Тот факт, что 
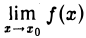≠ В с помощью логических символов формулируется так:
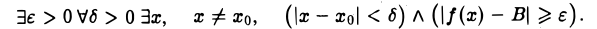
Воспользовавшись неравенством ||а| — |b|| ≤ |а — b|, получаем
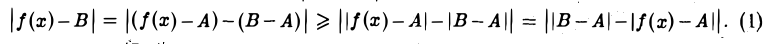
Возьмем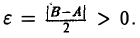 
Поскольку 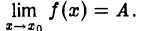, для выбранного ε > 0 найдется δ > 0 такое, что
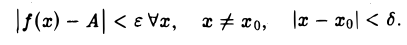
Из соотношения (1) для указанных значений х имеем
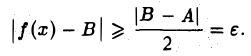
Итак, нашлось ε > 0 такое, что каким бы малым ни было δ > 0, существуют х ≠ х0,
такие, что 0 < |х — хо| < δ и вместе с тем |f(х) — В| ≥ ε . Отсюда В ≠ .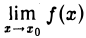
Определение:
Функция f(x) называется ограниченной в окрестности точки хо, если существуют числа М > 0 и δ > 0 такие, что
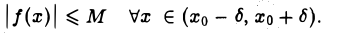
Теорема:
Ограниченность функции, имеющей предел. Если функция f{х) определена в окрестности точки хо и имеет в точке Хо конечный предел, то она ограничена в некоторой окрестности этой точки.
Пусть
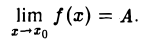
Тогда для любого ε > 0, например, для ε = 1, найдется такое δ > 0, что для всех х ≠ хо. удовлетворяющих условию |х — х0| < δ , будет верно неравенство
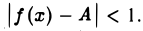
Замечая, что всегда
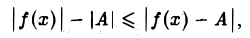
получим
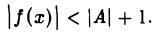
Положим M = mах{|A| + 1, |f(х0)|}- Тогда в каждой точке х интервала (хо — δ, х0 + δ) будем иметь
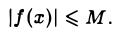
Это означает, согласно определению, что функция f(х) ограничена в окрестности точки х0.
Напротив, из ограниченности функции f(х) в окрестности точки хо не следует существования предела функции f(х) в точке хо. Например, функция f(х) = sin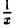 ограничена в окрестности точки х = 0:
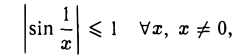
но не имеет предела в точке х = 0.
Сформулируем еще две теоремы, геометрический смысл которыхдостаточно ясен.
Теорема:
Переход к пределу в неравенстве. Если f(x) ≤ φ(х) для всех х из некоторой окрестности точки хо, кроме, быть может, самой точки Хо, и каждая из функций f(x) и φ(х) в точке Хо имеет предел, то
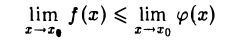
(рис.8).
Заметим, что из строгого неравенства f(х) < φ(х) для функций не обязательно следует строгое неравенство для их пределов. Если эти пределы существуют, то мы можем утверждать лишь, что
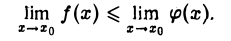
Так, например, для функций
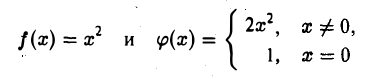
выполнено неравенство f(х) < φ(x) ∀ x, в то время как
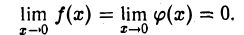
Теорема:
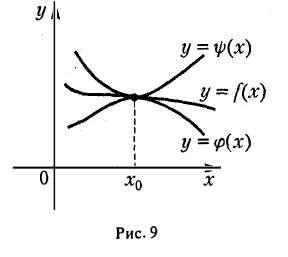
Предел промежуточной функции. Если φ(х) ≤ f(х) ≤ ψ(x) для всех х в некоторой окрестности точки x0, кроме, быть может, самой точки xо (рис. 9), и функции φ(х) и ψ(x) в точке хо имеют один и тот же предел А, то и функцияf(х) в точке хо имеет предел, равный этому же числу А.
Предел функции в бесконечности
Пусть функция f(х) определена либо на всей числовой оси, либо по крайней мере для всех х, удовлетворяющих условию |х| > К при некотором К > 0.
Определение:
Число А называют пределом функции f(x) при х, стремящемся к бесконечности, и пишут
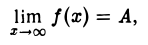
если для любого ε > 0 существует число N > 0 такое, что для всех х, удовлетворяющих условию |х| > N, верно неравенство
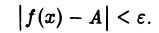
Заменив в этом определении условие |х| > N на х > N или на х < -N соответственно, получим определения
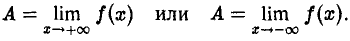
Из этих определений следует, что
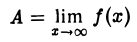
тогда и только тогда, когда одновременно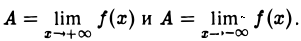 
Тот факт, что 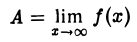, геометрически означает следующее: какой бы узкой ни была с-полоска между прямыми у = А- ε и у = А + ε, найдется такая прямая х = N > 0, что правее нее график функции у = f(x) целиком содержится в указанной е-полоске (рис. 10). В этом случае говорят, что при х —> + ∞ график функции у = f(х) асимптотически приближается к прямой у = А.
Пример:
Функция f(х) =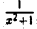
определена на всей числовой оси и представляет собой дробь, у которой числитель постоянен, а знаменатель неограниченно возрастает при |x| → + ∞. Естественно ожидать, что 
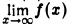=0. Покажем это.
Возьмем любое ε > 0, подчиненное условию 0 < ε ≤ 1. Чтобы имело место соотношение
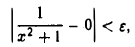
должно выполняться неравенство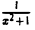 
< ε или, что то же, 
,
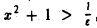откуда |z| >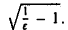 
Таким образом, если взять N =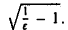, то при |r| > N будем иметь |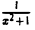| < ε. Это означает, что число 4=0 есть предел данной функции при х → ∞.
Заметим, что подкоренное выражение 1/ε — 1 ≥ 0 лишь для ε ≤ 1. В случае, когда ε > I, неравенство 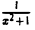< ε выполняется автоматически для всех х ∈ R.
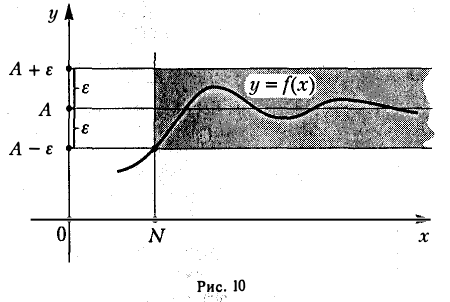
График четной функции у = 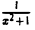асимптотически приближается к прямой у = 0 при х ± ∞.
Задача:
Сформулировать с помощью неравенств, что означает
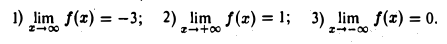
Бесконечно малые функции
Пусть функция а(х) определена в некоторой окрестности точки хо, кроме, быть может, самой точки х0.
Определение:
Функция а(х) называется бесконечно малой функцией (сокращенно б. м. ф.) при х, стремящемся к хо, если
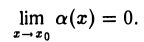
Например, функция а(х) = х — 1 является б. м. ф. при х → 1, так как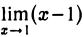 
. График функции у = х-1 изображен на рис. 11.
Вообще, функция а(х) = х-х0 является простейшим примером б. м. ф. при х → хо.
Принимая во внимание определение предела функции в точке, определение б. м. ф. можно сформулировать так.
Определение:
Функция а(х) называется бесконечно малой при х → хо, если для любого ε > 0 существует такое δ > 0, что для всех х, удовлетворяющих условию 0 < |х — хо| < δ, верно неравенство
|а(х)| < ε.
Наряду с понятием бесконечно малой функции при х → х0 вводится понятие бесконечно малой функции при х → ∞, х → + ∞ и х → — ∞ .
Определение:
Функция а(х) называется бесконечно малой при х → ∞, если
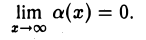
Если
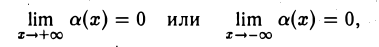
то функция а(х) называется бесконечно малой соответственно при х → + ∞ или при х → — ∞.
Например, функция а(х) =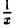, х ≠ 0, является бесконечно малой при х → ∞ , поскольку 
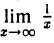= 0. Функция а(х) = е-x есть бесконечно малая функция при х → + ∞ , так как 
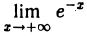= 0.
В дальнейшем все понятия и теоремы, связанные с пределами функций, мы будем, как правило, рассматривать только применительно к случаю предела функции в точке, предоставляя читателю самому сформулировать соответствующие понятия и доказать аналогичные теоремы для случаев, когда х → + ∞, х → + ∞ или х → — ∞.
Свойства бесконечно малых функций
Теорема:
Если а(х) и β (х) — б.м. ф. при х → хо, то их сумма а(х) + β (х) есть также б. м. ф. при х → хо.
Возьмем любое ε > 0. Так как а(х) — б. м. ф. при х → хо, то найдется δ1 > 0 такое, что для всех х ≠ хо, удовлетворяющих условию
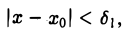
верно неравенство
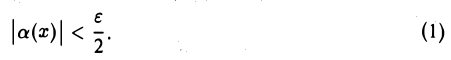
По условию β(х) также б.м.ф. при х → хо, поэтому найдется δ2 > 0. такое, что для всех х ≠ хо, удовлетворяющих условию
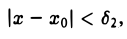
верно неравенство
Положим δ = min{δ1,< δ2}. Тогда для всех х ≠ хо, удовлетворяющих условию |х — xо| < δ, будут одновременно верны неравенства (1) и (2). Поэтому
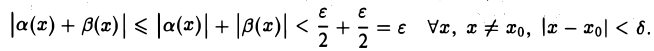
Это означает, что сумма а(х) + β(х) есть б. м. ф. при х → хо.
Замечание:
Теорема остается справедливой для суммы любого конечного числа функций, б. м. при х → xо.
Теорема:
Произведение б. м. ф. на ограниченную функцию. Если функция а(х) является б. м. ф. при х → х0» а функция f(x) ограничена в окрестности точки Xq, то произведение a(x)f(x) есть б. м. ф. при х → х0.
По условию функция f(x) ограничена в окрестности точки хо. Это означает, что существуют такие числа δ1 > 0 и М > 0, что
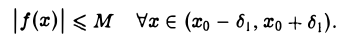
Возьмем любое ε > 0. Так как по условию а(х) — б. м. ф. при х —» хо, то найдется такое δ2 > 0, что для всех х ≠ хо. удовлетворяющих условию |х —х0| < δ2, будет верно неравенство
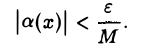
Положим δ = min{ δ1, δ2}- Тогда для всех х ≠ хо, удовлетворяющих условию |х — хо| < δ , будут одновременно верны неравенства
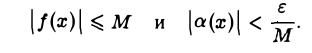
Поэтому
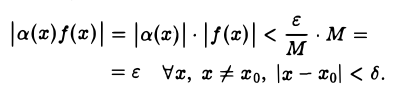
Это означает, что произведение а(х)f(х) есть б. м. ф. при х —» xo.
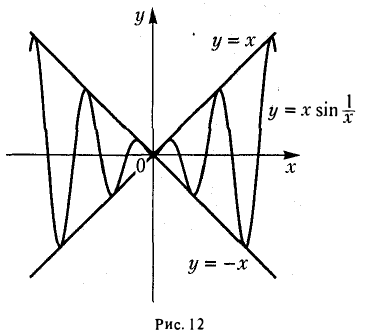
Пример:
Функцию у = х sin 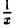{рис. 12) можно рассматривать как произведение функций а(х) = х и f(х) = sin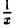. Функция а(х) есть б. м. ф. при х -> x0, а функция f(x) = sin 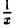определена всюду, исключая точку х = 0, и ограничена в любой проколотой окрестности этой точки. Поэтому, в силу теоремы 6, функция у = х sin 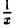есть б. м. ф. при х -> x0, так что
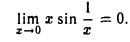
Следствие:
Если а(х) — б. м. ф. при х → xo, а функция f(х) в точке xо имеет (конечный) предел, то произведение a(x)f(x) есть б. м. ф. при х → xo.
Это вытекает из того, что функция, имеющая в точке хо предел, ограничена в проколотой окрестности точки хо.
Лемма:
Если функция f(х) в точке xo имеет предел, отличный от нуля, то функция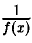 
ограничена в проколотой окрестности точки xo.
Пусть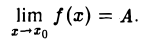 ≠ 0. Тогда для любого ε > 0, в частности для 
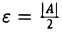, найдется δ > 0 такое, что для всех х, удовлетворяющих условию 0 < |х — хо| < δ, будет верно неравенство
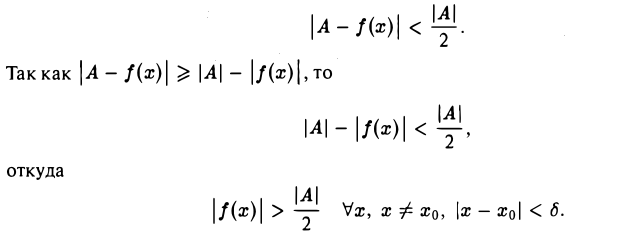
Значит, для указанных значений х определена функция 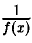, причем
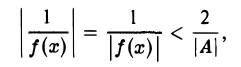
так что 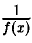ограничена в проколотой окрестности точки х0.
Теорема:
Если а(х) — б. м. ф. при х → х0, а функция f(x) имеет в точке х0 предел, отличный от нуля, то частное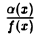 
есть б. м. ф. при х → xо.
Представим частное 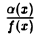в виде
В силу леммы функция 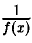ограничена в проколотой окрестности точки х0 и, следовательно, а(х) • 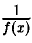— б. м. ф. при х → х0 как произведение б. м. ф. на ограниченную. Условие 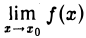≠ 0 является существенным. Рассмотрим, например, функции а(х) = х и f(х) = х2, являющиеся б. м. ф. при х → 0. Частное 
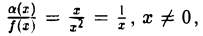очевидно, не является б. м. ф. при х → 0, так что отношение двух бесконечно малых функций в общем случае не есть бесконечно малая функция.
Теорема:
Связь функции, имеющей предел, с ее пределом и бесконечно малой функцией. Пусть функция f(x) определена в некоторой окрестности точки Хо, кроме, может быть, самой точки Хо. Для того, чтобы функция f(x) в точке Хо имела пределом число А, необходимо и достаточно, чтобы f(x) можно было представить в виде суммы
f(x) = А + а(х),
где а(х) — б. м. ф. при х → x0.
Необходимость. Пусть функция f(х) имеет в точке хо предел, равный числу А,
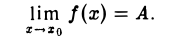
Положим
a(x)=f(x)-A (1)
и докажем, что а(х) — б. м. ф. при х → хо. Возьмем любое ε > 0. Так как по условию
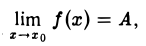
то для выбранного ε > 0 найдется такое δ > 0, что для всех х, х ≠ хо, удовлетворяющих условию |х — х0| < δ, верно неравенство
|f(х) — А| < ε.
В силу (1) последнее можно записать в виде
|а(х)| < ε.
Это означает, что а(х) — б. м. ф. при х → хо.
Достаточность. Пусть функцию f(х) можно представить в виде
f(х) = А + а(х), (2)
где А — постоянная, а а(х) — б.м.ф. при х → х0. Докажем, что функция f(х) в точке хо имеет предел, равный числу А. Возьмем любое ε > 0. Так как по условию а(х) — б.м.ф. при х → хо, то найдется такое δ > 0, что для всех х, х ≠ хо, удовлетворяющих условию |х — хо| < δ, будет выполняться неравенство
|а(х)| < ε.
Но в силу (2) а(х) = f(x)-A. Поэтому |f(х) — A| < ε для тех же значений х. Согласно определению это означает, что А = .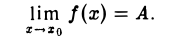
Арифметические операции над пределами
Пусть функции f(х) и φ(x) определены в некоторой окрестности точки хо, кроме, быть может, самой точки хо.
Теорема:
Если функции f(х) и φ(x) в точке Хо имеют пределы, то в этой точке имеют пределы также их сумма f(x) + φ(х), разность f(х) — φ(x), произведение f(x) ⋅ φ(x) и, при дополнительном условии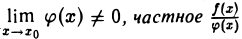 
, частное причем
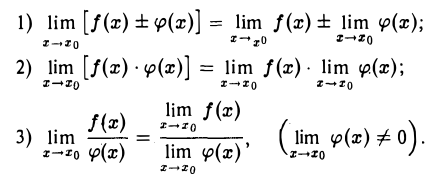
Ограничимся доказательством утверждения 2) о пределе произведения.
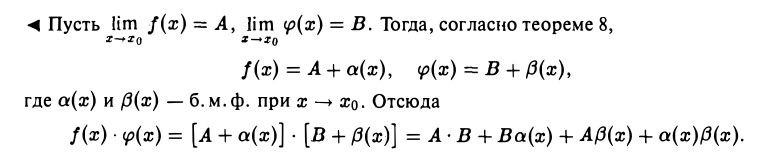
Так как Ва(х), А β(х), а(х) β(х) — б.м.ф. при х → хо (как произведение б.м.ф. на ограниченную), то и их сумма есть б. м. ф. при х → х0.
Таким образом, функция f(x)< φ(x) представлена как сумма постоянной АВ и б.м.ф. при х → хо. Отсюда на основании теоремы 8 заключаем, что функция f(х) • φ{х) .имеет предел в точке х0, равный числу АВ:
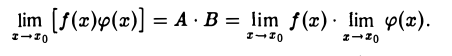
Утверждения 1) и 3) доказываются подобным же образом (докажите!).
Замечание:
Теорема о пределе суммы (произведения) обобщается на случай любого фиксированного числа слагаемых (сомножителей), имеющих предел.
Следствие:
Постоянный множитель можно выносить за знак предела.
Задача:
Пусть функция f(х) имеет предел в точке Хо, а функция φ(x) не имеет предела. Будут ли существовать пределы
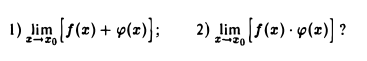
Задача. Пусть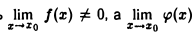 
не существует. Доказать, что 
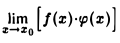не существует.
Приведем несколько примеров на вычисление пределов функций. Пример:
Найти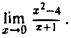 
Будем рассматривать данную функцию как частное двух функций f(х) = х2 — 4 и φ(x) = х + 1. Каждая из этих функций в точке х = 0 имеет предел:
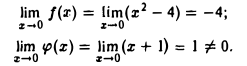
Так как предел знаменателя φ(х) заданного отношения не равен нулю, то можно воспользоваться теоремой о пределе частного, что дает
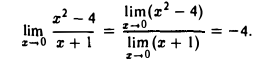
Пример:
Найти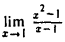 
Полагая f(x) = x2 — I, φ(x) = x — 1, имеем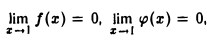 
т.е., как говорят, имеет место неопределенность вида 0/0. Пользоваться теоремой о пределе частного нельзя. Для раскрытия неопределенности поступаем так. В определении предела функции в точке х = 1 сама точка х = 1 из рассмотрения исключается. Заметив это, представим данную функцию в виде
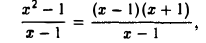
откуда, сокращая на х — 1 ≠ 0, получим
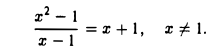
Поэтому
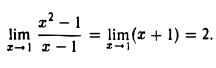
Пример:
Найти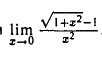 
.
Пределы числителя и знаменателя в точке х = 0 равны нулю, т.е. опять имеем неопределенность вида 0/0. Для ее раскрытия умножим числитель и знаменатель данной дроби на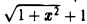 
. При х ≠ 0 имеем
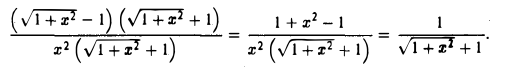
К полученной функции применима теорема о пределе частного, так что
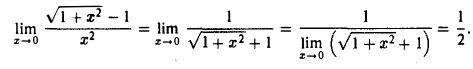
Пример:
Рассмотрим функцию f(х) = sin x2. Она определена на всей числовой Оси, четна, ограничена 
и обращается в нуль при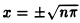 
, где п = 0, 1, 2, … .
Покажем, что эта функция — не периодическая. Возьмем два соседних нуля функции; пусть это будут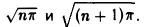 
Расстояние между ними равно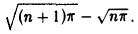 
Найдем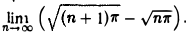 
Здесь имеет место неопределенность вида ∞ — ∞. Чтобы ее раскрыть, умножим и разделим выражени
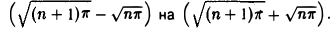
Будем иметь
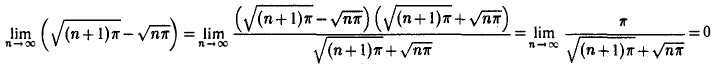
(поскольку числитель последней дроби постоянен, а знаменатель неограниченно возрастает при п → ∞).
Таким образом, расстояние между двумя соседними нулями функции стремится к нулю при п → ∞ . Следовательно, функция sin x2 —непериодическая.
Бесконечно большие функции. Их связь с бесконечно малыми функциями
Наряду с понятием бесконечно малых функций вводится понятие бесконечно больших функций (б. б. ф.).
Пусть функция /(х) определена в некоторой окрестности точки х0, кроме, быть может, самой точки хо.
Определение:
Если для любого, как угодно большого, числа М > 0 существует такое число δ > 0, что для всех х ≠ хо, удовлетворяющих условию
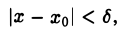
выполняется неравенство
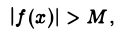
то функцию f(x) называют бесконечно большой функцией при х —> xо и пишут
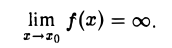
При этом говорят также, что f(х) при х → хо имеет бесконечный предел.
С помощью логических символов определение функции f(x), бесконечно большой при х → хо, запишется так
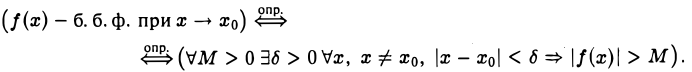
Заменяя в приведенном определении неравенство |f(х)| > М на f(х) > М или на f(х) < -М соответственно, получим определение положительной б.б.ф. f(х),
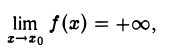
или отрицательной б. б. ф. f(х),
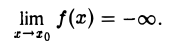
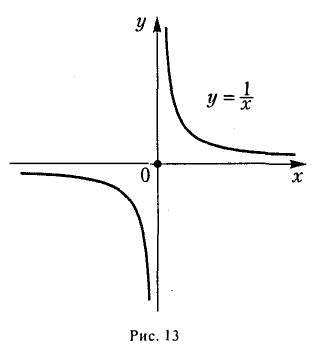
Пример:
Функция f(х) =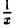, определенная для всех х ≠ 0 (рис. 13), есть б. б. ф. при х → 0.
Возьмем любое М > 0, как угодно большое. Неравенство |f(x)| =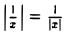
> M равносильно неравенству |z| = |х -0| < 
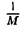. Поэтому, если взять δ = 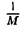, то для ∀x, х ≠ 0, таких, что |х — 0| = |x| < 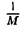, будет верно неравенство |f(x)| = 
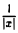> М . Согласно определению это означает, что f(x) = 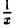— б. б. ф. при х -> 0.
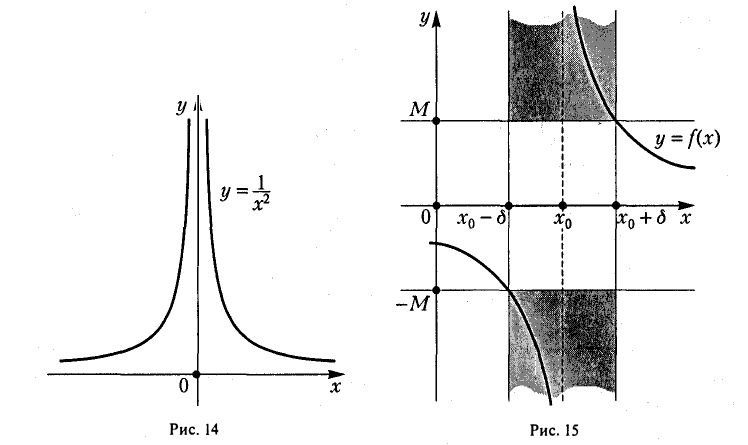
Функция f(х) =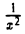 
, определенная для всех х ≠ 0 (рис. 14), при х —» 0 есть положительная б. б. ф.
Геометрическое пояснение б.б.ф.: функция f(х) является б.б.ф. при х —» хо, если для любой горизонтальной полосы между прямыми у = — М и у = М, сколь бы широкой она ни была, можно указать такие две вертикальные прямые х = хо — δ и х = хо + δ, что между этими прямыми часть графика функции у = f(х), х ≠ хо, целиком расположена вне этой горизонтальной полосы (рис. 15).
Заметим, что функция /(х) может быть неограниченной в окрестности точки хо и не быть бесконечно большой при х —» хо. Например, функция f(х) =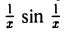 
не ограничена в окрестности точки х = 0, но не является б. б. ф. при х —» 0 (попробуйте сделать рисунок).
Определение:
Будем говорить, что f(х) есть бесконечно большая функция при х —> ∞ и писать
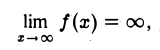
если для любого числа М > О, хотя бы и как угодно большого, найдется число п > 0 такое, что для всех х, удовлетворяющих условию |х| > N, верно неравенство
|f(х)|>М.
Пример:
f(х) = х — б. б.ф. при х -» ∞. В самом деле, ∀ M > 0 ∃N > 0, например, N = М, такое, что ∀x, |x| > N, верно неравенство |f(x)| = |x| > M.
Подобным же образом можно сформулировать определение бесконечно больших функций при х —> + ∞ и при х —> — ∞.
Между бесконечно большими и бесконечно малыми функциями существует зависимость, которая выражается следующими теоремами.
Теорема:
Если функция f(x) — бесконечно большая при х —» x0, то функция а(х) = 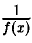— бесконечно малая при х —» хо.
Возьмем любое, как угодно малое ε > 0. Так как по условию функция f(х) — бесконечно большая при х —» хо, то для любого М > 0, в частности для М=1/ε, найдется такое δ > 0, что при всех значениях х, х Ф х0,изусловия |х — х0| < δ будет следовать неравенство
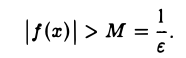
Для таких значений х определена функция а(х) = 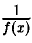, и для нее
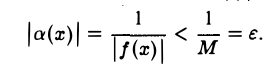
Итак,
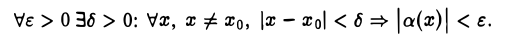
Это означает, что а(х) = 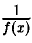— б. м. ф. при х —» хо. Аналогично доказывается обратное утверждение.
Теорема:
Если а(х) — бесконечно малая функция при х —> х0 и в некоторой окрестности (х0 — δ, х0 + δ) точки xо, кроме, быть может, самой точки xо, ос(х) отлична от нуля, то функция f(х) =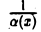
бесконечно большая при х —» хо.
Задача:
Сформулировать на языке неравенств, что значит
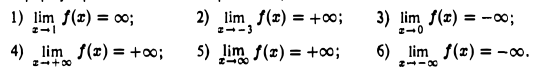
Пример:
Рассмотрим дробно-рациональную функцию
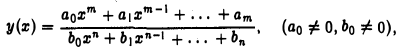
представляющую собой отношение двух многочленов относительно х степеней тип соответственно, и исследуем поведение этой функции при х → ∞,
При достаточно больших |х| знаменатель этой дроби отличен от нуля, и рассматриваемое отношение имеет смысл. Разделив числитель и знаменатель дроби на хn, получим
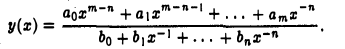
Ясно, что при х → ∞ знаменатель дроби имеет пределом число bо ≠ 0. Числитель дроби при т > п неограниченно возрастает по абсолютной величине; при т = п предел числителя равен коэффициенту ao; при т < п предел числителя равен нулю. Таким образом,
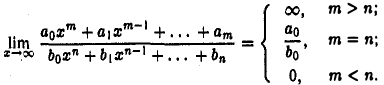
Односторонние пределы функции в точке
Пусть функция f(х) определена на интервале (а, х0).
Определение:
Число А называется пределом функции f(x) в точке х0 слева, если для любого ε > 0 существует δ > 0, такое, что для всех х, удовлетворяющих условию х0 — δ < х < х0, верно неравенство
|f(х) -А|< ε.
В этом случае пишут
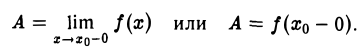
Пусть функция f(х) определена на интервале (х0, b).
Определение:
Число А называют пределом функции f(x) в точке xo справа и пишут
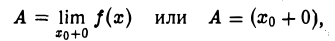
если для любого ε > 0 существует такое δ > 0, что для всех х, удовлетворяющих условию хо < х < xq + δ, верно неравенство
|f(х) -A|< ε.
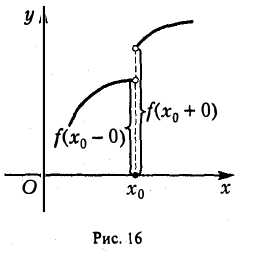
Пусть теперь функция f(x) определена в двусторонней окрестности точки хо, кроме, быть может, самой точки хо (рис. 16).
Теорема:
Для того, чтобы функция f(x) имела предел в точке хо, необходимо и достаточно, чтобы существовали пределы функции f(х) в точке xо слева и справа и они были равны между собой. Тогда
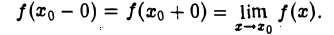
Пусть 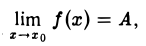. Тогда для всякого ε > О существует δ > 0 такое, что для всех х из интервала (хо — δ, хо + δ), х Ф хо, верно неравенство
|f(х) -A|< ε. (1)
Так как неравенство (1) имеет место как на интервале (хо — δ , хо), так и на интервале (хо, хо + δ), то согласно определению
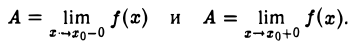
Обратно, пусть
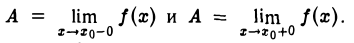
Тогда для любого ε > 0 существуют такие δ1 > 0 и δ2 > 0, что если х0 — δ1 < х < х0 и соответственно хо < х < хо + δ2, то |(х) — А| < ε. Обозначая через 6 наименьшее из чисел 62, получим, что |f(х) — А| < ε для всех х таких, что 0 < |х — х0| < δ. Это означает, что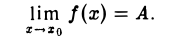
Примеры:
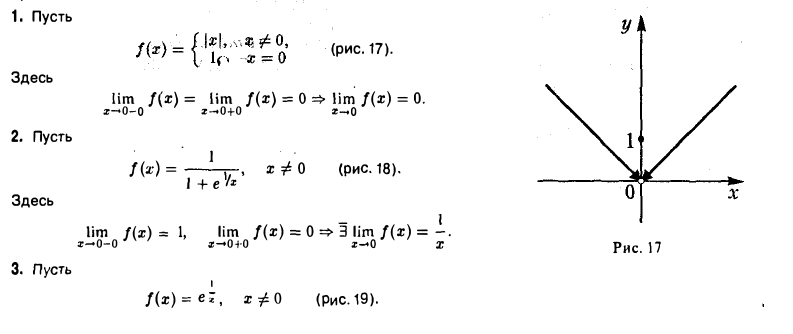
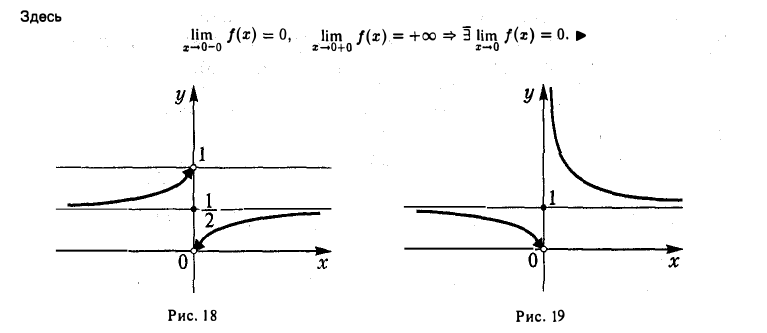
Если функция f(х) задана на отрезке [а, b] или на интервале (а, b), то в точке а она может иметь только предел справа, a в точке b — только слева.
Непрерывность функции
Пусть функция f(х) определена в некоторой окрестности Ω точки хо.
Определение:
Функция f(х) называется непрерывной в точке хо, если
1) она имеет предел вточке хо;
2) этот предел равен f(х0) — значению функции f(х) в точке хо,
Так как хо =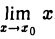 
то равенству (1) можно придать следующую форму
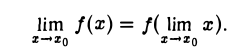
Следовательно, для непрерывной функции символ lim предельного перехода и символ f функции можно менять местами.
На языке ε — δ определение непрерывности выглядит так.
Определение:
Функция f(х) называется непрерывной в точке хо, если для любого числа ε > 0 существует число δ > 0, такое, что для всех х ∈ Ω1, удовлетворяющих условию |х — xo| < δ , выполняется неравенство
При этом в общем случае величина 6 зависит как от числа е > 0, так и от точки хо: δ = δ ( ε , х0).
С помощью логических символов определение 2 записывается в виде
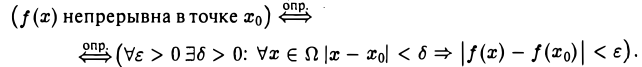
Подчеркнем, что теперь (в отличие от предыдущих параграфов) мы не требуем, чтобы х ≠ xo.
Приведем еще одну формулировку понятия непрерывности функции в точке. Пусть функция у = f(х) определена в некоторой окрестности Ω точки хо (рис.20).
Считая хо исходной точкой, возьмем другое значение аргумента х = хо + ∆х ∈ Ω , отличающееся от первоначального значения х0 на некоторую величину ∆х (все равно, положительную или отрицательную), которую будем называть приращением аргумента. Величину изменения функции
∆y = f(xо + ∆х) — f(х0) (3)
назовем приращением функции f в точке хо, отвечающим приращению ∆х аргумента х. Условие непрерывности функции f(х) в точке хо
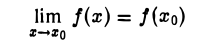
можно записать так
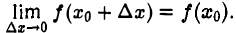
Это равносильно тому, что
(4)
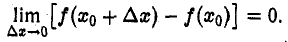
Замечая, что f(х0 + ∆ х) — f(х0) = ∆у, равенство (4) можно представить в виде
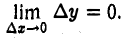
Определение:
Функция у = f(х) называется непрерывной в точке хо £ П, если приращение ∆у функции в этой точке, отвечающее приращению ∆х аргумента, стремится к нулю при ∆х → 0.
Пример:
Покажем, что функция у = х1 непрерывна во всякой точке хо числовой оси.
В самом деле, для любого приращения ∆x в точке хо имеем
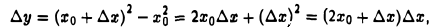
откуда видно, что величина ∆у → 0 при ∆х → 0.
В ряде случаев удобно пользоваться следующим определением непрерывности функции в точке.
Определение Гейне:
Пусть функция f(х) задана на произвольном множестве Е действительных чисел и пусть точка хо ∈ Е. Функция f(х) называется непрерывной в точке х0, если для любой последовательности точек {хn} ,хп ∈ Е, сходящейся к точке хо, соответствующая последовательность {f(хn)} значений функции сходится к f(х0).
Пользуясь определением 4, можно показать, что функция Дирихле
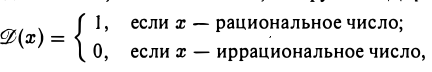
не является непрерывной в любой точке xo ∈ R.
Все четыре определения непрерывности функции равносильны. В каждом конкретном случае пользуются тем определением, которое оказывается более удобным.
Следующие теоремы выражают локальные свойства функции, непрерывной в точке.
Теорема:
Если функция f(х) непрерывна в точке хо и f(х0) > А (соответственно f(х0) < А), то существует такое δ > 0, что f(x) > А (соответственно f(x) < А) для всех х из интервала (хо — δ, xо + δ).
Пусть для определенности f(х0) > А, так что
f(х0) = A + h,
где h > 0. Возьмем ε = В силу непрерывности f(х) в точке хо существует такое δ > 0, что для всех х, удовлетворяющих условию |х — хо| < δ, верно неравенство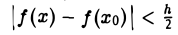 
или
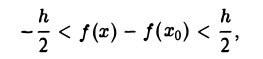
откуда
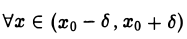
имеем
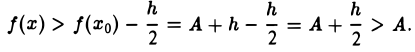
Теорема:
Устойчивость знака непрерывной функции. Если функция f(х) непрерывна в точке xо и f(х0) ≠ 0, то существует окрестность (хо — δ, х0 + δ) точки х0, в которой функция f(х) не обращается в нуль и сохраняет один и тот же знак (знак числа f(х0)).
Чтобы убедиться в этом, достаточно в предыдущей теореме взять А = 0.
Основные элементарные функции. Их непрерывность
Основными элементарными функциями называются следующие функции.
- Степенная функция
у = хa, где а — любое действительное число; область определения х > 0.
2. Показательная функция
у = аx, а > 0, а ≠ 1; область определения — ∞ < х < + ∞.
3. Логарифмическая функция
y = logaх, а > 0, а ≠ 1; область определения х > 0.
4. Тригонометрические функции
у = sin х; область определения — ∞ < х < + ∞;
у = cos х; область определения — ∞ < х < + ∞;
у = tg х; область определения х ≠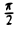
+ п π, п = 0, ± I,. ±2,
у = ctg х; область определения х ≠ п π, п = 0, ±1, ±2,… .
5. Обратные тригонометрические функции
У = arcsin х; область определения -1 1;
У = arccos х; область определения 1;
У = arctg х; область определения — ∞ < х < + ∞;
У = arcctg х; область определения — ∞ < X < + ∞.
Функции, которые получаются из основных с помощью конечного числа арифметических операций, а также операций взятия функции от функции, примененных конечное число раз, называются элементарными функциями.
Можно показать, что все основные элементарные функции непрерывны в каждой точке своих областей определения.
Пример:
Покажем, например, непрерывность функции у = cos х, — ∞ < х < + ∞.
Предварительно докажем неравенство
(1)
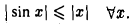
Рассмотрим окружность радикса 1 (рис.21).
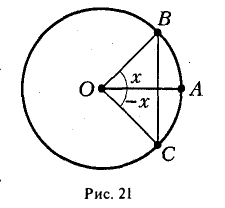
Пусть угол АОВ имеет радианную величину х, 0 < х < 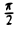, и пусть LAOB = LAOC. Очевидно, длина отрезка ВС равна 2 sin х; длина дуги —- ВС равна 2x. Так как длина дуги больше длины хорды, стягивающей эту дугу, то 2 sin х < 2х и, значит, sin < х. Для рассматриваемых значений х
∈ (0, 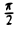) этo неравенство можно записать в виде |sinx| < |х|. Учитывая, что |sin(-x)| = | -sinx| = |sinx| и | — х| = |х|, замечаем, что неравенство | sin х| < |х| верно и для х ∈ (-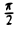, o). Так как sin0 = 0, то неравенство (1) справедливо для всех х ∈ (—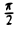> 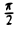), eсли же х ∉ (-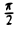, 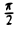), то |x| ≥ 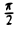> 1, тогда как |sinx| ≤ 1 ∀ x. Следовательно, неравенство
| sin х| ≤ |х|
верно для любых х.
Функция у = cos x определена на всей числовой оси. Возьмем любую точку x ∈ R, Дадим этому значению х приращение ∆х. Тогда функция у = cos х получит приращение
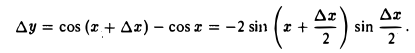
Отсюда
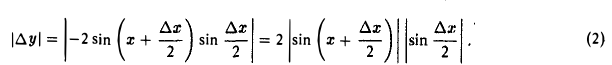
Воспользовавшись тем, что всегда
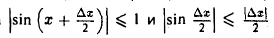
в силу неравенства (1), из (2) получаем, что
(при фиксированном х ∆у есть функция от ∆х). Отсюда, в силу теоремы о пределе промежуточной функции, при ∆x → 0 получаем
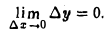
Это означает, что функция у = cos х непрерывна в любой точке х числовой оси.
Замечательные пределы
Первый замечательный предел
Если угол х выражен в радианах, то
(1)
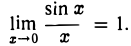
Предположим, что угол х заключен в границах 0 < х <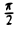. Рассмотрим окружность радиуса 1 и проведем некоторые построения (рис. 22).
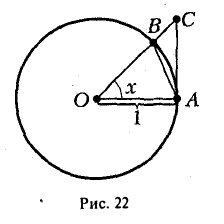
Из рисунка видно, что площ. ∆ОАВ < площ. сектора ОАВ < площ. ∆О АС.
Так как указанные площади равны соответственно
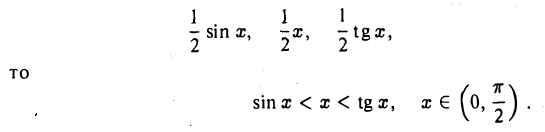
Разделив все члены этого неравенства на sin х > 0, получим
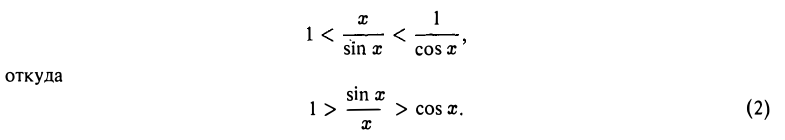
Неравенство (2) доказано для х ∈ (0, 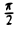), но оно верно и для х ∈ (- 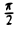, 0), так как
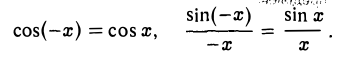
Функция у = cos х непрерывна в любой точке х, в частности, в точке х = 0, так что
Таким образом, обе функции φ(x) = cosx и φ(x) = 1 имеют в точке х = 0 предел, равный единице. По теореме о пределе промежуточной функции из (2) и (3) получаем
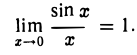
Второй замечательный предел
Мы установили выше, что
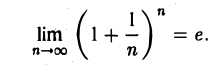
Положим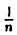 
= z. Легко видеть, что z принимает значения 1, 
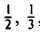,… и z → o при п → ∞.
Будем очевидно иметь
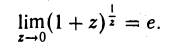
Можно показать, что
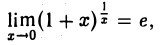
когда х стремится к нулю произвольным образом, пробегая любую последовательность значений, отличных от нуля.
Операции над непрерывными функциями
Теорема:
Пусть функции f(x) и φ(х) определены в некоторой окрестности точки хо-Если функции f(x) и φ(х) непрерывны в точке X0, то непрерывны в точке Хо их сумма f(х) + φ(х), разность f{х) — φ(х), произведение f{х) ⋅ φ(x), а также частное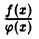
(при дополнительном условии φ(хо) ≠ 0).
Докажем непрерывность частного функций.
Пусть функции f(х) и φ(х) непрерывны в точке io. причем у(хо) ≠ 0. В силу теоремы об устойчивости знака непрерывной функции существует окрестность точки хо, в которой функция φ(х) ≠ 0. Поэтому функция F(x) = 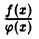определена в некоторой окрестности точки хо — Так как
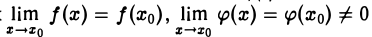
то по теореме о пределе частного имеем
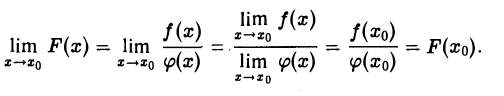
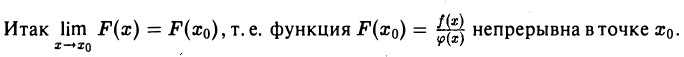
Остальные утверждения теоремы доказываются аналогично.
Сложная функция. Непрерывность сложной функции
Пусть на некотором множестве Е точек числовой оси задана функция и = φ(х). Обозначим через Е1 множество значений и, соответствующих значениям х из множества Е. Пусть далее на множестве Е1 определена функция у = f(u). Таким образом, каждому х ∈ Е соответствует определенное и ∈ Е1, а этому и ∈ Е1, в свою очередь, соответствует определенное значение у = f(u) (рис. 23). Следовательно, величина у в конечном счете является функцией от х, определенной на множестве Е. В этом случае у мы будем называть сложной функцией от x и обозначать
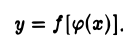
Например, если и = sinx, у = еu, то мы имеем сложную функцию y=esinx, определенную для всех х.
Теорема:
Переход к пределу под знаком непрерывной функции. Если функция и = φ (х) в точке хо имеет предел, равный числу А, а функция у = f(и) непрерывна в точке и = А, то сложная функция у = f [ φ (х)] в точке х0 имеет предел, равный f(A).
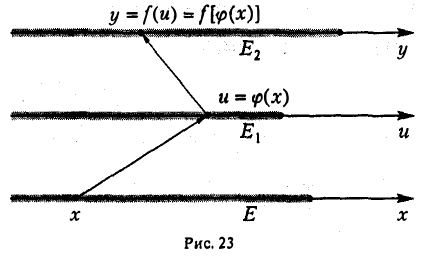
Возьмем любое ε > 0. Так как функция f(и) непрерывна в точке и = A, то для выбранного ε > 0 существует такое число η > 0, что для всех и, удовлетворяющих условию
|и-A|< η, (1)
верно неравенство
|f(u)-f(A)|< ε. (2)
По условию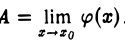 
. Поэтому, каким бы ни было число η > 0, найдется такое δ > 0, что для всех х, удовлетворяющих условию
будет верно неравенство
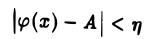
или, что то же самое,неравенство (1). А из неравенства (1) следует неравенство (2), которое можно записать в виде
Итак, для любого ε > 0 существует δ > 0 такое, что для всех х, удовлетворяющих условию
0 < |х — х0| < δ,
верно неравенствo
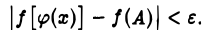
Согласно определению это означает, что число f(A) есть предел сложной функции f[ φ(х)] в точке хо.
Таким образом, при выполнении условий теоремы
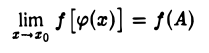
или, что то же
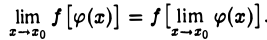
Это соотношение выражает правило перехода к пределу под знаком непрерывной функции.
Пример:
Показать, что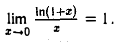 
Заметим, что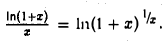 
Функция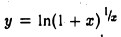 
является сложной функцией, составленной из функций у = ln и, 
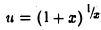. Так как 
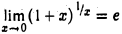, и функция у = ln u непрерывна в точке и = е, то на основании теоремы 16 получаем
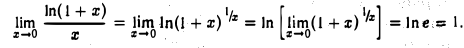
Теорема:
Непрерывность сложной функции. Если функция и = φ(х) непрерывна в точке xq, а функция у = f(и) непрерывна в точке u0 = φ(xo), то сложная функция у = f[ φ(х)] непрерывна в точке xo.
По условию функция и = φ (х) в точке хо имеет предел, равный φ(хо) = и0. Кроме того, функция у = f{и) непрерывна в точке ио. На основании теоремы 16 о переходе к пределу под знаком непрерывной функции сложная функция у = f[φ(x)] в точке хо имеет предел, равный f(ио) = f[φ(хо)],
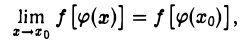
что означает непрерывность сложной функции f[ φ (х)] в точке хо.
Точки разрыва функции. Их классификация
Пусть функция f(х) определена в некоторой окрестности точки хо- Согласно определению, непрерывность функции f(х) в точке хо выражается соотношением
Пользуясь односторонними пределами функции, равенство (1) можно заменить равносильным ему двойным равенством
(2)
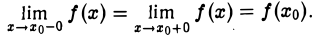
Таким образом, функция /(х) непрерывна в точке хо тогда и только тогда, когда в этой точке существуют пределы слева и справа, они равны между собой и равны значению функции f(х) в точке хо-
Определение:
Если в точке хо функция f(x) не является непрерывной, то говорят, что f(х) разрывна в этой точке, и точку хо называют точкой разрыва функции f(х). ( Если функция f(х) не определена в точке xo, то точку xo также называют точкой разрыва функции. )
Точки разрыва функции классифицируются в зависимости от того, как именно нарушено условие ее непрерывности (2).
Определение:
Если в точке х0 функция f(х) имеет предел слева и предел справа и они равны между собой, но не равны значению функции в точке xo,
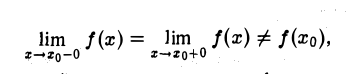
то точка хо называется точкой устранимого разрыва функции f(x).
Такое название оправдывается тем, что в этом случае достаточно изменить значение функции только в одной точке хо, чтобы получить новую функцию, уже непрерывную в точке хо. Именно, если f(х) имеет в точке хо устранимый разрыв, то функция
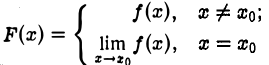
непрерывна в точке хо. Мы «устранили» разрыв, изменив значение функции в одной точке хо.
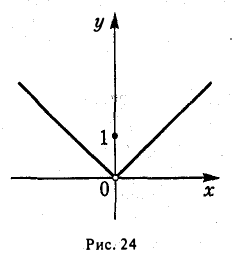
Пример:
Пусть
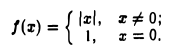
Имеем
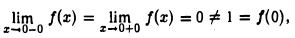
так что точка х = 0 есть точка устранимого разрыва для функции f(x) (рис. 24). Если изменить значение данной функции f в точке х = 0, положив f(0) = 0, то получим непрерывную в точке х = 0 функцию F(x) =|x|.
Вообще, графиком функции, непрерывной на множестве (х0 — δ1 ,xo) U (хо, х0 + δ2) и имеющей в точке xо устранимый разрыв, служит непрерывная кривая, из которой удалена точка с абсциссой хо (рис. 25).
Подчеркнем, что в точке хо устранимого разрыва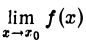 
существует.
Если 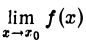не существует, то точка хо называется точкой неустранимого разрыва.
Определение:
Если в точке хо функция f(х) имеет конечные пределы слева и справа, но они разные,
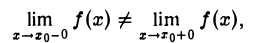
то точка хо называется точкой разрыва функции f(х) с конечным скачком функции. (При этом безразлично, совпадает или нет f(хо) с одним из односторонних пределов.)
Такое название точки разрыва обусловлено тем, что при переходе х через точку хо значения функции f(х) претерпевают скачок, измеряемый разностью f(xо + 0) -f(х0 — 0) предельных значений /(х) в точке хо справа и слева.
Пример:
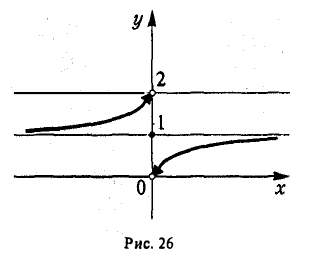
Пусть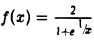 
, f(0) = I (рис.26).
Для данной функции точка х = 0 есть точка разрыва с конечным скачком функции, равным -2:
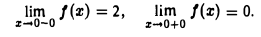
Точки устранимого разрыва и точки разрыва с конечным скачком функции называются точками разрыва первого рода. Каждая точка разрыва 1-го рода функции f(х) характеризуется тем, что в этой точке функция f(х) имеет конечный предел как слева, так и справа.
Все другие точки разрыва функции называются точками разрыва второго рода. Каждая точка разрыва второго рода функции f(x) характеризуется тем, что в этой точке функция f(x) не имеет конечного предела по крайней мере с одной стороны — слева или справа.
Примеры:
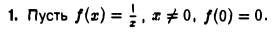
Для данной функции точка х = 0 есть точка разрыва второго рода, так как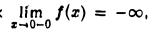 
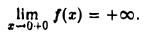
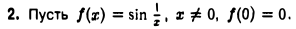
Эта функция в точке х = 0 не имеет ни конечного, ни бесконечного предела как слева, так и справа (чтобы убедиться в этом, можно воспользоваться определением предела функции по Гейне). Поэтому для данной функции точка х = 0 является точкой разрыва второго рода.
Для функции Дирихле
любая точка хо есть точка разрыва 2-го рода.
Будем говорить, что функция f(х) в точке хо непрерывна справа, если
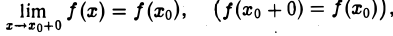
и непрерывна слева, если
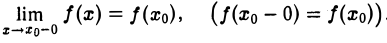
Функция f(х) называется непрерывной на интервале (а, b), если она непрерывна о каждой точке этого интервала. Множество всех функций, непрерывных на интервале (а, b) обозначают С (а, b).
Функция f(х) называется непрерывной на отрезке [а, b], если она непрерывна на интервале (а, b) и в точке а непрерывна справа, а в точке b — непрерывна слева. Множество всех таких функций обозначают С [а, bJ.
Свойства функций, непрерывных на отрезке
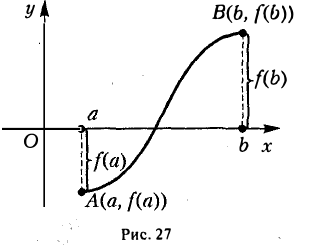
Теорема: Больцано—Коши о нуле функции:
Если функция f(х) непрерывна на отрезке [а, b] и в концах его имеет значения, противоположные по знаку, то f (х) обращается в нуль по крайней мере в одной точке интервала (а, b).
Пусть числа f(а) и f(b) противоположны по знаку. Точка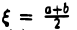 
делит отрезок [а, b] пополам. Если f( ξ ) = 0, то теорема верна. Пусть f( ξ ) ≠ 0. Тогда один из отрезков [а, ξ ] или [ ξ , b] будет таким, что в его концах значения функции f(х) имеют разные знаки. Обозначим этот отрезок через [а1, b1] и разделим его пополам точкой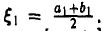 
Если = 0, то теорема верна. Пусть f( ξ1) ≠ 0. Тогда один из отрезков [а1, ξ1] или [а2, ξ2] будет таким, что в его концах значения функции f(x) имеют разные знаки. Обозначим этот отрезок через [a2, b2] и разделим его пополам.
Продолжая этот процесс, мы либо встретим на очередном этапе рассуждений точку a ∈ (a, b), для которой f(a) = 0, и тогда теорема доказана. Либо получим бесконечную последовательность вложенных друг в друга отрезков, длины которых стремятся к нулю,
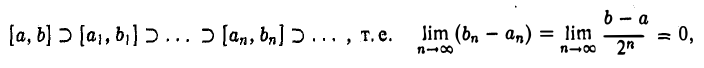
и на концах каждого из которых функция f(x) имеет значения разных знаков.
В силу леммы Кантора существует единственная точка а, принадлежащая всем отрезкам [аn, bn].
Докажем, что f(a) = 0. Допустим противное: f(а) ≠ 0. Функция f(х) непрерывна в точке a ∈ [a, b] и, о силу устойчивости знака непрерывной функции, найдется такой интервал (а — δ, а + δ), в котором f(х) сохраняет знак. Так как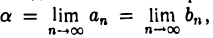 
то п можно взять настолько большим, что отрезок [аn, bn] будет содержаться в интервале (а — δ, а + δ), и поэтому числа f(an) и f(bn) будут одного знака. Но по построению отрезков [аn, bn] при любом п числа f(аn) и f(b„) противоположны по знаку. Полученное противоречие доказывает, что наше допущение f(а) ≠ 0 неверно. Следовательно f(а) = 0, где а < а < b (точка а ∈ [а, b], но не может совпадать ни с точкой а, ни с точкой b, так как f(a) ≠ 0, f(b) ≠ 0).
Геометрически результат теоремы очевиден. Если f(a)f(b) < 0.то точки А(а, f(a)) и В(b, f(b)) лежат в разных полуплоскостях, на которые ось Ох делит плоскость хОу. График непрерывной функции у = f(х), соединяющий эти точки, обязательно пересечет ось Ох по край ней мере в одной точке (рис.27).
Требование непрерывности функции f(х) на [а, b] существенно: функция, имеющая разрыв хотя бы в одной точке, может перейти от отрицательного значения к положительному и не обращаясь в нуль. Так будет, например, с функцией
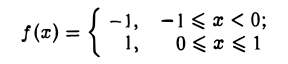
(рис.28).
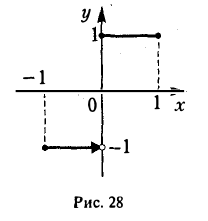
Укажем одно из применений доказанной теоремы. Рассмотрим многочлен нечетной степени с действительными коэффициентами
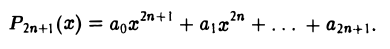
Пусть для определенности ао > 0. При достаточно больших по абсолютной величине отрицательных значениях х знак многочлена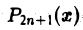 
будет отрицательным, а при достаточно больших положительных значениях х — положительным. Так как многочлен есть всюду непрерывная функция, то найдется некоторая точка, в которой он необходимо обращается в нуль. Отсюда следует, что всякий многочлен нечетной степени с действительными коэффициентами имеет по крайней мере один действительный корень.
Теоремой 18 можно пользоваться и для приближенного вычисления корня.
Пример:
Найдем приближенно корень многочлена
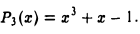
Это — многочлен нечетной степени и потому заведомо имеет по крайней мере один действительный корень.
На концах отрезка (0. 1] многочлен Р3(х) принимает значения разных знаков: Pз(0) = -1 < 0, Р3(1) = 1 >о. Следовательно, в интервале (0, 1) имеется корень этого многочлена.
Если взять точку ξ = 1/2 — середину отрезка (0, 1]. то получим
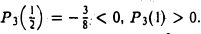
Значит, корень находится в интервале ( 1/2, l ). Возьмем теперь точку ξ1= 3/4 — середину отрезка [ 1/2, l]. Будем иметь
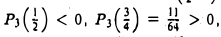
так что корень содержится в интервале (1/2,3/4) Продолжая этот процесс, мы можем найти все более тесные границы для корня многочлена Pз(х).
Теорема Коши:
О промежуточных значениях непрерывной функции. Пусть функция f(x) непрерывна на отрезке [а, b], причем f(a) = A, f(b) = В. Тогда каким бы ни было число С, заключенное между числами А и В, на отрезке [а, b] найдется по крайней мере одна точка а такая, что f(а) = С.
Иными словами, непрерывная на отрезке [а, b] функция принимает все промежуточные значения между ее значениями на концах отрезка.
Пусть, для определенности, А < В. Рассмотрим функцию
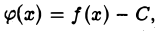
где А < С < В. Очевидно, функция φ(х) непрерывна на отрезке [а, b], причем на концах этого отрезка φ(х) принимает значения противоположного знака,
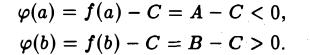
По теореме 18 в интервале (а, b) найдется точка а такая, что φ(а) = f(а) — С = 0, т.е. f(a) = C.
Теорема:
Первая теорема Вейерштрасса. Если функция f(x) непрерывна на отрезке [а, b], то она ограничена на нем, т. е. существует такое число К > 0, что для всех х ∈ [а, b] верно неравенств
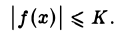
Замечание:
Если функция f(х) непрерывна на интервале (а, b) (или на полуинтервале [а, b), или на полуинтервале (а, b]), то f(х) не обязательно ограничена на нем. Например, функция f(х) = 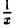непрерывна на полуинтервале (0, 1], но не ограничена на нем.
Пусть функция f(x) определена и ограничена на некотором множестве Е. Назовем точной верхней гранью М функции f(x) на множестве Е точную верхнюю грань множества значений функции f(x) на множестве Е
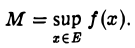
Аналогично определяется точная нижняя грань т. функции f(x) на Е:
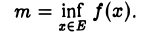
Теорема:
Вторая теорема Вейерштрасса. Если функция f(х) непрерывна на отрезке [а, b], то она достигает на этом отрезке своих точной нижней и верхней граней, т.е. на отрезке [а, b] найдутся такие точки ξ и η, что
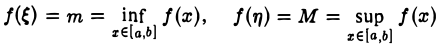
(рис. 29).
Замечание:
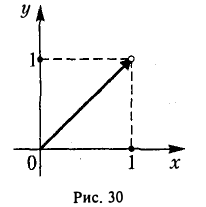
Условие непрерывности функции f(x) на отрезке [а, b) существенно: функция f(x) = х непрерывна на интервале (-1, 1) и ограничена на нем, но ее точная верхняя грань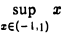 
= 1 не достигается, т.е. нет такого хo ∈ (-1, 1), значение этой функции для которого равно единице. Другой пример: f(x) = х — [х] на (0, 1| (рис.30). Здесь 
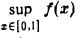= 1, но он не достигается на отрезке [0, 1]. Это связано с тем, что функция f(х) разрывна на (0, 1].
Назовем точную верхнюю грань наибольшим значением, а точную нижнюю грань — наименьшим значением функции f(x) на отрезке [а, b]. Тогда второй теореме Вейерштрасса можно придать следующую формулировку.
Теорема:
Если функция f(x) непрерывна на отрезке [а, b], то она на этом отрезке принимает свои наименьшее и наибольшее значения.
Равномерная непрерывность
Пусть функция f(x) непрерывна на интервале (а, b). Тогда в любой точке хо ∈ (а, b) для любого ε > 0 существует такое δ > 0, что для всех х ∈ (а, b), удовлетворяющих условию |z — х0| < δ, верно неравенство |(x) — (xо)| < δ. При этом величина δ зависит как от е, так и от точки хо: δ = δ( ε, xo) Так что при одном и том же ε > 0 в разных точках х ∈ (а, b) число δ может оказаться разным и ниоткуда не следует, что существует единое δ для всех х ∈ (а, b). Требование, чтобы такое δ = δ( ε ) > 0 существовало, является более сильным, чем требование просто непрерывности функции f(x) на интервале (а, b).
Определение:
Функция f(x) называется равномерно непрерывной на интервале (d,b), если для всякого ε > 0 существует такое δ = δ ( ε ) > 0, что для любых точек х’ и х» из интервала (а, b), удовлетворяющих условию
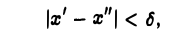
верно неравенство
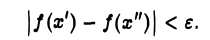
Здесь существенно, что для всякого ε > 0 существует δ > 0, обеспечивающее выполнение неравенства 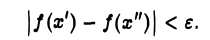сразу для всех х’, х» из интервала (а, b) при единственном условии \х’ — х»\ < δ.
Пример:
Функция f(х) = х равномерно непрерывна на всей числовой оси. Здесь достаточно взять δ = ε.
Ясно, что если функция f(x) равномерно непрерывна на интервале (а, b), то она непрерывна в каждой точке х ∈ (а, b). Обратное утверждение неверно.
Пример:
Функция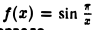 
непрерывна на интервале (0, I), но не является равномерно непрерывной на этом интервале.
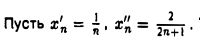
Тогда величина
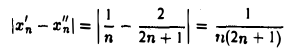
за счет выбора п может быть сделана меньше любого числа δ > 0, в то время как
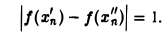
Тем самым, существует ε > 0 (например, ε = 1/2 ) такое, что при любом δ > 0 найдутся точки х’n и х»п из (0, 1) такие, что | х’n — х»п |< δ, но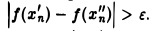 
Следовательно, функция f(x) = 
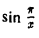не является равномерно непрерывной на интервале (0, I).
Пример:
Функция f(x) = 1/x непрерывна на интервале (0, 1), но не является равномерно непрерывной на этом интервале.
Пусть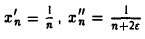 
( ε > 0 — любое). Тогда величина
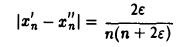
при достаточно большом п может быть сделана меньше любого δ > 0. Вместе с тем, |f(х’n) -f(x»n)| = 2ε > ε. Следовательно, функция f(х) = 1/x не является равномерно непрерывной на интервале (0, I).
Тем более интересно, что если функция f(x) непрерывна на отрезке [а, b], то она на этом отрезке обладает свойством равномерной непрерывности.
Теорема Кантора:
Если функция f(x) непрерывна на отрезке [а, b], то она равномерно непрерывна на этом отрезке.
Сравнение бесконечно малых функций
Пусть а(х) и β(х) — б. м. ф. при х → хо.
Определение:
Если
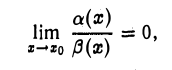
то а(х) называется б. м. более высокого порядка, чем β(х) и пишут а(х) = o ( β(х)), х → хо (читается «альфа равно о-малое от бета»). Символ о( β (х)), х → хо, означает любую б. м.ф., имеющую в точке х0 более высокий порядок малости, чем б. м. в этой точке функция β(х).
Пример:
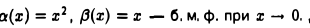
Для них
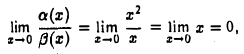
так что х2 = о(х), х → 0.
Определение:
Если
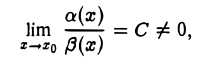
то a(z) и β(x) называют бесконечно малыми функциями одного порядка.
Так, a(x) = 2х, β(х) = х, х → 0, — б. м. ф. одного порядка, поскольку
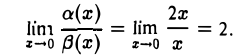
lim -тт-f = lim — = 2. х-0 р(х) г-0 X
Определение:
Говорят, что б. м. при х → хо функции а(х) и β(х) не сравнимы, если отношение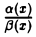 
при х —> хо не имеет предела, ни конечного, ни бесконечного.
Например, б. м. при х → 0 функции а(х) = xsin \ и /3(х) = х не сравнимы, поскольку их отношение 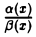= sin 1/x не имеет конечного предела в точке х = 0 и не является б. б. ф. при х → 0.
Определение:
Говорят, что б. м. при х → 0 функция а(х) имеет порядок малости т ∈ N относительно основной б. м. при х → хо функции w(х) = х — хо, если
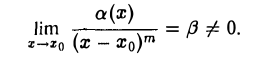
Например, функция а(х) = 3 sin2 х, б. м. при х 0, имеет порядок малости т = 2 относительно б. м. при х → 0 функции и(х) = х, так как
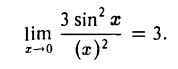
Эквивалентные бесконечно малые функции
Определение:
Две бесконечно малые при х → хо функции а(х) и β(х) называются эквивалентными, если предел их отношения в точке хо равен единице:
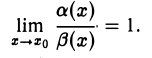
Эквивалентные б. м. ф. представляют частный случай б. м. одного порядка. Эквивалентность б. м. ф. а(х) и β(х) обозначается так:
а(х) ~ β(х), х → хо.
Про эквивалентные б. м. ф. а(х) и β(х) говорят также, что они равны асимптотически при х → xo.
Замечание:
Пусть a(х), β(х) и γ(x) — б. м.ф. при х — ю. Нетрудно видеть, что
1) а(х) ~ а(х), х → xo,
2) если а(х) ~ β{х), то β(х) ~ a(х), х → xo;
3) если а(х) ~ β(х), а β(х) ~ γ(1), то а(х) ~ γ(1), х → хо,
так что отношение эквивалентности обладает свойством рефлексивности, симметричности и транзитивности.
Приведем примеры эквивалентных бесконечно малых функций. В свое время мы установили, что
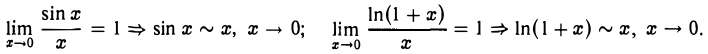
Нетрудно показать, что
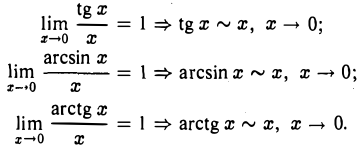
Докажем, что
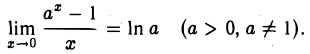
Положим аx — 1= y. Отсюда аx = 1 + у, х =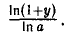 
. Ясно, что у → 0 при х → 0. Следовательно,
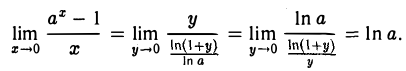
Поэтому аx — 1 ~ х ln а, х —» 0. В частности, при а = е получаем
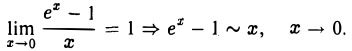
Докажем, что
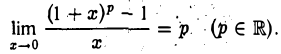
Положим (1 + х)р — 1 = у. Тогда (1 + х)р — 1 + у, откуда
Ясно, что y → 0 при х → 0. Используя равенство (1), получим
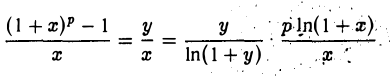
Переходя к пределу при х → 0 (у → 0), найдем
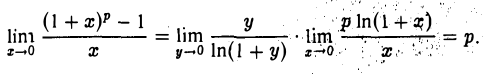
Итак,
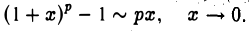
Таблица эквивалентных бесконечно малых функций (асимптотических равенств)
(2)
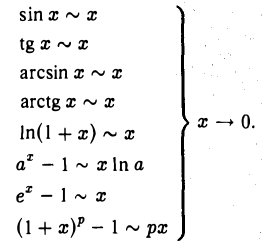
Определение:
Если для функции f(x) можно подобрать числа а и т, а ≠ 0, т ∈ N, такие, что f(х) ~ axm, х → 0, то говорят, что функция axm есть главный степенной член функции f(х) при х → 0.
Правые части написанных выше асимптотических равенств есть главные степенные члены левых частей.
Теорема:
Замена б.м.ф. эквивалентными. Пусть а(х), β(х), а1(х), β1(х) — бесконечно малые при х → xо функции, причем а(х) ~ a1(x), β(х) ~ β1(х). Если в точке xо отношение 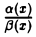имеет конечный или бесконечный предел, то он не изменится при замене а(х) на a1(х) и β(х) на β1(х).
Представим отношение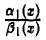 
в виде
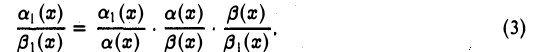
По условию
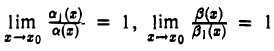
Если отношение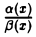 в точке x0 имеет предел А, то, воспользовавшись теоремой о пределе произведения, из (3) будем иметь
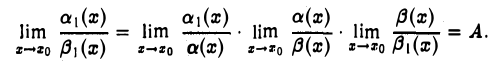
Если же 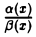бесконечно большая функция при х → xо, то вся правая часть равенства (3) и, значит, 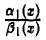также будет б. б. ф. при х → x0.
Пример:
Вычислить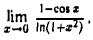 
Пользуясь теоремой о замене б.м.ф. им эквивалентными и таблицей (2), получаем
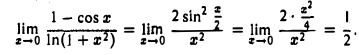
Теорема:
Условие эквивалентности. Для того, чтобы две бесконечно малые при х —> xо функции а(х) и β(х) были эквивалентными, необходимо и достаточно, чтобы их разность при х —> хо была бы б. м. ф. более высокого порядка, чем они сами.
Необходимость. Пусть а(х) и β(х) — эквивалентные б. м. ф. при х → x0. Докажем, что их разность
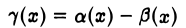
(б. м. ф. при x → x0) является б. м. более высокого порядка, чем β(x), а, следовательно, и а(x). Действительно, по условию а(x) ~ β(x), x → xо, и значит
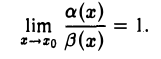
Отсюда
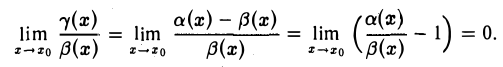
Это означает, что при x → x0 б. м. ф. γ(х) есть б. м. более высокого порядка, чем β(х). Достаточность, Пусть разность
γ(x) = а(x) — β(x)
функций а(x) и р(х), б. м. при x —> x0, есть б. м. ф. более высокого порядка, чем β(x) (или а(x)). Докажем, что а(x) ~ β(x), x → x0. По условию
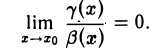
Отсюда
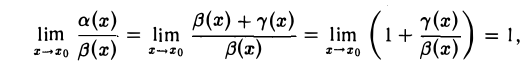
что означает эквивалентность б. м. ф. а(x) и β(х) при x → x0.
Пример:
Функции а(х) = х+2х1 и β(х) = х есть б. м. ф. при х0. Их разность γ(1) = 2х3 при х → 0 является б. м. более высокого порядка, чем а(х) и β(х). Следовательно, a(z) ~ β(х), х → 0.
Символы о и О (символы Ландау)
Пусть функции f(х) и φ(x) определены в некоторой окрестности Ω точки хо, кроме, быть может, самой точки хо, и пусть в некоторой окрестности Ωо точки хо, х ≠ хо, φ(х) ≠ 0 (здесь точка хо может быть конечной и бесконечной). Говорят, что f(х) есть о-малое от φ(х) и пишут
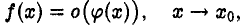
если
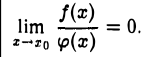
Соотношение f(x) = о( φ(х)), х → хо, означает таким образом, что функция f(х) есть бесконечно малая по сравнению с φ (х) при х → хо. В частности, соотношение f(х) = о(1), х → хо, означает, что f(х) — бесконечно малая функция при х → xo.
Примеры:
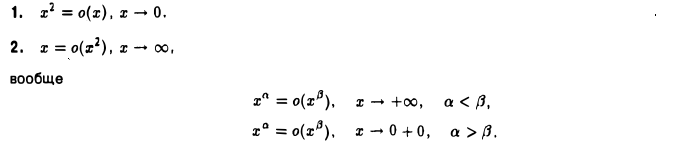
Говорят, что f(х) есть О-большое от φ(х) при х → х0, х ∈ Ω, и пишут
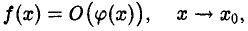
если существует число М > 0 и окрестность Ω0 точки xo такие, что
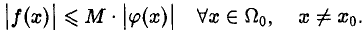
Соотношение f(х) = 0(1), х → хо, означает, что f(x) ограничена в окрестности точки xo.
Примеры:
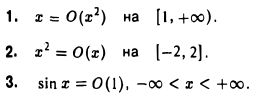
Использование знака равенства в рассматриваемой ситуации является чисто условным, так как некоторые свойства знака равенства не сохраняются. Например, из «равенства»
не следует, что 0(1) = sin х.
Справедливы следующие формулы:
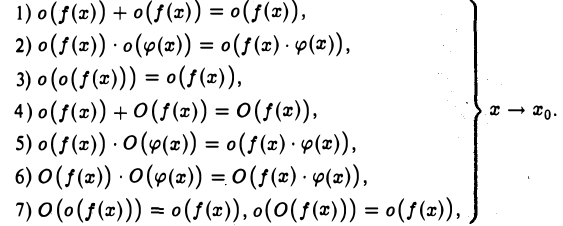
Напомним, что если
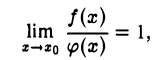
то функции f(x) и φ(x) называют эквивалентными или асимптотически равными при х → х0 и пишут f(х) ~ φ(х), х → Х0.
Пользуясь таблицей (2) эквивалентных б. м. ф. и теоремой 25, получаем асимптотические формулы
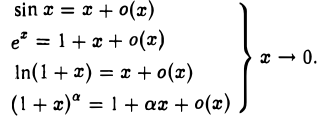
Всю группу соотношений f(x) ~ φ{х), f{х) = о(φ(х)), f(x) = O(φ{х)), х → х0, называют асимптотическими формулами или асимптотическими оценками.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
