Матрицы в математике с примерами решения и образцами выполнения

Понятие матрицы имеет большое значение. Объясняется это тем. что многие математические модели процессов и состояний в технике записываются в простой и компактной матричной форме.

Матрицей называется прямоугольная таблица чисел, переменных, функций, или других математических объектов. Эти математические объекты (числа, переменные и т.д.) называются элементами матрицы и в общем виде снабжаются двойной индексацией для обозначения места элемента в матрице.

Матрица обозначается круглыми скобками по бокам таблицы. Матрицы также обозначают большими латинскими буквами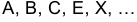

Примеры матриц:

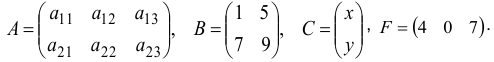
Здесь показаны различные типы матриц. Матрица 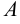— прямоугольная, размерностью (2×3), первая цифра указывает количество строк, вторая цифра — количество столбцов.

Матрица 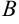— квадратная, у неё число строк равно числу столбцов.

Матрица состоит из одного столбца (матрица-столбец), матрица состоит из одной строки (матрица-строка).

Различают также диагональные матрицы — квадратные матрицы, у которых все элементы, кроме элементов, стоящих в главной диагонали, равны нулю.

Единичные матрицы — диагональные матрицы, у которых в главной диагонали стоят единицы. Например,

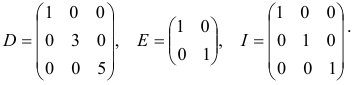
Здесь — диагональная матрица; 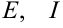— единичные матрицы разной размерности.

Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:

Высшая математика для 1 курса

Возможно вам будут полезны эти страницы:

Операции с матрицами: определения и пример с решением

Определители 2 и 3 порядков, вычисление, свойства

Основные свойства и приложения двойного интеграла

Вычисление двойного интеграла в декартовых координатах

Матрицы

Терминология и обозначения:

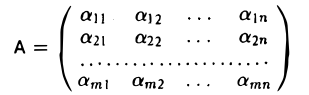
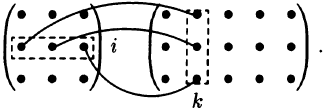
Матрицей А размера m х n называется набор m • n чисел — элементов матрицы

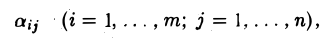
записанных в виде прямоугольной таблицы (1)

или

Символ a_ij читается так: «альфа-и-жи». Набор

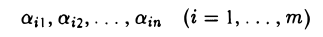
называется i-й строкой матрицы А:

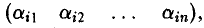
а набор

называется j-м столбцом матрицы А:

Таким образом, данная матрица А имеет m строк и n столбцов, а элемент a_ij расположен в i-й строке и в j-м столбце матрицы А — в позиции (i, j) (рис. 1). Числа i и j определяют расположение элемента a_ij в матрице А и являются как бы координатами этого элемента в прямоугольной таблице А.

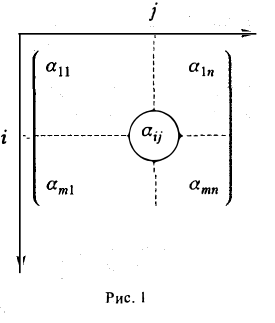
Если размер матрицы известен, то часто пишут кратко

А = (a_ij)

Матрица размера 1 х n называется просто строкой, а матрица размера m х 1 — столбцом. В случае m = n матрица

называется квадратной матрицей порядка n. В частности, квадратной матрицей первого порядка является одноэлементная матрица А = ( a₁₁ ). Набор элементов

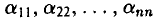
образует главную диагональ матрицы А.

Матрица, все элементы которой равны нулю, называется нулевой, а квадратная матрица, на главной диагонали которой стоят единицы, а все остальные элементы равны нулю, (2)

называется единичной. Подчеркнем, что для каждого размера m х n существует своя нулевая матрица, а для каждого числа n — своя единичная матрица порядка n.

Множество всех матриц размера m х n часто обозначают через R_mxn. Введенное обозначение требует дополнительных пояснений (для определенности мы ограничиваемся здесь рассмотрением только матриц, элементами которых являются вещественные числа). Множество вещественных чисел принято обозначать через R. Отсюда и символ K_mxn (множество матриц размера m х n, элементами которых являются комплексные числа, принято обозначать так: C_mxn см. главу XXV). С учетом этого обозначения матрицу (1) можно записать так

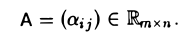
Матрицы А = (a_ij) и В = (β_ij ) называются равными, если они имеют одинаковый размер и их элементы, находящиеся в одинаковых позициях, совпадают, т. е.

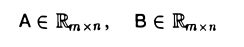
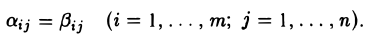
Обозначение: А = В.

Операции над матрицами

Сложение матриц

Пусть А и В — матрицы одного размера:

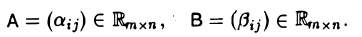
Суммой матриц А и В называется матрица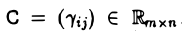 элементы которой вычисляются по формуле (3)

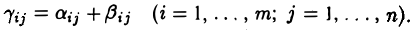
Обозначение: С = A + В.

Умножение матрицы на число

Произведением матрицы 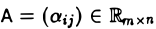на число λ называется матрица В = ( β_ij) ∈ R_mxn , элементы которой вычисляются по формуле (4)

Обозначение: В = λ А.

Запишем эти операции подробнее:

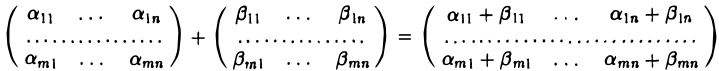
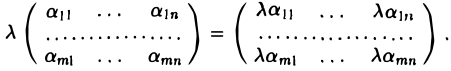
Линейное пространство строк

Рассмотрим введенные операции сложения и умножения не число на множестве матриц размера 1 х п — п-мерных строках. Пусть

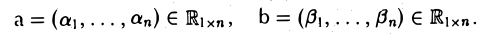
Тогда, согласно формулам (3) и (4), (5)

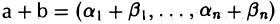
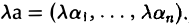
(6)
Правила (5) и (6) обладают легко проверяемыми свойствам (7)

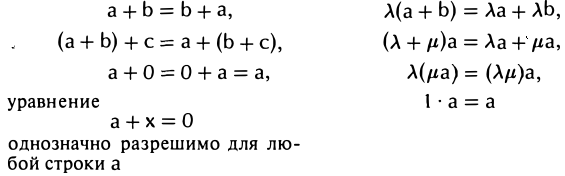
(здесь λ и μ — произвольные числа; а, b, с и х — n-мерные строки, 0 — нулевая п-мерная строка) и задают на множестве n-строк структуру линейного пространства.

Линейная зависимость

Введем важное понятие линейной зависимости. Пусть а1…, am — n-мерные строки. Строка b, определяемая равенством (8)

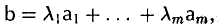
называется линейной комбинацией строк al,…, am с коэффициентами λl …, λm. Линейная комбинация (8) называется нетривиальной, если хотя бы одно из чисел λl,…, λm отлично от нуля, и тривиальной, если λm = … = λm = 0 (ясно, что в последнем случае b — нулевая строка). Строки называются линейно зависимыми, если некоторая их нетривиальная линейная комбинация равна нулевой строке 0. Строки называются линейно независимыми, если нулевой строке равна только их тривиальная линейная комбинация.

Покажем, что
если строки линейно зависимы, то одна из них является линейной комбинацией остальных.

Пусть строки al,…, аm линейно зависимы: найдутся числа λl,…, λm, не все равные нулю и такие, что

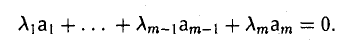
Пусть, например, λm ≠ 0. Перенесем все слагаемые, кроме последнего, из левой части формулы в правую,

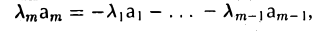
и, поделив обе части полученного равенства на λm ≠ 0, придем к тому, что строка аm является линейной комбинацией остальных строк —

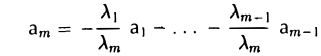
Верно и обратное: если одна из строк является линейной комбинацией остальных, например,

то существует нетривиальная линейная комбинация строк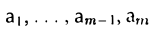

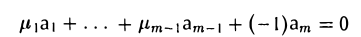
(коэффициент при аm равен — 1 ≠ 0), равная нулевой строке. Значит, эти строки линейно зависимы.

Аналогичными: свойствами обладает множество R_mxl m-мерных столбцов.
Общее определение линейного пространства будет рассмотрено в главе V.

Правило сокращенного суммирования

Сумму вида

часто удобно записывать так

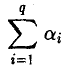
(знак сокращенного суммирования принято обозначать прописной греческой буквой Σ — «сигма»).

Умножение матриц

Пусть А = (a_ik) и В = (β_kj) — квадратные матрицы порядка n. Произведением матрицы А на матрицу В называется матрица

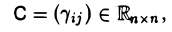
элементы которой вычисляются по формуле
(9)

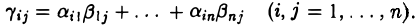
Обозначение: С = АВ.

Правило (9) можно проиллюстрировать следующей схемой

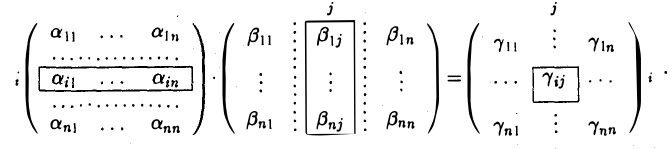
С использованием знака сокращенного суммирования формула (9) записывается так:

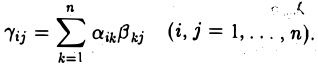
Порядок матриц-сомножителей существен.

Следующий пример показывает, что, вообще говоря, АВ ≠ ВА. Пример 1. Пусть

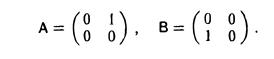
Тогда

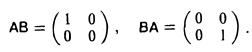
Аналогичные примеры можно построить для матриц А и В любого порядка.

Пример:

Пусть А — матрица третьего порядка

Покажем, что умножение матрицы А на матрицу

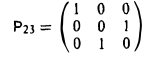
слева меняет местами 2-ю и 3-ю строки. Имеем

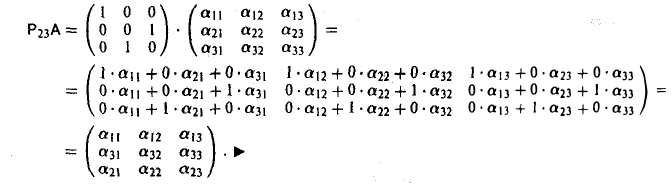
Аналогично можно убедиться в том, что умножение матрицы А на матрицу Р₂₃ справа меняет местами 2-й и 3-й столбцы.

Пример:

Для любой матрицы А выполняются равенства (10)

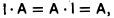
где I — единичная матрица.
Пусть, например,
А — матрица третьего порядка

Тогда

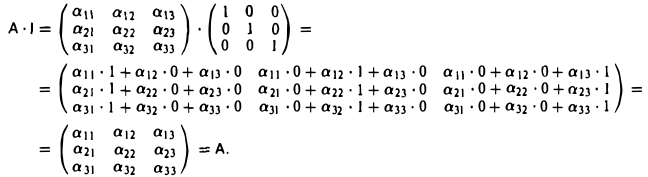
Справедливость равенства
проверяется аналогично.

I • А = А

Доказанные формулы (10) объясняют название матрицы I. Умножение матриц обладает следующими свойствами.

Если А, В, С, D — квадратные матрицы (n-го порядка), то

А. (АВ)С = А(ВС),

Б. А(В+С) = АВ + АС, (В +C)D = BD + CD.

Докажем, например, первую из формул Б.

Нетрудно видеть, что все три матрицы АВ, АС и А(В + С) имеют одинаковый порядок п. Вычисляя их элементы в позиции (i, j), получаем соответственно

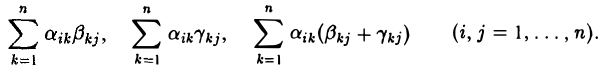
Ясно, что

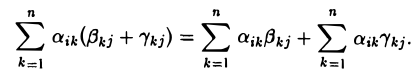
Требуемое равенство доказано.

Похожими рассуждениями доказываются и две другие формулы.

Замечание:

Операцию умножения можно определить и для прямоугольных матриц.
Пусть даны матрицы

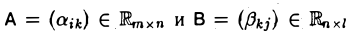
Тогда элементы 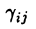матрицы 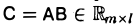вычисляются по формуле (11)

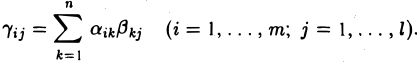
Произведение двух прямоугольных матриц существует не всегда: для того чтобы матрицу А можно было умножить на матрицу В, необходимо, чтобы число столбцов матрицы А совпадало с числом строк матрицы В (см. формулу (11) и рис. 2).

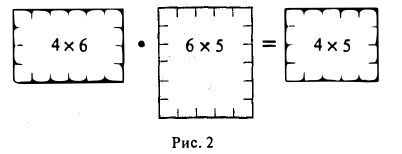
Для прямоугольных матриц справедливы формулы (10), А и Б (при условии, разумеется, что соответствующие произведения имеют смысл).

Пример:

Найти произведение матрицы

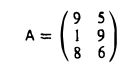
на матрицу

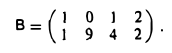
Прежде всего, проверяем, что число столбцов матрицы А (два) совпадает с числом строк матрицы В (две). Значит, умножать матрицу А на матрицу В можно. Вычислим это произведение. Имеем

О порядке суммирования

Сумму Н всех элементов прямоугольной матрицы

можно вычислить двумя способами:

1-й способ. Найдем суммы элементов каждого столбца

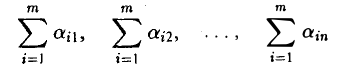
и сложим полученные числа:

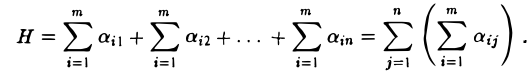
2-й способ. Найдем суммы элементов каждой строки

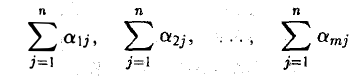
и сложим полученные числа:

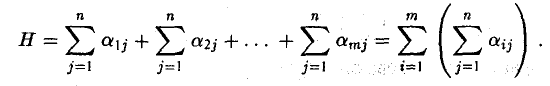
Отсюда вытекает, что

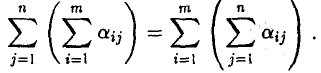
Транспонирование матрицы

Матрица

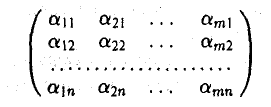
называется транспонированной по отношению к матрице

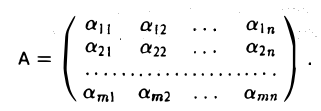
Обозначение: А^Т.

Пример:

Транспонировав матрицу

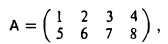
согласно определению, получим

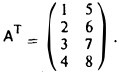
Подчеркнем, что элемент матрицы А^Т, находящийся в позиции (j, i), совпадает с элементом матрицы А, находящимся в позиции (i, j). При транспонировании строки матрицы А переходят в столбцы матрицы А^Т , а столбцы — в строки. Таким образом, если у матрицы А m строк и n столбцов, то у транспонированной матрицы А^Т n строки m столбцов.
Укажем некоторые свойства операции транспонирования:

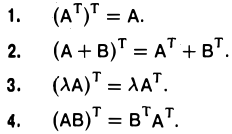
Элементарные преобразования матрицы

Пусть А и — произвольные матрицы одинакового размера m х n. Обозначим последовательные строки матрицы А через

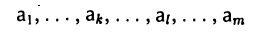
соответственно.

Будем говорить, что матрица 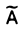получена из матрицы А

1.перестановкой двух строк, если 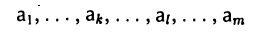— последовательные строки матрицы ;

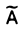2. умножением строки на не равное нулю число β, еcли — последовательные строки матрицы ;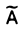

3. прибавлением к строке матрицы А другой ее строки, умноженной на числом, если 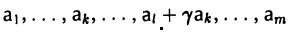— последовательные строки матрицы .

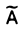Замечание:

Во всех трех типах преобразований отмеченные многоточием строки не претерпевают никаких изменений.

Преобразования указанных трех типов называются элементарными преобразованиями строк матрицы А. Аналогично определяются элементарные преобразования столбцов матрицы.

Пример:

Матрица

получена из матрицы

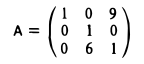
перестановкой 2-й и 3-й строк, а матрица

получена из матрицы А перестановкой 1-го и 2-го столбцов.

Если к 1-й строке матрицы А прибавить 3-ю, умноженную на -2, то получим матрицу

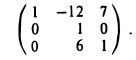
Замечание:

Нетрудно увидеть, что если матрица 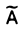получена из матрицы А элементарным преобразованием строк любого из трех типов, то и матрицу А можно получить из матрицы 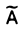элементарным преобразованием строк, причем того же типа (либо вновь меняя местами k-ю и l-ю строки, либо умножая k-ю строку на ‘/ β, либо прибавляя к l-Й строке k—ю строку, умноженную на — λ).

Основной процесс:

Опишем метод, который позволяет при помощи элементарных преобразований строк приводить произвольную матрицу к матрице более простого вида.

Пусть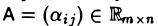 — ненулевая матрица.

1-й шаг. То, что матрица А — ненулевая, означает, что в ней есть хотя бы один элемент, не равный нулю. Так как он расположен в какой-то строке, то в матрице А есть ненулевые строки. Выберем ту из них, в которой первый отличный от нуля элемент расположен в столбце с наименьшим номером k1 ≥ 1. Применив к матрице А преобразование 1-го типа, переставим эту строку на место первой строки. В результате этого преобразования матрица А переходит в матрицу

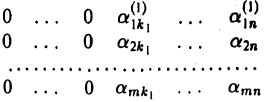
где .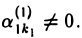

Покажем теперь, как добиться того, чтобы все элементы k1 -го столбца матрицы (12), кроме первого его элемента 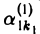, оказались равными нулю.

Если к i-й строке матрицы (12) (i = 2,… ,m) прибавить первую строку, умноженную на

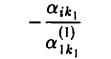
(это преобразование 3-го типа), то в результате получим матрицу, у которой элемент в позиции (i, k1) будет равен нулю. Проведя эту операцию с каждой из строк, содержащих ненулевые элементы в k1 -м столбце, приходим к матрице вида
(13)

Конец 1-го шага.

В дальнейших преобразованиях первая строка не участвует.

Возможны два случая:

1. Все строки матрицы (13), кроме первой, нулевые. В этом случае считаем процесс преобразований завершенным.
2. У матрицы (13) есть ненулевые строки, кроме первой.

2-й шаг. Выберем ту из них, в которой первый ненулевой элемент располагается в столбце с наименьшим номером, например, k2 (вследствие специального выбора строки на первом шаге и выполненных выше преобразований k1< k2). Применив к матрице (13) преобразование первого типа, переставим эту строку на место второй строки. Имеем (14)

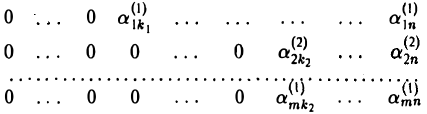
где 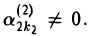Прибавляя к i-й строке (i = 3,…, m) матрицы (14) вторую строку, умноженную на

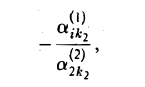
далее действуем по той же схеме, что и при первом шаге. Конец 2-го шага.

В общем случае может возникнуть необходимость 3-го и последующих шагов. Однако суммарное число шагов не превосходит min(m,n). Поэтому обязательно наступит момент, когда процесс преобразований завершится, и мы получим матрицу следующего ступенчатого вида —
(15)

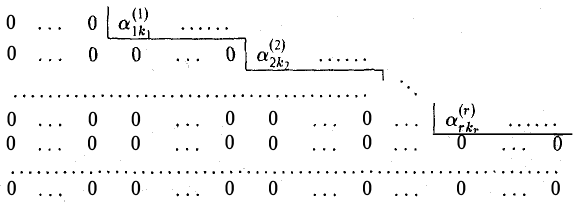
где 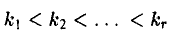и

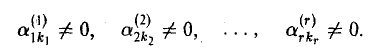
Матрица вида (15) называется ступенчатой. Тем самым, доказано следующее утверждение.

Теорема:

Любую матрицу можно привести к ступенчатой матрице при помощи конечного числа элементарных преобразований строк (1 -го и 3-го типов).

Пример:

Привести матрицу

к матрице ступенчатого вида.

Поменяем местами 1-ю и 4-ю строки матрицы А:

Поменяем местами 3-ю и 4-ю строки матрицы А1.

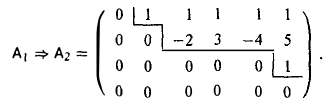
Матрица А2 — ступенчатая.

Пример:

Привести матрицу

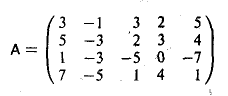
к ступенчатой.

Поменяем местами первую и третью строки

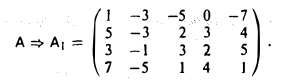
1-й шаг. Вычитаем из второй, третьей и четвертой строк первую строку, умноженную соответственно на числа 5, 3 и 7. Тогда

2-й шаг. Для простоты последующих вычислений воспользуемся элементарным преобразованием строк 2-го типа (хотя они и не использовались в описанном выше процессе, но их применение часто упрощает вычисления): умножим вторую строку на 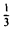, третью — на 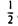, четвертую — на 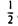. Тогда

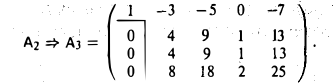
Вычитаем из третьей и четвертой строк вторую строку, умноженную на 1 и 2 соответственно. Тогда

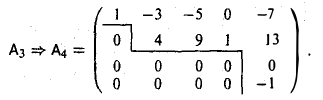
3-й шаг. Замечая, что третья строка нулевая, переставим ее с четвертой. Тогда

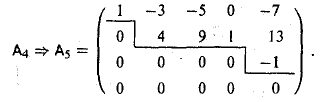
Полученная матрица А5 является ступенчатой.
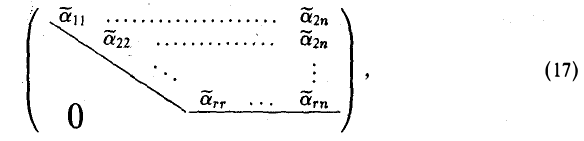
Ступенчатую матрицу при помоши элементарных преобразований ее столбцов можно привести к матрице, имеющей еще более простой вид (16)

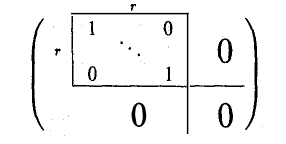
(все элементы матрицы, кроме единиц, стоящих в позициях (l, 1), (2,2), (r, r) равны нулю).

Путем перестановки в матрице (15) столбцов с номерами 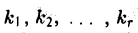на места первого, второго, …, r-го столбцов соответственно (это преобразования 1-го типа) получаем трапециевидную матрицу

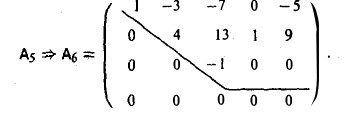
Пример:

Например, переставляя 3-й и 5-й столбцы матрицы А5, получаем, что

Прибавляя к j-му столбцу матрицы (17) первый столбец, умноженный на

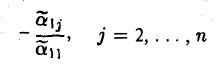
(преобразования 3-го типа), получим в результате всех таких преобразований матрицу, первая строка которой содержит только один ненулевой элемент — :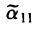

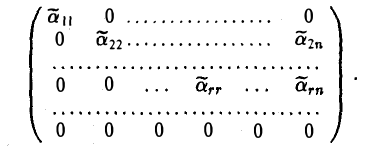
Упрощая аналогично 2-ю, 3-ю, …, r-ю строки, в итоге получим

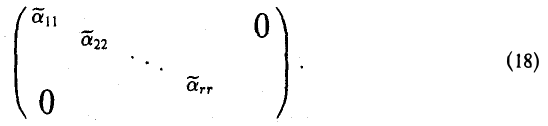
К виду (16) матрица (18) приводится элементарными преобразованиями 2-го типа.

Пример:

Подвергая матрицу Аб таким преобразованиям, приходим к матрице

и, далее,

Матрицы элементарных преобразований

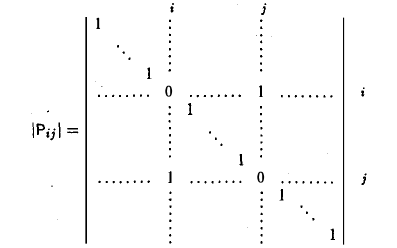
С элементарными преобразованиями тесно связаны квадратные матрицы — матрицы элементарных преобразований. Так называются матрицы следующих трех типов.

1-й тип. Матрицы, получающиеся из единичной матрицы перестановкой любых двух строк. Например, матрица

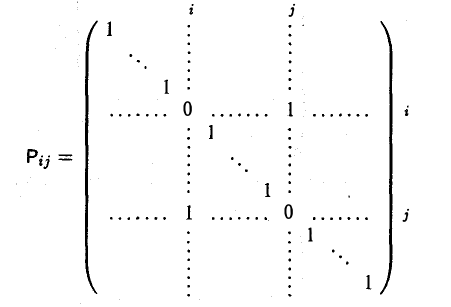
получена из единичной матрицы

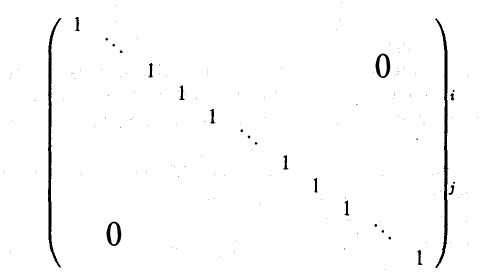
перестановкой i-й и j-й строк (в матрице все элементы вне главной диагонали кроме тех, которые располагаются в позициях (i, j) и (j, i), равны нулю).

2-й тип. Матрицы, получающиеся из единичной заменой диагонального элемента на произвольное не равное нулю число. Например, матрица

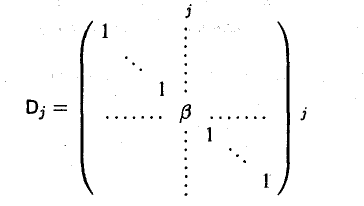
отличается от единичной матрицы лишь элементом β ≠ 0 в позиции (j, j) (в матрице Dj все элементы вне главной диагонали равны нулю).

3-й тип. Матрицы, отличающиеся от единичной матрицы лишь одним внедиаго-нальным элементом. Например, матрица

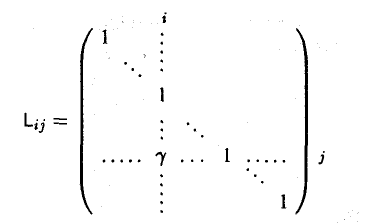
отличается от единичной лишь элементом γ в позиции (i, j), а матрица

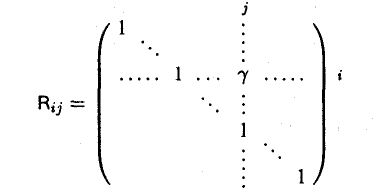
отличается от единичной тоже элементом γ, но в позиции (j, i) (все другие внедиаго-нальные элементы матриц L_ij и R_ij , кроме указанных, равны нулю).

Сформулируем основное свойство матриц элементарных преобразований.
Теорема:

Элементарные преобразования произвольной матрицы равносильны умножению этой матрицы на матрицы элементарных преобразований:

А. Элементарные преобразования строк матрицы А —

1. Умножение матрицы А на матрицу Р _ij — слева переставляет строки с номерами i и j.
2. Умножение матрицы А на матрицу D _j — слева равносильно умножению j-й строки матрицы А на число β.
3. Прибавление к j-й строке матрицы А ее i-й строки, умноженной на число γ, равносильно умножению матрицы А на матрицу L_ij слева.

Б. Элементарные преобразования столбцов матрицы А —

1. Умножение матрицы А на матрицу Р_ij справа переставляет столбцы с номерами i и j.
2. Умножение матрицы А на матрицу D_j — справа равносильно умножению j -го столбца матрицы А на число β.
3. Прибавление к j -му столбцу матрицы А ее i-го столбца, умноженного на число γ, равносильно умножению матрицы А на матрицу R_ij справа.
   

Для простоты ограничимся случаем m = n = 3. Пусть А — квадратная матрица третьего порядка

1. В п. 1.4 («Умножение матриц») было показано (см. пример 2), что при умножении матрицы А на матрицу

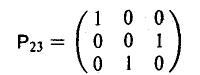
слева получается матрица

приумножении А на Р₂₃ справа — матрица

Нетрудно заметить, что матрица В отличается от матрицы А порядком строк, а матрица С — порядком столбцов.

Аналогично проверяется справедливость свойства 1 для матриц Р₁₂ и P₁₃ —

2. Умножим матрицу А на

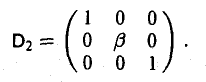
Имеем:

а) приумножении слева

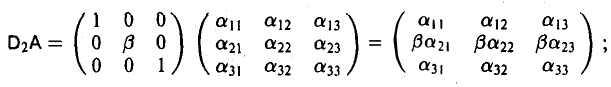
б) при умножении справа

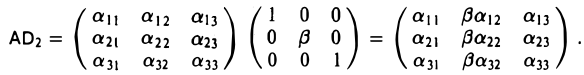
Аналогично проверяется справедливость свойства 2 для матриц D1 и D3. Подобным же образом можно убедиться в справедливости свойства 3.

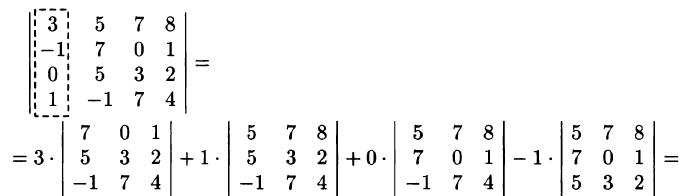
Определители

Свяжем с каждой квадратной матрицей число — определитель матрицы — по следующему правилу.

Будем считать, что определитель матрицы

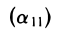
первого порядка равен числу .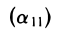

Определителем матрицы второго порядка

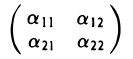
называется число, равное .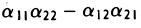

Обозначение:
(1)

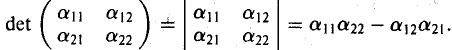
Определителем матрицы третьего порядка

называется число, равное

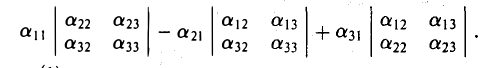
С учетом формулы (1) получаем:

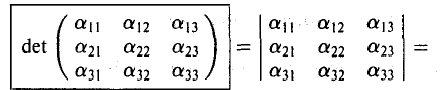
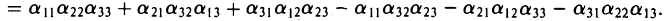
Формулу (2) легче запомнить, если воспользоваться двумя правилами для построения слагаемых определителя, символически описанными на рисунке 4. На левом рисунке показано, как выбирать сомножители первых трех слагаемых определителя, а на правом — трех последних.

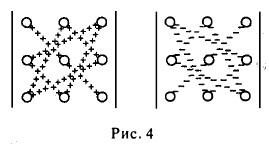
Предположим теперь, что определители матриц, порядок которых меньше n, уже введены. Определителем матрицы n-го порядка

называется число, равное
(4)

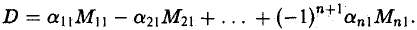
Здесь Mil (i = l,… , n) — определитель матрицы порядка n — 1:

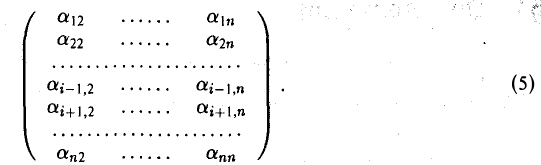
Матрица (5) получена из матрицы А путем вычеркивания первого столбца и i-й строки.
Обозначение:
(6)

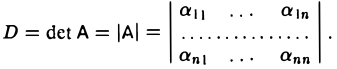
Формула (4) называется разложением определителя по первому столбцу. Нетрудно проверить непосредственно, что при n = 2 и n = 3 эта формула дает те же числа, что и формулы (1) и (2) соответственно. Например, при n = 3 имеем

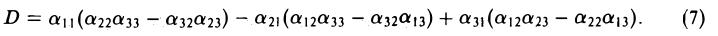
Формула (4) допускает сокращенную запись
(8)

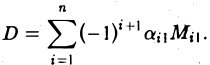
Пример:

Вычислим определитель треугольной матрицы

Имеем

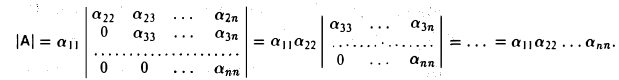
Таким образом,

определитель треугольной матрицы (матрицы треугольного вида) равен произведению ее элементов, стоящих на главной диагонали.

Обратимся к общей ситуации. Пусть теперь i и j — произвольные числа из набора 1,2, … , n — 1, n. Определитель матрицы порядка n — 1, которая получается из матрицы А вычеркиванием элементов i-й строки и j-го столбца, называется дополнительным минором элемента a_ij и обозначается через (рис.5). Таким образом, M_ij — дополнительный минор элемента a_il.

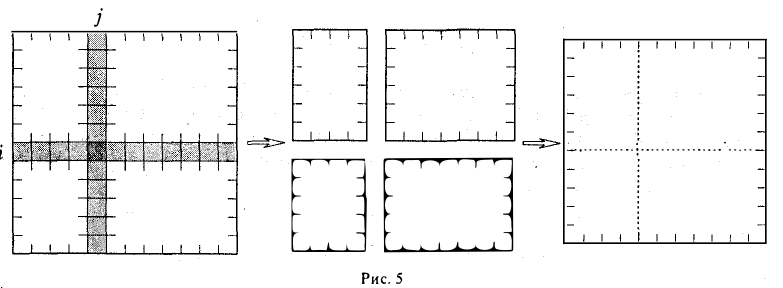
По аналогии с формулой (8) введем числа D_j
(9)

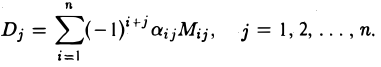
Покажем, что все числа D = D1,D2…., Dn равны между собой.

Для простоты ограничимся рассмотрением случая n = 3. Тогда из формул (9) при j = 2 получаем

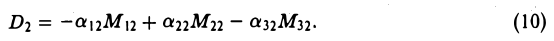
Каждый минор М₁₂ (i = 1, 2, 3) является определителем второго порядка —

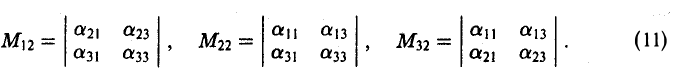
Вычислим определители (11) в соответствии с правилом (1) и, подставляя результаты

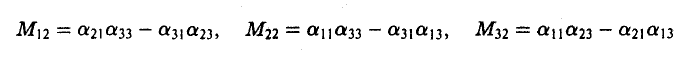
в формулу (10), получим, что

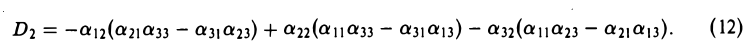
Сравнивая правые части соотношений (7) и (12), убеждаемся в том, что D = D2. Подобным же образом проверяется равенство D = D3.

Замечание:

Равенства D = D1 = …= Dn в общем случае также доказываются путем сведения к вычислению определителей меньшего порядка ((n — 1)-гои (n — 2)-го).
Таким образом, доказана формула
(13)

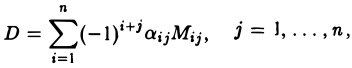
коротко называемая разложением определителя по j -му столбцу. Придадим полученному результату несколько иной вид. Число
(14)

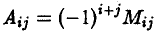
называется алгебраическим дополнением элемента a_ij в определителе |А|. Заметим, что алгебраическое дополнение А_ij элемента a_ij зависит только от его позиции (t, j) в матрице А. При замене элемента a_ij матрицы на любое другое число алгебраическое дополнение не изменяется. С учетом обозначения (14) формулу (13) можно записать в следующем виде:
(15)

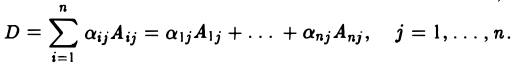
Тем самым, показано, что
определитель квадратной матрицы равен сумме попарных произведений элементов произвольного столбца на их алгебраические дополнения.

По аналогии с формулами (9) вводятся числа (16)

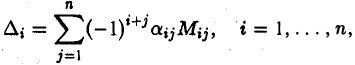
также равные между собой. Чтобы убедиться в этом, достаточно, поменяв ролями строки и столбцы, дословно повторить предыдущие рассуждения. Имеет место следующий замечательный факт.

Теорема:

Для любого i = 1…..n

Иными словами, справедливо разложение определителя по i-й строке.

Достаточно убедиться в том, что (18)

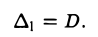
Вновь ограничимся случаем n = 3. Согласно правилу (16), имеем

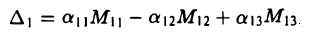
и далее

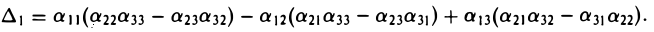
Сравнивая полученный результат с формулой (7), убеждаемся в справедливости требуемого равенства (18).

Замечание:

В общем случае равенство 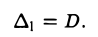также доказывается путем сведения к вычислению определителей меньшего порядка ((n — 1)-го и (n — 2)-то).

С учетом обозначения (14) полученный результат можно записать следующим образом:

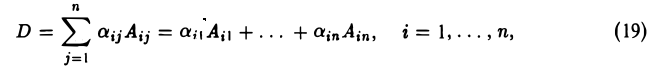
— определитель квадратной матрицы равен сумме попарных произведений элементов произвольной строки на их алгебраические дополнения.

Пример:

Вычислим определители матриц элементарных преобразований.

Раскладывая определитель матрицы Р_ij.

по 1-й строке и затем повторяя эту операцию достаточное число раз (n — 2), придем в результате к следующей формуле

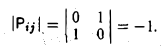
Так как матрица Dj элементарных преобразований 2-го типа имеет диагональный вид, то

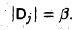
Для матрицы L_ij третьего Типа получаем

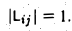
Свойства определителя

Линейность

Пусть в определителе D i-я строка является линейной комбинацией двух n-строк:

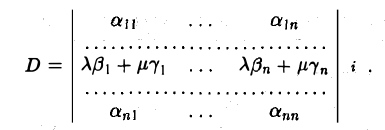
Тогда

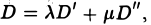
где определители

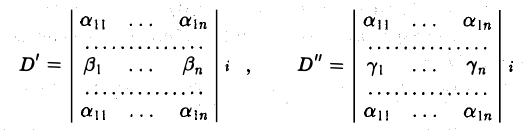
отличаются от определителя D только i -ми строками.

Чтобы убедиться в справедливости этого свойства, достаточно разложить определители D, D’ и D» по i-й строке. Так как алгебраические дополнения А_ij элементов i-й строки у всех трех определителей одинаковы, то согласно формуле (19) имеем

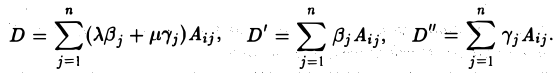
Отсюда следует, что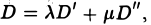

Антисимметричность

Если определитель 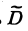получен из определителя D перестановкой двух строк,

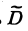= -D.

Предположим, что определитель 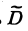получен из определителя D перестановкой первых двух строк:

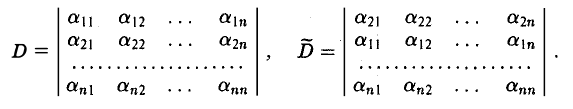
Разложим определитель D по второй строке, а определитель 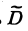— по первой строке. Согласно формуле (17) получим соответственно

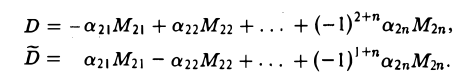
Нетрудно видеть, что 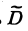= — D.

При перестановке любых двух строк определителя D доказательство проводится аналогично.

Транспонирование определителя

При транспонировании матрицы определитель не изменяется

|А^T| = |А|.

Это свойство непосредственно вытекает из доказанной выше теоремы: разложение определителя |А| по первой строке совпадает с разложением определителя | А^T | по первому столбцу.

Заметим, чтосвойства 1 и 2 справедливы и для столбцов (это следует из свойства 3).

Определитель произведения квадратных матриц

Определитель произведения квадратных матриц равен произведению определителей этих матриц, т. е. если А и В — квадратные матрицы одного порядка, то

|АВ| = |А| • |В|.

Сформулируем свойства определителя, удобные при практических вычислениях.

1. Определитель матрицы с двумя одинаковыми строками равен нулю.

В самом деле, при перестановке двух любых строк, согласно свойству 2, определитель должен изменить знак на противоположный; с другой стороны, при перестановке двух одинаковых строк определитель не меняется. Значит, D = -D, откуда вытекает, что D = 0.

2. Умножение строки определителя на число равносильно умножению самого определителя на это число.

Это вытекает из свойства 1 при μ = 0.

3. Определитель с нулевой строкой равен нулю.

Достаточно разложить определитель по нулевой строке.

4. Определитель, одна и з строк которого равна произведению другой его строки на число, равен нулю.

В силу свойства 2 множитель можно вынести за знак определителя, после чего остается определитель с двумя равными строками.

5. Если к строке определителя прибавить другую его строку, умноженную на любое число, то полученный определитель будет равен исходному.

Полученный определитель согласно свойству 1 равен сумме двух определителей — исходного и определителя, одна из строк которого равна произведению другой его строки на число.
Итог: определитель не изменится, если к любой его cmроке прибавить линейную комбинацию других строк определителя.

То же самое справедливо и для столбцов определителя.

Задача:

Доказать, что сумма произведений элементов строки определителя на алгебраические дополнения соответствующих элементов другой строки определителя равна нулю.

Заменим в определителе

элементы k-й строки соответствующими элементами i-й строки. Получим определитель

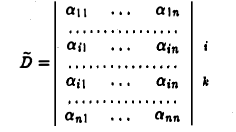
с двумя одинаковыми строками — i -й и k-й. Согласно свойству 1, 5 = 0.

Раскладывая определитель D по k-й строке, получим требуемое равенство

(напомним, что изменение элементов строки определителя не изменяет алгебраических дополнений этих элементов).

Вычисление определителя

Прежде чем обратиться к описанию вычисления определителя при помощи элементарных преобразований, отметим, что при преобразованиях первого типа определитель изменяет знак (свойство I), при преобразованиях второго типа определитель умножается на то же число (свойство 2), а при преобразованиях третьего типа определитель не изменяется.

Пример:

Вычислить определитель матрицы

Элемент а₁₁ ≠ 0. Не все элементы первого столбца делятся на а₁₁ нацело. Чтобы избежать деления элементов матрицы, умножим 2-ю строку на -2, 3-ю на -1 и четвертую на 2. Получим

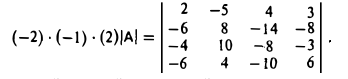
1-й шаг. Прибавляем ко второй, третьей и четвертой строкам первую строку, умноженную соответственно на 3, 2 и 3. Тогда

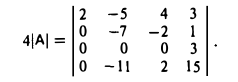
2-й шаг. Чтобы избежать деления, умножим последнюю строку на -7. Тогда

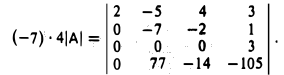
Прибавляя к четвертой строке вторую строку, умноженную на 11, получим

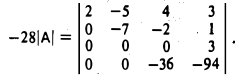
3-й шаг. Переставляем третью и четвертую строки:

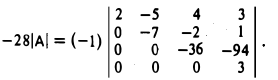
Вычисляя определитель полученной треугольной матрицы, имеем

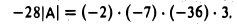
Отсюда окончательно получаем, что

|А| = 54.

Обратная матрица

Квадратная матрица называется невырожденной, если определитель этой матрицы не равен нулю.

Пусть А = (a_ij) — невырожденная матрица порядка n. Построим новую квадратную матрицу В порядка п по следующему правилу: в i -ю строку и j -й столбец матрицы В — в позицию (i, j) — помещается число, равное алгебраическому дополнению A_ij элемента a_ij матрицы А:

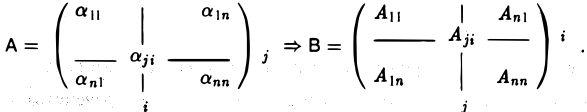
Матрица В обладает следующим важным свойством:
(1)

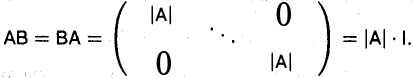
Докажем, например, равенство

АВ = |А| • I.

Элемент произведения АВ, находящийся в позиции (i, j) вычисляется по формуле

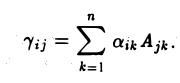
При i = j получаем разложение определителя матрицы А по i-й строке:

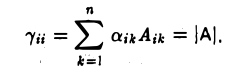
При i ≠ j согласно разобранной выше задаче

Равенство

ВА = |А| • I

обосновывается аналогично. Матрица

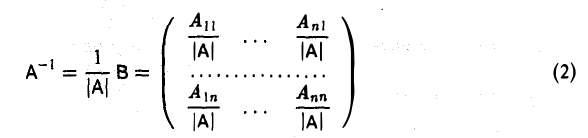
называется обратной к матрице А.

Из формулы (1) вытекают равенства
(3)

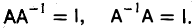
Это означает, что матрицу А 1 можно рассматривать как решение сразу двух матричных уравнений

АХ = I и ХА = I,

где

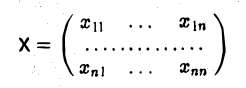
— неизвестная матрица.

Покажем, что других общих решений у этих матричных уравнений нет. < Предположим, что для некоторой матрицы С выполняются равенства

АС = I и СА = I.

Умножим обе части каждого из равенств на матрицу А-1: левого — слева, правого — справа. Получим

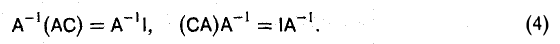
Пользуясь свойствами операции умножения матриц, преобразуем правые части равенств (4):

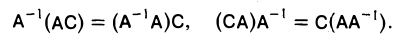
В соответствии с формулой (3) и формулами (10) каждое из равенств (4) дает требуемое соотношение: С = А-1.

Метод Жордана

Укажем простой и эффективный способ вычисления обратной матрицы при помощи элементарных преобразований. Начнем с обоснования метода.

Теорема:

Произвольную невырожденную матрицу элементарными преобразованиями строк можно привести к единичной матрице.
Согласно теореме 1 любую матрицу при помощи элементарных преобразований строк (1-го и 3-го типов) можно привести к матрице ступенчатого вида. Если исходная матрица является квадратной и невырожденной, то она преобразуется к матрице, имеющей треугольный вид

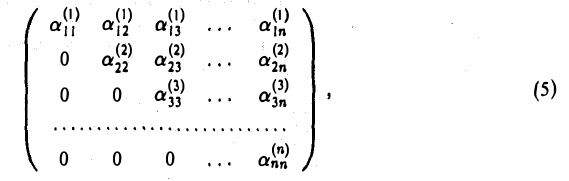
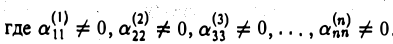
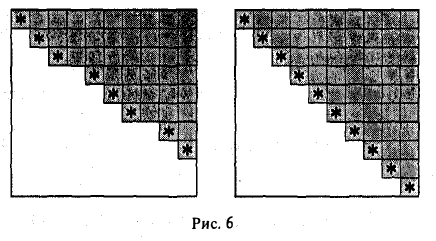
Покажем это. Элементарные преобразования строк матрицы равносильны умножению этой матрицы слева на соответствующие матрицы элементарных преобразований (теорема 2). Как показано выше, матрицы элементарных преобразований невырождены. В силу свойства 4 определителя при умножении квадратных матриц их определители перемножаются. Поэтому при умножении невырожденной матрицы на любую из матриц элементарных преобразований вновь получаем невырожденную матрицу. Если ширина хотя бы одной «ступеньки» у получившейся в результате ступенчатой матрицы была бы больше одного элемента (см. рис. 6), то ее определитель равнялся бы нулю. Это противоречит предыдущему рассуждению. Тем самым, матрица (5) оказывается невырожденной, т. е.

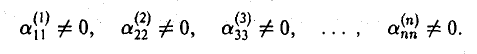
Элементарными преобразованиями строк 2-го типа полученная матрица (5) приводится к следующему виду

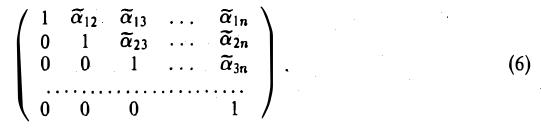
Единичная матрица получается из матрицы (6) элементарными преобразованиями третьего типа: последовательно прибавляя к первым n — 1 строкам последнюю, умноженную соответственно на — 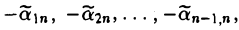, приводим ее к матрице, у которой все элементы n-го столбца, кроме последнего, равны нулю:

Аналогичным образом, прибавляя к первым n — 2 строкам полученной матрицы (n — 1)-ю строку, умноженную соответственно на 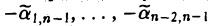придем к матрице, у которой все элементы последних двух столбцов, кроме расположенных на главной диагонали, равны нулю, и т. д. Наконец, прибавляя к первой строке вторую, умноженную на 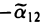, придем к единичной матрице

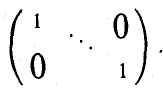
Доказанное утверждение позволяет переформулировать теорему 4 в матричной форме:

Теорема:

Для любой невырожденной матрицы (к можно указать матрицы элементарных преобразований такие, что

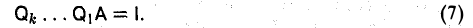
Умножим обе части равенства (7) на матрицу справа. Получаем, что

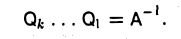
Способ построения обратной матрицы

Пусть А — невырожденная матрица порядка n. Составим расширенную матрицу
(АI) (8)
размера n х (2n). Если подвергнуть строки этой матрицы элементарным преобразованиям, соответствующим матрицам , то на месте матрицы А получится единичная матрица l, а на месте единичной матрицы l — матрица 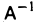, обратная А. Иными словами, элементарными преобразованиями строк матрица (8) преобразуется в матрицу

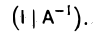
Таким образом, чтобы построить матрицу, обратную заданной квадратной невырожденной матрице А = (aij), следует поступать так: 1. Составить расширенную матрицу

2. Элементарными преобразованиями строк расширенной матрицы (А | I) привести матрицу А к треугольному виду

(см. описание основного процесса, положенного в основу доказательства теоремы 1).

3. Элементарными преобразованиями строк матрицы (А | В) привести матрицу А к единичной

(см. описание сведения матрицы (6) к единичной в теореме 4). 4. Полученная матрица С является обратной к матрице А:

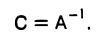
Пример:

Найти матрицу, обратную матрице

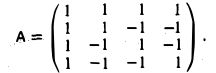
Составим расширенную матрицу

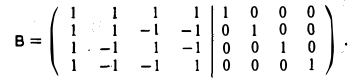
1-й шаг. Вычитаем первую строку из всех последующих строк:

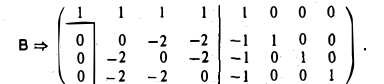
2-й шаг. Элемент а22 = 0. Меняем местами вторую и третью строки, затем вычитаем из четвертой строки полученную вторую:

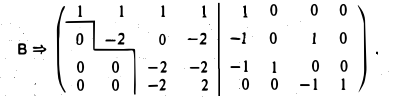
3-й шаг. Вычитаем из четвертой строки третью и делим все строки на их диагональные элементы:

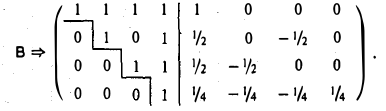
4-й шаг. Вычитаем последнюю строку из первых трех строк:

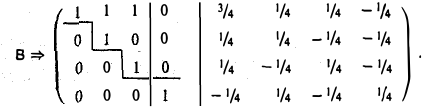
5-й шаг. Вычитаем третью строку из первой строки:

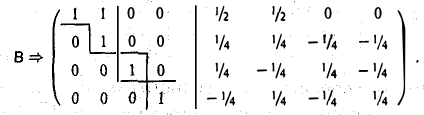
6-й шаг. Вычитаем вторую строку из первой строки:

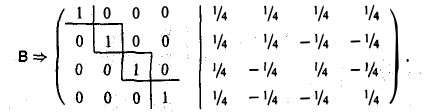
Отсюда следует, что

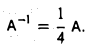
Ранг матрицы

Выберем в матрице

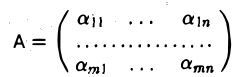
k строк и k столбцов. Пусть

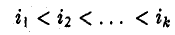
— номера выбранных строк и

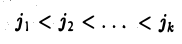
— номера выбранных столбцов. Построим матрицу k -го порядка

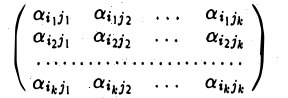
Определитель Мк этой матрицы называется минором к-го порядка матрицы А. Ясно, что у матрицы размера m х n есть миноры, порядок которых равен 1,2,…, min(m, n).

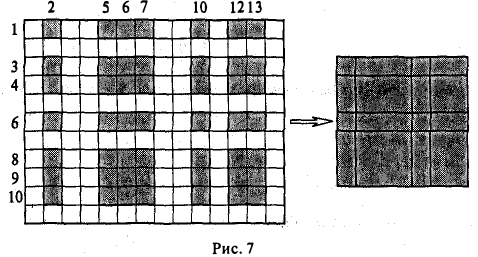
Пример:

Выберем в матрице А размера 11 х 14 7 строк и 7 столбцов:

1, 3, 4, 6, 8, 9, 10 — номера выбранных строк;

2, 5, 6, 7, 10. 12, 13 — номера выбранных столбцов.

Построим матрицу порядка 7 из элементов, располагающихся одновременно и в отобранных строках и в отобранных столбцах, сохранив их взаимное расположение. Получим матрицу, схематически изображенную на рис. 7 справа. Определитель этой матрицы будет минором 7-го порядка исходной матрицы.

Пусть матрица А ненулевая. Тогда найдется число r такое, что

1) некоторый минор r-го порядка матрицы А отличен от нуля;

2) любой минор порядка s (s > r) матрицы А (если таковой существует) равен нулю.

Число rназывается рангом матрицы А. Обозначение: rang А.

Ранг нулевой матрицы считаем равным нулю. Таким образом, для любой матрицы А размера m х n

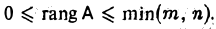
Отличный от нуля минор Mr, порядок которого равен рангу матрицы А, называется базисным минором матрицы А. Строки и столбцы матрицы А, которые содержат элементы базисного минора, называются базисными.

Теорема:

1. Базисные строки матрицы А линейно независимы.
2. Каждая строка матрицы А может быть представлена в виде линейной комбинации базисных строк.

Аналогичное утверждение справедливо и для базисных столбцов.
Предположим для определенности, что базисный минор матрицы А имеет порядок г и расположен в ее левом верхнем углу:

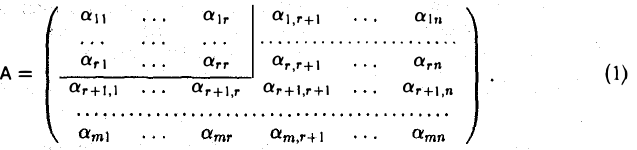
Тогда первые r строк a1,…, аr будут базисными.

1. Покажем, что строки a1,…, аr линейно независимы. Будем рассуждать от противного. Пусть строки a1,…, аr линейно зависимы. Тогда согласно утверждению п. 3 одна из строк является линейной комбинацией остальных. Пусть, например,

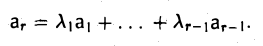
Это означает, что в базисном миноре 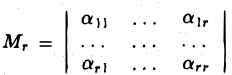r-я строка является линейной комбинацией остальных строк Мr. Отсюда в силу свойства определителя вытекает равенство Мr = 0, которое противоречит определению базисного минора. Тем самым, наше предположение о линейной зависимости строк a1,…, аr неверно. Значит, они линейно независимы.

2. Перейдем к доказательству второго утверждения теоремы. Покажем сначала, что для любых i и j () выполняется равенство

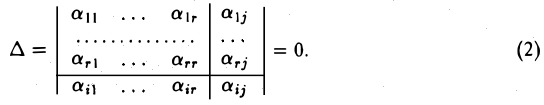
В самом деле, при i ≤ r у определителя ∆ две одинаковых строки, при j ≤ r — два одинаковых столбца, а в остальных случаях (при t > г и j > г) ∆ является минором матрицы А порядка г + 1. Тем самым, он оказывается равным нулю при всех обстоятельствах.

Зафиксируем t (1 ≤ t ≤ m) и разложим определитель ∆ по последнему столбцу. Имеем

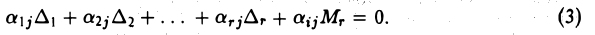
Полученное равенство (3) выполняется для любого j (l ≤ j ≤ n); при этом числа ∆1,…, ∆r от j не зависят. Полагая

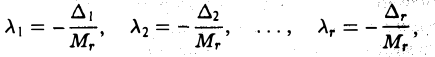
перепишем равенство (3) в следующем виде

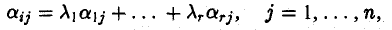
или, подробно,

На основании полученных соотношений (4) заключаем, чтo

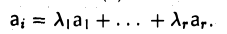
Тем самым, i-я строка матрицы А является линейной комбинацией базисных строк а1,…, аr. Ввиду произвольности выбора i (1 ≤ i ≤ m) отсюда заключаем, что каждая строка матрицы является линейной комбинацией базисных.

Утверждение:

Элементарные преобразования матрицы не увеличивают ее ранга.
Пусть матриц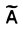а ранга 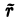получена из матрицы А ранга r элементарным преобразованием строк 1-го типа. Рассмотрим в матрице 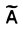произвольный минор 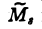, порядка s и выберем в матрице А минор Мs того же порядка s по следующему правилу. Элементы минора Мs расположены в матрице А в тех же строках и в столбцах с теми же номерами, что и элементы минора 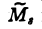в матрице 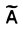. Так как преобразование 1-го типа, переставляя строки матрицы, не изменяет их, то строки миноров Мs и 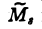могут различаться только порядком расположения в минорах. Отсюда вытекает, что либо 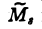= +Мs либо 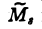= ~Мs.

По определению ранга все миноры матрицы А, порядок которых больше г, равны нулю. Поэтому из полученных равенств вытекает, что любой минор матрицы 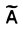порядка s > r равен нулю: 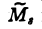= 0. Это означает, что ранг матрицы 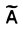не может быть больше ранга матрицы A: 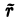≤ r.

Похожими рассуждениями можно убедиться в справедливости неравенства

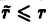
и для случая, когда матрица получена из матрицы А элементарными преобразованиями строк 2-го и 3-го типов.

Для столбцов доказательство проводится аналогично.
Теорема:

Элементарные преобразования не изменяют ранга матрицы.

Достаточно вспомнить, что если матрица получена из матрицы А элементарным преобразованием, то и матрицу А можно получить из матрицы элементарным преобразованием (причем того же типа). С учетом доказанного выше утверждения из этого факта можно заключить, что и

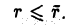
Сопоставляя неравенства 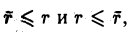получаем требуемое

Замечание:

Число ненулевых строк ступенчатой матрицы равно ее рангу.

В самом деле, минор порядка r ступенчатой матрицы, элементы которого расположены в ее первых r

строках и в столбцах с номерами k1, k2,…, kr, отличен от нуля,

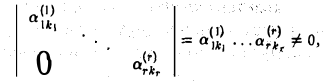
а любой минор порядка s > r содержит нулевую строку и, значит, равен нулю.

Тем самым, элементарные преобразования матрицы предоставляют простой и эффективный способ отыскания ранга произвольной матрицы.

Пример:

Найти ранг матрицы

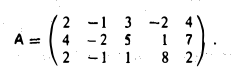
1-й шаг. Вычитая из второй и третьей строк первую строку, умноженную соответственно на 2 и 1, получим, что

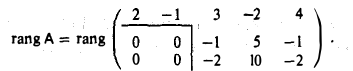
2-й шаг. Вычитаем из третьей строки вторую строку, умноженную на 2. Тогда

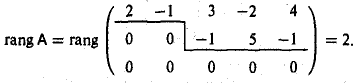
Система линейных уравнений

Пусть дана матрица

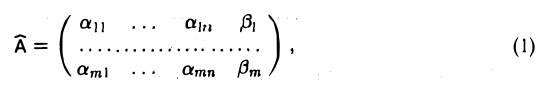
первые n столбцов которой ненулевые. Совокупность соотношений
(2)

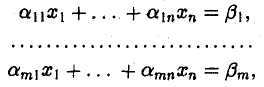
где числа х1,…, хn рассматриваются как величины, подлежащие определению (неизвестные), называется системой m линейных уравнений с n неизвестными, или, коротко, — линейной системой. Числа а_ij (i = 1,…, m; j = 1, … , n) называются коэффициентами линейной системы (2), а числа β_i (i = 1,…, m) — ее свободными членами.

Решением линейной системы (2) называется упорядоченная совокупность чисел γ1,…γn. которая при подстановке в каждое уравнение системы (2) вместо совокупности неизвестных х1,… ,хn обращает его в тождество. Линейная система называется совместной, если она имеет решение, и несовместной, если решений нет. Решения γ1,…γn и γ’ 1,…γ’ n системы (2) называются различными, если нарушено хотя бы одно из равенств

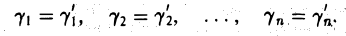
Совместная система называется определенной, если она имеет ровно одно решение, и неопределенной, если она имеет не менее двух различных решений.

Линейная система (2) допускает более компактную (матричную) запись: AX = b (3)

где

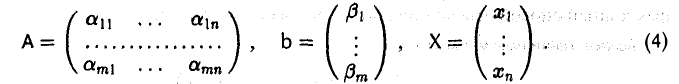
Матрица А называется матрицей системы (2), b — столбцом свободных членов, X — столбцом неизвестных. Исходная матрица

А = (А | b)

называется расширенной матрицей системы (2). Решением матричной системы (3) является столбец Г, элементы которого суть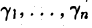

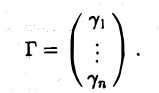
Теорема Кронекера—Капелли:

Линейная система совместна в том и только в том случае, если ранг матрицы системы и ранг расширенной матрицы равны.

Пусть линейная система (2) совместна. Это означает, что некоторый упорядоченный набор чисел 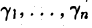обращает каждое из уравнений этой системы в тождество:

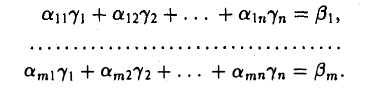
Полученные соотношения можно понимать так: столбец свободных членов расширенной матрицы = (А | b) является линейной комбинацией ее первых п столбцов, т. е. столбцов матрицы А. Прибавим к последнему столбцу матрицы 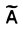первый столбец, умноженный на — γ1, затем второй столбец, умноженный на — γ2,… , и, наконец, n-й столбец, умноженный на — γn. B результате получим матрицу

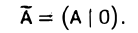
Ранг матрицы 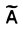совпадает с рангом матрицы , так как проведенные элементарные преобразования столбцов 3-го типа не изменяют ранга матрицы (теорема 7). С другой стороны, ясно, что ранги матриц 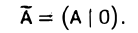и А также равны. Тем самым,

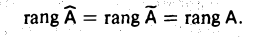
Пусть теперь ранг матрицы системы равен рангу расширенной матрицы. Так как = (А | b), то у матриц А и есть общий базисный минор. Предположим для определенности, что порядок базисного минора равен r, и он расположен в левом верхнем углу обеих матриц. Этого всегда можно добиться путем перестановки уравнений и (в случае необходимости) перенумерации неизвестных. Согласно теореме 6 любой столбец матрицы можно представить в виде линейной комбинации базисных столбцов. В частности, для столбца свободных членов (это последний столбец матрицы ) имеем

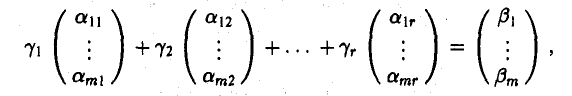
Или

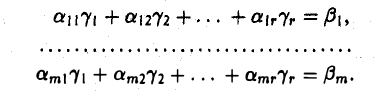
Нетрудно видеть, что упорядоченный набор n чисел

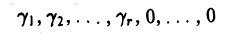
обращает каждое из уравнений исходной линейной системы в тождество. Это означает, что система (2) совместна.

Эквивалентные линейные системы

Совокупность всех решений линейной системы будем называть множеством решений системы. Две линейные системы с одинаковым числом неизвестных называются эквивалентными (равносильными), если множества их решений (возможно, пустые) совпадают. Другими словами, всякое решение одной системы является решением другой и, обратно, всякое решение второй системы является решением первой, либо обе системы не имеют решений.

Ясно, что линейная система однозначно задается своей расширенной матрицей. Возьмем две матрицы и 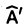одного размера m х (n+ 1) и рассмотрим соответствующие им линейные системы

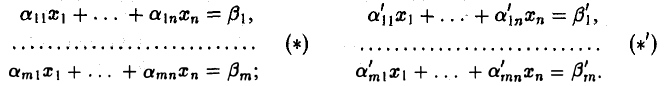
Будем говорить, что система (*‘) получена из системы (*) при помощи элементарных преобразований, если расширенная матрица 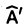системы (*‘) получается из расширенной матрицы системы (*) элементарными преобразованиями строк.
Теорема:

Если линейная система (*’) получена из линейной системы (*) элементарными преобразованиями, то системы (*) и (*’) эквивалентны.

Предположим сначала, что система (*) совместна. Пусть 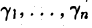— ее решение. Покажем, что этот набор при подстановке в каждое из уравнений системы (*’) вместо набора неизвестных х1… ,хn обращает его в тождество. Достаточно рассмотреть только те уравнения, которые подверглись преобразованиям.

Пусть система (*’) получена из системы (*) элементарным преобразованием:

1) первого типа — изменение порядка уравнений в системе не лишает набор 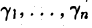возможности обратить каждое из них в тождество;

2) второго типа — после умножения fc-ro тождества

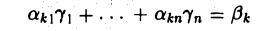
на А ≠ 0 получаем соотношение

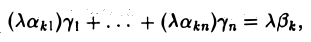
означающее, что набор 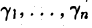обращает уравнение

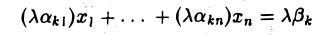
в тождество;

3) третьего типа ~ выпишем преобразованное уравнение

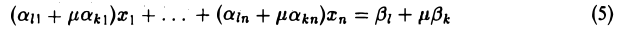
и тождества, полученные из k-то и l-го уравнений системы (*):

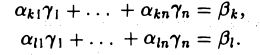
Умножим первое из этих тождеств на μ и, прибавив ко второму, получим тождество

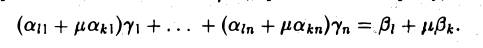
Подстановка набора в уравнение (5) приводит к тому же результату. Таким образом, в каждом из трех случаев система () оказывается совместной, и набор является ее решением — всякое решение системы (*) является решением системы (*’).

Так как система (*) также может быть получена из системы (*’) путем элементарных преобразований, то, повторяя приведенные выше рассуждения для систем (*’) и (*), убеждаемся в том, что всякое решение системы (*‘) является решением системы (*).

В том случае, когда система (*) несовместна, несовместна также и система (*’). В этом легко убедиться, рассуждая от противного: совместность системы (*‘), согласно доказанному выше, неизбежно влечет совместность системы (*), которая по условию не имеет решений.

Ясно, что если система (*’) получена из системы* () при помощи конечного числа элементарных преобразований, то эти системы эквивалентны.

Метод Гаусса

Решить линейную систему — это значит:

1) выяснить, является ли система совместной или несовместной;

2) если система совместна, то найти множество ее решений.

Укажем способ решения линейной системы, состоящий в следующем: элементарными преобразованиями заданная система приводится к системе простого вида, для которой ответить на поставленные вопросы уже нетрудно.

Так как элементарные преобразования системы напрямую связаны с элементарными преобразованиями строк ее расширенной матрицы, будет удобно рассматривать их одновременно:

Как доказано в теореме 1 элементарными преобразованиями строк матрицу можно привести к ступенчатой

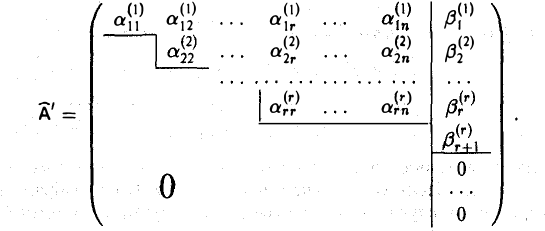
Соответственно преобразуется и система (*).

Если свободный член 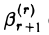отличен от нуля, то полученная (а значит, и исходная) система будет несовместна. В самом деле, (r + 1)-е уравнение имеет следующий вид:

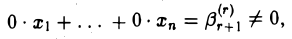
и никакой набор чисел 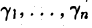не может обратить его в тождество.

Обратимся к случаю, когда 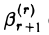= 0. Тогда только первые г строк матрицы 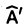будут отличными от нуля. Выпишем соответствующие уравнения. Для простоты записи будем считать, что

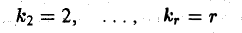
(этого можно добиться, временно перенумеровав искомые неизвестные: у1 = х1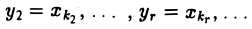). Имеем

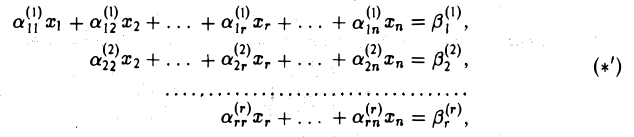
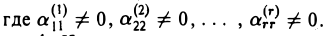
Возможны два случая:

1. Число неизвестных n и число уравнений r в системе (*’) равны, r — n. Тогда система (*’) имеет вид:

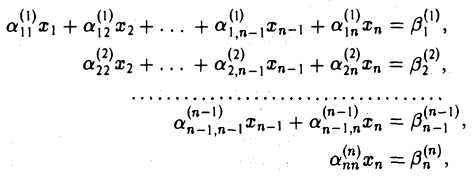
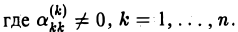
Из последнего уравнения однозначно определяется значение неизвестного хn. Подставляя его в предыдущее (n — 1) -е уравнение, находим значение неизвестного xn_1 и т. д. Наконец, подставляя найденные значения неизвестных x2,…, хn в первое уравнение, однозначно определяем значение неизвестного х1.

Таким образом, в рассматриваемом случае (при r = n) система (*‘) имеет единственное решение. Это же верно и для системы (*).

2. Число неизвестных n больше числа уравнений r, n > r. Придадим неизвестным xr+1,… , хn (их называют свободными) произвольные значения и, перенося соответствующие слагаемые в правые части уравнений системы, получим

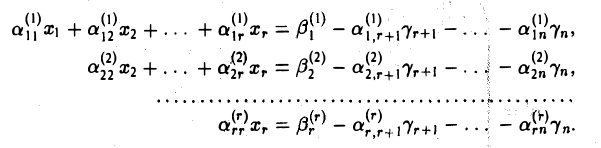
Как и выше, мы можем последовательно определить значения главных неизвестных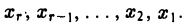

Поскольку значения были выбраны произвольно, то в рассматриваемом случае множество решений линейной системы бесконечно.

Пример:

Решить систему

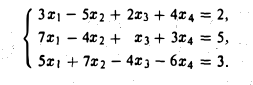
Составим расширенную матрицу системы,

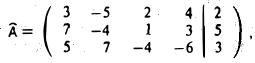
и приведем ее при помощи элементарных преобразований строк к ступенчатой матрице.

1-й шаг. Чтобы получить элемент в позиции (1,1) равным 1, вычитаем из второй строки удвоенную первую строку и затем меняем их местами. Тогда

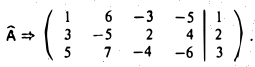
Вычитаем из второй и третьей строк первую, умноженную на 3 и 5 соответственно. Получим, что

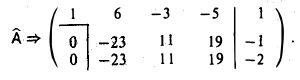
2-й шаг. Вычитаем из третьей строки вторую:

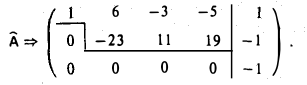
Система несовместна, так как rang А = 2, a rang = 3.

Пример:

Решить систему

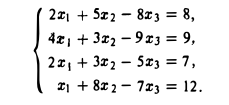
Составим расширенную матрицу системы:

Прямой ход.

1-й шаг. Переставим первую и четвертую строки. Тогда элемент в позиции (1,1) будет равен I. Вычитая затем из всех строк первую строку, умноженную соответственно на 4 , 2 и 2, получаем

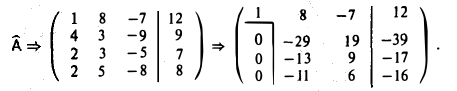
2-й шаг. Во избежание громоздких вычислений вычитаем из второй строки удвоенную третью строку, а из третьей четвертую. Затем у полученной матрицы вычитаем из второй строки третью:

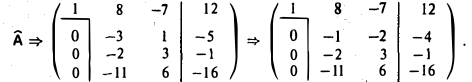
Вычитая из третьей и четвертой строк вторую строку, умноженную на 2 и 11 соответственно, получаем, что

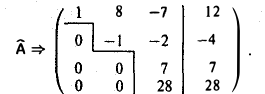
3-й шаг. Вычитаем из четвертой строки третью, умноженную на 4. Затем умножаем элементы третьей строки на :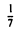

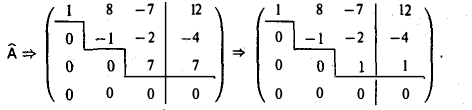
Система совместна, так как rang А = rang = 3, и имеет единственное решение, так как ранг матрицы равен числу неизвестных.

Таким образом, исходная система эквивалентна системе

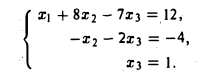
Обратный ход.

Из третьего уравнения сразу видим, что x3 = 1. Подставив это значение x3 во второе уравнение, получаем -х2 — 2 = -4, откуда x2 = 2. После подстановки найденных значений для x3 и x2 в первое уравнение получаем х1+ 16 — 7 = 12, откуда х1 = 3.

Система имеет единственное решение:

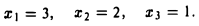
Пример:

Решить систему

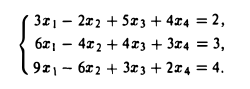
Соcтавим расширенную матрицу системы:

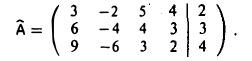
1-й шаг. Вычитаем из второй и третьей строк первую строку, умноженную на 2 и 3 соответственно:

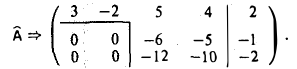
2-й шаг. Вычитаем из третьей строки удвоенную вторую

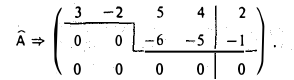
Система совместна (rang А = rang = 2) и имеет бесконечное число решений (rang А < 4). Исходная система эквивалентна системе следующего вида

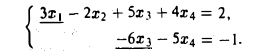
Найдем общее решение системы. Придадим свободным неизвестным x2 и х4 произвольные значения γ2 и γ4 соответственно и, перенося соответствующие слагаемые в правые части уравнений, получим

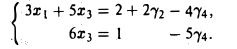
Из последнего уравнения находим

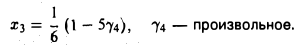
Подставляя выражение для х3 в первое уравнение, получим, что

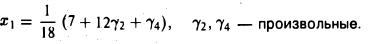
Общее решение системы имеет вид

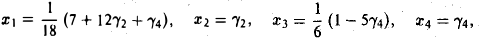
где γ2 и γ4 — произвольные числа. Частное решение можно получить из общего, если придать свободным неизвестным конкретные значения. Например, положив γ2 = 1, γ4 = -1, получим, что х1 = х3 = 1. Итак, частное решение системы:

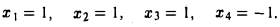
Правило Крамера

Рассмотрим систему n линейных уравнений с n неизвестными — квадратную систему
(6)

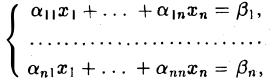
или, в матричной записи,

АХ = b (7)

Если квадратная матрица А невырождена, то система (6) совместна и имеет единственное решение, так как rang А = n.

Умножая обе части равенства (7) слева на матрицу 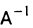, обратную к А, получаем, что

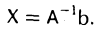
С учетом формулы (2) для обратной матрицы имеем

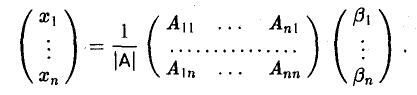
Проведем необходимые вычисления в правой части и получим, что

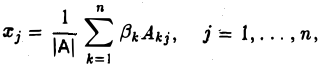
или, подробнее,

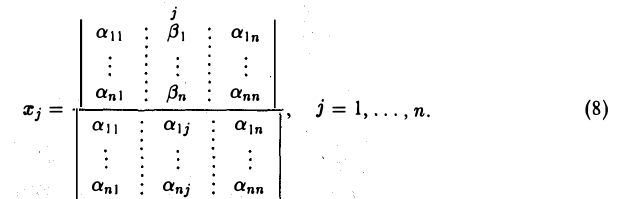
В числителе располагается определитель матрицы, полученной из матрицы А линейной системы путем замены j -го столбца на столбец свободных членов, а в знаменателе — определитель матрицы А.

Важное замечание:

Приведенное правило (8) имеет в значительной степени теоретический интерес, и в практических вычислениях (за исключением квадратных систем с двумя или тремя неизвестными) не применяется ввиду громоздкости.

Замечание:

Необходимость вычисления n + 1 определителя n-го порядка сильно увеличивает количество вычислений по сравнению с методом Гаусса: при непосредственном раскрытии определителей решение квадратной системы с п неизвестными требует порядка п!п арифметических операций. Уже при n = 30 такое число операций для современных ЭВМ недоступно.

Общее число арифметических действий в методе Гаусса имеет порядок n3.

Большинство распространенныхточных методов решения линейных систем можно рассматривать как варианты метода Гаусса, различающиеся между собой лишь некоторыми деталями. Количество арифметических операций для всех таких методов примерно одно и тоже.

Чтобы найти решение линейной системы

АХ = b

с квадратной невырожденной матрицей А, следует поступать так:

1. Составить расширенную матрицу системы:

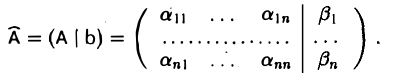
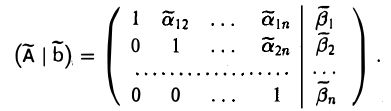
2. Элементарными преобразованиями строк расширенной матрицы привести матрицу системы к треугольному виду:

3. Элементарными преобразованиями строк матрицы 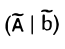привести матрицу А к единичной:

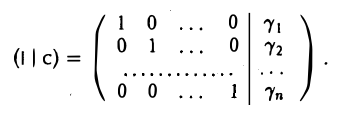
4. Записать линейную систему, соответствующую полученной расширенной матрице (l | с):

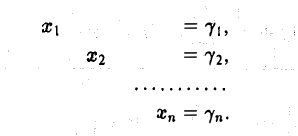
Набор

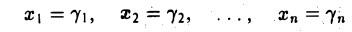
— решение исходной системы.

Однородные линейные системы

Линейная система называется однородной, если все свободные члены системы равны нулю: (9)

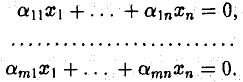
Основные свойства однородной системы:

1.Однородная система всегда совместна.

Набор x1 = 0,…, хn = 0 — нулевое решение, существующее у системы (9) всегда.

2. Если число m уравнений однородной системы меньше числа п неизвестных, то эта система имеет ненулевые решения.

Согласно сформулированному условию ранг г матрицы системы (9) удовлетворяет неравенству r ≤ m< n. Это позволяет утверждать, что исходная система является неопределенной (см. п. 1).

3. Сумма решений однородной системы (9) также является ее решением. Пусть 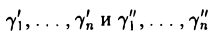— решения системы (9). Это означает, что

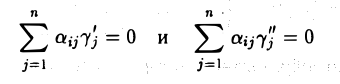
для любого i = 1,…, m. Так как

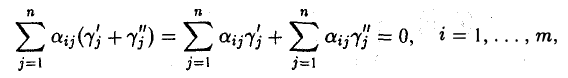
то набор

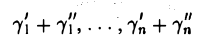
— сумма решений 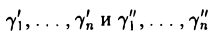— решение однородной системы (9).

Произведение решения однородной системы (9) на любое число также является решением этой системы.

Пусть 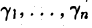— решение системы (9):

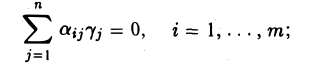
μ — произвольное число. Тогда

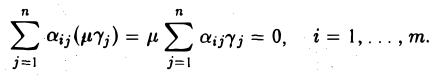
Тем самым, набор — произведение решения 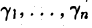на число μ — решение системы (9).

Часто оказывается удобной матричная запись однородной системы

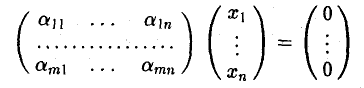
или, короче,

АХ = 0. (10)

Проведем доказательство свойств 3 и 4 в матричной записи.

Доказательство свойства 3.

Пусть столбцы Г’ и Г» — решения системы (10): АГ’ = 0 и АГ» = 0. Тогда столбец Г’ + Г» также является решением системы (10), так как

А(Г’ + Г») = АГ’ + АГ» = 0+0 = 0.

Доказательство свойства 4.

Пусть АГ =’ 0. Вычислим А( μГ), где μ — любое число. Имеем

А(μГ) = μ(АГ) = μ0 = 0.

Свойства 3 и 4 означают, что множество решений однородной системы с естественными правилами сложения решений и умножения решения на число является линейным пространством 2′).

Познакомимся с одним важным свойством линейного пространства решений однородной системы.

Применив к однородной системе (9) метод Гаусса, приведем ее к следующему виду:

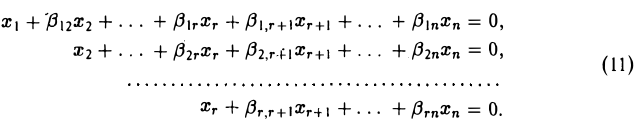
Здесь мы считаем для простоты, что неизвестные х1,…,хr — главные (напомним, что этого всегда можно добиться путем временной перенумерации неизвестных).
2) Обшеe понятие линейного пространства будет рассмотрено.

Пусть ранг г матрицы системы (11) меньше числа n неизвестных, r < n. Построим п-г решений системы (11), придавая свободным неизвестным хr+1,… ,хn значения в соответствии со следующей таблицей

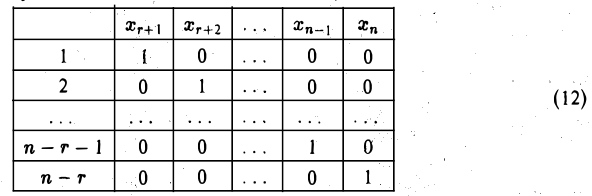
Каждому набору значений свободных неизвестных соответствует решение системы (11):

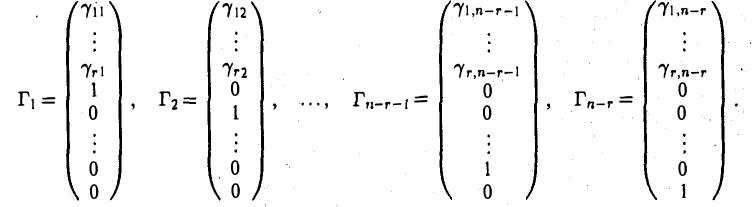
Построенная совокупность решений Г1 …, Гn-r линейно независима. Покажем это. м Рассмотрим линейную комбинацию

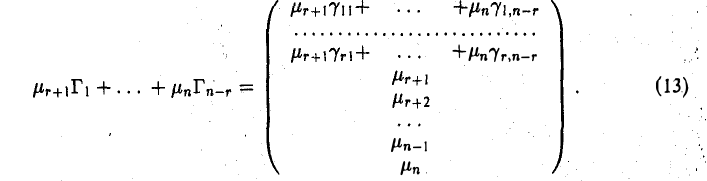
Легко заметить, что линейная комбинация (13) равна нулевому столбцу в том и только в том случае, когда

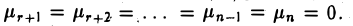
Это означает, что нулевому решению системы (11) равна лишь тривиальная линейная комбинация решений Г1 …, Гn-r.

В силу доказанных выше свойств 3 и 4 линейная комбинация (13) является решением системы (11) при любых

Покажем, что любое решение

однородной системы (11) можно представить в виде линейной комбинации вида (13)’.

Умножая решения Г1,…, Гn-r на соответственно и складывая, получим решение системы (11) в виде (13). Сравнивая формулы (13) и (14), нетрудно убедиться в том, что эти решения имеют одинаковый набор значений свободных неизвестных. А так как по заданным значениям свободных неизвестных главные определяются однозначно, то сами решения совпадают:

Таким образом, построенная совокупность решений Г1,…, Гn-r однородной системы (9) обладает следующими свойствами:

1. оналинейно независима;
2. любое решение системы (9) можно представить в виде линейной комбинации решений Г1…..Гn-r.
   

Определение:

Любая совокупность из n — r решений однородной системы (9), удовлетворяюшая условиям 1 и 2, называется фундаментальной системой решений однородной системы (9).
Пример:

Решить систему

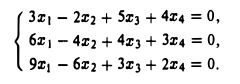
Применив метод Гаусса, получим

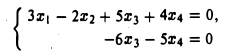
(см. пример 3 п.З). Свободные неизвестные — х2 и x4. Составим таблицу

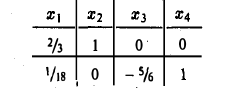
Фундаментальную систему решений образуют решения

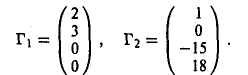
Любое решение Г заданной системы можно представить в следующем виде:

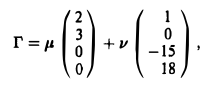
где μ и v — произвольные постоянные.
Итог. Для того, чтобы описать множество решений однородной системы, достаточно найти ее фундаментальную систему решений (ФСР), так как всевозможные линейные комбинации элементов ФСР и составляют это множество.
Нетрудно заметить, что в таблицу (12) заключена единичная матрица порядка n — r.

Замечание:

Требование (12) на набор свободных неизвестных не является обязательным для построения ФСР. Можно поместить в таблицу (12) любую невырожденную матрицу (n — r).-го порядка.

Замечание:

Любая однородная линейная система, имеющая ненулевые решения, обладает ФСР.

Матрицы в линейной алгебре

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или п столбцов одинаковой длины). Матрица записывается в виде

или, сокращенно, 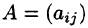, где) строки, — номер столбца

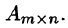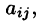Матрицу А называют матрицей размера m х п и пишут Числа составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.

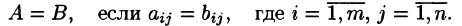
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера п х п называют матрицей п-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.

Пример:

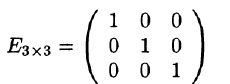
— единичная матрица 3-го порядка.

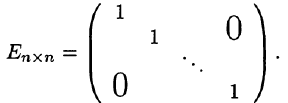
— единичная матрица n-го порядка.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Имеет вид

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

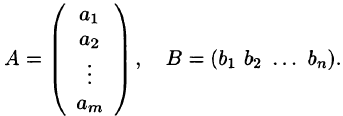
Матрица размера 1 x 1, состоящая из одного числа, отождествляется с этим числом, т. е. 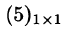есть 5.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается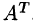

Так, если

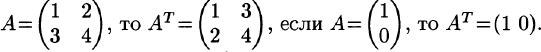
Транспонированная матрица обладает следующим свойством: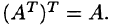

Действия над матрицами

Сложение:

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц 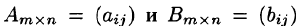называется матрица 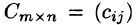такая, что 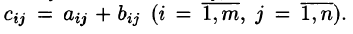Записывают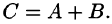

Пример:

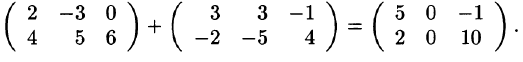
Аналогично определяется разность матриц.

Умножение на число:

Произведением матрицы 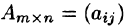на число k называется матрица 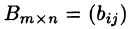такая, что 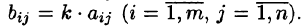Записывают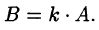

Пример:

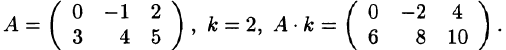
Матрица 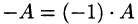называется противоположной матрице А.

Разность матриц А — В можно определить так: А — В = А + (—В). Операции сложения матриц и умножения матрицы на число обла-
дают следующими свойствами:

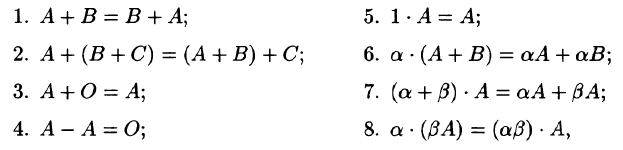
где А, В, С — матрицы, — числа.

Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы A и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например

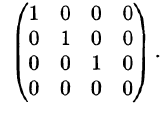
Пример:

Привести к каноническому виду матрицу

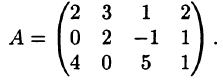
Решение: Выполняя элементарные преобразования, получаем

Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы 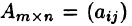на матрицу 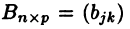называется матрица 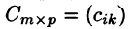такая, что

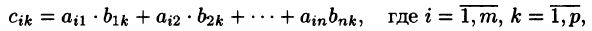
т. е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Получение элемента 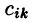схематично изображается так:

Если матрицы A и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что 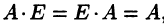, где А — квадратная матрица, Е — единичная матрица того же размера.

Пример:

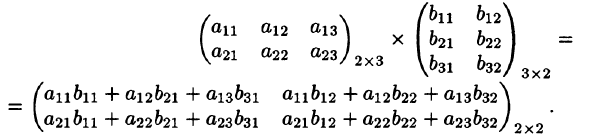
Пример:

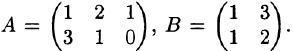Тогда произведение

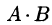не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определено произведение 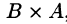, которое считают следующим образом:

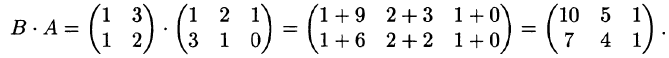
Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами:

если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

Определители

Квадратной матрице А порядка п можно сопоставить число det А (или |A|, или ), называемое ее определителем, следующим образом:

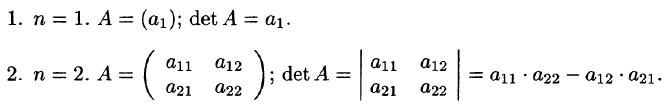
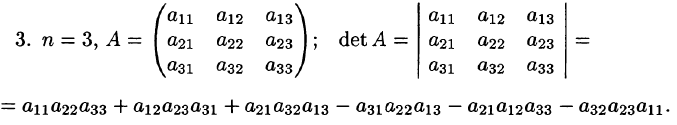
Определитель матрицы А также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (с. 23, свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

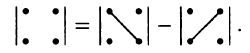
Пример:

Найти определители матриц

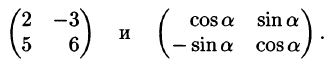
Решение:

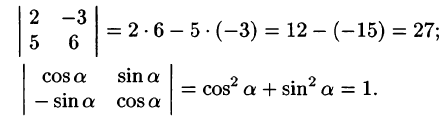
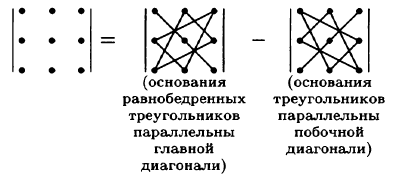
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

Пример:

Вычислить определитель матрицы

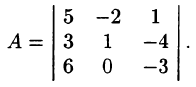
Решение:

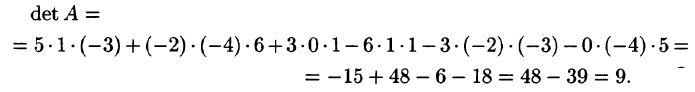
Свойства определителей

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.

Иными словами,

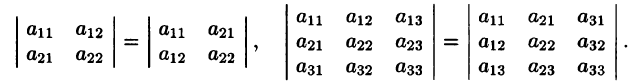
В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

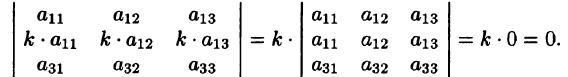
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей. Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Пример:

Доказать, что

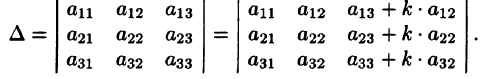
Решение:

Действительно, используя свойства 5, 4 и 3, получим

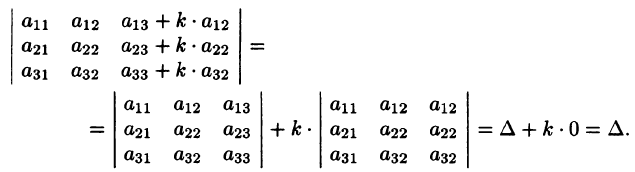
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения

Минором некоторого элемента 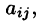определителя n-го порядка называется определитель п — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается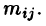

Так, если

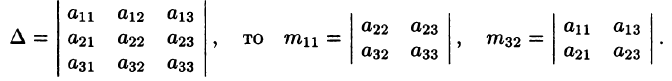
Алгебраическим дополнением элемента 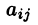определителя называется его минор, взятый со знаком «плюс», если сумма i+j — четное число, и со знаком «минус», если эта сумма нечетная. Обозначается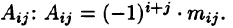

Так,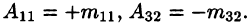

Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что

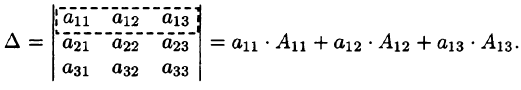
В самом деле, имеем

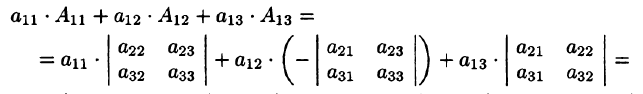
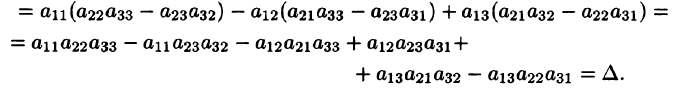
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Пример:

Вычислите определитель матрицы

Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.

Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Так, например,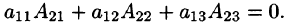

Невырожденные матрицы

Пусть А — квадратная матрица n-го порядка

Квадратная матрица А называется невырожденной, если определитель 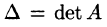не равен нулю: 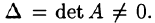В противном случае 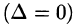матрица А называется вырожденной.

Матрицей, союзной к матрице A, называется матрица

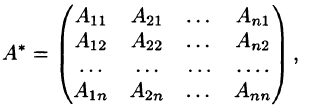
где 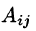— алгебраическое дополнение элемента 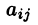данной матрицы А (оно определяется так же, каик и алгебраическое дополнение элемента определителя).

Матрица 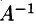называется обратной матрице , если выполняется условие

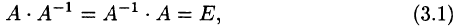
где Е — единичная матрица того же порядка, что и матрица A. Матрица 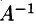имеет те же размеры, что и матрица A.

Обратная матрица

Теорема 3.1. Всякая невырожденная матрица имеет обратную.
Проведем доказательство для случая матрицы 3-го порядка. Пусть

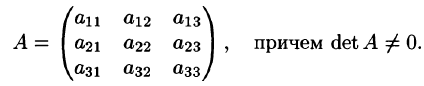
Составим союзную матрицу

и найдем произведение матриц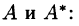

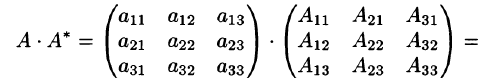
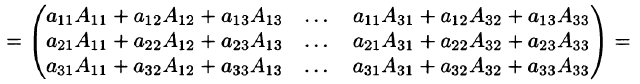
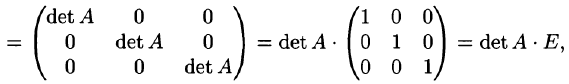
т. е.

Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).

Аналогично убеждаемся, что

Равенства (3.2) и (3.3) перепишем в виде

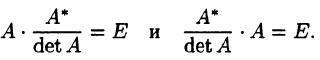
Сравнивая полученные результаты с определением (3.1), получаем

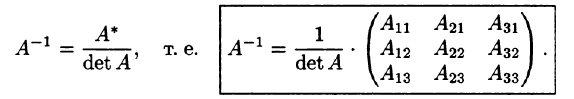
Отметим свойства обратной матрицы:

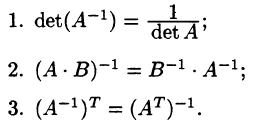
Пример:

Найти 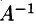, если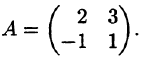

Решение: 1) Находим det A: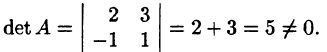

2) Находим

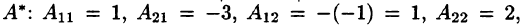
поэтому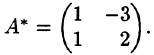

Проверка:

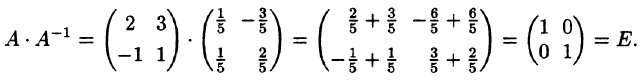
Пример:

Определить, при каких значениях существует матрица, обратная данной:

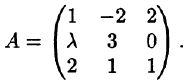
Решение: Всякая невырожденная матрица имеет обратную. Найдем определитель матрицы А:

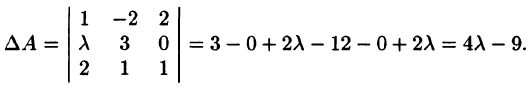
Если 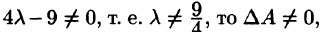т. е. матрица А невырожденная, имеет обратную.

Пример:

Показать, что матрица А является обратной для В,
если

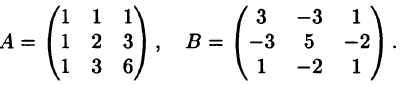
Решение: Найдем произведение матриц А и В:

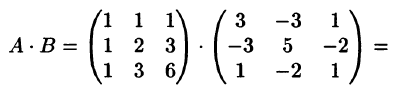
Аналогично 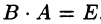. Следовательно, матрица А является обратной для В.

Ранг матрицы

Рассмотрим матрицу А размера m х п.

Выделим в ней k строк и k столбцов 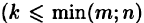). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -гo порядка. Все такие определители называются ми-норами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить 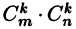штук, где 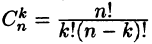— число сочетаний из п элементов по k.)

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается 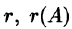или rang A.

Очевидно, что 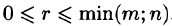, где 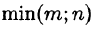— меньшее из чисел тип.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

Пример:

Найти ранг матрицы:

Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля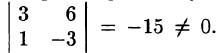 Значит, r (А) = 2.
Базисный минор стоит на пересечении 2 и 3 строки с 1 и 3 столбцами.

Отметим свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы (см. с. 18).

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

Пример:

Найти ранг матрицы

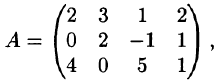
используя результаты примера 1.4.

Решение: В примере 1.4 показано, что

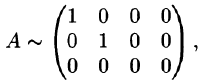
то есть

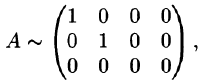
Таким образом, ранг матрицы А равен r(A) = 2.

Виды матриц и операции над матрицами

Матрицей А называется таблица чисел. Матрицы обозначаются различными способами:

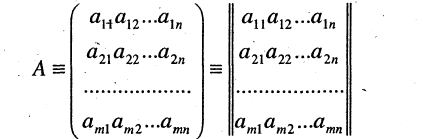
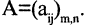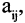или сокращенно Числа составляющие матрицу, называются ее элементами. Первый индекс указывает номер строки, второй — номер столбца. Если матрица состоит из m строк и n столбцов, то говорят, что размерность матрицы есть m на n. Количество элементов в такой матрице равно произведению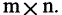

Матрица называется прямоугольной, е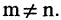сли Если 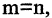то матрица называется квадратной и число n — порядком матрицы. Матрица, содержащая один столбец, называется матрица-столбец. Матрица, состоящая из одной строки, — матрица-строка. Матрица, все элементы которой равны нулю, называется нулевой матрицей.

Для квадратной матрицы порядка п, т. е. 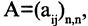совокупность элементов 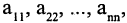у которых оба индекса совпадают, образует главную диагональ. Сумма элементов главной диагонали называется следом матрицы и обозначается

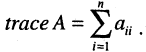
Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали, равны нулю: 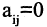при 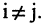Диагональная матрица обозначается так:

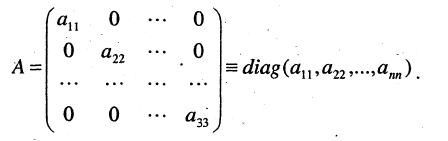
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной и обозначается

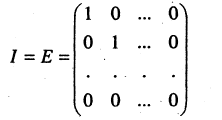
Квадратная матрица называется треугольной, если все элементы, стоящие ниже (или выше) главной диагонали, равны нулю:

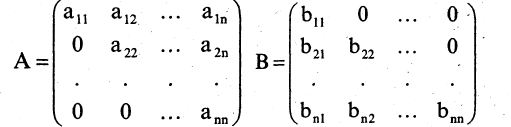
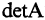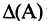Каждой, квадратной матрице ставится в соответствие число, называемое детерминантом или определителем. Обозначается определитель символами или или 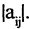Определитель квадратной матрицы А представляет собой числовую функцию, аргументы которой есть элементы этой матрицы. Общее выражение определителя матрицы n-го порядка задается в следующем виде:

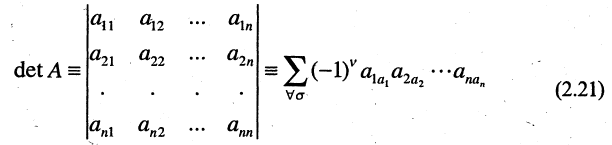
В правой части выражения (2.21) стоит сумма всех произведений, которые можно образовать из n элементов матрицы по правилу: по одному из каждой ее строки и из каждого столбца, т. е. в каждом произведении среди всех первых и всех вторых индексов не должно быть одинаковых. Первые индексы располагают в возрастающем порядке. Следовательно, каждое произведение в (2.21) образует подстановку n-ой степени:

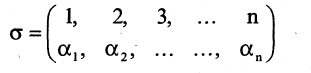
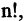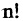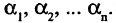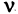Поскольку число подстановок из п чисел равно то в (2.21) входит слагаемых вида Число равно числу инверсий соответствующей перестановки 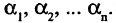Частные случаи для формулы (2.21)

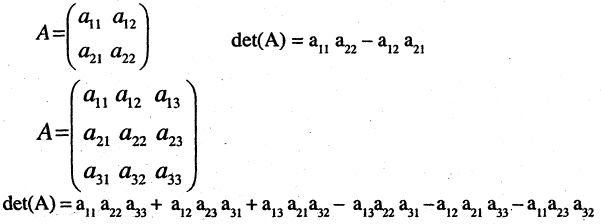
Пример:

Вычислить определитель матрицы

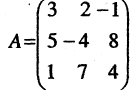
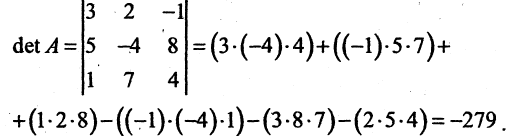
Очевидно, что определитель единичной матрицы равен единице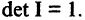

Квадратная матрица называется невырожденной (неособенной), если 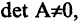и вырожденной (особенной), если 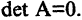Легко проверить, что определитель треугольной матрицы равен произведению диагональных элементов:

Отсюда следует, что если все диагональные элементы в треугольной матрице отличны от нуля, то матрица невырожденная.

Действия над матрицами

Равенство матриц

Две матрицы 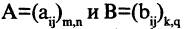называются равными, если они одинаковых размеров 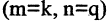и их соответствующие элементы равны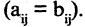

Сложение матриц

Складывать можно лишь матрицы одинакового размера. Суммой двух матриц 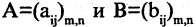называется матрица 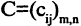тех же размеров. Элементы матрицы С равны суммам соответствующих элементов матриц А и В, т. е. 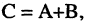если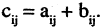

Пример:

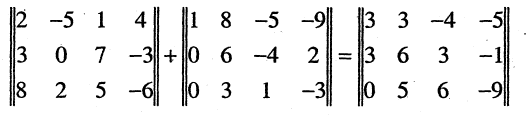
Умножение матрицы на число

Произведением матрицы 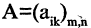на число 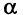называется матрица 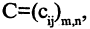элементы которой получаются из соответствующих элементов матрицы А умножением на число :

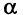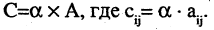
Пример:

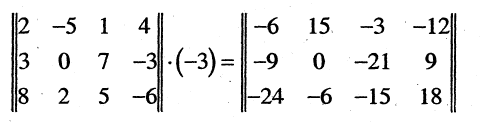
Легко проверить, что операции сложения матриц и умножения матриц на число обладают следующими свойствами:

(перестановочный закон);

(сочетательный закон); (распределительный закон);

где 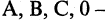матрицы одного размера, 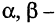числа.

Операции сложения матриц и умножения матрицы на число называются линейными операциями.

Замечание:

Пусть А, В — квадратные матрицы порядка 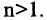Линейные операции над матрицами не переносятся на их определители, т. е.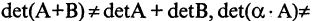

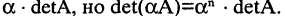
Произведение матриц

Произведение матриц А • В определено в том и только в том случае, если число столбцов матрицы А равно числу строк матрицы В. Произведением матрицы А размера m • k на матрицу В размера k • n называется матрица 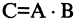размера элементы которой определяются по формуле

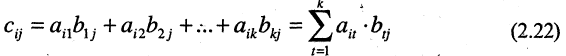
Сумма в (2.22) представляет собой скалярное произведение вектора-строки i матрицы А на вектор-столбец j матрицы В (см. главу 2.5). Поэтому говорят, что умножение матриц производится по правилу «строка на столбец», т. е. для получения элемента 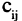необходимо скалярно умножить строку i матрицы А на столбец j матрицы В.

Пример:

Требуется перемножить матрицы

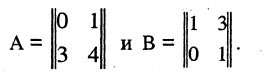
Поскольку это матрицы квадратные и одного размера, то умножение таких матриц возможно всегда. В соответствии с (2.22) имеем:

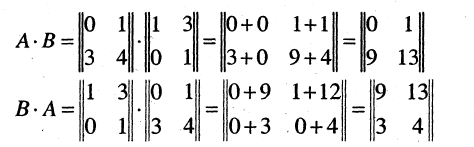
Из примера следует важное правило: «Произведение матриц не-перестановочно», т. е. в общем случае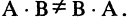

Пример:

Найти произведение матриц

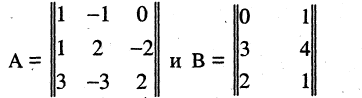
В соответствии с правилом умножения матриц произведение 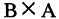не существует, а произведение

Можно проверить, что умножение матриц удовлетворяет свойствам:

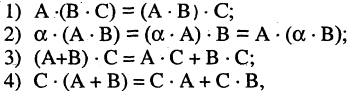
где — число, А, В, С — матрицы, для которых произведения существуют;

5) если А, В — квадратные матрицы одного порядка, то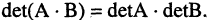

Транспонирование матриц

Рассмотрим произвольную матрицу

полученная из матрицы А заменой строк столбцами, называется транспонированной по отношению к А. Например,

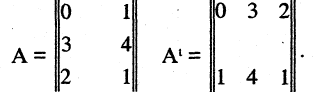
Можно доказать, что:

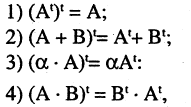
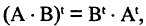где А и В — матрицы, — число;

5) Если А — квадратная матрица, то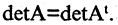

Квадратная матрица называется симметрической, если 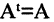и кососимметрической, если 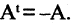У симметрической матрицы 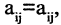т. е. все элементы, стоящие ниже главной диагонали, равны соответствующим элементам, расположенным выше диагонали. Пример симметрической матрицы.

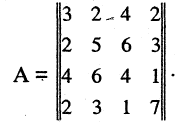
У кососимметрической матрицы 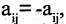следовательно,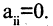

Пример кососимметрической матрицы.

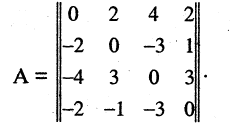
Произведение матрицы А на транспонированную матрицу 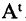есть симметрическая матрица. Для доказательства этого факта проверим, что 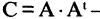симметрическая матрица. Действительно,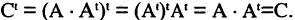

Пусть в определителе матрицы А размером выделено произвольных строк и столько же произвольных столбцов. Элементы, расположенные на пересечении этих строк и столбцов, образуют определитель k-го, порядка называемый минором k-го порядка матрицы А. Например, для матрицы

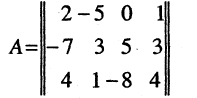
все ее элементы являются минорами первого порядка: 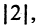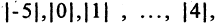(здесь знак 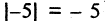означает минор первого порядка, а не модуль числа -5). Определители

миноры второго порядка, а миноры третьего порядка для этой матрицы следующие:

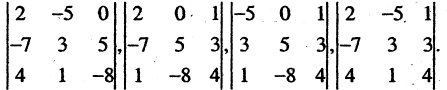
Число r называется рангом матрицы А (обозначается rgА), если у нее существует хотя бы один минор порядка r, не равный нулю, а все миноры большего порядка, если они существуют, равны нулю. Ранг матрицы не может превышать наименьшего из чисел m, n. Если ранг матрицы равен r, то ее минор порядка r, не равный нулю, называется базисным минором. Базисных миноров у матрицы может быть несколько. Миноры, образованные строками и столбцами с одинаковыми номерами, называются главными.

Пример:

Найти ранг и базисный минор матрицы

Все четыре минора третьего порядка этой матрицы равны нулю. Если же построить определитель из строк 1,3 и столбцов 1,3, то он не равен нулю, т.к. 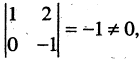следовательно,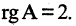

Элементарными называются следующие преобразования матрицы:

1) перестановка двух строк (столбцов);

2) умножение одной из строк (столбцов) на число, не равное нулю;

3) прибавление к одной из строк (столбцов) другой строки (столбца), умноженной предварительно на произвольный не равный нулю множитель.

Все матрицы, полученные из данной путем элементарных преобразований, — разные матрицы. Вместе с тем все они обладают некоторыми одинаковыми свойствами, например, имеют одинаковый ранг. По этой причине матрицы, полученные в результате элементарных преобразований, называют эквивалентными. При переходе к эквивалентной матрице вместо знака 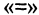часто используют знак соответствия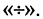

Обратная матрица

Пусть А — квадратная матрица n-го порядка, а 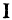— единичная матрица того же порядка. Матрица В называется обратной по отношению к матрице А, если выполняются равенства

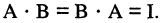
Матрицу, обратную к матрице А, обозначают символом 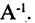Если у матрицы А существует обратная матрица, то она единственна.

Алгебраическим дополнением элемента 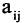матрицы А называется определитель, получаемый из определителя исходной матрицы А путем изъятия из него строки i и столбца j и взятый со знаком 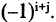Например, если матрица А имеет определитель

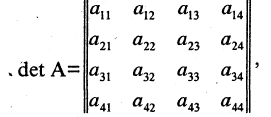
то алгебраическим дополнением элемента 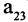этой матрицы, поскольку 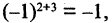является определитель

Присоединенной (или союзной) к матрице А называется матрица 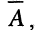элементами которой являются алгебраические дополнения соответствующих элементов исходной матрицы А, расположенные как элементы в транспонированной по отношению к А матрице.

Присоединенная матрица обладает свойством

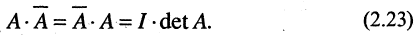
Критерий существования обратной матрицы

Для того, чтобы для матрицы А существовала обратная, необходимо и достаточно; чтобы матрица А была невырожденной, т. е. 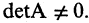Свойства обратной матрицы следуют из ее определения.

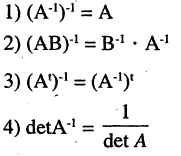
Пример:

Найти обратную матрицу для

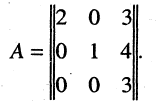
Определитель матрицы: 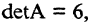следовательно, обратная матрица 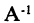существует. Построим присоединенную к А матрицу А . Для этого вычислим алгебраические дополнения для всех элементов А:

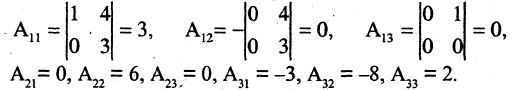
Присоединенная по отношению к А матрица

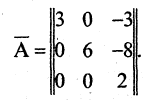
Обратная к А матрица

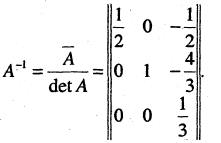
Как найти матрицу — подробная инструкция

Матрицей размера m х n называется прямоугольная таблица из m строк и n столбцов выражений, называемых элементами матрицы:

Здесь 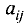— элемент матрицы, стоящий на пересечении i-й
строки и j-го столбца, i = 1, 2,…, m , j = 1,2,…, n.

Элементами матрицы являются, как правило, числа, но иногда
и другие математические объекты, например векторы. Матрицу
обозначают следующим образом:

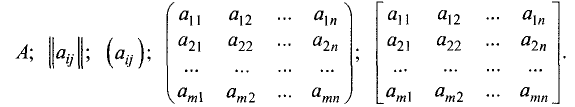
Квадратная матрица порядка n — это матрица размера n х n .

Диагональной называется квадратная матрица, у которой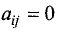
при всех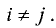

Единичной называется диагональная матрица, у которой
диагональные элементы равны единице. Например,

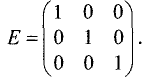
Диагональ, проходящая из левого верхнего угла в правый нижний, называется главной диагональю квадратной матрицы. Элементы,
стоящие на этой диагонали, называются главными диагональными. Их сумма называется следом и обозначается SpA (SpurA), ТrА (TraceA).

Матрица (вектор)-строка — это матрица размера 1 х n:

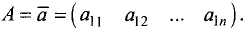
Матрица (вектор)-столбец это матрица размера m х 1:

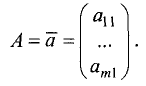
Матрица размера m x n называется нулевой, если все ее элементы
равны нулю. Обозначается 0.

Транспонированной к матрице 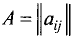называется матрица 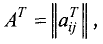получаемая расстановкой строк матрицы 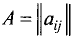в столбцы матрицы 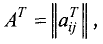а столбцов — в строки.
Например,

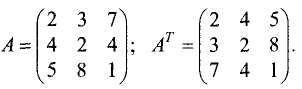
Определитель квадратной матрицы

Определителем квадратной матрицы порядка n называется число D, которое может быть рассчитано, например, с помощью метода разложения на алгебраические дополнения.

Этот метод рассмотрен в §1.7. Обозначение:

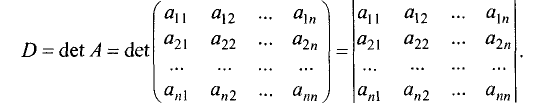
► Пример 1.8. Найти определитель матрицы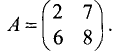

Решение. Определитель второго порядка вычисляем по формуле

Свойства определителей

1.Общий для всех элементов строки (столбца) множитель можно выносить за знак определителя.

Действительно,

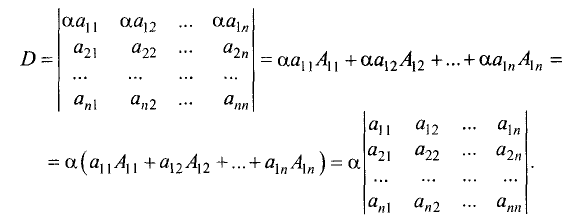
Заметим, что за знак матрицы можно выносить только общий
множитель всех элементов.

2.При перестановке двух соседних строк (столбцов) матрицы ее
определитель меняет знак на противоположный.

Действительно, разложим определитель n-го порядка по первой
строке:

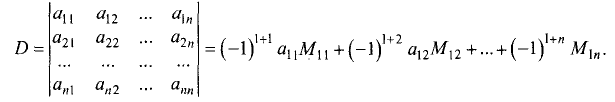
Поменяем местами первую и вторую строки и разложим новый
определитель n-го порядка по второй строке:

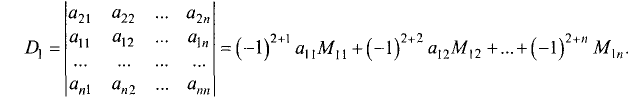
Если сравнить это выражение с предыдущим, то легко увидеть,
что все слагаемые разложения определителей имеют
противоположные знаки. Значит, и сами определители имеют
противоположные знаки. Точно так же доказывается данное свойство определителя для других соседних строк и столбцов.

3.Если квадратная матрица содержит две одинаковые строки
(столбца), то ее определитель равен нулю.

Действительно, если эти строки соседние, то переставим их.
Знак новой матрицы изменится на противоположный. Но так как
строки одинаковы, то это две одинаковые матрицы. Такая ситуация
возможна, если исходные матрицы равны нулю.

Если эти строки не являются соседними, то путем
последовательных перестановок строк построим определитель с двумя одинаковыми соседними строками. Такой определитель равен нулю. А исходный определитель отличается от него, по крайней мере,
только знаком. Поэтому он тоже равен нулю.

4.От прибавления (вычитания) к строке (столбцу) элементов
другой строки (столбца) или линейной комбинации элементов
другой строки (столбца) величина определителя не изменится.

Пусть определитель 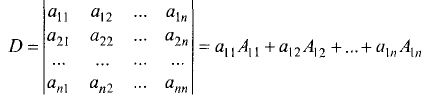разложен по первой строке.

Умножим элементы второй строки на и сложим с первой
строкой. Определитель новой матрицы запишем в виде

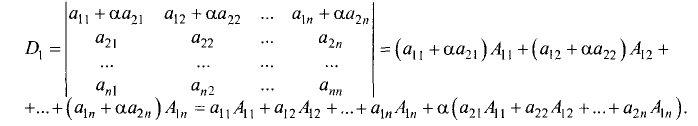
Сопоставив D с видим, что где

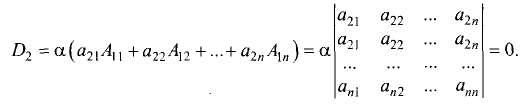
Определитель 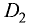равен нулю, так как имеет две одинаковые
строки. Таким образом, 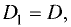что и требовалось доказать.

5.В предыдущем пункте доказано важное свойство определителей.
Сумма произведений всех элементов некоторого столбца
определителя на алгебраические дополнения соответствующих
элементов другого столбца равна нулю.

6.Определитель не изменит своей величины, если заменить его
строки столбцами.

Пример:

Рассчитать определитель

Решение:

Умножим первую строку на -1, а результат сложим со второй и третьей строками:

В последнем столбце получили четыре нуля и единицу. Поэтому
при разложении определителя по последнему столбцу все слагаемые,
кроме первого, будут равны нулю. После разложения по последнему
столбцу получим

Умножим первую строку на -2 и сложим со второй:

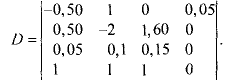
Разложим результат по последнему столбцу:

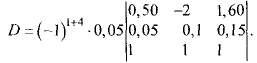
Умножим первый столбец на —1 и сложим со вторым и третьим
столбцами:

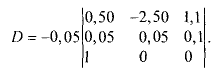
Разложим данный определитель по последней строке:

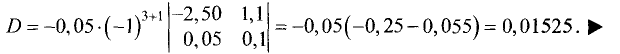
Алгебра матриц

Две матрицы называются равными, если они имеют одинаковый
размер и все элементы, стоящие на одних и тех же местах, равны
между собой.

Суммой двух матриц одинакового размера 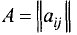и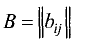
является матрица 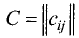того же размера с элементами 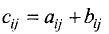для всех i и j.

Матрицы размера m х n и размера r х s
называются сцепленными, если n = r.

Произведением двух сцепленных матриц 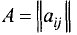размера m х n и
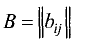размера n x s является матрица 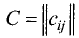размера m х s, где

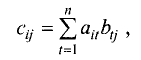
т.е. элемент, стоящий в i-й строке и j-м столбце матрицы
произведения, получается в виде скалярного произведения i-го вектора строки матрицы 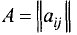и j-го вектора столбца матрицы .

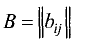Пример:

Вычислить произведение матриц А*В и В*А , где

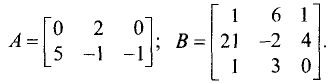
Размер матрицы произведения равен 2×3. Вычислим элементы
матрицы С, скалярно перемножая i-й вектор строки матрицы А и
соответствующий j-й вектор столбца матрицы В:

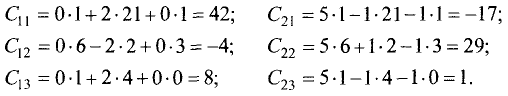
Матрица С имеет вид

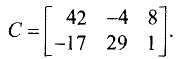
Матрица В*А не существует, так как количество столбцов матрицы
В не равно количеству строк матрицы А. ►

Многие операции, совершаемые над числами, справедливы и
для матриц. К ним относятся:

А+В=В+А;

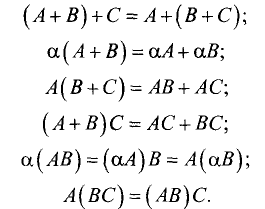
Однако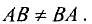

Для единичных матриц Е справедливы равенства ЕА = АЕ = А.
Иными словами, произведение любой матрицы на единичную
матрицу не изменяет исходной матрицы.

Обратная матрица

Матрица 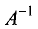называется обратной по отношению к квадратной матрице А, если при перемножении этих матриц получается единичная матрица Е, т.е.

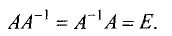
Вырожденной называется матрица, определитель которой равен нулю. В противном случае матрица называется невырожденной.

Необходимое и достаточное условие существования обратной
матрицы состоит в следующем: обратная матрица существует и
единственна тогда и только тогда, когда исходная матрица невырожденная.

Обратной матрицей 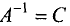по отношению к матрице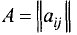
называется матрица

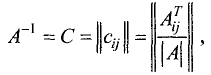
где 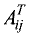— алгебраическое дополнение элемента 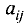в определителе матрицы 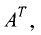транспонированной к матрице А. (Напомним, что
алгебраическое дополнение есть умноженный на 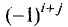минор, полученный из 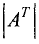вычеркиванием i-й строки и j-го столбца.)

Пример:

Найти матрицу, обратную данной:

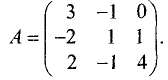
Решение. Определитель матрицы А

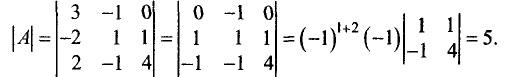
Составим определитель матрицы 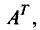транспонированной к матрице А:

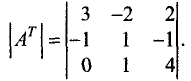
Находим алгебраические дополнения определителя матрицы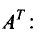

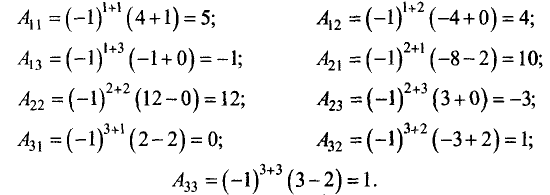
Составляем матрицу 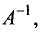обратную матрице А:

Проведем проверку, умножив А на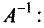

Ранг матрицы

Пусть дана матрица

где m — количество строк, n — количество столбцов.

Выбираем в матрице А произвольные k строк и k столбцов,
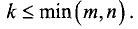Элементы, стоящие на пересечении данных строк и столбцов, составляют квадратную матрицу k-го порядка матрицы А . Определитель квадратной матрицы А называется минором. Нас интересуют порядки тех миноров матрицы А, которые отличны от нуля.

Наивысший порядок минора, отличного от нуля, называется рангом матрицы.

Обозначается rang А или r(А).

При отыскании ранга матрицы полезно знать, что если все миноры k-го порядка матрицы А равны нулю, то равны нулю и все миноры более высоких порядков.

При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор k-го порядка D, отличный от нуля, то требуется вычислить лишь миноры (k + 1)-го порядка, окаймляющие минор D. Если все они равны нулю, то ранг матрицы равен k.

Пример:

Найти ранг матрицы

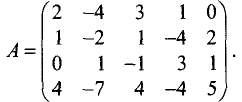
Решение:

Возьмем отличный от нуля минор второго порядка

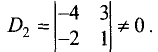
Минор третьего порядка 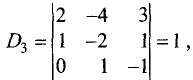окаймляющий минор
отличен от нуля. Два минора четвертого порядка, окаймляющие
минор равны нулю. Действительно,

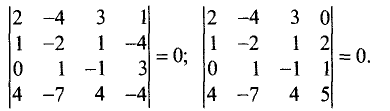
Таким образом, ранг матрицы А равен трем (rang А = 3). ►

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические функции числового аргумента
101. Тригонометрические выражения и их преобразования
102. Преобразование тригонометрических выражений
103. Комбинаторика
104. Вычислительная математика
105. Прямая линия на плоскости и ее уравнения
106. Прямая и плоскость
107. Линии и уравнения
108. Прямая линия
109. Уравнения прямой и плоскости в пространстве
110. Кривые второго порядка
111. Кривые и поверхности второго порядка
112. Числовые ряды
113. Степенные ряды
114. Ряды Фурье
115. Преобразование Фурье
116. Функциональные ряды
117. Функции многих переменных
118. Метод координат
119. Гармонический анализ
120. Вещественные числа
121. Предел последовательности
122. Аналитическая геометрия
123. Аналитическая геометрия на плоскости
124. Аналитическая геометрия в пространстве
125. Функции одной переменной
126. Высшая алгебра
127. Векторная алгебра
128. Векторный анализ
129. Векторы
130. Скалярное произведение векторов
131. Векторное произведение векторов
132. Смешанное произведение векторов
133. Операции над векторами
134. Непрерывность функций
135. Предел и непрерывность функций нескольких переменных
136. Предел и непрерывность функции одной переменной
137. Производные и дифференциалы функции одной переменной
138. Частные производные и дифференцируемость функций нескольких переменных
139. Дифференциальное исчисление функции одной переменной
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат