Оглавление:
Многочлен (некоторые сведения справочного характера):
Функция вида
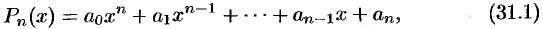
где 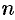 — натуральное число,
— натуральное число, 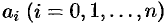 — постоянные коэффициенты, называется многочленом (или целой рациональной функцией). Число
— постоянные коэффициенты, называется многочленом (или целой рациональной функцией). Число 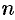 называется степенью многочлена.
называется степенью многочлена.
Корнем многочлена (31.1) называется такое значение 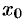 (вообще говоря, комплексное) переменной
(вообще говоря, комплексное) переменной 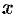 , при котором многочлен обращается в нуль, т. е.
, при котором многочлен обращается в нуль, т. е. 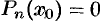 .
.
Теорема:
Если 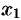 есть корень многочлена
есть корень многочлена 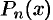 , то многочлен делится без остатка на
, то многочлен делится без остатка на 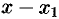 , т. е.
, т. е.
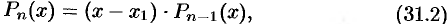
где 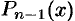 — многочлен степени
— многочлен степени  .
.
Возникает вопрос: всякий ли многочлен имеет корень? Положительный ответ на этот вопрос дает следующее утверждение.
Теорема:
Основная теорема алгебры. Всякий многочлен 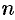 -й степени (
-й степени (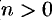 ) имеет по крайней мере один корень, действительный или комплексный.
) имеет по крайней мере один корень, действительный или комплексный.
Доказательство этой теоремы мы не приводим.
Пользуясь основной теоремой алгебры, докажем теорему о разложении многочлена на линейные множители.
Теорема:
Всякий многочлен 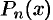 можно представить в виде
можно представить в виде
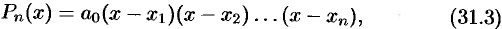
где 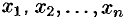 — корни многочлена,
— корни многочлена, 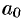 — коэффициент многочлена при
— коэффициент многочлена при 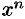 .
.
Рассмотрим многочлен (31.1). По теореме 31.2 он имеет корень. Обозначим его через 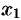 . Тогда имеет место соотношение (31.2). А так как
. Тогда имеет место соотношение (31.2). А так как 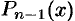 — также многочлен, то он имеет корень. Обозначим его через
— также многочлен, то он имеет корень. Обозначим его через 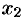 . Тогда
. Тогда 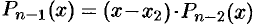 , где
, где 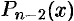 — многочлен (
— многочлен (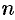 -2)-й степени. Следовательно,
-2)-й степени. Следовательно, 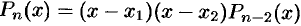 .
.
Продолжая этот процесс, получим в итоге:
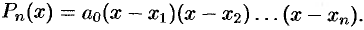
Множители 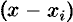 в равенстве (31.3) называются линейными множителями.
в равенстве (31.3) называются линейными множителями.
Пример:
Разложить многочлен 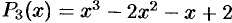 на множители.
на множители.
Решение:
Многочлен 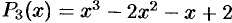 обращается в нуль при
обращается в нуль при 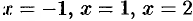 . Следовательно,
. Следовательно,
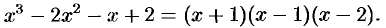
Пример:
Представить выражение 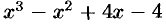 в виде произведения линейных множителей.
в виде произведения линейных множителей.
Решение:
Легко проверить, что
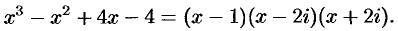
Если в разложении многочлена (31.3) какой-либо корень встретился 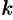 раз, то он называется корнем кратности
раз, то он называется корнем кратности 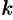 . В случае
. В случае 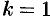 (т. е. корень встретился один раз) корень называется простым.
(т. е. корень встретился один раз) корень называется простым.
Разложение многочлена (31.3) можно записать в виде
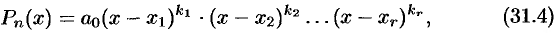
если корень 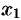 имеет кратность
имеет кратность 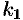 , корень
, корень 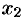 — кратность
— кратность 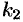 и так далее. При этом
и так далее. При этом  , a
, a 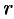 — число различных корней.
— число различных корней.
Например, разложение
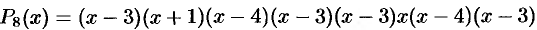
можно записать так:
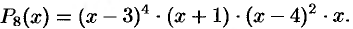
Пользуясь теоремой 31.3, можно доказать следующие утверждения.
Теорема:
Если многочлен 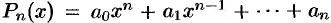 тождественно равен нулю, то все его коэффициенты равны нулю.
тождественно равен нулю, то все его коэффициенты равны нулю.
Теорема:
Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Например, если 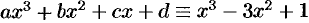 , то
, то 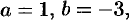
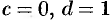 .
.
Теорема:
Если многочлен 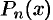 с действительными коэффициентами имеет комплексный корень
с действительными коэффициентами имеет комплексный корень 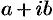 , то он имеет и сопряженный корень
, то он имеет и сопряженный корень 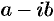 .
.
В разложении многочлена (31.3) комплексные корни входят сопряженными парами. Перемножив линейные множители
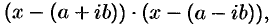
получим трехчлен второй степени с действительными коэффициентами 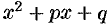 . В самом деле,
. В самом деле,
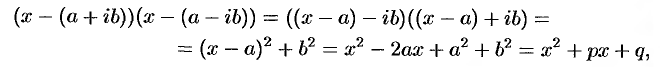
где 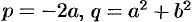 .
.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами.
С учетом вышеизложенного справедлив следующий факт.
Теорема:
Всякий многочлен с действительными коэффициентами разлагается на линейные и квадратные множители с действительными коэффициентами, т. е. многочлен 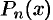 можно представить в виде
можно представить в виде
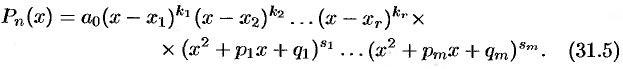
При этом 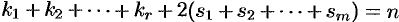 , все квадратные трехчлены не имеют вещественных корней.
, все квадратные трехчлены не имеют вещественных корней.
Примеры разложений (31.5):
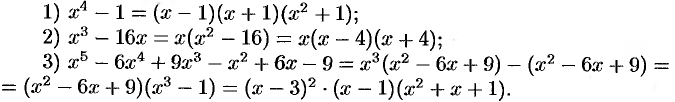
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Метод интегрирования подстановкой |
| Метод интегрирования по частям |
| Дробно-рациональная функция |
| Интегрирование рациональных дробей |
Рациональная функция одной переменной
Рациональной функцией или рациональной дробью называется функция, равная частному от деления двух многочленов:
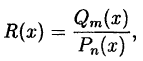
где
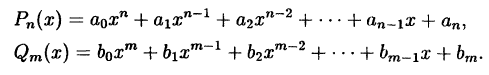
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя и неправильной — в противном случае. Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной дроби.
Пример:
Представить в виде суммы многочлена и правильной
дроби следующую неправильную дробь:
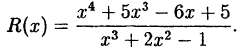
Решение:
Разделив числитель на знаменатель получим в частном 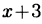 в остатке
в остатке 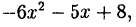 т.е.,
т.е.,
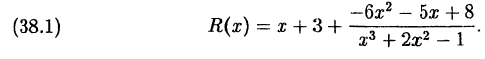
Остаток от деления многочлена 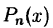 на разность
на разность 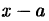 можно найти, не выполняя самого процесса деления на основании следующей теоремы.
можно найти, не выполняя самого процесса деления на основании следующей теоремы.
Теорема Везу:
Остаток от деления многочлена 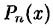 на разность
на разность 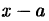 равен значению многочлена
равен значению многочлена 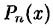 при
при 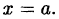
Пример:
Найти остаток от деления многочлена 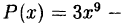
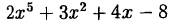 на двучлен
на двучлен 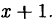
Решение:
Здесь 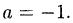 Поэтому искомый остаток равен:
Поэтому искомый остаток равен:
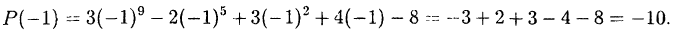
Некоторые сведения о многочленах
Рассмотрим кратко
некоторые сведения о многочленах, которые понадобятся нам в
дальнейшем.
- Корнем многочлена
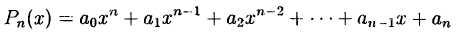
называется всякое число 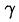 (действительное или комплексное), которое обращает многочлен в нуль, т.е. такое, что
(действительное или комплексное), которое обращает многочлен в нуль, т.е. такое, что 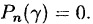
Пример:
Проверить, что 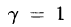 является корнем многочлена
является корнем многочлена 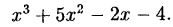
Решение: Действительно: 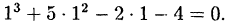
2. Имеет место следующая теорема, принимаемая без доказательства:
Теорема:
Всякий многочлен степени 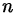 может быть
может быть
представлен в виде произведения 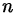 множителей вида
множителей вида  и множителя при старшей степени
и множителя при старшей степени 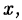 т.е
т.е
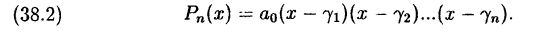
Числа 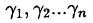 очевидно являются корнями многочлена.
очевидно являются корнями многочлена.
Если в разложении 38.2 раскрыть скобки, то свободный член
многочлена будет равен произведению корней многочлена 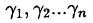
Отсюда вытекает следующее правило: Если многочлен 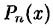 имеет
имеет
целые корни, то эти корни являются делителями свободного члена.
Так как любое число имеет конечное множество целых делителей, то
это правило позволяет решать алгебраические уравнения степени выше двух при условии, что хотя бы один корень — целое число.
Пример:
Решить уравнение

Решение:
Если у него есть целые корни, то только 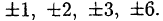 Подставив в уравнение, например,
Подставив в уравнение, например, 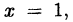 получим тождество. Следовательно, на основании теоремы Безу многочлен
получим тождество. Следовательно, на основании теоремы Безу многочлен 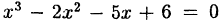 делится на разность
делится на разность 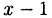 без остатка. Выполнив это деление, получим:
без остатка. Выполнив это деление, получим:
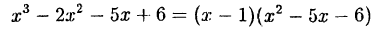
Решив квадратное уравнение
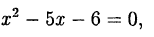
найдем корни: -3 и 2. Следовательно, корни уравнения (38.3):
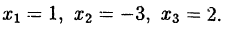
Пример:
Легко проверить, что 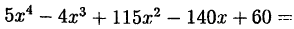
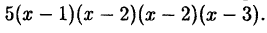
Пример:
Многочлен 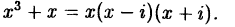
3. Среди линейных множителей в (38.2) могут быть одинаковые.
Объединяя их, можем записать разложение многочлена на множители в виде:
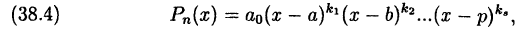
где все корни 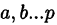 различны, и сумма показателей степени равна
различны, и сумма показателей степени равна 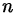 .
.
Корни 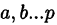 называются кратными корнями многочлена, а именно
называются кратными корнями многочлена, а именно 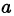 — корень кратности
— корень кратности 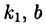 — корень кратности,
— корень кратности, 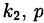 — корень кратности
— корень кратности
4. Среди корней в разложении (38.2) могут быть комплексное 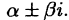
В алгебре доказывается: если 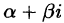 является корнем многочлена кратности
является корнем многочлена кратности 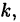 то и сопряженное число
то и сопряженное число 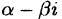 так же является корнем этого же многочлена той же кратности.
так же является корнем этого же многочлена той же кратности.
5. Поэтому, если в разложении (38.4) есть множитель 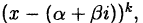 то в этом разложении присутствует множитель
то в этом разложении присутствует множитель 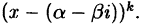
Перемножив два множителя, соответствующие комплексным
сопряженным корням, получим (см. 37.7):
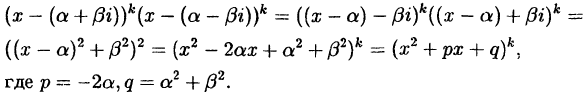
Обратите внимание что трехчлен 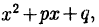 равный сумме двух
равный сумме двух
квадратов имеет отрицательный дискриминант.
6. Все вышесказанное позволяет сформулировать утверждение:
всякий многочлен с действительными коэффициентами можно представить в следующем виде:
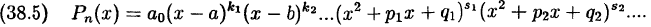
В 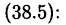
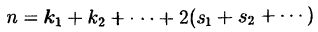
В нем линейные множители соответствуют действительным корням,
а квадратные трехчлены, имеющие по два корня — комплексным корням многочлена.
Разложение правильной рациональной дроби на простейшие
Определение:
Дроби
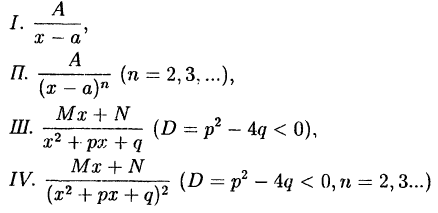
называются простейшими дробями первого, второго, третьего и
четвертого типов.
В высшей алгебре доказывается следующая теорема, которую мы
принимаем без доказательства:
Теорема:
Правильную рациональную дробь 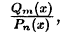 где
где 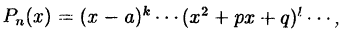 можно единственным образом
можно единственным образом
разложить на сумму простейших дробей:
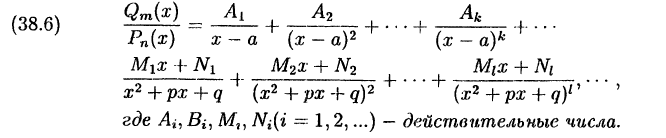
В формуле (38.6) первое многоточие в разложении многочлена 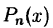 на множители соответствует другим, кроме
на множители соответствует другим, кроме 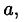 действительным корням, a второе — комплексным.
действительным корням, a второе — комплексным.
Из формулы (38.6) следует, что линейным множителям в разложении знаменателя соответствуют дроби I и II типов, а квадратичным множителям соответствуют простейшие дроби III и IV типов.
При этом число простейших дробей, соответствующих данному
множителю, равно степени, с которой этот множитель входит в разложение знаменателя дроби на множители.
Правило разложения правильной рациональной дроби остается
справедливым при любом числе линейных и квадратичных множителей в разложении знаменателя 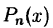
Рассмотрим два способа нахождения коэффициентов разложения (38.6).
Метод неопределенных коэффициентов
Этот метод основан
на следующем утверждении, принимаемом без доказательства: если два многочлена тождественно равны, то равны и коэффициенты при
одинаковых степенях неизвестной в обеих частях тождества.
Поэтому приводя в правой части разложения (38.6) к общему
знаменателю, получаем тождественное равенство двух рациональных дробей с равными знаменателями.
Следовательно, числители тождественно равны. Приравнивая
коэффициенты при одинаковых степенях неизвестной, получим систему линейных уравнений, относительно неизвестных коэффициентов 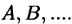 Рассмотрим примеры.
Рассмотрим примеры.
Пример:
Разложить на простейшие дроби: 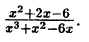
Решение:
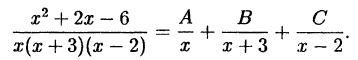
Приводим правую часть этого тождества к общему знаменателю:
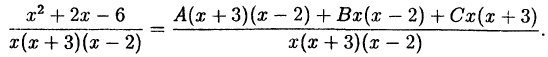
Приравниваем числители:
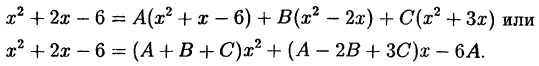
Приравниваем коэффициенты при одинаковых степенях 
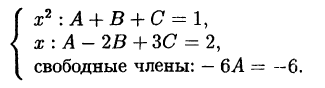
Можно показать, что эта система всегда имеет единственное решение.
Это решение следующее:
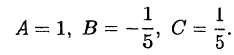
Подставив найденные коэффициенты в разложение (38.7),
окончательно получим:
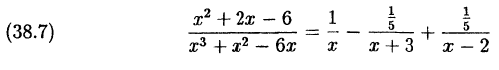
Пример:
Разложить на простейшие дроби:
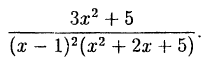
Решение:
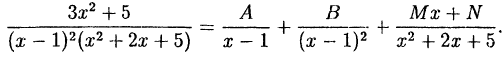
Приведем правую часть к общему знаменателю:
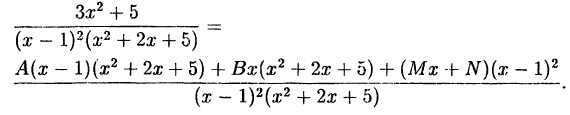
Приравнивая числители, получаем:
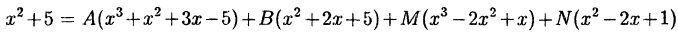
или
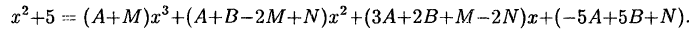
Приравнивая коэффициенты при одинаковых степенях ж получаем
систему:
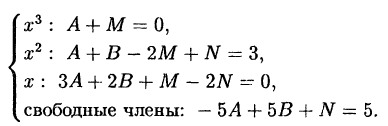
Ее решение: 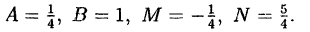
Следовательно, подставив найденные коэффициенты в (38.8), получим:
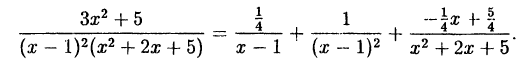
Метод произвольных значений
Этот метод основан на
утверждении: если два многочлена тождественно 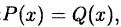 то они равны при любом значении независимой переменной
то они равны при любом значении независимой переменной 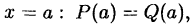 где
где 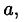 произвольное число.
произвольное число.
Поэтому вместо приравнивания коэффициентов при одинаковых
степенях неизвестной в разложении (38.6) можно подставлять туда вместо 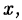 несколько произвольных чисел.
несколько произвольных чисел.
Этот метод особенно эффективен когда многочлен 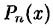 стоящий в
стоящий в
знаменателе имеет различные действительные корни и в качестве
произвольных значений берутся числа, равные действительным корням знаменателя.
Пример:
Разложить на простейшие дроби функцию из примера (38.7).
Решение:
Ранее, при использовании метода неопределенных
коэффициентов было получено:
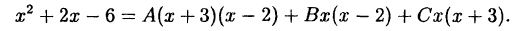
Подставим в это тождество последовательно три значения 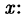
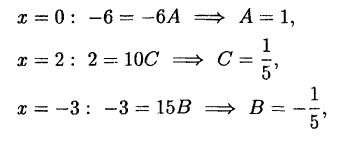
Опять получаем соотношение (38.7).
Рассмотрим теперь пример, в котором для разложения знаменателя на множители можно использовать операцию извлечения корня из комплексного числа.
Пример:
Разложить на простейшие дроби 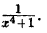
Решение:
Многочлен 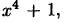 стоящий в знаменателе имеет лишь
стоящий в знаменателе имеет лишь
комплексные корни, которые мы нашли в лекции 37:
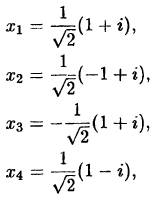
Таким образом,
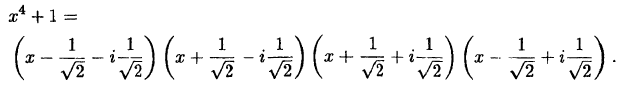
Объединив первую скобку с последней, вторую с третьей, получим:
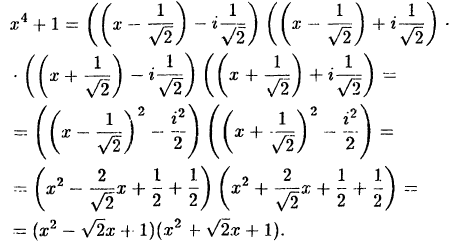
В соответствии с формулой (38.6) и методом неопределенных
коэффициентов, находим:
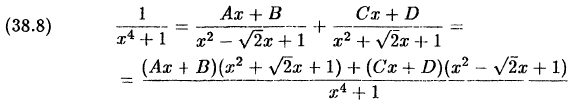
и, следовательно,
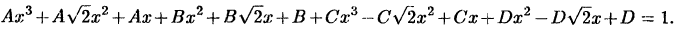
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях равенства, получим систему уравнений для определения неизвестных 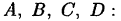
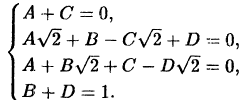
Выразив из первого уравнения С через А, а из последнего D через В и подставив 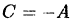 и
и 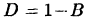 во второе и третье уравнения системы, получим:
во второе и третье уравнения системы, получим:
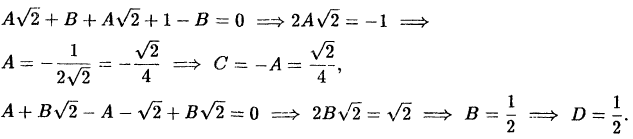
Подставляя найденные значения 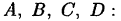 в (38.8) найдем разложение дроби
в (38.8) найдем разложение дроби 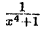 на простейшие:
на простейшие:
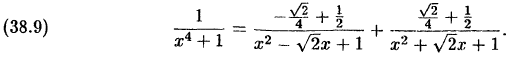
Замечание:
Разложение (38.9) многочлена 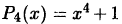 на
на
множители можно было бы получить и методом неопределенных коэффициентов.
Учитывая, что комплексные корни входят в разложение многочлена на множители как корни квадратных трехчленов вида 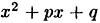 при
при 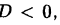 запишем:
запишем:
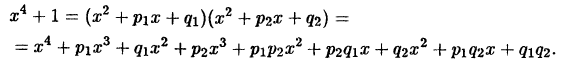
Приравнивая коэффициенты при одинаковых степенях 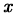 слева и справа в полученном тождестве, получим уравнения для определения
слева и справа в полученном тождестве, получим уравнения для определения 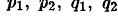 и найдем их так:
и найдем их так:
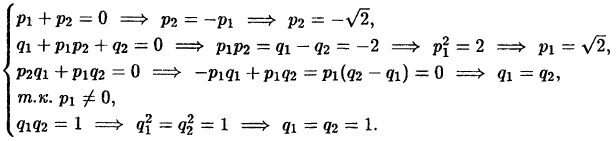
Отметим, что 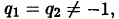 так как в этом случае из второго уравнения следовало бы, что
так как в этом случае из второго уравнения следовало бы, что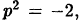 что невозможно. Таким образом, мы получили опять разложение (38.9).
что невозможно. Таким образом, мы получили опять разложение (38.9).
Замечание:
Разложить 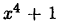 на множители можно еще и так. Прибавим и вычтем
на множители можно еще и так. Прибавим и вычтем 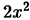 и воспользуемся формулой сокращенного умножения:
и воспользуемся формулой сокращенного умножения:
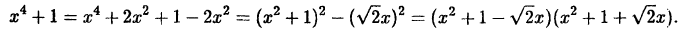
Этот пример показывает, что нестандартные приемы решения часто очень эффективны!
Разложение рациональных дробей на простейшие
Рассмотрим прежде всего примеры на выделение целой части в
неправильной дроби.
Пример:
Представить неправильную дробь 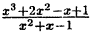 в виде суммы целой части и правильной дроби.
в виде суммы целой части и правильной дроби.
Решение:
Разделим числитель на знаменатель
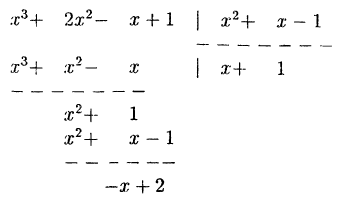
Следовательно,
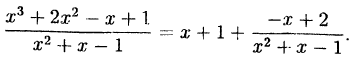
В следующих примерах представим (без отыскания коэффициентов)
правильную дробь в виде суммы элементарных дробей.
Пример:
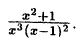
Решение:
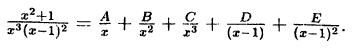
Пример:
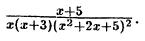
Решение:
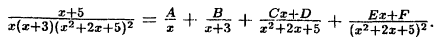
В следующих примерах разложить правильную дробь на простейшие и найти коэффициенты разложения с помощью метода произвольных значений.
Пример:
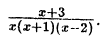
Решение:
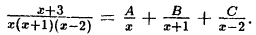
В правой части тождества приводим к общему знаменателю и
приравниваем числители:
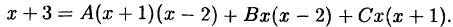
Подставляем в обе части тождества произвольные значения 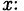
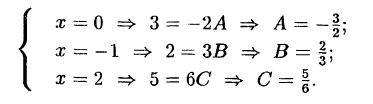
Следовательно,
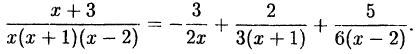
Пример:
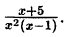
Решение:
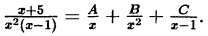
Далее:
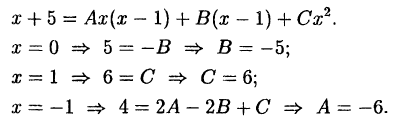
Следовательно,
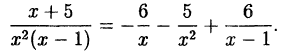
В следующих примерах разложить правильную дробь на простейшие и найти коэффициенты с помощью метода неопределенных коэффициентов.
Пример:
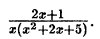
Решение:
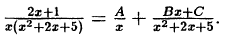
Приведем в правой части к общему знаменателю и приравняем
числители
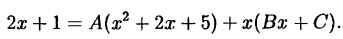
Раскроем скобки и приведем подобные члены
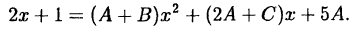
Приравняем коэффициенты при одинаковых степенях 
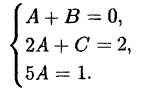
Решив эту систему, найдем
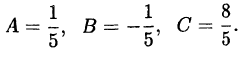
Следовательно,
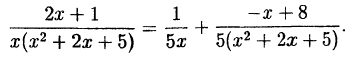
Пример:
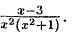
Решение:
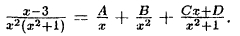
Далее
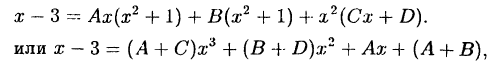
получаем систему:
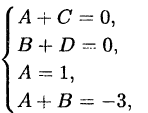
откуда 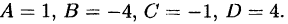
Поэтому
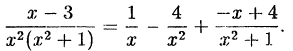
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
