Непрерывные дроби в математике с примерами решения и образцами выполнения

Определение непрерывной дроби:

Непрерывной, или цепной, дробью называется дробь вида: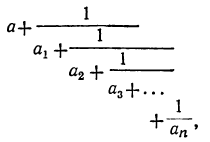

где целое число а складывается с дробью, у которой числитель есть 1, а знаменатель целое число α₁, сложенное с дробью, у которой числитель есть 1, а знаменатель целое число α₂, сложенное с дробью,…, и т. д. (все целые числа предполагаются положительными).

Дроби 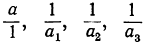и т. д. называются составляющими дробями или звеньями.

Написанную выше непрерывную дробь сокращённо изображают так:
(α, α₁, α₂, α₃,…, ).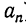

Например дроби: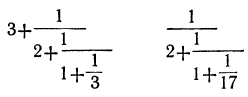

сокращённо изображаются: (3, 2, 1, 3) и (0, 2, 1, 17).

Обращение непрерывной дроби в обыкновенную

Всякую непрерывную дробь можно обратить в обыкновенную; для этого достаточно произвести по правилам арифметики все действия, указанные в изображении непрерывной дроби.

Пусть, например, мы имеем такую дробь: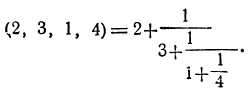

Производим указанные действия: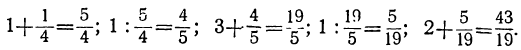

Это и есть обыкновенная дробь, представляющая точное значение данной непрерывной.

Обращение обыкновенной дроби в непрерывную

Всякую обыкновенную дробь можно обратить в непрерывную. Пусть, например, дана дробь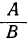. Исключив из неё целое число, получим: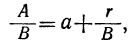

где а есть целое частное, а r₁ — остаток от деления А на В (если дробь 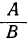правильная, то а=0 и r=А).

Разделив оба члена дроби 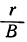на r, получим: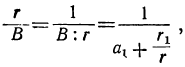

где α₁ есть целое частное, a r₁ — остаток от деления В на r.

Разделив оба члена дроби 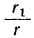на r₁, получим: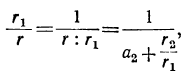

где α₂ есть целое частное, a r₂ — остаток от деления r на r₁. Продолжая этот приём далее, будем последовательно получать: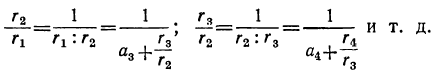

Так как B>r>r₁>r₂>r₃,…, то, продолжив этот приём, дойдём до остатка, равного 0. Пусть 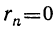, т. е..

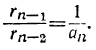Тогда путём подстановки получим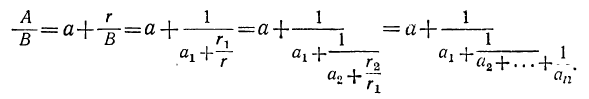

Замечание. Из рассмотрения этого приёма следует, что a a₁, a₂,…, 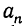— целые частные, получаемые при последовательном делении А на В, потом В на первый остаток, первого остатка на второй и т. д., иначе говоря, это — целые частные, получаемые при нахождении общего наибольшего делителя между AnB способами последовательного деления. Вследствие этого числа a a₁, a₂,…, 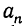называются частными непрерывной дроби.

Примеры:
1) Обратить в непрерывную дробь число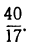
Так как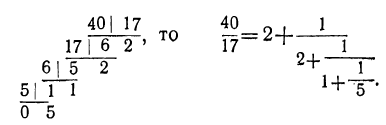

2) Обратить в непрерывную дробь число.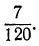
Так как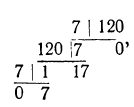
то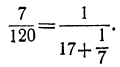

Подходящие дроби

Если в непрерывной дроби возьмём несколько звеньев с начала, отбросив все остальные, и составленную
ими непрерывную дробь обратим в обыкновенную, то получим так называемую подходящую дробь. Первая подходящая дробь получится, когда возьмём одно первое звено: вторая — когда возьмём два первых звена, и т. д. Таким образом, для непрерывной дроби: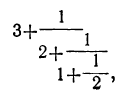

первая подходящая дробь есть ;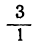
вторая „ „ „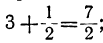
третья „ „ „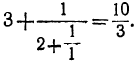

Четвёртая подходящая дробь представит в этом примере точную величину непрерывной дроби .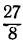

Когда в непрерывной дроби нет целого числа, то первая подходящая дробь есть 0.

Закон составления подходящих дробей

Составим для непрерывной дроби ( a a₁, a₂,…, 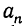) первые три подходящие дроби: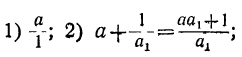

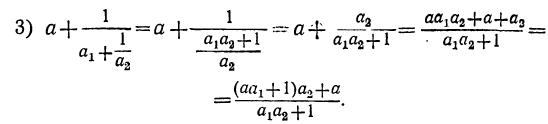
Сравнивая третью подходящую дробь с двумя первыми, заметим, что числитель третьей подходящей дроби получится, если числитель второй подходящей дроби умножим на соответствующее частное (т. е. на α₂) и к полученному произведению прибавим числитель первой подходящей дроби; знаменатель третьей подходящей дроби получится подобным же образом из. знаменателей предыдущих двух подходящих дробей.

Докажем, что этот закон применим ко всякой подходящей дроби, следующей за третьей, т. е. мы докажем, что вообще числитель (n+1)-й подходящей дроби получится, если числитель n-й подходящей дроби умножим на соответствующее частное (т. е. на 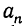) и произведение сложим с числителем (n— 1)-й подходящей дроби, и что знаменатель (n+l)-й подходящей дроби подобным же способом получится из знаменателей n-й и (n — 1)-й подходящих дробей. Употребим доказательство от n к (n+1), т. е. докажем, что если этот закон применим к n-й подходящей дроби, то он применим и к (n+1)-й подходящей дроби.

Обозначим первую, вторую, третью и т. д. подходящие дроби последовательно через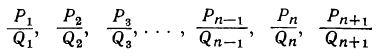

и заметим, что соответствующие им частные будут: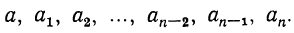

Допустим, что верны равенства: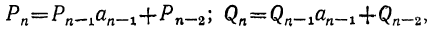
(1)
и, следовательно: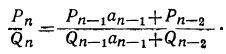
(2)

Требуется доказать, что в таком случае и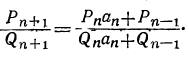
(3)

Из сравнения двух подходящих дробей: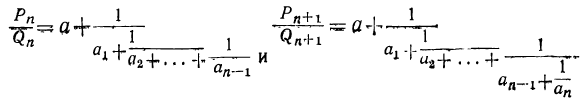

усматриваем, что (n+1)-я подходящая дробь получится из n-й, если в последней заменим число 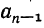на сумму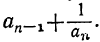

Поэтому равенство (2) даёт: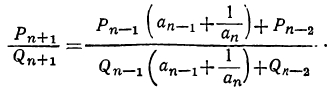

Раскрыв скобки и умножив оба члена дроби на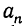, получим: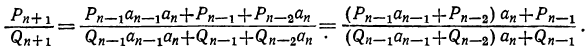

Приняв во внимание равенство (1), можем окончательно написать: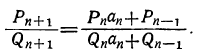

Это и есть равенство (3), которое требовалось доказать.

Таким образом, если доказываемый закон верен для n-й подходящей дроби, то он будет верен и для (n+l)-й подходящей дроби. Но мы непосредственно видели, что он верен для третьей подходящей дроби; следовательно, по доказанному, он применим для четвёртой подходящей дроби; а если для четвёртой, то и для пятой и т. д.

Пользуясь этим законом, составим все подходящие дроби для следующего примера: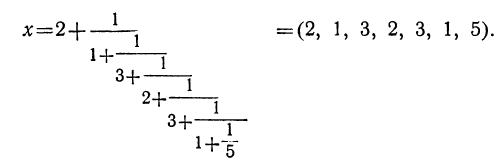

Вычисления всего удобнее расположить так:

		3	2	3	1	5
2	3	11	25	86	111	641
1	1	4	9	31	40	231

Первые две подходящие дроби найдём непосредственно, это будут 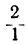и 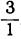. Остальные подходящие дроби получим, основываясь на доказанном законе. Для памяти размещаем в верхней строке целые частные с третьего до последнего.

Теорема:

Точное значение непрерывной дроби заключается между двумя последовательными подходящими дробями, причём оно ближе к последующей, чем к предыдущей.

Доказательство:

Пусть имеем непрерывную дробь: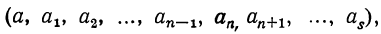

точную величину которой обозначим через А. Возьмём какие-нибудь три последовательные подходящие дроби: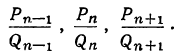

По доказанному, имеем: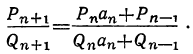

Если в правую часть этого равенства мы вместо 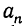подставим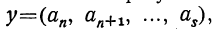, то в левой части получим точную величину А непрерывной дроби, значит: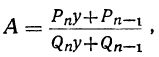

откуда: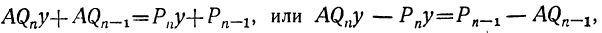

и значит: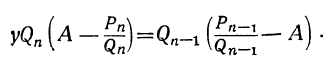

Из последнего равенства можем вывести два следующих заключения:
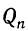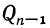1) Так как числа у, и положительные, то разности, стоящие внутри скобок, должны быть одновременно положительны или одновременно отрицательны; значит:
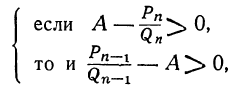или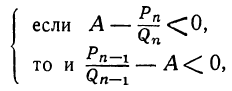
т.е. 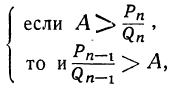или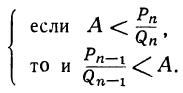

Следовательно, А заключено между всякими двумя последовательными подходящими дробями.

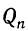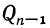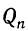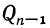2) Так как у>1 и >, причём числа и положительные, то из того же равенства выводим: абсолютная величина 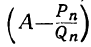меньше абсолютной величины.

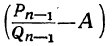Отсюда следует, что 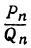ближе к А, чем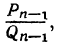, что и требовалось доказать.

Замечание:

Так как, очевидно, A>а, т. е. 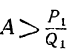, то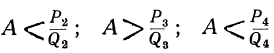
и т. д.

Точное значение непрерывной дроби более всякой подходящей дроби нечётного порядка и менее всякой подходящей дроби чётного порядка.

Теорема:

Разность между двумя рядом стоящими подходящими дробями равна + 1, делённой на произведение знаменателей этих подходящих дробей.

Доказательство:

Так как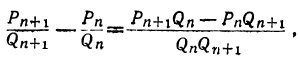

то очевидно, что знаменатель этой разности удовлетворяет требованию теоремы. Остаётся доказать, что числитель равен ±1.

Так как
Pn+1=Pnαn+Pn-1 и Q,,+ι=Qnαn+Qn-ι,
то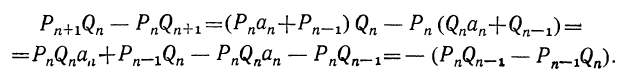

Выражение, стоящее в скобках, представляет собой числитель P P —
дроби, которая получится от вычитания из 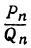дроби

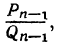
Следовательно, мы доказали, что абсолютная величина числителя дроби, получаемой от вычитания 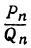из 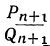, равна абсолютной величине числителя дроби, получаемой от вычитания 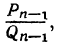из 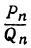, другими словами, абсолютная величина числителя дроби, получаемой от вычитания одной из другой двух рядом стоящих подходящих дробей, есть величина постоянная для всех подходящих дробей. Но разность между второй и первой подходящими дробями есть: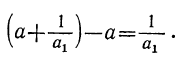

Следовательно, числитель разности между всякими двумя рядом стоящими подходящими дробями по абсолютной своей величине равен 1.

Так, если взять пример, приведённый, то найдём: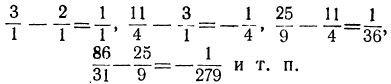

Следствия:

1. Всякая подходящая дробь есть дробь несократимая, потому что, если бы 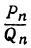могло быть сокращено на некоторый делитель 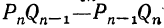делилось бы на m, что невозможно, так как эта разность равна ±1.

2. Если вместо точной величины непрерывной дроби возьмём подходящую дробь 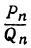, то сделаем ошибку, меньшую каждого из трёх
следующих чисел: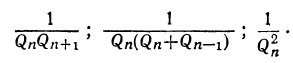

Действительно, если А есть точное значение непрерывной дроби, то 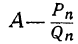численно меньше разности 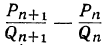, абсолютная величина которой, по доказанному, равна .

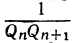C другой стороны, так как 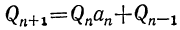, где, то 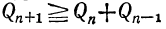и, следовательно: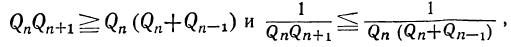

и потому абсолютная величина разности 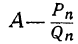меньше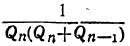

Наконец, так как 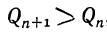, то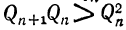 и потому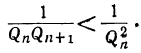

Следовательно, абсолютная величина разности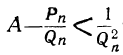

Из трёх указанных пределов погрешности самый меньший есть 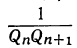но его вычисление предполагает известным знаменатель подходящей дроби, следующей за той, которую мы приняли за приближение. Вычисление предела 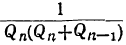может быть выполнено только тогда, когда известен знаменатель предшествующей подходящей дроби.

Когда же известна одна подходящая дробь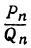 возможно только
указание предела погрешности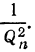

Например, если мы знаем, что некоторая подходящая дробь данной непрерывной дроби есть 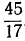, то можно сказать, что 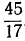точно до
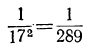. Если, кроме того, знаем, что знаменатель предшествующей подходящей дроби есть, например, 8, то можем сказать, что 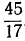точно до 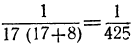• Наконец,
когда знаем, что знаменатель следующей подходящей дроби есть, например, 37, то можем ручаться, что 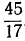разнится от точного значения непрерывной дроби менее, чем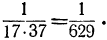

Теорема:

Подходящая дробь ближе к точному значению непрерывной дроби, чем всякая другая дробь с меньшим знаменателем.

Доказательство:

Допустим, что существует дробь 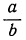, менее отличающаяся от точного значения непрерывной дроби А, чем под-р
холящая дробь 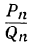, и пусть. Докажем, что это предположение ведёт к противоречию. Так как 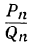ближе к А, чем 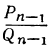, и 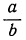ближе к A, чем 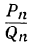то и подавно 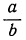ближе к А. чем 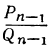; так как, кроме того, А заключается между 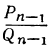и 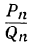, то абсолютная величина разности 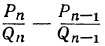больше абсолютной величины разности 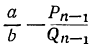; значит, обращая внимание только на абсолютные величины, можно написать: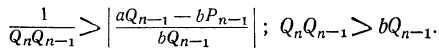

Перемножив почленно эти неравенства, получим: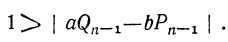

Так как 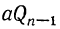и 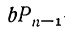числа целые, то это неравенство возможно только при условии:
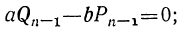, откуда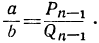

Но это равенство невозможно, так как, по предположению, 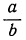ближе подходит к А, чем 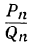тогда как 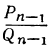, по доказанному, больше разнится от А, чем 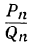. Полученное противоречие доказывает справедливость теоремы 3.

Приближённые значения данной арифметической дроби

Когда числитель и знаменатель данной несократимой арифметической дроби выражены большими числами, часто является потребность получить приближённое значение этой дроби в возможно более простом виде. Для этого достаточно обратить данную дробь в непрерывную и найти ту или другую подходящую дробь, смотря по желаемой степени приближения.

Пример:

Зная, что число π, представляющее отношение окружности к её диаметру, заключено между двумя дробями: 3,141592653 и 3,141592654, найти простейшее приближение π.

Обратив обе дроби в непрерывные и взяв только общие неполные частные, найдём:
π =(3, 7, 15, 1, …).

Подходящие дроби будут:

		15	1
3	22	333	355
1	7	106	113

Приближение 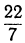было найдено Архимедом; оно верно до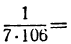 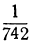значит, и подавно верно до 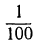. Число 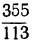было указано Адрианом Мецием; взяв это число вместо π, сделаем ошибку, меньшую 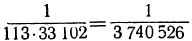т. e. во всяком случае меньшую одной миллионной. Приближения Архимеда и Меция, как подходящие дроби чётного порядка, более π.

Извлечение квадратного корня

Пусть требуется найти 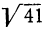при помощи непрерывных дробей. Рассуждаем так: наибольшее целое число, заключающееся в 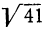, есть 6; поэтому можем положить:

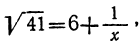
откуда: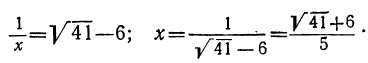
(1)

Так как 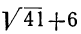равняется 12 с дробью, то наибольшее число, заключающееся в 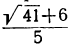, ecть 2; поэтому можем положить: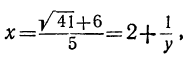

откуда: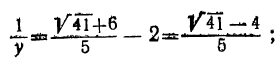
(2)

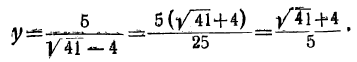
Так как 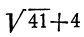равняется 10 с дробью, то и наибольшее целое число, заключающееся в 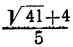; поэтому можем положить:
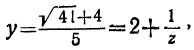(3)
откуда: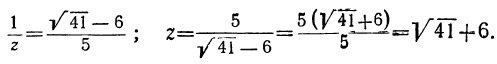

Наибольшее целое число, заключающееся в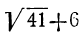, есть 12; поэтому можем положить: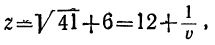

откуда: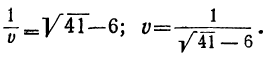

Сравнивая формулу для v с формулой для х, находим, что υ = х. Пользуясь равенствами (1), (2), (3) и (4), получим: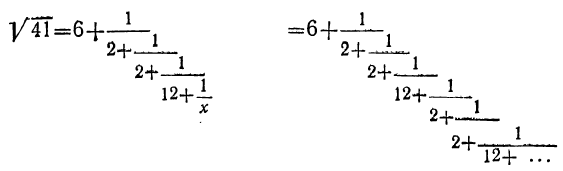

Таким образом, 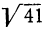выразился периодической непрерывной дробью. Найдя подходящие дроби, получим приближённые значения :

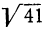		2	12	2	2	…
6	13	32	397	826	2049	…
1	2	5	62	129	320	…

Подобным же образом найдём:
√13=(3; 1; 1; 1; 1; 6; 1; 1; …); √29=(5; 2; 1; 1; 2; 10; …).

Нахождение решения неопределённого уравнения

Непрерывные дроби дают средство найти одно решение неопределённого уравнения ax+by=c. Покажем это на примерах. Пусть имеем уравнение:
43x+15y=8.

Возьмём дробь 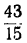и обратим её в непрерывную: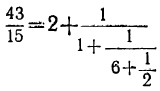

Найдём теперь предпоследнюю подходящую дробь; это будет .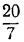
Так как последняя подходящая дробь есть точное значение непрерывной дроби, т. е. 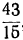, а 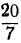есть подходящая дробь нечётного порядка, то на основании теоремы (замечание) можем написать: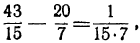

откуда:
43‧7—15‧20=1.

Чтобы уподобить последнее тождество данному уравнению, умножим все его члены на 8 и представим его так:
43‧56+15 (—160)=8.

Сравнив теперь это тождество с нашим уравнением, находим, что в последнем за х можно принять число 56, а за у число—160. Тогда всевозможные решения выразятся формулами:
x=56-15t; у=—160+43t.

Эти формулы можно упростить, заменив t на t+3 (что можно сделать вследствие произвольности числа t):
х=56—15(t+3) = 11-15t; у= —160+43 (t+3)= -31 +43t.

Возьмём ещё пример: 7x—19y=5.

Обратив дробь 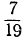в непрерывную, найдём: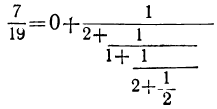

Предпоследняя подходящая дробь будет 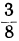. Так как она чётного порядка, то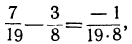

откуда:
7‧8—19∙3=-1.

Умножив все члены этого равенства на 5, получим:
7‧40—19‧15=-5, или 7∙ (—40)-19∙(-15)=5.

Сравнивая последнее тождество с данным уравнением, находим, что в последнем за х можно принять число—40, а за у число —15.

Тогда:
x = -40+19t; у= —15+7t.

Эти формулы можно упростить, заменив t на t+2:
x = -40+19 (t+2) = -2+19t;
у= -15+7 (t+2) =—1+7t.

Вычисление логарифма

Пусть требуется вычислить lg 2 по основанию 10; другими словами, требуется решить уравнение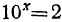. Сначала находим для х ближайшее целое число. Так как 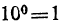, a 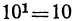, то х заключается между 0 и 1; следовательно, можно положить, что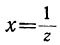, тогда 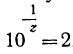, или 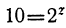. Нетрудно видеть, что z заключается между 3 и 4; следовательно, можно положить 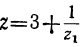. Тогда: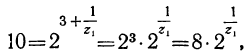

откуда: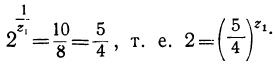

Испытанием находим, что z₁ заключается между 3 и 4, поэтому можно положить: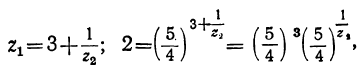

откуда: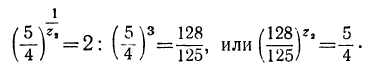

Снова испытанием находим, что z₂ заключается между 9 и 10. Этот приём можно продолжать далее. Довольствуясь приближённой величиной z₂, можем положить z₂=9; следовательно: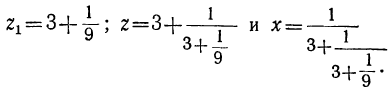

Обратив эту непрерывную дробь в обыкновенную, получим: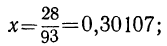

этот результат верен до четвёртого десятичного знака; более точные изыскания дают: x=0,3010300.

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Функция
24. Исследование функций
25. Предел
26. Интеграл
27. Двойной интеграл
28. Тройной интеграл
29. Интегрирование
30. Неопределённый интеграл
31. Определенный интеграл
32. Криволинейные интегралы
33. Поверхностные интегралы
34. Несобственные интегралы
35. Кратные интегралы
36. Интегралы, зависящие от параметра
37. Квадратный трехчлен
38. Производная
39. Применение производной к исследованию функций
40. Приложения производной
41. Дифференциал функции
42. Дифференцирование в математике
43. Формулы и правила дифференцирования
44. Дифференциальное исчисление
45. Дифференциальные уравнения
46. Дифференциальные уравнения первого порядка
47. Дифференциальные уравнения высших порядков
48. Дифференциальные уравнения в частных производных
49. Тригонометрические функции
50. Тригонометрические уравнения и неравенства
51. Показательная функция
52. Показательные уравнения
53. Обобщенная степень
54. Взаимно обратные функции
55. Логарифмическая функция
56. Уравнения и неравенства
57. Положительные и отрицательные числа
58. Алгебраические выражения
59. Иррациональные алгебраические выражения
60. Преобразование алгебраических выражений
61. Преобразование дробных алгебраических выражений
62. Разложение многочленов на множители
63. Многочлены от одного переменного
64. Алгебраические дроби
65. Пропорции
66. Уравнения
67. Системы уравнений
68. Системы уравнений высших степеней
69. Системы алгебраических уравнений
70. Системы линейных уравнений
71. Системы дифференциальных уравнений
72. Арифметический квадратный корень
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат