Оглавление:
Прямая принадлежит плоскости, если: 1) она проходит через две точки, лежащие в данной плоскости.
Прямая и плоскость
Зафиксируем на плоскости некоторую точку О. Положение произвольно взятой прямой L на плоскости будет вполне определено, если задать следующие величины: расстояние до нее от начальной точки О, т. е. длину р отрезка О Т перпендикуляра, опущенного из точки О на эту прямую, и единичный вектор n°, |n°| = 1, перпендикулярный прямой L и направленный из начальной точки О к этой прямой (рис. 1).
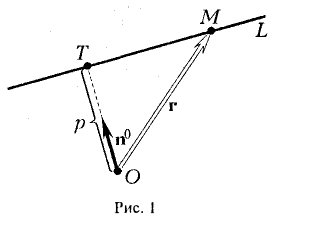
Когда текущая точка М движется по прямой L, ее радиус-вектор r меняется так, чтобы (1)
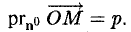
Соотношение (I) выполняется для каждой точки прямой L и нарушается, если точка М лежит вне этой прямой. Тем самым, равенство (1) выражает свойство, присущее всем точкам прямой L и только им. Иными словами, оно является уравнением этой прямой. Замечая, что
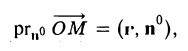
перепишем уравнение (1) в следующем виде (2)
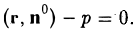
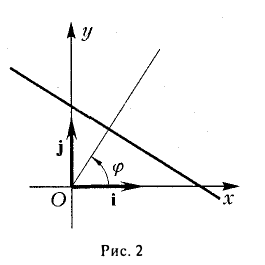
Уравнение (2) называется нормальным (нормированным) уравнением прямой в векторной форме. Радиус-вектор r произвольной точки прямой называется текущим радиусом-вектором прямой.
Введем на плоскости прямоугольную декартову систему координат, поместив ее начало в точку О. Тогда векторы n° и r можно записать так
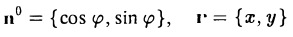
(рис. 2), и уравнение (2) примет вид (3)
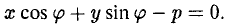
Это нормальное уравнение прямой в координатной форме.
Относительно переменных х и у уравнение (3) является уравнением первой степени. Тем самым, в прямоугольной декартовой системе координат всякая прямая на плоскости определяется уравнением первой степени относительно переменных x и у. Верно и обратное:
всякое уравнение первой степени относительно переменных х и у определяет на плоскости прямую.
В самом деле, возьмем уравнение первой степени общего вида относительно переменных x и у (4)
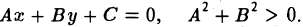
Умножим каждый член уравнения (4) на один и тот же постоянный множитель μ,

и подберем множитель μ так, чтобы уравнение (5) оказалось нормальным уравнением. Для этого достаточно положить
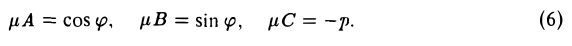
Из формул (6) находим
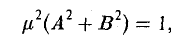
откуда
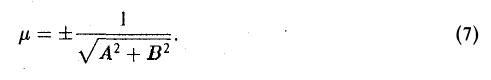
Из условия
μС = -р
вытекает, что в формуле (7) надо брать знак, противоположный знаку свободного члена С. Подставив полученное значение μ в равенства (6), найдем cos φ, sin φ и р и, тем самым, преобразуем уравнение (4) к нормальному виду. Так как нормальное уравнение определяет прямую, то и уравнение (4) определяет прямую.
Множитель μ, выбираемый по указанному правилу, называют нормирующим множителем для данного уравнения прямой. Уравнение (4) называется общим уравнением прямой на плоскости.
Итак, всякое уравнение первой степени относительно переменных хну определяет прямую как множество точек М плоскости, декартовы координаты хну которых удовлетворяют этому уравнению.
Условимся называть нормальным вектором прямой L всякий ненулевой (необязательно единичный) вектор, перпендикулярный этой прямой. Из приведенных выше рассуждений следует, что вектор
n = {A,В}
будет нормальным вектором прямой, заданной уравнением (4).
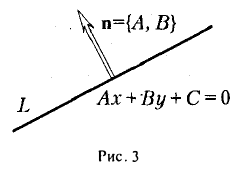
Таким образом, коэффициенты А и В при текущих координатах х и у в общем уравнении прямой (4) имеют простой геометрический смысл: они являются координатами нормального вектора n = {A, В) этой прямой (рис. 3). Все другие нормальные векторы прямой можно получить, умножая вектор п на произвольное не равное нулю число.
Отметим два интересных частных случая, а) Если В ≠ 0, то, положив
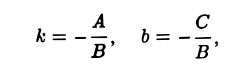
получим уравнение прямой с угловым коэффициентом
у = kx + b
(рис.4).
б) Если ABC ≠ 0, то, положив
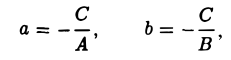
получим уравнение прямой в отрезках
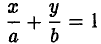
(рис. 5).
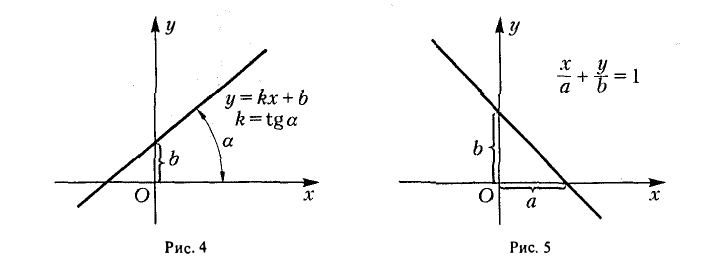
Уравнение прямой на плоскости, проходящей через заданную точку перпендикулярно заданному направлению
Для того, чтобы найти уравнение прямой L, проходящей через точку Мо, заданную радиус-вектором
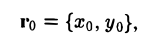
перпендикулярно вектору
n = {А,В},
проведем радиус-вектор r = {х, у} в произвольную точку М этой прямой. Вектор
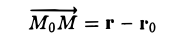
лежит на прямой L и, значит, перпендикулярен вектору n (рис.6).
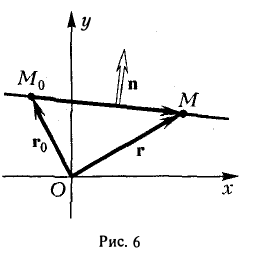
Поэтому их скалярное произведение равно нулю (8)
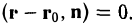
Равенство (8) справедливо для всех точек М прямой L и нарушается, если точка М не принадлежит этой прямой. Тем самым, уравнение (8) является векторным уравнением искомой прямой.
Выражая скалярное произведение векторов r-rо и n через их координаты, получим уравнение этой же прямой L в координатной форме
А(х — х0) + В(у- у0) = 0. (9)
Расстояние от точки до прямой на плоскости
Расстоянием от точки М* до прямой L называется длина отрезка M*N перпендикуляра L⊥, опушенного из точки М* на эту прямую (рис. 7). Пусть М*(х*, у*) — заданная точка и
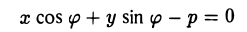
— нормальное уравнение прямой L. Тогда расстояние от точки М* до прямой L можно вычислить по формуле
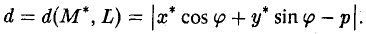
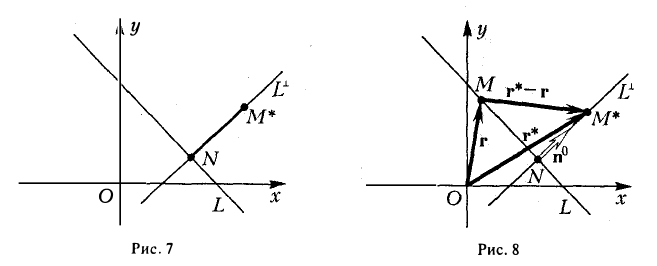
Пусть r — радиус-вектор произвольной точки М прямой L (рис.8). Тогда выполнено равенство
(r, n°) = р.
Обозначим через r* радиус-вектор точки M*. Разность
(r*,n°) -р
равна проекции вектора r* — r на ось L⊥, определяемую вектором n°:
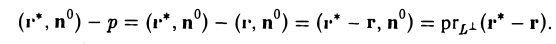
Взяв разность (r*, n°) — р по абсолютной величине, получим, что
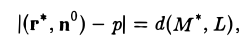
или, в координатах,
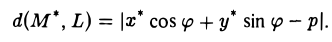
Если прямая L задана обшим уравнением
Ах + By + С = 0,
то расстояние от точки М’ до этой прямой вычисляется по формуле (10)
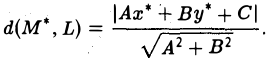
Угол между двумя прямыми
Пусть L1 и L2 — две прямые, заданные уравнениями
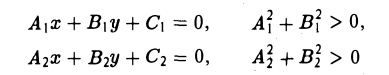
соответственно. Угол φ между прямыми L1 и L2 равен углу между нормальными векторами 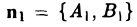 , и
, и 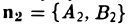 этих прямых (рис. 9).
этих прямых (рис. 9).
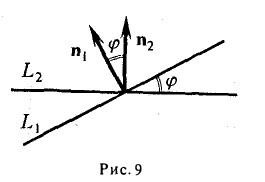
Отсюда вытекает, что
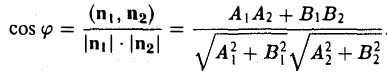
Условие перпендикулярности двух прямых на плоскости
В случае перпендикулярности прямых L1 и L2 их нормальные векторы также перпендикулярны, т. е. справедливо равенство
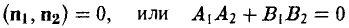
— условие перпендикулярности прямых.
Условие параллельности двух прямых на плоскости
В случае параллельности прямых L1 и L2 их нормальные векторы коллинеарны, т.е. справедливо равенство
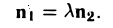
Переходя к координатам этих векторов, получаем, что
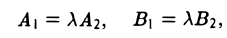
Или
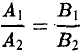
— условие параллельности прямых.
Плоскость
К рассмотрению свойств плоскости можно подойти совершено аналогично.
Нормальное уравнение плоскости. Общее уравнение плоскости
Зафиксируем в пространстве некоторую точку О. Положение плоскости П в пространстве будет вполне определено, если задать следующие величины: расстояние до нее от начальной точки О, т.е. длину р отрезка ОТ перпендикуляра, опущенного из точки О на плоскость П, и единичный вектор n°, |n°| = 1, перпендикулярный плоскости П и направленный из начальной точки О к этой плоскости (рис. 10).
Когда текущая точка М движется по плоскости П, ее радиус-вектор r меняется так, что (1)
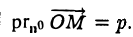
Соотношение (1) выполняется для каждой точки плоскости П и нарушается, если точка М лежит вне этой плоскости. Тем самым, равенство (1) выражает свойство, присущее всем точкам плоскости П и только им. Иными словами, (1) является уравнением этой плоскости. Замечая, что
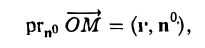
перепишем уравнение (1) в следующем виде
(r,n°)-р = 0. (2)
Уравнение (2) называется нормальным (нормированным) уравнением плоскости в векторной форме. Радиус-вектор г произвольной точки плоскости называется ее текущим радиус-вектором.
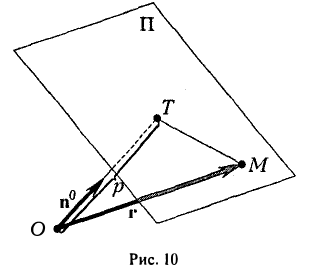
Введем в пространстве прямоугольную декартову систему координат, поместив ее начало в точку О. Тогда векторы n° и r можно записать так
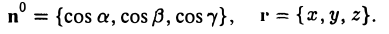
При этом уравнение (2) примет следующий вид (3)
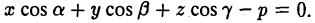
Это нормальное уравнение плоскости в координатной форме.
Особенности нормального уравнения плоскости (3):
1) сумма квадратов коэффициентов при текущих координатах равна 1,
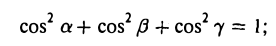
2) свободный член (-р) неположителен.
Относительно переменных х, у и z уравнение (3) является уравнением первой степени, так что в прямоугольной декартовой системе координат всякая плоскость определяется уравнением первой степени относительно текущих координат х, у и z. Верно и обратное утверждение:
всякое уравнение первой степени относительно переменных х, у и z определяет плоскость.
В самом деле, возьмем уравнение первой степени общего вида относительно переменных x, у И z (4)
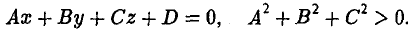
Умножим каждый член уравнения (4) на один и тот же постоянный множитель μ, (5)
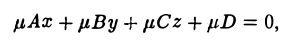
и подберем еготак, чтобы уравнение (5) оказалосьнормальным уравнением. Для этого достаточно положить
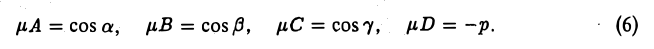
Из формул (6) находим
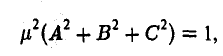
откуда
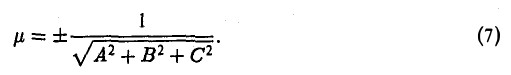
Из условия
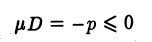
вытекает, что в формуле (7) надо брать знак, противоположный знаку свободного члена D. Подставив полученное значение μ в равенство (6), найдем cos α, cos β, cos γ и р и, тем самым, преобразуем уравнение (4) к нормальному виду. Так как нормальное уравнение определяет плоскость, то и уравнение (4) также определяет плоскость.
Множитель μ, выбираемый по указанному правилу, называют нормирующим множителем для данного уравнения плоскости. Уравнение (4) называется общим уравнением плоскости.
Итак, всякое уравнение первой степени относительно переменных х, у и z определяет плоскость как множество точек М пространства, декартовы координаты х, у и z которых удовлетворяют этому уравнению.
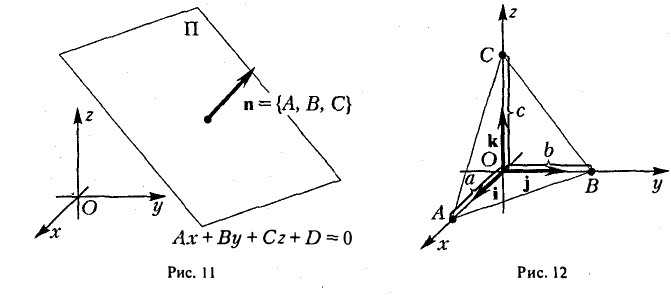
Условимся называть всякий ненулевой (не обязательно единичный) вектор, перпендикулярный плоскости П, нормальным вектором этой плоскости. Из приведенных выше рассуждений следует, что вектор
n = {А, В, С}
будет нормальным вектором прямой, заданной уравнением (4). Таким образом, коэффициенты А, В и С при текущих координатах х, у и z в общем уравнении плоскости (4) имеют простой геометрический смысл: они являются координатами нормального вектора n = {A, В, С} этой плоскости (рис. 11). Все другие нормальные векторы плоскости можно получить, умножая вектор п на произвольное не равное нулю число.
Отметим интересный частный случай.
Если ABCD ≠ 0, то, положив
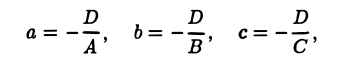
получим уравнение плоскости в отрезках
(рис. 12).
Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному направлению
Для того, чтобы найти уравнение плоскости П, проходящей через точку Мо, заданную радиус-вектором
перпендикулярно вектору
n = {А,В,С},
проведем радиус-вектор r = (x, у, z} в произвольную точку М этой плоскости. Вектор
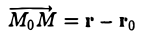
лежит в плоскости П и, значит, перпендикулярен вектору r (рис. 13). Поэтому их скалярное произведение равно нулю
(r — ro, n) = 0. (8)
Равенство (8) справедливо для всех точек М плоскости П и нарушается, если точка М этой плоскости не принадлежит. Тем самым, уравнение (8) является векторным уравнением искомой плоскости.
Выражая скалярное произведение векторов r-rо и n через их координаты, получим уравнение этой же плоскости П в координатной форме
А{х — х0) + В{у — у0) + C(z — z0) = 0. (9)
Расстояние от точки до плоскости
Расстоянием от точки М* до плоскости П называется длина отрезка М*N перпендикуляра Z1, опущенного из точки М* на эту плоскость (рис. 14). Пусть М*(х*,у*, z*) — заданная точка и
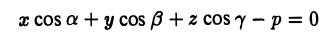
— нормальное уравнение плоскости П. Тогда расстояние отточки М* до плоскости П можно вычислить по формуле
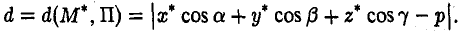
Пусть r — радиус-вектор произвольной точки М плоскости П. Тогда выполнено равенство
(r, n°) = р.
Обозначим через r* радиус-вектор точки М*. Разность
(r*, n°) — р
равна проекции вектора r* — r на ось L⊥, определяемую вектором n°:
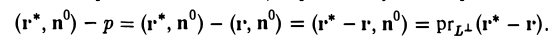
Взяв разность (r*, n°) — р по абсолютной величине, получим, что
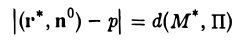
или, в координатах,
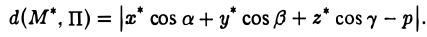
Если плоскость П задана общим уравнением
Ах + By + Cz + D = 0,
то расстояние отточки М* до этой плоскости вычисляется по формуле (10)
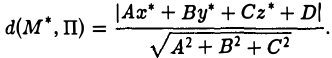
Угол между двумя плоскостями
Пусть П1 и П2 — две плоскости, заданные уравнениями
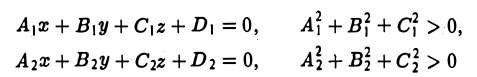
соответственно. Углом между двумя плоскостями будем называть любой из двух смежных двугранных углов, образованных этими плоскостями (рис. 15) (в случае параллельности плоскостей угол между ними равен или 0, или π).
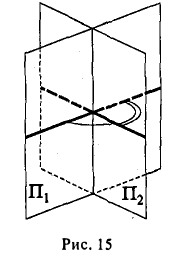
Один их этих двугранных углов равен углу φ между нормальными векторами n1 = {A1,В1,С1} и n2 = {А2, В2, С2} этих плоскостей. Отсюда вытекает, что
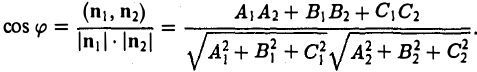
Условие перпендикулярности двух плоскостей
В случае перпендикулярности плоскостей П1 и П2 их нормальные векторы также перпендикулярны, т. е. справедливо равенство
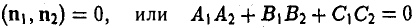
— условие перпендикулярности плоскостей.
Условие параллельности двух плоскостей
В случае параллельности плоскостей П1 и П2 их нормальные векторы коллинеарны, т. е. справедливо равенство
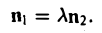
Переходя к координатам этих векторов, получаем, что
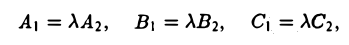
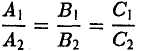
— условие параллельности плоскостей.
Прямая линия в пространстве
Уравнения прямой линии
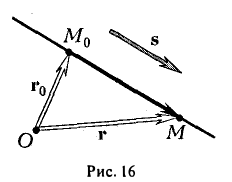
Положение прямой линии в пространстве будет вполне определено, если задать точку М 0 на прямой (при помощи радиус-вектора r0 ) и ненулевой вектор s, которому прямая параллельна. Вектор s называют направляющим вектором прямой.
Переменной точке М прямой соответствует ее радиус-вектор 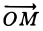 = r. Из рис. 16 получаем (1)
= r. Из рис. 16 получаем (1)
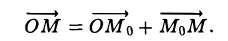
Вектор 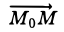 параллелен вектору s, так что
параллелен вектору s, так что 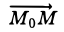 = st (числовой множитель t (параметр) может принимать любые значения в зависимости от положения точки М на прямой). Следовательно, равенство (1) можно записать так (2)
= st (числовой множитель t (параметр) может принимать любые значения в зависимости от положения точки М на прямой). Следовательно, равенство (1) можно записать так (2)
r = r0 + St.
Уравнение (2) называется векторным уравнением прямой.
Введем в пространстве прямоугольные декартовы координаты, поместив начало координат в точку О. Обозначим декартовы координаты точки Мо (координаты вектора r0) через х 0 , у 0 и z 0 , текущие координаты точки М (координаты вектора r) через х, у и z, а координаты направляющего вектора s через l, m и n. Тогда, записав векторное уравнение (2) в координатах, получим (3)
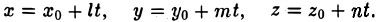
Уравнения (3) называются параметрическими уравнениями прямой. Числа l, m, n называют направляющими коэффициентами этой прямой. Исключим из уравнений (3) параметр t. Имеем
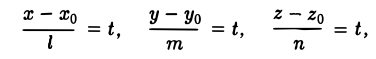
откуда (4)
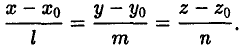
Уравнения (4) называют каноническими уравнениями прямой. В них х0 , у0 и z0 — координаты точки M0, лежащей на прямой, а l, m и n — координаты направляющего вектора прямой (l2 + m2 + n2 > 0). Система уравнений (4) определяет прямую как линию пересечения двух плоскостей, описываемых, например, уравнениями
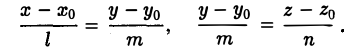
Уравнения прямой, проходящей через две данные точки
Пусть требуется найти уравнения прямой, проходящей через точки M1 { х1, у1, z1}, M 2 { х2, у2, z2 } . Будем искать эти уравнения в канонической форме. Для решения задачи надо знать координаты одной из точек, лежащих на прямой, и направляющий вектор. За точку на прямой можно взять любую из двух данных, например, M1{ х1, у1, z1}. За направляющий вектор прямой примем вектор
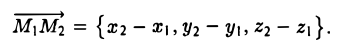
Уравнения искомой прямой — (5)
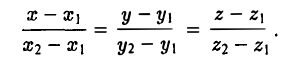
Замечание:
Если точки M1 и M2 лежат в плоскости Оzy, т.е. z1 = z2 = 0, то уравнения проходящей через них прямой имеют следующий вид
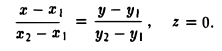
Пример:
Найти уравнения прямой, проходящей через точки
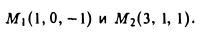
Пользуясь формулой (5), сразу получаем искомые уравнения
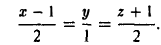
Общие уравнения прямой. Переход к каноническим уравнениям
Всякие две не параллельные между собой и несовпадающие плоскости определяют прямую как линию их пересечения. Пусть уравнения этих плоскостей суть
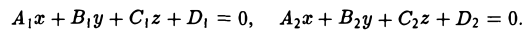
Рассматриваемые совместно, (6)
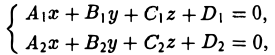
эти уравнения называются общими уравнениями прямой.
От общих уравнений прямой (6) можно перейти к ее каноническим уравнениям. Для этого надо знать какую-нибудь точку прямой и ее направляющий вектор. Координаты точки прямой найдем из системы (6), выбирая одну из координат произвольно и решая полученную после этого систему относительно оставшихся двух координат. Для отыскания направляющего вектора s прямой заметим, что этот вектор, направленный по линии пересечения данных плоскостей, должен быть перпендикулярен нормальным векторам n1 = {А 1 , В 1 ,С 1 ) и n2 = {А 2 , В 2 , С 2 } этих плоскостей. Обратно, всякий вектор, перпендикулярный векторам n1 и n2, будет параллелен обеим плоскостям, т. е. параллелен их линии пересечения. Так как векторное произведение [n1, n2] перпендикулярно каждому из векторов n1 и n2, то в качестве направляющего вектора прямой можно взять вектор s = [n1, n2].
Пример:
Привести к каноническому виду уравнения прямой (7)
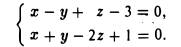
Находим какую-нибудь точку, принадлежащую прямой (7). Полагая, например, z = 0, приходим к системе двух уравнений с двумя неизвестными
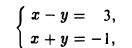
откуда х = l, у =— 2. Итак, M0 (1, -2,0) — точка данной прямой.
2) Нормальный вектор первой плоскости n1 = {1, -1, 1}, второй плоскости — n1 = {1, 1, -2}.
3) В качестве направляющего вектора прямой берем вектор
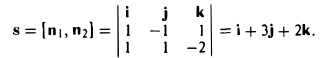
4) Канонические уравнения прямой (7) имеют вид
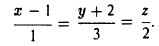
Угол между прямой и плоскостью
Пусть даны прямая (8)
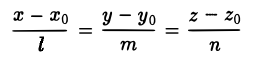
и плоскость
Ах + By + Cz + D = 0.
Углом φ между прямой и плоскостью называют наименьший из углов, образованных прямой с ее проекцией на плоскость (рис. 17).
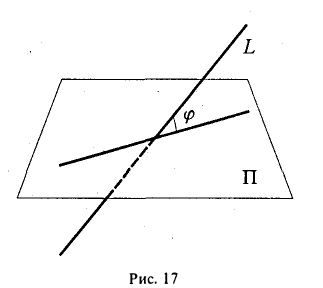
Обозначим через а угол между прямой (8) и перпендикуляром к плоскости (9) (рис. 18). Для cos а получаем выражение
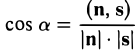
где II — нормальный вектор плоскости (9), as — направляющий вектор прямой (8). Замечая, что | cos а| = sin φ, находим (10)
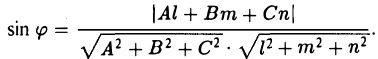
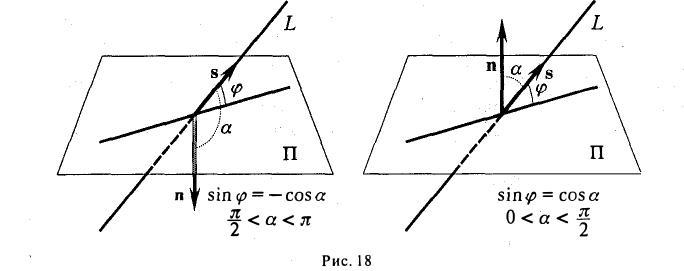
Если прямая (8) параллельна плоскости (9), то направляющий вектор s прямой перпендикулярен нормальному вектору n плоскости, так что
(n, s) = 0,
или (11)
Аl + Вm + Сn = 0.
Это условие параллельности прямой и плоскости.
Если прямая (8) перпендикулярна плоскости (9), то s || n (векторы s и n параллельны), так что (12)
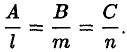
Это условие перпендикулярности прямой к плоскости.
Пересечение прямой с плоскостью
Координаты точки пересечения прямой (13)
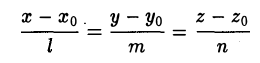
с плоскостью
Ах + By + Cz + D = 0 (14)
должны одновременно удовлетворять уравнениям (13) и (14), и, чтобы найти эти координаты, надо решить эти уравнения совместно, считая х, у и z неизвестными.
Перейдем от канонических уравнений прямой (13) к параметрическим уравнениям:
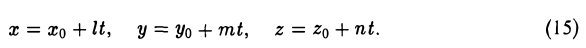
Подставляя эти выражения для х, у и z в уравнение (14), получим
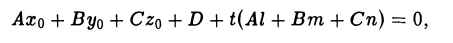
откуда
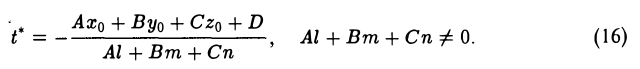
По найденному значению t из формул (15) получаем координаты искомой точки. Если
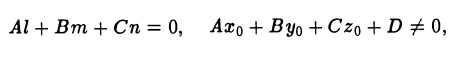
то прямая (13) параллельна плоскости (14), а точка (х0 , у0 , z0). через которую прямая проходит, лежит вне этой плоскости. Следовательно, прямая (13) в этом случае не имеете плоскостью (14) ни одной обшей точки.
Если Аl + Вm + Сn = 0 и Ах0 + Бу0 + Cz0 + D = 0, то в силу первого равенства прямая параллельна плоскости (14), а в силу второго равенства точка (х0, у0, г0) прямой лежит в этой плоскости. Следовательно, в этом случае вся прямая лежит в этой плоскости.
Пример:
Найти точку пересечения прямой

и плоскости

Переходим от канонических уравнений (17) к параметрическим (19)
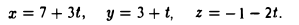
Подставляем найденные выражения для х, у и z в формулу (16)
6t + 14 + t + 3 — 14t- 7 — 3 = 0
или
-7t + 7 = 0,
откуда t = 1. Теперь из (19) находим х = 10, у = 4, z = -3 — координаты точки пересечения прямой и плоскости.
Задача:
Найти расстояние от точки М1(х1, у1, z1) до прямой
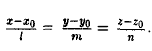
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
