Числовые множества: определение, обозначение, с примерами решения и образцами выполнения

Оглавление:

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

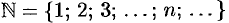Числовые множества — множество натуральных чисел;

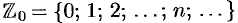Числовые множества — множество целых неотрицательных чисел;

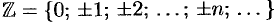Числовые множества — множество целых чисел;

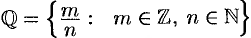Числовые множества — множество рациональных чисел.

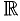Числовые множества — множество действительных чисел.

Между этими множествами существует соотношение

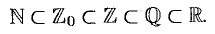
Множество 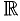Числовые множества содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 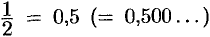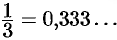Числовые множества , — рациональные числа.

Действительные числа, не являющиеся рациональными, называются иррациональными.

Теорема:

Не существует рационального числа, квадрат которого равен числу 2.

Допустим, что существует рациональное число, представленное несократимой дробью 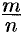Числовые множества квадрат которого равен 2. Тогда имеем:

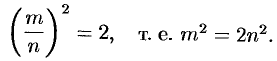
Отсюда следует, что 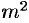Числовые множества (а значит, и 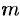) — четное число, т. е. 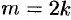. Подставив 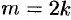к равенство 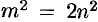, получим 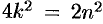, т. е. 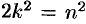. Отсюда следует, что число 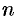— четное, т. е. 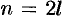. Но тогда дробь 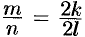сократима. Это противоречит допущению, что 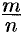Числовые множества дробь несократима. Следовательно, не существует рационального числа, квадрат которого равен числу 2.

Иррациональное число выражается бесконечной непериодической дробью. Так, 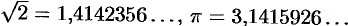Числовые множества — иррациональные числа. Можно сказать: множество действительных чисел есть множество всех бесконечных десятичных дробей. И записать

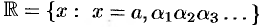Числовые множества , где .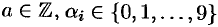

Множество 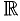Числовые множества действительных чисел обладает следующими свойствами.

1. Оно упорядоченное: для любых двух различных чисел 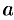Числовые множества и 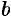имеет место одно из двух соотношений 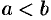либо .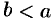

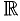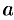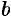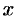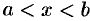2. Множество Числовые множества плотное: между любыми двумя различными числами и содержится бесконечное множество действительных чисел , т. е. чисел, удовлетворяющих неравенству Числовые множества .

Так, если 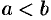Числовые множества , то одним из них является число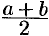

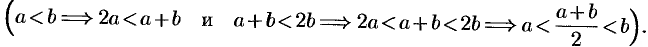
3. Множество Числовые множества непрерывное. Пусть множество разбито на два непустых класса 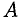и 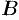таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел 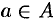Числовые множества и 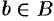выполнено неравенство 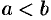. Тогда (свойство непрерывности) существует единственное число 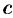, удовлетворяющее неравенству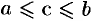 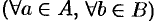. Оно отделяет числа класса 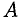Числовые множества от чисел класса 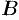. Число 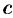является либо наибольшим числом в классе 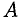(тогда в классе 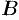нет наименьшего числа), либо наименьшим числом в классе 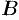(тогда в классе 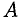Числовые множества нет наибольшего).

Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает, что каждому числу 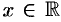Числовые множества соответствует определенная (единственная) точка числовой оси и, наоборот, каждой точке оси соответствует определенное (единственное) действительное число. Поэтому вместо слова «число» часто говорят «точка».

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Поверхности вращения

Множество действительных чисел

Числовые промежутки

Предельный переход в неравенствах

Числовые множества

Множество 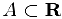Числовые множества называется ограниченным сверху (снизу), если существует действительное число 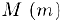такое, что для всех чисел 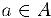выполняется неравенство

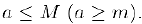
Числа 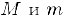Числовые множества называются, соответственно, мажорантой и минорантой множества А.

Ограниченное снизу и сверху множество, называется ограниченным.

Наименьшая из мажорант (наибольшая из минорант) называется верхней (нижней) гранью множества А. Верхняя грань обозначается через 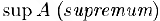Числовые множества . Для нижней грани используется обозначение .

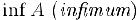В качестве примера рассмотрим множество

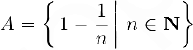
Здесь 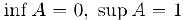Числовые множества .

Докажем теперь теорему о существовании граней множества.

Теорема:

Ограниченное сверху (снизу) множество имеет. верхнюю (нижнюю) грань.

Доказательство:

Предположим, для определенности, что множество А ограничено сверху. Обозначим через В множество его мажорант. Тогда для любых чисел 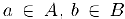Числовые множества выполняется неравенство 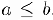. По свойству полноты множества действительных чисел (§1. свойство 9)) существует число-разделитель с такое, иго для всех 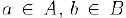Числовые множества имеет место неравенство

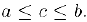
Таким образом, с одной стороны, число с: является мажорантой, а, с другой стороны, оно нс превосходит любой из мажорант и, следовательно, 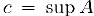Числовые множества . Аналогично доказывается существование нижней грани.

Рассмотрим систему вложенных отрезков

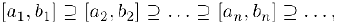
т. е.

Принцип вложенных отрезков. Любая система вложенных отрезков имеет непустое пересечение.

Доказательство. Пусть множества А и В состоят из левых и правых концов отрезков, соответственно. Так как для любых 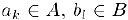Числовые множества справедливо неравенство ,

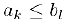то по свойству полноты множества действительных чисел найдется разделитель 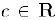Числовые множества . этих множеств и, следовательно, дня всех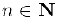

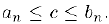
Таким образом, число с принадлежит всех отрезкам системы. Принцип доказан.

Множества можно сравнивать по количеству элементов, содержащихся в них. Конечные множества считаются равномощными, если они имеют одинаковое ’тело элементов. Если множество содержит бесконечное количество элементов, то можно попытаться сравнить его с другим бесконечным множеством простой структуры. например, с множеством натуральных чисел.

Бесконе’шое множество называется счетным, если его элементы можно пронумеровать, т. с. каждый элемент множества получает свой, отличный от других номер, выражающийся натуральным числом.

Примерами счетных множеств могут служить, например, множества целых и рациональных чисел. Целые числа можно пересчитать, расположив их в ряд:

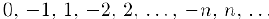
Для того, чтобы пронумеровать рациональные числа, расположим их в следующей бесконечной матрице:

В строках этой матрицы записаны все несократимые рациональные дроби с фиксированным знаменателем. Ясно, что каждому рациональному числу однозначно найдется место в этой матрице. Занумеруем теперь числа матрицы по диагоналям, на’шная с левого верхнего угла, т. е.

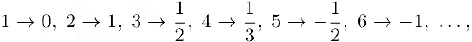
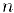где запись Числовые множества означает, что рациональное число получает номер . Таким образом, каждое рациональное число будет пронумеровано и, следовательно, множество 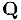счетно.

На этих примерах мы наблюдаем любопыппдй парадокс, который является особенностью бесконечных множеств: бесконечное множество может быть равномощно своей части, т. с. содержать столько же элементов, сколько их имеется в собственном подмножестве.

В заключение этого параграфа покажем что существуют множества, которые являются более мощными, чем счетные.

Теорема:

Любой отрезок множества действительных чисел является несчетным множеством.

Доказательство:

Предположим, наоборот, что отрезок 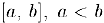Числовые множества является счетным множеством и пусть

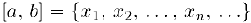
— пронумерованное множество чисел этого отрезка. Выберем внутри данного отрезка отрезок 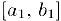Числовые множества , который нс содержит число 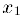, внутри отрезка 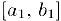найдется отрезок 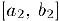. не содержащий число 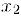, …, внутри отрезка 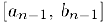возьмем отрезок 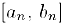, в котором не содержится число 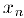Числовые множества , …. В результате мы получим систему вложенных отрезков

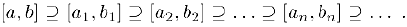
В соответствии с принципом вложенных отрезков, найдется число с, общее для всех отрезков. Пусть Числовые множества — номер этого числа, т. е. 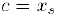и, следовательно, 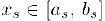. Полученное противоречие и доказывает утверждение теоремы.

Числовые множества и числовые последовательности

Множества

Понятие м ножества принадлежит к числу первичных, неопределяемых понятий. Употребляя термин «множество», будем понимать под этим любое собрание (совокупность) определенных и различимых между собой элементов, мыслимое как единое целое. Например, мы можем говорить о множестве букв на данной странице, о множестве песчинок на морском берегу, о множестве всех корней уравнения, о множестве всех четных чисел и т. д.

Если А — произвольное множество элементов, то утверждение «элемент о принадлежит множеству А символически записывается так: a ∈ А. Запись a ∈ А (или a∉А) означает, что элемент о не принадлежит множеству А. Если каждый элемент из множества А входит и в множество В, то мы называем А подмножеством множества В и пишем А ⊂ В. Так, множество всех четных чисел Z’ является подмножеством множества Z всех целых чисел. Заметим, что всегда А ⊂ А.

Если А ⊂ В и В ⊂ А, т.е. если каждый элемент множества А есть также и элемент В и наоборот, то мы говорим, что множества А и В равны и пишем А = В. Тем самым множество однозначно определено своими элементами. Пользуясь этим, мы будем иногда обозначать множество его элементами, заключенными в фигурные скобки. Так

А = {а}, A = {а,b}, А = {а, b, с}

суть множества, соответственно состоящие из одного элемента а, двух элементов a и b, трех элементов а, b и с. Часто все элементы множества выписать затруднительно, или невозможно. В таких случаях невыписанные элементы будем заменять точками:

А = {а, b, с,… }

есть множество, состоящее из элементов а, b, с и, может быть, еше некоторых других. Какие эти другие элементы, обозначенные точками, должно быть указано, например:

множество натуральных чисел {1, 2, 3…..п,… };

множество квадратов натуральных чисел {1, 4, 9,…, п2,… }; множество простых чисел {2, 3,5,7,… }.

Если А ⊂ В, но А ≠ В, то А называют правильной частью множества В (истинным подмножеством множества В).

Иногда мы не знаем заранее, содержит ли некоторое множество хотя бы один элемент. Поэтому целесообразно ввести понятие пустого множества, т. е. множества, не содержащего ни одного элемента. Будем обозначать пустое множество символом ∅. Любое множество содержит пустое множество в качестве подмножества.

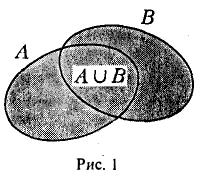
Пусть А и В — два множества. Их суммой или объединением С = A ∪ В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств A и В (рис. 1).

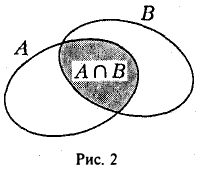
Числовые множества и числовые последовательности

Назовем пересечением множеств А и В множество С = А ∩ В, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В (рис. 2). Например, если А = {1, 2, 3}, В = {2, 3, 4, 5}, то A U В = {1,2, 3, 4, 5}, A ∩ В = {2,3}.

Аналогично определяются объединение и пересечение любого числа множеств.

Если А ∩ В = ∅, то говорят, что множества А и В не пересекаются.

Множество называется конечным, если оно состоит из некоторого натурального числа элементов. Например, конечным является множество всехжителейданного города, а также множество всех людей, населяющих планету Земля. Непустое множество называется бесконечным, если оно не является конечным. Так, множество N = {1, 2,… } всех натуральных чисел является бесконечным множеством.

Пусть А и В — некоторые множества. Говорят, что между множествами А и В установлено взаимнооднозначное соответствие, если каждому элементу множества А поставлен в соответствие один элемент множества В так, что: 1) разным элементам множества А поставлены в соответствие разные элементы множества В и 2) каждый элемент множества В поставлен в соответствие некоторому элементу множества А. Если между двумя конечными множествами А и В удалось установить взаимнооднозначное соответствие, то множество А и В имеют одинаковое число элементов. Множества А и В, между которыми можно установить взаимнооднозначное соответствие, называются эквивалентными.

Обозначение: А ~ В.

Бесконечное множество А называется счетным, если можно установить взаимнооднозначное соответствие между множеством А и множеством N натуральных чисел, т. е. если А ~ N. Каждое бесконечное множество содержит счетное подмножество.

Действительные числа. Абсолютная величина

Числа 1, 2, 3,…, п, п + 1,… называются натуральными числами. Дроби вида

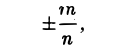
где т и п — натуральные числа, а также число 0 называются рациональными числами. В частности, рациональным будет каждое натуральное и каждое целое отрицательное число. Любое рациональное число выражается либо конечной, либо бесконечной периодической десятичной дробью.

Кроме рациональных чисел существуют еще иррациональные числа, которые выражаются бесконечными непериодическими десятичными дробями. Например,

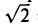Числовые множества и числовые последовательности = 1,41… , π = 3,14… .

Рациональные и иррациональные числа называются действительными (вещественными) числами.

Можно показать, что множество всех рациональных чисел счетно. Множество всех действительных чисел счетным не является.

Мы будем предполагать, что основные свойства действительных чисел и арифметические действия над ними известны из школьного курса математики.

Определение:

Абсолютной величиной (модулем) числа a называется само число а, если a — положительно, и число -а, если а — отрицательно. Абсолютная величина нуля есть нуль.
Абсолютная величина числа a обозначается символом |a|. Таким образом, по определению

Если а > 0, то отношение |х| ≤ а эквивалентно отношению

-а ≤ х ≤ а (проверьте это!).

Для абсолютных величин верны следующие соотношения:

1. |а • b| = |а| • |b|;

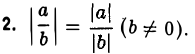
Справедливость этих соотношений вытекает из правила умножения и деления действительных чисел и из определения абсолютной величины.

3.|а + b| ≤ |а| + |b|.

Сложив почленно очевидные неравенства

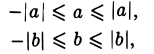
получим двойное неравенство

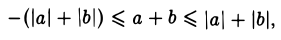
равносильное неравенству

|а + b| ≤ |а| + |b|.

4. ||а|-|Ь|| ≤ |а-b|

Так как

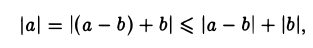
то

Из неравенства

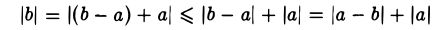
получаем,что

Из соотношений (1) и (2) следует

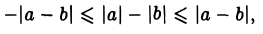
что равносильно неравенству

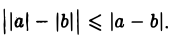
Числовая ось. Простейшие множества чисел

Действительные числа изображаются точками прямой. Делается это так.

На некоторой прямой (будем считать ее расположенной горизонтально, рис. 3) выберем положительное направление, начало отсчета О и единицу масштаба и. Для изображения положительного числа а возьмем на нашей прямой справа от начала О точку на расстоянии (в принятом масштабе), равном данному числу а; для изображения отрицательного числа а возьмем точку слева от начала О на расстоянии, равном |a|; числу а = 0 будет отвечать точка О — начало отсчета.

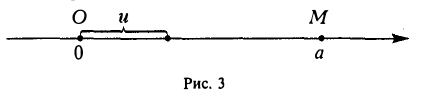
Таким приемом мы устанавливаем взаимнооднозначное соответствие между всеми точками прямой и множеством действительных чисел: каждое действительное число будет изображено одной определенной точкой прямой, причем каждая точка прямой будет изображением одного определенного действительного числа.

Определение:

Прямая, для всех точек которой установлено указанное взаимооднозначное соответствие с множеством всех действительных чисел, называется числовой осью или числовой прямой.
В дальнейшем мы будем обозначать одним и тем же символом х действительное число х и точку х числовой оси.

Числовая ось позволяет дать наглядное представление о расположении действительных чисел. Неравенство x1 < х2 означает, что точка х1 лежит левее точки х2; двойное неравенство х1 < х3 < х2 означает, что точка xз лежит между точками x1 и х2.

Простейшие множества чисел

Дадим определения простейших числовых множеств, с которыми нам особенно часто придется иметьдело в дальнейшем.

Для наиболее важных множеств приняты стандартные обозначения. Так например, буквами N, Z, Q, R обозначают соответственно множества натуральных, целых, рациональных и действительных чисел.

Множество всех действительных чисел х (всех точек числовой оси), удовлетворяющих условию а ≤ х ≤ b, где а < b, называется отрезком (сегментом) и обозначается [а, b]. Множество всех действительных чисел х, удовлетворяющих условию а < х < b, называется интервалом и обозначается (а,b). Множество всех действительных чисел х, определяемых неравенствами а ≤ х < b, а < х ≤ b мы будем обозначать соответственно [а, b) и (а, b] и употреблять в обоих случаях равносильные термины: полуинтервал и полуотрезок. Мы будем рассматривать также бесконечные интервалы и полуинтервалы, вводя несобственные точки (числа) + ∞ и — ∞ . Таким образом, (о, + ∞) — множество всех действительных чисел х > а;

[а, + ∞) — множество всех действительных чисел х ≥ а; (— ∞, b — множество всех действительных чисел х < b; (— ∞, b] — множество всех действительных чисел х ≤ b; (- ∞, + ∞) — множество R всех действительных чисел (числовая прямая).

Определение:

Окрестностью точки х0 числовой оси называется любой интервал, содержащий точку х0.
Пусть δ — положительное число.

Определение:

δ -окрестностью точки хо называется интервал (хо — δ, хо + δ), симметричный относительно точки х0 (рис.4). Это — совокупность всех чисел х, удовлетворяющих неравенств

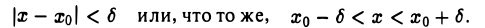
Определение:

Интервал (xo — δ, х0 + δ), из которого выброшена точка х0, иногда называют проколотой δ -окрестностью точки xо.

Обозначение: (х0 — δ, х0) U (х0, х0 + δ ).

Точная верхняя и точная нижняя грани множества

Определение:

Множество Е действительных чисел называется ограниченным сверху, если существует число а такое, что для всякого числа х ∈ Е выполнено неравенство

х ≤ b.

Например, множество Е = (- ∞, 1] ограничено сверху.
Определение. Множество Е называется ограниченным снизу, если существует число а такое, что для всякого числа х ∈ Е выполнено неравенство

а ≤ х.

Так, множество всех натуральных чисел ограничено снизу.

Определение:

Множество Е называется ограниченным, если оно ограничено снизу и сверху, т. е. если существуют такие числа а и b, что для всякого числа х ∈ Е имеем

а ≤ х ≤ b.

Отсюда следует, что множество Е ограничено, если оно содержится в некотором отрезке [а, b].

Множество, не являющееся ограниченным сверху (снизу), называется неограниченным сверху (снизу). Например, множество всех натуральных чисел является неограниченным сверху (но ограниченным снизу); множество всех отрицательных чисел является неограниченным снизу (но ограниченным сверху). Множество всех целых чисел, множество всех рациональных чисел, а также множество всех действительных чисел являются множествами, не ограниченными как сверху, так и снизу.

Если множество Е ограничено сверху числом b, то это число b называют верхней гранью множества Е. В этом случае любое число b’, большее b, тоже будет верхней гранью множества Е.

Определение:

Число М называется точной верхней гранью множества Е, если

1) для любого х ∈ Е выполняется неравенство

х ≤ М.

2) для любого как угодно малого числа е > 0 найдется число х* ∈ Е такое, что

М — е < х* ≤ М.

Иными словами, точная верхняя грань множества Е есть наименьшая из всех верхних граней множества Е.

Точная верхняя грань множества Е обозначается

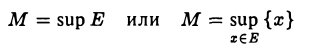
(сокращение от латинского слова supremum — наивысший). Для множества Е, не ограниченного сверху, будем считать по определению точную верхнюю грань равной + ∞ и писать

sup Е = + ∞.

Если множество Е ограничено снизу числом а, то это число а называют нижней гранью множества Е. Ясно, что всякое число, меньшее а, тоже будет нижней гранью множества Е.

Определение:

Число m называется точной нижней гранью множества Е, если

1) для любого х ∈ Е выполняется неравенство

х ≥ т.

2) для любого сколь угодно малого числа е > 0 найдется число х* 6 Е такое, что

т ≤ х* < т + е.

Таким образом, точная нижняя грань множества Е есть наибольшая из нижних граней этого множества.

Точная нижняя грань множества Е обозначается

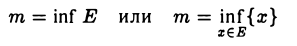
(сокращение от латинского слова intimum — наинизший). Для множества Е, не ограниченного снизу, полагаем

inf Е = — ∞.

Примеры:

Если Е = [а, b], то inf Е = а, sup Е = b.

Если Е = (а, b), то опять inf E = а, sup E = b. В первом случае inf E и sup E принадлежат множеству Е, во втором — нет. Для множества

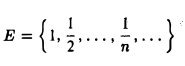
имеем inf Е = 0, sup Е = 1.

Справедливо следующее утверждение.

Теорема:

Всякое ограниченное сверху непустое множество действительных чисел имеет точную верхнюю грань, а всякое ограниченное снизу — точную нижнюю грань.

Логические символы. Логические высказывания

В дальнейшем изложении для сокращения записи и для упрощения построения определений мы будем пользоваться некоторыми логическими символами и отношениями.

Квантор существования ∃ соответствует словам «существует», «существуют», «найдется». Квантор общности ∀ соответствует словам «для всякого», «для любого», «для каждого», «для всех».

Будем называть высказыванием всякое повествовательное предложение, в отношении которого имеет смысл утверждать, истинно оно или ложно. Например, высказываниями являются предложения «Математика есть наука», «2 меньше 3», «6 есть простое число». Напротив, предложения «Закройте дверь», «Сколько Вам лет?» не являются высказываниями. Условимся обозначать высказывания буквами а, β, γ и т. д.

Импликация а => β (читается «если а, то β» или «а влечет за собой β») означает высказывание, которое ложно в том и только в том случае, когда а истинно, а β ложно. Соотношение «если а, то β» не следует понимать как отношение основания и следствия. Напротив, высказывание а => β истинно всякий раз, когда а есть ложное высказывание. Иными словами, из неверного суждения следует любое суждение: если 2×2 = 5, то существуют ведьмы.

Эквиваленция а ⇔ β («а тогда и только тогда, когда β») означает логическую равносильность высказываний а и β.

Конъюнкция а ∧ β означает высказывание, составленное из высказываний а и β при помощи союза «и» (читается «а и β»), Конъюнкция а ∧ β считается истинным высказыванием тогда и только тогда, когда оба высказывания а и β истинны.

Дизъюнкция а ∨ β означает высказывание, образованное из высказываний а и β при помощи союза «или» (читается «а или β»), Дизъюнкция a ∨ β считается истинным высказыванием тогда и только тогда, когда истинно хотя бы одно из данных высказываний.

Отрицание. Пусть а — некоторое высказывание. Высказывание -а называют отрицанием высказывания а (читается «а с чертой» или «не а»). Высказывание -а истинно, если а ложно и, наоборот, ложно, если а истинно.

Отрицание некоторого свойства, содержащего кванторы ∀, ∃ и свойство А, получается заменой каждого квантора на двойственный (т. е. квантора общности на квантор существования и наоборот) и заменой свойства А на его отрицание -А. При этом, если

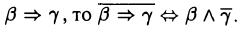
Необходимое и достаточное условия

Пусть β — некоторое высказывание. Всякое высказывание а, из которого следует β, называется достаточным условием для β. Всякое высказывание а, которое вытекает из β, называется необходимым условием для β. Например, пусть высказывания а и β таковы: а: «число х равно нулю»; β: «произведение ху равно нулю».

Тогда а является достаточным условием для β. Действительно, для того, чтобы произведение ху равнялось нулю, достаточно, чтобы число х было равно нулю. Для того, чтобы х было равно нулю, необходимо, чтобы произведение ху было равно нулю. Однако, β не является достаточным для а: из того, что произведение ху равно нулю, не вытекает, что обязательно число х равно нулю.

Теорему: «если истинно высказывание а, то истинно высказывание β», можно записать так: а => β и выразить любой из следующих формулировок:

«а является достаточным условием для β»;

«β является необходимым условием для а».

Если высказывания а и β таковы, что из каждого из них вытекает другое, т.е. а β и β => а, то говорят, что каждое из высказываний а и β является необходимым и достаточным условием для другого и пишут

а ⇔ β.

Другие употребительные формулировки:

1) для справедливости а необходимо и достаточно, чтобы имело место β;

2) а имеет место в том и только в том случае, если выполняется β;

3) а истинно тогда и только тогда, когда истинно β.

Метод математической индукции

Многочисленные примеры убеждают нас в том, что некоторое утверждение может быть справедливо в целом ряде частных случаев и в то же время быть несправедливым вообще. Вот один из таких примеров. Подставляя в выражение 991 п² + 1 вместо п последовательные натуральные числа 1, 2, 3,…, 10¹⁰, мы будем получать числа, не являющиеся полными квадратами. Однако делать отсюда вывод, что все числа такого вида не являются квадратами, было бы преждевременным: существуют п, при которых число 991 п² + 1 есть полный квадрат. Вот наименьшее из таких значений п:

12055735790331359447442538767

Поэтому естественно возникает следующий вопрос. Имеется утверждение а, зависящее от натурального параметра (числа) п и справедливое в нескольких частных случаях. Как узнать справедливо ли это утверждение вообще (при всех значениях параметра п)?

Этот вопрос иногда удается решить методом математической индукции (полной индукции). В основе этого метода лежит принцип математической индукции, заключающийся в следующем.

Принцип математической индукции. Если

1) утверждение а(п) справедливо для п = 1;
2) из справедливости утверждения а(п) для какого-либо натурального числа п = к следует его справедливость для п = к + 1,
то утверждение а(п) справедливо для всякого натурального п.

Этот принцип принимают в качестве основного положения математического мышления.

В качестве его применения установим одно неравенство, называемое неравенством Бернулли: если h > -1, то (*)

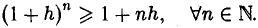
В самом деле, неравенство (*) верно для п = 1. Допустим, что оно доказано для некоторого натурального п = т > 1, т. е.

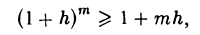
и покажем, что оно справедливо при п = т + 1. Умножим обе части последнего неравенства на 1 + h > 0. Имеем

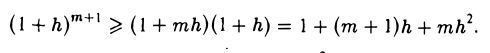
Отбрасывая справа неотрицательное слагаемое mh², получим

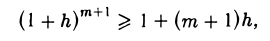
т. е. неравенство оказывается верным и для т + 1. Следовательно, согласно принципу математической индукции, неравенство (*) верно для всякого натурального числа п.

Числовая последовательность и ее предел

Если каждому натуральному числу п по некоторому закону поставлено в соответствие определенное действительное число аn, то говорят, что задана числовая последовательность

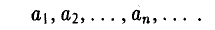
Числа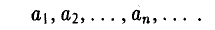 Числовые множества и числовые последовательности называются членами последовательности; аn называют общим членом последовательности. Он содержит закон образования членов последовательности.

Ради сокращения записи последовательность 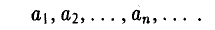Числовые множества и числовые последовательности будем обозначать . 1)

Примеры последовательностей:

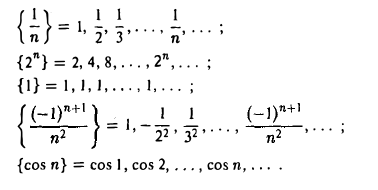
Введем важное понятие предела числовой последовательности. Число А называется пределом числовой последовательности Числовые множества и числовые последовательности , если для любого как угодно малого положительного числа е существует номер N такой, что все члены последовательности ап с номерами п > N удовлетворяют неравенству

1) Не следует путать последовательность Числовые множества и числовые последовательности с множеством . Так, например, последовательность {5} = 5, 5,…, 5…..в то время как множество {5} состоит из одного элемента 5.

Обозначения:

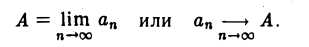
С помощью логических символов определение предела последовательности Числовые множества и числовые последовательности выражается следующим образом:

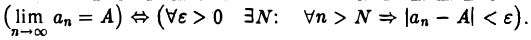
Геометрический смысл предела последовательности

Изобразим члены последовательности Числовые множества и числовые последовательности точками числовой оси (рис.5). Неравенство |ап -А| < ε, равносильное двойному неравенству А- ε < ап < A+ ε.

А + ε, означает, что точка аn находится в е-окрестности точки А.

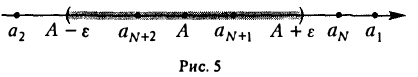
Таким образом, число А есть предел последовательности Числовые множества и числовые последовательности , если какова бы ни была ε -окрестность точки А, найдется такой номер N, что все точки ап с номерами п > N будут содержаться в этой окрестности точки А, т.е. в интервале (А — ε , А + ε ); вне этого интервала может оказаться лишь конечное множество точек данной последовательности.

Определение:

Последовательность {а„} называется сходящейся, если она имеет (конечный) предел, и расходящейся, если она предела не имеет.

Пример:

Последовательность Числовые множества и числовые последовательности , все члены которой равны одному и тому же числу A (стационарная последовательность), имеет предел, равный этому числу А.

Пример:

Рассмотрим последовательность

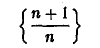
с общим членом

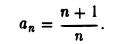
Очевидно, что при больших п дробь 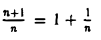Числовые множества и числовые последовательности мало отличается от единицы. Это дает основание предполагать, что

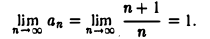
Докажем, что это действительно так. Возьмем произвольное ε > 0 и найдем натуральное число N такое, что при всех значениях п> N будет верно неравенство

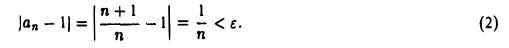
Решим неравенство 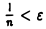Числовые множества и числовые последовательности , считая п неизвестным:

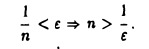
Если взять в качестве N целое число, большее 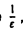Числовые множества и числовые последовательности , то для всех п > N будет выполняться соотношение

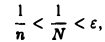
а следовательно, и неравенство (2). Согласно определению, это означает, что

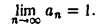
Номер N в определении понятия предела, вообще говоря, зависит от ε:

N = N( ε ).

Так в приведенном примере при ε = 0,1 в качестве N можно взять число 10 (или любое большее), а при ε = 0,01 в качестве N следует брать число, не меньшее, чем 100.

Замечание:

Номер N, фигурирующий в определении понятия предела последовательности, определяется заданием числа ε неоднозначно в следующем смысле: если неравенство (I) выполнено при всех п > N1, то оно выполнено и при n > N2, где N2 > N1. Как правило, не возникает необходимости искать среди этих номеров наименьший.

Сформулируем теорему, которая дает необходимое и достаточное условие существования предела последовательности.

Теорема:

Критерий Коши. Для сходимости последовательности

необходимо и достаточно, чтобы для любого числа ε > 0 существовал номер N такой, что для всех п > N и всех т > N было бы верно неравенство

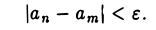
Последовательность Числовые множества и числовые последовательности , удовлетворяющая условию Коши, называется фундаментальной.

Теорема:

Единственность предела последовательности. Последовательность Числовые множества и числовые последовательности не может иметь двух различных пределов.

Пусть последовательность Числовые множества и числовые последовательности имеет пределом число А. Докажем, что тогда никакое число В ≠ А не может быть пределом {ап}. Для этой цели возьмем е-окрестности точек А и В столь малыми, чтобы они не пересекались, например, возьмем

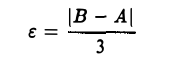
(рис.6).

Так как 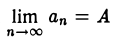Числовые множества и числовые последовательности , то вне интервала (А — ε, А + ε), в частности, в интервале (В — ε, В + ε) может располагаться лишь конечное число точек из последовательности Числовые множества и числовые последовательности . Поэтому число В и не может быть пределом последовательности .

Определение:

Последовательность Числовые множества и числовые последовательности называется ограниченной сверху, если существует число М такое, что

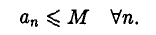
Пример:

Последовательность … — п,-(п — 1),…,-3, — 2, — 1 ограничена сверху: любой член этой последовательности меньше нуля.

Определение:

Последовательность Числовые множества и числовые последовательности называется ограниченной снизу, если существует число т такое, что

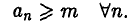
Пример:

Последовательность 1, 2, 3………. ограничена снизу: любой член этой последовательности не меньше единицы.

Определение:

Последовательность Числовые множества и числовые последовательности называется ограниченной, если она ограничена и сверху, и снизу, т. е. если существуют числа m и М такие, что

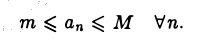
Геометрически это означает, что все точки, изображающие члены последовательности Числовые множества и числовые последовательности , лежат на отрезке [т, М].

Пример:

Последовательность Числовые множества и числовые последовательности с общим членом 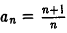ограничена: при всяком п имеем

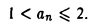
Иногда бывает удобнее другое, равносильное определение.

Определение:

Последовательность Числовые множества и числовые последовательности называется ограниченной, если существуют число К > 0 такое, что для любого п выполнено неравенство

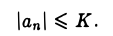
Сформулируем определение ограниченности последовательности с помощью логических символов:

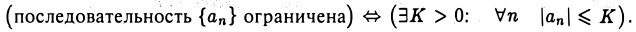
Определение неограниченной последовательности получаем из предыдущего заменой квантора существования на квантор общности, квантора общности на квантор существования и обращения неравенства:

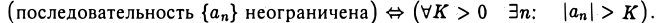
Пример:

Последовательность {2ⁿ} — неограниченная.

Каково бы ни было число К > 0, найдется п такое, что 2ⁿ > К, именно п > log2 К. Тем самым, последовательность { 2ⁿ } неограничена.

Определение:

Последовательность {ап} называется бесконечно большой, если для любого как угодно большого числа М > 0 существует номер N такой, что

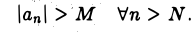
Мы пишем в этом случае, что

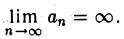
Если последовательность {ап} такова, что

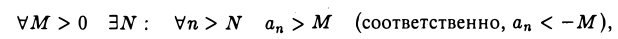
то эту последовательность также называют бесконечно большой и пишут

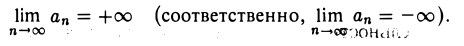
Любая бесконечно большая последовательность является неограниченной. Напротив, неограниченная последовательность Числовые множества и числовые последовательности может и не быть бесконечно большой. Такова, например, последовательность .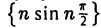

Теорема:

Об ограниченности сходящейся последовательности. Всякая сходящаяся последовательность ограничена, т. е. существуют числа т и М такие, что

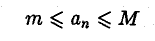
для всех членов данной последовательности.
Пусть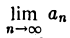 Числовые множества и числовые последовательности = А. Возьмем какое угодно ε > 0. Тогда найдется такой номер N, что все члены аn с номерами п > N будут содержаться в интервале (А- ε, А+ ε), а вне этого интервала могут оказаться только точки 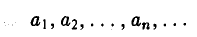Числовые множества и числовые последовательности (рис. 7). Последних конечное множество. Поэтому среди них есть самая левая точка а_ и самая правая точка а+. Обозначим через т меньшее из двух чисел а_ и А — ε

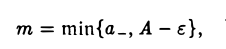
а через М — большее из чисел а+ и А + ε

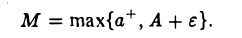
Тогда на отрезке [т, М] будут находиться точки 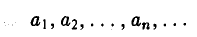Числовые множества и числовые последовательности также интервал (A — ε, А + ε), содержащий все точки аn с номерами п ≥ N + 1.

Следовательно, отрезок [т, М] будет содержать все члены данной последовательности Числовые множества и числовые последовательности , что и означает ее ограниченность.

Из теоремы 4 следует, что необходимым условием сходимости последовательности является ее ограниченность. Однако для сходимости последовательности условие ограниченности достаточным не является.

Пример:

Ограниченная последовательность

1,0,1,0,1,… (3)

расходится.

Предположим противное, т.е. что последовательность (3) имеет предел, равный числу А. Тогда для любого ≥ > 0, в частности, для ε =1/4 должно найтись натуральное число N такое, что

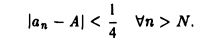
Поскольку члены последовательности (3) равны то единице, то нулю, будут выполняться неравенства

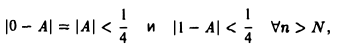
откуда легко вытекает, что

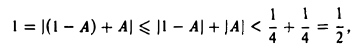
т.е. I < 1/2

Полученное противоречие свидетельствует о том, что наше допущение о сходимости последовательности (3) неверно. Значит, последовательность (3) предела не имеет, т. е. расходится.

Арифметические операции над сходящимися последовательностями

Теорема:

Если последовательности {ап} и {bп} сходятся, то сходится и последовательность {аn + bп}, причем

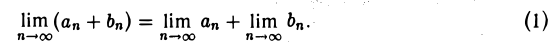
Пусть 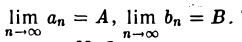Числовые множества и числовые последовательности Тогда для любого ε > 0 найдется номер N1 такой, что для всех п > N1 будет верно неравенство

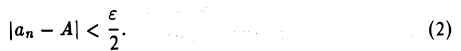
Аналогично найдется номер N2 такой, что для всех п > N1 будем иметь

Положим N = max{N1, N2}. Тогда для всякого п > N будут одновременно выполняться неравенства (2) и (3). Поэтому для всех п > N будем иметь

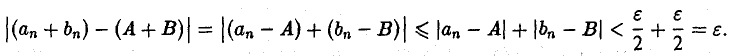
Согласно определению, это означает, что последовательность { аn +bn} сходится и имеет место равенство (1).

Теорема остается справедливой для суммы любого конечного числа сходящихся последовательностей.

Похожими рассуждениями доказываются следующие утверждения.

Теорема:

Если последовательности {аn} и {bn} сходятся, то сходится и последовательность {аn — bn}, причем

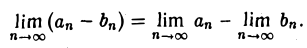
Теорема:

Если последовательности {аn} и {bn} сходятся, то сходится и поcледовательность {аn • bп}, причем

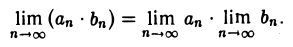
Теорема:

Если последовательности {аn} и {bn} сходятся, причем 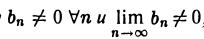Числовые множества и числовые последовательности , то последовательность 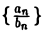также сходится и

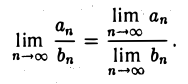
Монотонные последовательности

Определение:

Последовательность {ап} называется неубывающей, если

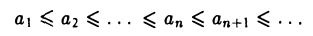
Последовательность {аn} называется невозрастающей, если

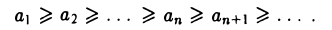
Определение:

Последовательность {аn} называется монотонной, если она является либо неубывающей, либо невозрастающей.

Неубывающая последовательность {аn} будет ограниченной, если она ограничена сверху, т. е. если существует такое число М, что аn ≤ М ∀ n.

В самом деле, в этом случае все члены последовательности лежат на отрезке [а1,М].

Невозрастающая последовательность {ап} будет ограниченной, если она ограничена снизу, т. е. если существует число т такое, что ап ≥ т ∀ n.

Все члены последовательности {аn} будут лежать на отрезке [m, a1].

Теорема:

Всякая монотонная ограниченная последовательность имеет предел.
Так как последовательность {аn} ограничена, то множество ее элементов имеет точную верхнюю и точную нижнюю грани. Пусть М — точная верхняя грань множества элементов последовательности {аn}. Покажем, что если {ап} — неубывающая последовательность, то

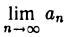Числовые множества и числовые последовательности = М.

Согласно определению точной верхней грани, для любого числа ε > О можно указать элемент a_N такой, что a_N > М — ε и a_N < М. Из этих двух неравенств следует двойное неравенство 0 ≤ М — a_N < ε. Так как {аn} — неубывающая последовательность, то при ∀n ≥ N верны неравенства

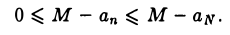
Отсюда вытекает, что

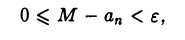
или

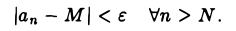
Это означает, что число М есть предел последовательности (an}.

Аналогично доказывается, что если {аn} — невозрастающая ограниченная последовательность и т — точная нижняя грань множества элементов последовательности, то 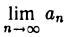Числовые множества и числовые последовательности = m.

Замечание:

Монотонность не является необходимым условием сходимости последовательности. Например, немонотонная последовательность 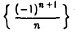Числовые множества и числовые последовательности сходится: 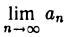= 0.

Из теоремы 9 следует важное свойство стягивающейся системы вложенных отрезков.

Лемма (Кантор):

Пусть задана последовательность отрезков

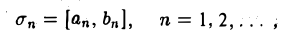
вложенных друг в друга, т. е. таких, что 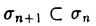Числовые множества и числовые последовательности (п = 1,2,…), с длинами, стремящимися к нулю: аn = bn — аn —» 0 при п —» ∞. Тогда существует и притом единственная точка, принадлежащая всем отрезкам ап.

Эта лемма выражает замечательное свойство непрерывности множества действительных чисел или свойство полноты числовой прямой (сплошное, без «дырок», заполнение этой прямой действительными числами).

Число е

Рассмотрим последовательность {an} с общим членом

Выпишем несколько ее первых членов:

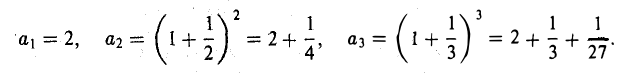
Легко видеть, что а1 < а2 < аз.

Пользуясь формулой бинома Ньютона 2), можно показать, что последовательность 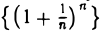Числовые множества и числовые последовательности монотонно возрастает и ограничена, причем

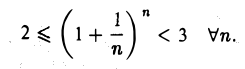
Значит, эта последовательность имеет предел, который обозначают буквой е,

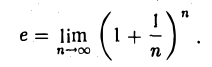
Число е иррациональное, е ≈ 2,7183 … . По некоторым соображениям число е удобно выбрать в качестве основания для системы логарифмов. Логарифмы по основанию е называются натуральными логарифмами. Натуральный логарифм числа х > 0 обозначается символом In x.

2) Формулой бинома Ньютона называется формула

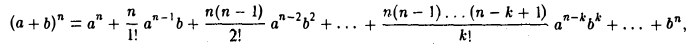
где, по определению, k = 1 • 2 • 3 • • • k.

В частности,

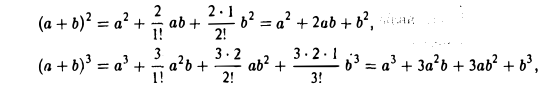
т.е. получаем знакомые формулы квадрата суммы и куба суммы двух слагаемых.

Замечание:

Существование предела последовательности Числовые множества и числовые последовательности 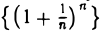можно доказать, если воспользоваться неравенством Бернулли.

В самом деле, в силу этого неравенства 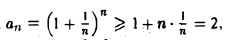Числовые множества и числовые последовательности т. е. последовательность {an} ограничена снизу. Рассмотрим последовательность {bn}, где

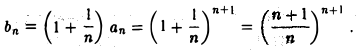
Ясно, что 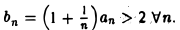Числовые множества и числовые последовательности Имеем

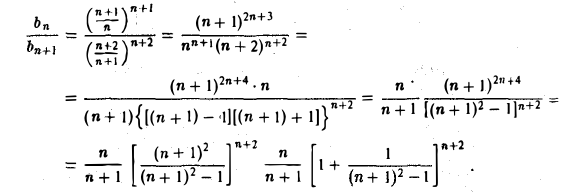
Применив опять неравенство Бернулли к выражению

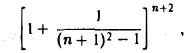
получим

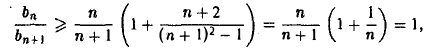
т.е. Числовые множества и числовые последовательности .

Таким образом, последовательность {bn} — невозрастающая и ограниченная снизу и потому имеет предел. Но тогда существует и предел последовательности {аn}, причем

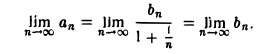
Комплексные числа и действия над ними

В этом параграфе изложены основные определения и факты, относящиеся к понятию комплексного числа, действиям с комплексными числами и их геометрической интерпретации.

Комплексным числом называется выражение вида

z = х + iy

(алгебраическая форма записи комплексного числа), где х и у — произвольные действительные числа, а i — мнимая единица — удовлетворяет условию i2 = — 1. Числа х и у называются соответственно действительной (вещественной) и мнимой частями комплексного числа z = х + iy.

Обозначения: х = Re z, у = Im z.

Комплексное число вида х + i0 отождествляется с действительным числом х. Комплексные числа z1 = х1 + iy1, и z2 = х2 + iу2 называются равными, z1 = z2, если х1 = х2 и у1 = у2.

Введем алгебраические операции над комплексными числами.

1) Сложение. Суммой z1 + z2 комплексных чисел z1 = x1 + iy1 и z2 = х2 + iy2 называется комплексное число (1)

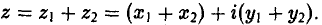
Непосредственно проверяются основные законы сложения — переместительный:

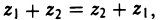
и сочетательный:

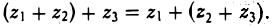
Сложение допускает обратную операцию — вычитание: для любых двух комплексных чисел z1 и z2 можно указать такое число z, что z1 = z + z2. Это комплексное число z называется разностью комплексных чисел z1 и z2 и обозначается черезz1 — z2:
(2)

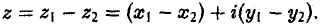
2) Умножение. Произведением Z1Z2 комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число
(3)

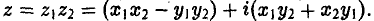
Эту формулу легко запомнить: достаточно при обычном перемножении (z1 + iy1) и (х2 + iy2) учесть, что i² = — 1. Если z1 и z2 — действительные числа, то правило (3) совпадает с обычным.

Несложно проверить, что при таком определении произведения сохраняются основные законы умножения — переместительный:

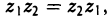
сочетательный:

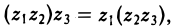
распределительный (относительно сложения):

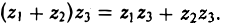
Умножение допускает обратную операцию — деление: для любых двух комплексных чисел z1 и z2 (z2 ≠ 0) можно найти такое комплексное число z, что

z1 = z2z. (4).

Комплексное число z называется частным от деления z1 на z2 и обозначается через 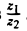Числовые множества и числовые последовательности .

Укажем формулу для вычисления частного. Пусть

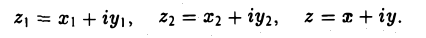
Тогда из формулы (4) вытекает, что (5)

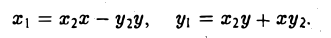
Полученная система (5) при z2 ≠ 0 всегда разрешима относительно х и у. Имеем
(6)

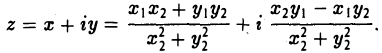
Комплексное число

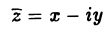
называется сопряженным комплексному числу z = x + iy. Укажем некоторые свойства операции сопряжения:
(7)

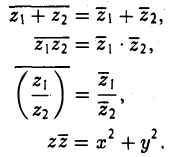
Тригонометрическая и показательная формы записи комплексного числа

Комплексное число z = х + iy изображается на плоскости хОу точкой М с координатами (х, у) либо вектором, начало которого находится в точке 0(0,0), а конец — в точке М (х, у) (рис. 8). Такую плоскость будем называть комплексной плоскостью z; ось Ох — действительной (вещественной) осью, а ось Оу — мнимой осью.

Для определения положения точки М ≠ 0 на координатной плоскости удобно пользоваться полярными координатами (r, θ), где r — длина вектора Числовые множества и числовые последовательности , а θ — угол между вектором 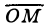и осью Ох (рис.9). Переходя в алгебраической форме записи комплексного числа z = х + iy к полярным координатам

х = r cos θ, у — r sin θ,

получим тригонометрическую форму записи комплексного числа

r = r(cos θ + r sin θ), z ≠ 0. (8)

Полярный радиус r называется модулем комплексного числа z, а полярный угол θ — его аргументом.

Обозначение: r = \z\, θ = Argz.

Модуль комплексного числа определяется однозначно:
(9)

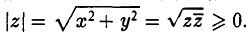
Аргумент комплексного числа z ≠ 0 определен с точностью до слагаемого, кратного 2 π: (10)

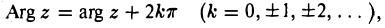
где arg z — главное значение аргумента, задаваемое следующими условиями (11)

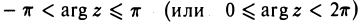
и (12)

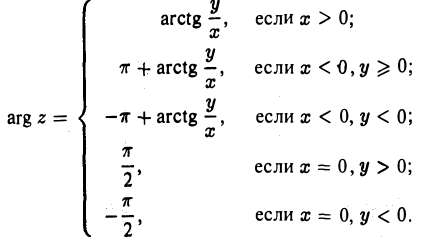
Аргумент комплексного числа z = 0 вообще не определен, а модуль этого числа равен нулю.

Два отличны от нуля комплексных числа z1 и z2 равны между собой в том и только в том случае, когда их модули равны, а их аргументы либо равны, либо отличаются на слагаемое, кратное 2 π: (13)

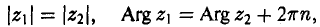
где п — целое число.

Пример:

Найти модуль и аргумент комплексного числа

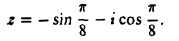
Имеем

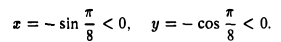
Главным значением аргумента, согласно (12) будет

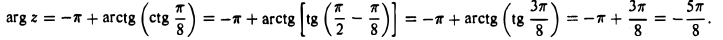
Следовательно,

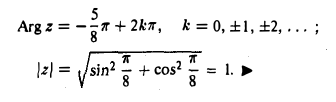
Отмеченное выше соответствие между комплексными числами и векторами на плоскости придает естественный геометрический смысл операциям сложения и вычитания комплексных чисел (см. рис. 10, где изображена сумма и разность комплексных чисел z1 и z2).

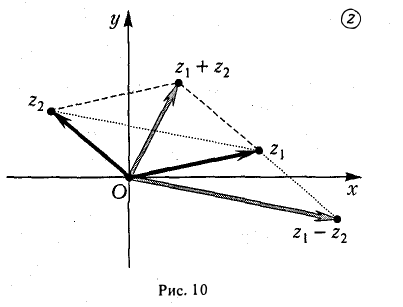
Легко устанавливаются следующие неравенства. (14)

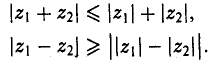
Для простоты письма введем сокращенное обозначение (15)

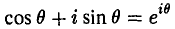
(полный смысл введенного обозначения будет установлен в дальнейшем). Это пoзволяет записать комплексное число (8) в показательной форме
(16)

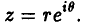
Тригонометрическая и показательная формы записи комплексного числа удобны для выполнения операции умножения и деления комплексных чисел. Если 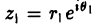Числовые множества и числовые последовательности и 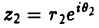, то (17)

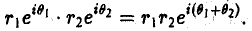
В самом деле

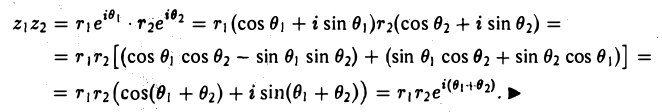
Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются: (18)

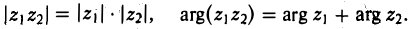
Так же просто выполняется операция деления комплексных чисел:
(19)

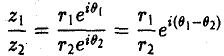
(при r2 ≠ 0). Из формулы (19) видно, что
(20)

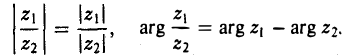
Определим операцию возведения комплексного числа z в натуральную степень п:

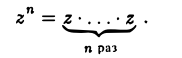
В силу формулы (17) возведение комплексного числа

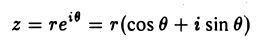
в степень п можно производить по правилу
(21)

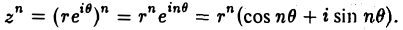
Из последнего соотношения при r = 1 получается формула Муавра
(22)

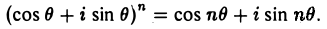
Обратная операция — извлечение корня — определяется следующим образом. Комплексное число w называется корнем п-й степени из комплексного числа z, если
(23)

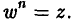
Обозначение: 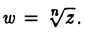Числовые множества и числовые последовательности

Покажем, что для любого z ≠ 0 корень 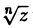Числовые множества и числовые последовательности имеет п различных значений. Подставляя

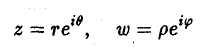
в формулу (23), получаем
(24)

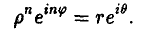
Напомним, что из равенства комплексных чисел вытекает равенство их модулей, а аргументы чисел либо совпадают, либо различаются на слагаемое, кратное 2 π. Поэтому из соотношения (24) вытекают равенства

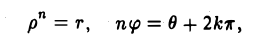
или, что тоже,
(25)

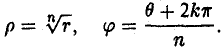
Первое из равенств (25) показывает, что модули всех корней п-й степени из z одинаковы, а второе — что их аргументы различаются на слагаемое, кратное 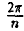Числовые множества и числовые последовательности . Отсюда вытекает, что точки на комплексной плоскости, соответствующие различным значениям корня n-й степени из комплексного числа z ≠ 0, расположены в вершинах правильного n-угольника, вписанного в окружность радиуса 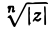Числовые множества и числовые последовательности с центром в точке w = 0 (рис. 11).

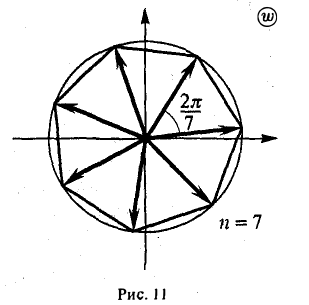
Придавая в формуле (25) числу к значения 0, 1,2,… ,п— 1, получим п различных комплексных чисел

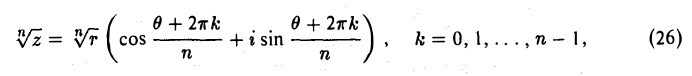
или

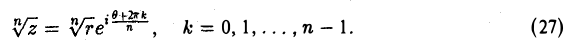
Пример:

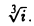
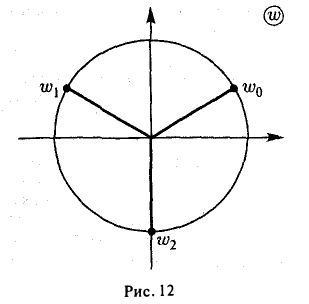
Найти все значения Числовые множества и числовые последовательности

Запишем комплексное число z = i в показательной форме

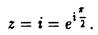
В соответствии с формулами (27) получаем

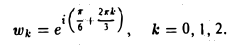
Отсюда

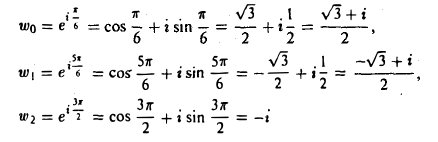
(рис. 12).

Предел последовательности комплексных чисел

Пусть {zn} — последовательность комплексных чисел.

Определение:

Комплексное число z называется пределом последовательности {zn}, если для любого ε > 0 найдется номер N = N( ε ) такой, что для всех п ≥ N выполняется неравенство

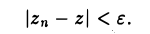
Последовательность {zn}, имеющая пределом комплексное число z, называется сходящейся к числу z.

Обозначения: 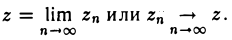Числовые множества и числовые последовательности

Каждый элемент zn = xn + iyn последовательности {zn} характеризуется парой действительных чисел хп и уп. Поэтому последовательности комплексных чисел {zn} соответствуют две последовательности вещественных чисел {in} и {уп}, составленные из действительных и из мнимых частей элементов zn последовательности {zn}.

Теорема:

Последовательность комплексных чисел {zn} является сходящейся в том и только в том случае, когда одновременно сходятся обе последовательности действительных чисел {хn} и {уп} (zn = хn + iyn).

Пусть последовательность {zn} сходится к числу z. Это означает, что для любого ε > 0 можно указать номер N, такой, что для всех п ^ N выполняется неравенство |zn — z| < ε. Так как |хn — х| ≤ |zn — z| и |уп — y| ≤ |zn — z| < ε, то отсюда следует, что

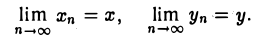
Обратно, если 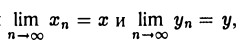Числовые множества и числовые последовательности то тогда для любого ε > 0 найдется номер N1 такой, что

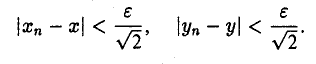
Поэтому

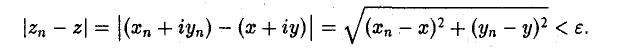
Тем самым,

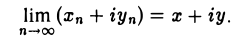
Доказанное утверждение позволяет переносить на последовательности комплексных чисел все основные факты, установленные для сходящихся последовательностей действительных чисел.

Простейшие виды числовых множеств

Числовыми множествами называют множества, элементы которых являются числами. Простейшими среди них являются множество натуральных чисел

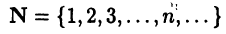
и множество целых чисел

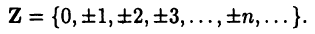
Они являются подмножествами множества рациональных чисел

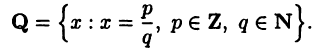
Рациональные числа определяются как обыкновенные дроби. Можно показать, что каждая обыкновенная дробь представима в виде бесконечной периодической десятичной дроби. Например, 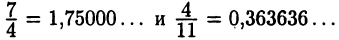Множества Верно и обратное: каждая бесконечная периодическая десятичная дробь записывается в виде обыкновенной дроби. Поэтому рациональные числа можно также определять как бесконечные периодические десятичные дроби.

Бесконечные непериодические десятичные дроби называются иррациональными числами. Таковым, например, является число 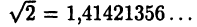Множества Отметим следующие иррациональные числа, играющие особую роль в математике и ее приложениях:

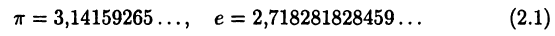
Обозначим множество иррациональных чисел через I.

Пример:

Покажем, что число 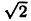Множества является иррациональным. В предположении противного оно является рациональным числом, т. е. найдутся натуральные числа 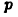и 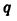такие, что 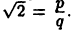Можно считать, что числа 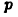Множества и 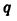несократимы, в частности, по крайней мере, одно из них является нечетным. Возведя

в квадрат обе части равенства 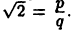Множества получим 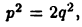т. е. число 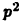и, следовательно, само 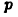четно. Тогда 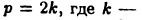некоторое натуральное число. Отсюда получим 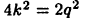и, следовательно, 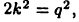т. е. число 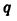также является четным, что противоречит предположению. Таким образом, число 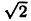Множества является иррациональным.

Множество вещественных чисел

Множество вещественных (действительных) чисел определяется равенством 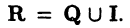Множества Другими словами, вещественные числа определяются как числа либо рациональные, либо иррациональные.

Множество вещественный чисел является наиболее широким из рассмотренных выше числовых множеств: оно содержит как подмножества множества N натуральных чисел, Z целых чисел, Q рациональных чисел и I иррациональных чисел.

Непрерывность множества вещественных чисел

Множество R вещественных чисел обладает важным свойством, называемым непрерывностью этого множества.

• Пусть 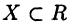Множества и 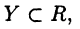при этом 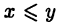для 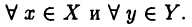Тогда 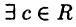такое, что 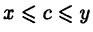для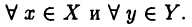

Это свойство говорит о том, что между множествами Х и 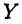не может быть «дырки», т. е. пустого множества. Поэтому его и называют «непрерывностью» множества вещественных чисел.

Множество Q рациональных чисел таким свойством не обладает. Действительно, если рассмотреть два его подмножества

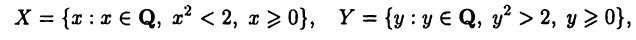
то 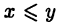Множества для 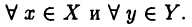В то же время не найдется числа 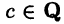такого, что 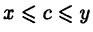для 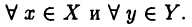так как таким числом может быть только 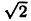, которое не является рациональным.

Наиболее употребительные числовые множества

Пусть 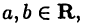Множества причем 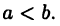Ниже будут использоваться обозначения:

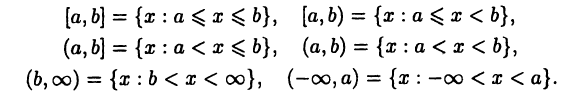
При этом множество вещественных чисел будет обозначаться в виде:

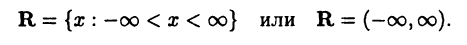
Введенные в рассмотрение числовые множества называются промежутками, при этом множество 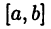— отрезком, множество 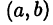— интервалом, а множества 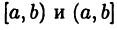— полуинтервалами.

Абсолютное значение вещественного числа

Абсолютным значением или модулем числа 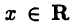Множества называется неотрицательное число 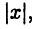определяемое равенством:

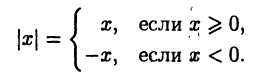
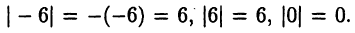Множества Отметим следующие полезные неравенства

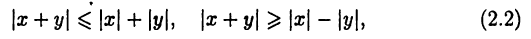
верные для любых вещественных чисел 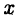Множества и 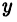(докажите их!).

Грани числовых множеств

Множество 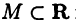называется ограниченным сверху (снизу), если 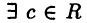такое, что 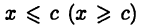для 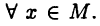При этом число с называется верхней (нижней) гранью множества М. Если М является одновременно ограниченным и сверху и снизу, то оно называется ограниченным.

Каждый промежуток вида 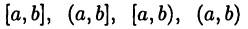Множества является, очевидно, ограниченным множеством (покажите это). Промежуток 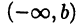является ограниченным сверху и неограниченным снизу, а промежуток 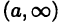— наоборот. Наконец, множество R всех вещественных чисел неограниченно и сверху и снизу.

Пусть М — ограниченное сверху множество. Естественен вопрос о том, имеет ли это множество «максимальный» элемент, т. е. найдется ли число 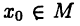такое, что 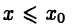для 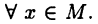Если такой «максимальный» элемент существует, то пишут 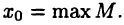Аналогично определяется понятие «минимального» элемента для ограниченного снизу множества М; если «минимальный» элемент существует и равен то пишут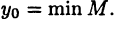

Пример:

Рассмотрим множества

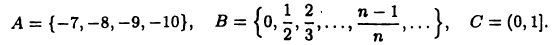
Очевидно, что эти множества ограниченные, причем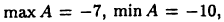 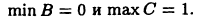В то же время множество В не имеет максимального элемента (покажите!), а множество С не имеет минимального элемента (покажите!).

Приведенный пример показывает, что максимальный или мини-г мальный элемент у ограниченного бесконечного множества может не существовать (покажите, что для конечных множеств такие элементы всегда существуют!).

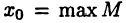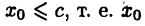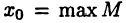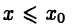Пусть М. — ограниченное сверху множество и пусть существует max М. Докажем, что число является верхней гранью множества М, при этом для любой другой верхней грани с выполнено неравенство является наименьшей верхней гранью множества М. Действительно, так как то для 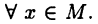следовательно, число 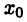является верхней гранью множества М. Далее, если с — другая верхняя грань множества М, то 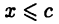для 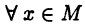и так как 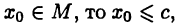что и требовалось доказать.

Таким образом, если М — ограниченное сверху множество и существует 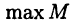, то существует наименьшая верхняя грань этого множества (совпадающая в этом случае с 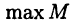). Правомерен вопрос о существовании наименьшей верхней грани для произвольного ограниченного сверху множества М. Оказывается, такая верхняя грань всегда существует (даже если не существует 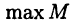); ее называют точной верхней гранью множества М и обозначают символом sup М (читается «супремум» множества М). Аналогично определяется понятие точной нижней грани множества М, которая обозначается символом inf М (читается «инфимум» множества М). Сформулируем сказанное в виде теоремы.

Теорема:

Если множество М ограничено сверху (снизу), то существует sup М (inf М).

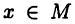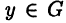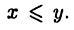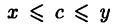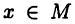► Пусть множество М ограничено сверху. Обозначим через G множество верхних граней множества М. Тогда для любых и выполнено неравенство В силу свойства непрерывности вещественных чисел найдется вещественное число с такое, что любых и 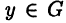. Тогда, во-первых, число с является верхней гранью множества М и, во-вторых, с не превосходит любую другую верхнюю грань этого множества, т. е. с = sup М. Аналогично рассматривается случай, когда множество М ограничено снизу.

Пример:

Пусть М = (3,5). Тогда supM = 5 и inf М = 3. Покажем, например, справедливость первого равенства. Так как х < 5 для 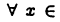(3,5), то число с = 5 является верхней гранью множества М. Остается показать, что оно является наименьшей верхней гранью. Допустим противное, т. е. существует верхняя грань 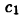множества М такая, что 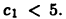Через 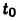обозначим среднее арифметическое чисел 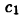и 5, т. е. 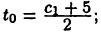тогда с одной стороны, 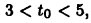т. е. 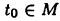, а с другой стороны, 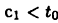, что противоречит предположению о том, что 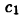верхняя грань множества М.

Пример:

Пусть 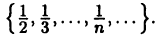А = Тогда 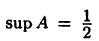и inf А = 0. Действительно, так как множество А имеет максимальный элемент, то 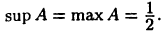Покажем теперь, что inf А = 0. Так как элементы множества А положительны, то число 0 является нижней гранью этого множества. Пусть теперь с — какая-либо другая нижняя грань множества А. Тогда 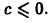Действительно, допустим, что с > 0. Очевидно найдется, натуральное число 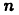такое, что 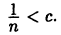Так как 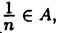то это противоречит тому, что с является нижней гранью множества А. Итак, 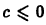и, следовательно, inf А = 0.

Отметим следующее важное свойство точных верхних и нижних граней.

Теорема:

Пусть М — ограниченное сверху (снизу) множество и 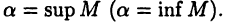Множества Тогда для 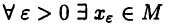такое, что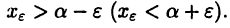

► Рассмотрим только случай, когда М ограничено сверху. Допустим, что утверждение теоремы не верно, т. е. 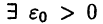такое, что для 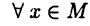выполнено неравенство 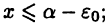тогда число 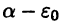является верхней гранью множества М, причем меньшей, чем a = supM. Это противоречит тому, что sup М является наименьшей верхней гранью.

Теорема 2.2 указывает на тот факт, что если множество М ограничено сверху (снизу) и 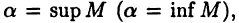Множества то в нем найдутся числа, как угодно близкие к 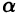(которые могут, конечно, и совпадать с 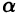, если множество М имеет максимальный (минимальный) элемент).

Понятие супрермума (инфимума) было дано для ограниченного сверху (снизу) множества. Если же множество М не ограничено сверху (снизу), то естественно полагать: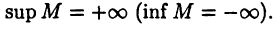

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: