Оглавление:
Линейное отображение — обобщение линейной числовой функции, а точнее, функции на случай более общего множества аргументов и значений. Линейные отображения, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.
Определение линейного отображения. Образ и ядро линейного отображения
Пусть V и W — линейные пространства (либо оба вещественные, либо оба комплексные). Линейным отображением линейного пространства V в линейное пространство W называется правило А, согласно которому каждому элементу х из пространства V ставится в соответствие (единственный) элемент у = Ах из пространства W так, что
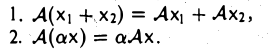
Эти два требования можно объединить в одно:
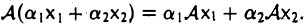
Обозначение: A:V → W.
Примеры линейных отображений
- Пусть V = W = Мп, где Мп — пространство многочленов, степень которых не выше п. Правило
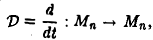
согласно которому каждому многочлену из Мп ставится в соответствие его производная, является линейным отображением (производная суммы равна сумме производных, постоянный сомножитель можно выносить из-под знака производной).
2. Правило, по которому каждому элементу х из V ставится в соответствие элемент λх из V ( λ ≠ 0 и фиксировано), — преобразование подобия — является линейным отображением (рис. 1).
3. Пусть у = (еi…, еn) — базис пространства V. Поставим произвольному элементу
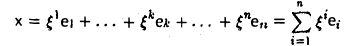
в соответствие элемент
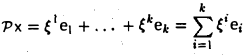
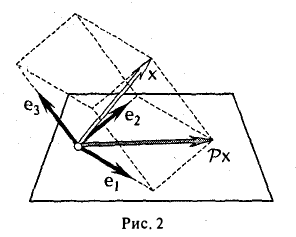
(здесь k < п фиксировано). Правило V : V → V является линейным отображением и называется отображением проектирования (рис. 2).
4. Cовокупность Т2 тригонометрических многочленов вида
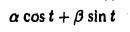
образует линейное пространство. Правило
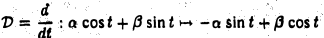
является линейным отображением
5. Пусть 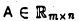 — фиксированная матрица, X — произвольный столбец высоты п. Умножение столбца X на матрицу А слева является линейным отображением пространства столбцов высоты п в пространство столбцов высоты m,
— фиксированная матрица, X — произвольный столбец высоты п. Умножение столбца X на матрицу А слева является линейным отображением пространства столбцов высоты п в пространство столбцов высоты m,
Образом линейного отображения А: V → W называется множество im А всех элементов из пространства W, обладающих следующим свойством элемент у лежит в im А, если в пространстве V найдется элемент х, такой, что Ах = у. Примеры.
1′. Образом операции дифференцирования V : Мn — Мп является совокупность многочленов, степень которых не выше п — 1,
2′. Образ отображения подобия совпадает со всем пространством V.
3′. Образ отображения проектирования V : V → V является подпространством
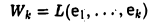
пространства V.
4′. Образ операции дифференцирования V : T2 → Т2 совпадает со всем пространством Т2
Теорема:
Образ im А линейного отображения А: V → W является линейным подпространством пространства W.
Пусть у1 и у2 — элементы из im А. Это означает, что в пространстве V найдутся элементы x1 и х2, такие, что -Ax1 = y1 и Ах2 = у2. Из формулы
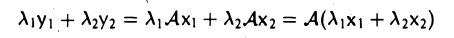
вытекает, что произвольная линейная комбинация элементов y1 и у2 также лежит в im А.
Размерность образа линейного отображения называется рангом этого линейного отображения.
Обозначение: rang А.
Определение:
Линейные отображения А: V → W и В: V W называются равными, если для любого элемента х из пространства V выполняется равенство Ах = Вх.
Обозначение: А = В.
Теорема:
Построение линейного отображения. Пусть V и W — линейные пространства, e = (e1… , еn) — базис пространства V, a f1. . ., fn — произвольные элементы из пространства W. Тогда существует и притом ровно одно линейное отображение
A :V → W,
для которого
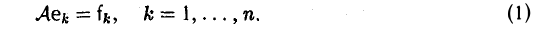
А. Существование. Разложим произвольный элемент х из пространства V по базису с этого пространства,
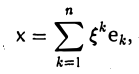
и построим отображение А: V → W по следующему правилу:
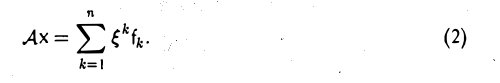
Ясно, что
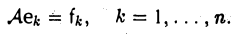
В линейности отображения А убедимся непосредственно. Пусть
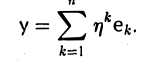
Тогда согласно правилу (2)
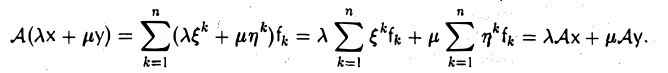
Б. Единственность. Покажем, что требованием (1) линейное отображение А определяется однозначно.
Пусть В: V → W — линейное отображение и
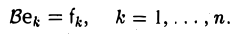
Вычисляя действия А и В на произвольный элемент х из V, убеждаемся в том, что в обоих случаях результат один и тот же —
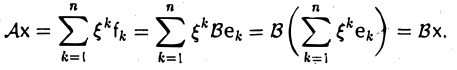
Значит, отображения A и В совпадают.
Таким образом, линейное отображение можно задать его действием только на элементы базиса.
Ядром линейного отображения А: V → W называется множество ker А всех элементов из пространства V, каждый из которых отображение А переводит в нулевой элемент θw пространства W.
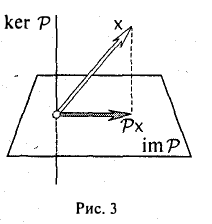
Примеры:
1″. Многочлены нулевой степени образуют ядро операции дифференцирования V: Мп -> Мп.
2″. Ядро отображения подобия состоит из нулевого элемента θv пространства V.
3″. Ядром отображения проектирования P: V→V является линейное подпространство L(ek+1,…, еn) (рис. 3).
4″. Ядро операции дифференцирования D:T2→Т2 состоит из нуля.
5″. Ядром отображения
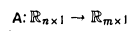
является множество решений однородной линейной системы
АХ = 0.
Теорема:
Ядро линейного отображения А: V
→W является линейным подпространством пространства V.
Из равенств Ах = θw и Ay = θw вытекает, что
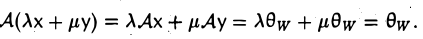
Размерность ядра линейного отображения называется дефектом этого отображения.
Обозначение: defect .<4.
Для любого линейного отображения А: V→W справедливо равенство
rang А + defect А = dim V. (*)
Операции над линейными отображениям
Пусть V и W — линейные пространства и A:V W, B:V→W — линейные отображения. Суммой линейных отображений А и В называется отображение С: V→W, определяемое п о следующему правилу:
Сх = Ах + Вх
для любого элемента х из V. Нетрудно убедиться в том, что отображение С является линейным. В самом деле,
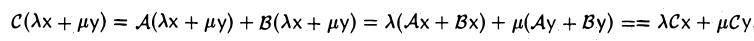
Обозначение: С = А + В.
Произведением линейного отображения A:V→W на число а называется отображение В: V —> W, определяемое по правилу:
Вх = аАх
для любого элемента х из V. Отображение В линейно:
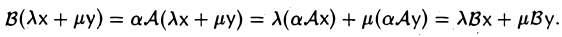
Обозначение: В = а А.
В дальнейшем мы ограничимся рассмотрением линейных операторов — линейных отображений, действующих из пространства V в это же пространство V. Среди рассмотренных выше примеров отображений линейными операторами являются дифференцирование, подобие и проектирование; умножение столбца на квадратную матрицу также является линейным оператором.
Оператор I: V —> V, задаваемый правилом Ix = х для любого элемента х из V, называется тождественным.
Введем операцию умножения линейных операторов. Пусть А: V → V и В: V→V — линейные операторы. Произведением оператора А на оператор В называется отображение С: V → V, определяемое по правилу
Сх = В(Ах),
где х — произвольный элемент из V. Покажем, что С — линейный оператор:
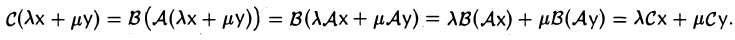
Обозначение: С = В А.
Замечание:
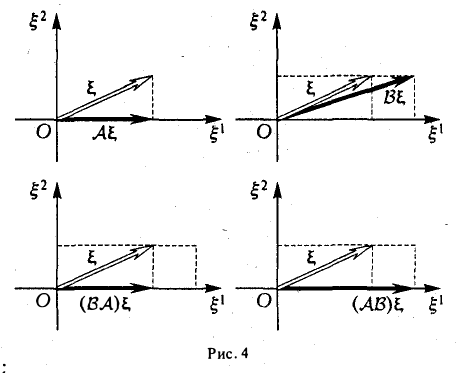
Порядок сомножителей в произведении линейных операторов является существенным, как показывает следующий пример.
Пример:
Пусть V = R2. Отображения
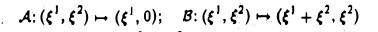
— линейные операторы, действующие из R2 в R2 (рис. 4). Тогда
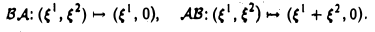
Ясно, что при ξ2 ≠ 0
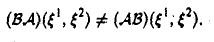
Пусть A: V → V — линейный оператор. Линейный оператор В: V → V называется обратным оператору А, если выполнены следующие равенства
ВА = АВ= I,
где I: V —> V — тождественный оператор.
Теорема:
Для того, чтобы у линейного оператора А: V → V был обратный, необходимо и достаточно, чтобы образ оператора А совпадал со всем пространством,
im А = V.
Предположим сначала, что обратный оператор В у заданного оператора А существует и покажем, что произвольно взятый элемент у из пространства V непременно лежит в im А. Подействовав оператором А на элемент х = В у, согласно определению (1), получим
Ах = А(Ву) = (АВ)у = Iу — у.
Значит, элемент у является образом элемента х = By и, следовательно, лежит в im А. Тем самым imA = V.
Пусть теперь образ оператора А совпадает со всем пространством V:
imA = V.
Тогда
rang А = dim V.
Поэтому оператор А переводит базис пространства V снова в базис:
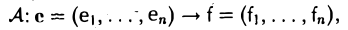
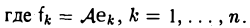
Построим линейный оператор В по следующему правилу

Согласно теореме 1, условием (2) оператор В определяется однозначно.
Пусть х — произвольный элемент пространства V. Вычислим (ВA)х и (АВ)х. Разложим х по базису с. Имеем
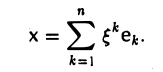
Подействовав на него оператором В А, с учетом формул (2) получаем, что
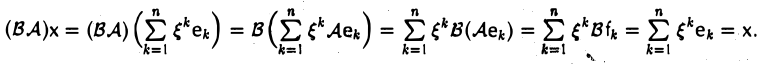
Аналогично, раскладывая элемент х по базису f,
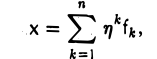
и действуя на него оператором АВ, имеем
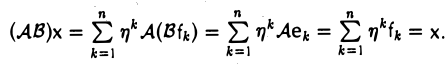
Тем самым,
ВAх = х, АВх = х
для любого элемента х из V и, значит,
В А = АВ = I.
Замечание:
В ходе доказательства этой теоремы мы установили также, что обратный к А оператор В определен однозначно.
Для оператора, обратного к А, принято следующее обозначение: А-1.
Следствие:
Линейный оператор А: V → V обратим (имеет обратный) тогда и только тогда, когда его ядро тривиально,
ker А= { θ v}.
Справедливость этого утверждения вытекает из теоремы 3 и формулы.
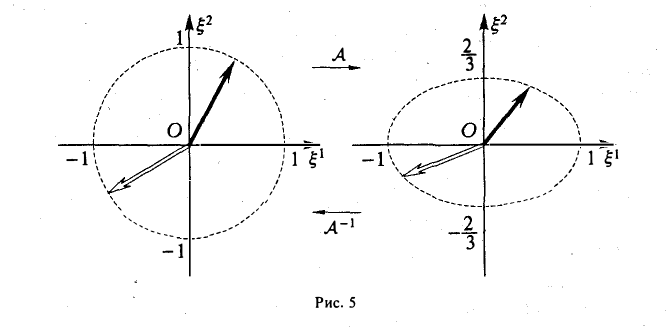
Пример:
Линейный оператор
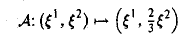
осуществляет равномерное сжатие плоскости к оси ξ 1 (с коэффициентом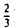 ); обратный оператор
); обратный оператор
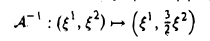
— равномерное растяжение (с коэффициентом 3/2) (рис. 5).
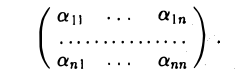
Матрица линейного оператора
Пусть линейный оператор А: V —> V преобразует элементы базиса e = (e1,…, еn) пространства V по следующему правилу
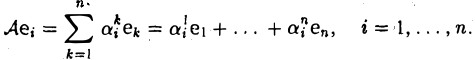
Матрица
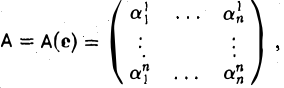
столбцами которой являются координаты образов базисных элементов, называется матрицей линейного оператора А в базисе e.
Пример:
Матрица D(с) оператора дифференцирования V: Мз → Mз в базисе ео = l. e1 = t, 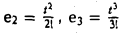 имеет вид
имеет вид
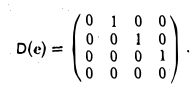
Пример:
Матрица D(e) оператора дифференцирования V: T2 → T2 в базисе e1 = cos t, е2 = sin t имеет вид
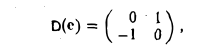
так как
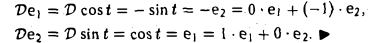
Пусть
У = Ax.
Разложим элементы x и у no базису e:
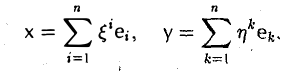
Координатные столбцы
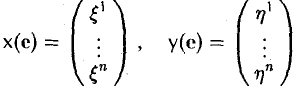
элементов х и у в базисе с связаны соотношением
у(e) = A(e)х(e). (1)
Сравнивая формулы
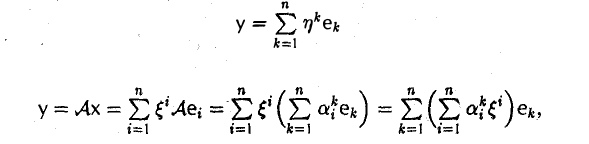
в силу единственности разложения элемента у по базису e получаем
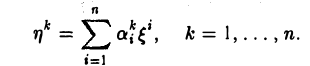
Записывая полученные п равенств в матричной форме
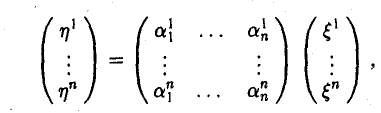
получаем требуемое равенство (1).
Теорема:
Ранг матрицы А(с) линейного оператора А: V —> V не зависит от выбора базиса с и равен рангу rang А оператора А.
Так как
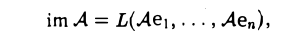
то rang A равен максимальному числу линейно независимых элементов в системе Ае1,…, Аеn. В силу теоремы 4 главы V, последнее совпадает с максимальным числом линейно независимых столбцов матрицы А(e), т. е. с ее рангом. Таким образом,
rang А(с) = rang A.
Легко убедиться в том, что при сложении линейных операторов их матрицы (вычисленные в одном базисе) складываются, а при умножении линейного оператора на число его матрица умножается на это число.
Матрица произведения С = ВА операторов А и B равна произведению матриц этих операторов (относительно одного и того же базиса e):
С(e) = В(e)А(e). (2)
Пусть
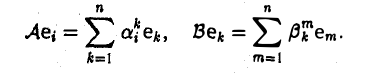
Тогда
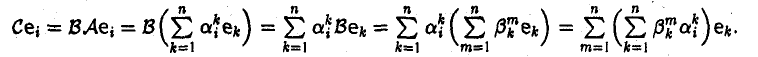
Положим
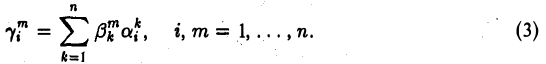
Тем самым,

Вследствие того, что 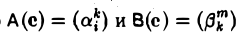 из формул (3) и (4) получаем
из формул (3) и (4) получаем
С (e) = В(e)А(e).
Отсюда, в частности, вытекает, что
матрица оператора A-1 , обратного к A, является обратной к его матрице А.
В самом деле, из соотношений
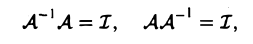
определяющих обратный оператор, получаем, что его матрица В удовлетворяет равенствам
ВА = I, АВ = I,
и, значит, является обратной к А:
В = A-1.
Теорема:
Матрицы А = А(е) и А’ = А(е’) линейного оператора А: V → V относительно базисов с и с’ пространства V связаны равенством

где S — матрица перехода от базиса е к базису е’.
Пусть у = Ах. Координатные столбцы элементов х и у относительно базисов с и с’ связаны равенствами
у(е) = Ах (е), у(е’) = А’х(е’) (6)
соответственно. Согласно свойству 2 матрицы перехода имеем
х(е) = Sx(c’), у(е) = Sy(е’). (7)
Заменяя в первом из равенств (6) столбцы х(е) и у(е) их выражениями (7), получаем
Sy(е’) = ASx(е’).
Пользуясь вторым равенством (6), имеем
SA’x(е’) = ASx(е’).
Отсюда в силу произвольности столбца х(е’) получаем, что
SA’ = AS.
Так как матрица перехода S невырождена и, значит, обратима, то умножая обе части последнего равенства на матрицу S -1 слева приходим к требуемой формуле (5).
Следствие:
Определитель матрицы линейного оператора не зависит от выбора базиса.
Вычислим определитель матрицы
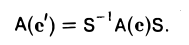
Имеем

Последнее равенство выполняется в силу того, что
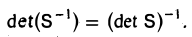
Таким же свойством обладает и определитель матрицы линейного оператора
А — tI,
где I — тождественный оператор, a t — произвольное число. * Рассмотрим матрицы этого оператора в базисах e и e’ соответственно:
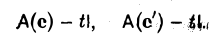
Воспользовавшись равенством (5)
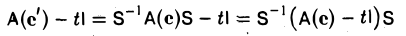
и доказанным выше следствием, получаем, что
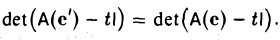
Пусть 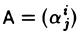 — матрица линейного оператора A в каком-нибудь базисе. Функция
— матрица линейного оператора A в каком-нибудь базисе. Функция
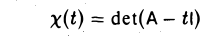
является многочленом от t и, согласно только что доказанному, не зависит от выбора базиса. Расписав определитель матрицы А — t1 подробнее, получаем, что
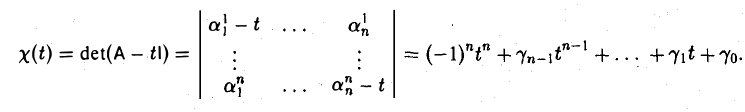
Многочлен
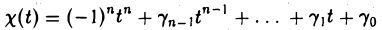
называется характеристическим многочленом линейного оператора А (матрицы А). Его корни называются характеристическими, или собственными, числами линейного оператора А (матрицы А).
Собственные значения и собственные элементы
Ненулевой элемент х ∈ V называется собственным элементом линейного оператора А: V —> V, если найдется такое число λ — собственное значение линейного оператора А, что
Ах = λх.
Пример:
Всякий многочлен нулевой степени является собственным элементом оператора дифференцирования
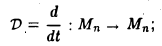
соответствующее собственное значение равно нулю:
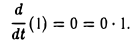
Пример:
Оператор дифференцирования собственных элементов не имеет.
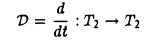
Пусть некоторый тригонометрический многочлен a cos t + β sin t после дифференцирования переходит в пропорциональный:
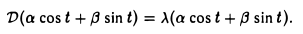
Это означает, что
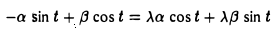
или, что то же,
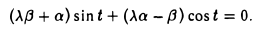
Последнее равенство выполняется в том и только в том случае, если
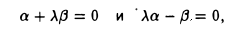
откуда вытекает, что а = β = 0 и, значит, многочлен может быть только нулевым.
Теорема:
Вещественное число λ является собственным значением линейного оператора А в том и только в том случае, когда это число — корень его характеристического многочлена: х( λ ) = 0.
Необходимость, Пусть λ — собственное значение оператора А. Тогда найдется ненулевой элемент х, для которого Ах = λх.
Пусть е = (е1 …, еп) — базис пространства. Тогда последнее равенство можно переписать в эквивалентном матричном виде
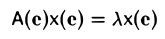
или, что то же,

Из того, что х — собственный элемент, вытекает, что его координатный столбец х(е) ненулевой. Это означает, что линейная система (1) имеет ненулевое решение. Последнее возможно лишь при условии, что
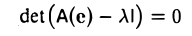
или, что то же,
x (λ) = у.
Достаточность. Способ построения собственного элемента
Пусть λ — корень многочлена т- е-
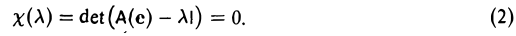
Рассмотрим однородную линейную систему с матрицей А(е) — λ1:
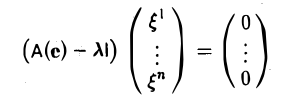
или, подробнее,
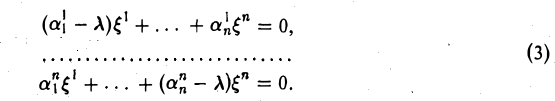
В силу условия (2) эта система имеет ненулевое решение 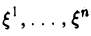 .
.
Построим элемент х по правилу
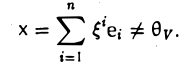
Координатный столбец х(е) этого элемента удовлетворяет условию
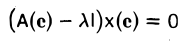
или, что то же,
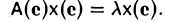
Последнее эквивалентно тому, что
Ах = λх.
Следовательно, х — собственный элемент линейного оператора λ, а А — соответствующее ему собственное значение.
Замечание:
Для нахождения всех собственных элементов, отвечающих заданному собственному значению λ, необходимо построить ФСР системы (3).
Пример:
Найти собственные векторы линейного оператора
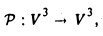
действующего по правилу
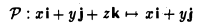
(оператор проектирования) (рис.6).
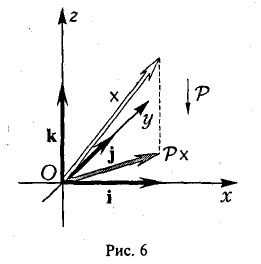
Рассмотрим действия линейного оператора Р на базисные векторы. Имеем
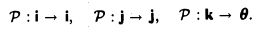
Запишем матрицу оператора:
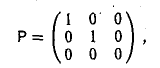
построим характеристический многочлен
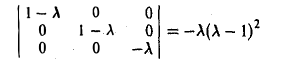
и найдем его корни. Имеем λ1 = λ2,з = 1. Построим однородные линейные системы с матрицами:
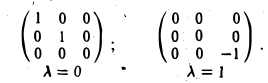
Получим соответственно:
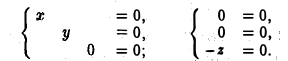
Найдем фундаментальные системы решений для каждой из этих систем. Имеем
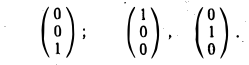
Таким образом, собственными векторами этого оператора проектирования являются: вектор к с собственным значением 0 и любой вектор 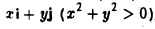 с собственным значением 1.
с собственным значением 1.
Пример:
Найти собственные элементы линейного оператора дифференцирования D, действующего в пространстве M3 многочленов степени не выше двух:
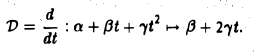
Матрица D заданного оператора в базисе I, t, t 2 имеет вид
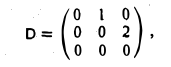
характеристический многочлен — λ 3 имеет ровно один корень λ = 0. Решением системы
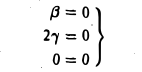
является набор 1,0,0, которому соответствует многочлен нулевой степени.
Сопряженный оператор
В евклидовом пространстве над линейными операторами можно ввести еще одно действие — операцию сопряжения.
Пусть V — n-мерное евклидово пространство. С каждым линейным оператором
A: V → V,
действующим в этом пространстве; естественно связан другой линейный оператор, сопряженный данному.
Определение:
Линейный оператор
Л*: V → V
(читается: «а со звездой») называется сопряженным линейному оператору А: V → , если для любых элементов х и у из пространства V выполняется равенство
(Ах, у) = (х, A*у). (1)
Линейный оператор А*, сопряженный данному оператору А, всегда существует.
Пусть e = (e1…..еn) — ортобазис пространства V и А = А(e) = 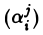 — матрица линейного оператора А в этом базисе, т. е.
— матрица линейного оператора А в этом базисе, т. е.
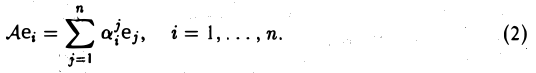
Непосредственными вычислениями можно убедиться в том, что для линейного оператора А*: V —> V, определяемого по правилу
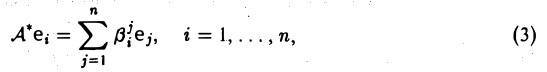
где
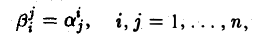
равенство (1) выполнено при любых х и у. Напомним. что согласно теореме 1, для того, чтобы построить линейный оператор, достаточно задать его действие на базисные элементы.
Пример:
Введем в линейном пространстве М\ многочленов с вещественными коэффициентами степени не выше первой операцию скалярного умножения по следующему правилу. Пусть
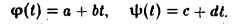
Положим

Тем самым, М1 — двумерное евклидово пространство.
Пусть D: М1 — М1 — оператор дифференцирования-. D(a + bt) = b. Построим сопряженный оператор D*: М1 → М1.
Многочлены l и t образуют ортобазис пространства Af (, так как согласно правилу (*) (1. 1) = (t, t) = 1. (l, t) = 0. Матрица оператора D в этом базисе имеет вид
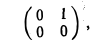
т.к. D(1) = 0, D(t) = 1. Тогда
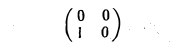
— матрица сопряженного оператора D* действующего по правилу:
D*(l)=l, D*(t)=0.
Для произвольного многочлена φ(t) = а +bt получаем
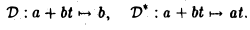
Свойства операции сопряжения
- У каждого линейного оператора существует ровно один сопряженный ему оператор.
Пусть В и С — операторы, сопряженные заданному оператору A. Это означает, что для любых элементов х и у из пространства V выполняются равенства
(Ах, у) = (х, By), (Ах, у) = (х, Су).
Отсюда вытекает, что
(х, Ву)=(х, Су)
и, далее,
(х, By — Су) = 0.
В силу произвольности выбора элемента х заключаем, что элемент Ву-Су ортогонален любому элементу пространства V и, в частности, себе самому. Последнее возможно лишь в случае, когда By — Су = θ и, значит, By = Су. Вследствие того, что у — произвольный элемент, получаем В = С.
2. (аA)* = аA*, где а — произвольное вещественное число.
Пусть A: V —> V н B: V → V — линейные операторы. Тогда
3. (А+ В)* = А* + В*;
4. (АВ)* = В*А*
5. (А*)*=А.
Свойства 2-5 легко вытекают из единственности сопряженного оператора.
6. Пусть e — ортобазис пространства V. Для того, чтобы операторы А: V —> V и В: V —> V были взаимносопряженными, т.е. выполнялись равенства В = А, А= В, необходимо и достаточно, чтобы их матрицы А = А(e) и В = В(e) получались одна из другой транспонированием.
Замечание:
Подчеркнем, что свойство 6 справедливо только для матриц, построенных в ортонормиро-ванном базисе. Для произвольного базиса оно неверно.
7. Если линейный оператор А невырожден, то сопряженный ему оператор А* также невырожден и выполняется равенство
Симметричный оператор
Линейный оператор А называется самосопряженным (или симметричным), если он совпадает с сопряженным ему оператором А*, т. е.
А* = А.
В силу свойства 6 из предыдущего параграфа матрица самосопряженного оператора в ортобазисе симметрична, т. е. не изменяется при транспонировании. Поэтому самосопряженный оператор называют также симметричным оператором.
Пример:
Рассмотрим оператор Р ортогонального проектирования трехмерного евклидова пространства Oxyz на координатную плоскость Оху (рис. 7). В ортобазисе i,j,k матрица этого оператора имеет следующий вид

(так как Рi = i, Рj = j, Pk = θ, т. е. является симметричной. Значит, оператор проектирования P симметричен.
Симметричный оператор обладает рядом замечательных свойств.
Свойства симметричного оператора
Первые два вытекают из его определения.
- Для того, чтобы линейный оператор А: V → V был симметричным, необходимо и достаточно, чтобы для любых элементов х и у из пространства V выполнялось равенство
(Ах, У) = (х, Aу). (6) - Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в (каком-нибудь) ортонормированном базисе была симметрична.
- Характеристический многочлен симметричного оператора (и симметричной матрицы) имеет только вещественные корни.
Напомним, что вещественный корень λ характеристического многочлена линейного оператора А является его собственным значением, т.е. существует ненулевой элемент х (собственный вектор оператора А), который оператор А преобразует так: Ах = λх.
4. Собственные элементы симметричного оператора, отвечающие различным собственным значениям, ортогональны.
Пусть x1 и х2 — собственные элементы оператора А,
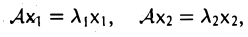
И 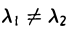 . В силу симметричности оператора имеем
. В силу симметричности оператора имеем
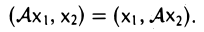
С другой стороны,
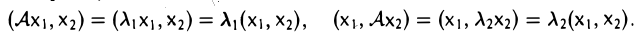
Из вытекающего отсюда равенства
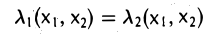
получаем, что
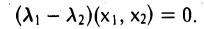
Отсюда в силу неравенства 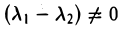 имеем
имеем
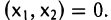
5. Пусть А: V —> V — симметричный оператор. Тогда в пространстве V существует ортонормированный базис е = (е1,… ,еп), состоящий из собственных элементов оператора А:
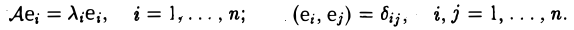
В приведенном выше примере таким базисом является тройка i, j, к: векторы i и j — собственные векторы оператора проектирования Р с собственными значениями, равными единице, а к — его собственный вектор с нулевым собственным значением.
6. Пусть А: V —» V — невырожденный симметричный оператор. Тогда обратный ему оператор А -1: V —> V также является симметричным.
Замечание:
Все собственные значения невырожденного оператора отличны от нуля. Если λ ≠ 0 — собственное значение оператора А, то 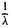 — собственное значение обратного оператора А -1 .
— собственное значение обратного оператора А -1 .
Симметричный оператор называется положительным, если для любого ненулевого элемента х из пространства V выполняется неравенство (Ах, х) > 0.
Свойства положительного оператора
- Симметричный оператор А: V —» V является положительным в том и только в том случае, когда все его собственные значения λ1…, λп положительны.
- Положительный оператор невырожден (обратим).
- Оператор, обратный положительному, также положителен.
Квадратичные формы
Пусть А = (aij) — симметричная матрица порядка п, ajj = Выражение
(1)
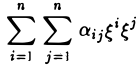
называется квадратичной формой переменных 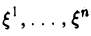 . Матрица А называется матрицей этой квадратичной формы.
. Матрица А называется матрицей этой квадратичной формы.
Примером квадратичной формы двух переменных х и у может служить выражение ах2 + 2bху + су2, где а, b и с — некоторые действительные числа; ее матрица
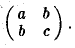
Набор чисел 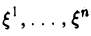 можно рассматривать как координаты элемента п-мерного евклидова пространства V в некотором фиксированном ортобазисе e = (e1,…, еn) этого пространства,
можно рассматривать как координаты элемента п-мерного евклидова пространства V в некотором фиксированном ортобазисе e = (e1,…, еn) этого пространства,
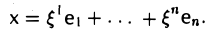
Тогда выражение (1) будет представлять собой числовую функцию аргумента х, заданную на всем пространстве V. Эту функцию принято обозначать так: A(х, х). О такой квадратичной форме
(2)
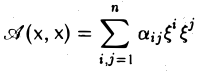
говорят, что она задана в n-мерном евклидовом пространстве
Со всякой квадратичной формой A(x, x) естественно связана симметричная билинейная форма
(3)
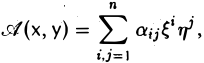
где  — координаты элемента у в ортобазисе e:
— координаты элемента у в ортобазисе e:
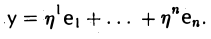
Замечание:
Форма (3) называется билинейной, так как она линейна по каждому аргументу — и по х, и по у :
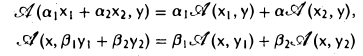
(здесь a1, a2, β1, β2 — произвольные числа).
Билинейная форма (3) называется симметричной вследствие того, что ее значение не зависит от порядка аргументов,
A(y,x) = A{x,y).
Вычисляя значения билинейной формы A (x, у) на базисных элементах, т. е. полагая х = еk, у = ет, получаем, что (4)
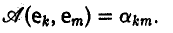
Это означает, что элементы матрицы А квадратичной формы (2) суть значения билинейной формы на элементах базиса с.
Примером билинейной формы может служить скалярное произведение векторов n-мерного координатного пространства Rn
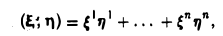
где 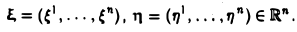 Соответствующая квадратичная форма
Соответствующая квадратичная форма
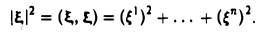
определяет квадрат длины вектора ξ.
При переходе к другому базису координаты элемента х изменяются. Меняется и матрица А = А(e) квадратичной формы.
В приложениях часто возникает необходимость приведения квадратичной формы к наиболее простому виду. Таким видом является диагональный, или нормальный вид. Будем говорить, что квадратичная форма в базисе с имеет нормальный вид, если все коэффициенты при произведениях различных координат равны нулю, т.е. аij = 0 при i ≠ j. Тогда
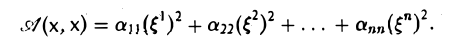
Матрица квадратичной формы в этом базисе имеет диагональный вид:

Теорема:
Для каждой квадратичной формы, заданной в евклидовом пространстве, можно указать (ортонормированный) базис, в котором ее матрица имеет диагональный вид.
Чтобы убедиться в справедливости этого утверждения, воспользуемся свойствами симметричного оператора. Построим линейный оператор А: V → V так, чтобы его матрица 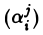 в базисе е совпадала с матрицей (aij) квадратичной формы в этом же базисе е, т.е. положим
в базисе е совпадала с матрицей (aij) квадратичной формы в этом же базисе е, т.е. положим 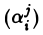 = aij. В силу симметричности матрицы
= aij. В силу симметричности матрицы 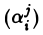 оператор А симметричен.’
оператор А симметричен.’
Вычислим (Aх, х). Замечая, что
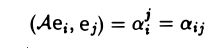
вследствие ортонормированности базиса e, получаем
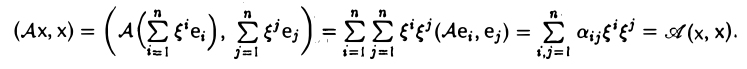
Тем самым, м ы установили важную связь
A(х, х) = (Aх, х) (5)
между квадратичной формой, заданной в евклидовом пространстве V, и действующим в нем симметричным оператором.
В силу симметричности построенного оператора А в евклидовом пространстве V существует ортонормированный базис f = (f1,… ,fn) состоящий из собственных элементов оператора А:
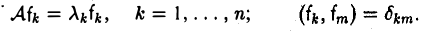
Заметим, что
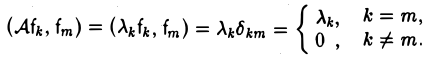
Разложим элемент х по базису f,
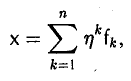
и вновь вычислим (Aх, х). Имеем
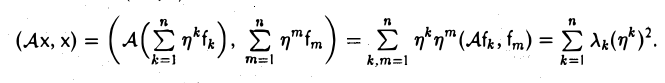
Отсюда в силу равенства (5) получаем, что
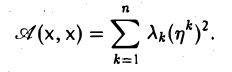
Тем самым, матрица A(f) исходной квадратичной формы в базисе f является диагональной:
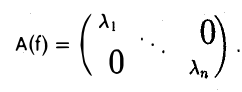
Сам диагональный вид квадратичной формы можно (с точностью до порядка слагаемых) записать и не вычисляя элементов базиса f. Достаточно найти собственные значения линейного оператора А или, что тоже самое, собственные значения матрицы А = (aij) и выписать их с учетом кратности.
Пример:
Привести квадратичную форму
A(х, х) = 2ху + 2yz + 2xz
к диагональному виду.
Запишем матрицу квадратичной формы
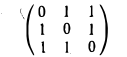
и построим ее характеристический многочлен:
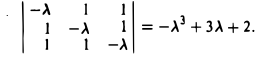
Приравняв полученное выражение к нулю, найдем его корни:
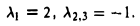
Тем самым,
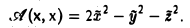
Построение соответствующего ортобазиxа сложнее.
Собственные векторы симметричного оператора А суть собственные векторы матрицы квадратичной формы. Найдем их.
Пусть λ = 2. Рассмотрим однородную линейную систему с матрицей
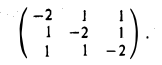
Все решения системы
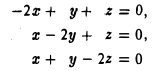
пропорциональны набору (1 1 1 ) т.
Пусть λ = — I. Однородная линейная система с матрицей

сводится к одному уравнению
х + y + z = 0
и имеет два линейно независимых решения. Выберем их так, чтобы они были ортогональны: (1 -2 1 )Т, (1 0 — 1 )Т. Легко убедиться в том, что векторы с найденными координатными столбцами попарно ортогональны. Пронормируем их:
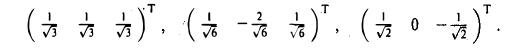
Искомый базис построен:
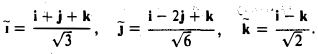
Замечание:
В качестве пространства V можно взять любое п-мерное евклидово пространство. Однако в задачах наиболее часто встречается координатное пространство Rn, элементами которого являются всевозможные упорядоченные наборы действительных чисел — ξ = ( ), стандартный базис состоит из наборов (1,0,…, 0,0), (0,1…..0,0),… , (0,0,….,), 0), (0,0…..0, I), а скалярное произведение наборов ξ = (
), стандартный базис состоит из наборов (1,0,…, 0,0), (0,1…..0,0),… , (0,0,….,), 0), (0,0…..0, I), а скалярное произведение наборов ξ = ( ) и η = (
) и η = ( ) определяется формулой
) определяется формулой
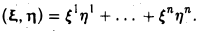
Опишем алгоритм, посредством которого для произвольной квадратичной формы, заданной в n-мерном координатном пространстве, строится базис, в котором эта квадратичная форма имеет диагональный вид.
Пусть
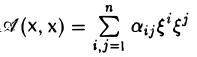
— заданная квадратичная форма.
- Выпишем матрицу квадратичной формы
2. Построим характеристический многочлен
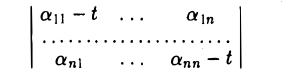
и найдем его корни (в силу симметричности матрицы все корни вещественны). Запишем их с учетом кратности:

3. Пусть λ — один из этих корней, кратности k. Однородная линейная система с матрицей
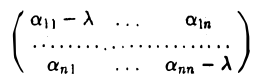
имеет ровно к линейно независимых решений (образующих фундаментальную систему решений). Ортонормировав ее, получим к попарно ортогональных решений единичной длины.
4. Поступая так с каждым корнем характеристического многочлена, получаем набор ровной попарно ортогональных элементов единичной длины, т. с. ортобазис f1 …, fn пространства Rn.
В построенном ортобазисе f = (f1,…,fn) заданная квадратичная форма имеет диагональный вид:
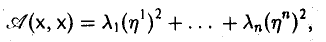
где
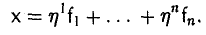
Определение:
Квадратичная форма

называется положительно определенной или знакоположительной, если для любого ненулевого элемента х (или, что то же, для любого ненулевого набора 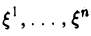 , выполняется неравенство
, выполняется неравенство
A(х, х) > 0.
Примером знакоположительной квадратичной формы может служить скалярный квадрат произвольного вектора ξ = (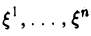 ) координатного пространства:
) координатного пространства:
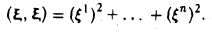
После приведения знакоположительной квадратичной формы к диагональному виду получаем
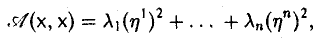
где λ1 > 0, …, λn > 0
Критерий Сильвестра (знакоположительное квадратичной формы)
Для того, чтобы квадратичная форма (6) была знакоположительной, необходимо и достаточно, чтобы все миноры ее матрицы, расположенные в левом верхнем углу, были положительны, т. е.

Метод Лагранжа
Существует еще один (простой) метод приведения квадратичной формы к диагональному виду, удобный, например, при получении ответа на вопрос, является ли квадратичная форма знакоопределенной или нет. Этот метод Лагранжа, или метод выделения полного квадрата, заключается в следующем. Пусть
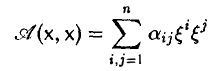
— заданная квадратичная форма и a11 ≠ 0. Выпишем сначала все слагаемые, содержащие переменную ξ1 и преобразуем их так:
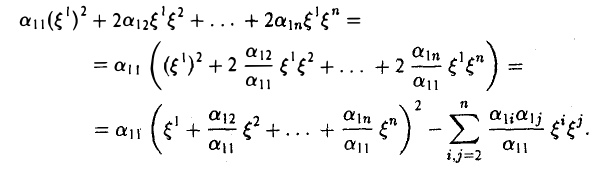
Полагая
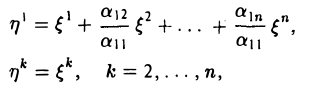
получаем, что
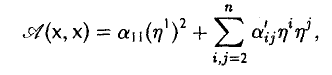
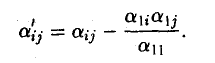
Замечая, что выражение
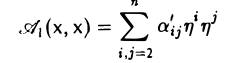
также является квадратичной формой, но уже зависящей от меньшего числа переменных, вновь выделяем полный квадрат и т.д.
Если a11 = 0, но отлично от нуля аii(2 < i < п), то применяем тот же прием, но уже к переменной ξi.
Если все коэффициенты при квадратах неизвестных равны нулю, a11 = … = aпп = 0, то тогда следует начинать с преобразования координат вида
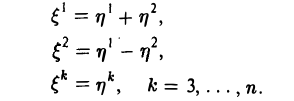
В результате проведенного преобразования координат, в частности, получим
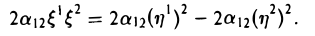
И, тем самым, придем к общему случаю.
Пример:
Методом Лагранжа привести к диагональному виду квадратичную форму
A(x, х) = 2ху + 2yz + 2zx.
Введем новые координаты 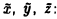
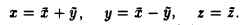
Тогда
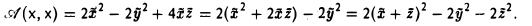
Положим
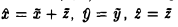
и получим
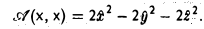
Замечание:
Недостаток метола Лагранжа состоит в том, что при указанных преобразованиях координат новые координатные оси уже не являются попарно ортогональными.
Существуют и другие способы приведения квадратичной формы к диагональному виду.
Сравнивая результаты описанных выше двух способов приведения квадратичной формы 2ху + 2yz + 2zx к диагональному виду (речь идет о последних двух разобранных примерах), можно заметить, что в них соответственно одинаковы: число отрицательных коэффициентов и число положительных коэффициентов. Это совпадение не случайно, а является важным свойством квадратичных форм, называемым законом инерции:
число положительных, число отрицательных и число нулевых коэффициентов при квадратах неизвестных в диагональном виде квадратичной формы всегда одни и те же и не зависят от способа приведения квадратичной формы к этому виду.
Классификация кривых и поверхностей второго порядка
Применим описанный выше алгоритм приведения квадратичной формы к диагональному виду для классификации кривых и поверхностей второго порядка.
Кривые
Рассмотрим общее уравнение кривой второго порядка на плоскости Оху :
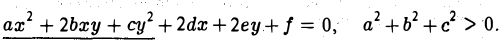
Построим матрицу квадратичной части ах2 + 2bху+су2:
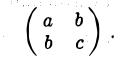
Найдем корни λ1 и λ2 характеристического многочлена и соответствующие им собственные векторы i и j (единичные и взаимноортогональные).. Возьмем эти векторы за орты новых осей Ох и Оу (рис. 8).
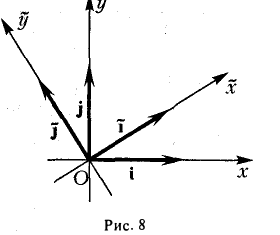
Переходя к новым координатам  , получим
, получим
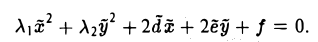
Возможны два случая: 1) λ1 • λ2 ≠ 0, 2) λ1 (или λ2 ) равно нулю.
В первом случае сдвигом точки начала отсчета
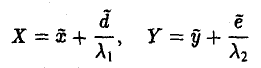
добиваемся исчезновения линейных членов
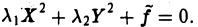
Далее, как это и делалось, рассматриваем всевозможные сочетания знаков у коэффициентов λ1, λ2 и f. В результате получаем: эллипс, гиперболу, пару пересекающихся прямых, точку, пустое множество.
Во втором случае (положим для определенности λ1 = 0, λ2 ≠ 0) сдвигом начала отсчета
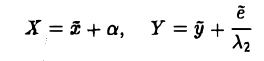
от уравнения
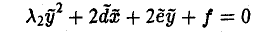
приходим к уравнению
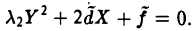

соответственно получим
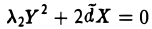
{парабола).
Если же d= 0,то взяв а = 0, имеем
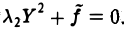
В зависимости от знака 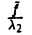 получаем: пару параллельных прямых, пару совпадающих прямых, пустое множество.
получаем: пару параллельных прямых, пару совпадающих прямых, пустое множество.
Замечание:
Операция отыскания корней характеристического многочлена квадратичной части уравнения кривой и взаимноортогональных единичных собственных векторов, описанная здесь, заменяет уничтожение произведения разноименных координат путем поворота на подходящий угол. В случае поверхностей второго порядка дело обстоит сложнее (и для того, чтобы разобраться с классификацией до конца, нужны и внимание и терпение).
Поверхности
Общее уравнение поверхности второго порядка имеет следующий вид
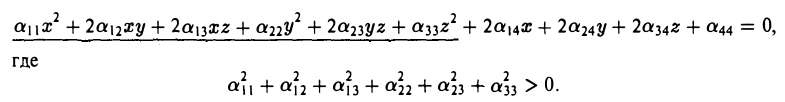
Упростим вид квадратичной части этого уравнения (подчеркнута), пользуясь описанным выше алгоритмом. Построим матрицу

найдем корни λ1, λ2, λз характеристического многочлена
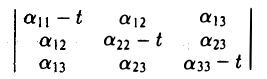
и соответствующие им собственные векторы i, J, k так, чтобы они образовывали ортонормированную тройку (это всегда возможно). Возьмем векторы i, J и k за орты новых координатных осей Ox, Ox, Oz. Производя замену координат, получим (*)
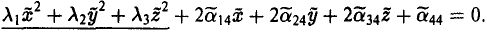
Возможны три случая:
(I) Все три корня λ1, λ2, λ3 отличны от нуля. Путем сдвига начала
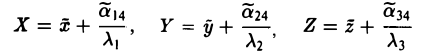
уравнение (*) поверхности приводится к следующему виду
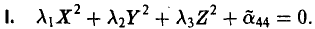
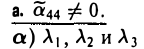
имеют один и тот же знак, противоположный знаку 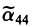 .
.
Полагая
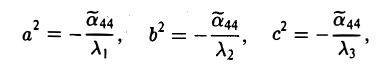
получаем уравнение эллипсоида
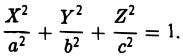
β ) Знаки λ1 и λ2 противоположны знаку 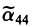 , а знаки A3 и
, а знаки A3 и 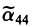 совпадают. Полагая
совпадают. Полагая
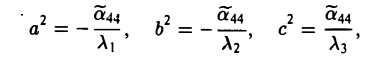
получаем уравнение однополостного гиперболоида
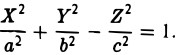
γ ) Знаки λ1 и λ2 совпадают со знаком 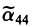 , а знаки λ3 и
, а знаки λ3 и 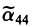 противоположны. Полагая
противоположны. Полагая
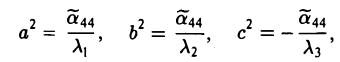
получаем уравнение двуполостного гиперболоида
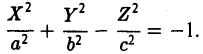
б. 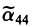 = 0.
= 0.
а) Если λ1, λ2 и λз имеют один и тот же знак, то получаем точку (0, 0, 0).
β) Если одно из λ, имеет знак, противоположный знаку двух других, то получаем уравнение конуса второго порядка
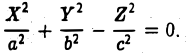
(II) Ровно один корень равен нулю (для определенности λз = 0). Полагая
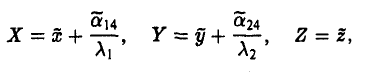
получим
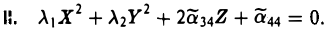
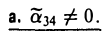 Тогда сдвигом точки начала отсчета
Тогда сдвигом точки начала отсчета
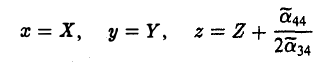
получаем уравнение вида
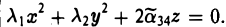
а) Если λ1 и λ2 — одного знака, то, полагая
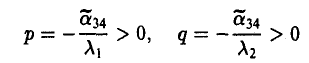
(можно считать, что знак 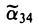 противоположен знаку λ1 и λ2; этого всегда можно добиться, поменяв в случае необходимости ориентацию оси z на противоположную), получаем уравнение эллиптического параболоида
противоположен знаку λ1 и λ2; этого всегда можно добиться, поменяв в случае необходимости ориентацию оси z на противоположную), получаем уравнение эллиптического параболоида
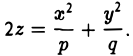
β) Если λ1 и λ2 имеют противоположные знаки, то, положив
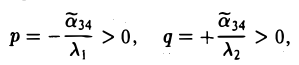
получим уравнение гиперболического параболоида
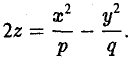
б. 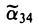 =0. Тогда уравнение поверхности имеет следующий вид
=0. Тогда уравнение поверхности имеет следующий вид
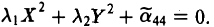
Классификация поверхностей с уравнениями такого типа приводится в таблице.
Замечание:
Отсутствие третьей координаты (точнее, ее неявное присутствие) приводит к цилиндрическим поверхностям, направляющими которых являются кривые второго порядка, лежащие в плоскости Z = 0 и имеющие уравнения вила
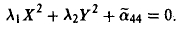

(III) Ровно два корня равны нулю (для определенности λ2 = λ3 = 0). Преобразованием координат
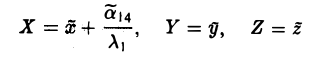
приходим к уравнению
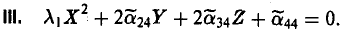
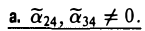 Покажем, что этот случай всегда можно свести к такому:
Покажем, что этот случай всегда можно свести к такому: 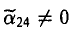 ,
, 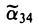 = 0. Преобразованием координат
= 0. Преобразованием координат
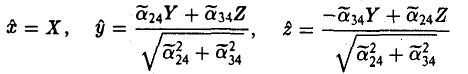
уравнение поверхности приводится к следующему виду
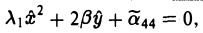
где
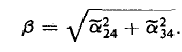
Замечание:
Преобразование координат, упрощающее вид уравнения, выбирается так, чтобы новая координатная система вновь была прямоугольной декартовой.
Сдвигом начала координат
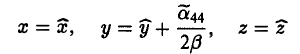
получаем уравнение параболического цилиндра
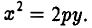
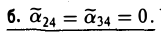
Уравнение
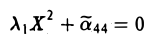
описывает либо пару параллельных плоскостей ( λ1 •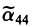 < 0), либо пару совпадающих плоскостей (
< 0), либо пару совпадающих плоскостей (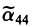 = 0), либо пустое множество ( λ1 •
= 0), либо пустое множество ( λ1 • 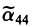 > 0).
> 0).
Дополнение к линейным отображениям






Смотрите также:
Решение задач по математическому анализу
| Отображения. | Дифференцируемые отображения. |
| Векторные отображения. | Отображения с неравным нулю якобианом. |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
