Оглавление:
Предел последовательности — это пространство которое содержит все все элементы последовательности начиная с какого-то значения. А простыми словами, предел последовательности, простыми словами, это такая «область» куда попадают все значения после определенного порога (в нашем случае – А). На изображении ниже она условно показана синей полоской.
Понятие предела и понятие функции — фундаментальные понятия математического анализа. Начало изучению понятия предела положено в элементарной математике, где с помощью предельных переходов определяются длина окружности, объем цилиндра, конуса и т. д. Оно также было использовано при определении суммы бесконечно убывающей геометрической прогрессии. Операция предельного перехода является одной из основных операций анализа. В настоящей главе рассматривается простейшая форма операции предельного перехода, основанная на понятии предела числовой последовательности. Понятие предела числовой последовательности позволит в дальнейшем определить и другие более сложные формы операции предельного перехода.
Предел числовой последовательности:
Числовую функцию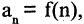 
определенную на множестве натуральных чисел, называют числовой последовательностью и обозначают 
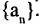Последовательность задана, если каждому натуральному числу n по некоторому закону f поставлено в соответствие число 
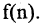Если закон f задан формулой, т. е. существует аналитическое выражение для 
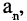называемого общим членом последовательности, то говорят об аналитическом способе задании последовательности. Например, последовательность квадратов целых чисел
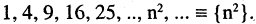
Если закон, по которому задается последовательность, позволяет построить очередной член последовательности по известным предыдущим членам, то такой способ задания называется рекуррентным. Например, арифметическая последовательность (арифметическая прогрессия)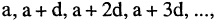 
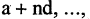может быть задана при помощи рекуррентного соотношения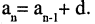 
Геометрическая последовательность (геометрическая прогрессия)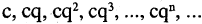 
может быть задана при помощи следующего рекуррентного соотношения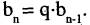 
Кроме рекуррентного соотношения, задаются также первые члены последовательности, и, возможно, некоторые параметры. Так для арифметической и геометрической последовательностей достаточно задать лишь их первые члены а и b, а также и параметры прогрессий d и q соответственно.
Последовательность называется ограниченной сверху, если существует число М (верхняя граница), такое, что,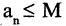 
для всех n. Последовательность 
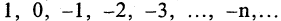ограничена сверху, например, числом 2. Если для всех n выполняется условие 
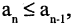то это убывающая последовательность.
Последовательность 
называется ограниченной снизу, если существует такое число m (нижняя граница), что 
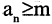для всех п, если для всех n выполняется условие 
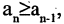то она называется возрастающей. Последовательность 
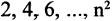является ограниченной снизу возрастающей последовательностью.
Последовательность называется ограниченной, если она ограничена и сверху, и снизу. Очевидно, что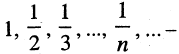 
ограниченная убывающая последовательность.
Сходимость последовательности. Последовательность сходится к числу А, если для любого сколь угодно малого числа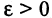 
можно указать такое натуральное число 
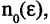что для всех n больших 
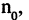т. е. для 
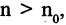выполняется неравенство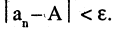 
Этот факт записывается так:
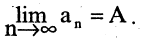
Само число А называется пределом последовательности . Следовательно, при неограниченном увеличении номера общий член последовательности стремится к пределу А. Если число А конечно, то последовательность называют сходящейся. Если последовательность не имеет конечного предела или не имеет предела вообще, то ее называют расходящейся. Так последовательность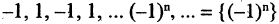 
расходится, так как в этом случае 
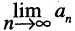не существует. Последовательность 
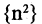тоже является расходящейся, так как по мере возрастания n члены последовательности становятся больше любого наперед заданного числа, то есть 
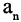стремится к бесконечности. В этом случае пишут: 
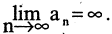Заметим, что хотя здесь предел формально и существует, но он не является конечным числом.
Если последовательность имеет пределом точку А, то для всех номеров последовательности, начиная с некоторого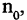 
члены последовательности находятся внутри отрезка 
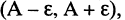называемого 
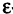-окрестностью числа А. Если 
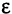очень мало, то число 
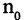может быть весьма большим. Следовательно, много членов последовательности окажутся вне 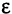-окрестности, однако их всегда будет лишь конечное число. Все остальные члены последовательности, начиная с номера 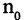и более, попадают в 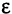— окрестность. Таким образом, если последовательность сходится к А, то какую бы окрестность точки А ни взять, почти все числа 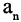попадают в выбранную окрестность. Отсюда следует, что добавление или исключение конечного числа членов такой последовательности не влияет на ее сходимость. Геометрический смысл сходимости последовательности проиллюстрирован на рис. 3.1. Каждому члену числовой последовательности соответствует точка на числовой оси.
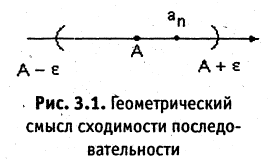
Пример:
Рассмотрим последовательность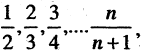 
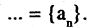Отклонение общего члена последовательности от 1 равно 
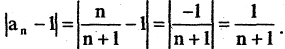С возрастанием n это отклонение, уменьшаясь, стремится к нулю. Пусть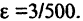 
Вычислим отклонение для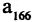 
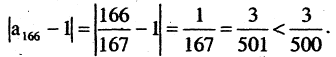
Тем самым, начиная с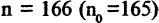 
выполняется неравенство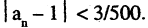 
Предел функции:
Пусть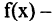 
функция непрерывного аргумента. Число А называется пределом функции 
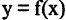при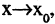 
если для каждого сколь угодно малого числа 
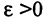можно указать зависящее от 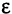число 
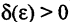такое, что для всех х, удовлетворяющих неравенству 
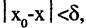имеет место неравенство 
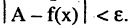Запись
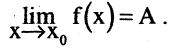
Наличие у функции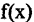 
предела А в точке 
означает, что как только независимая переменная х достаточно близко приблизится к значению , так функция будет сколь угодно близка к А.
Справедливы следующие свойства пределов функций:
1.Если предел функции существует, то он единственный.
2.Предел постоянной величины равен самой постоянной.
Если при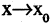 
существуют конечные пределы функций 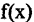и 
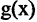, то
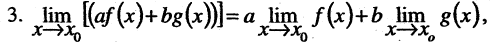
где а и b числа.
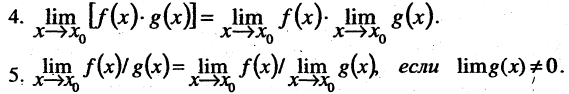
6.Если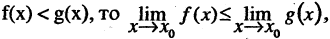 
в частности, если
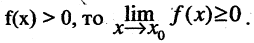
В качестве примера вычислим два предела.
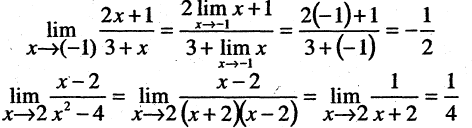
На практике при вычислении пределов часто используют так называемые замечательные пределы
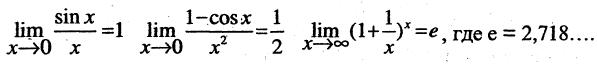
Бесконечно малые и бесконечно большие величины:
Если при 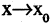функция 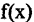стремится к 0, то ее называют бесконечно малой величиной (или просто бесконечно малой) в
окрестности точки . Бесконечно малые обозначают греческими буквами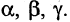 
Примеры бесконечно малых величин: 
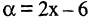при 
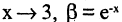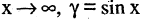при 
при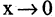 
и т.п. Справедливы следующие утверждения:
1.Сумма бесконечно малых величин есть величина бесконечно малая.
2.Произведение бесконечно малых величин есть величина бесконечно-малая.
3.Произведение бесконечно малой на число есть величина бесконечно малая.
4.Разность между функцией и ее пределом в точке а есть величина бесконечно малая, т. е., если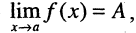 
то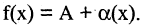 
Функция называется бесконечно большой величиной в окрестности точки , если для любого сколь угодно большого числа М можно указать зависящее от М число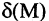 
такое, что для всех х, удовлетворяющих неравенству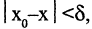 
имеет место неравенство 
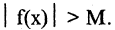Запись 
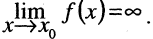К бесконечно большим относятся, например, 
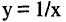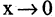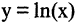при , 
при 
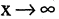и при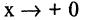 
и др. Между бесконечно малой и бесконечно большой величинами существует простое соотношение: если 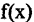— бесконечно малая величина, не равная тождественно нулю, то 
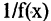— бесконечно большая величина и наоборот. Поэтому, если 
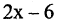является бесконечно малой величиной в окрестности точки 
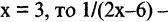бесконечно большая в окрестности той же точки.
Замечание:
Бесконечность (обозначаемая знаком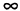 
) не является числом.
Функция 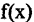называется непрерывной в точке , если она определена в этой точке и некоторой ее окрестности, а также
Точки, в которых равенство (3.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка. Непрерывные функции обладают рядом свойств.
Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.
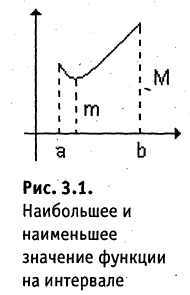
Если функция непрерывна на замкнутом промежутке [а, b], то она достигает на этом промежутке наибольшего М и наименьшего m значений (рис. 3.2).
Числовые последовательности
Числовые последовательности и арифметические действия над ними. Числовые последовательности изучают уже в средней школе. Примерами таких последовательностей могут служить: 1) последовательность всех членов арифметической и геометрической прогрессий; 2) последовательность периметров правильных л-угольников, вписанных в данную окружность; 3) последовательность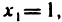 
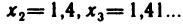приближенных значений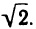 
Уточним и расширим понятие числовой последовательности.
Определение:
Если каждому числу п из натурального ряда чисел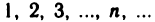 
поставлено в соответствие вещественное число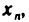 
то множество вещественных чисел
называется числовой последовательностью или просто последовательностью*
Числа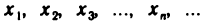 
будем называть элементами (или членами) последовательности (1), символ 
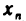— общим элементом (или членом) последовательности, а число п — его номером. Сокращенно последовательность (1) будем обозначать символом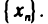 
Так, например, символ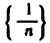 
обозначает последовательность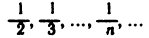 
Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула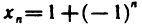 
*Другими словами, числовую последовательность можно определить как множество пар чисел, в которых первое число принимает последовательно значения 1, 2, 3, … задает последовательность: 0,2, 0,2, … Обращая дробь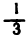 
в десятичную и оставляя один, два, три и т. д. знака после запятой, получаем последовательность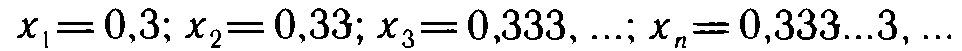
По самому определению, последовательность содержит бесконечное число элементов: любые два ее элемента отличаются, по крайней мере, своими номерами.
Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. На рис. 6, а
и б изображены соответственно последовательност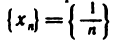и 
и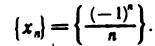 
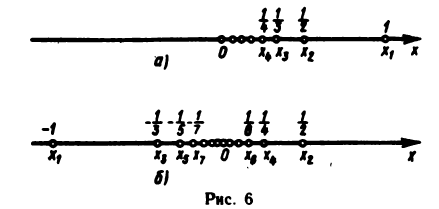
Введем арифметические действия над числовыми последовательностями. Пусть даны последовательности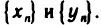 
Произведением последовательности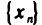 
на число m назовем последовательность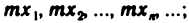 
суммой данных последовательностей назовем последовательность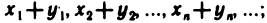 
разностью — последовательность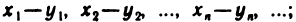 
произведением — последовательность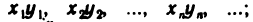 
частным — последовательность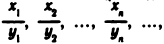 
если все члены последовательности 
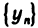отличны от нуля.
Указанные действия над последовательностями символически записываются так: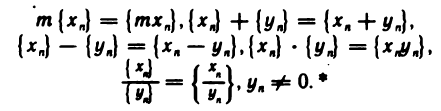
Ограниченные и неограниченные последовательности
Определение:
Последовательность 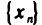называется ограниченной сверху (снизу), если существует число М (число m) такое, что любой элемент 
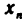этой последовательности удовлетворяет неравенству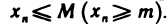 
Определение:
Последовательность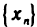 
называется ограниченной, если она ограничена и сверху и снизу, т. е. существуют числа m и М такие, что любой элемент 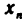этой последовательности удовлетворяет неравенствам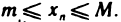 
Пусть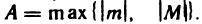 
Тогда условие ограниченности последовательности можно записать в виде 
Определение:
Последовательность 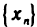называется неограниченной, если для любого положительного числа А существует элемент 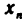этой последовательности, удовлетворяющий неравенству 
Из данных определений следует, что если последовательность ограничена сверху, то все ее элементы принадлежат промежутку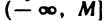 
; если она ограничена снизу — промежутку 
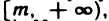а если ограничена и сверху и снизу — промежутку [m, М]. Неограниченная последовательность может быть ограничена сверху (снизу).
Рассмотрим примеры ограниченных и неограниченных последовательностей.
1. Последовательность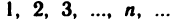 
ограничена снизу, но не ограничена сверху.
2. Последовательность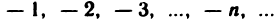 
ограничена сверху, но не ограничена снизу.
3. Последовательность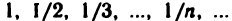 
ограничена, так как любой элемент 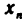этой последовательности удовлетворяет неравенствам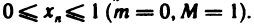 
4. Последовательность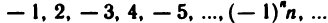 
неограниченная. В самом деле, каково бы ни было число А среди элементов 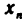этой последовательности, найдутся элементы, для которых будет выполняться неравенство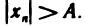 
С помощью логических символов данные выше определения можно записать следующим образом:
Сравнивая запись с помощью логических символов двух последних определений, видим, что при построении отрицаний символы 
и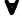 
заменяют друг друга.
Бесконечно большие и бесконечно малые последовательности
Определение:
Последовательность 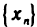называется бесконечно большой, если для любого положительного числа А существует номер N такой, что при 
выполняется неравенство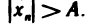 
Символическая запись определения бесконечно большой последовательности: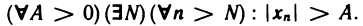 
Замечание:
Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограничен-ная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n, 1, n+1… не является бесконечно большой, поскольку при A > 1 неравенство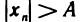 
выполняется не для всех элементов 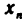с нечетными номерами.
Определение:
Последовательность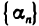 
называется бесконечно малой, если для любого положительного числа е существует номер N такой, что при n>N выполняется неравенство 
Символическая запись определения бесконечно малой последовательности: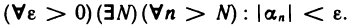
Пример:
Используя определение 1, докажем, что последовательность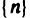 
является бесконечно большой.
Возьмем любое число A>0. Из неравенства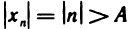 
получаем n>А. Если взять 
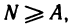то для всех n>N будет выполняться неравенство 
т. е. согласно определению 1 последовательность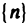 
бесконечно большая.
Пример:
Используя определение 2, докажем, что последовательность [1 /n] является бесконечной малой.
Возьмем любое число 
Из неравенства 
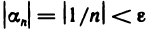получаем 
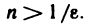Если взять 
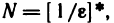то для всех n>N будет выполняться неравенство 
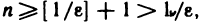откуда 
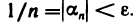Таким образом, согласно определению 2 последовательность [1 /n] является бесконечно малой.
Докажем теорему, устанавливающую связь между бесконечно большими и бесконечно малыми последовательностями.
Теорема:
Если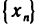 
— бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность 
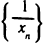бесконечно малая, и, обратно, если 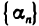— бесконечно малая последовательность и 
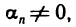то последовательность 
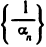— бесконечно большая.
Доказательство:
Пусть 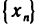— бесконечно большая последовательность. Возьмем любое 
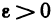и положим 
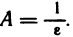Согласно определению 1 для этого А существует номер N такой, что при n> N будет 
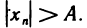Отсюда получаем, что 
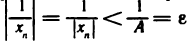для всех n>N. А это значит, что последовательность 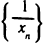бесконечно малая.
Доказательство второй части теоремы проводится аналогично.
Основные свойства бесконечно малых последовательностей
Теорема:
Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности.
Доказательство:
Пусть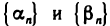 
— бесконечно малые последовательности. Требуется доказать, что последовательность 
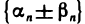бесконечно малая. Пусть 
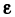— произвольное положительное число, 
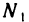— номер, начиная с которого 
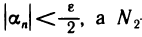—номер, начиная с которого 
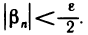(Такие номера 
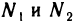найдутся по определению бесконечно малой последовательности.) Возьмем 
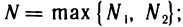тогда при n>N будут одновременно выполняться два неравенства: 
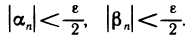Следовательно, при n>N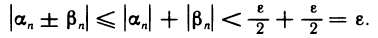
Это значит, что последовательность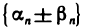 
бесконечно малая.
Следствие:
Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема:
Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство:
Пусть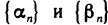 
— бесконечно малые последовательности. Требуется доказать, что последовательность 
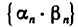бесконечно малая. Так как последовательность 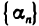бесконечно малая, то для любого 
существует номер 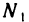, такой, что 
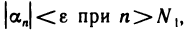а так как 
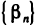также бесконечно малая последовательность, то для 
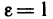существует номер 
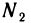такой, что
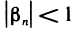при 
Возьмем 
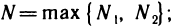тогда при n>N будут выполняться оба неравенства. Следовательно, при п> N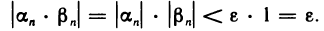
Это означает, что последовательность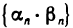 
бесконечно малая.
Следствие:
Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Замечание:
Частное двух бесконечно малых последовательностей может не быть бесконечно малой последовательностью и может даже не иметь смысла. Например, если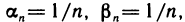 
то все элементы 
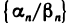равны единице и данная последовательность является ограниченной. Если 
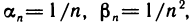то последовательность 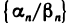бесконечно большая, а если 
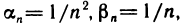то — бесконечно малая. Если, начиная с некоторого номера, элементы 
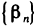равны нулю, то 
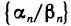не имеет смысла.
Теорема:
Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
Доказательство:
Пусть 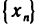— ограниченная, а 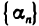— бесконечно малая последовательности. Требуется доказать, что последовательность 
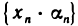бесконечно малая. Так как последовательность 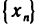ограничена, то существует число А>0 такое, что любой элемент 
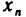удовлетворяет неравенству 
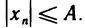Возьмем любое . Поскольку последовательность 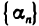бесконечно малая, для положительного числа 
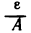существует номер N такой, что при n>N выполняется неравенство 
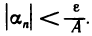Следовательно, при n>N: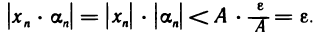
Это означает, что последовательность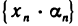 
бесконечно малая.
Следствие:
Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
Перейдем теперь к одному из важнейших в математическом анализе понятию предела числовой последовательности.
Сходящиеся последовательности
Понятие сходящейся последовательности и её определение:
Число а называется пределом последовательности 
, если для любого положительного числа г существует номер N такой, что при n > N выполняется неравенство
С помощью логических символов это определение можно записать в виде
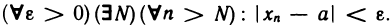
Последовательность, имеющая предел, называется сходящейся.
Если последовательность сходится и имеет своим пределом число а. то символически это записывается так:
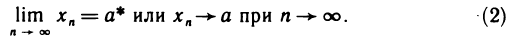
Последовательность, не являющаяся сходящейся, называется pасходящейся.
Пример:
Используя определение предела последоватeльности. Докажем, что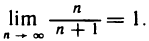 
Возьмем любое число е>0. Так как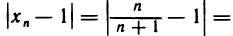 
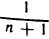то для нахождения значений n, удовлетворяющих неравенству 
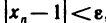достаточно решить неравенство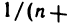 
, откуда получаем 
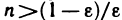. Следовательно, в качестве N можно взять целую часть числа 
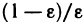, т. е. N =
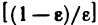. Тогда неравенство 
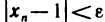будет выполняться при всех n>N. Этим и доказано, что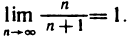 
Замечание:
Пусть последовательность имеет своим пределом число а. Тогда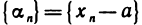 
является бесконечно малой последовательностью, так как для любого е>0 существует номер N такой, что при n>N выполняется неравенство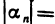 
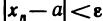. Следовательно, любой элемент 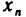последовательности, имеющей пределом число а, можно представить в виде
где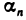 
— элемент бесконечно малой последовательности 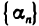. Очевидно, справедливо и обратное: если 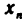можно представить в ви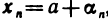де 
, где 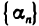—бесконечно малая последовательность, то 
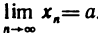. Представление (3) используется при доказательствах теорем о пределах последовательностей.
Замечание:
Неравенство (1) равносильно неравенствам
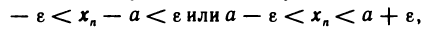
которые означают, что элемент 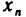находится в е-окрестности точки а (рис. 7). Поэтому определение предела последовательности можно сформулировать следующим образом: число а называется пределом последовательности , если для любой е-окрестности точки а существует номер N такой, что все элементы 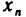с номерами n>N находятся в этой е-окрестности.
Замечание:
Очевидно, что бесконечно большая последовательность не имеет предела. Иногда говорят, что она имеет бесконечный предел, и пишут
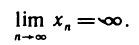
Если при этом, начиная с некоторого номера, все члены последовательности положительны (отрицательны), то пишут
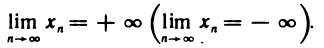
Предел последовательности, как он был определен ранее, будем называть иногда в отличие от бесконечного предела конечным пределом.
Замечание:
Очевидно, всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число а=0.
2. Основные свойства сходящихся последовательностей. Докажем лемму, которая понадобится при доказательстве теоремы 2.5.
Лемма:
Если все элементы бесконечно малой последовательности 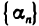равны одному и тому же числу с, то с = 0.
Доказательство:
Предположим противное, т. е. что с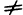
0. Положим 
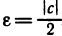. Тогда по определению бесконечно малой последовательности существует номер N такой, что при выполняется неравенство 
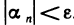. Так как 
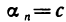, a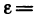 
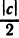, то последнее неравенство можно переписать в виде 
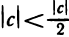, откуда 
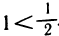. Полученное противоречие доказывает, что неравенство с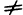0 не может иметь места и, значит, с=0.
Теорема:
Сходящаяся последовательность имеет только один предел.
Доказательство:
Предположим противное, т. е. что сходящаяся последовательность имеет два предела а и b. Тогда по формуле (3) для элементов 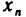получаем
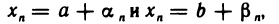
где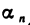 
и 
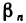— элементы бесконечно малых последовательностей 
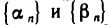Приравнивая правые части этих соотношений, найдем, что 
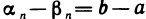. Так как все элементы бесконечно малой последовательности 
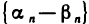равны одному и тому же числу Ь — а, то по лемме 2.1 b — а = 0, т. е. b = а.
Теорема:
Сходящаяся последовательность ограничена.
Доказательство:
Пусть — сходящаяся последовательность и число а — ее предел. Пусть, далее, е — произвольное положительное число и N — номер, начиная с которого выполняется неравенство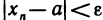 
. Тогда
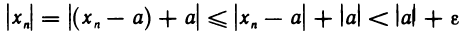
для всех n>N. Пусть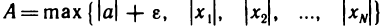 
.
Очевидно,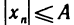 
для всех номеров п, что и означает ограниченность последовательности .
Замечание:
Ограниченная последовательность может и не быть сходящейся. Например, последовательность —1, 1, —1, …,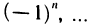 
очевидно ограничена, но не сходится. Докажем это. Предположим, что данная последовательность имеет предел число а. Тогда для е= 1/2 существует номер N такой, что при n>N будет 
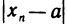<1/2. Так как 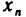принимает поперемеyно значения 1 и —1, то 
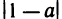<1/2 и 
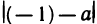<1/2. Используя эти неравенства, получаем
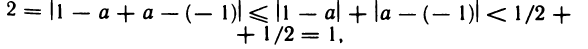
т. е. 2<1. Полученное противоречие доказывает расходимость данной последовательности.
Теорема:
Сумма (разность) двух сходящихся последовательностей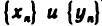 
есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей .
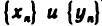Доказательство:
Пусть а и b — соответственно пределы последовательностей 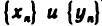. Тогда по формуле (3):
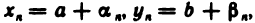
где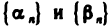 
— бесконечно малые последовательности. Следовательно,
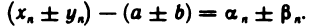
По теореме 2.2 последовательность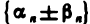 
бесконечно малая. Таким образом, последовательность 
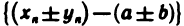также бесконечно малая, и поэтому последовательность 
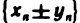сходится и имеет своим пределом число а ± b.
Теорема:
Произведение сходящихся последовательностей 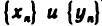есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей .
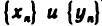Доказательство:
Пусть а и b — соответственно пределы последовательностей 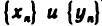. Тогда по формуле (3):
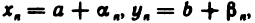
где 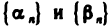—бесконечно малые последовательности. Следовательно,
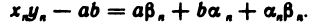
Согласно теоремам 2.2—2.4 последовательность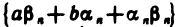 
бесконечно малая. Таким образом, последовательность 
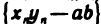также бесконечно малая, и поэтому последовательность 
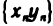сходится и имеет своим пределом число аb.
Теорема:
Частное двух сходящихся последовательностей 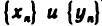при условии, что предел 
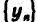отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей .
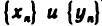Доказательство:
Пусть а и b (b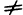0) — соответственно пределы последовательностей 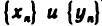. Тогда по формуле (3):
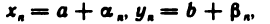
где 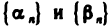— бесконечно малые последовательности. Следовательно,
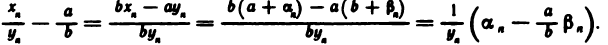
В силу свойств бесконечно малых последовательностей последовательность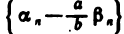 
бесконечно малая. Покажем, что 
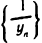— ограниченная последовательность. Так как 
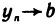при 
, то для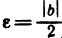 
найдется номер N такой, что для всех n>N будет 
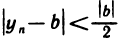. Поэтому
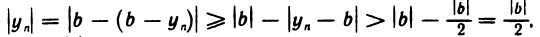
т. е.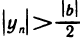 
и, следовательно, 
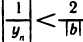для всех n>N, что означает ограниченность последовательности 
.
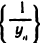По теореме 2.4 последовательность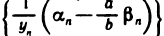 
бесконечно малая, поэтому последовательность 
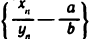также бесконечно малая. Следовательно, последовательность 
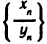сходится и имеет своим пределом число 
.
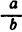Теоремы, доказанные в этом пункте, имеют большое не только теоретическое, но и практическое значение.
Пример:
Найдем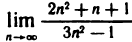 
При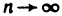 
числитель и знаменатель дроби стремятся к бесконечности, следовательно, применить теорему о пределе частного нельзя, так как в условии этой теоремы предполагается существование конечных пределов. Поэтому сначала преобразуем данную последовательность, разделив числитель и знаменатель на 
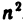. Затем, применяя теоремы о пределе частного и о пределе суммы, найдём
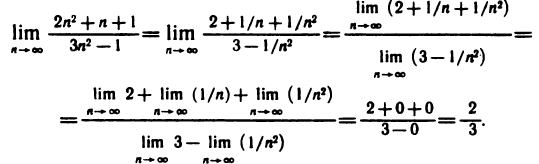
Предельный переход в неравенствах. Теорема 2.10.
Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству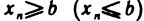 
, то и предел а этой последовательности удовлетворяет неравенству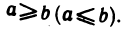 
Доказательство:
Пусть все элементы 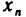, начиная с некоторого номера, удовлетворяют неравенству 
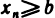. Требуется доказать неравенство 
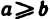. Предположим противное, т. е. что а < b.
Так как а — предел , то для 
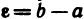существует номер N такой, что при n>N выполняется неравенство 
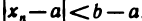, которое равносильно следующим двум неравенствам: 
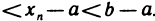Из правого неравенства получаем: 
при n>N, а это противоречит условию теоремы. Следовательно,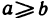 
. Случай 
рассматривается аналогично.
Следствие:
Если элементы сходящихся последовательностей 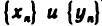, начиная с некоторого номера, удовлетворяют неравенству 
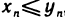, то их пределы удовлетворяют неравенству
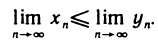
В самом деле, начиная с некоторого номера, элементы последовательности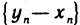 
— неотрицательны, а поэтому неотрицателен и ее предел: 
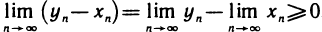. Отсюда следует, что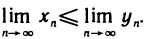 
Следствие:
Если все элементы сходящейся последовательности сходятся на отрезке [а, b], то и ее предел с также находится на этом отрезке.
В самом деле, так как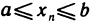 
, то 
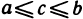. Следующая теорема играет важную роль в различных приложениях.
Теорема:
Пусть даны три последовательност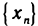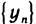и 
, 
и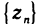 
, причем 
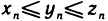для всех п, и пусть последовательност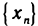и и 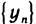имеют один и тот же предел а. Тогда последовательность 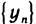также имеет предел а.
Доказательство:
Возьмем любое е>0. По этому е для последовательности 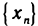найдется номер 
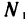, такой, что 
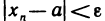при 
т. е.
По тому же е для последовательности 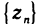найдется номер 
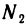такой, что 
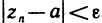при 
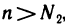т. е.
Пусть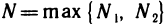 
. Тогда при n>N будут выполняться одновременно неравенства (4) и (5). Используя подчеркнутые неравенства, а также неравенства, данные в условии теоремы, получаем
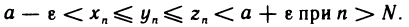
Отсюда
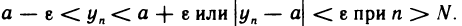
Это означает, что предел последовательности 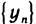равен а.
Монотонные последовательности
Определение и признак сходимости монотонных последовательностей. Определение. Последовательность 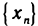называется возрастающей, если 
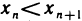для всех п; неубывающей, если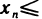 
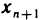, для всех л; убывающей, если 
для всех n; невозрастающей, если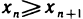 
для всех n.
Все такие последовательности объединяются общим названием: монотонные последовательности. Возрастающие и убывающие последовательности называются также строго монотонными.
Рассмотрим примеры монотонных последовательностей.
- Последовательность 1, 1/2, 1/3, …, 1/n, … убывающая и ограниченная.
- Последовательность 1, 1, 1/2, 1/2, 1/3, 1/3, …1/n, 1/n, … невозрастающая и ограниченная.
- Последовательность 1, 2, 3, … n, … возрастающая и неограниченная.
- Последовательность 1, 1, 2, 2, 3, 3….. n, n, … неубывающая и неограниченная.
- Последовательность 1/2, 2/3, 3/4….. n/(n+1), … возрастающая и ограниченная.
Отметим, что монотонные последовательности ограничены, по крайней мере, с одной стороны: неубывающие последовательности—снизу (
для всех n), невозрастающие — сверху (
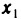, для всех n). Оказывается, что если монотонная последовательность ограничена с обеих сторон, т. е. просто ограничена, то она сходится. Немонотонные последовательности этим свойством не обладают. Например, немонотонная последовательность 
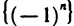ограничена, но не сходится (см. замечание к теореме 2.6).
Имеет место следующая основная теорема о монотонных последовательностях.
Теорема:
Монотонная ограниченная последовательность сходится.
Доказательство:
Рассмотрим случай неубывающей последовательности.
Пусть 
для всех n и существует число М такое, что все элементы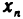 
не больше М , т. е. 
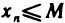. Рассмотрим числовое множество X, состоящее из элементов данной последовательности. По условию это множество ограничено сверху и непусто. Поэтому в силу теоремы 1.1 множество X имеет точную верхнюю грань. Обозначим ее через а и докажем, что а является пределом данной последовательности.
Так как а — точная верхняя грань множества элементов последовательности 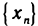, то согласно свойству точной верхней грани Для любого е>0 найдется номер N такой, что 
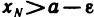. Поскольку 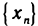—неубывающая последовательность, то при n>N будет 
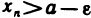. С другой стороны, по определению верхней грани 
для всех n. Таким образом, при n>N получаем неравенства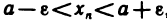 
, т. е. 
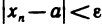при n>N. Это и означает, что число а — предел последовательности .
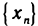Случай невозрастающей последовательности рассматривается аналогично.
Замечание:
Ограниченность монотонной последовательности является необходимым и достаточным условием сходимости.
В самом деле, если монотонная последовательность ограничена, то в силу теоремы 2.12 она сходится; если же монотонная последовательность сходится, то по теореме 2.6 она ограничена.
2.Число е. Рассмотрим последовательность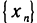 
с общим членом 
:
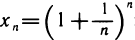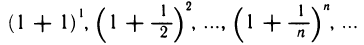
Докажем, что она сходится. Для этого достаточно доказать, что последовательность 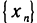— возрастающая и ограничена сверху. Применив формулу бинома Ньютона [гл. 6, § 3, п. 4, формула (10) ], получим
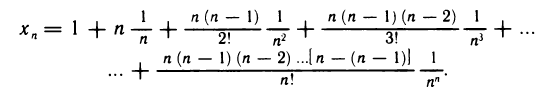
Представим это выражение в следующей форме:
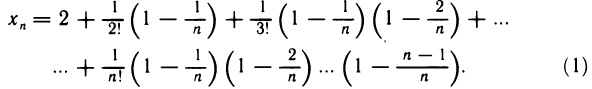
Аналогичным образом представим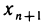 
:
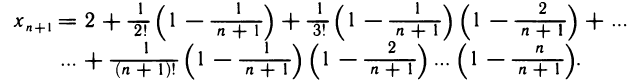
Заметим теперь, что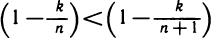 
при 0<k<n. Поэтому каждое слагаемое в выражении для 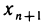больше соответствующего слагаемого в выражении для 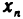и, кроме того, у 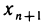по сравнению с 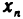добавляется еще одно положительное слагаемое. Следовательно, 
, т. е. последовательность 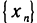возрастающая.
Для доказательства ограниченности сверху данной последовательности заметим, что каждое выражение в круглых скобках в соотношении (1) меньше единицы. Учитывая также, что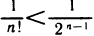 
при n>2, получаем
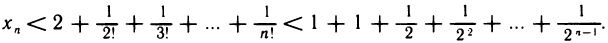
Используя формулу суммы геометрической прогрессии, придем к неравенству
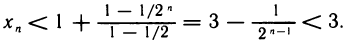
Таким образом, доказано, что последовательность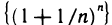 
— возрастающая и ограничена сверху. По теореме 2.12 она имеет предел. Этот предел обозначают буквой е. Итак, по определению,
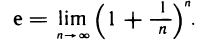
Отметим, что число е играет большую роль во многих вопросах математики. Оно, в частности, является основанием натуральных логарифмов. В настоящем параграфе дано только определение числа е. Далее будет рассмотрен способ вычисления этого числа с любой степенью точности.
Здесь лишь отметим, что так как 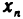<3 и из (1) непосредственно очевидно, что 2<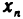, то число е заключено в пределах 
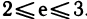Доказано, что число е иррациональное.
Докажем теорему, которая в дальнейшем неоднократно используется при доказательстве других теорем.
Теорема о вложенных отрезках
Пусть дана последовательность отрезков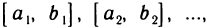 
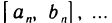таких, что каждый последующий содержится в предыдущем: 
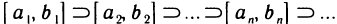,т. е
для всех n (1)
и пусть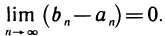 
Будем называть эту последовательность последовательностью вложенных отрезков.
Теорема:
Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности.
Доказательство:
Из неравенств (1) следует, что левые концы отрезков образуют неубывающую последовательность
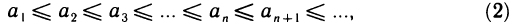
а правые концы — невозрастающую последовательность
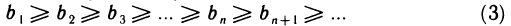
При этом последовательность (2) ограничена сверху, а последовательность (3) ограничена снизу, так как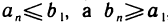 
, для любого n. Следовательно, на основании теоремы 2.12 эти последовательности имеют пределы. Пусть 
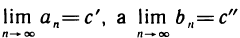. Тогда из условия
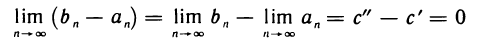
следует, что с’ = с», т. е. последовательности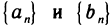 
имеют общий предел. Обозначая этот предел буквой с, получаем, что для любого п справедливы неравенства 
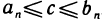, т. е. точка с принадлежит всем отрезкам последовательности (1).
Докажем теперь, что такая точка только одна. Допустим, что существует еще одна точка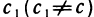 
, принадлежащая всем отрезкам последовательности (1). Тогда для любого п должно выполняться неравенство 
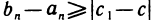и, следовательно, 
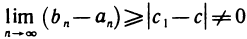, что противоречит условию теоремы.
Замечание. Теорема неверна, если вместо отрезков рассматривать интервалы. Например, для последовательности вложенных интервалов
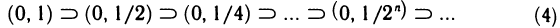
не существует точки, принадлежащей всем интервалам. В самом деле, какую бы точку с на интервале (0, 1) ни взять, всегда найдется номер N такой, что при n>N будет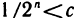 
и, следовательно, точка с не будет принадлежать интервалам последовательности (4), начиная с интервала 
.
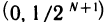Для дальнейшего изложения нам понадобятся некоторые сведения из аналитической геометрии. Поэтому следующая глава посвящена этому разделу математики.
Дополнение к пределу последовательности
Смотрите также:
| Переменные величины | Признаки существования предела последовательности |
| Понятие числовой последовательности | Число е |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
