Линейные пространства с примерами решения и образцами выполнения

Оглавление:

Определение линейного пространства:

Линейным пространством называется множество, для элементов которого определены операции сложения и умножения на число, удовлетворяющие условиям (см. главу 1.3):

1.Коммутативность 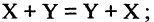Линейные пространства

2.Ассоциативность 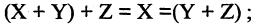Линейные пространства

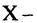
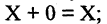
3.Существует нулевой элемент 0 такой, что для любого Линейные пространства

4.Для любого элемента X существует противоположный ему элемент 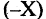Линейные пространства такой, что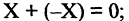

5.Пусть с и d — числа, тогда

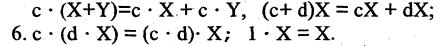
7.Кроме того: 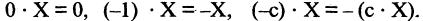Линейные пространства

Примерами линейного пространства являются: пространство действительных чисел, все множество геометрических векторов на плоскости, пространство матриц фиксированной размерно-

сти, пространство решений однородных линейных систем и др. Элементами линейного пространства являются n-мерные векторы — упорядоченные наборы из n вещественных чисел 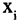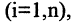Линейные пространства называемых координатами или компонентами векторов, 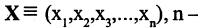размерность вектора. Линейное пространство n-мерных векторов обычно называют n-мерным вещественным векторным пространством и обозначают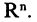 Линейные пространства

Суммой двух n-мерных векторов X и У называется вектор Z, составляющие которого равны суммам соответствующих составляющих складываемых векторов

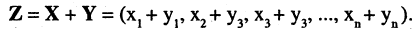
Складывать можно лишь векторы одинаковой размерности. Например, (2, -1,0,4) + (-5,0,2,2) = (-3, -1,2,6). Но операция (3, -1,9) + (6, 2) не определена. В то время как, например, (3, -1, 9) + (6, 0, 2) = (9, 1, 11). При этом следует помнить, что 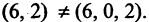Линейные пространства

Произведение вектора X на число 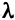Линейные пространства есть новый вектор Y, составляющие которого равны произведению каждой составляющей вектора X на это число, т. е.

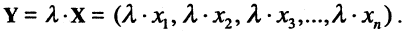
Из m векторов 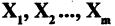Линейные пространства в лилейном пространстве может быть построена линейная комбинация векторов L(Х)

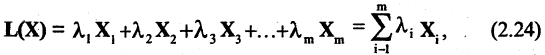
где 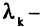Линейные пространства числа.

Скалярное произведение векторов X и Y есть число, равное сумме парных произведений соответствующих составляющих этих векторов, т. е.

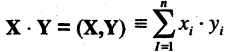
Например, скалярное произведение двух 5-мерных векторов

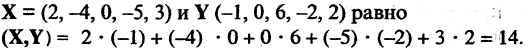
Вещественное векторное пространство, в котором введено скалярное произведение, называется Евклидовым пространством. Из определения следуют основные свойства скалярного произведения:

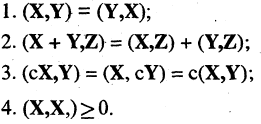
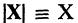
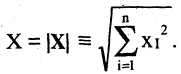
Нормой (или длиной) вектора X называется число Линейные пространства

Два вектора называются ортогональными, если их скалярное произведение равно нулю, т. е. 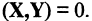Линейные пространства Система векторов называется ортогональной, если любые два вектора из этой системы ортогональны. Примером ортогонального векторного пространства может служить система трех взаимно перпендикулярных векторов (декартова система координат в трехмерном геометрическом пространстве).

Линейная независимость векторов

Вектора называются коллинеарными, если они параллельны одной прямой; компланарными — если они лежат в одной и той же плоскости. Рассмотрим три компланарных трехмерных вектора X, Y, Z. В этом случае один из них, например, X, можно представить как линейную комбинацию векторов Y и Z (рис. 2.18)

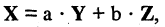
где а, b — числовые множители.
Если X, Y, Z не компланарны, то ни один из них в виде линейной комбинации представить нельзя.
Пусть задана система из m штук n-мерных векторов:

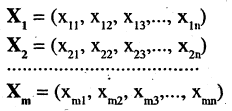
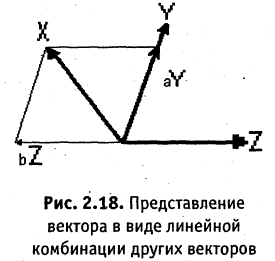
Векторы называются линейно зависимыми, если линейная комбинация векторов равна нулю, но хотя бы одно из чисел 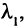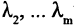Линейные пространства не равно нулю

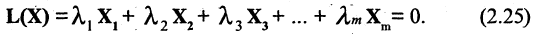
В развернутом виде через проекции векторов это можно записать так

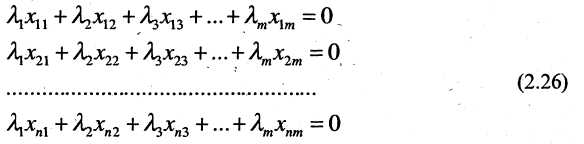
Векторы 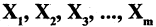Линейные пространства называются линейно независимыми, если линейная комбинация векторов равна нулю, только тогда, когда все 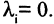Для того, чтобы векторы были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из них являлся линейной комбинацией других.

Для того, чтобы векторы 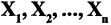Линейные пространства в пространстве 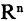были линейно независимы, необходимо и достаточно, чтобы определитель, составленный из компонент этих векторов, был отличен от нуля.

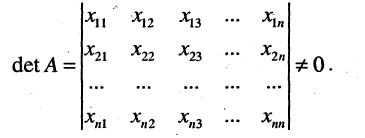
Замечание:

Система векторов, содержащая нулевой вектор, всегда линейно зависима.

Пример:

Дана система векторов

Определить: линейно зависимы или независимы эти векторы? Составим определитель:

Следовательно, данные векторы линейно независимы.

Замечание:

Такая система векторов называется стандартной.

Базис системы векторов

Совокупность n-мерных векторов 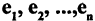Линейные пространства называется базисом (системой координат) векторного пространства 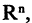если эти векторы линейно независимы и любой другой вектор этого пространства является их линейной комбинацией:

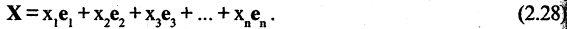
Равенство (2.28) называется разложением вектора X по базису 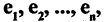Линейные пространства компоненты вектора 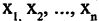называются его координатами в этом базисе. Совокупность базисных векторої обозначается 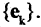Имеют место следующие утверждения:

1.Каждый вектор системы может быть разложен по базизу единственным способом.

2.Два различных базиса одной и той же системы векторов содержат одинаковое количество векторов.

3.Система n линейно независимых векторов 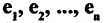Линейные пространства образует базис в пространстве .

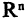4.В пространстве 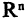Линейные пространства система, состоящая более чем из n векторов, линейно зависима.

Размерностью конечномерного линейного пространства Линейные пространства 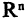называется число векторов его базиса.

Пример:

Можно ли принять за базис пространства 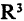Линейные пространства следующие векторы:

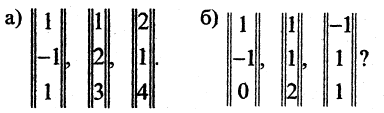
Составим из этих столбцов определители и вычислим их значения

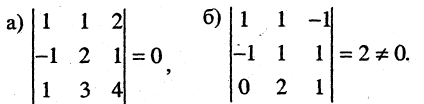
Следовательно, векторы «а» базис не образуют, а векторы «б» — образуют.

Преобразование координат в пространстве

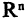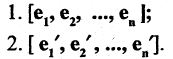
Пусть задано два базиса в пространстве Линейные пространства :

Любой вектор можно разложить по базисным векторам как 1-й, так и 2-й системы:

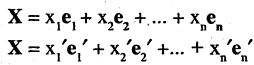
или в компактной форме

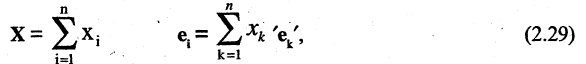
Формулы преобразования координат вектора X при переходе от одного базиса к другому получают, разлагая каждый вектор второго базиса по элементам первого базиса:

Подставляем в (2.29) вместо 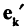Линейные пространства формулу (2.30)

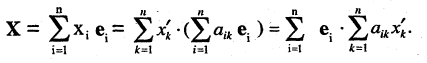
В силу единственности разложения вектора по базису 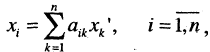Линейные пространства т. е. координаты вектора X в первом базисе 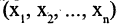связаны с координатами этого же вектора во втором базисе 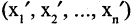следующим образом:

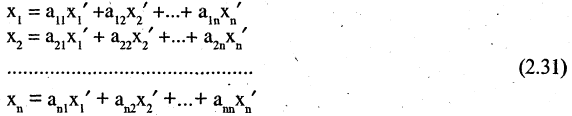
Из координат 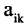Линейные пространства векторов 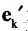в первой системе базисных векторов формируют матрицу, называемую матрицей перехода от базиса 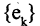к базису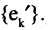

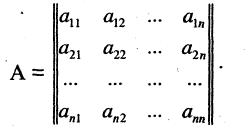
Базисные векторы 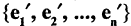Линейные пространства линейно независимы, следовательно, матрица А будет невырожденной 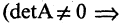существует обратная матрица 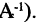Матричная форма формулы перехода (2.31)

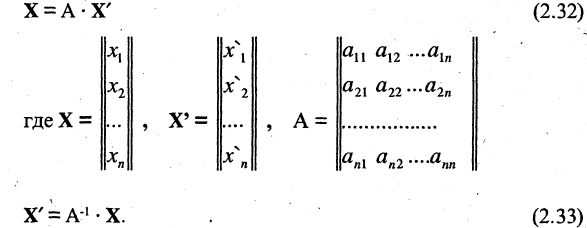
Пример:

Пусть задан вектор 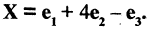Линейные пространства При помощи матрицы перехода

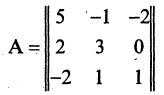Линейные пространства перешли к новому базису 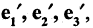т. е.

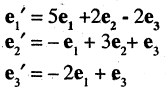
Найти вектор X в новом базисе, т. е. вектор 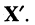Линейные пространства

Решение:

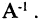
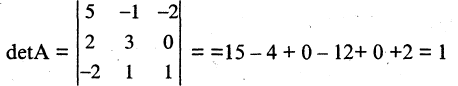
Найдем обратную к А матрицу Линейные пространства

Так как определитель матрицы А равен единице, то присоединенная к А матрица 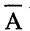Линейные пространства равна обратной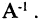

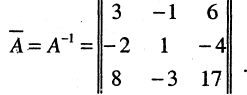
Теперь найдем вектор X в новом базисе

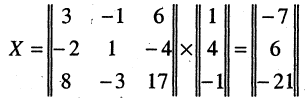
или в виде разложения по новому базису 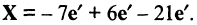Линейные пространства

Линейные пространства

Смотрите также:

Производная преобразования Фурье функции.	Нормированные и полуиормированные пространства.
Метрические пространства.	Примеры нормированных и полунормированных пространств.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: