Оглавление:
Прямая линия — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий, их свойства и связь с другими понятиями (например, точки и плоскости) определяются аксиомами геометрии. Прямая, наряду с окружностью, относится к числу древнейших геометрических фигур.
Векторный базис на плоскости
Из школьного курса известно, что если векторы a и b не коллинеарны, то любой вектор c, компланарный с a и b, можно представить единственным образом в виде
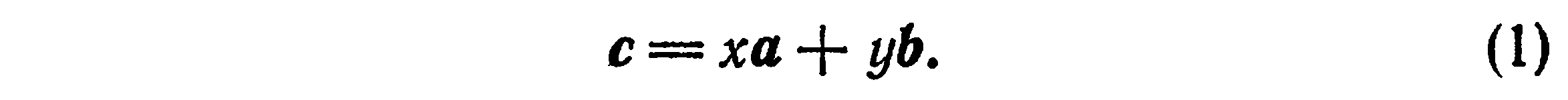
Определение:
Линейной комбинацией векторов  называется любой вектор вида
называется любой вектор вида 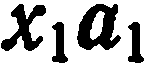
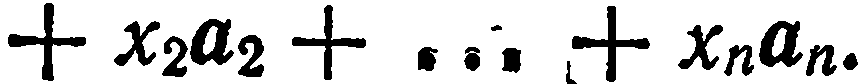
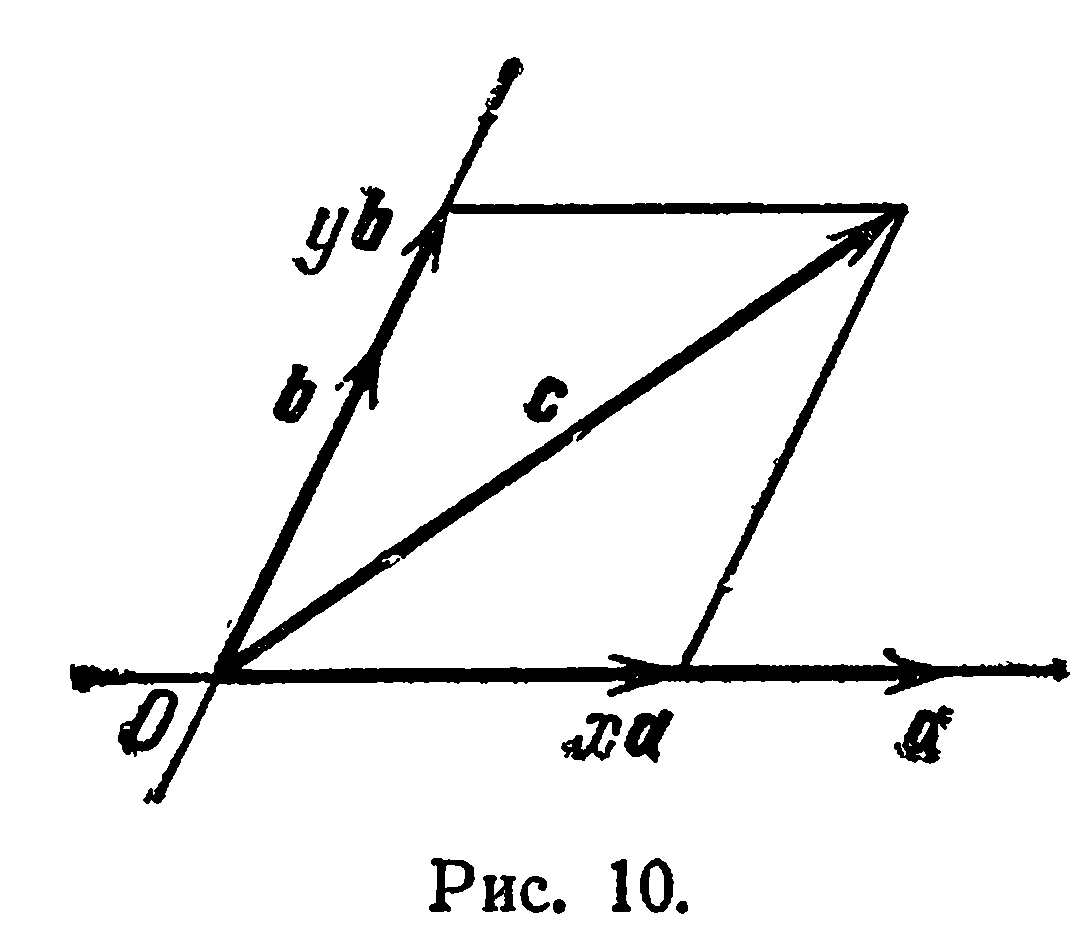
Здесь  — числа, называемые коэффициентами линейной комбинации. Если вектор представлен в виде линейной комбинации каких-то векторов, то говорят, что он разложен по этим векторам. Так, вектор с из равенства (1) представлен в виде линейной комбинации вектора
— числа, называемые коэффициентами линейной комбинации. Если вектор представлен в виде линейной комбинации каких-то векторов, то говорят, что он разложен по этим векторам. Так, вектор с из равенства (1) представлен в виде линейной комбинации вектора 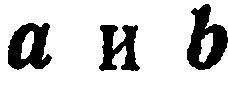 , поэтому можно
, поэтому можно
сказать, что он разложен по векторам 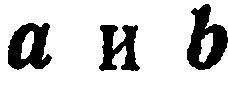 (рис. 10).
(рис. 10).
Определение:
Векторным базисом на плоскости называются два произвольных неколлинеарных вектора этой плоскости, взятые в
определенном порядке. Легко видеть, что в любой плоскости существует бесконечное множество базисов.
Пусть 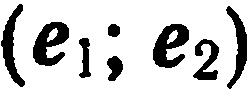 — один из базисов некоторой плоскости. Тогда любой вектор а этой плоскости может быть единственным образом представлен в виде линейной комбинации базисных векторов, т. е.
— один из базисов некоторой плоскости. Тогда любой вектор а этой плоскости может быть единственным образом представлен в виде линейной комбинации базисных векторов, т. е.
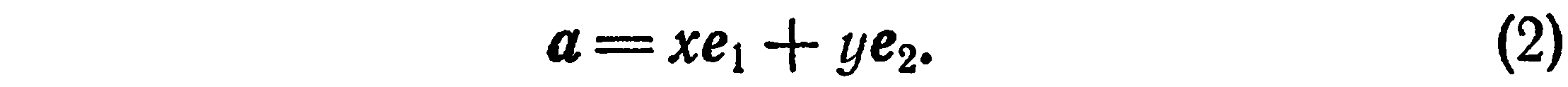
Это означает, что если на плоскости выбран базис 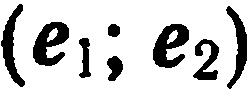 , то каждому вектору а этой плоскости однозначно сопоставлена упорядоченная пара чисел x и y и, наоборот, каждой упорядоченной паре чисел х и у
, то каждому вектору а этой плоскости однозначно сопоставлена упорядоченная пара чисел x и y и, наоборот, каждой упорядоченной паре чисел х и у
соответствует на плоскости единственный вектор а, определяемый равенством (2). Числа х и у называются координатами вектора а в базисе 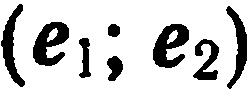 при этом пишут:
при этом пишут: 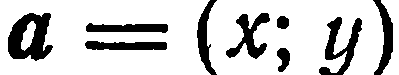 .
.
Пример:
Найти координаты векторов а, b и c в базисе 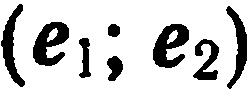 , если
, если 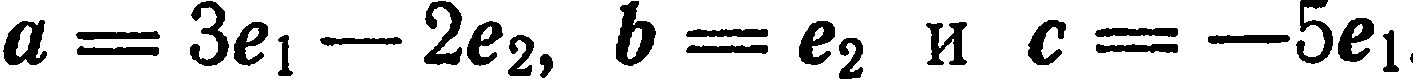 .
.
Решение:
Векторы а, b и с заданы своими разложениями в базисе 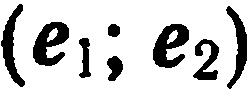 поэтому
поэтому 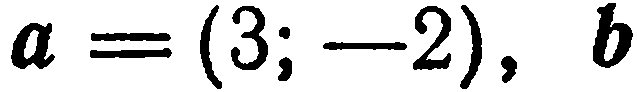
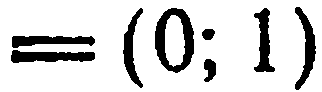 и
и 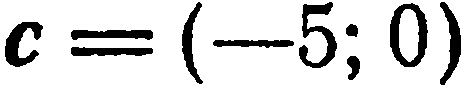 .
.
Базис 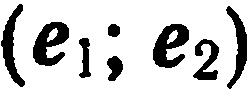 называется прямоугольным, если
называется прямоугольным, если 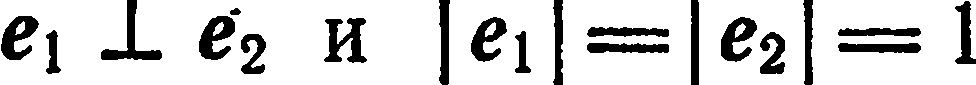 т. е. если базисные векторы единичны и взаимно перпендикулярны. В прямоугольном базисе единичные векторы принято обозначать через i и j, следовательно, разложение вектора
т. е. если базисные векторы единичны и взаимно перпендикулярны. В прямоугольном базисе единичные векторы принято обозначать через i и j, следовательно, разложение вектора 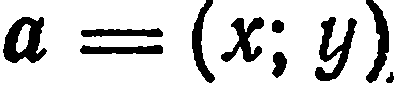 по базису ( i ; j )имеет вид
по базису ( i ; j )имеет вид 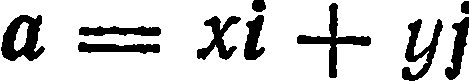 .
.
Пример:
Найти координаты векторов 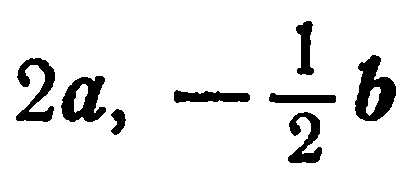
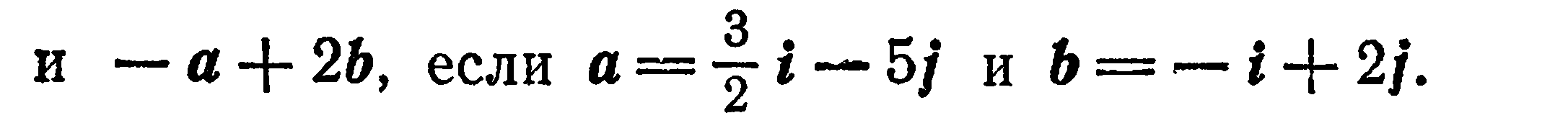
Решение:
Применив правила действия над векторами, заданными своими координатами, получим:
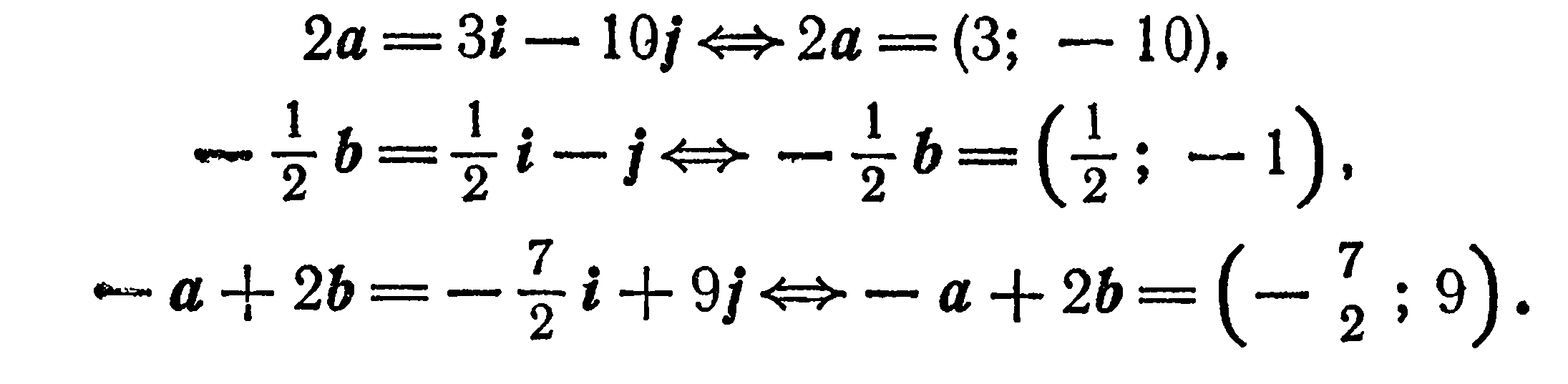
Прямоугольные координаты
Пусть  — произвольная точка некоторой плоскости, а
— произвольная точка некоторой плоскости, а 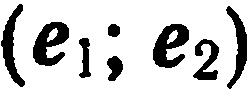 —один из базисов той же плоскости.
—один из базисов той же плоскости.
Определение:
Декартовой системой координат
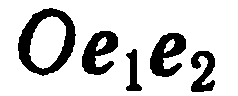 на плоскости называется совокупность точки
на плоскости называется совокупность точки  и
и
базиса 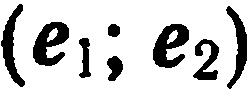 .
.
Точка  называется началом координат, прямые
называется началом координат, прямые  и
и 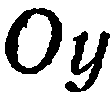 , проходящие через начало координат в направлении базисных векторов
, проходящие через начало координат в направлении базисных векторов  (рис 11), называются осями координат:
(рис 11), называются осями координат:  — ось абсцисс,
— ось абсцисс, 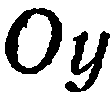 — ось ординат. При этом систему координат
— ось ординат. При этом систему координат 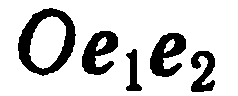 будем обозначать также
будем обозначать также 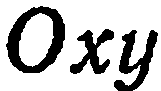 , а плоскость с соответствующей системой координат будем называть плоскостью
, а плоскость с соответствующей системой координат будем называть плоскостью 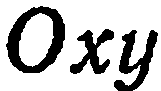 .
.
Рассмотрим произвольную точку  плоскости
плоскости 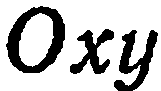 .
.
Радиусом-вектором точки  по отношению к точке
по отношению к точке 
называется вектор  Координатами точки
Координатами точки  в системе координат
в системе координат 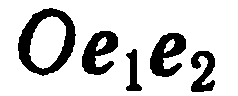 называются координаты радиуса-вектора
называются координаты радиуса-вектора  в базисе
в базисе 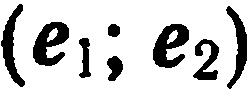 . Если
. Если 
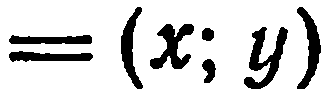 , то координаты точки
, то координаты точки  записывают
записывают 
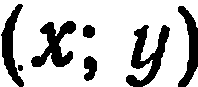 ; число
; число 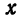 называется абсциссой
называется абсциссой 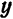 — ординатой.
— ординатой.
Например, точка  , изображенная на рис. 11, имеет
, изображенная на рис. 11, имеет
координаты (2; 1), так как 

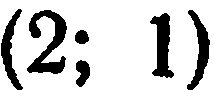
Определение:
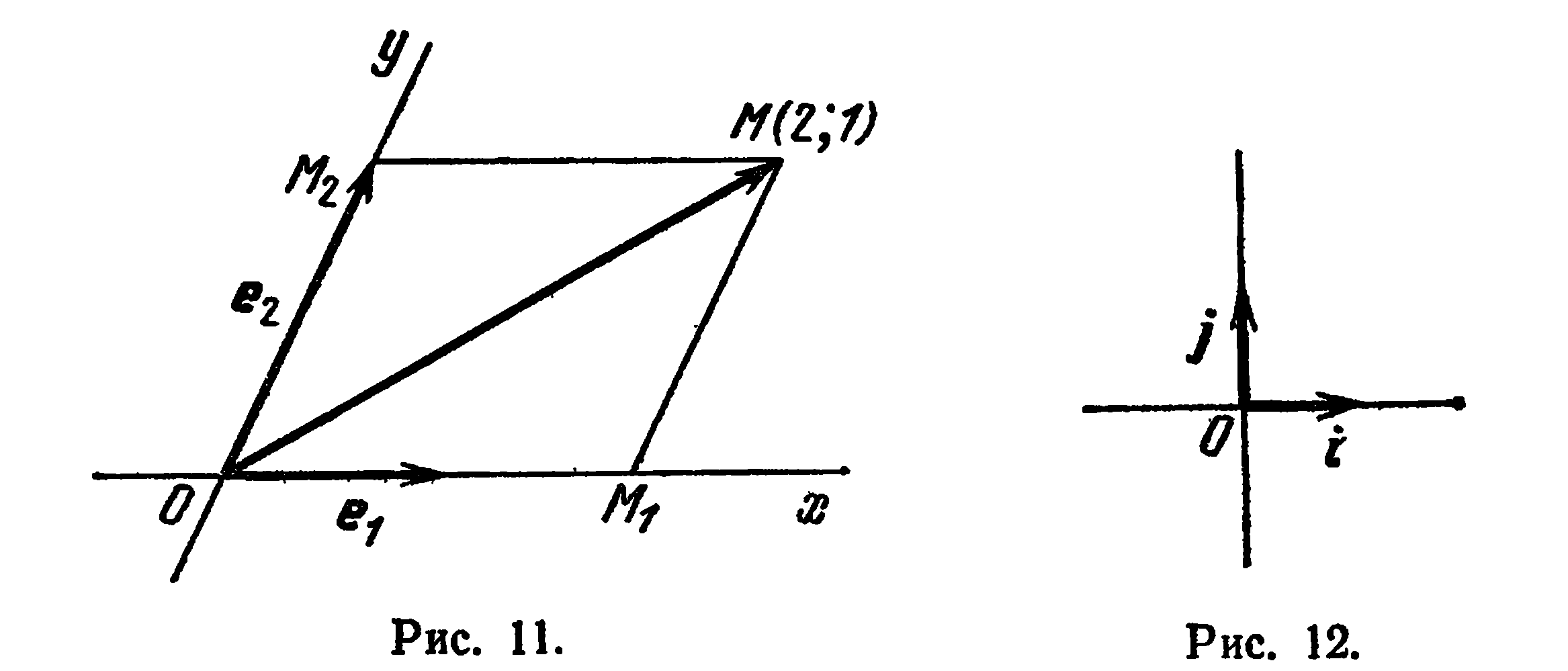
Декартова система координат называется прямоугольной, если координатные (базисные) векторы единичны и взаимно перпендикулярны, т. е. если базис прямоугольный. Единичные координатные векторы прямоугольной декартовой системы координат также обозначают через  и
и 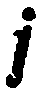 (рис. 12).
(рис. 12).
Полярные координаты
Наряду с прямоугольной системой координат, которая хорошо известна по школьному курсу, довольно часто применяется так называемая полярная система координат, рассмотрим ее.
Зададим на плоскости некоторый луч  , на которром отложим единичный вектор
, на которром отложим единичный вектор 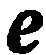 . Возьмем на той же плоскости точку
. Возьмем на той же плоскости точку 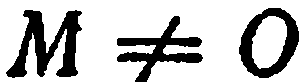 (рис. 13), Пусть
(рис. 13), Пусть 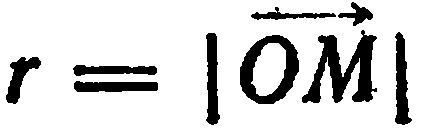 и
и
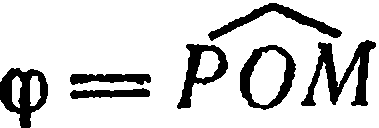 — величина направленного угла
— величина направленного угла  . Очевидно, что числа
. Очевидно, что числа  и
и  определяют положение единственной точки
определяют положение единственной точки  на плоскости. Они называются полярными координатами точки
на плоскости. Они называются полярными координатами точки  :
:  — полярный радиус,
— полярный радиус,  — полярный угол. Пишут:
— полярный угол. Пишут: 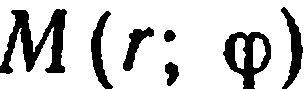 .
.
Если 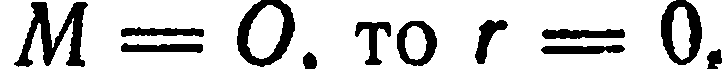 а число
а число  — неопределенное. Для всех других
— неопределенное. Для всех других
точек плоскости  , а
, а  определено с точностью до
определено с точностью до  , т. е, пары чисел
, т. е, пары чисел  — любое целое
— любое целое
число, представляют собой координаты одной и той же точки.
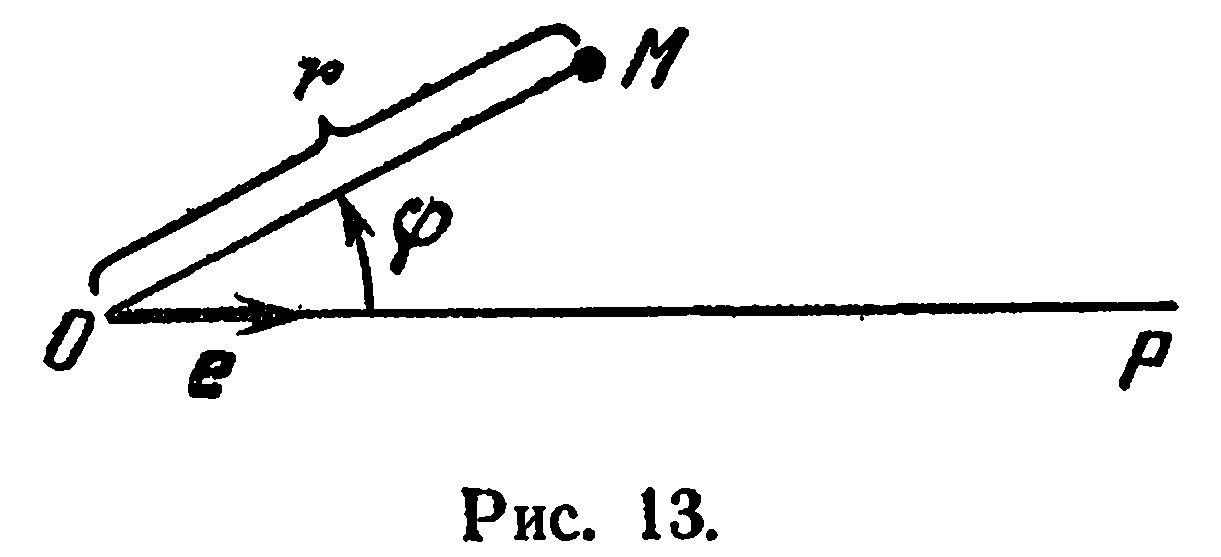
Таким образом, полярная система координат определяется заданием луча  и единичного вектора
и единичного вектора 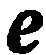 , сонаправленного с ним.
, сонаправленного с ним.
Пример:
Построить в полярной системе координат точку 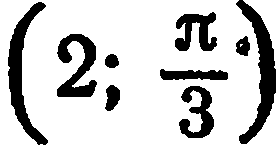
Решение:
Проводим через полюс  луч
луч 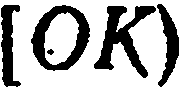 под углом
под углом 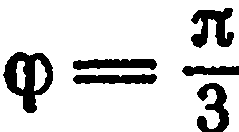 к полярной оси
к полярной оси  и откладываем от полюса отрезок
и откладываем от полюса отрезок 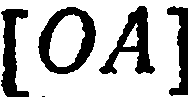 , длина которого равна
, длина которого равна  . Конец этого отрезка
. Конец этого отрезка 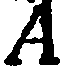 будет искомой точкой (рис. 14).
будет искомой точкой (рис. 14).
Связь между прямоугольными и полярными координатами
Рассмотрим такую полярную систему координат, что:
1) ее полюс  совпадает с началом прямоугольной системы координат
совпадает с началом прямоугольной системы координат  ;
;
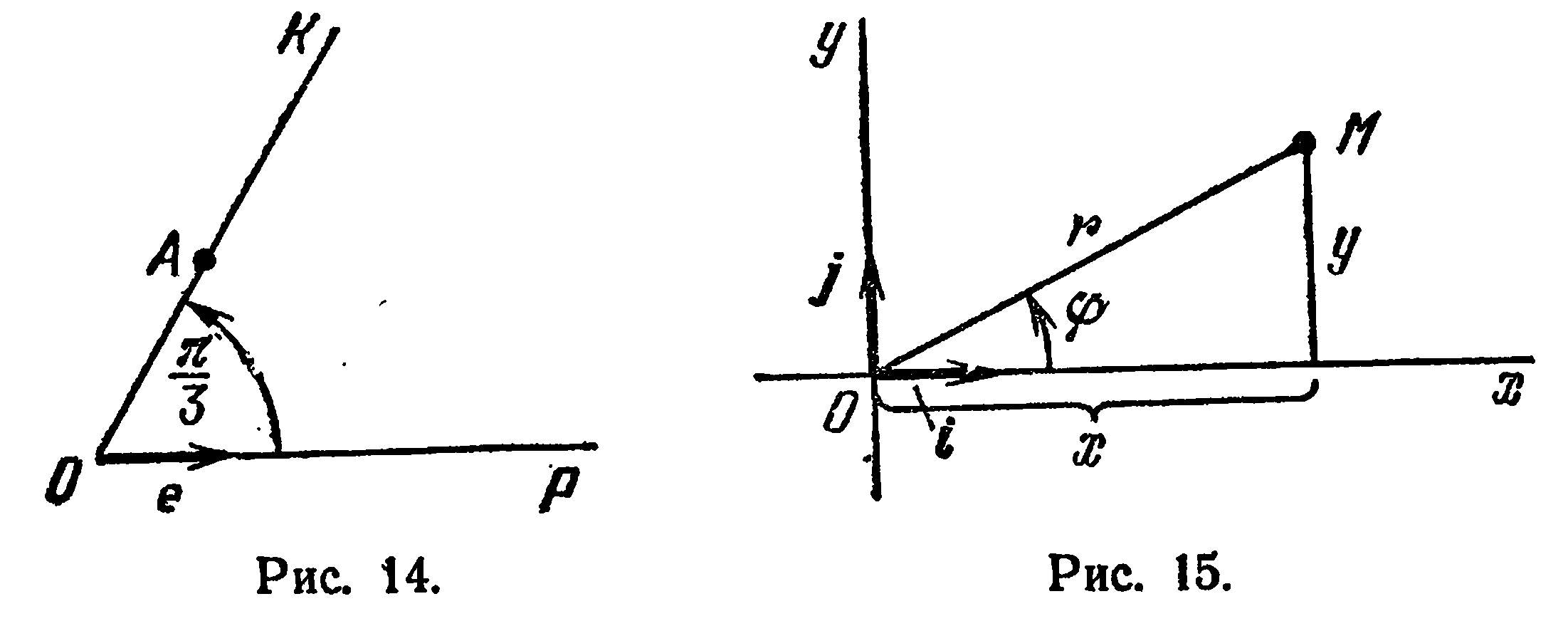
2) полярная ось совпадает с положительной полуосью абсцисс (рис. 15).
Пусть 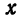 и
и 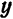 —- прямоугольные координаты некоторой точки
—- прямоугольные координаты некоторой точки  , а
, а  и
и  — ее полярные координаты. Из рис. 15 видно, что прямоугольные координаты точки
— ее полярные координаты. Из рис. 15 видно, что прямоугольные координаты точки  выразятся через ее полярные координаты равенствами:
выразятся через ее полярные координаты равенствами:

Обратно, 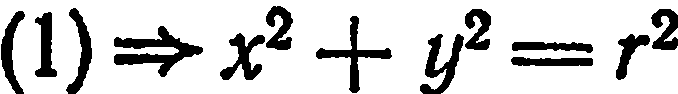 откуда
откуда

(перед радикалом берем знак 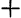 , так как
, так как 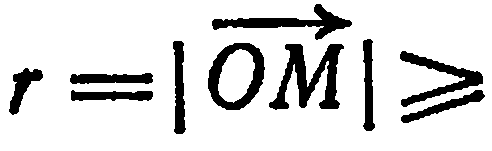

Если  то из (1) и (2) имеем:
то из (1) и (2) имеем:
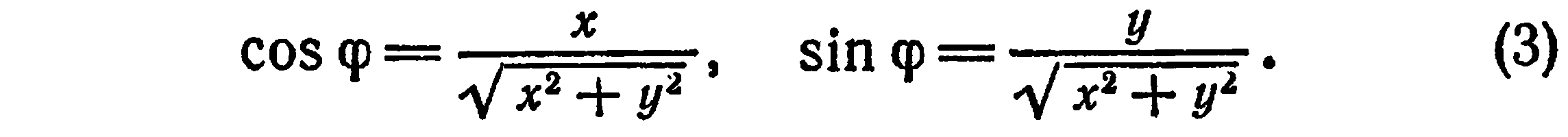
По формулам (2) и (3) находят полярные координаты  и
и  точки
точки 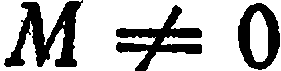 , зная ее прямоугольные координаты
, зная ее прямоугольные координаты 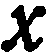 и
и 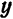
Пример:
Найти прямоугольные координаты точки  с полярными координатами
с полярными координатами 
Решение:
Имеем: 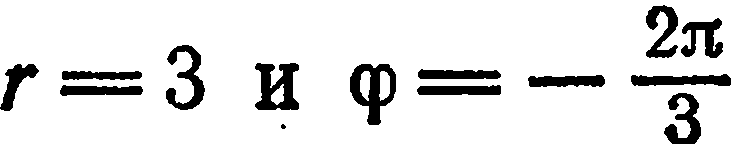 По формулам (1) находим:
По формулам (1) находим:
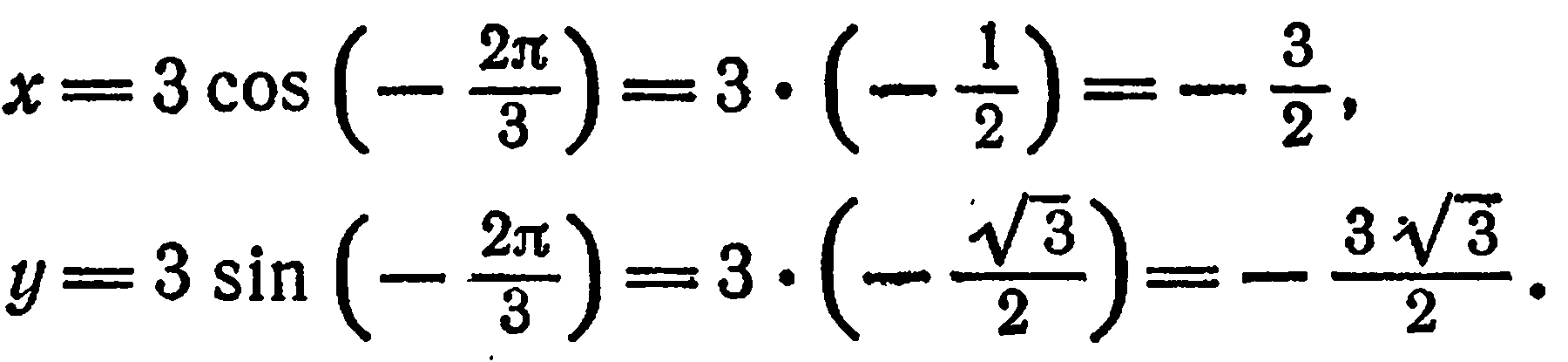
Итак, 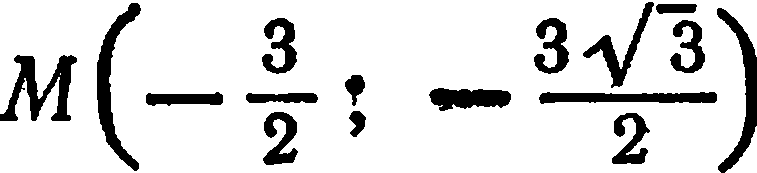 .
.
Пример:
Найти полярные координаты точки  с прямоугольными координатами
с прямоугольными координатами 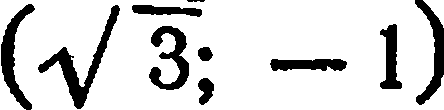 .
.
Решение:
Имеем: 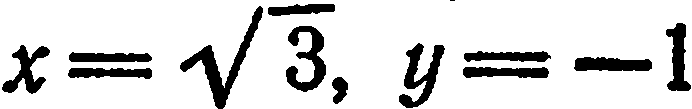 . По формуле (2)
. По формуле (2)
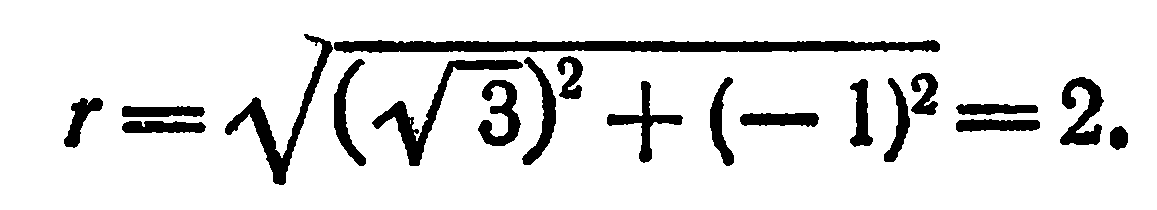
По формулам (3) получаем:
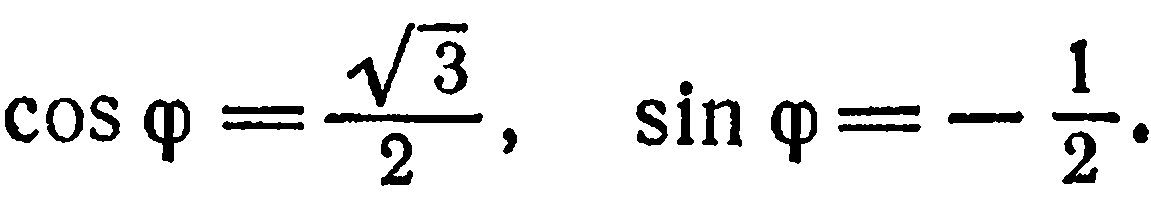
Отсюда 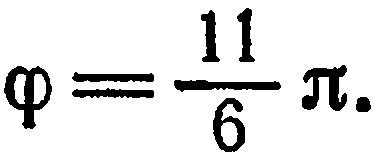 Итак,
Итак, 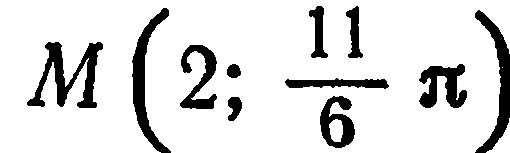
Преобразование прямоугольных координат
В практике встречаются случаи, когда в одной и той же плоскости рассматриваются одновременно две и более системы координат. При этом одна и та же точка плоскости относительно различных систем координат будет иметь, вообще говоря, различные координаты, В связи с этим целесообразно иметь формулы, устанавливающие взаимосвязь между координатами произвольной точки плоскости в разных системах координат.
Параллельный перенос осей координат
Пусть дана некоторая система координат 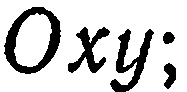 назовем ее
назовем ее
«старой». Под параллельным переносом осей координат понимают такой переход от старой системы координат 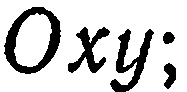 к новой системе
к новой системе
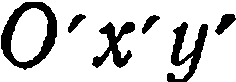 при котором меняется положение начала координат, а направление осей (и масштаб) остаются неизменными (рис. 16).
при котором меняется положение начала координат, а направление осей (и масштаб) остаются неизменными (рис. 16).
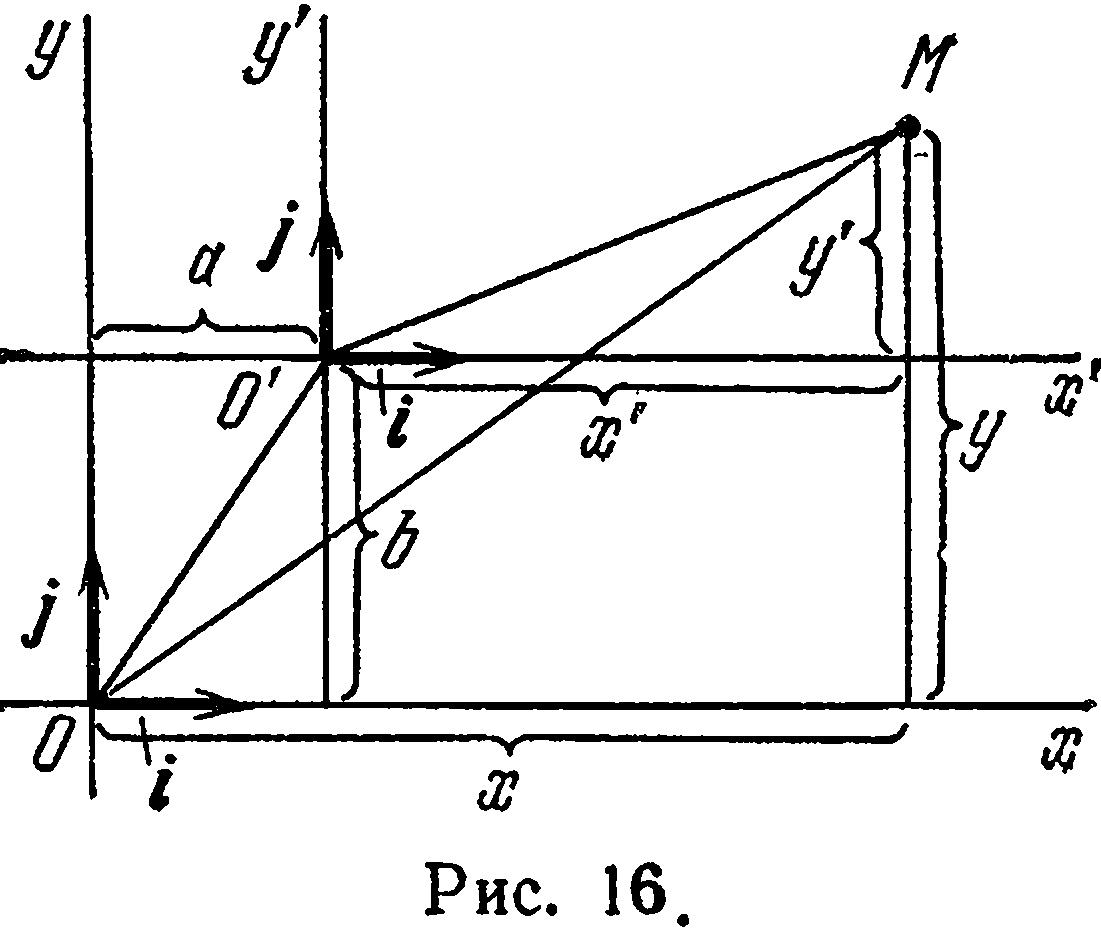
Положение новой системы координат 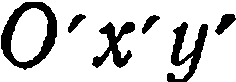 относительно старой
относительно старой 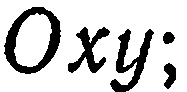 определяется заданием координат
определяется заданием координат 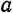 и
и 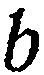 нового начала
нового начала  в старой системе координат.
в старой системе координат.
Пусть произвольная точка  имеет в старой системе координаты
имеет в старой системе координаты 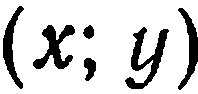 и эта же точка
и эта же точка  имеет в новой системе координаты
имеет в новой системе координаты 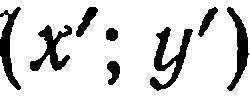 . Найдем связь между координатами точки
. Найдем связь между координатами точки  в старой системе
в старой системе 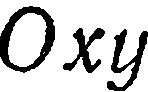 и в новой системе
и в новой системе 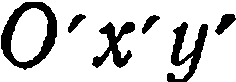 .
.
Рассмотрим векторы
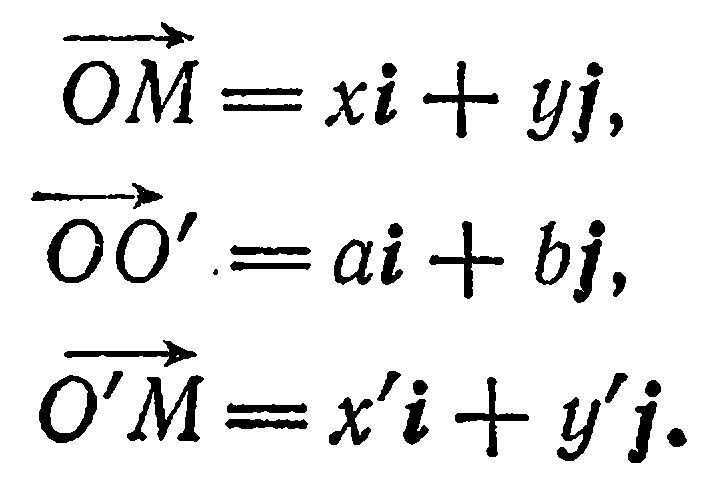
Так как 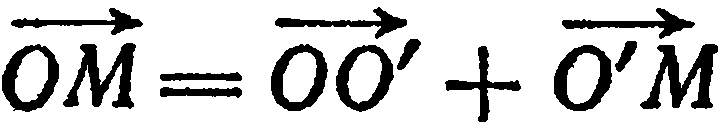 , то
, то
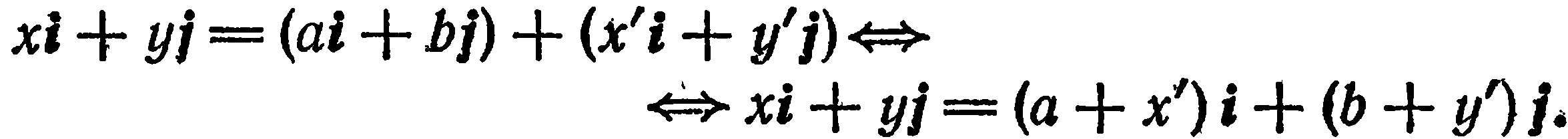
Отсюда
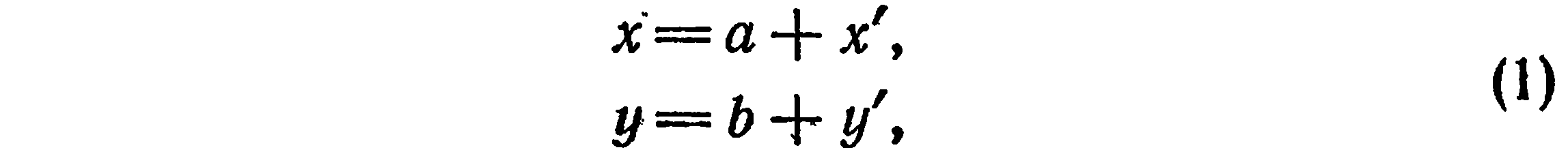
или
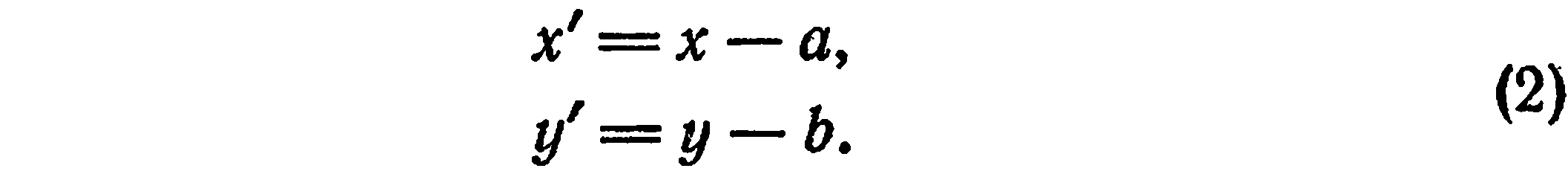
Формулы (1) служат для нахождения старых координат 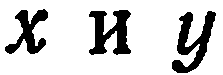 по известным новым
по известным новым 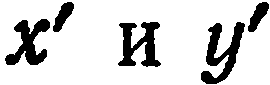 , а формулы (2) служат для нахождения новых координат
, а формулы (2) служат для нахождения новых координат 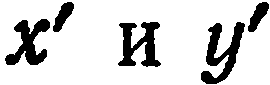 по известным старым
по известным старым 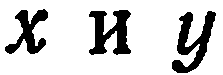 где
где 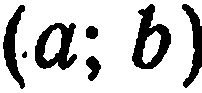 —координаты начала новой системы в старой системе.
—координаты начала новой системы в старой системе.
Пример:
Известны координаты точки  и нового начала
и нового начала 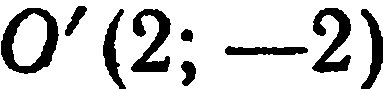 в старой системе. Найти координаты точки
в старой системе. Найти координаты точки  в новой системе.
в новой системе.
Решение:
Из условия задачи имеем:
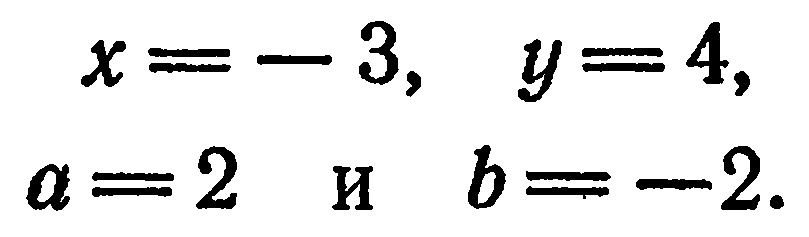
По формулам (2) находим:
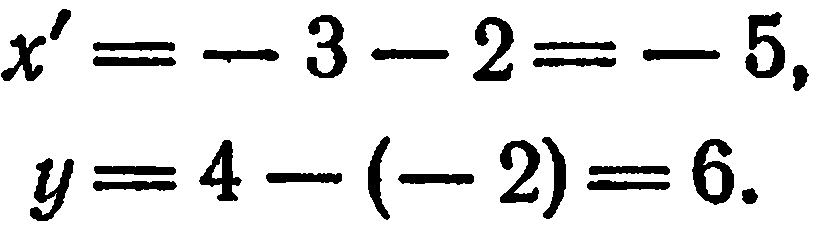
В новой системе точка  имеет координаты
имеет координаты 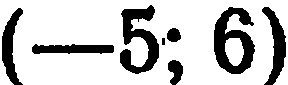 .
.
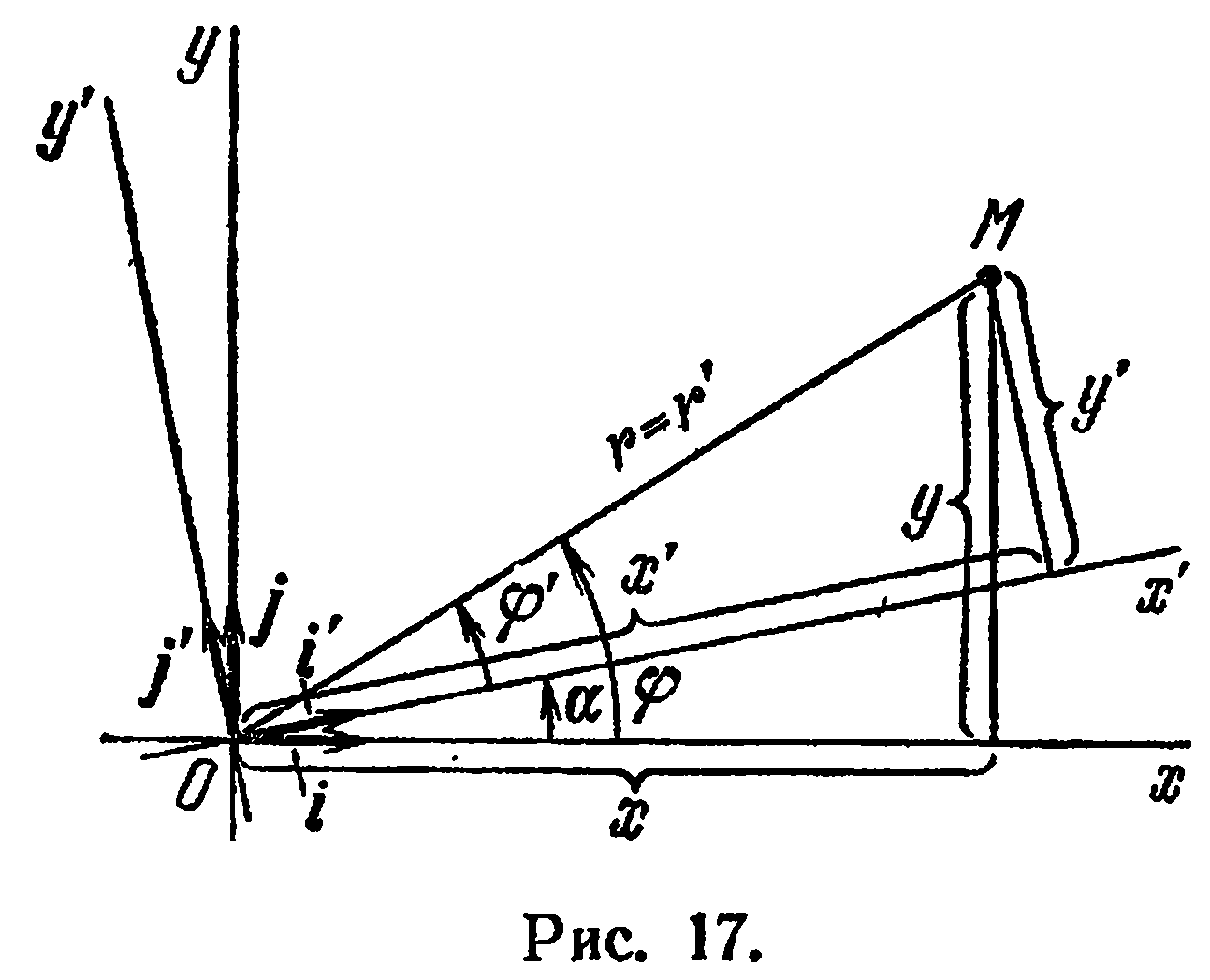
Поворот осей координат
Под поворотом осей координат понимают такое преобразование прямоугольных координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными (рис. 17).
Положение новой системы координат 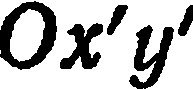 относительно старой
относительно старой 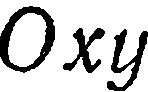 определяется заданием угла
определяется заданием угла 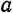 поворота, совмещающего старые оси
поворота, совмещающего старые оси  с новыми
с новыми 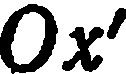

Пусть  — произвольная точка плоскости,
— произвольная точка плоскости, 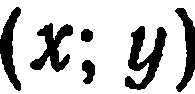 — ее координаты в старой системе и
— ее координаты в старой системе и 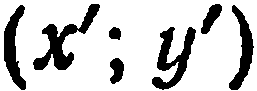 — в новой системе.
— в новой системе.
Рассмотрим две полярные системы координат с общим полюсом  , с тем же масштабом, что и прямоугольные системы, и полярными осями
, с тем же масштабом, что и прямоугольные системы, и полярными осями 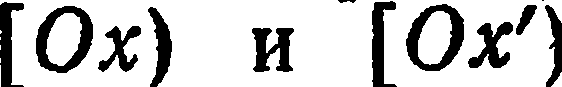 . Обозначим полярные координаты точки
. Обозначим полярные координаты точки  в этих
в этих
системах соответственно через 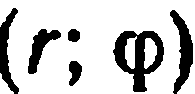 и
и 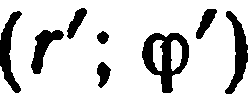 . Ясно, что
. Ясно, что 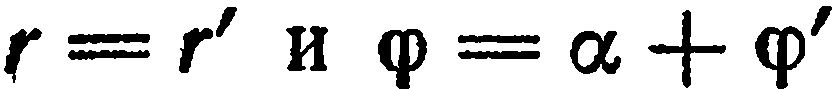 По формулам перехода от полярных координат к прямоугольным (§ 2, (1)) имеем:
По формулам перехода от полярных координат к прямоугольным (§ 2, (1)) имеем:
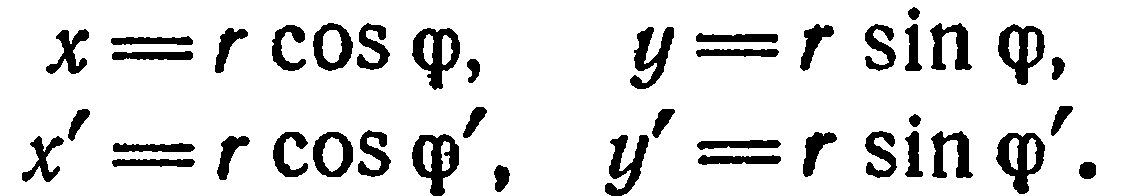
Но 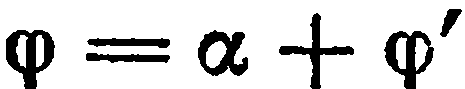 , поэтому
, поэтому
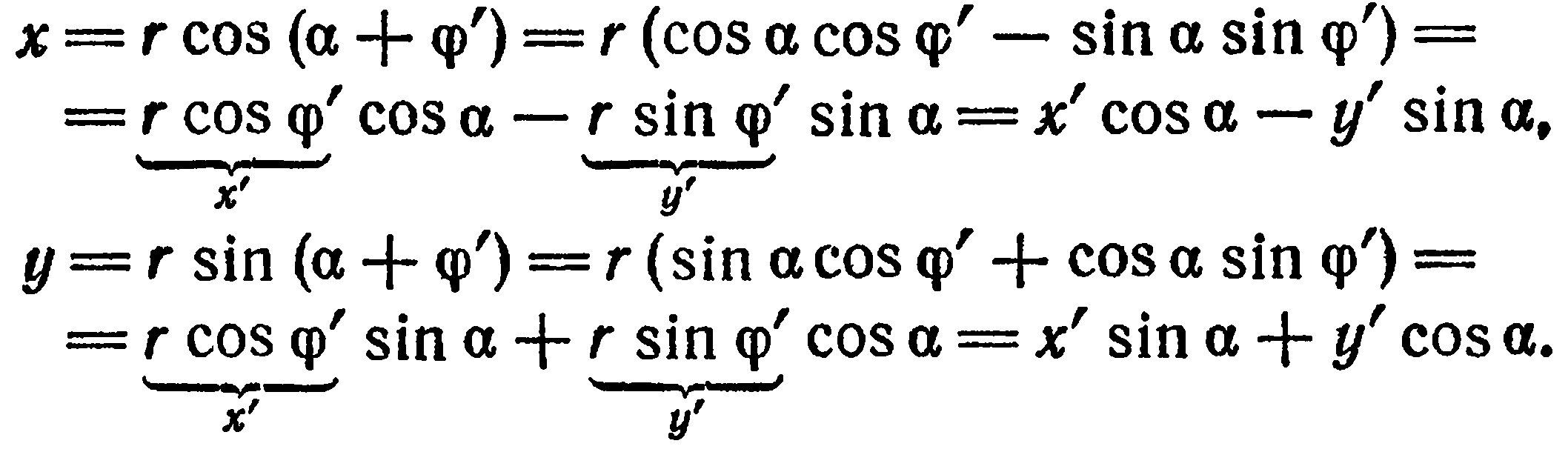
Таким образом,
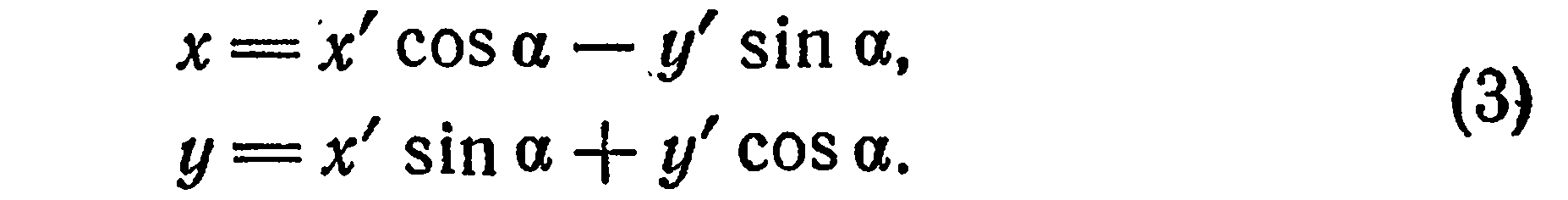
выражающие новые координаты 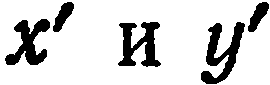 точки
точки  через ее старые координаты
через ее старые координаты 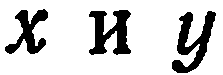 .
.
Пример:
Зная координаты точки  в старой системе
в старой системе 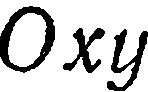 , найти ее координаты в новой системе
, найти ее координаты в новой системе 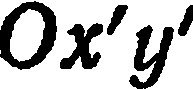 полученной из данной поворотом осей на угол
полученной из данной поворотом осей на угол 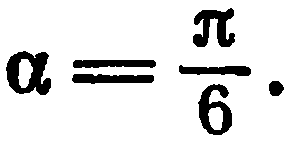
Решение:
По формулам (4) находим:
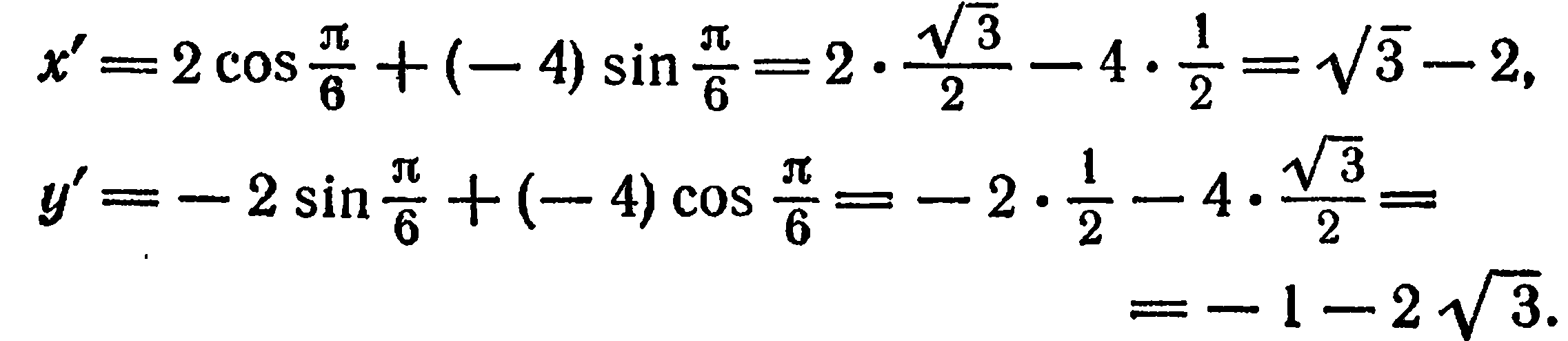
Деление отрезка в данном отношении
Пусть на плоскости 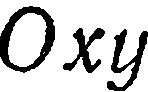 заданы две произвольные различные точки
заданы две произвольные различные точки 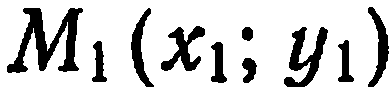 и
и 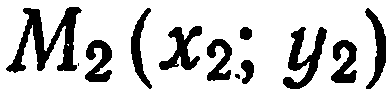 . Проведем через эти точки прямую
. Проведем через эти точки прямую 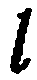 и сделаем ее осью, выбрав на ней определенное направление Пусть
и сделаем ее осью, выбрав на ней определенное направление Пусть 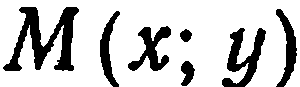 — любая точка прямой
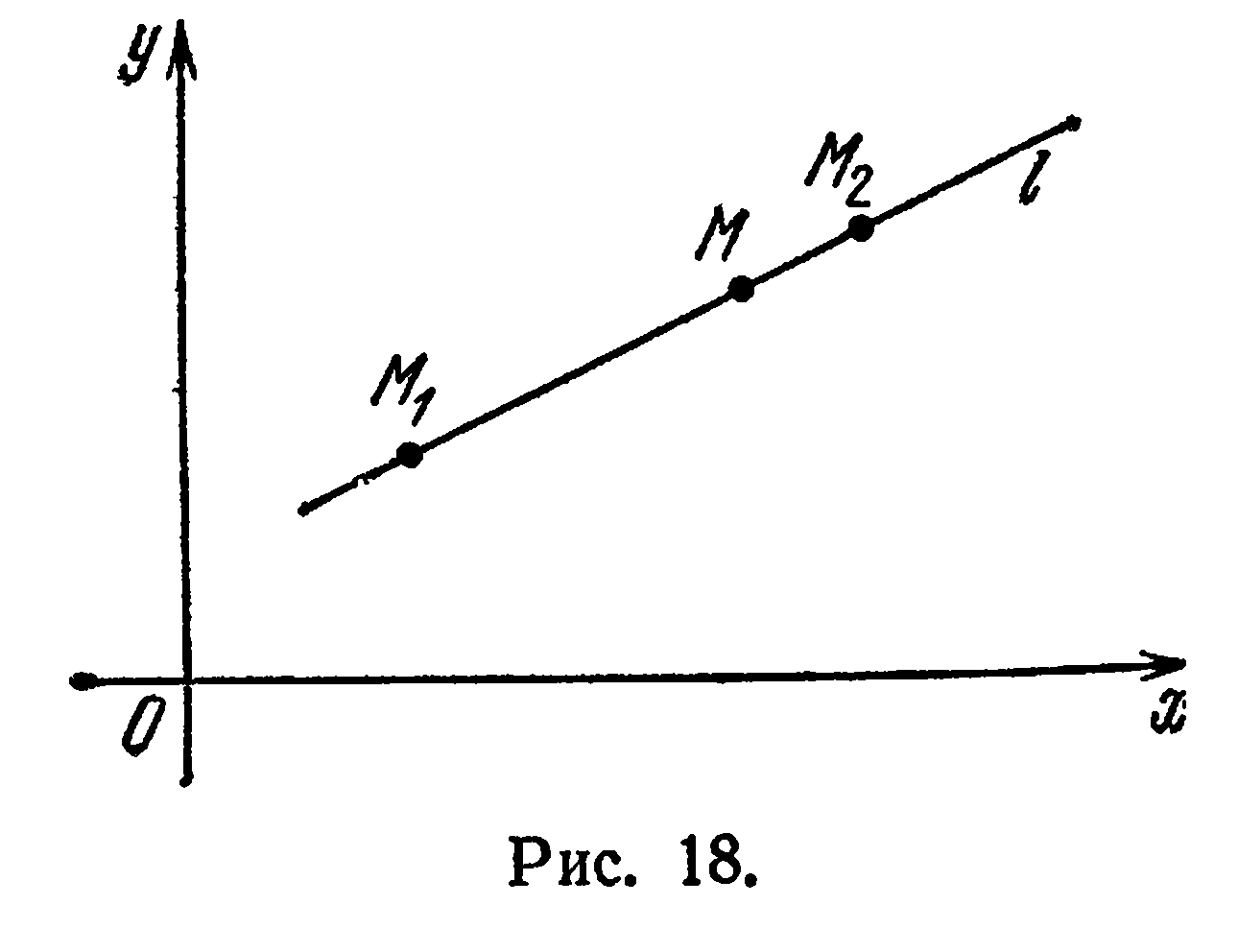
— любая точка прямой 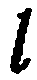 , не совпадающая с
, не совпадающая с 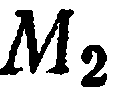 (рис. 18). Говорят, что точка
(рис. 18). Говорят, что точка  делит отрезок
делит отрезок 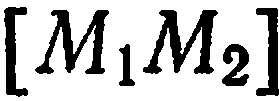 в отношении
в отношении 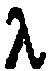 , если
, если
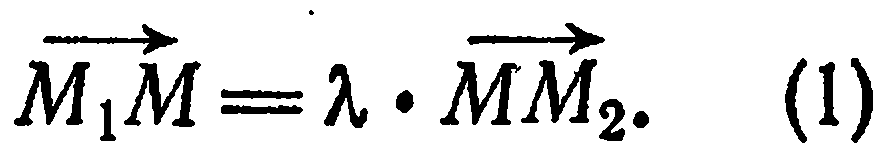
Очевидно, что: 1)  лишь в случае, когда точка
лишь в случае, когда точка  лежит между точками
лежит между точками 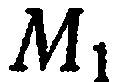 и
и 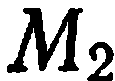 ;
;
2) 
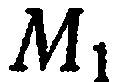 ;
;
3)  в случае, когда
в случае, когда 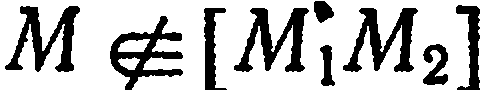 ;
;
4) 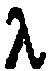 не зависит от того, как выбрано направление на прямой
не зависит от того, как выбрано направление на прямой 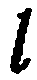 .
.
Наша задача заключается в том, чтобы найти координаты 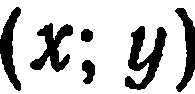 точки
точки  , делящей отрезок
, делящей отрезок 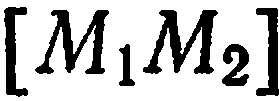 в заданном отношении
в заданном отношении 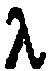 , если известны координаты
, если известны координаты 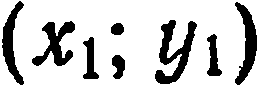 и
и 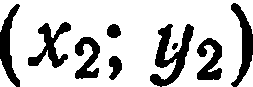 точек
точек 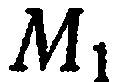 и
и 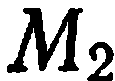 .
.
Перепишем равенство (1) в координатной форме;
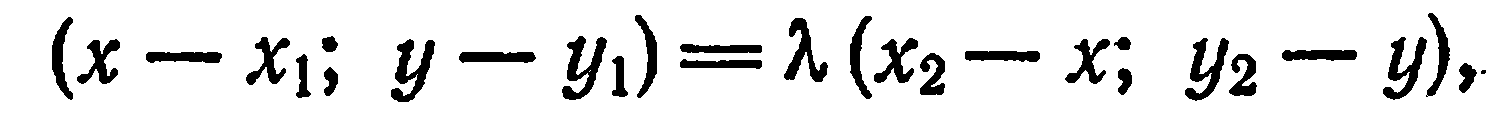
откуда
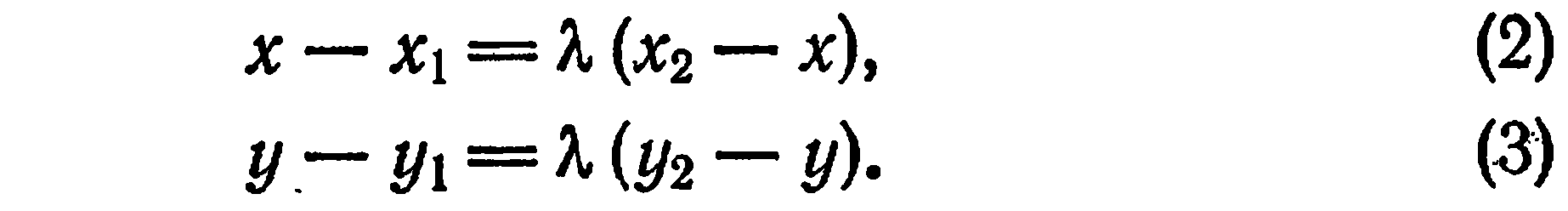
Формулы (4) называются формулами деления отрезка в данном отношении. В частности, если 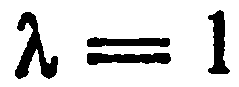 , то формулы (4) примут вид:
, то формулы (4) примут вид:
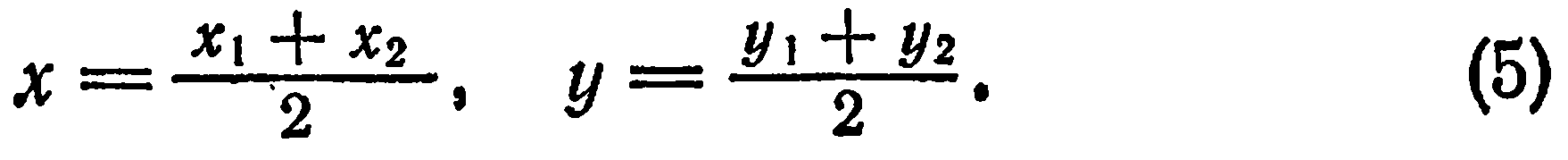
В этом случае точка 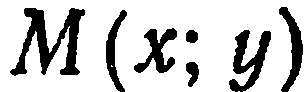 является серединой отрезка
является серединой отрезка 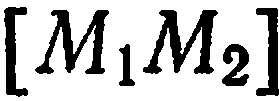 . Следовательно, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
. Следовательно, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Пример:
Даны точки 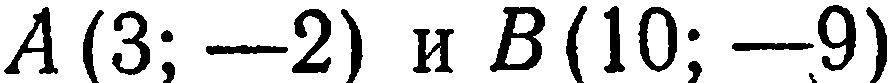 ; Найти точку
; Найти точку 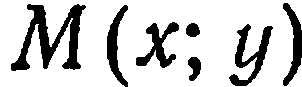 , делящую отрезок
, делящую отрезок 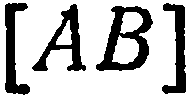 в отношении
в отношении 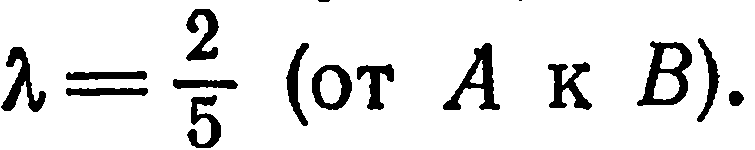
Решение:
Так как точка  делит отрезок
делит отрезок 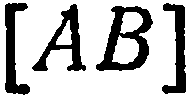
от 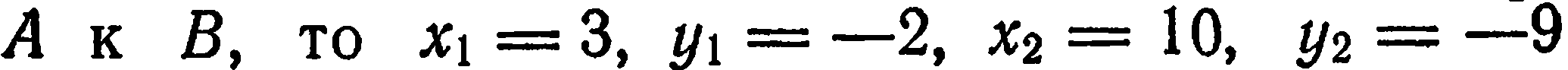 и
и 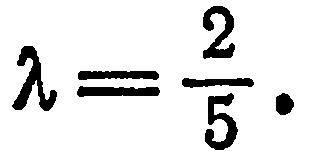 . Подставив эти данные в формулы (4), найдем координаты точки
. Подставив эти данные в формулы (4), найдем координаты точки  :
:
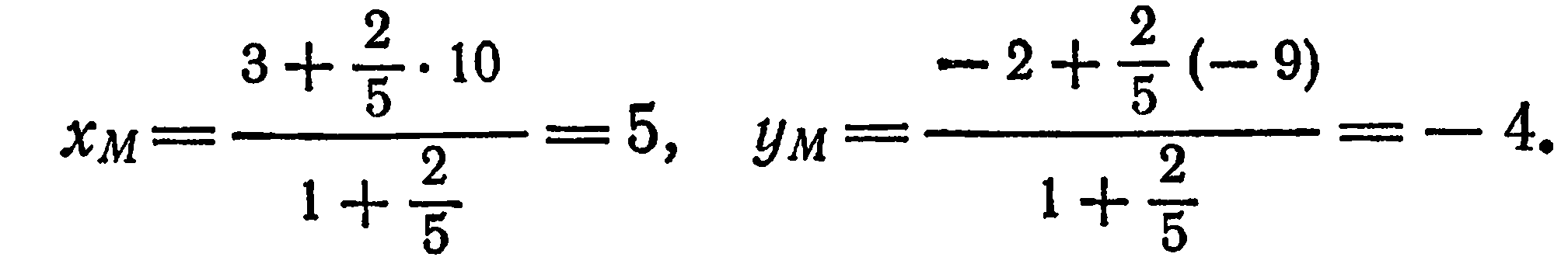
Получили точку 

Понятие об уравнении линии на плоскости
Рассмотрим уравнение

где 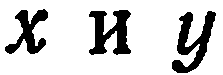 — произвольные переменные, принимающие действительные значения.
— произвольные переменные, принимающие действительные значения.
Известно, что решением уравнения (1) является любая упорядоченная пара значений переменных 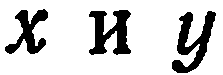 , обращающая это уравнение в верное равенство. Заметим, что уравнению (1) может удовлетворять одна пара действительных чисел, несколько и даже бесконечное
, обращающая это уравнение в верное равенство. Заметим, что уравнению (1) может удовлетворять одна пара действительных чисел, несколько и даже бесконечное
множество таких пар. Например, уравнению 
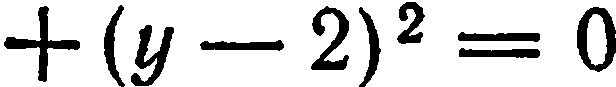 удовлетворяет-единственная пара чисел:
удовлетворяет-единственная пара чисел: 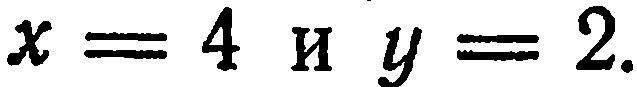 Уравнению
Уравнению 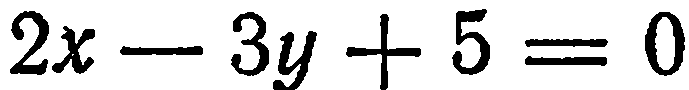 удовлетворяет любая пара чисел
удовлетворяет любая пара чисел 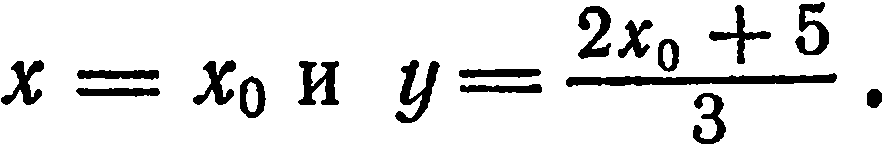
Существуют уравнения вида (1), которым не удовлетворяет ни одна пара действительных чисел. Такими, например, являются уравнения 
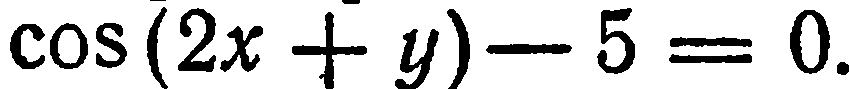
Зададим на плоскости систему координат 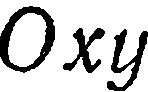 . Если рассматривать множество пар значений переменных
. Если рассматривать множество пар значений переменных 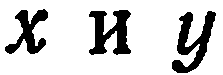 , удовлетворяющих уравнению (1), как координаты точек на плоскости, то изображение этого множества на координатной плоскости дает график уравнения (l), который, вообще говоря, есть некоторая линия
, удовлетворяющих уравнению (1), как координаты точек на плоскости, то изображение этого множества на координатной плоскости дает график уравнения (l), который, вообще говоря, есть некоторая линия 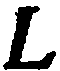 .
.
Таким образом, уравнению с переменными  и
и 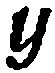 соответствует на плоскости, вообще говоря, некоторая линия, координаты точек которой удовлетворяют данному уравнению. Построение графиков функций можно рассматривать как примеры нахождения линий,
соответствует на плоскости, вообще говоря, некоторая линия, координаты точек которой удовлетворяют данному уравнению. Построение графиков функций можно рассматривать как примеры нахождения линий,
соответствующих данным уравнениям.
Не Менее важной является обратная задача: по
данной на плоскости линии найти соответствующее ей
уравнение.
Определение Уравнением данной линии (в выбранной на плоскости системе координат) называется такое уравнение с переменными  и
и 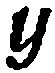 , которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
, которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Рассмотрим конкретный пример. Пусть дана на плоскости окружность с центром в точке 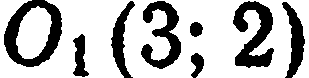 и радиусом, равным 1,5
и радиусом, равным 1,5
(рис. 19). Требуется найти уравнение этой окружности.
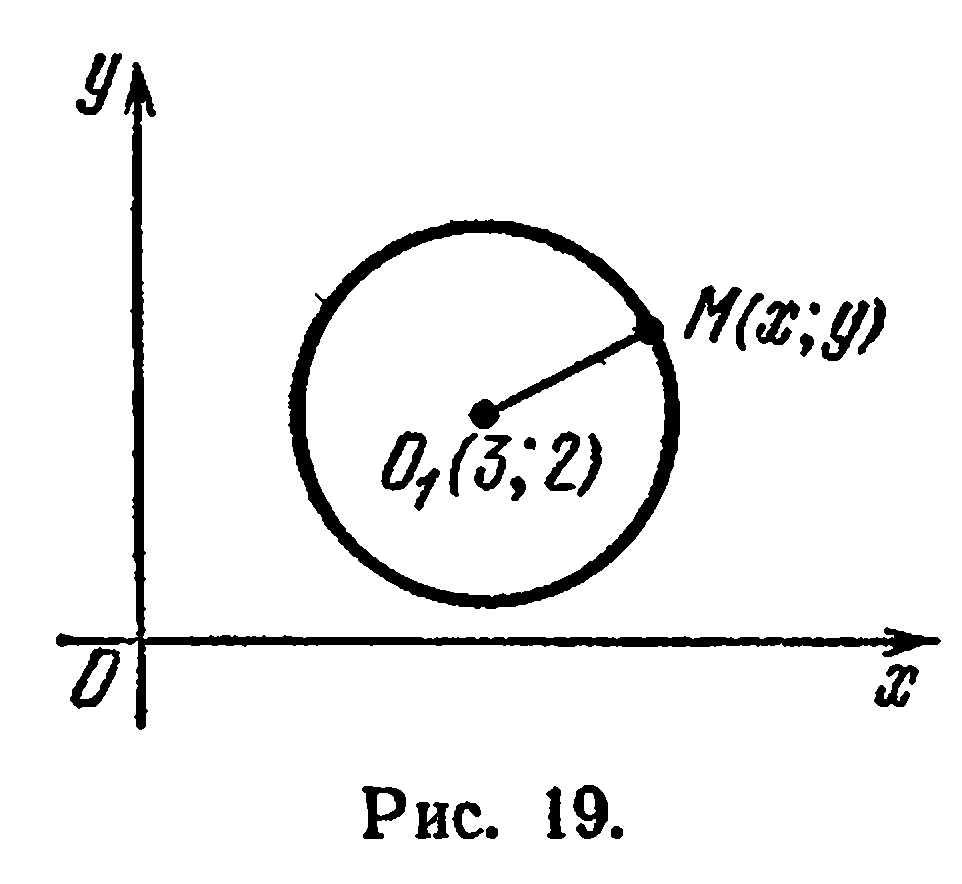
Возьмем на окружности произвольную точку 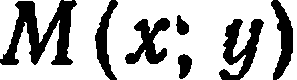 Из определения окружности следует, что
Из определения окружности следует, что 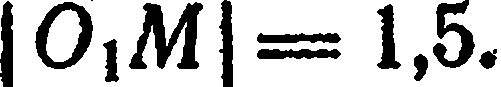
Имеем:
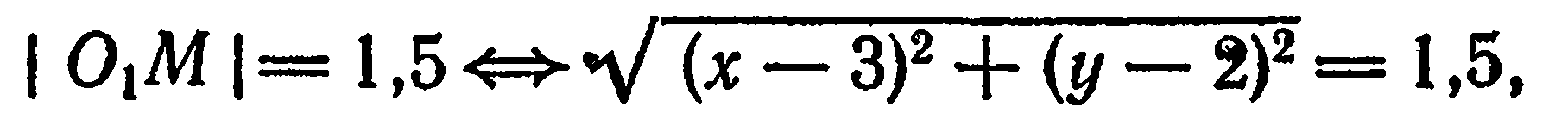
откуда
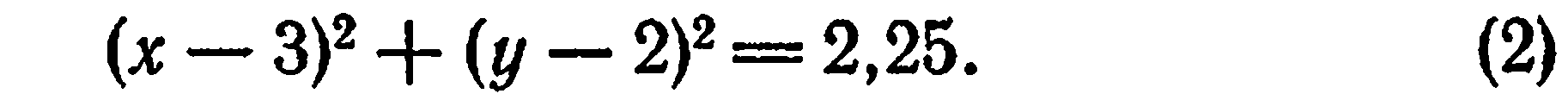
Так как 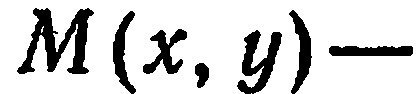 произвольная точка окружности, то координаты любой точки данной окружности удовлетворяют уравнению (2). Нетрудно убедиться в том, что координаты любой точки, не лежащей на данной окружности, не удовлетворяют уравнению (2).
произвольная точка окружности, то координаты любой точки данной окружности удовлетворяют уравнению (2). Нетрудно убедиться в том, что координаты любой точки, не лежащей на данной окружности, не удовлетворяют уравнению (2).
В самом деле, пусть 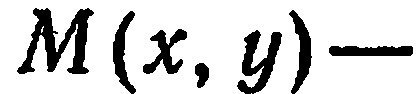 любая точка, не принадлежащая данной окружности. Тогда ее расстояние от
любая точка, не принадлежащая данной окружности. Тогда ее расстояние от 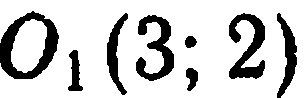 либо больше, либо меньше, чем 1,5, т. е. либо
либо больше, либо меньше, чем 1,5, т. е. либо 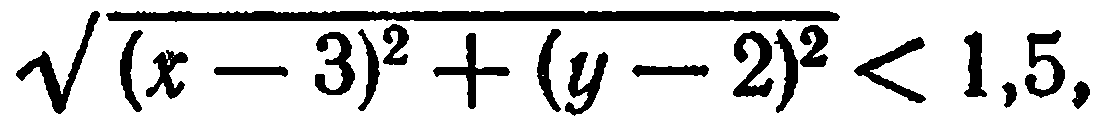
либо 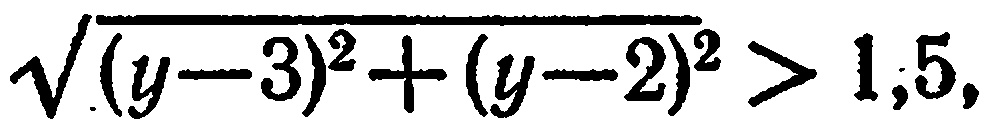 или, что то же, либо
или, что то же, либо 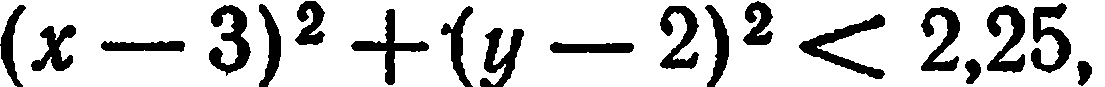 либо
либо 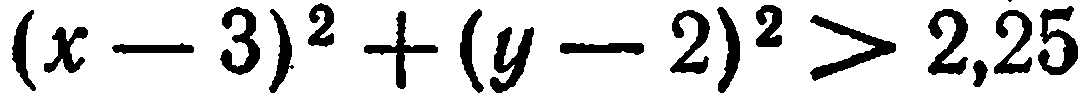 . А это означает, что координаты точек, не принадлежащих данной окружности, не
. А это означает, что координаты точек, не принадлежащих данной окружности, не
удовлетворяют уравнению (2).
Итак, уравнение (2) вполне определяет данную окружность, а поэтому оно называется уравнением этой окружности.
Заметим, что если известно уравнение некоторой линии, то для любой точки плоскости можно решить задачу: лежит она на этой линии или нет. Для этого достаточно подставить в данное уравнение вместо переменных  и
и 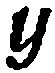 координаты исследуемой точки; если
координаты исследуемой точки; если
координаты удовлетворяют данному уравнению, то точка лежит на линии, если не удовлетворяет, — не лежит.
Пример:
Лежат ли точки 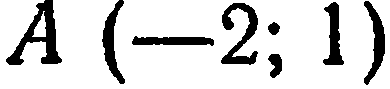 и
и 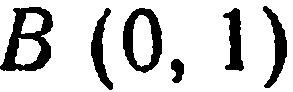 на линии
на линии 
Решение:
Подставив в данное уравнение вместо  и
и 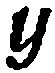 координаты точки
координаты точки 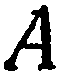 , получим
, получим
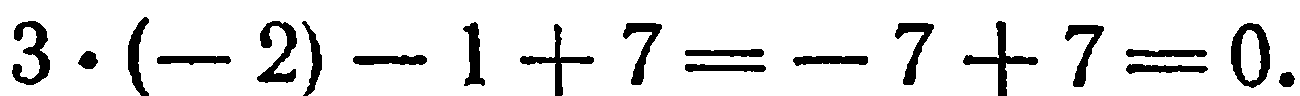
Следовательно, точка 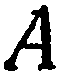 лежит на данной линии. Подставим координаты точки
лежит на данной линии. Подставим координаты точки 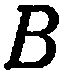 :
:
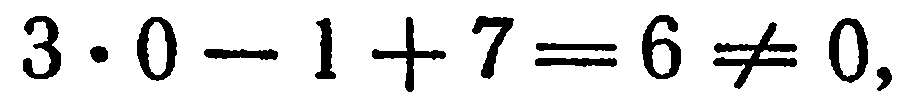
т е. точка 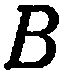 не лежит на данной линии.
не лежит на данной линии.
Уравнение прямой, проходящей через данную точку с заданным нормальным вектором
Пусть в плоскости 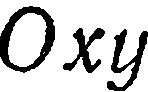 задана некоторая точка
задана некоторая точка 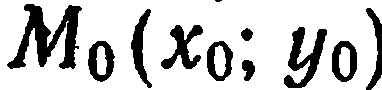 и ненулевой вектор
и ненулевой вектор 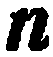 с координатами
с координатами 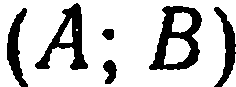 . Требуется составить уравнение прямой
. Требуется составить уравнение прямой 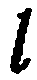 , проходящей через точку
, проходящей через точку 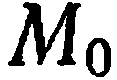 .и перпендикулярной вектору
.и перпендикулярной вектору 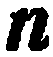 (рис. 20).
(рис. 20).
Определение:
Любой ненулевой вектор 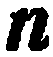 , перпендикулярный прямой
, перпендикулярный прямой 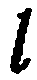 , называется нормальным вектором этой прямой.
, называется нормальным вектором этой прямой.
Очевидно, что через точку Рис. 20. 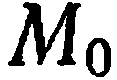 в плоскости
в плоскости 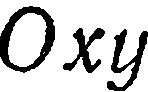 проходит
проходит
единственная прямая 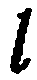 имеющая нормальный вектор
имеющая нормальный вектор 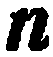 . Возьмем на прямой
. Возьмем на прямой 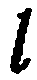 произвольную точку
произвольную точку 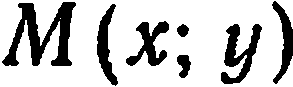 . Ясно, что условие
. Ясно, что условие  эквивалентно условию
эквивалентно условию 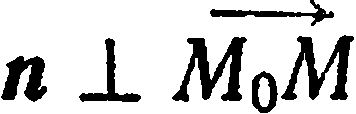 которое в свою очередь эквивалентно
которое в свою очередь эквивалентно

Учитывая, что 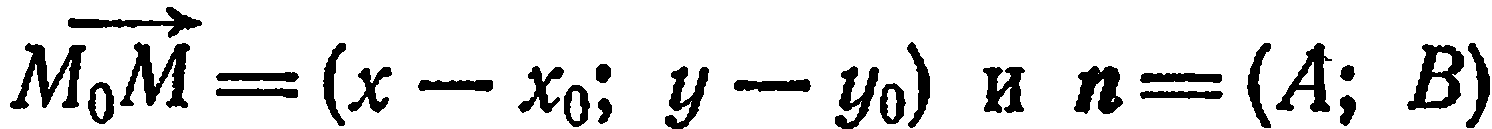 , выразим равенство (1) в координатной форме:
, выразим равенство (1) в координатной форме:
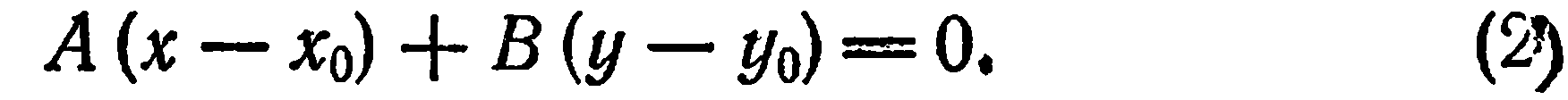
Уравнение (2) называется уравнением прямой, проходящей через точку 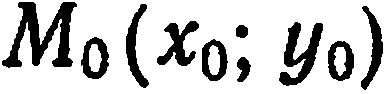 с заданным нормальным вектором
с заданным нормальным вектором 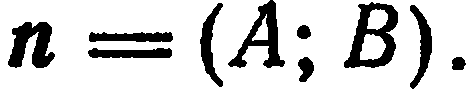
Пример:
Составить уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 
Решение:
Из условия задачи имеем:
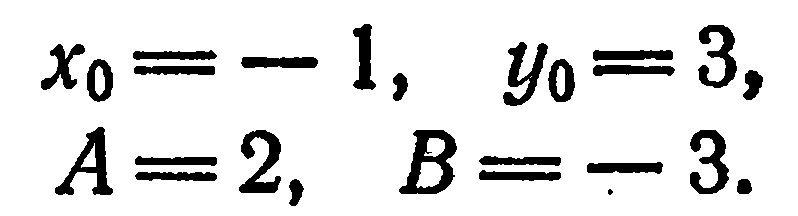
Подставив эти значения уравнение (2), получим:
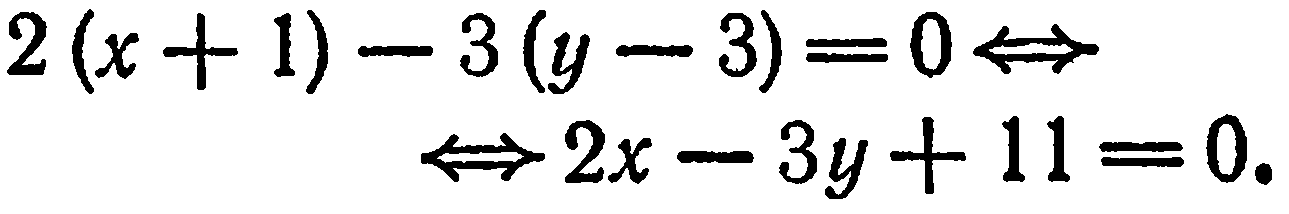
Пример:
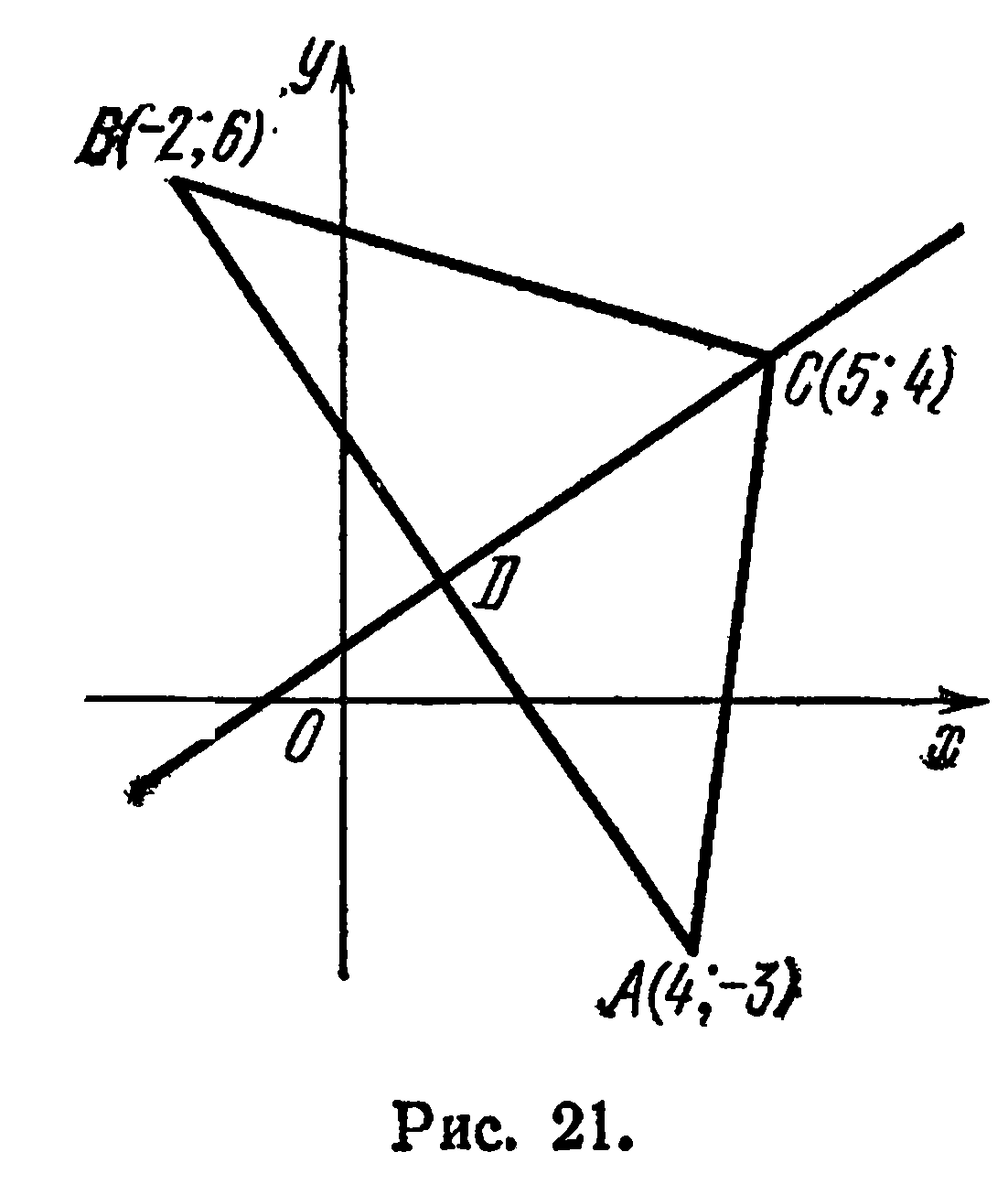
Дан треугольник 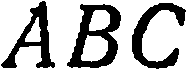 с вершинами
с вершинами 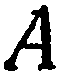
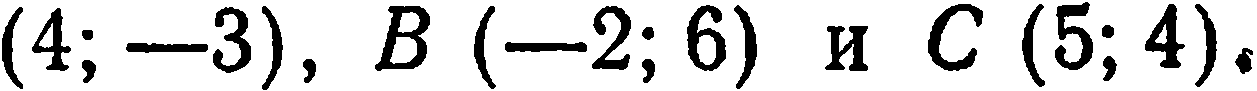 Составить уравнение высоты
Составить уравнение высоты
 (рис. 21).
(рис. 21).
Решение:
Высота  проходит через точку
проходит через точку 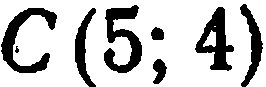 , поэтому можно положить
, поэтому можно положить 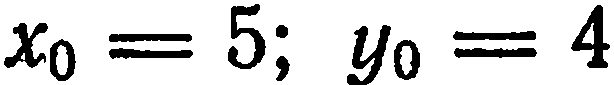 . За нормальный вектор прямой
. За нормальный вектор прямой  можно взять вектор
можно взять вектор 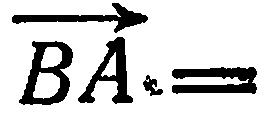
 . Следовательно, искомое уравнение имеет вид
. Следовательно, искомое уравнение имеет вид  , или
, или 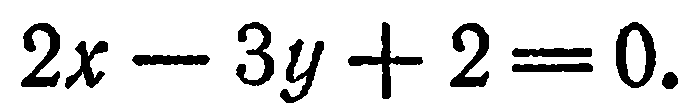
Общее уравнение прямой и его частные случаи
В предыдущем параграфе мы показали, что если на плоскости задана одна фиксированная точка 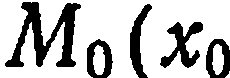 ;
;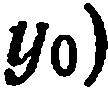 и нормальный вектор
и нормальный вектор 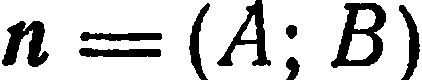 произвольной прямой
произвольной прямой  , то уравнение этой прямой имеет вид
, то уравнение этой прямой имеет вид
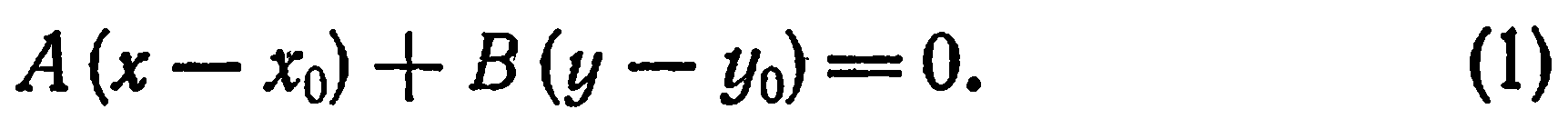
Так как нормальный вектор 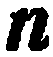 отличен от нуля, то хотя бы одно из чисел
отличен от нуля, то хотя бы одно из чисел 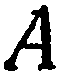 и
и 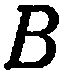 отлично от нуля. А это значит, что уравнение (1) является уравнением первой степени.
отлично от нуля. А это значит, что уравнение (1) является уравнением первой степени.
Таким образом, всякая прямая в прямоугольной системе координат определяется уравнением первой степени относительно переменных  и
и 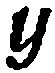 .
.
Теперь покажем обратное: всякое уравнение первой
степени

в прямоугольной системе координат определяет прямую и притом единственную.
Так как (2) —уравнение первой степени, то по крайней мере хотя бы один из коэффициентов 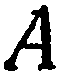 или
или 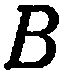 отличен от нуля. Допустим, для определенности, что
отличен от нуля. Допустим, для определенности, что 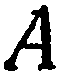
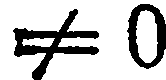 Тогда уравнение (2) можно представить в виде
Тогда уравнение (2) можно представить в виде
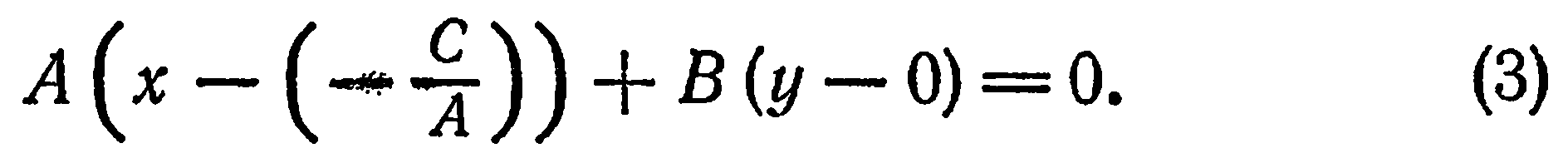
Уравнение (3) имеет вид уравнения (1) и, следовательно, определяет единственную прямую, проходящую через точку 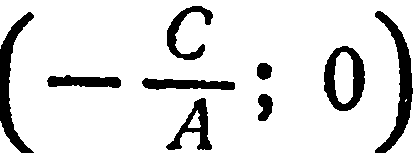 и перпендикулярную вектору
и перпендикулярную вектору 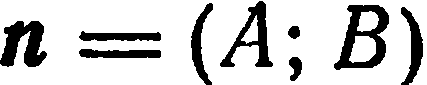 . Но тогда и уравнение (2), равносильное уравнению (3), определяет прямую. Уравнение (2)
. Но тогда и уравнение (2), равносильное уравнению (3), определяет прямую. Уравнение (2)
называется общим уравнением прямой.
В общем уравнении прямой 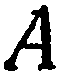 ,
, 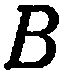 и
и  могут принимать различные действительные значения, исключая одновременное равенство нулю
могут принимать различные действительные значения, исключая одновременное равенство нулю 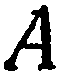 и
и 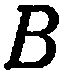 . Рассмотрим некоторые частные случаи уравнения (2), получающиеся при равенстве нулю отдельных его коэффициентов.
. Рассмотрим некоторые частные случаи уравнения (2), получающиеся при равенстве нулю отдельных его коэффициентов.
1. Пусть в уравнении (2)  ; тогда
; тогда

Положив 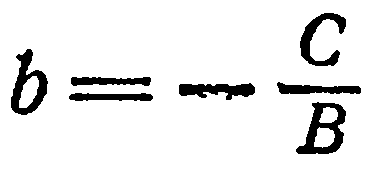 , получим
, получим

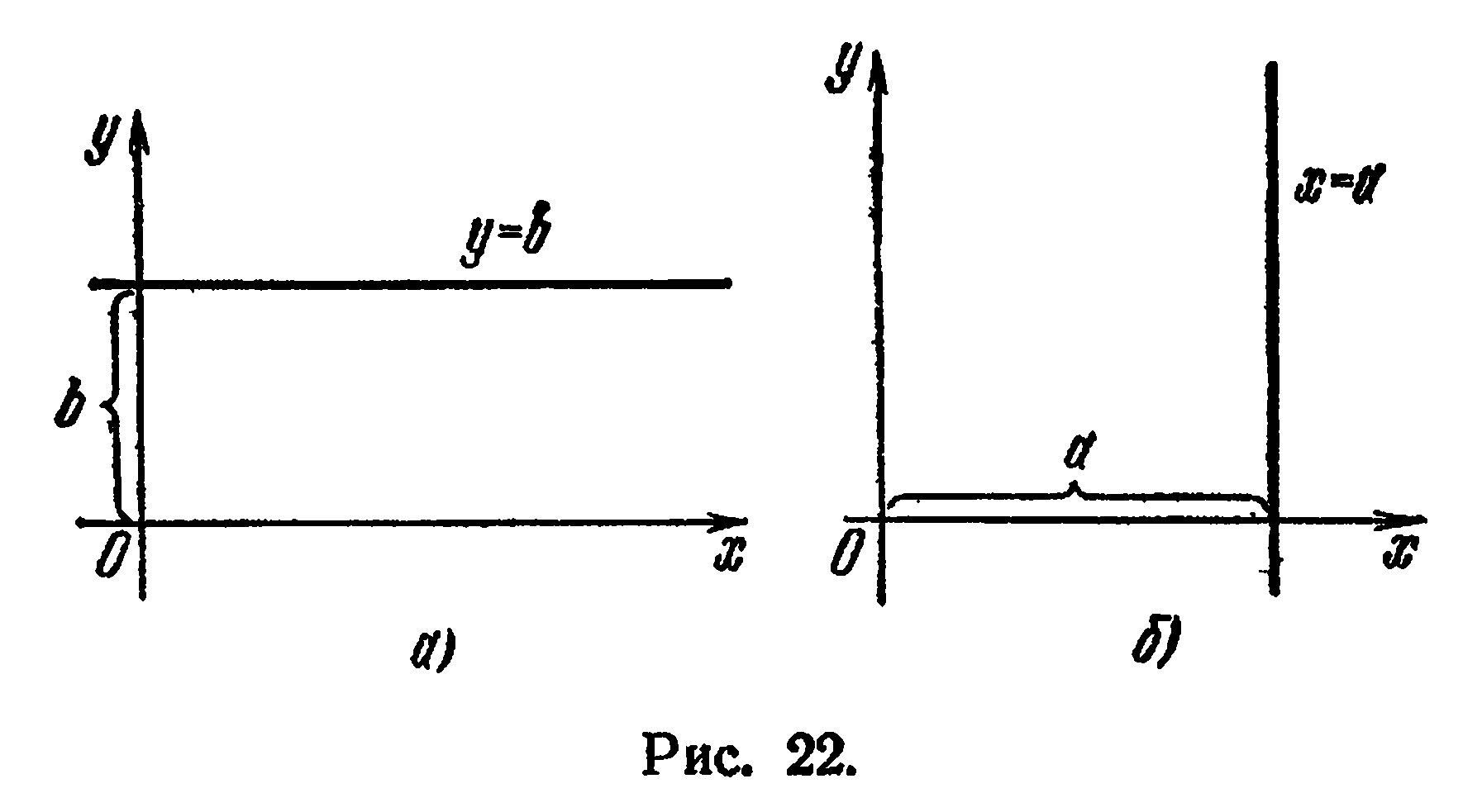
Уравнение (4) определяет прямую, все точки которой имеют одну и туже ординату, равную 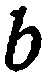 . Следовательно, прямая параллельна оси
. Следовательно, прямая параллельна оси  (рис. 22, а).
(рис. 22, а).
Если, кроме того, 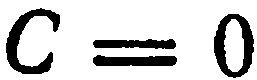 , уравнение (4) примет вид
, уравнение (4) примет вид

Уравнение (5) определяет прямую, все точки которой имеют ординату, равную нулю. Следовательно, прямая совпадает с осью  .
.
1. Пусть  ; тогда уравнение (2) примет вид
; тогда уравнение (2) примет вид  , или
, или
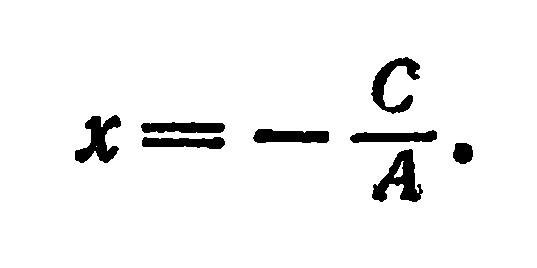
Положив 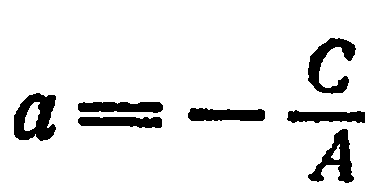 , получаем
, получаем

Уравнение (6) определяет прямую, все точки которой имеют одну и ту же абсциссу, равную 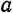 . Следовательно, прямая параллельна оси
. Следовательно, прямая параллельна оси  (рис. 22, б).
(рис. 22, б).
Если, кроме того,  то уравнение (6) примет вид
то уравнение (6) примет вид

Уравнение (7) определяет прямую, все точки которой имеют абсциссу, равную нулю, Следовательно, прямая совпадает с осью ординат.
3. Пусть в уравнении 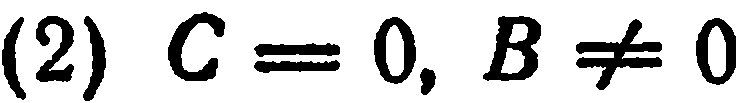 ; тогда
; тогда

Положив

получим

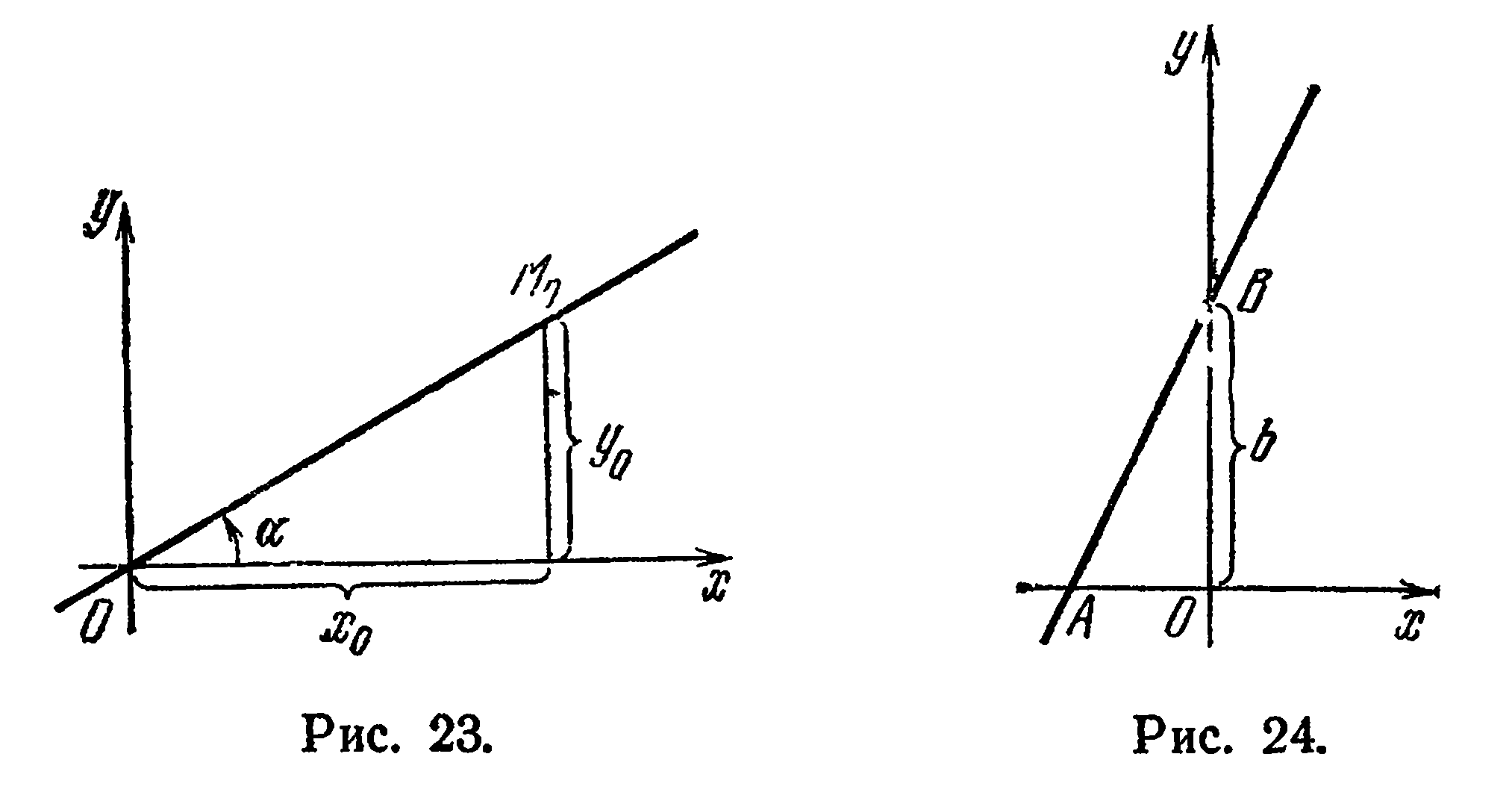
Уравнению (9) удовлетворяют координаты точки 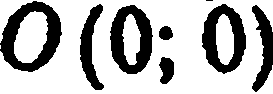 ; следовательно, прямая, определяемая этим уравнением, проходит через начало координат. Возьмем на этой прямой произвольную точку
; следовательно, прямая, определяемая этим уравнением, проходит через начало координат. Возьмем на этой прямой произвольную точку 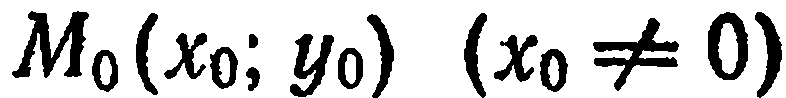 (рис. 23). Тогда
(рис. 23). Тогда 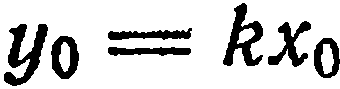 , откуда
, откуда 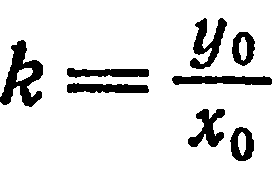 .
.
Из рис. 23 видно что 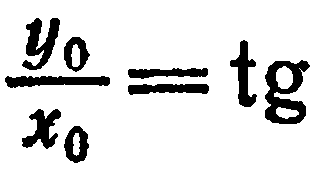 следовательно,
следовательно,

Определение:
Тангенс угла наклона прямой к положительному направлению оси  называется угловым коэффициентом прямой и обозначается буквой
называется угловым коэффициентом прямой и обозначается буквой 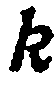 .
.
Угловой коэффициент прямой можно вычислить по одной из формул (8) или (10).
4. Пусть 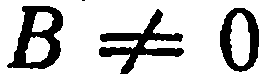 ; тогда уравнение (2) можно преобразовать следующим образом:
; тогда уравнение (2) можно преобразовать следующим образом:
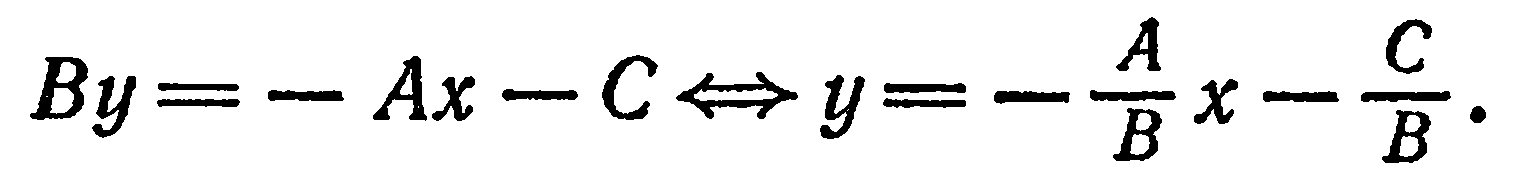
Учитывая, что 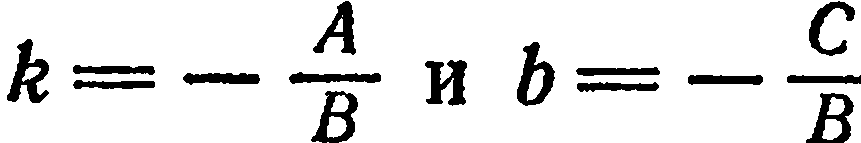 получим
получим

Очевидно, что если  , то
, то  ; следовательно, прямая, определяемая уравнением (11), пересекает ось
; следовательно, прямая, определяемая уравнением (11), пересекает ось  в точке
в точке 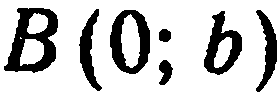
(рис. 24). Число 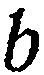 называется начальной ординатой прямой, а уравнение (11) — уравнением прямой с угловым коэффициентом и начальной ординатой.
называется начальной ординатой прямой, а уравнение (11) — уравнением прямой с угловым коэффициентом и начальной ординатой.
Пример:
Построить прямую  .
.
Решение:
Для построения прямой достаточно построить две ее точки. Проще всего найти точки переселения прямой с осями координат, если, конечно, они существуют и помещаются на чертеже. Положив в данном уравнении  , получим:
, получим:
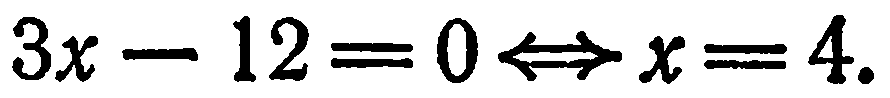
Следовательно, точка пересечения данной прямой с осью  имеет координаты (4; 0).
имеет координаты (4; 0).
Положив в том же уравнении 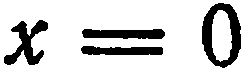 , найдем
, найдем  , т. е. координаты точки пересечения прямой с осью
, т. е. координаты точки пересечения прямой с осью  будут (0;3).
будут (0;3).
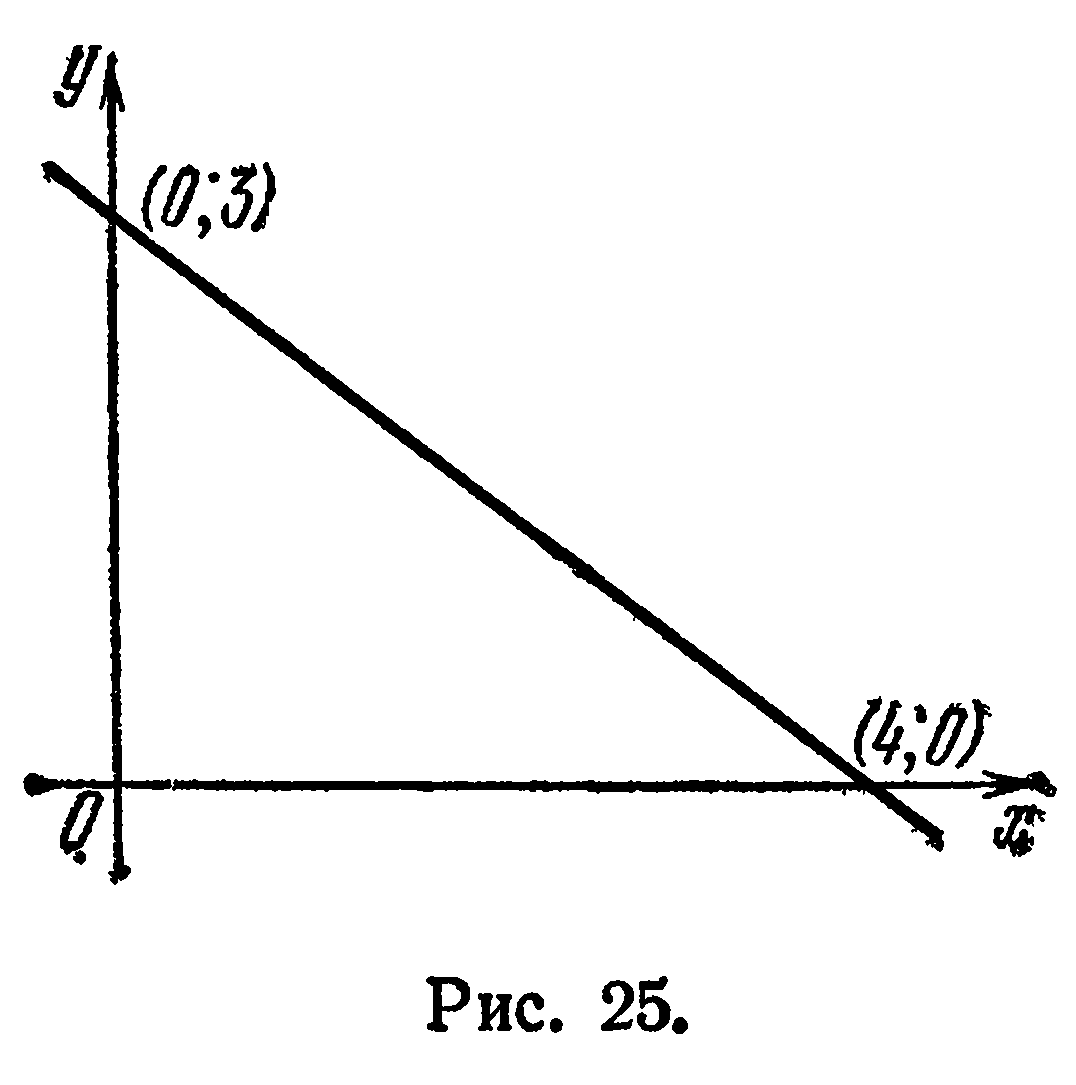
Строим найденные точки и проводим через них прямую (рис. 25).
Пример:
Найти угловой коэффициент и начальную ординату прямой 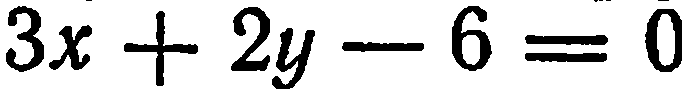 .
.
Решение:
Угловой коэффициент находим по формуле 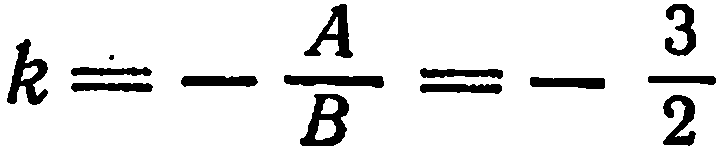 , а начальную ординату — по формуле
, а начальную ординату — по формуле 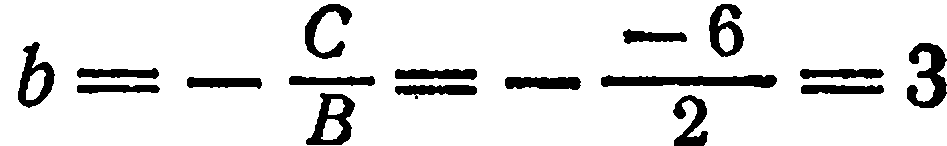
Угловой коэффициент и начальную ординату можно найти и другим путем.
Преобразуем данное уравнение к виду 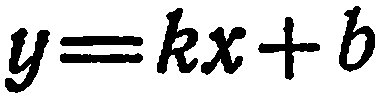 для этого решаем
для этого решаем
его«.относительно 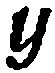 :
: 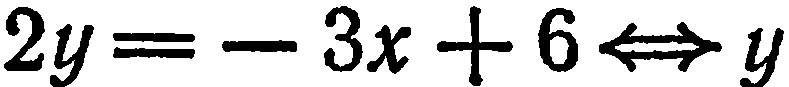
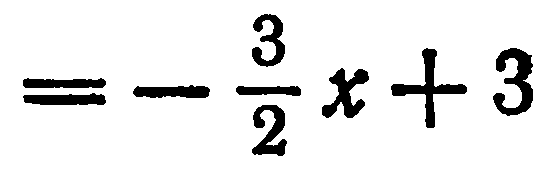 .
.
Сравнивая полученное уравнение с уравнением 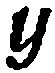
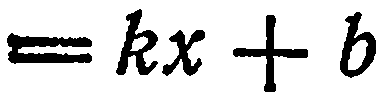 находим:
находим: 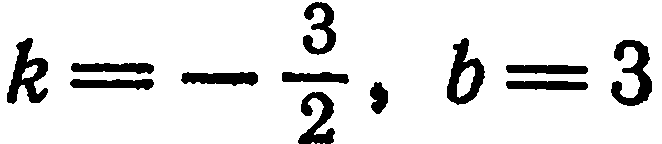
Другие формы уравнения прямой на плоскости
В этом параграфе мы познакомимся с некоторыми другими формами уравнения прямой на плоскости.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть даны точка 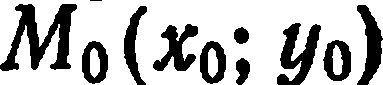 и угловой коэффициент
и угловой коэффициент 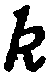 прямой, проходящей через точку
прямой, проходящей через точку 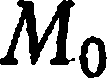 : требуется составить уравнение этой прямой.
: требуется составить уравнение этой прямой.
Запишем уравнение искомой прямой в виде
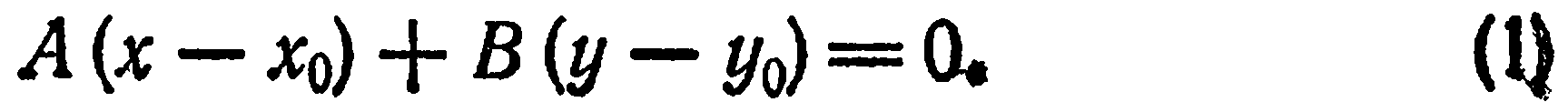
В этом уравнении координаты  и
и 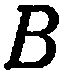 нормального вектора
нормального вектора 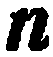 нам неизвестны, поэтому постараемся их исключить. Для этого разделим уравнение (1) на
нам неизвестны, поэтому постараемся их исключить. Для этого разделим уравнение (1) на 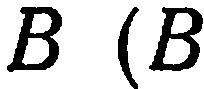
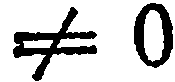 в противном случае
в противном случае 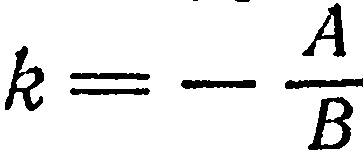 не существует ):
не существует ):
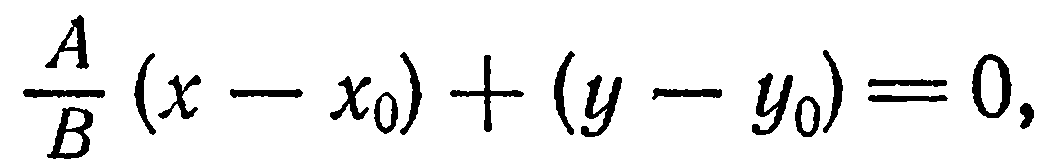
откуда
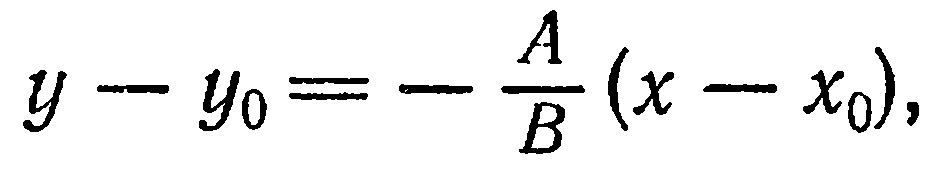
или
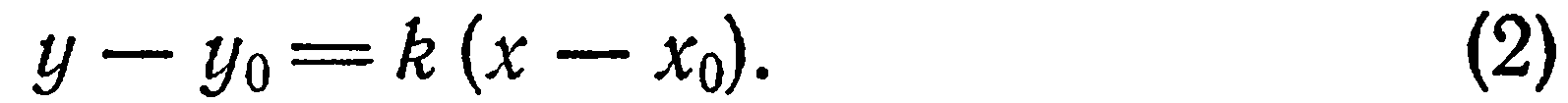
Уравнение (2) называется уравнением прямой, проходящей через данную точку в данном направлении.
Пример:
Составить уравнение прямой, проходящей через точку  и образующей с положительным направлением оси
и образующей с положительным направлением оси  угол
угол 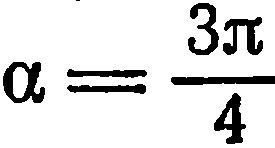 .
.
Решение:
Находим угловой коэффициент 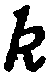 искомой прямой:
искомой прямой:
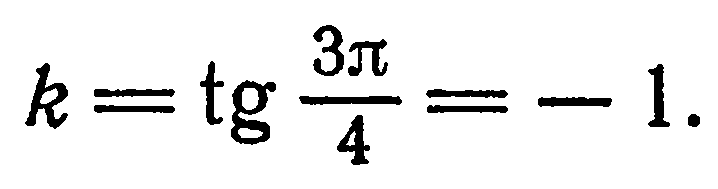
Заменив в формуле (2)  и
и 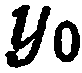 координатами точки
координатами точки 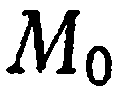 и
и 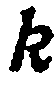 его найденным значением, получим:
его найденным значением, получим: 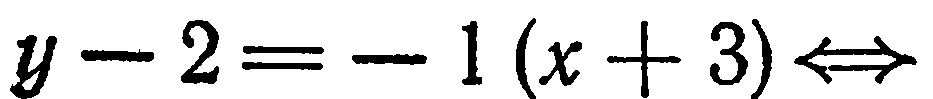
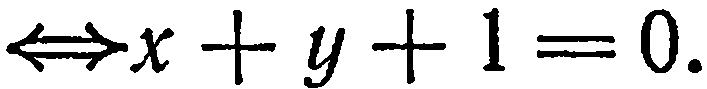
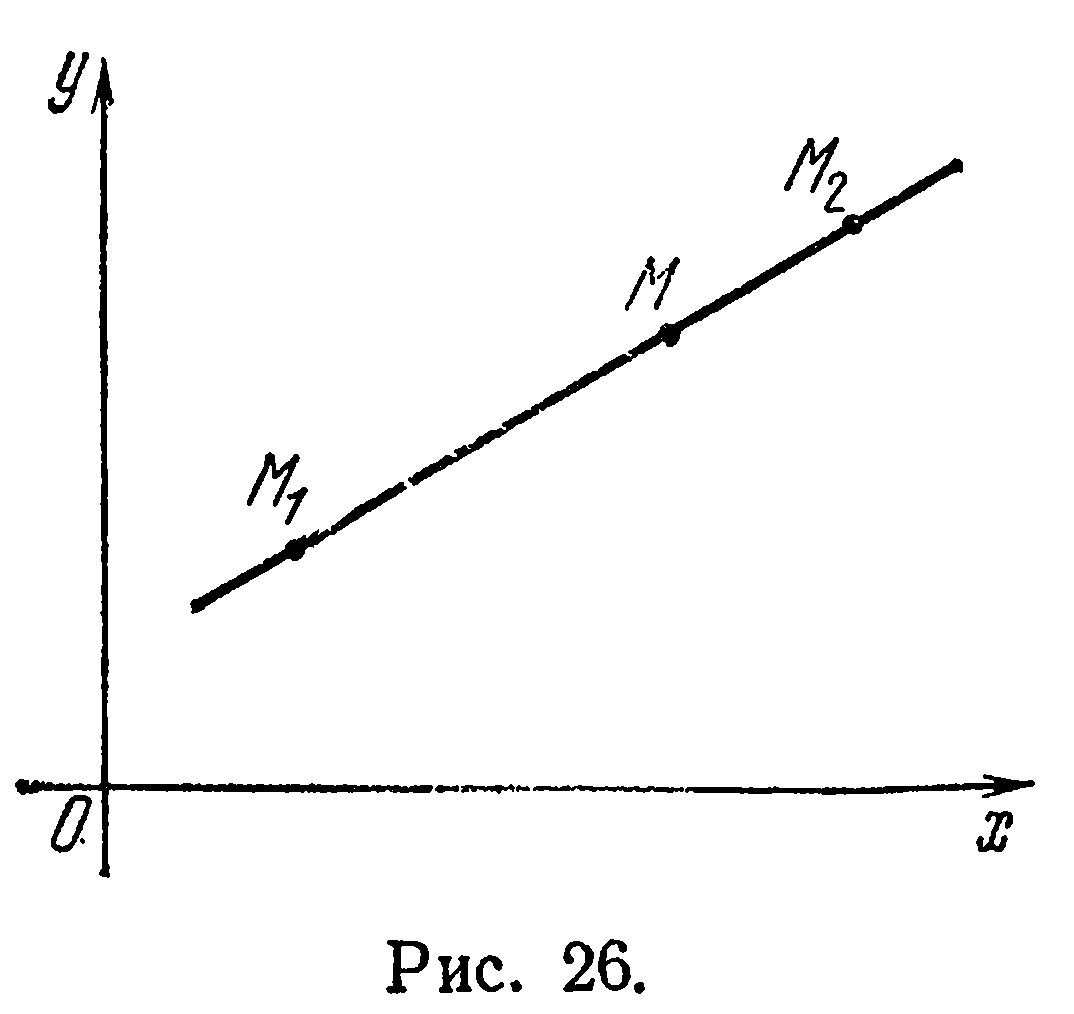
Уравнение прямой, проходящей через две данные точки
Пусть даны две различные точки 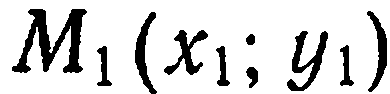 и
и 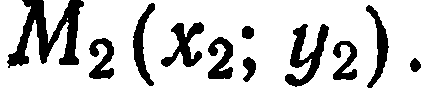 Требуется составить уравнение прямой, проводящей через эти точки. Возьмем произвольную точку
Требуется составить уравнение прямой, проводящей через эти точки. Возьмем произвольную точку 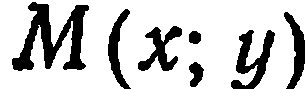 на этой прямой (рис. 26). Рассмотрим векторы
на этой прямой (рис. 26). Рассмотрим векторы 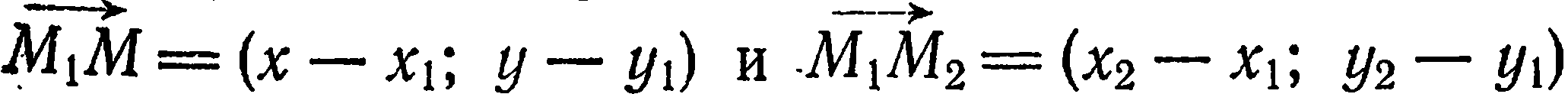 Так
Так
как точки 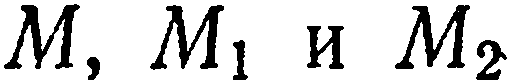 лежат на одной прямой, то эти векторы коллинеарны и, следовательно, их координаты пропорциональны:
лежат на одной прямой, то эти векторы коллинеарны и, следовательно, их координаты пропорциональны:
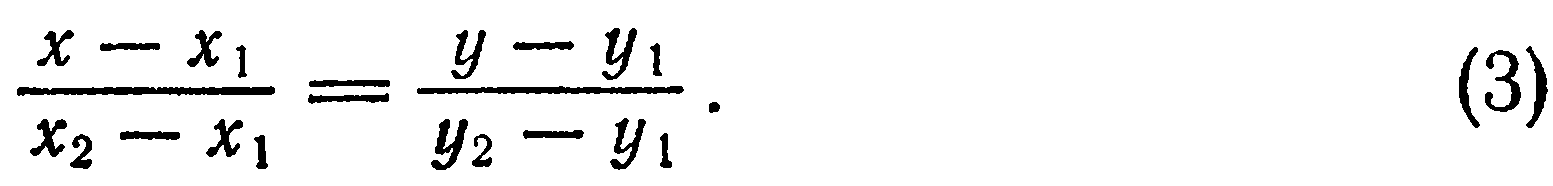
Уравнение (3) называется уравнением прямой, проходящей через две данные точки.
Очевидно, что если  или
или 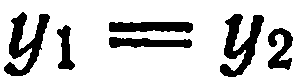 то уравнение (3) теряет смысл. В первом случае прямая параллельна оси
то уравнение (3) теряет смысл. В первом случае прямая параллельна оси  и ее уравнение имеет вид
и ее уравнение имеет вид  Во втором случае прямая параллельна оси
Во втором случае прямая параллельна оси  и имеет уравнение
и имеет уравнение 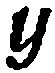

Пример:
Даны координаты вершин треугольника 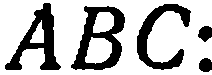
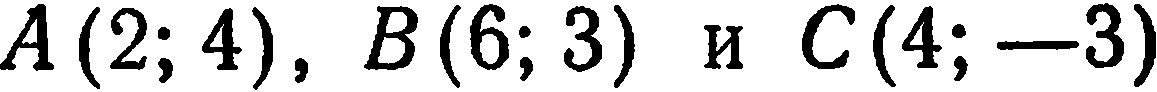 . Составить уравнение
. Составить уравнение
медианы 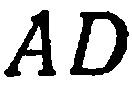 (рис.27).
(рис.27).
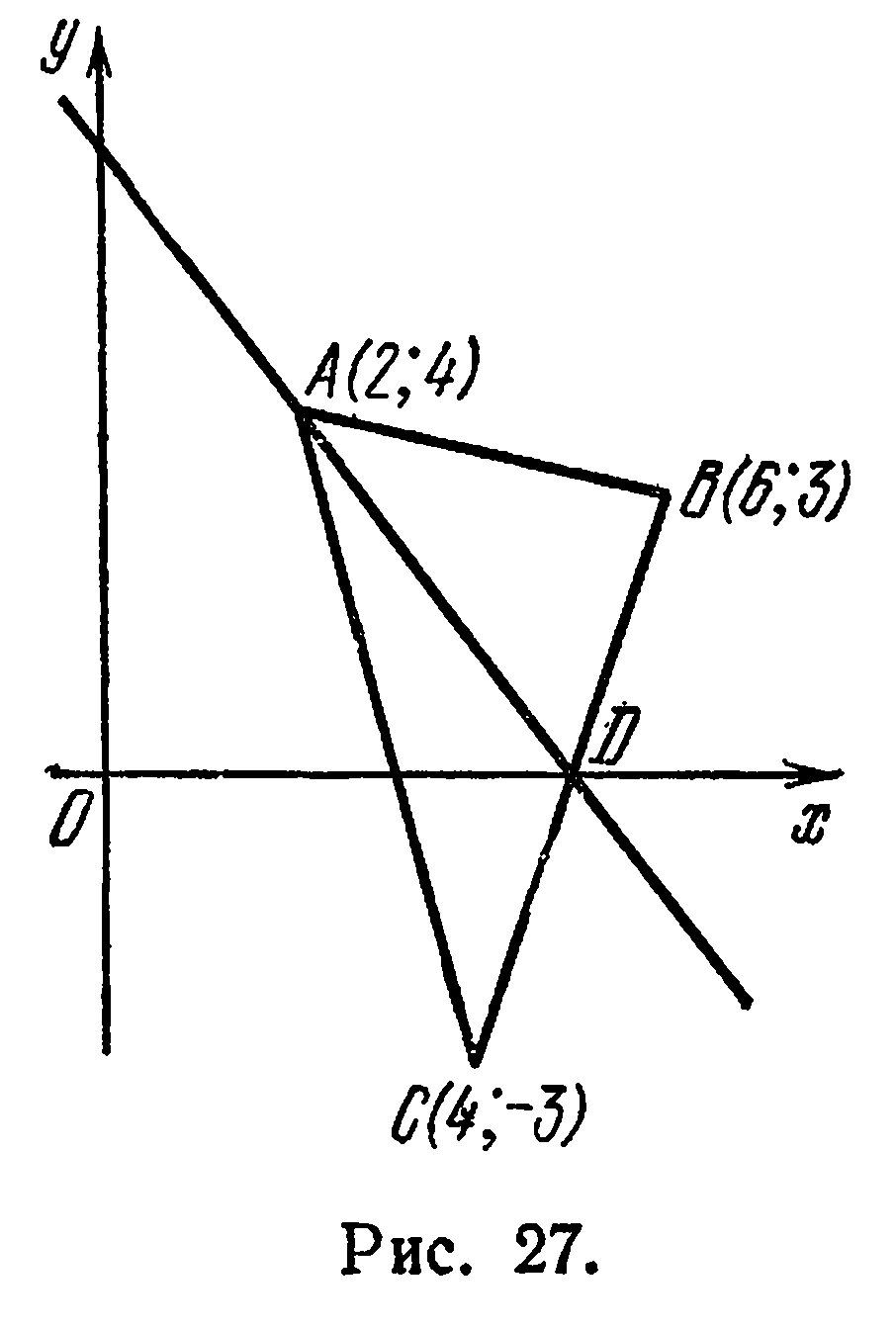
Решение:
Координаты точки  (середины
(середины 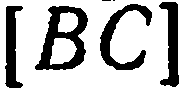 ) находим по
) находим по
формулам (5) § 3:
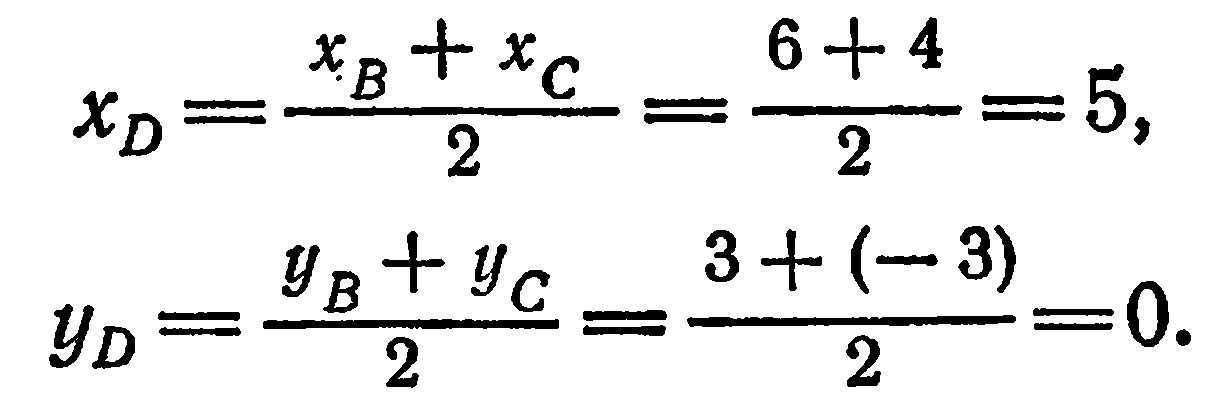
Подставив в уравнение (3) вместо 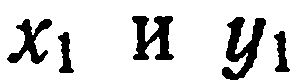 координаты
координаты
точки 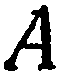 , а вместо
, а вместо  координаты точки
координаты точки  , получим:
, получим:
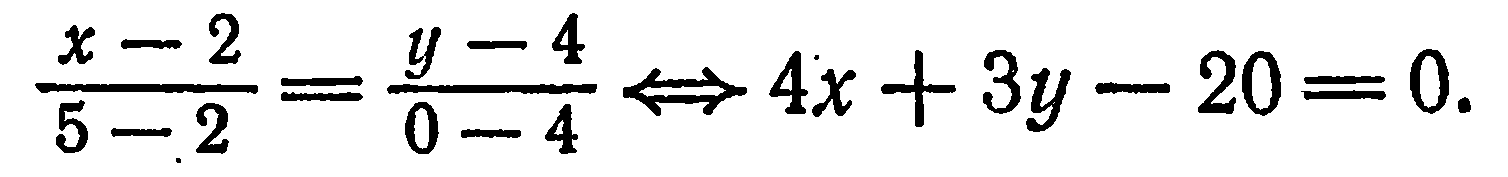
Уравнение прямой в отрезках
Пусть требуется составить уравнение прямой 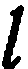 , отсекающей на оси
, отсекающей на оси 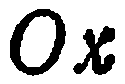
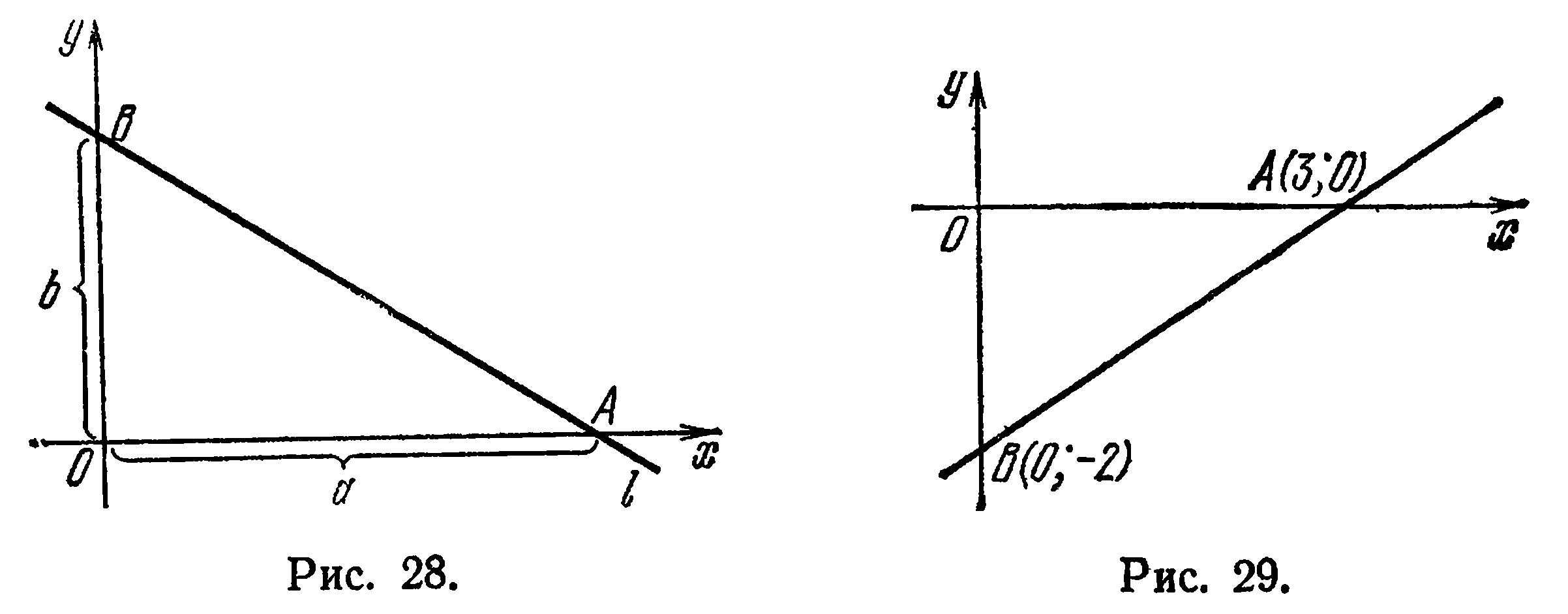
отрезок величины 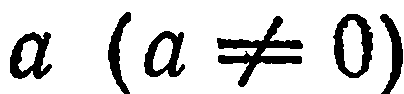 , а на оси
, а на оси  — отрезок величины
— отрезок величины 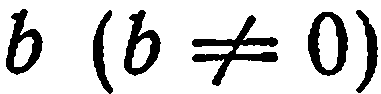 (рис. 28). Обозначим точки пересечения прямой
(рис. 28). Обозначим точки пересечения прямой 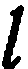 с осями координат
с осями координат  соответственно через
соответственно через 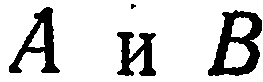 . Тогда точка
. Тогда точка 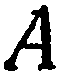 имеет координаты
имеет координаты 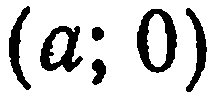 , а точка
, а точка 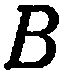 — координаты
— координаты 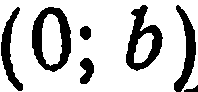 . Составим уравнение прямой
. Составим уравнение прямой 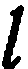 как прямой, проходящей через две
как прямой, проходящей через две
точки 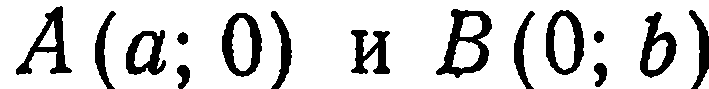 . Заменив в (3)
. Заменив в (3) 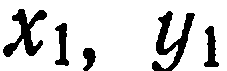 координатами
координатами
точки 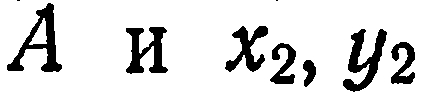 координатами точки
координатами точки 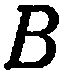 , получим
, получим
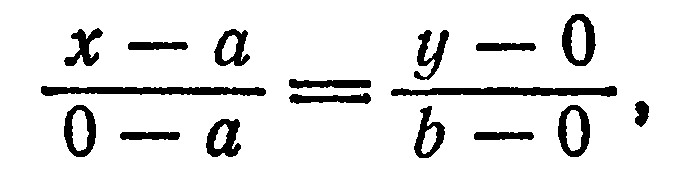
откуда

Уравнение (4) называется уравнением прямой в отрезках (оно связывает текущие координаты  отрезки
отрезки 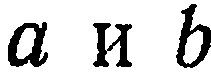 отсекаемые прямой на осях координат).
отсекаемые прямой на осях координат).
Пример:
Построить прямую 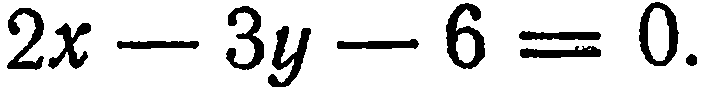
Решение:
Преобразуем данное уравнение к виду (4); для этого перенесем свободный член вправо и разделим обе части на него:
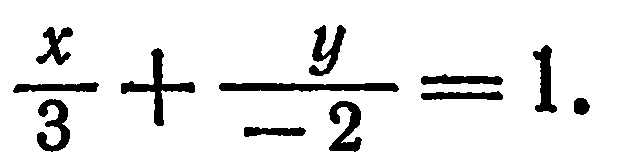
Сравнивая полученное уравнение с уравнением (4), найдем 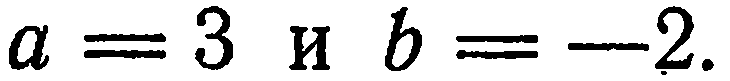 Отложим на оси
Отложим на оси 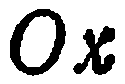 отрезок
отрезок 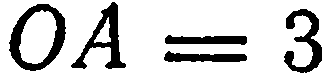 и на оси
и на оси  отрезок
отрезок 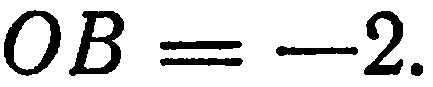 Прямая, проведенная через точки
Прямая, проведенная через точки 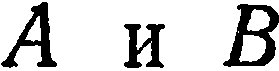 , будет искомой (рис. 29)
, будет искомой (рис. 29)
Пересечение двух прямых
Пусть даны прямые:
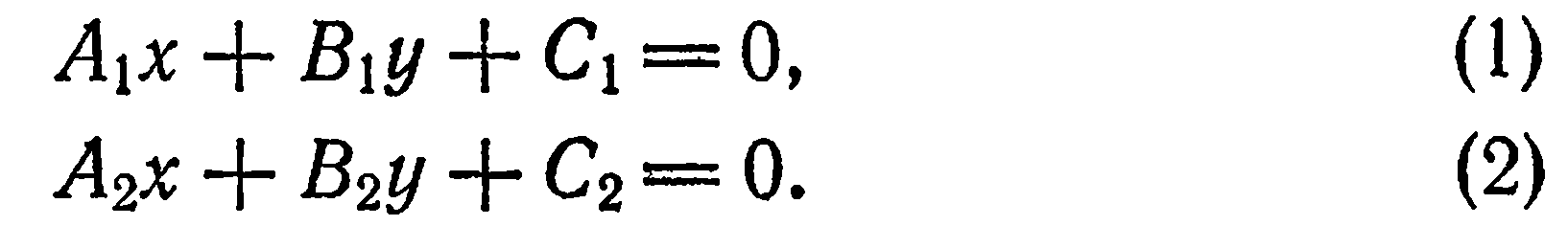
Если данные прямые пересекаются, то координаты их общей точки удовлетворяют каждому из уравнений (1) и (2) (точка пересечения принадлежит как уравнению (1), так и уравнению (2)). Это значит, что координаты точки пересечения данных прямых представляют собой
общее решение уравнений (1) и (2). Справедливо и обратное: чтобы найти координаты точки пересечения прямых (1) и (2), нужно найти общие решения этих уравнений, а для этого нужно решить систему
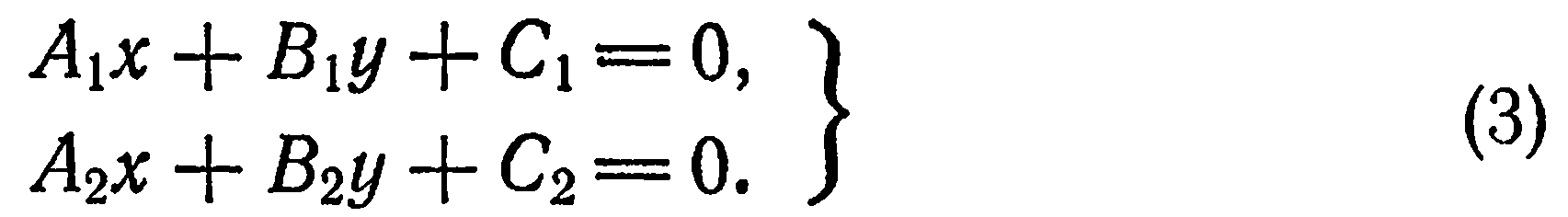
Замечание:
Если случится, что система (3) не имеет решений, то прямые, заданные этими уравнениями, не имеют общей точки, т. е. они параллельны. Если же система (3) имеет бесконечное множество решений, то прямые имеют бесконечное множество общих точек,
т. е. они совпадают.
Пример:
Найти точку пересечения прямых 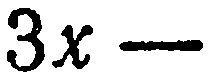
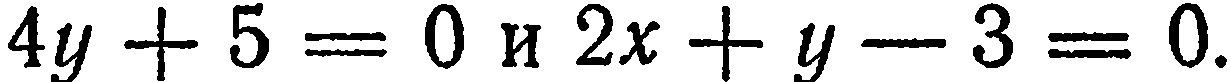
Решение:
Решив систему
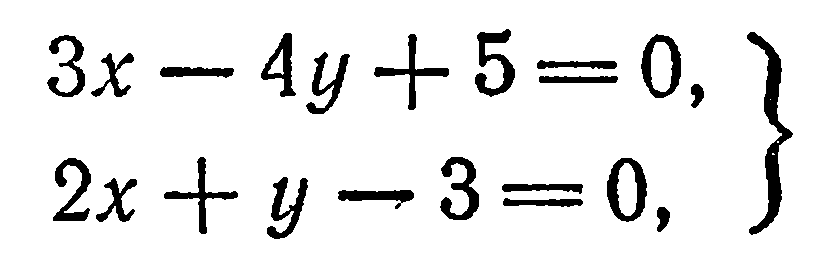
найдем 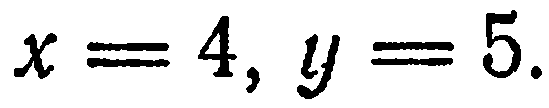 Следовательно, искомая точка есть (4; 5).
Следовательно, искомая точка есть (4; 5).
Угол между двумя прямыми
Пусть требуется определить угол между прямыми  , заданными в плоскости
, заданными в плоскости  уравнениями.
уравнениями.
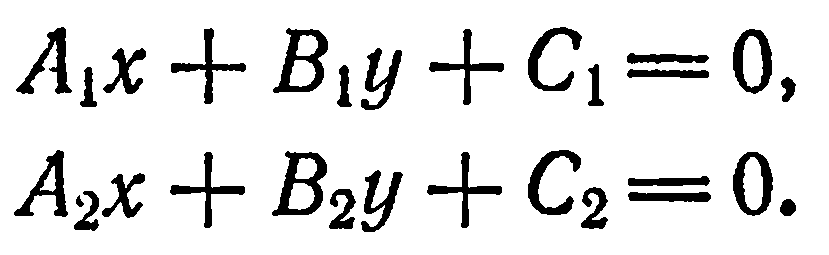
Очевидно, что 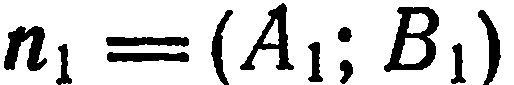 является нормальным вектором прямой
является нормальным вектором прямой 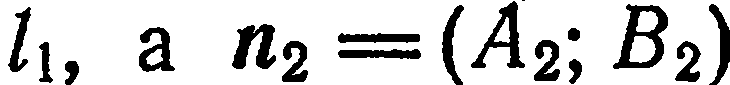 —нормальным вектором прямой
—нормальным вектором прямой 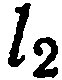 . Кроме этого, угол
. Кроме этого, угол  между нормальными векторами
между нормальными векторами 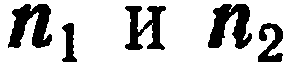 равен одному из углов, образованных прямыми
равен одному из углов, образованных прямыми 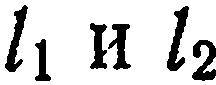 (рис. 30, а):
(рис. 30, а):
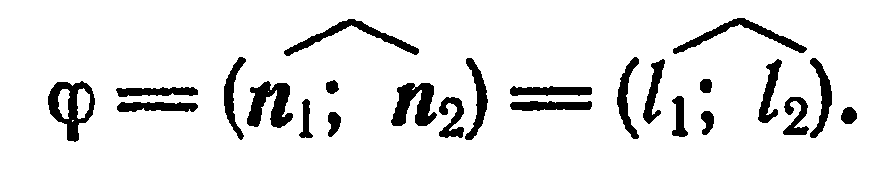
Но
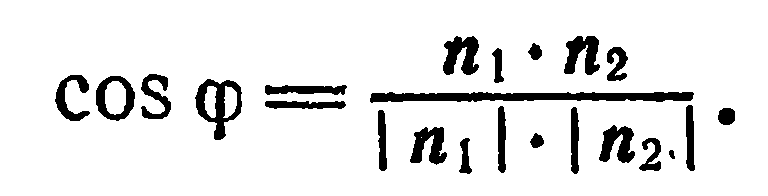
Записав правую часть последнего равенства в координатной форме, получаем
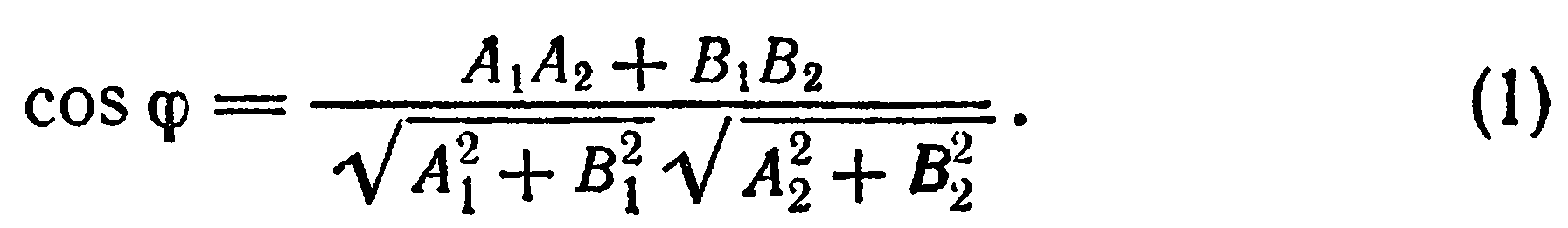
Формула (1) служит для определения угла между двумя прямыми, заданными их общими уравнениями.
Пример 1. Найти угол между прямыми


Решение:
По формуле (1) находим:
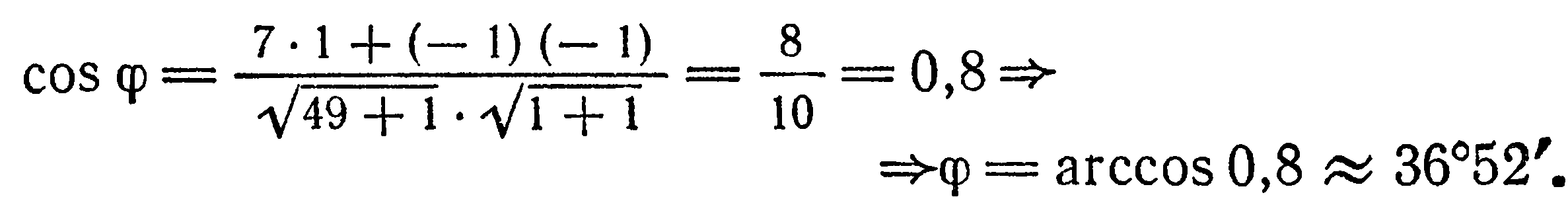
Если прямые 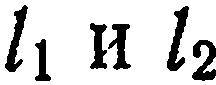 заданы соответственно уравнениями
заданы соответственно уравнениями

то угол  , на который, нужно повернуть прямую
, на который, нужно повернуть прямую 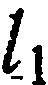 в положительном направлении до совпадения с прямой
в положительном направлении до совпадения с прямой 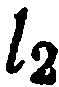
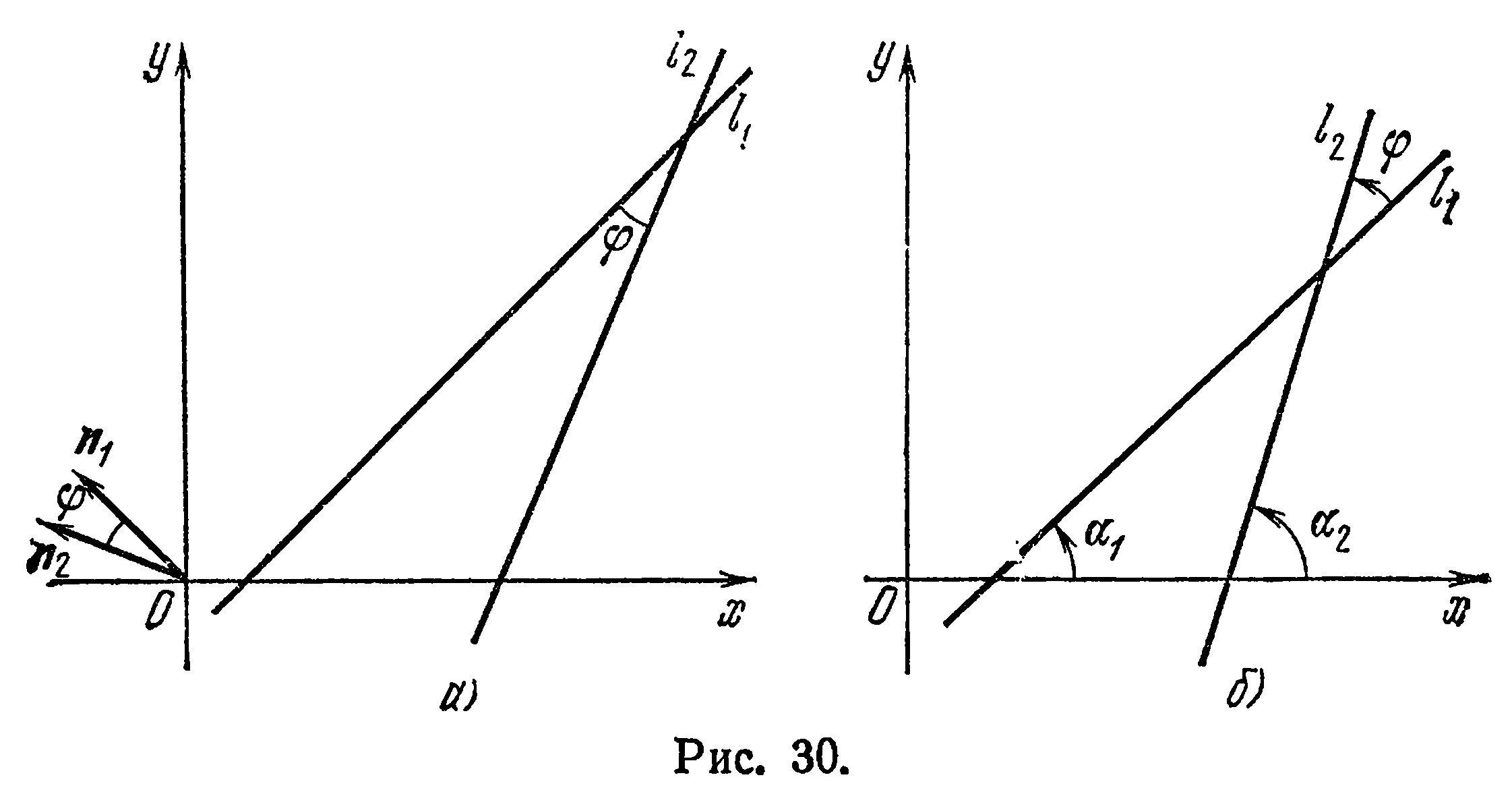
можно вычислить через угловые коэффициенты 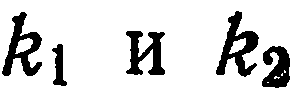 этих прямых. Из рис. 30. б видно, что
этих прямых. Из рис. 30. б видно, что 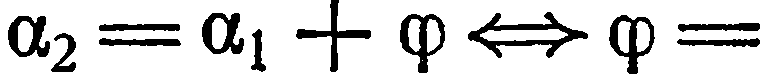

Если прямые 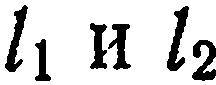 не перпендикулярны, т. е. имеет смысл
не перпендикулярны, т. е. имеет смысл 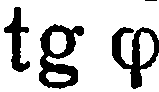 , то
, то
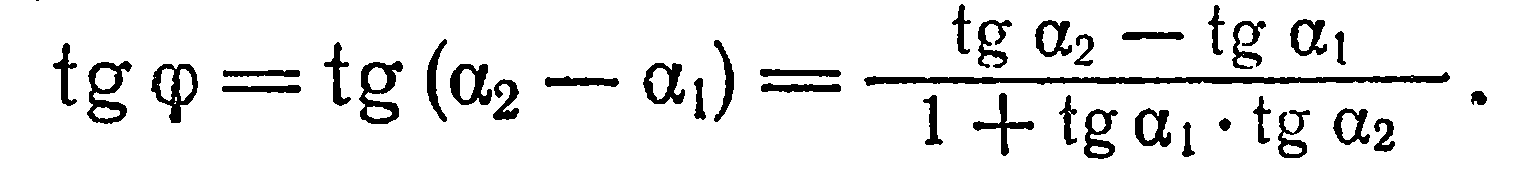
Но 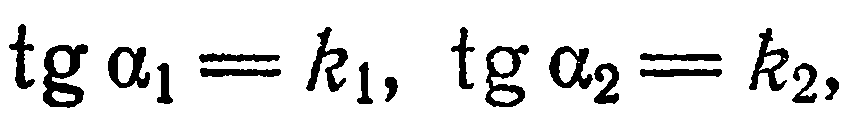 поэтому
поэтому 
Условие параллельности прямых. Если прямые 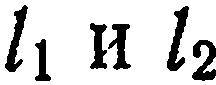 параллельны между собой, то их нормальные векторы
параллельны между собой, то их нормальные векторы 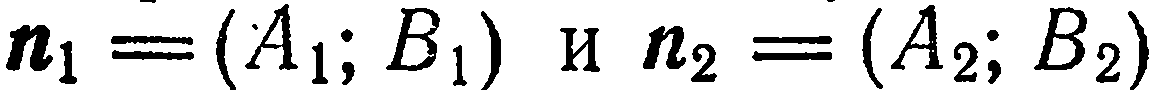 коллинеарны. Считая, что ни одна из прямых не коллинеарна осям координат, запишем условие коллинеарности векторов
коллинеарны. Считая, что ни одна из прямых не коллинеарна осям координат, запишем условие коллинеарности векторов 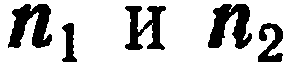 в
в
координатной форме:
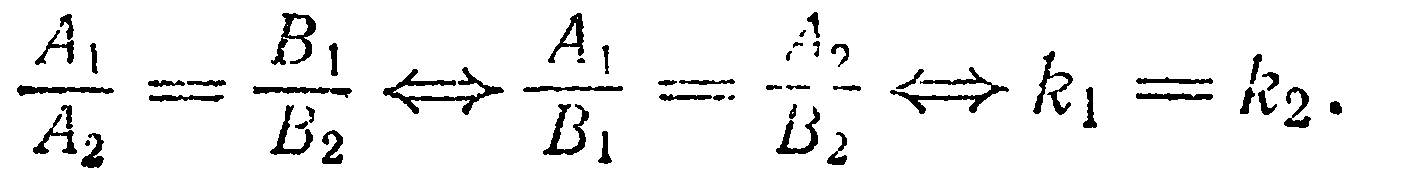
К этому же выводу можно прийти из геометрических соображений. Если  (рис. 31). Следовательно,
(рис. 31). Следовательно,  (при условии, что
(при условии, что 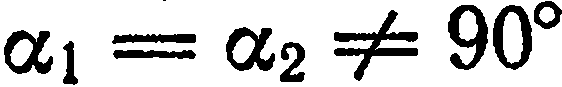 ), или
), или  . Обратно, если
. Обратно, если  то числитель дроби равенства (2) обращается в нуль, и, следовательно,
то числитель дроби равенства (2) обращается в нуль, и, следовательно, 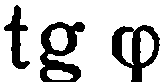
 . А это значит, что прямые параллельны.
. А это значит, что прямые параллельны.
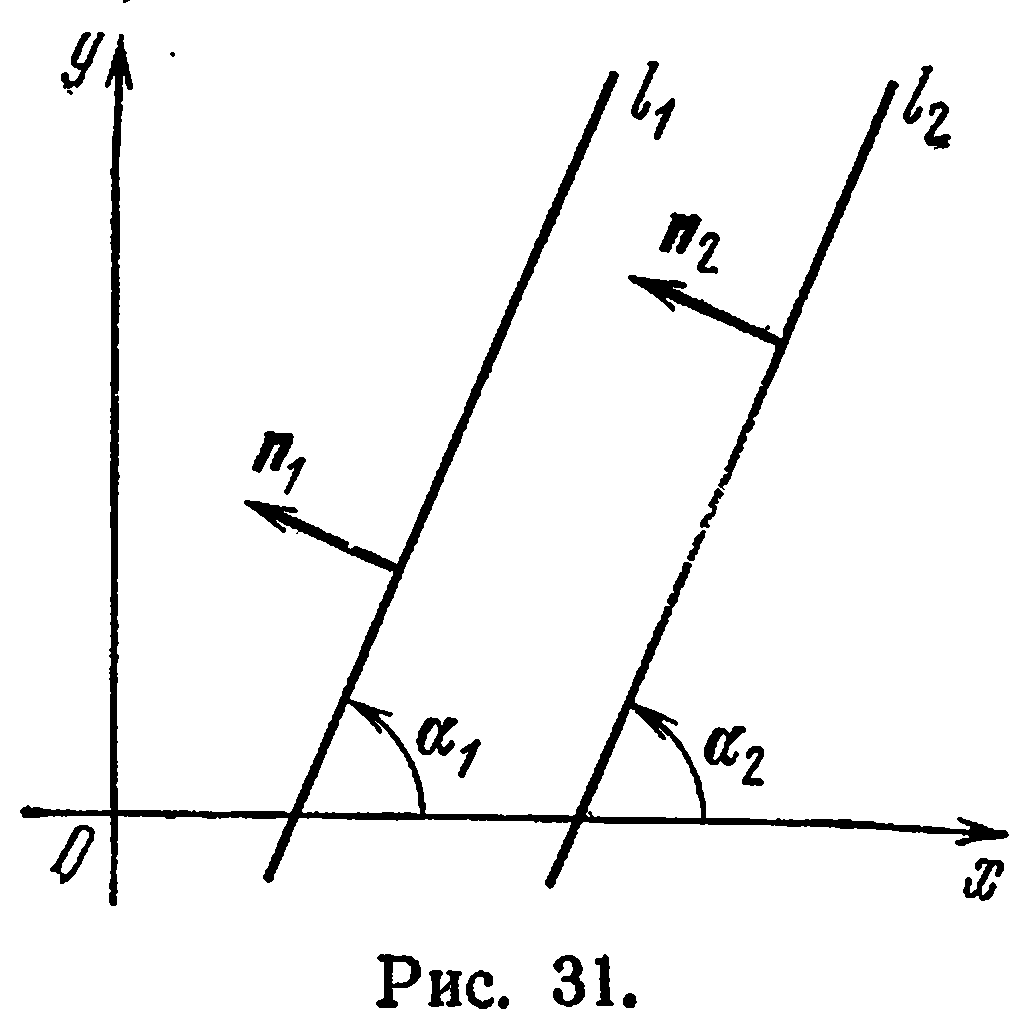
Таким образом, прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты.
Пример:
Параллельны ли прямые
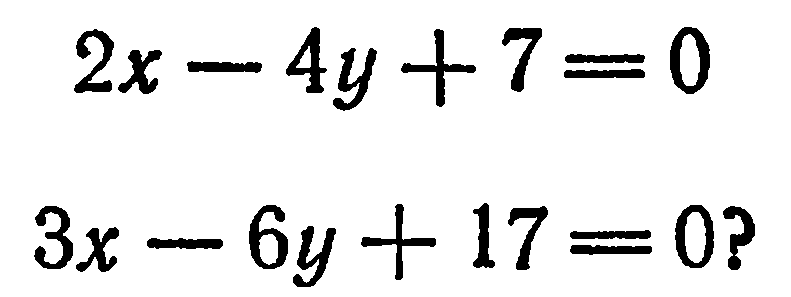
Решение:
Прямые параллельны потому, что их угловые коэффициенты равны между собой, а именно:
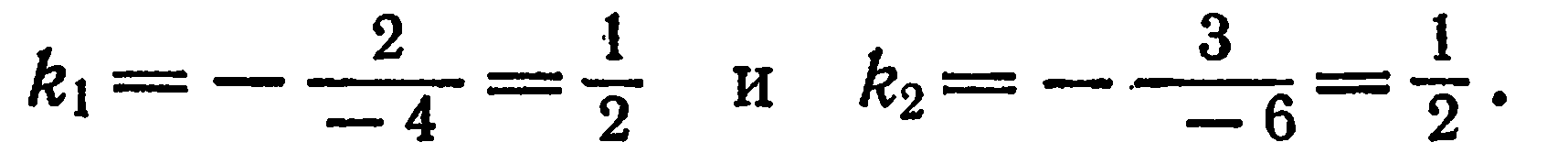
Условие перпендикулярности прямых
Если прямые  взаимно перпендикулярны, то взаимно перпендикулярны и их нормальные векторы
взаимно перпендикулярны, то взаимно перпендикулярны и их нормальные векторы 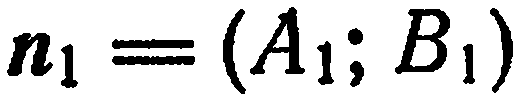 и
и 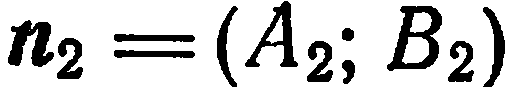 .
.
Запишем условие перпендикулярности векторов 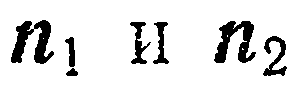 в координатной форме:
в координатной форме:
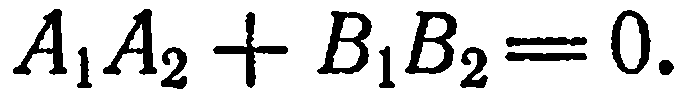
Считая 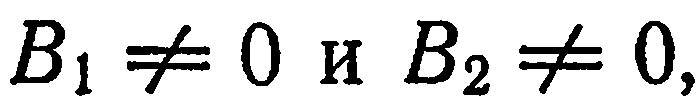 имеем:
имеем:
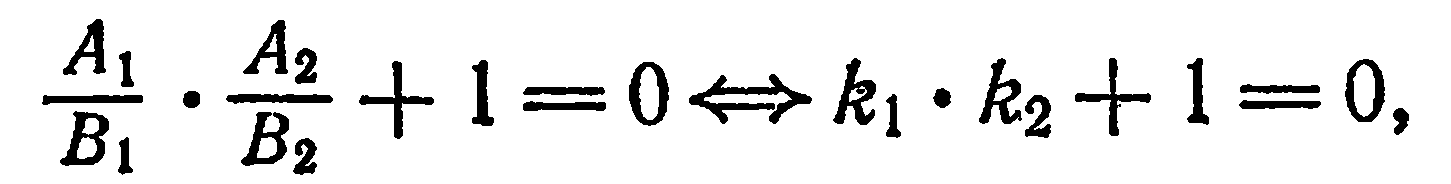
или

Таким образом, прямые взаимно перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположены по знаку.
Пример:
Перпендикулярны ли прямые

Решение:
Находим:
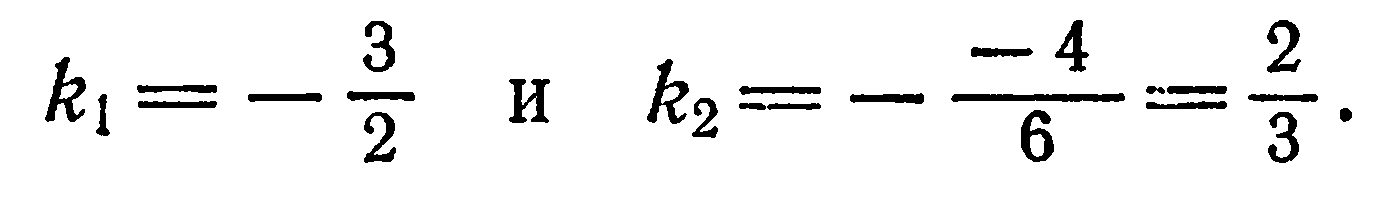
Прямые перпендикулярны потому, что их угловые коэффициенты обратны по величине и противоположны по знаку.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
