Оглавление:
Графики функций вида 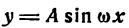 .
.
В дальнейшем изложении нам придется использовать функции вида 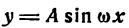 , а также их графики. Покажем на примерах, как строятся графики таких функций.
, а также их графики. Покажем на примерах, как строятся графики таких функций.
Пример:
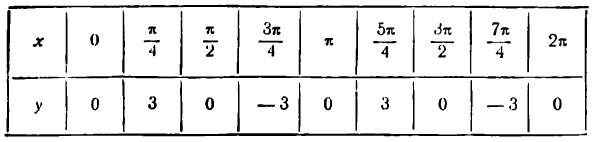
Построить график функции у = sin Зx
Решение:
Данная функция — периодическая; областью ее существования служат все действительные числа. Построим график этой функции для значений аргумента от х = 0 до х = 2 , составив предварительно следующую таблицу значений x и у.
, составив предварительно следующую таблицу значений x и у.
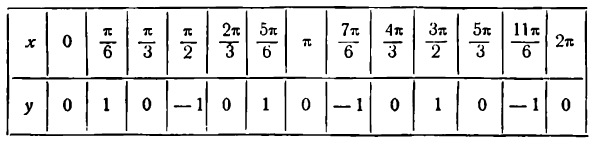
Рассматривая каждую пару значений х и у как координаты точек графика данной функции, построим эти точки и, проведя через них плавную линию, получим график функции у = sin Зx , представленный на рисеже 132 в виде сплошной линии — синусоиды с наименьшим периодом 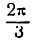 .
.
Как видно из рисежа, этот график можно получить из графика функции у = sin x , изображенного на том же рисеже пунктирной линией, уменьшив масштаб по оси Ох в три раза.
Пример:
Построить график функции у = 3 sin 2x .
Решение:
Составим таблицу значений х и у.
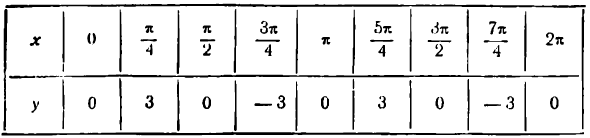
График, построенный по точкам с вычисленными координатами, представляет синусоиду с наименьшим периодом
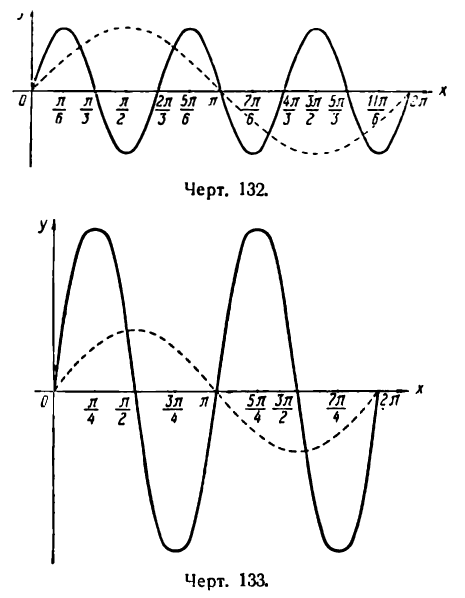
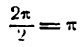 (на рисеже 133 эта синусоида изображена сплошной линией).
(на рисеже 133 эта синусоида изображена сплошной линией).
График функции у = 3 sin 2x можно получить и из графика функции у = sin х, представленного на том же рисеже пунктирной линией, уменьшив масштаб по оси Ох вдвое и увеличив его по оси Оу втрое.
Гармонические колебания
1. Простые гармонические колебания. В естествознании и технике часто наблюдаются периодические процессы, т. е. такие явления, которые повторяются через определенный промежуток времени. Например, колебания маятника, явления переменного тока и др.
Простейшее периодическое явление — гармоническое колебание, совершаемое по закону
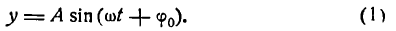
В равенстве (1) постоянный множитель А, представляющий наибольшую величину, которую может иметь у, называется амплитудой колебания, 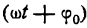 — фазой колебания, а
— фазой колебания, а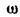 — частотой колебания.
— частотой колебания.
Функция (1) — периодическая с наименьшим-периодом 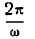 от прибавления которого к аргументу t функция не меняет своего значения. В самом деле,
от прибавления которого к аргументу t функция не меняет своего значения. В самом деле,
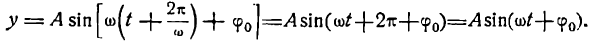
Величина 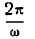 определяет время, в течение которого происходит одно колебательное движение, поэтому ее называют периодом колебания. Обозначив ее буквой T, можно написать:
определяет время, в течение которого происходит одно колебательное движение, поэтому ее называют периодом колебания. Обозначив ее буквой T, можно написать:
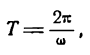
откуда
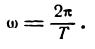
Так как Т—время одного колебания, то 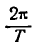 — число колебаний за время 2
— число колебаний за время 2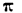 . Таким образом, величина
. Таким образом, величина 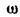 определяет частоту колебаний. Преобразуем равенство (1), применяя формулу для синуса суммы двух углов:
определяет частоту колебаний. Преобразуем равенство (1), применяя формулу для синуса суммы двух углов:
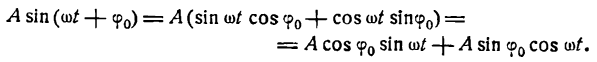
Решение:
Составим таблицу значений х и у.
График, построенный по точкам с вычисленными координатами, представляет синусоиду с наименьшим периодом
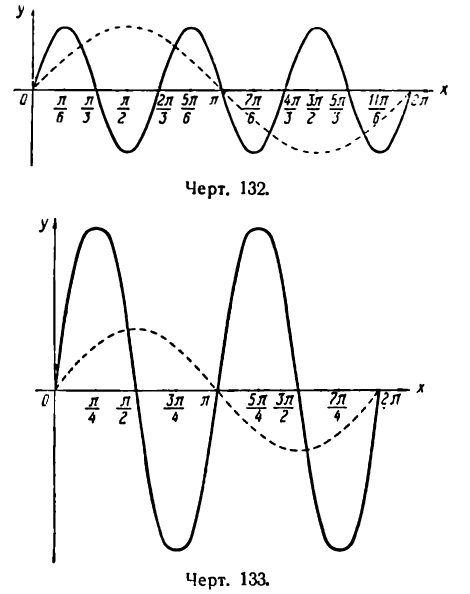
 (на рисеже 133 эта синусоида изображена сплошной линией).
(на рисеже 133 эта синусоида изображена сплошной линией).
График функции у = 3 sin 2x можно получить и из графика функции у = sin х, представленного на том же рисеже пунктирной линией, уменьшив масштаб по оси Ох вдвое и увеличив его по оси Оу втрое.
Гармонические колебания. I. Простые гармонические колебания. В естествознании и технике часто наблюдаются периодические процессы, т. е. такие явления, которые повторяются через определенный промежуток времени. Например, колебания маятника, явления переменного тока и др.
Простейшее периодическое явление — гармоническое колебание, совершаемое по закону
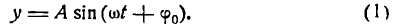
В равенстве (1) постоянный множитель А, представляющий наибольшую величину, которую может иметь у, называется амплитудой колебания, 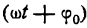 — фазой колебания, а
— фазой колебания, а 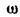 — частотой колебания.
— частотой колебания.
Функция (1) — периодическая с наименьшим-периодом 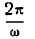 ,от прибавления которого к аргументу t функция не меняет своего значения. В самом деле,
,от прибавления которого к аргументу t функция не меняет своего значения. В самом деле,
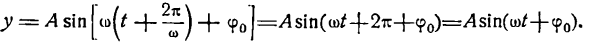
Величина 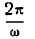 определяет время, в течение которого происходит одно колебательное движение, поэтому ее называют периодом колебания. Обозначив ее буквой Т можно написать:
определяет время, в течение которого происходит одно колебательное движение, поэтому ее называют периодом колебания. Обозначив ее буквой Т можно написать:
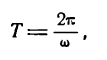
откуда
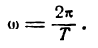
Так как Т—время одного колебания, 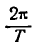 — число колебаний за время 2
— число колебаний за время 2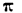 . Таким образом, величина
. Таким образом, величина  определяет частоту колебаний. Преобразуем равенство (1), применяя формулу для синуса суммы двух углов:
определяет частоту колебаний. Преобразуем равенство (1), применяя формулу для синуса суммы двух углов:
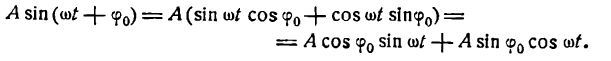
Обозначив
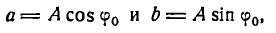
получим:
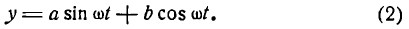
Колебательное движение, происходящее по закону функции (1) или, что то же, по закону функции (2), называется простым гармоническим колебанием, а график его — простой гармоникой.
ІІ. Сложные гармонические колебания. Не всякий периодический процесс можно рассматривать как простое гармоническое колебание. Очень часты случаи,
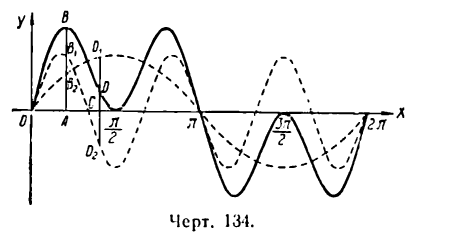
когда периодическое явление есть результат сложения нескольких простых гармонических колебаний. Полученное результирующее движение называется сложным гармоническим колебанием, а график его — сложной гармоникой.
Итак, сложная гармоника есть результат сложения нескольких простых гармоник или иначе — результат наложения простых гармоник друг на друга.
Рассмотрим пример. Пусть даны две простые гармоники, определяемые уравнениями:
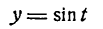
и
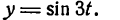
На рисеже 134 эти гармоники изображены пунктирными линиями, сложная же гармоника, являющаяся графиком функции
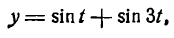
представлена сплошной линией. Любая точка сложной гармоники имеет ординату, равную сумме ординат точек, лежащих на простых гармониках и имеющих одну и ту же абсциссу. Так, например,
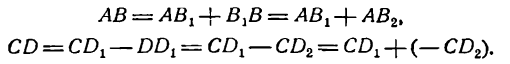
Как видно из рисежа, результирующая гармоника будет повторяться через каждый промежуток  будет периодической, но по своей форме она уже теряет характер синусоиды.
будет периодической, но по своей форме она уже теряет характер синусоиды.
Можно доказать, что вообще при сложении простых гармоник с разными частотами получается сложная гармоника не синусоидального вида, а при сложении гармоник с одинаковыми частотами — гармоника того же вида, что и простые.
Тригонометрические ряды
Как было указано, наблюдаются периодические процессы, которые нельзя рассматривать как простые колебательные явления. Положим, что какое-либо периодическое движение задано при помощи некоторой периодической функции, отличной от (1). Чтобы иметь представление о характере этого движения, данную функцию разлагают в ряд простых гармоник, имеющий следующий вид:
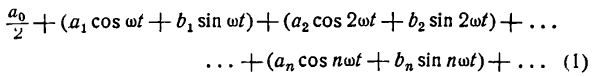
Ряд (1) называется тригонометрическим рядом, а числа

— коэффициентами ряда.
Положим для простоты
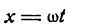
и будем считать, что ряд (1) сходится при всех действительных значениях х к данной функции [т. е. сумма ряда равна функции f(х)], тогда можно написать:
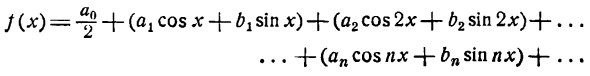
или короче
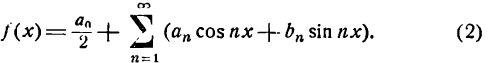
Как видно, функция f(x) — периодическая с периодом 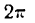 так как прибавляя к х (или вычитая из x)
так как прибавляя к х (или вычитая из x) 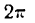 целое число раз, мы не изменим величины каждого члена ряда (2), а, следовательно, не изменим и величины суммы (2).
целое число раз, мы не изменим величины каждого члена ряда (2), а, следовательно, не изменим и величины суммы (2).
Отсюда следует, что тригонометрический ряд достаточно рассматривать только для значений x от 0 до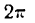 (или от —
(или от —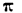 до +
до + 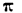 ), так как за пределами указанного промежутка значений аргумента величина каждого члена ряда будет периодически повторяться.
), так как за пределами указанного промежутка значений аргумента величина каждого члена ряда будет периодически повторяться.
Чем больше простых гармоник ряда (2) мы сложим, тем точнее результирующая гармоника будет представлять периодическое движение, заданное функцией f(x). Поэтому вопрос о разложении функции в тригонометрический ряд приобретает очень важное значение в прикладных науках.
Процесс разложения функции, представляющей сложное периодическое движение, в тригонометрический ряд называется гармоническим анализом.
Коэффициенты Фурье
Ряд Фурье. Чтобы разложить периодическую функцию f(x) с периодом 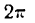 в тригонометрический ряд, нужно найти коэффициенты этого ряда. Мы приводим здесь без вывода формулы, по которым производится вычисление этих коэффициентов:
в тригонометрический ряд, нужно найти коэффициенты этого ряда. Мы приводим здесь без вывода формулы, по которым производится вычисление этих коэффициентов:
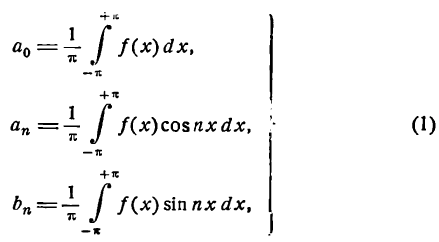
где n = 1, 2, 3, 4, ……….
Числа, полученные по формулам (1), называются коэффициентами Фурье *), а тригонометрический ряд с этими коэффициентами — рядом Фурье.
*) Формулы (1) были даны еще Эйлером (1707—1783), но широко использовал их французский математик Ж. Фурье (1768—1830).
Определение:
Ряд
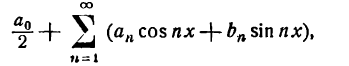
где
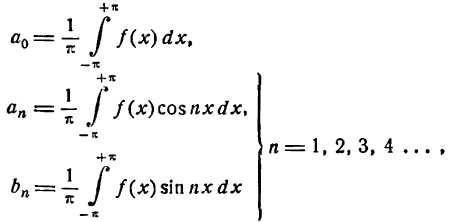
называется рядом Фурье функции f(x).
Если ряд Фурье сходится к функции f(x), то можно записать:
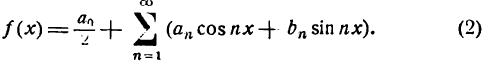
Следует заметить, что величина интегралов в формулах (1) не изменится, если пределами их взять 0 и 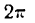 . В этом случае формулы для определения коэффициентов Фурье можно написать в следующем виде:
. В этом случае формулы для определения коэффициентов Фурье можно написать в следующем виде:
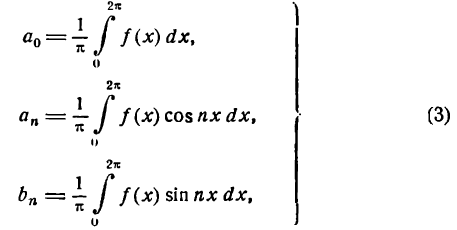
где п = 1, 2, 3, 4 …
Формулы (3) представляют иногда большие удобства, чем формулы (1).
Возможность разложения непериодической функции в ряд Фурье
Периодическая функция, как мы уже знаем, определяет колебательное движение. Однако бывают колебательные явления, которые совершаются по закону непериодической функции. Поэтому для изучения колебательного движения, подчиняющегося непериодической функции, выгодно разложить эту функцию в ряд Фурье, что оказывается возможным при некоторых условиях.
Пусть, например, задана функция
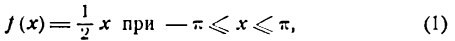
график которой изображен на рисеже 135 отрезком прямой АВ. Покажем, что для разложения данной функции в ряд Фурье
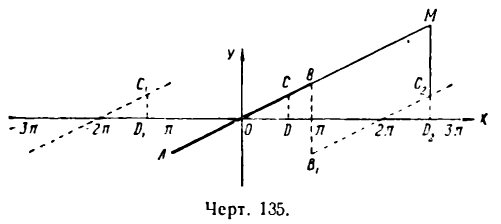
можно и к ней применить правила. Для этого введем вспомогательную периодическую функцию  с периодом
с периодом  при условии:
при условии:
 в промежутке значений х от —
в промежутке значений х от —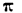 до +
до +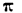 , (2)
, (2)
за пределами же указанного промежутка 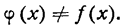
К функции 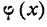 , как к периодической, можно применить формулы. Но мы знаем, что тригонометрический ряд достаточно рассматривать для промежутка значений аргумента от —
, как к периодической, можно применить формулы. Но мы знаем, что тригонометрический ряд достаточно рассматривать для промежутка значений аргумента от —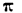 до +
до + 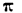 ), поэтому формулы имеем право применить не только к функции
), поэтому формулы имеем право применить не только к функции 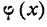 , но, согласно условию (2), и к заданной.
, но, согласно условию (2), и к заданной.
Величина суммы ряда Фурье, полученного для функции (1), вследствие периодичности его членов будет повторяться через каждый промежуток, равный 2 , и принимать значения данной функции (1). Поясним это геометрически. С этой целью перенесем отрезок АВ (рис. 135), сохраняя его направление, вдоль оси Ох на расстояния, равные 2
, и принимать значения данной функции (1). Поясним это геометрически. С этой целью перенесем отрезок АВ (рис. 135), сохраняя его направление, вдоль оси Ох на расстояния, равные 2 , 4
, 4 и т. д., вправо и влево от начала координат или, как говорят, продолжим периодически график функции (1). Возьмем значение х внутри промежутка от —
и т. д., вправо и влево от начала координат или, как говорят, продолжим периодически график функции (1). Возьмем значение х внутри промежутка от — до +
до + , например,
, например,
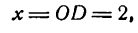
тогда ордината
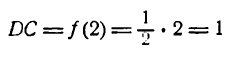
даст величину суммы ряда Фурье функции (1) при х = 2. Ясно, что при
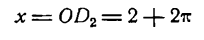
или
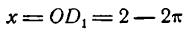
величина ординат D2С2 и D1С1, а следовательно, и сумма ряда при тех же значениях х не изменится и будет равна по-прежнему единице.
Обратим внимание, что для значений х вне промежутка от — до +
до +  сумма ряда Фурье функции (1) и значения этой функции не равны между собой. Действительно, сумма этого ряда при х = 2 + 2
сумма ряда Фурье функции (1) и значения этой функции не равны между собой. Действительно, сумма этого ряда при х = 2 + 2 , как мы узнали, равна 1, а значение функции
, как мы узнали, равна 1, а значение функции
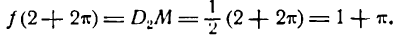
Все сказанное выше подтверждает мысль, что ряд Фурье функции имеет смысл рассматривать только в промежутке
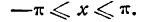
Условия Дирихле
Теорема Дирихле:
Как было уже сказано, функция f(х) с областью существования 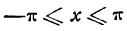 может быть разложена в ряд Фурье, сходящийся к данной функции f(х) при определенных условиях. Эти условия, называемые условиями Дирихле, заключаются в следующем:
может быть разложена в ряд Фурье, сходящийся к данной функции f(х) при определенных условиях. Эти условия, называемые условиями Дирихле, заключаются в следующем:
1) функция должна быть непрерывной в промежутке значений х от — до +
до +  или может иметь в указанном промежутке разрывы первого рода, но только в конечном числе;
или может иметь в указанном промежутке разрывы первого рода, но только в конечном числе;
2) функция должна иметь конечное число максимумов и минимумов ила не иметь их совсем.
Одной из основных теорем, применяемых при исследовании рядов Фурье, является теорема Дирихле.
Теорема Дирихле:
Если функция f(х) с областью существования —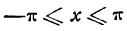 удовлетворяет условиям Дирихле, то
удовлетворяет условиям Дирихле, то
1) ряд Фурье функции f(x) сходится в указанном промежутке значений х;
2) сумма этого ряда сходится к функции f(x) во всех точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна половине скачка функции;
4) при х =  и х = —
и х = —  сумма ряда одинакова и равна
сумма ряда одинакова и равна
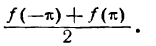
Примем указанную теорему без доказательства.
Заметим, что в дальнейшем изложении мы будем пользоваться только функциями, удовлетворяющими условиям Дирихле, а потому в каждом разбираемом примере не будем останавливаться на этих условиях.
Прежде чем перейти к разложению функций в ряды Фурье мы должны познакомиться с методом интегрирования по частям, без которого нельзя определять коэффициенты Фурье.
Интегрирование по частям
Пусть и и 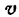 — дифференцируемые функции х, тогда по правилу IV имеем:
— дифференцируемые функции х, тогда по правилу IV имеем:
и
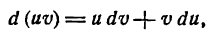
откуда
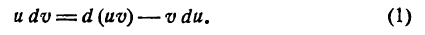
Взяв интеграл от обеих частей равенства (1), получим:
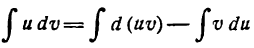
или
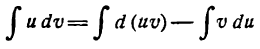
Равенство (2) служит формулой интегрирования по частям.
Пример:
Найти 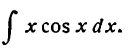
Решение:
Положим
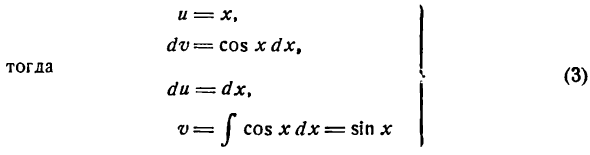
(произвольное постоянное интегрирования напишем в окончательном результате).
Подставив (3) во (2), получим:
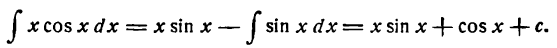
Пример:
Найти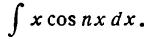
Решение:
Положим
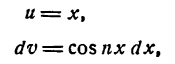
тогда
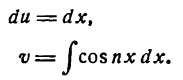
Применяя метод подстановки
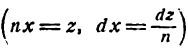
получим:
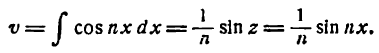
Согласно формуле (2) имеем:
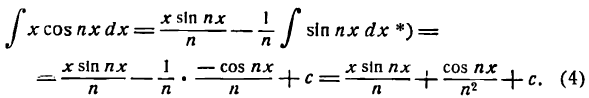
Аналогично можно найти:
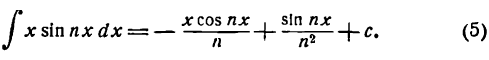
Пример:
Найти 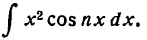
Решение:
Положим
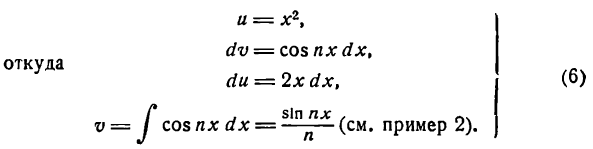
Подставив (6) во (2), получим:
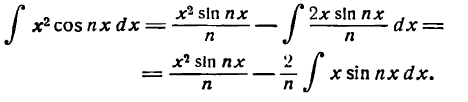
Приняв во внимание равенство (5), будем иметь:
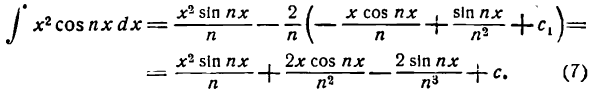
Таким же образом найдем:
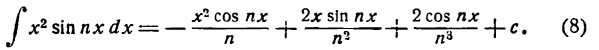
*) Применяется подстановка
Примеры разложения функций в ряд Фурье
Пример:
Разложить в ряд Фурье функцию:
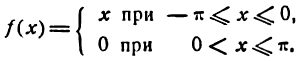
Решение:
По формулам (1) найдем коэффициенты Фурье
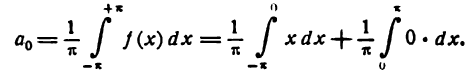
Но
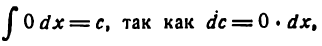
кроме того,
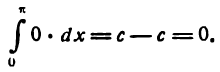
Поэтому
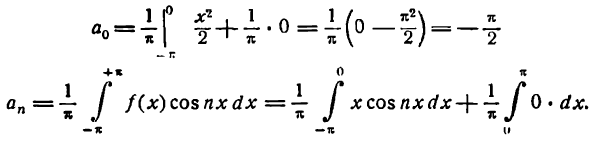
Приняв во внимание равенство (4) получим:
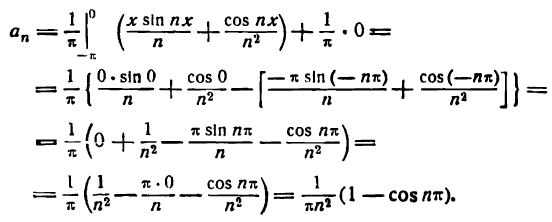
Отсюда
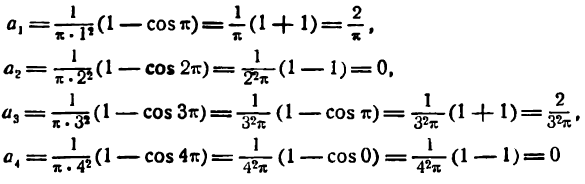
и т.д.
Как видно, при четном значении n коэффициенты 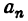 равны нулю.
равны нулю.
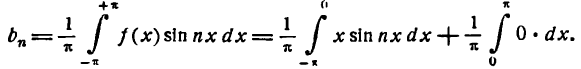
Согласно равенству (5) получим:
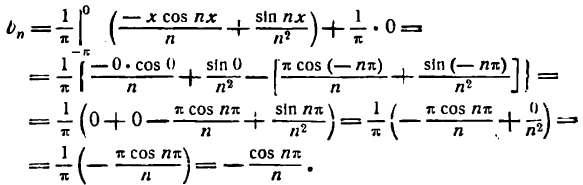
Отсюда
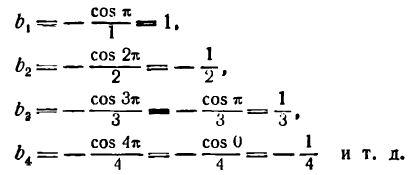
Искомый ряд напишется так:
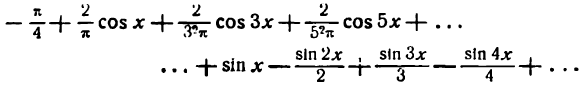
Согласно теореме Дирихле этот ряд сходится к данной функции во всех точках промежутка значений x от —  до +
до +  кроме x = —
кроме x = —  и х =
и х =  . В самом деле, при х = —
. В самом деле, при х = —  и x =
и x =  сумма ряда равна
сумма ряда равна
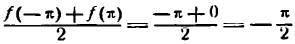
между тем как значения функции при х = —  и x =
и x =  соответственно равны —
соответственно равны — и 0, т. е. не совпадают с суммой ряда.
и 0, т. е. не совпадают с суммой ряда.
Таким образом, можно написать:
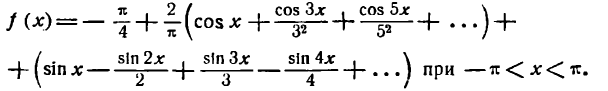
Пример:
Разложить в ряд Фурье функцию

Решение:
Здесь для определения коэффициентов Фурье используем формулы (3) .
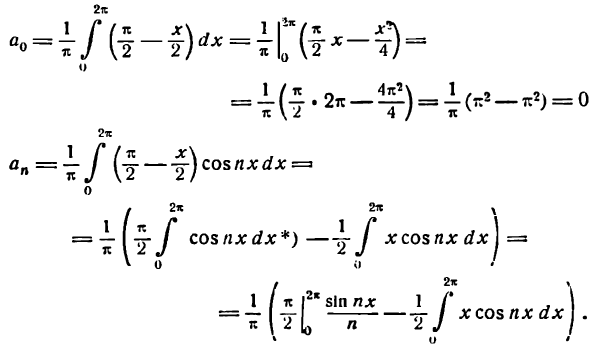
*) 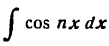 находится подстановкой: nx — z и
находится подстановкой: nx — z и 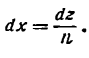
Приняв во внимание равенство (4) , будем иметь:
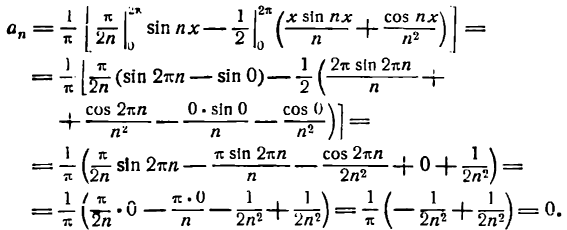
Таким образом, все коэффициенты
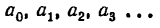
равны нулю.
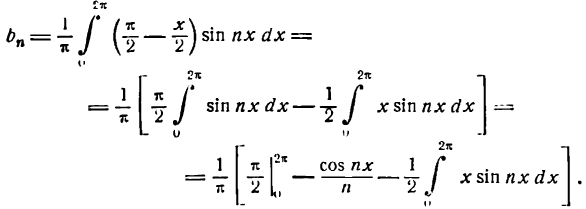
Применяя к  формулу (5) , получим:
формулу (5) , получим:
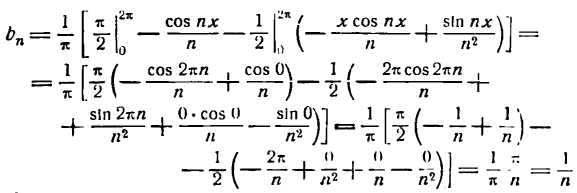
Итак,
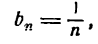
откуда
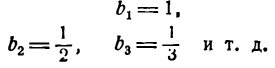
Искомое разложение будет:
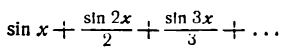
Полученный ряд сходится к функции 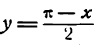 при всех
при всех
значениях х в промежутке от 0 до 2 , кроме х = 0 и х = 2
, кроме х = 0 и х = 2 как это и следует из теоремы Дирихле. Таким образом,
как это и следует из теоремы Дирихле. Таким образом,
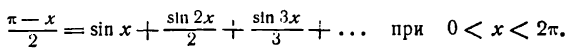
Ряды Фурье для четных и нечетных функций
Функция f(x) называется четной, если при подстановке вместо х величины —х знак функции не меняется, т. е. f(—x) = f(x). Например, 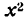 , cos x — четные функции, так как
, cos x — четные функции, так как 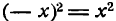 , cos(—x) = cos x.
, cos(—x) = cos x.
Функция f(x) называется нечетной, если при подстановке вместо х величины —х знак функции меняется на противоположный, т. е. f(—х) = — f(х). Например, 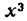 , sin х— нечетные функции, так как
, sin х— нечетные функции, так как 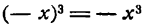 , sin (—x) = — sin x.
, sin (—x) = — sin x.
Заметим, что произведение двух четных или двух нечетных функций есть четная функция, а произведение четной функции на нечетную есть функция нечетная.
В самом деле,
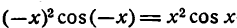
—произведение двух четных функций,

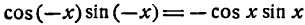
— произведение четной функции на нечетную.
График четной функции симметричен относительно оси Оу, график нечетной функции симметричен относительно начала координат. Примеры таких графиков даны на рисеже 136 для четной функции, на рисеже 137 — для нечетной. Если f(x)—четная функция, то
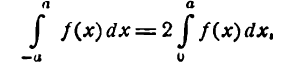
если f(x)—нечетная функция, то
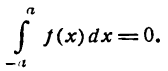
Эти равенства можно подтвердить геометрическими соображениями. Пусть 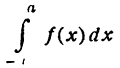 выражает площадь фигуры, заключенной между графиком функции f(x), двумя прямыми х = — а и х = а и осью Ох, тогда в случае четной функции f(x) эта площадь равна удвоенной площади фигуры,
выражает площадь фигуры, заключенной между графиком функции f(x), двумя прямыми х = — а и х = а и осью Ох, тогда в случае четной функции f(x) эта площадь равна удвоенной площади фигуры,
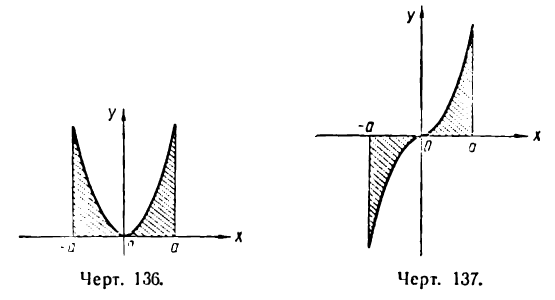
образованной тем же графиком, осью Ох и прямыми x = 0 и х = а (рис. 136); в случае нечетной функции площадь равна нулю, так как она состоит из двух равных площадей с противоположными знаками (рис. 137).
Приняв во внимание сказанное, можно упростить формулы (1) , написав их в следующем виде: для случая четной функции
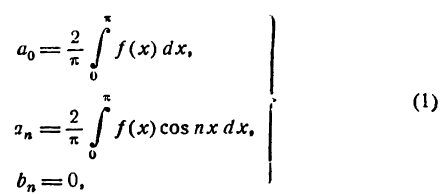
для случая нечетной функции
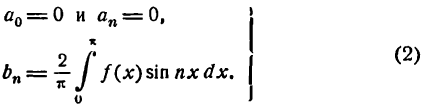
Как видно, ряд Фурье (2) для четной функции будет состоять только из косинусов, т. е.
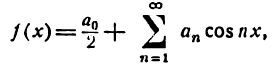
а для нечетной функции — только из синусов, т. е.
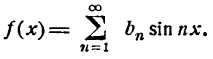
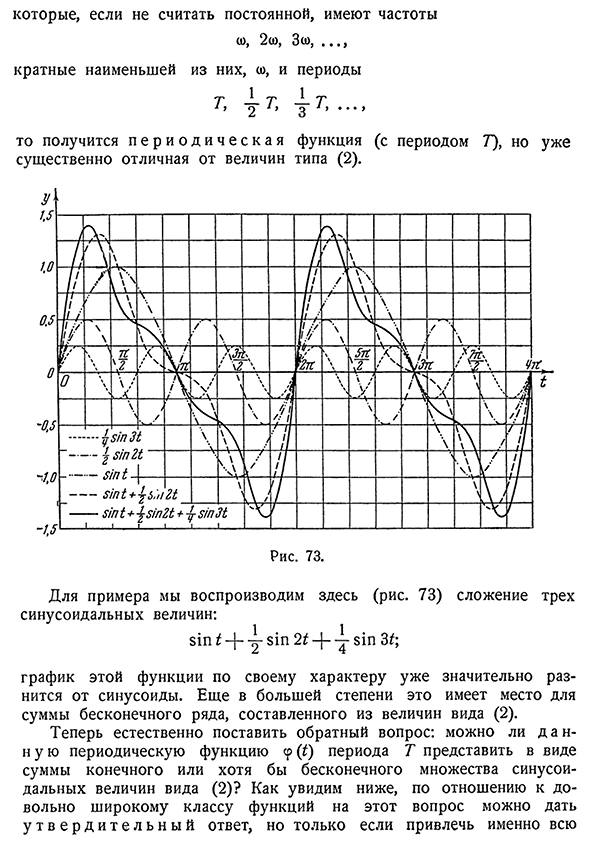
Пример:
Разложить в ряд Фурье функцию
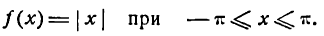
Решение:
Функция у = | х | — четная (см. рис. 73), а потому согласно формулам (1) имеем:
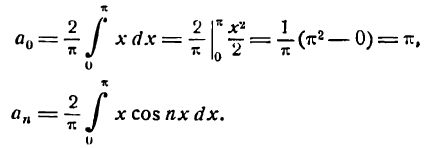
Приняв во внимание равенство (4), найдем:
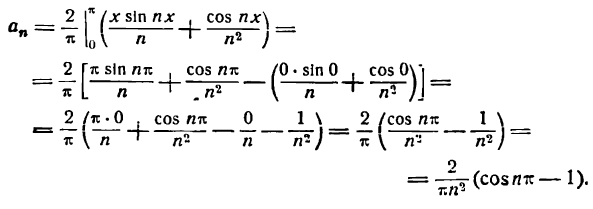
Отсюда
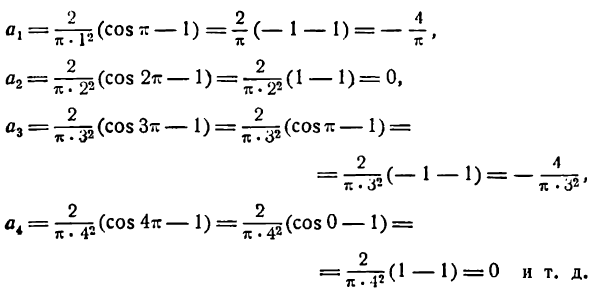
Искомое разложение будет:
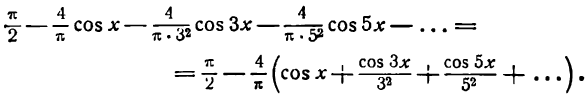
Применяя теорему Дирихле, можно показать, что полученный ряд сходится к данной функции при всех значениях х от — до +
до + 
Следовательно, можно написать:
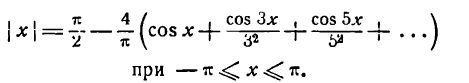
Пример:
Разложить в ряд Фурье функцию
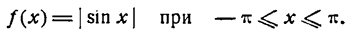
Решение:
Данная функция четная; применяя формулы (1), получим:
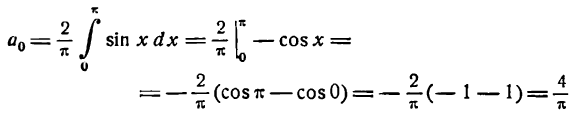
Положив п = 1 в формуле для 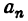 , будем иметь:
, будем иметь:
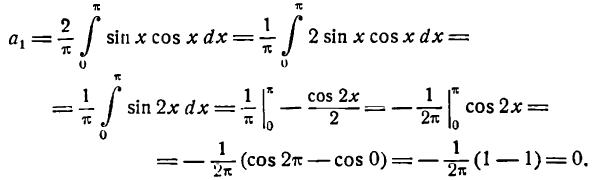
Для n = 2, 3, 4 … получим:
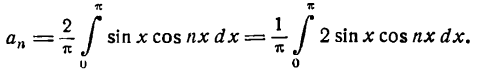
Представим произведение 2 sin x cos nx в следующем виде:
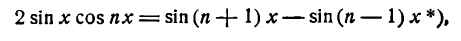
*) Это равенство легко проверить, применив к правой части его формулу для разности синусов двух углов.
тогда
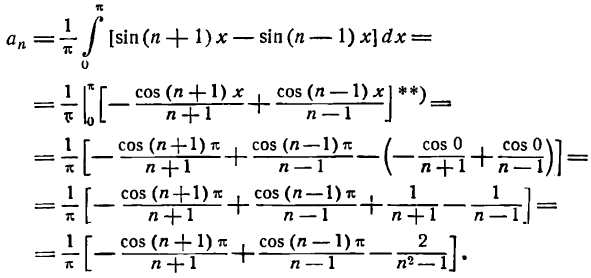
**) 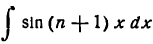 находится подстановкой: (n + 1) х = z и
находится подстановкой: (n + 1) х = z и 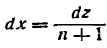 . Аналогичную подстановку применяем и к
. Аналогичную подстановку применяем и к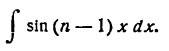
Отсюда
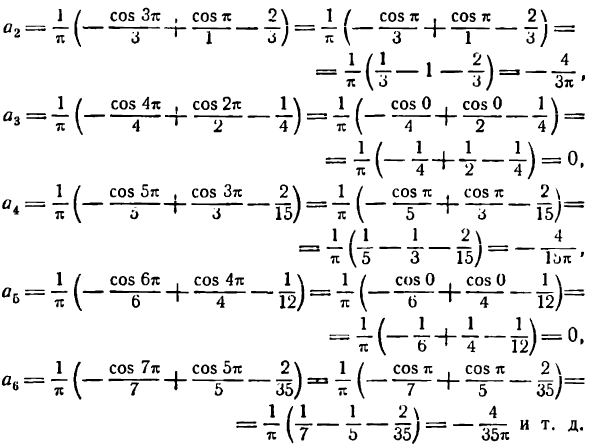
Искомое разложение напишется так:
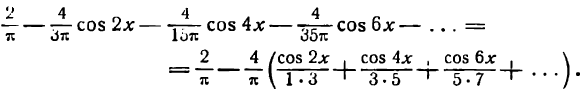
Согласно теореме Дирихле полученный ряд сходится к данной функции при 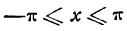 поэтому
поэтому
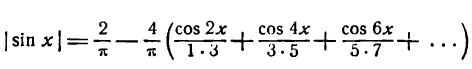
при всех значениях х указанного промежутка.
Пример:
Разложить в ряд Фурье функцию
f(x) = x при 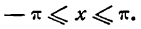
Решение:
Применим формулы (2), так как функция f(x) = x нечетная.
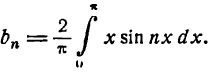
Согласно равенству (5) найдем:
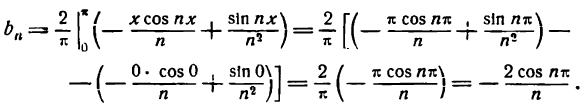
Отсюда
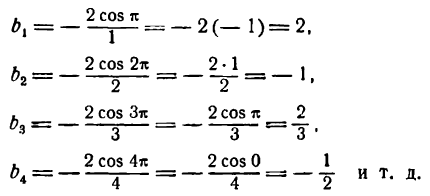
Искомое разложение таково:
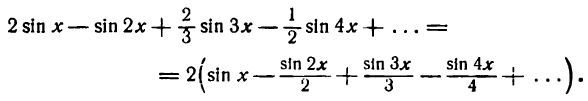
Этот-ряд представляет функцию f(х) = х при всех значениях х промежутка от — до +
до +  кроме
кроме 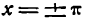 . Действительно, по теореме Дирихле при
. Действительно, по теореме Дирихле при 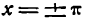 сумма ряда равна
сумма ряда равна
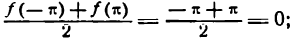
значения же функции при х = —  и x =
и x =  соответственно равны —
соответственно равны — и
и  , т. е. не совпадают с суммой ряда. Таким образом,
, т. е. не совпадают с суммой ряда. Таким образом,
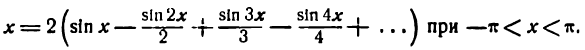
Пример:
Разложить в ряд Фурье функцию
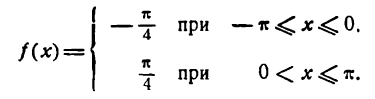
Решение:
Данная функция — нечетная, а потому, применяя формулу (2), получим:
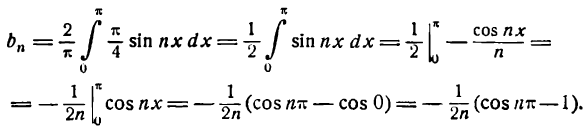
Отсюда
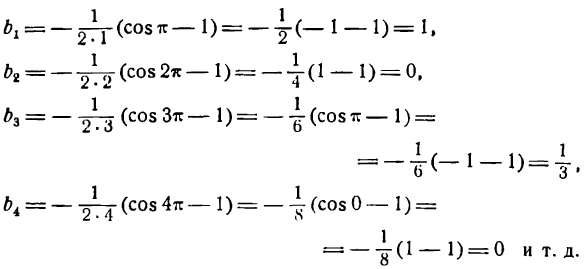
Разложение напишется следующим образам:
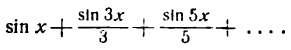
При х = —  , x = 0 и х =
, x = 0 и х =  сумма полученного ряда не совпадает со значениями данной функции, поэтому указанный ряд сходится к функции f(x) при
сумма полученного ряда не совпадает со значениями данной функции, поэтому указанный ряд сходится к функции f(x) при 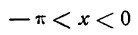 и
и 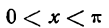
Следовательно,
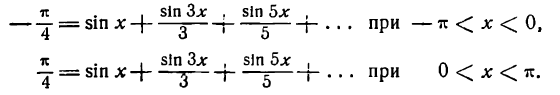
Покажем на примере разложения в ряд этой функции, что по мере увеличения числа слагаемых (простых гармоник) частичная сумма ряда (результирующая гармоника) все лучше и лучше представляет данную функцию.
На рисеже 138 I показана первая гармоника (sin х) ряда. На рисеже 138 II изображены первые две гармоники ряда (sin х и 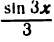 — пунктирные линии) и их сумма (sin х +
— пунктирные линии) и их сумма (sin х + 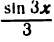 — сплошная линия)
— сплошная линия)
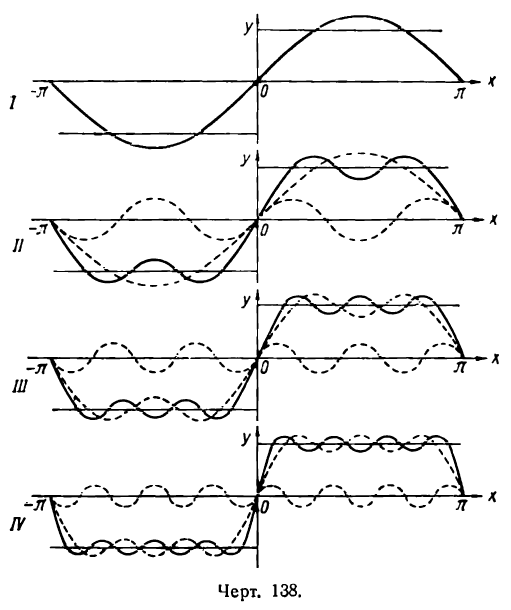
На рисеже 138 III показаны найденная сумма двух первых гармоник (sin х + 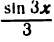 пунктирная линия) и третья гармоника (
пунктирная линия) и третья гармоника (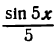 — пунктирная линия), а также сумма трех первых гармоник
— пунктирная линия), а также сумма трех первых гармоник
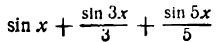
— сплошная линия).
На рисеже 138 IV — найденная сумма трех первых гармоник
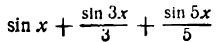
— пунктирная линия), четвертая гармоника ( 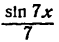 — пунктирная линия) и сумма первых четырех гармоник (
— пунктирная линия) и сумма первых четырех гармоник (
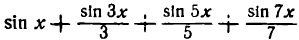
— сплошная линия).
Продолжая операцию сложения простых гармоник и дальше, мы будем получать результирующую гармонику (частичную сумму ряда), все больше и больше приближающуюся к двум параллельным отрезкам, изображающим данную функцию.
Вследствие периодичности ряда Фурье данной функции результирующая гармоника будет точно повторяться через каждый промежуток значений x, равный 2 .
.
Периодические величины и гармонический анализ



Смотрите также:
| Геометрическая интерпретация | Механические приложения |
| Полнота множества вещественных чисел | Некоторые конкретные множества вещественных чисел |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
