Оглавление:
Математические познания, достигнутые в последующие века, изучаются в соответствующих высших учебных заведениях.
В общеобразовательных школах изучаются следующие математические предметы: арифметика, элементарная алгебра, элементарная геометрия и плоская тригонометрия.
Арифметика, элементарная алгебра, элементарная геометрия и тригонометрия относятся к так называемой «элементарной математике». Математические же дисциплины, изучаемые в высших учебных заведениях, относятся к высшей математике.
Однако надо иметь в виду, что современная элементарная математика не изолирована от идей высшей математики. Например, в книгах по элементарной математике можно встретить сведения о функциях, координатах иа плоскости, графическом методе, пределах, суммировании рядов, производной и интеграле, т. е. понятия, относящиеся к началам высшей математики.
Математика и ее значение
Математика, так же как и другие науки, возникла, становилась и развивается на основе производственно-практической деятельности людей. Так, начала арифметики и геометрии возникли в связи с самыми простейшими запросами хозяйственной жизни. Счет предметов, потребность измерять количества продуктов и производить расчеты при их обмене, знать протяженность дорог, площади земельных участков, размеры и вместимость сосудов, исчислять время — все это и приводило к возникновению и развитию первоначальных понятий арифметики и геометрии. Вопросы астрономии привели к появлению зачатков тригонометрии еще в Вавилонии (Месопотамия) за много веков до нашей эры.
Слово «математика» происходит от греческого слова «ματηеμα», что означает «познание», «наука».
Содержание и происхождение математики как науки точно и полно характеризуется следующими словами Энгельса: «Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть — весьма реальный материал. Тот факт, что это материал принимает чрезвычайно абстрактную форму, может лишь слабо затушевать его происхождение из внешнего мира. Но чтобы быть в состоянии исследовать эти формы и отношения в чистом виде, необходимо совершенно отделить их от их содержания, оставить это последнее в стороне как нечто безразличное; таким путем мы получаем точки, лишенные измерений, линии, лишенные толщины и ширины, разные а и b, х и у, постоянные и переменные величины… Как и все другие науки, математика возникла из практических нужд людей: из измерения площадей земельных участков и вместимости сосудов, из счисления времени и из механики». (Ф. Э и г е л ь с, Аити-Дюрииг, 1948, стр. 37).
Богатство содержания этого классического определения будет раскрываться все полнее по мере расширения математических познаний читателя.
Остановим свое внимание сначала на том, что математика есть наука, изучающая связи между величинами и изучающая формы тел, поверхностей и линий. Поясним это на примерах.
Пример:
Пусть требуется вычислить следующую сумму:
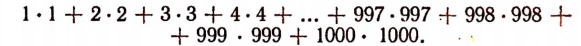
Эта сумма содержит тысячу слагаемых; каждое слагаемое есть произведение.
Если находить ее непосредственно, то нам придется тысячу раз умножить, а затем сложить тысячу слагаемых в виде полученных произведений. На все это понадобится не менее 20 часов. Между тем, если воспользоваться соответствующим математическим законом *, то за одну минуту можно обнаружить, что искомая сумма равна

Это число мы получили, вычислив выражение
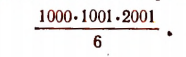
Здесь 1000 есть число слагаемых в данной сумме; число 1001 больше числа слагаемых на единицу; число 2001 взято как сумма этих двух чисел. Знаменатель не зависит от числа слагаемых. Например,
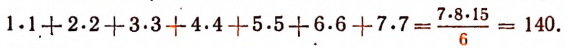
Числа 7, 8 и 15 взяты по тому же правилу, по которому составлены числа 1000, 1001 и 2001 раньше. В знаменателе стоит опять число 6, так как оно не зависит от числа слагаемых.
Пример:
Пусть нужно найти следующую сумму:
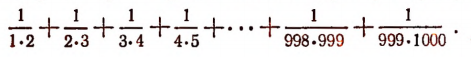
Обратим внимание на то, что каждое слагаемое этой суммы можно представить в ввде разности двух дробей, а именно:
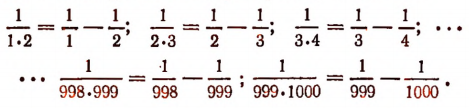
Благодаря этому наша первоначальная сумма примет вид:
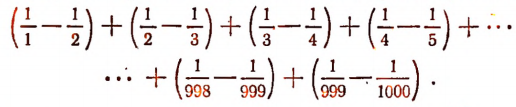
Легко видеть, что эта сумма равна 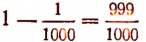
Пример:
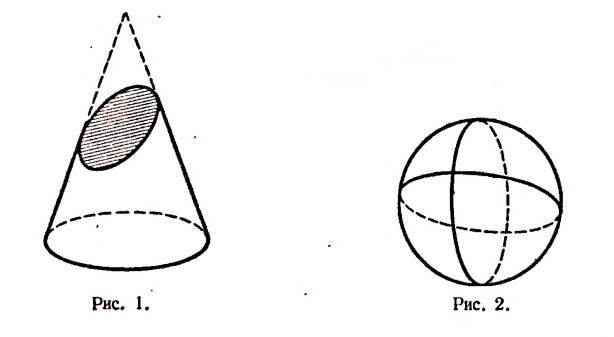
Посредством математических методов можно, например, теоретически обнаружить все особенности линии пересечения конической поверхности с плоскостью. Если такая линия пересечения замкнутая (рис. 1), то можно вычислить ее длину, площадь плоской фигуры, ею ограниченной, и многое другое. Можно вычислить объем шара, если известна площадь его поверхности (рис. 2) и т. д.
Математика нужна при проектировании инженерных сооружений. Без математических методов нельзя достаточно полно усвоить физику, механику, электротехнику, радиотехнику и прочие инженерные науки. Начала арифметики необходимы каждому человеку. При современном развитии техники элементарные знания по геометрии или умение пользоваться буквенными формулами и графиками необходимы всякому мастеру, всякому квалифицированному рабочему. В целом же математика , как и всякая другая наука, является одним из средств познания закономерностей окружающего нас материального мира и раскрытия путей использования этих закономерностей в практической деятельности людей.
Но математика изучает не все содержание окружающих нас предметов и явлений. Например, с помощью только математики нельзя определить химический состав воды или изучить процессы, происходящие в живом организме. Математика изучает лишь количественные отношения и пространственные формы действительного мира, реальных явлений и предметов.
Под выражением «количественные отношения действительного мнра» следует понимать, например, законы движения планет вокруг Солнца, законы движения комет нлн, скажем, взаимосвязь между величиной атмосферного давления и высотой над уровнем моря. (По атмосферному давлению летчик определяет высоту полета.)
Под выражением «пространственные формы действительного мира» можно понимать, например, формы планет, формы орбит, по которым планеты движутся вокруг Солнца, формы предметов, находящихся на Земле, формы земных материков, гор, рек, морей.
Таким образом, математика изучает только две стороны явления или предмета, а именно количественные отношения и пространственные формы. Другие же стороны явлений изучают иные науки (физика, химия, аэродинамика, радиотехника и т. д.). Сложные технические вопросы разрешаются совместными усилиями ученых и практиков различных специальностей, т. е. путем применения не одной науки, а одновременно нескольких соответствующих наук. Поэтому, зная только математику, нельзя построить, например, мост через Волгу. Вместе с тем такой мост нельзя построить и без математических расчетов. Следовательно, для сооружения крупного моста математические знания являются необходимыми, но не достаточными. Кроме математики, нужны еще строительная механика, материаловедение и многое другое.
Из сказанного выше ясно, что математика, выделяя количественные отношения и пространственные формы, оставляет в стороне все остальное, не являющееся предметом математического исследования. Например, изучая свойства шара, математика не интересуется ни его цветом, ни материалом, из которого он сделан. Изучая свойства чисел и правила действий над ними, математика оставляет в стороне конкретные величины и формулирует полученные результаты независимо от того, что этими числами выражено. Наряду с этим математика отличается еще той особенностью, что все объекты, ею изучаемые, мыслятся абсолютно точными,идеальными. Поясним, что это значит.
Никакое физическое шарообразное тело (например, мяч, глобус или игрушечный воздушный шар) не может иметь абсолютно гладкую или, точнее говоря, идеально шаровую поверхность. Шарообразные же формы, изучаемые в математике, мыслятся абсолютно точными, имеющими абсолютно гладкую, идеальную шаровую поверхность.
Всякая линия, начерченная тушью или проведенная карандашом, имеет ширину и толщину. Линии же, изучаемые в математике, мыслятся имеющими только длину и не обладающими ни шириной, ни толщиной.
Всякая точка, изображённая тушью или карандашом, имеет какие-то размеры (длину, ширину и толщину). Все же без исключения размеры математической точки мыслятся равными нулю.
Никакой треугольник, вырезанный из дерева, картона или металла, либо просто изображенный на чертеже, не может иметь идеально прямой угол, идеально прямолинейные края или границы. Длину сторон такого треугольника никогда нельзя определить абсолютно точно. Треугольники же, изучаемые в математике,1 мыслятся идеальными, т.е. имеющими абсолютно точную прямолинейность сторон, абсолютно точные углы, абсолютно точную длину сторон и т.д.
Особенность математики изучать количественные отношения и пространственные формы изолированно от всего прочего и при этом в их идеальном виде — является основным условием существования математической науки и ее силой. Без этой особенности математика как наука не существовала бы. Поясним сказанное.
Еще за две тысячи лет до нашей эры египетские землемеры пользовались для построения прямых углов веревочным треугольником со сторонами 3, 4 и 5. (Очевидно, что  ) Были известны и другие прямоугольные треугольники, стороны которых выражались целыми числами, например 5, 12, 13. Но этот замеченный факт тогда не могли еще обоснованно обобщить. И только в VI веке до нашей эры Пифагор доказал, что площадь квадрата, построенного на гипотенузе любого прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. Но Пифагор сумел прийти к этому открытию только потому, что он отвлекся от физических треугольных форм и стал рассматривать треугольник математический, воображаемый, идеальный, т.е. такой, в котором прямолинейность сторон, прямой угол и длина сторон мыслятся абсолютно точными. При этом его исследования и суждения относились не к отдельному треугольнику, а ко всему множеству прямоугольных треугольников.
) Были известны и другие прямоугольные треугольники, стороны которых выражались целыми числами, например 5, 12, 13. Но этот замеченный факт тогда не могли еще обоснованно обобщить. И только в VI веке до нашей эры Пифагор доказал, что площадь квадрата, построенного на гипотенузе любого прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. Но Пифагор сумел прийти к этому открытию только потому, что он отвлекся от физических треугольных форм и стал рассматривать треугольник математический, воображаемый, идеальный, т.е. такой, в котором прямолинейность сторон, прямой угол и длина сторон мыслятся абсолютно точными. При этом его исследования и суждения относились не к отдельному треугольнику, а ко всему множеству прямоугольных треугольников.
Такой метод исследования геометрических форм появился далеко не сразу, а лишь в результате длительной работы многих предшественников Пифагора и самого Пифагора. Надо было от египетских веревок и от намеченных вехами или заборами границ земельных участков перейти к отвлеченному понятию линии, в частности прямой линии, не имеющей ни ширины, ни толщины. Надо было установить добытые практикой первоначальные геометрические истины (аксиомы), установить признаки равенства треугольников, научиться определять площадь треугольника и т. д. и т. п.
Если бы мы отказались пользоваться таким методом исследования пространственных форм, тогда геометрия как наука не могла бы существовать. В самом деле, изучая только веревочные треугольники и другие веревочные фигуры, мы обнаружили бы лишь отдельные случайные факты и не смогли бы из них сделать далеко идущие выводы общего порядка. Мы не сумели бы, например, установить сколько-нибудь полно взаимосвязь между сторонами и углами треугольника, между его площадью и сторонами и т. д.
Первоначальным источником всякого познания являются наши чувственные восприятия, получаемые из опыта, из наблюдений. Но данные, полученные из опыта, из наблюдений — это лишь первый шаг познания. Вторым его шагом является обобщение этих данных и их логическая обработка, т. е. создание теории. Но теория имеет значение только тогда, когда она применяется на практике. Поэтому третьим шагом познания является применение теории к практике, а вместе с тем и проверка на практике выводов теории.
Таким образом, всякое познание вырастает только из практики человеческого общества. (Здесь слово «практика» понимается в самом широком смысле. Под практикой понимается опыт, наблюдения, производство, техника, наука, искусство и культура.)
Математические теории имеют огромную ценность, так как без них невозможно решение крупных практических проблем*, связанных с техникой, производством и строительством, и теоретических проблем во многих других науках (механике, физике, аэродинамике, гидродинамике, радиолокации и т. д.).
* Проблема — это сложный практический или теоретический вопрос, подлежащий изучению, исследованию и разрешению. Слово «проблема» происходит от греческого слова
, что означает «задача». Буквальный перевод этого греческого слова — «нечто, брошенное вперед»*
Когда мы мысленно отвлекаемся от всего прочего содержания явления или предмета и изучаем только какую-нибудь одну существенную его сторону, например форму предмета или количественные отношения между его элементами, то говорят, что мы изучаем эту сторону явления или предмета абстрактно. Таким образом, математика есть наука абстрактная. Слово «абстракция» происходит от латинского слова «abstraciо», что означает «отвлечение». Поясним сказанное на примере.
Пусть предметом нашего изучения служит шар. Отвлекаясь от многих свойств шара (его цвета, материала, из которого он сделан, его веса и т. д.), выделим мысленно только одно его свойство: иметь объем. Но свойством иметь объем обладают и другие тела. Поэтому возникает такая задача: «Найти общий метод вычисления объемов тел любой формы, а не только шара». Силой абстракции такой общий метод в математике уже создан.
Абстрактное мышление есть более высокая ступень отражения в нашем сознании закономерностей и связей объективного мира, нежели живое созерцание или чувственные восприятия. Например, мы не слышим и не видим непрестанно распространяющиеся вокруг нас радиоволны. Несмотря на это, в ходе практической деятельности людей при помощи абстрактного мышления это явление познано и изучено настолько глубоко, что получило в руках людей широчайшее практическое применение (радиоприемники, телевизоры, радиолокационные приборы и т. д.).
Чувственным восприятием нельзя охватить движение со скоростью света, а абстрактному мышлению оно доступно. С помощью созерцания или чувственного восприятия мы не можем видеть ту закономерную зависимость, которая объективно существует между площадью и длинами сторон треугольника. С помощью же абстрактного мышления на базе уже ранее добытых практикой и теорией познаний мы эту зависимость в состоянии обнаружить. Таким образом, благодаря абстракции мы овладеваем правилом, позволяющим определять точно площадь треугольника по заданной длине его сторон.
Роль абстракции велика не только для познания окружающей нас природы, не только для построения математических и других естественнонаучных теорий. Она не в меньшей мере велика и для познания сущности явлений и законов развития общества. Приведем хотя бы одни пример.
Цена товара и его стоимость представляют собой совершенно различные понятия. Цены товаров на капиталистическом рынке колеблются в зависимости от спроса и предложения. Когда спрос на товары превышает их предложение, цены поднимаются и, наоборот, уменьшение спроса ведет к понижению цен. Не зная, что такое стоимость товара, можно подумать, что цена товара и есть его стоимость. В действительности же это совершенно неверно. Стоимость не зависит от спроса и предложения. Стоимость товара определяется количеством затраченного на его производство общественно необходимого труда.
В том случае, когда спрос и предложение находятся в равновесии, цена товара представляет собой денежное выражение стоимости. Однако такой идеальный случай на капиталистическом рынке никогда не может иметь места в силу анархии капиталистического способа производства. Стоимость есть важнейшая экономическая категория, хотя и не вечная. Особенно важное значение понятие стоимости имеет для анализа общественных отношений при капитализме. Сущность этих общественных отношений невозможно познать глубоко без понятия стоимости. Но понятие стоимости не могло бы возникнуть без абстракции. К. Маркс вывел его именно путем абстракции. Вот что он говорит по этому поводу: «…при анализе экономических форм нельзя пользоваться ни микроскопом, ни химическими реактивами. То и другое должна заменить сила абстракции» (К. Маркс, Капитал, т. 1, предисловие к первому изданию).
История дает множество примеров предвидения с помощью научной абстракции. В. И. Ленин в своем произведении «Что такое «друзья народа» и как они воюют против социал-демократов?», написанном нм еще в 1894 году (В. И. Ленин, Сочинения, т. 1, 1958) на основе научной революционной теории предвидел неизбежность социалистической революции в России. Гениальность этого величайшего предвидения В. И. Ленина подтвердила Великая Октябрьская социалистическая революция.
Д. И. Менделеев на основе открытого нм периодического закона предсказал свойства трех еще не открытых химических элементов. Вскоре после этого (с 1875 до 1886 г.) все эти три элемента были открыты. Предсказанные Д. И. Менделеевым свойства этих элементов подтвердились с большой точностью.
Изучая неправильность в движении Урана, французский астроном Леверье с помощью вычислений установил существование за пределами орбиты Урана другой, еще никому не известной планеты. Леверье указал момент времени и место на небесном своде, где должна была находиться эта планета. Точно в указанный момент времени и точно в указанном нм месте была действительно обнаружена берлинским астрономом Галле в сентябре месяце 1846 года неизвестная планета (позже названная Нептуном).
В заключение приведем замечательное высказывание В. И. Ленина о значимости абстракции. «Абстракция материи, закона природы, абстракция стоимости и т. д., одним словом все научные (правильные, серьезные, не вздорные) абстракции отражают природу глубже, .вернее, полнее». (В. И. Ленин, Философские тетради, 1947, стр. 146).
Возвращаясь к математике, заметим, что абстракция в математике, так же как и во всякой другой науке, не означает отрыва науки от материальной действительности. Например, запас количественных отношений и пространственных форм, изучаемых математикой, непрерывно расширяется именно в неразрывной связи с запросами производства, техники и естествознания.
Запросы производства и техники приводят к рождению в математике новых идей, новых методов. Усилиями ученых эти идеи и методы теоретически развиваются, обобщаются и после этого в свою очередь становятся на службу дальнейшему прогрессу техники и производства. Между техникой и наукой (в частности, математикой) происходит непрестанное чередующееся взаимодействие. Практика двигает вперед науку, наука двигает вперед практику.
Например, созданная промышленностью сложная аппаратура обеспечила физикам возможность проведения таких экспериментов, которые после теоретической обработки привели к открытию атомной энергии. В свою очередь физика атома сыграла огромную роль для дальнейшего развития техники. Например, современная металлургия, создающая новые сплавы с заданными свойствами, была бы немыслимой без исследования атомной структуры кристаллов.
Чередующееся взаимодействие наблюдается не только между практикой и наукой, но и между самими науками. Например, новые задачи, возникавшие в физике при изучении колебательных процессов, повлияли на развитие в математике теории дифференциальных уравнений. Достижения же по теории дифференциальных уравнений становились реальным орудием для разрешения в физике вопросов по теории колебаний, не только раньше возникших, нон более сложных, новых.
Новые методы и идеи в математике возникают не только из потребностей производства или других наук, но и из внутренних проблем самой математики (например, геометрия Лобачевского, теория функций комплексного переменного и многое другое).
Созданное великим Лобачевским в первой половине XIX века новое более широкое понимание предмета геометрии привело в конце XIX и начале XX века к перестройке всей системы математических знаний. То более широкое понятие пространства, которое возникло в геометрии Лобачевского, в дальнейшем оказалось тесно связанным с развитием физики в первую очередь теории относительности (начало этой теории положено Эйнштейном). Взаимосвязь, установленная в этой теории между массой и энергией, явилась основой всего учения об атомной энергии.
Вся история развития наук ярко свидетельствует о том, что обогащение математики, физики, химии, астрономии и других областей естествознания происходило в тесной взаимосвязи, в условиях взаимного воздействия достижений одних наук на успехи в других.
О возникающих у учащихся ошибочных взглядах на математику
В заключение сделаем еще несколько замечаний с целью помочь учащемуся правильно определить свое отношение к математике.
Еще до сих пор среди части учащихся существует представление об алгебре и математике вообще как о науке сухой, скучной, как бы уже полностью законченной и застывшей, как о науке, оторванной от жизни. Такое представление является совершенно неправильным, ошибочным, основанным на незнании сути дела. Напротив, математика есть живая, непрестанно развивающаяся наука, теснейшим образом связанная с жизнью, с практической деятельностью людей. Ежегодно издаются тысячи работ по математике, в которых ставятся и решаются все новые и новые теоретические и практические задачи.
Современная математика является мощным орудием, широко применяемым для решения теоретических и практических вопросов физики, механики (теоретической, строительной, небесной), радиотехники, аэродинамики, газовой динамики, кораблестроения, самолетостроения и т. д. Чтобы проиллюстрировать важность математических теорий, приведем хотя бы несколько характерных исторических примеров.
Пример:
Операции над комплексными числами были использованы Эйлером при решении важных и трудных вопросов гидродинамики.
Пример:
С помощью функций комплексного переменного Софья Кавалевская разрешила важную для развития теории гироскопов и гироскопических приборов задачу огромной трудности о вращении твердого тела вокруг неподвижной точки.
Пример:
Н. Е. Жуковский и С. Я. Чаплыгин блестяще воспользовались теорией функции комплексного переменного для определения подъемной силы крыла самолета и решения других важных вопросов гидро- и аэромеханики.
Пример:
Теории, разработанные для расчета движения планет под действием притяжения к Солнцу и между собой, оказались применимыми к решению вопросов, связанных с волновой качкой корабля.
Теория качки корабля при любом волнении создана впервые выдающимся русским ученым академиком А. Н. Крыловым. Путем труднейших математических исследований и расчетов им определены усилия, возникающие в различных частях корабля при его качке.
Труды А. Н. Крылова по кораблестроению доставили ему мировую известность и способствовали установлению приоритета и ведущей роли отечественной науки в этой области.
Пример:
Математическая теория Пуассона о равновесии компасной стрелки на протяжении целых 40 лет не находила практического применения. Между тем из-за погрешностей в показаниях компаса корабли нередко терпели аварии. И только после того как в 1862 году на протяжении лишь одного месяца у берегов Ирландии из-за неправильных показаний компаса погибли два океанских парохода, ученые и специалисты обратились к теории Пуассона. На базе этой теории были разработаны практические способы устранения погрешностей в показаниях морских компасов. Таким образом, математическая теория Пуассона помогла повысить безопасность мореплавания.
Пример:
В 1858 году через Атлантический океан был проложен первый телеграфный кабель. Оказалось, что один сигнал (точка или тире) передавался по этому кабелю в виде множества путаных знаков, исключавшего возможность что-либо разобрать.
Казалось, что огромные средства и труд, затраченные на сооружение кабеля, пропали безвозвратно. И вот выдающийся английский физик Уильям Томсон делает из математической теории теплопроводности, созданной знаменитым французским математиком Фурье еще в 1808 году и английским математиком Грином в 1828 году, такие практические выводы, при помощи которых удается фактически бездействующий кабель превратить в кабель, работающий совершенно нормально.
Все современные математические теории, приобретшие важную прикладную роль в естествознании и технике, связаны с высшей математикой, связаны так или иначе с дифференциальным и интегральным исчислениями. Но это обстоятельство не умаляет значения самой элементарной математики. Во-первых, элементарная математика является основой всех современных математических теорий (операции, производимые в этих теориях, неразрывно связаны с операциями элементарной математики). Во-вторых, имеется немало и таких практических и теоретических задач, для решения которых необходимы и достаточны лишь средства элементарной математики. Для иллюстрации приведем несколько таких задач. Решать эти задачи сейчас не требуется.
Задача:
Путем наблюдения с берега моря определить скорость корабля (движущегося прямолинейно и равномерно).
Задача:
На плоскости расположены произвольным образом 100 точек. Найти центр и радиус наименьшего круга, охватывающего собой все эти точки (рис. 3).
Задача:
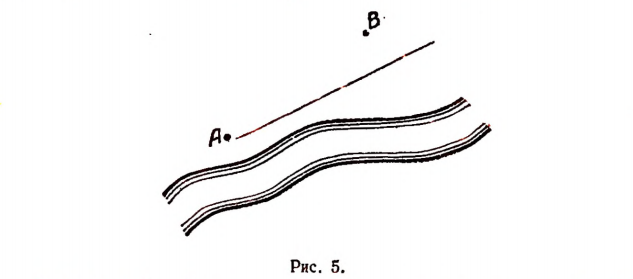
Дан прямоугольный лист железа размерами 80 см на 50 см (рис. 4). Требуется вырезать около всех его углов одинаковые квадраты так, чтобы после загибания остающихся кромок получилась открытая сверху коробка наибольшей вместимости.
3адача:
Не переходя реки, определить расстояние между пунктами А и В, расположенными за рекой (рис. 5).
3адача:
Доказать, что во всяком выпуклом многограннике сумма числа вершин и числа граней всегда на две единицы больше, чем число ребер (теорема Эйлера о многогранниках). Приведем иллюстрацию. В кубе (рис. 6) 8 вершин, 6 граней и 12 ребер. Сумма чисел 8 и 6 действительно на 2 больше, чем 12.
В пятиугольной пирамиде (рис. 7) 6 вершин, 6 граней и 10 ребер. Сумма чисел 6 и 6 действительно на 2 больше, чем 10.
Задача:
Доказать, что любое натуральное* число есть
сумма не более чем четырех квадратов. Например:
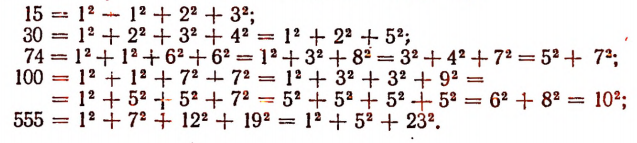
* Натуральным числом называется всякое целое число, большее нуля.
Задача:
Доказать, что сумма 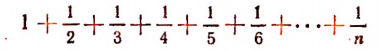
при достаточно большом значении целого положительного числа n может стать более любого числа, например более миллиарда, а сумма
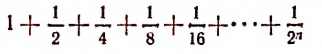
будет оставаться меньше 2, сколь большим ни брали бы мы число n .
Задача:
Разрезать равносторонний треугольник прямолинейными разрезами на 5 таких частей, из которых можно было бы составить квадрат, равновеликий этому равностороннему треугольнику (рис. 8).
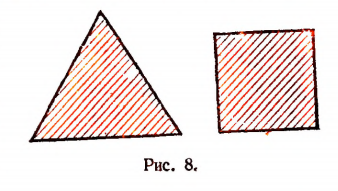
Математические решения задач о превращении одних фигур с помощью прямолинейных разрезов в другие, им равновеликие, применяются на практике в целях наиболее экономной раскройки промышленных материалов (листового Железа, кожи и других материалов).
В конце книги в приложении указана литература, в которой можно найти решения этих восьми задач. Разумеется, изучать эти решения удобнее после приобретения соответствующих знаний по алгебре, геометрии и тригонометрии.
Существует еще одно не совсем правильное представление о математике, а именно: часто считают, что для понимания и изучения математики требуются какие-то особые способности. В действительности это неверно. По совершенно справедливому мнению академика А. Н. Колмогорова, «Обычные средние человеческие способности вполне достаточны, чтобы при хорошем руководстве или по хорошим книгам не только сознательно усвоить математические знания, преподающиеся в средней школе, но и разобраться, например, в началах дифференциального и интегрального исчислений» (А. Н. Колмогоров, О профессии математика, «Советская наука», 1954). Изучить основы математики не труднее, чем основы какой-либо другой науки. В этом каждый может убедиться сам, если только станет приобретать математические знания шаг за шагом, соблюдая строгую последовательность в усвоении материала.
Мы сами являемся свидетелями того, как ежегодно десятки тысяч молодых людей, не ставивших себе задачу стать математиками, все же достаточно хорошо овладевают основами математики и становятся квалифицированными инженерами, техниками, агрономами или руководителями крупных предприятий.
Об инициативном подходе к изучению математики
Математика и свойственный ей стиль мышления представляют собой существенный элемент общей культуры современного человека, даже если он не занимается деятельностью в области точных наук или техники.
К изучению или решению всякого заслуживающего внимания вопроса надо подходить инициативно. Поясним это на простых примерах.
Пример:
Пусть требуется вычислить сумму всех целых чисел от 1 до 1000, т. е. следующую сумму:

Вычислять эту сумму путем последовательного прибавления каждого последующего слагаемого очень неудобно, так как на это потребуется много времени. Поэтому должна возникнуть мысль о том, нельзя ли определить эту сумму каким-нибудь косвенным рациональным способом.
Проявив наблюдательность, можно заметить, что: сумма двух крайних слагаемых равна 1001; сумма второго слагаемого и предпоследнего тоже равна 1001; сумма третьего слагаемого от начала и третьего от конца опять равна 1001 и т. д.
Легко видеть, что таких пар слагаемых будет 500. Следовательно, вся сумма равна произведению
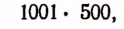
т. е. равна 500500.
Пример:
На прямой линии (рис. 9) найти такую точку, чтобы сумма ее расстояний до двух точек А и В, лежащих по одну сторону этой прямой, была бы наименьшей.
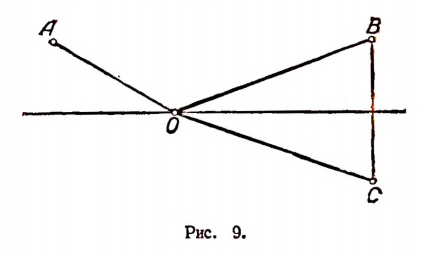
Выбор местоположения искомой точки на глаз не может гарантировать нам точность ответа. Находить положение искомой точки путем проб и измерений невозможно, так как такие пробы исчерпать нельзя. Значит, для решения поставленной задачи надо искать какое-то логическое суждение.
Нетрудно заметить, что путь по ломаной линии АОВ будет такой же, как и по ломаной линии АОС, где точка С есть точка, симметричная точке В относительно данной прямой. Но путь АОС будет самым коротким, если линия АОС окажется не ломаной, а прямой. Значит, искомая точка должна находиться на пересечении данной прямой с прямой, соединяющей точку А с точкой С, которая расположена симметрично точке В относительно данной прямой (рис. 10).
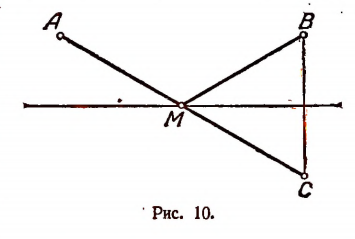
Пример:
Изучающий математику без инициативы, без наблюдательности, без собственных рассуждений и исканий не может развить свои математические способности. Например, такой человек, столкнувшись случайно с равенствами
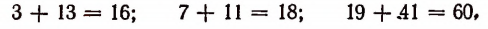
не обратит на них никакого внимания. Наблюдательный же человек может заметить между ними некоторое сходство. Он может заметить, что четные числа 16; 18; 60 являются суммами двух нечетных простых* чисел. У него может возникнуть вопрос: не является ли всякое четное число суммой двух простых нечетных чисел? Он начинает проверять это на других четных числах и получает следующую таблицу:

Эта таблица подтверждает его предположение.
* Простым числом называется всякое целое число, делящееся нацело только на себя и на единицу (последняя простым числом не считается). То, что последовательность простых чисел 2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47; 53; … конца не имеет, доказывается в теории чисел.
После этого у него возникает догадка, гипотеза следующего содержания: «Всякое четное число можно представить в виде суммы двух нечетных простых чисел». Но он еще не станет верить в эту догадку, в эту гипотезу. Ведь его опытная проверка не охватывает и не может никогда охватить все четные числа, так как им нет конца. Поэтому перед ним станет задача либо доказать эту гипотезу, либо ее опровергнуть. Эта гипотеза впервые была высказана в 1742 году Гольдбахом.
Попытки доказать или опровергнуть эту гипотезу Гольдбаха были безуспешными почти 200 лет. Один из лучших знатоков теории чисел начала нашего века — Ландау сказал на Международном математическом конгрессе 1912 года следующие слова: «Проблема Гольдбаха превосходит силы современной математики». Но в 1937 году советскому академику Виноградову удалось решить эту проблему для достаточно больших нечетных чисел.
Доказательство гипотезы Гольдбаха, найденное Виноградовым, быстро облетело математический мир. В докладах, прочитанных в математических обществах Франции, Англии и других стран, специалисты называли достижение Виноградова одним из самых блестящих проявлений человеческого гения в XX веке. Лондонское Королевское общество (Английская Академия наук) избрало Виноградова своим членом.
Мы привели один из классических примеров того, как из простого наблюдения может порой получиться в конце концов результат мирового значения.
Для того чтобы овладеть математическими знаниями и научиться применять их на практике умело, правильно и с пользой, надо усваивать эти знания шаг за шагом, систематически, добиваясь отчетливого понимания каждого вопроса. Надо помнить, что при изучении той или иной области любой науки ничто так не опасно, как знание наполовину, как заучивание без достаточного понимания. Кроме того, необходимо стремиться усваивать отдельные теоретические положения во взаимосвязи их друг с другом и во взаимосвязи с практикой. Вот что сказано о взаимосвязи теории и практики великим русским математиком П. Л. Чебышевым:
«Сближение теории с практикой дает самые благотворные результаты и не одна только практика от этого выигрывает: сами науки развиваются под влиянием ее; она открывает им новые предметы для исследования или новые стороны в предметах давно известных» (П. Л. Чебышев, Избранные математические труды, Огиз, 1946, стр. 150).
* * *
В заключение приведем несколько высказываний о математике, принадлежащих выдающимся деятелям науки, искусства и философии.
«Я глубоко почитаю математику, потому что знакомые с нею видят в ней средство к пониманию всего существующего». (Бхаскара— индийский ученый XII века.)
«Математика есть лучшее и даже единственное введение в изучение природы». (Писарев Д. И. — русский писатель и критик.)
«Многие, которым не представлялось случая более узнать математику, считают ее наукой сухой. В сущности же это наука, требующая наиболее фантазии, и один из первых математиков нашего столетия говорил совершенно верно, что нельзя быть математиком, не будучи поэтом в душе». (С. Ф. Ковалевская — выдающийся русский математик, первая в мире женщина-профессор.)
«В математике есть своя красота, как в живописи и поэзии». (Н. Е. Жуковский — великий русский ученый.)
«Подобно тому, как дар слова обогащает нас мнениями других, так язык математических знаков служит средством еще более совершенным, более точным и ясным, чтобы передавать другому понятия, которые он приобрел, истину, которую он открыл». (Н. И. Лобачевский — великий русский математик.)
В настоящее время математика празднует триумф в познании действительности и подчинении природы человеку. С помощью математики вычисляются орбиты искусственных спутников Земли и Солнца, траектории межпланетных кораблей и межконтинентальных ракет, рассчитываются плотины, гидроэлектростанции, атомные электростанции и другие гигантские сооружения современной техники, достигается автоматизация производства в крупных масштабах, удается давать долгосрочные прогнозы погоды, решать сложнейшие проблемы экономического планирования и проникать в тончайшие особенности строения вещества.
Римские цифры и алфавиты
В математике широко применяются латинские и греческие буквы для различных обозначений. Поэтому учащемуся, приступающему к изучению алгебры, необходимо предварительно ознакомиться с алфавитами этих букв, чтобы в дальнейшем по мере надобности усвоить их полнее и лучше.
Эти алфавиты, а также сведения о римских цифрах даны на следующих двух страницах.
Для обозначения того или иного века (до или после нашей эры), для нумерации глав в книгах и в некоторых других случаях иногда употребляют еще и до сих пор римскце цифры.
Римских цифр всего семь:
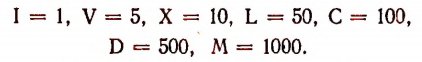
Числа первых двух десятков записываются так:
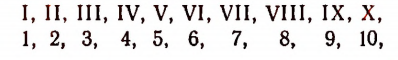

Если рядом стоят одинаковые цифры, то они складываются. Например:
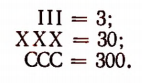
Если большая цифра предшествует меньшей, то они также складываются. Например:
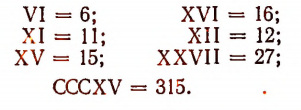
Если же большая цифра следует за меньшей, то из большей вычитается меньшая. Например:
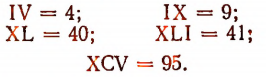
Записывать большие числа с помощью римских цифр крайне неудобно.
Что такое алгебра или предмет алгебры
Приступая к изучению какого-либо нового предмета, учащийся имеет право и обязан интересоваться тем, что представляет собой этот предмет и каким целям он служит.
Алгебра, так же как, например, арифметика или геометрия, является одним из разделов математики. О том, что такое математика, было сказано выше. Остается сказать о том, что такое алгебра.
Алгебра есть наука о числах более сложных, чем числа арифметические, и о способах решения задач, более общих и более мощных, чем способы арифметические.
Однако надо иметь в виду, что существуют и другие разделы математики, в которых изучаются числа, еще более сложные, чем те, которые изучаются в алгебре и которые дают способы решения задач, еще более общие и еще более мощные, чем алгебраические.
Преимущества алгебры перед арифметикой достигаются благодаря тому, что алгебра содержит учение о положительных и отрицательных числах, учение о правилах действий над числами в их буквенном изображении, и, наконец, благодаря тому, что в ней, кроме первых четырех действий, изучаются еще и другие, совершенно новые действия (возведение в степень, извлечение корня и логарифмирование).
Когда мы говорим, что алгебра по сравнению с арифметикой дает более мощные способы решения задач, то это означает, что с помощью алгебры можно разрешать не только такие задачи, которые разрешимы в арифметике, но и большой круг задач, которые средствами арифметики разрешить трудно или даже невозможно.
Значение алгебры очень велико. Алгебра есть такая основа, без которой не могли бы оформиться, развиваться и применяться на практике геометрия, тригонометрия, высшая математика и все пользующиеся математическими методами науки.
Чтобы хорошо усвоить алгебру, необходимо весь материал изучать систематически, последовательно, без пропусков. Ни в коем случае не следует практиковать заучивание без понимания.
Усвоение теории не может оказаться прочным и глубоким, если ее не применять на .практике. Поэтому, изучая теоретический материал, необходимо параллельно этому упражняться в решении примеров и задач. При этом полезно уделять внимание трудным задачам, для решения которых необходимы находчивость и изобретательность.
Положительные и отрицательные числа
Величины, отсчитываемые в двух противоположных направлениях:
Существуют величины, отсчет которых приходится производить в двух противоположных направлениях. Например, расстояние от ст. Бологое по Октябрьской железной дороге можно отсчитывать в сторону как Москвы, так и Ленинграда (рис. 11).
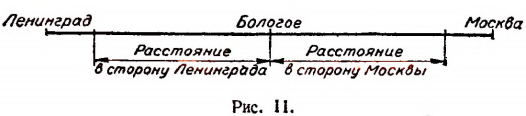
Температура отсчитывается в двух противоположных направлениях от температуры тающего льда, принимаемой за нулевую (рис. 12).
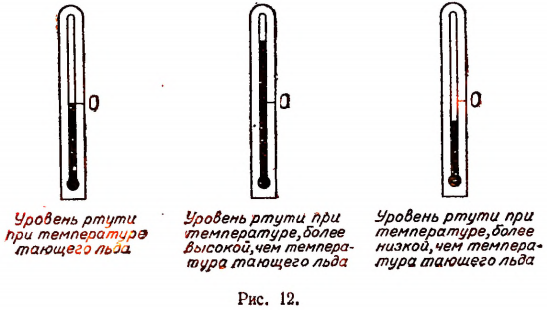
Отклонение маятника от вертикального положения можно отсчитывать как в сторону, противоположную движению часовой стрелки (вправо), так и в сторону движения часовой стрелки (влево) (рис. 13).
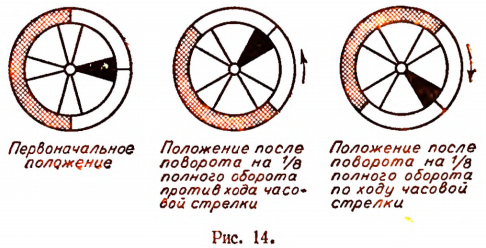
Поворот махового колеса можно отсчитывать как в сторону, противоположную движению часовой стрелки, так и в сторону движения часовой стрелки (рис. 14).
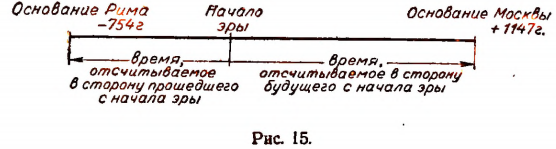
Время можно отсчитывать как в сторону будущего, так и в сторону прошедшего по отношению к тому или иному избранному моменту. Например, календарное время до сих ,пор почти во всех странах отсчитывается в ту и другую сторону с момента начала нашей эры (см. рис. 15).
Возникновение положительных и отрицательных чисел
Пусть мы имеем какую-либо величину, отсчет которой приходится производить в двух противоположных направлениях. Одно из этих направлений, безразлично какое, принято называть положительным, а другое отрицательным.
Число, полученное в результате измерения величины, отсчитанной в положительном направлении, называется положительным числом и изображается с помощью арифметического числа со знаком + (плюс) впереди. Например, +12 есть положительное число. (Арифметическими числами мы называем здесь числа, известные из арифметики.)
Число, полученное в результате измерения величины, отсчитанной в отрицательном направлении, называется отрицательным числом и изображается с помощью арифметического числа со знаком — (минус) впереди. Например, —12 есть отрицательное число.
Приведем примеры.
Пример:
Примем за положительное направление — направление от ст. Бологое в сторону Москвы. Тогда фраза «Локомотив находится от ст. Бологое на расстоянии + 25 км» будет означать, что локомотив находится от ст. Бологое на расстоянии 25 км в сторону Москвы, фраза же «Локомотив находится от ст. Бологое на расстоянии — 25 км будет означать , что локомотив находится от ст. Бологое на расстоянии 25 км в сторону Ленинграда.
Пример:
Примем за положительное направление вращения — вращение против хода часовой стрелки. Тогда фраза «Колесо повернулось на + оборота» будет означать, что колесо совершило
оборота» будет означать, что колесо совершило  оборота против хода часовой стрелки. Фраза же «Колесо повернулось на —
оборота против хода часовой стрелки. Фраза же «Колесо повернулось на —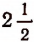 оборота» будет означать, что колесо совершило
оборота» будет означать, что колесо совершило 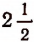 оборота по ходу часовой стрелки.
оборота по ходу часовой стрелки.
Пример:
Примем за положительное направление отсчета времени направление в сторону будущего с момента начала эры. Тогда фраза «Событие произошло в +1147 году» будет означать, что событие произошло в 1147 году после начала нашей эры. Фраза же «Событие произошло в — 754 году» будет означать, что событие произошло в 754 году до начала нашей эры (рис. 15).
Итак, все арифметические числа, кроме нуля, записанные со знаком + (плюс) впереди, будут числами положительными, а записанные со знаком — (минус) — отрицательными. Например,
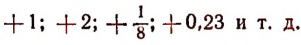
суть числа положительные;
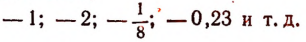
суть числа отрицательные.
3. О нуле
Ставить перед числом нуль какой-либо знак (+ или — ) не имеет смысла, так как символы + 0; — 0 и 0 представляют собой одно и то же. Среди положительных и отрицательных чисел нуль занимает особое место; нуль есть число не положительное и не отрицательное.
О величинах, отсчет которых в двух противоположных направлениях не производится
Наряду с величинами, отсчет которых приходится производить в двух противоположных направлениях, существуют величины, отсчет которых в различных направлениях не имеет смысла. Например, площадь комнаты, число жильцов в квартире и др. Действительно, бессмысленно говорить, что площадь комнаты равна —24 кв.м или что число жильцов в квартире равно —8 и т.д. Принято говорить, что площадь комнаты равна 24 кв.м, число жильцов в квартире равно 8.
Таким образом, величины, отсчет которых в двух противоположных направлениях не имеет смысла, изображаются просто арифметическими числами.
Упрощенное обозначение положительных чисел
Выше было сказано, что положительное число изображается арифметическим числом со знаком + (плюс) впереди. Наряду с этим принято и другое, более краткое обозначение положительного числа, а именно: для обозначения положительного числа употребляется просто арифметическое число. Например, вместо
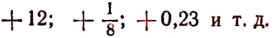
пишут просто
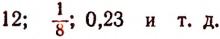
Таким образом, арифметические числа рассматриваются в алгебре как числа положительные. Следовательно, такие величины, как площадь комнаты, число жильцов в квартире, емкость сосуда и т.п., выражаются в алгебре только положительными числами.
Примечание:
Положительные и отрицательные числа, включая нуль, иногда называют относительными числами. Однако употреблять термин «относительные числа» не следует, так как в науке он не принят.
Противоположные числа
Отсчитаем 50 км от ст. Бологое в сторону Москвы и те же 50 км в сторону Ленинграда. Полученные числа + 50 и — 50 называются противоположными.
Определение:
Если какую-либо определенную величину, допускающую отсчет в двух противоположных направлениях, отсчитать в положительном и отрицательном направлениях, то полученные в результате этих двух отсчетов числа называются противоположными. Например, числа
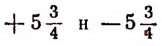
противоположны. Если данное число 7, то ему противоположным будет — 7. Если данное число — 7, то ему противоположным будет 7. Если данное число нуль, то ему противоположным будет также нуль.
Абсолютная величина числа
При решении различных вопросов, в которых встречаются положительные и отрицательные числа, мы обязаны, как правило, учитывать направление отсчета величин, изображаемых этими числами.
Например, решим такую задачу: «Локомотив прошел от ст. Бологое 4- 120 км, а затем еще — 140 км. Определить местоположение локомотива после этих двух пробегов». (Как и раньше, будем считать положительным направлением направление от ст. Бологое в сторону Москвы.) Для решения этой задачи нам необходимо учитывать направление движения локомотива как в первом, так и во втором случае.
Сначала локомотив прошел 120 км от ст. Бологое в сторону Москвы, а затем прошел 140 км в обратную сторону, т. е. в сторону Ленинграда. Очевидно, что после этих двух пробегов локомотив оказался на расстоянии 20 км от ст. Бологое в сторону Ленинграда.
Таким образом, для решения этой задачи нам пришлось учитывать направления движения локомотива как в первом, так и во втором случае.
Однако встречаются и такие задачи, для решения которых совершенно не нужно учитывать направление отсчета. Например, решим такую задачу: «Локомотив прошел сперва + 120 км, а затем еще — 140 км. Определить общий пробег локомотива в километрах». Для определения общего пробега достаточно сложить два положительных числа 120 и 140, т. е. нет никакой надобности учитывать направления движения локомотива. Очевидно, что общий пробег локомотива составляет 260 км.
Если бы локомотив прошел сперва — 120 км, а затем еще — 140 км, то общий пробег опять составил бы 260 км.
Таким образом, при решении этой задачи нам совершенно не нужно было учитывать направления отсчета. Вместо отрицательных чисел мы брали числа положительные, противоположные этим отрицательным числам. Например, вместо числа — 120 мы брали число 120.
Все это побуждает нас ввести новое важное понятие, а именно понятие абсолютной величины числа.
Определение:
Абсолютной величиной положительного числа называется само это число. Абсолютной величиной отрицательного числа называется число, ему противоположное.
Абсолютной величиной числа нуль называется само число нуль.
Обратим внимание на то, что абсолютная величина всякого, отрицательного числа есть число положительное.
Примеры:
Абсолютная величина числа + 5 (или 5) есть + 5 (или 5).
Абсолютная величина числа — 5 есть число + 5 (или 5).
Противоположные числа имеют одинаковую абсолютную величину. Например, числа + 10 и — 10 имеют одну и ту же абсолютную величину, равную + 10 или 10.
Абсолютная величина любого числа, например числа + 7, обозначается символом |+ 7|.
Символ |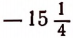 | обозначает абсолютную величину числа
| обозначает абсолютную величину числа 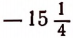 .
.
Таким образом, можно писать
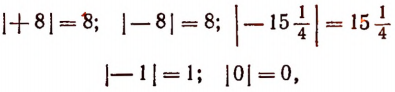
Четыре действия над положительными и отрицательными числами
1. Общие замечания
Для указания первых четырех действий над положительными и отрицательными числами употребляются те же знаки, что и в арифметике.
Правила сложения и умножения положительных и отрицательных чисел устанавливаются по определению, а потому не подлежат доказательству. Правила же вычитания и деления выводятся из принятых правил сложения и умножения.
2. Сложение
Как складывать положительные числа, известно из арифметики. Например:
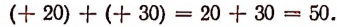
Прежде чем формулировать правила сложения для остальных случаев, мы рассмотрим задачи, решения которых подскажут нам целесообразные определения этих правил.
Пусть колесо повернулось на — 20°, иначе говоря, оно повернулось на 20° по ходу часовой стрелки; пусть после этого оно повернулось еще на — 30°. В результате этих двух поворотов колесо отклонится от первоначального положения по ходу часовой стрелки на 50°, иначе говоря, на — 50°. Следовательно,
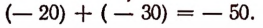
Правило 1. Чтобы сложить два отрицательных числа, надо сложить их абсолютные величины и перед полученной суммой поставить знак минус. Например:
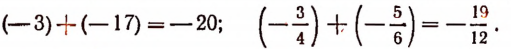
Пусть колесо повернулось на — 20°, а затем еще на + 12°. В результате этих двух поворотов колесо окажется отклоненным от первоначального положения на 8° по ходу часовой стрелки, иначе говоря, на — 8°. Следовательно,
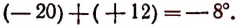
Правило 2. Чтобы сложить два числа, из которых одно положительное, а другое отрицательное и которые имеют разные абсолютные величины, надо из большей абсолютной величины вычесть меньшую и перед полученным результатом поставить знак того из слагаемых, у которого абсолютная величина больше. Например:
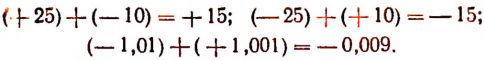
Правило 3. Сумма двух противоположных чисел равна нулю. Например:
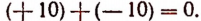
Замечание:
Сумма двух не противоположных чисел отлична от нуля.
Следствие:
Сумма двух чисел равна нулю лишь тогда, когда эти числа противоположны.
Правило 4. Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому. Например:
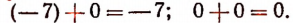
Сложение трех и более чисел
Чтобы найти сумму трех и более чисел, достаточно к первому числу прибавить второе, затем к полученному результату прибавить третье и т. д. Например:
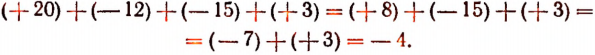
Основные свойства сложения
1.Сумма двух чисел не изменяется от изменения порядка слагаемых (переместительный или коммутативный закон сложения). Например:

Справедливость этого закона вытекает из того, что в правилах сложения оба слагаемых равноправны.
2. Сумма не изменится, если в ней часть слагаемых мы заменим их суммой (сочетательный или ассоциативный закон сложения). Например:
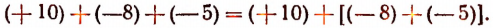
Из этих двух законов следует следующее общее правило.
Правило. При вычислении суммы любого числа слагаемых можно произвольно переставлять эти слагаемые, а также произвольно разбивать их на группы и каждую группу слагаемых заменять их суммой.
(Доказательство этого правила, так же как и сочетательного закона, опускается для облегчения курса). Из этого правила вытекает следствие.
Следствие:
Чтобы прибавить сумму, можно прибавить одно за другим все входящие в нее слагаемые. Например:
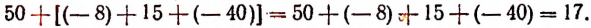
3. Вычитание
Вычитание есть действие, обратное сложению.
Пусть имеется два каких-нибудь числа.
Вычесть из первого числа второе — это значит найти такое третье число, сумма которого со вторым даст первое. (Здесь первое число называется уменьшаемым, второе — вычитаемым и третье — разностью.)
Правило вычитания нельзя устанавливать по определению, так как оно вытекает из правила сложения и определения действия вычитания.
Пусть требуется из числа + 10 вычесть число — 8, т. е. найти разность

Здесь 10 есть уменьшаемое, а — 8 вычитаемое.
Искомая разность должна быть таким числом, чтобы от прибавления его к вычитаемому получилось уменьшаемое. Легко проверить, что таким числом будет + 18. Это число + 18 мы можем получить путем прибавления к уменьшаемому числа, противоположного вычитаемому. Поэтому разность

представляет собой то же самое число, что и сумма
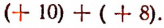
Отсюда вытекает следующее правило вычитания.
Правило. Чтобы вычесть из одного числа другое, достаточно к первому прибавить число, противоположное второму.
Примеры:
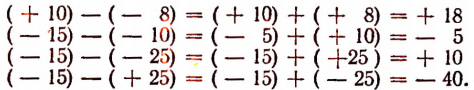
Таким образом, разность чисел всегда можно представить в виде соответствующей суммы, т. е. вычитание сводить к сложению.
Выше, в четвертом равенстве, мы получили, что
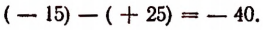
Вычитание здесь сделано правильно. В самом деле, если мы сложим числа + 25 и— 40, то получим — 15, т. е. как раз уменьшаемое.
Также можно проверять правильность произведенного вычитания и во всех других случаях.
Проиллюстрируем действие вычитания на практических примерах.
Пример:\
Пусть температура одного тела равна + 10°, а другого — 8°. Чтобы найти разность между температурой первого тела и температурой второго, мы должны из + 10° вычесть — 8°. Выполняя это действие, получим
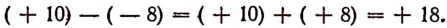
Этот результат соответствует действительности. В самом деле, если температура одного тела 10° выше нуля, а другого 8° ниже нуля, то скачок от одной температуры к другой действительно составляет 18°.
Рассмотрим тот же пример, поменяв местами уменьшаемое и вычитаемое. Пусть температура первого тела — 8°, а второго + 10°. Тогда разность между температурой первого тела и второго будет
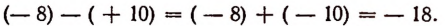
И здесь скачок от одной температуры к другой равен 18°.
Обратив внимание на знаки двух последних разностей, заметим следующее. Когда уменьшаемым служит число, выражающее более высокую температуру, а вычитаемым — более низкую, то разность оказывается числом положительным, а именно:

Когда же, наоборот, уменьшаемым служит число, выражающее более низкую температуру, а вычитаемым — более высокую, то разность оказывается числом отрицательным. Действительно,
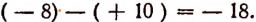
Пример:
На рисунке 16 изображены высоты известных гор с помощью вертикальных отрезков. Числа, проставленные над каждым вертикальным отрезком, выражают в метрах высоту соответствующей горы над уровнем моря. Выразим с помощью положительных и отрицательных чисел высоты этих гор, но не по отношению к уровню моря, а по отношению к уровню вершины Арарата, т. е. приняв уровень вершины Арарата равным нулю.
На рисунке 17 высоты тех же гор уже выражены с помощью положительных и отрицательных чисел.
Вычтем из числа ( + 3692) число (— 346):
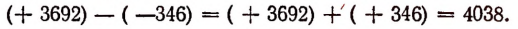
Число + 4038 показывает, что Эверест выше Монблана на 4038 м.
Эверест — высочайшая вершина земного шара; находится в Азии на Главном Гималайском хребте.
Пик Коммунизма — высшая точка Памира; находится в Азии, на территории СССР.
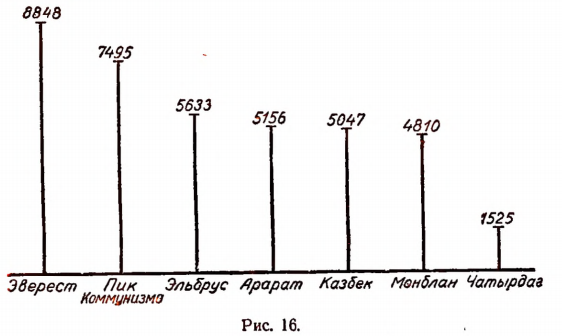
Эльбрус — высшая точка Кавказского хребта.
Арарат находится в Турции вблизи столицы Армении—Еревана.
Казбгк находится на территории Грузинской ССР.

Монблан — высшая точка Западной Европы; находится на границе Франции, Италии и Швейцарии.
Чатырдаг находится в Крыму.
В заключение сделаем следующее важное замечание.
Введение отрицательных чисел делает выполнимым действие вычитания во всех случаях.
Например:
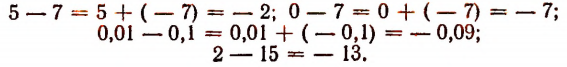
4. Умножение
Как умножаются положительные числа, известно из арифметики. Например:
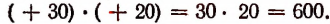
Теперь нам надо выяснить, как же следует умножать два отрицательных числа или два числа, из которых одно положительное, а другое отрицательное.
С этой целью рассмотрим одну из задач, решение которой подскажет нам целесообразное правило умножения положительных и отрицательных чисел для всех случаев. В качестве такой задачи рассмотрим задачу, в которой требуется вычислить работу, произведенную силой. Но прежде чем формулировать эту задачу, изложим необходимые предварительные сведения.
Пусть к твердому телу, расположенному на прямой Х1Х, приложены силы, действующие по этой прямой Х1Х в двух противоположных направлениях (рис. 18). Силу, действующую вправо,
условимся выражать положительным числом, а влево—отрицательным. Под действием таких сил тело может перемещаться по прямой Х1Х . Перемещение тела вправо будем выражать положительным числом, а влево — отрицательным.

Если перемещение тела происходит вдоль той же прямой, по которой действует сила, то произведение силы на перемещение называется работой, произведенной этой силой.
В том случае, когда направление силы совпадает с направлением перемещения, работу, произведенную этой силой, естественно считать положительной, в противном случае — отрицательной.
В самом деле, когда сила действует в направлении, противоположном перемещению, то она является силой, тормозящей движение, а потому естественно считать работу, производимую ею, отрицательной.
Таким образом, здесь нам приходится иметь дело с тремя величинами: силой, перемещением и работой.
Обратим внимание на то, что каждая из этих величии может иметь как положительное, так и отрицательное значение. Теперь поставим следующую задачу.
Задача:
К твердому телу, расположенному на прямой X1X, приложены две силы: — 12 кг и +4 кг, действующие по этой же прямой X1X . Пусть под действием этих сил тело переместилось вдоль прямой X1X на — 5 м. Найти работу, произведенную каждой силой в отдельности.
Решение:
Работа, произведенная первой силой, будет положительной, и равной 60 кгм (килограммометрам), так как направление ее действия совпадает с направлением происшедшего перемещения. Поэтому
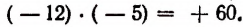
Работа, произведенная второй силой, будет отрицательной, равной — 20 килограммометрам, так как направление ее действия противоположно направлению происшедшего перемещения. Поэтому
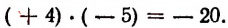
Рассматривая решения только что разобранной задачи и других подобных задач, естественно прийти к принятию следующих правил:
- Произведение двух отрицательных чисел равно произведению их абсолютных величин.
- Произведение двух чисел, из которых одно положительное, а второе отрицательное, равно отрицательному числу, абсолютная величина которого равна произведению абсолютных величин сомножителей.
- Произведение двух чисел равно нулю, если хотя бы одно из них равно нулю.
Приведем примеры на все эти правила.
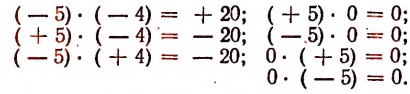
Следуя изложенному правилу умножения, мы всегда будем получать правильный результат. Подтвердим сказанное еще на одном примере.
Пример:
Пусть паровоз движется без остановок с постоянной скоростью по Октябрьской железной дороге и пусть в нуль часов, т. е. в полночь, он проходит ст. Бологое (рис. 19).

Расстояние от ст. Бологое до паровоза в сторону Москвы будем выражать положительным числом; тогда расстояние в сторону Ленинграда мы обязаны будем выражать числом отрицательным. Скорость паровоза условимся выражать положительным числом, если движение паровоза совершается по направлению от Ленинграда к Москве, и отрицательным числом в противном случае. Момент времени после момента нуль часов будем выражать положительным числом, а момент времени до момента нуль часов — числом отрицательным.

Таким образом, в этом примере нам приходится иметь дело с тремя величинами: расстоянием, скоростью и временем. Обратим внимание на то, что каждая из этих величин является величиной, отсчет которой ведется в двух противоположных направлениях. Таким образом, каждая из этих трех величин может иметь как положительные, так и отрицательные значения.
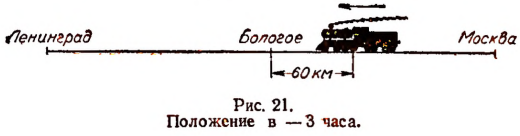
Вспомним, что в нуль часов, т. е. в полночь, паровоз проходит ст. Бологое и предположим для определенности, что скорость паровоза равна — 20 км в час, а время равно — 3 часам. Это значит, что паровоз движется по направлению от Москвы к Ленинграду и что момент времени, который мы рассматриваем, есть момент, предшествующий на 3 часа моменту нуль часов (рис. 20).
Очевидно, что в — 3 часа паровоз находился от станции Бологое на расстоянии 60 км в сторону Москвы (рис. 21).
С другой стороны мы знаем, что для отыскания расстояния от ст. Бологое до паровоза достаточно скорость — 20 км умножить на время — 3 часа. Выполняя это умножение по установленному правилу, получим
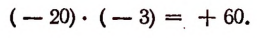
Число +60 как раз свидетельствует о том, что паровоз находится от ст. Бологое на расстоянии 60 км в сторону Москвы, что в точности согласуется с действительностью.
Рекомендуется рассмотреть этот пример при других выбранных значениях скорости и момента времени.
Произведение трех и более чисел
Чтобы найти произведение трех и более чисел, достаточно первое умножить на второе, затем полученный результат умножить на третье и т. д. Например:
Основные свойства умножения
1. Произведение чисел не меняется от перемены мест множителей (переместительный или коммутативный закон умножения). Например:

2. Произведение не изменится, если часть множителей заменить их произведением (сочетательный или ассоциативный закон умножения). Например:
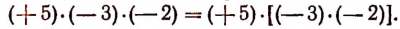
3. Произведение суммы чисел на число равно сумме произведений слагаемых на это число (распределительный или дистрибутивный закон умножения). Например:
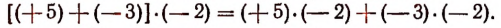
Из этих свойств вытекает следующее правило.
Правило. Произведение любого числа множителей не изменится, если произвольно переставлять множители, а также если их произвольно разбивать на группы и каждую группу множителей заменять их произведением.
(Доказательство этого правила, а также законов умножения опускается для облегчения курса.)
Пример:
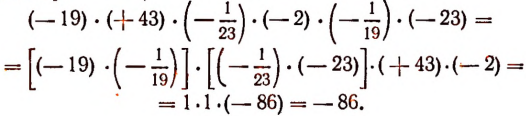
5. Деление
Деление есть действие обратное умножению.
Пусть имеется два каких-нибудь числа. Разделить первое на второе—это значит найти такое третье число, произведение которого на второе равно первому. (Здесь первое число называется делимым, второе—делителем и третье— частным.)
Правило деления нельзя устанавливать по определению, так как оно вытекает из правила умножения и определения действия деления. Исходя из правила умножения и определения действия деления, легко вывести следующие правила деления.
Правило. Абсолютная величина частного равна частному от деления абсолютной величины делимого на абсолютную величину делителя. При этом частное будет положительным, если делимое и делитель оба положительны или оба отрицательны. Частное будет отрицательным, если из двух чисел—делимого и делителя — одно положительно, а другое отрицательно. Частное равно нулю, если делимое равно нулю, а делитель отличен от нуля.
Деление невозможно, если делитель равен нулю.
Примеры:

Правильность деления можно проверить умножением делителя на частное. Очевидно, что
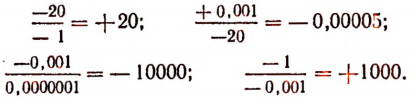
Упражнения. Найти значения следующих выражений:
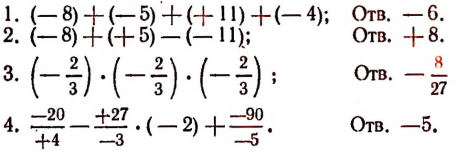
6. Несколько замечаний, относящихся к четырем действиям над числами
В выражении
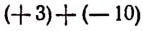
знак +, стоящий между скобками, есть знак действия сложения, остальные же знаки (+) и (—) являются не знаками действий, а лишь знаками, характеризующими направление отсчета.
Когда два числа, имеющие перед собой знаки + или —, соединяются между собой с помощью знака сложения или вычитания, то сами эти положительные или отрицательные числа записываются в скобках.
Выражение 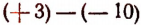 есть разность между числами + 3 и —10.
есть разность между числами + 3 и —10.
Выражение 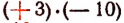 или
или 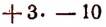 есть произведение чисел +3 и — 10.
есть произведение чисел +3 и — 10.
Выражение 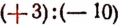 , или
, или 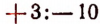 , или
, или 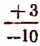 есть частное.
есть частное.
7. Особенности чисел 0 и 1
Особенности нуля
Нуль есть единственное число, обладающее следующими свойствами:
1. Если одно из двух слагаемых есть нуль, то сумма равна другому слагаемому. Например:
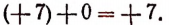
2. Если один из множителей есть нуль, а остальные несколько множителей какие угодно числа, то произведение также будет равно нулю. Например:
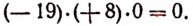
Следствие. Если делимое есть нуль, а делитель не нуль, то частное будет представлять собой также нуль. Например:
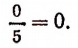
3. Деление на нуль невозможно. Например, выражения 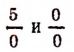
смысла не имеют.
Символ 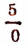 не представляет собой никакого числа, так как произведение любого числа на нуль будет равно нулю, между тем как делимое отлично от нуля.
не представляет собой никакого числа, так как произведение любого числа на нуль будет равно нулю, между тем как делимое отлично от нуля.
Бессмысленно спрашивать, во сколько раз 5 больше нуля.
Символ 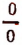 не представляет собой определенного числа, так как произведение любого числа на нуль будет равно нулю.
не представляет собой определенного числа, так как произведение любого числа на нуль будет равно нулю.
Бессмысленно спрашивать, во сколько раз нуль больше нуля.
Особенность положительной единицы
Положительная единица есть единственное число, обладающее следующим свойством.
Если один из двух множителей есть +1, то произведение равно другому множителю, каким бы числом он ни был. Например:
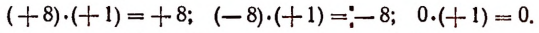
Следствие. Если делитель равен +1, то частное равно делимому. Например:
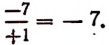
§ 3. ПОНЯТИЕ «БОЛЬШЕ» И «МЕНЬШЕ» ПРИМЕНИТЕЛЬНО К ПОЛОЖИТЕЛЬНЫМ И ОТРИЦАТЕЛЬНЫМ ЧИСЛАМ
Определение. Если разность между двумя числами положительна, то число, являющееся уменьшаемым, условились считать большим, числа, являющегося вычитаемым. Например, разность между числом —2 и числом —10, равная
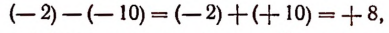
представляет собой число положительное. Следовательно,—2 больше, чем —10, или в краткой записи:
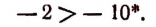
* Острие знака неравенства всегда обращается в сторону меньшего числа. Например, запись 5 > 3 читается так: пять больше трех. Запись 2 < 7 читается так: два меньше семи.
Если разность между двумя числами отрицательна, то число, являющееся уменьшаемым, следует считать меньшим числа, являющегося вычитаемым. Например, разность между числами —10 и — 2, равная
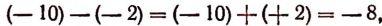
представляет собой число отрицательное. Следовательно, —10 меньше, чем —2 или кратко
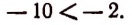
Из принятого определения следует, что:
1. Всякое положительное число больше нуля и больше всякого отрицательного числа. Например:
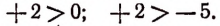
2. Всякое отрицательное число меньше нуля и меньше всякого положительного числа. Например:
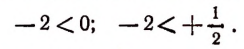
3. Из двух отрицательных чисел то больше, у которого абсолютная величина меньше. Например:
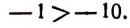
Изложенное о сравнении чисел проиллюстрируем на конкретных примерах.
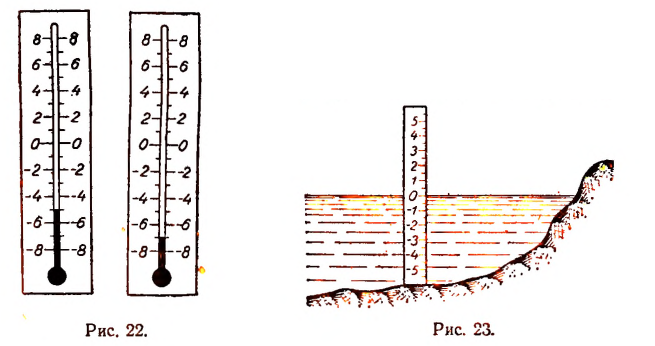
Пример:
Рассмотрим два показания термометра — 5° и — 7° (рис. 22).
По данному выше формальному определению число — 5 больше, чем число — 7, так как разность
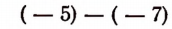
равна положительному числу.
Когда мы говорим, что — 5 больше, чем — 7, то в нашем конкретном примере это значит, что температура — 5° выше температуры — 7°.
Аналогично можно истолковать и смысл неравенств
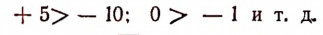
Отсюда становится понятным, почему всякое положительное число больше всякого отрицательного; почему нуль больше всякого отрицательного числа, почему — 10 больше, чем — 100.
Пример:
Пусть на водомерной рейке отметка нуль соответствует среднему уровню воды в озере, а отметки положительные — уровням выше среднего: отметки же отрицательные — уровням пониженным (рис. 23).
Рассмотрим два различных показания рейки, а именно — 1 и — 2 (рис. 24, 25).
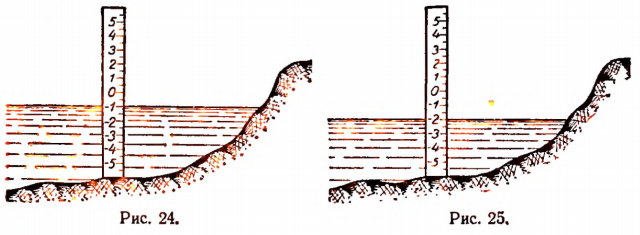
Число — 1 больше, чем число — 2, так как разность 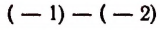 равна положительному числу.
равна положительному числу.
В этом конкретном примере неравенство 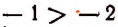 означает, что уровень воды в озере при показании— 1 выше, чем при показании — 2.
означает, что уровень воды в озере при показании— 1 выше, чем при показании — 2.
Аналогично можно истолковать смысл неравенств
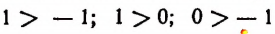
И т. д.
Примеры:
Расположив числа
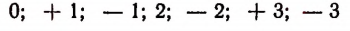
в порядке возрастания, получим
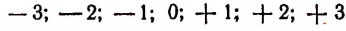
Расположив числа
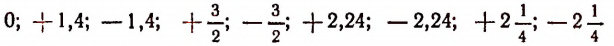
в порядке возрастания, получим
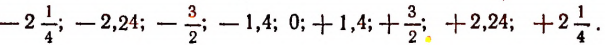
§ 4. ЧИСЛОВАЯ ОСЬ
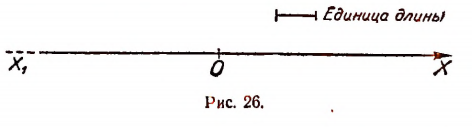
Многим свойствам чисел можно придать наглядность с помощью числовой оси. Возьмем прямую Х1Х с начальной на ней точкой О и примем длину некоторого отрезка за единицу (рис. 26). Эту прямую условимся называть осью.
Отложим по оси Х1Х от точки О единицу длины вправо и влево 1, 2, 3, 4, 5 и т. д. раз. Концы полученных отрезков, расположенных справа, отметим с помощью положительных чисел, + 1, + 2, +3, + 4, + 5 и т. д., а расположенные слева — с помощью отрицательных чисел —1, —2, —3, — 4, — 5 и т. д. (рис. 27).
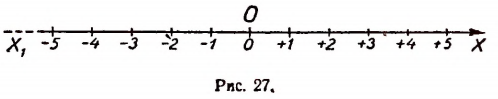
Числу нуль поставим в соответствие начальную точку О. Таким образом, каждое целое число (положительное, отрицательное и нуль) изобразится одной и только одной точкой оси Х1Х .
Чтобы отметить на оси Х1Х дробное число, например 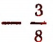 , разделим единицу длины на восемь равных частей и три такие части отложим влево от начальной точки О. Так же поступим и со всяким другим дробным или смешанным числом.. Таким образом, и каждое дробное число, как положительное, так и отрицательное, изобразится одной и только одной точкой оси Х1Х .
, разделим единицу длины на восемь равных частей и три такие части отложим влево от начальной точки О. Так же поступим и со всяким другим дробным или смешанным числом.. Таким образом, и каждое дробное число, как положительное, так и отрицательное, изобразится одной и только одной точкой оси Х1Х .
Когда мы говорим, что число изображается точкой, то это не следует понимать так, что точка и число представляют собой одно и то же.
Напротив, точка и число совершенно различные понятия, совершенно различные вещи. Поэтому, когда мы говорим, что данная точка есть изображение числа, например 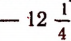 , то это значит, что эта точка находится на расстоянии
, то это значит, что эта точка находится на расстоянии 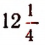 единиц длины влево от начальной точки О.
единиц длины влево от начальной точки О.
Прямая, на которой указанным выше способом отмечены точки, соответствующие положительным и отрицательным числам, называется числовой осью.
Вместо того чтобы говорить «точка соответствует числу  » , говорят просто «точка
» , говорят просто «точка  » и т. п.
» и т. п.
Число, которое изображается данной точкой, называется координатой этой точки.
Расположение чисел в порядке возрастания наглядно видно на числовой оси. А именно, из двух чисел большим будет то, которое на нашей числовой оси расположено правее изображения другого числа.
Например: 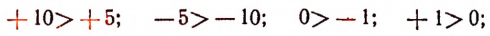
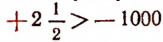 (см. рис. 28).
(см. рис. 28).

Изображения двух противоположных чисел симметричны относительно начальной точки О, например изображения чисел + 5 и —5 (рис. 29).

Два числа считаются равными, если их разность равна нулю. Например, —5 равно —5, так как 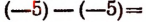
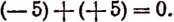
§ 5. ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ УМНОЖЕНИЯ
В § 4 была показана возможность изображать положительные и отрицательные числа точками числовой оси. Наряду с этим мы можем ввести еще одно геометрическое изображение положительных и отрицательных чисел. А именно, каждому числу поставим в соответствие вектор (т. е. направленный отрезок), началом которого служит начальная точка числовой оси, а концом — точка, являющаяся изображением данного числа на числовой оси.
Например, числам + 5 и — 2 соответствуют на числовой оси (рис. 30) векторы 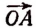 и
и 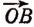 . (Вектором
. (Вектором 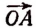 называется отрезок OA с направлением от О к А).
называется отрезок OA с направлением от О к А).
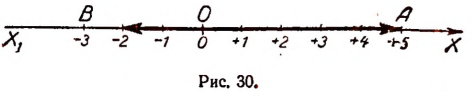
Теперь посмотрим, какая операция над векторами соответствует операции умножения двух чисел.
Примеры:
- Умножив число + 5 на число + 1, получим + 5; умножив число —5 на + 1, получим —5, т. е. при умножении числа на + 1 вектор, соответствующий произведению, совпадаете вектором, соответствующим множимому.
- Умножив число + 5 на число — 1, получим — 5; умножив число — 5 на — I, получим + 5, т. е. при умножении числа на — 1 вектор, соответствующий произведению, получается из вектора, соответствующего множимому, путем его поворота на 180°.
- Умножив + 5 на + 3, получим + 15; умножив — 5 на +3, получим — 15, т. е. при умножении на положительное число вектор, соответствующий произведению, получается из вектора, соответствующего множимому, путем только изменения его длины (т. е. путем растяжения или сжатия). Растяжение получается, когда абсолютная величина множителя больше единицы. Сжатие же, — когда эта абсолютная величина меньше единицы.
- Умножив + 5 на — 3, получим — 15; умножив — 5 на — 3, получим + 15, т. е. при умножении на отрицательное число вектор, соответствующий произведению, получается из вектора, соответствующего множимому, путем его поворота на 180° и изменения его длины (растяжения или сжатия). Не нужно забывать, что сомножители равноправны. Поэтому во всех этих примерах можно поменять ролями множимое и множитель.
§ 6. ИЗМЕНЕНИЕ ВЕЛИЧИН
С помощью положительных и отрицательных чисел в алгебре принято изображать не только сами величины, но также и их изменения.
Среди величин существуют и такие, которые могут изменяться лишь в одном направлении, и такие, которые могут изменяться в двух противоположных направлениях. Например, возраст человека может изменяться только в одном направлении — он может только увеличиваться; высота нормально растущего дерева также может только увеличиваться. Запас же горючего в изолированно летящем самолете может уменьшаться или оставаться некоторое время неизменным и никак не может увеличиваться.
Величинами, которые могут изменяться в двух противоположных направлениях, являются, например, наличность приходо-расходной кассы, температура, расстояние по железной дороге от станции до паровоза.
Условимся изображать изменение величины в одном из двух возможных направлений с помощью положительного числа, а в другом — с помощью отрицательного числа.
Под фразой «Наличность кассы изменилась на + 500 руб». будем понимать, что наличность кассы увеличилась на 500 руб.; тогда под фразой «Наличность кассы изменилась на — 500 руб.» мы обязаны будем понимать, что наличность кассы уменьшилась на 500 руб.
Под фразой «Температура изменилась на + 2° условимся понимать, что температура повысилась на 2°; тогда под фразой «Температура изменилась на— 2° » мы обязаны понимать, что температура понизилась на 2°.
Пусть первоначальная температура была + 20°. Тогда после ее изменения на + 2° она станет равной + 22°. Если же первоначальную температуру + 20° изменить на —2°, то она станет равной + 18°.
Пусть первоначальная температура была — 20°. Тогда после ее изменения на + 2°, она станет равной — 18°. Если же первоначальную температуру — 20° изменить на — 2°, то она станет равной — 22°.
Изменение расстояния по железной дороге от станции до паровоза мы рассмотрим на двух примерах, существенно отличающихся друг от друга.
Пример:
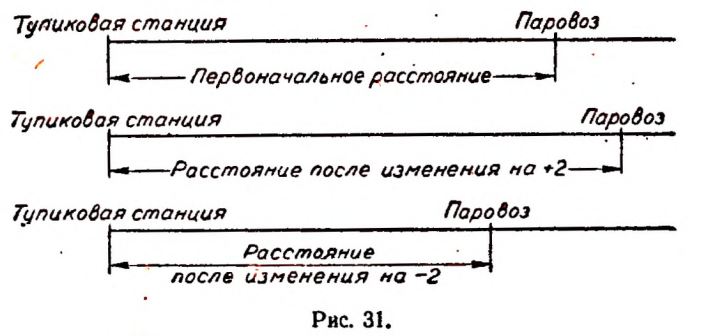
Пусть величина, изменение которой мы будем изучать, есть расстояние между тупиковой станцией и паровозом. Само это расстояние является величиной, отсчет которой в двух противоположных направлениях смысла не имеет, между тем как изменения этой:величины могут происходить в двух противоположных направлениях. (Расстояние между тупиковой станцией и паровозом может и увеличиваться и уменьшаться.)
Под фразой «Расстояние между тупиковой станцией и паровозом изменилось на + 2 км» будем понимать, что паровоз переместился на 2 км по направлению, противоположному станции; тогда под фразой «Расстояние между тупиковой станцией и паровозом изменилось на — 2 км» мы обязаны понимать, что паровоз переместился на 2 км в сторону станции (рис. 31).
Пример:
Пусть величина, изменение которой мы будем изучать, есть расстояние от ст. Бологое до паровоза. Это расстояние в сторону Москвы, как и раньше, условимся выражать положительным числом, а в сторону Ленинграда — отрицательным (рис. 32).
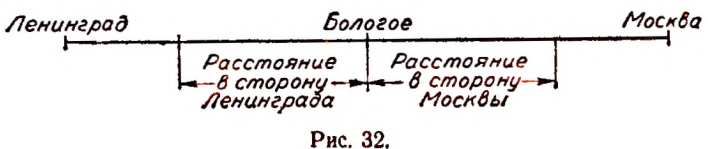
Условимся выражать изменение этого расстояния положительным числом в том случае, когда этому изменению соответствует перемещение паровоза от первоначального положения по направлению к Москве, а отрицательным— по направлению к Ленинграду.
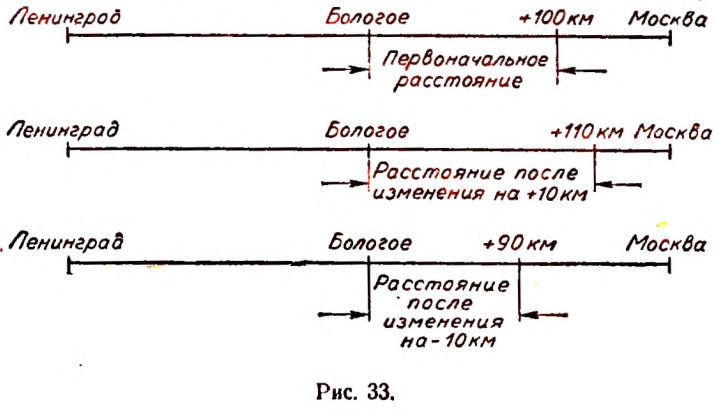
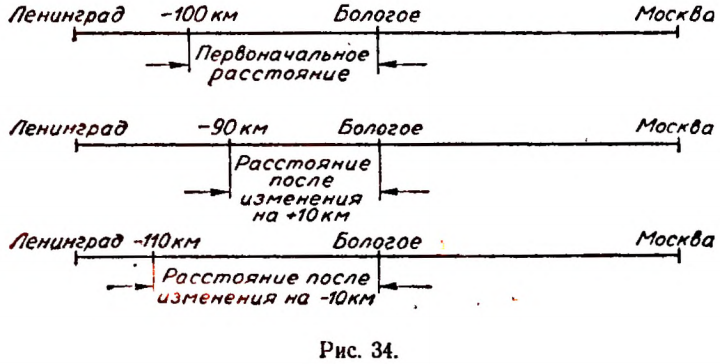
Пусть первоначальное расстояние равно + 100 км. Тогда при его изменении на + 10 км расстояние станет равным +110 км. Если же первоначальное расстояние + 100 км изменить на — 10 км, то расстояние станет равным + 90 км (рис. 33).
Пусть первоначальное расстояние равно — 100 км. Тогда при его изменении на + 10 км расстояние станет равным — 90 км. Если же первоначальное расстояние изменить на — 10 км, то оно станет равным — 110 км (рис. 34).
§ 7. О ВЫРАЖЕНИЯХ ВИДА 
Условимся считать, что знак плюс, поставленный перед каким-нибудь числом, оставляет это число без изменения. Например
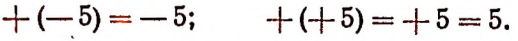
Условимся считать, что знак минус, поставленный перед каким-нибудь числом, изменяет это число на число, ему противоположное. Например:
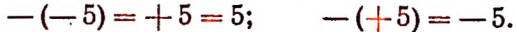
Очевидно, что
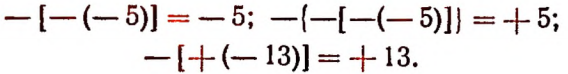
Числа, которые соответствуют точкам координатной прямой, лежащим правее начала отсчета, называют положительными.
Числа, которые соответствуют точкам координатной прямой, лежащим левее начала отсчета называю отрицательными.
Определение отрицательного числа
Содержание понятия числа не оставалось неизменным при историческом развитии общества и постепенно расширялось по мере расширения круга вопросов и задач, требовавших разрешения средствами математики. Учащимся при изучении математики тоже необходимо шаг : за шагом ознакомиться с расширением понятия числа. Первый шаг
в этом направлении делается в арифметике, когда к целым числам присоединяются дробные. Это расширение понятия числа значительно увеличивает круг вопросов и задач, допускающих решение при помощи арифметики.
Теперь пришло время сделать второй шаг. Этот шаг состоит в том, что к числам, изучавшимся в арифметике— целым и дробным— присоединяются новые —отрицательные числа.
Под этим названием понимаются числа —3, —5 (минус три, минус пять) и т. д. Один случай употребления такого рода чисел вошел в быт, именно при измерении температуры. Всем известны и понятны выражения, вроде: «Температура ночью от минус десяти до минус четырнадцати градусов.»
Введение новых чисел заставляет дать специальное название и для обыкновенных целых и дробных чисел, рассматриваемых в арифметике. Все они, кроме нуля, называются положительными числами. Число 0 не причисляется ни к положительным, ни отрицательным числам.
Раньше чем дать точное определение отрицательного числа, рассмотрим следующую задачу.
Задача. Во время сильных дождей уровень воды в реке поднялся на а сантиметров в течение суток. В течение следующих суток уровень воды понизился на b сантиметров. Какой будет уровень воды по истечении этих двух суток?
Решение. Решим прежде всего эту задачу, сравнивая уровень воды в конце вторых суток с уровнем в начале первых суток. При этом способе решения нам придется рассмотреть три случая.
Случай 1. Число а больше b. В этом случае уровень воды в конце вторых суток будет выше уровня воды в начале первых суток на (а — b) см.
Случай 2. Число а равно b. В этом случае уровень воды в конце вторых суток будет совпадать с начальным уровнем.
Случай 3. Число а меньше b, В этом случае уровень воды в конце вторых суток будет ниже начального уровня на (b — а) см.
Ответ задачи может быть сформулирован следующим образом.
За двое суток вода поднялась на (а — b) см, если а больше b осталась на том же уровне, если а равно Ъ, или опустилась на (b— а) см, если а меньше b. Таким образом, при самом простом способе решения этой задачи мы не можем дать одну формулу для ее решения, охватывающую всевозможные численные значения для данных чисел а и b.
Однако можно дать другой способ решения, при котором мы сможем одной формулой охватить все случаи. Для этого достаточно отсчитывать высоту уровня воды, например, от дна реки в глубоком месте.
Пусть в начале первых суток вода стояла на А см выше дна реки. Тогда в конце первых суток вода будет находиться на (A+ а) см выше дна, а к концу вторых суток на ( A+ а — b) см выше дна. Формулой А + а — b охватываются все случаи, которые могут представиться в задаче.
Решение выглядит так, как будто к числу А, определяющему уровень воды в начале первых суток, добавляется число а — b .
Например, если а =15 и b=10, то A+a — b = A+ 5.
Однако, если а меньше b, то разность а — b не имеет смысла, а для вычисления А+а — b нужно от числа А отнять некоторое число. Например, если а = 5 и b= 10, то
А + а — b = А — 5.
Таким образом, в этом случае, вместо добавления к числу А разности а — b, мы должны сделать вычитание из А некоторого числа.
Введение отрицательных чисел дает возможность сохранить первый способ истолкования формулы А + а — b . Именно, будем считать, что разность а — b имеет смысл не только при а, не меньшем b, но и при а, меньшем b, но в этом случае эта разность есть число,
называемое отрицательным числом, а именно такое, добавление которого равносильно вычитанию некоторого положительного числа. Так, 10— 15 есть отрицательное число «—5». Добавление этого числа равносильно вычитанию числа 5.
Дадим теперь точное определение отрицательного числа.
Определение:
Каждому положительному числу сопоставляется число, называемое отрицательным. При этом считается, что добавление к какому-либо числу отрицательного числа равносильно вычитанию соответствующего положительного.
Само собой разумеется, что то число, добавление к которому отрицательного числа равносильно вычитанию соответствующего положительного, нужно считать достаточно большим, чтобы это вычитание имело смысл.
Введем теперь некоторые названия и обозначения, необходимые при пользовании отрицательными числами.
Отрицательное число, соответствующее некоторому положительному числу а, называется противоположным числу а и обозначается —а. Так, число, противоположное числу 5, обозначается —5; число, противоположное числу 0,73, обозначается -0,73; число, противоположное числу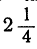 , обозначается
, обозначается 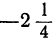 и т. д. Обозначение отрицательных чисел читаются словами так: «минус пять», «минус нуль целых семьдесят три сотых», «минус два и одна четверть» и т. д. Смысл этого обозначения тесно связан с определением отрицательного числа: добавление числа —а, согласно определению, равносильно вычитанию числа а.
и т. д. Обозначение отрицательных чисел читаются словами так: «минус пять», «минус нуль целых семьдесят три сотых», «минус два и одна четверть» и т. д. Смысл этого обозначения тесно связан с определением отрицательного числа: добавление числа —а, согласно определению, равносильно вычитанию числа а.
В свою очередь и положительное число, которому противоположно данное отрицательное число, называется противоположным этому отрицательному числу. Так, число, противоположное числу —5, есть 5;число, противоположное числу 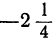 , есть
, есть 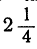 и т. д. Обозначение отрицательных чисел читаются словами так: «минус пять», «минус нуль целых семьдесят три сотых», «минус два и одна четверть» и т. д. Смысл этого обозначения тесно связан с определением отрицательного числа: добавление числа —а, согласно определению, равносильно вычитанию числа а.
и т. д. Обозначение отрицательных чисел читаются словами так: «минус пять», «минус нуль целых семьдесят три сотых», «минус два и одна четверть» и т. д. Смысл этого обозначения тесно связан с определением отрицательного числа: добавление числа —а, согласно определению, равносильно вычитанию числа а.
В свою очередь и положительное число, которому противоположно данное отрицательное число, называется противоположным этому отрицательному числу. Так, число, противоположное числу —5, есть 5; число, противоположное числу 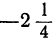 , есть
, есть 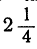 и т. д.
и т. д.
Можно поэтому говорить, что число 5 и —5 взаимно противоположны, так как —5 противоположно числу 5, и 5 противоположно числу —5.
Наконец за число, противоположное числу 0, принимается само число 0. Это естественно, так как добавление нуля к какому-либо числу или вычитание нуля из этого же числа приведет к одному результату — число не изменится.
Если некоторое число, положительное, отрицательное или 0, как- либо обозначено, то противоположное ему число обозначается таким же образом, но со знаком минус. Например, —0 есть число,
противоположное числу 0, и потому —0 = 0. Число — (—5) противоположно числу —5, и потому —(—5) = 5. Если число обозначено буквой а, то противоположное ему обозначается —а. Если а есть положительное число, то это обозначение совпадает с введенным выше обозначением для отрицательных чисел.
Часто бывает нужно подчеркнуть противопоставление положительных чисел отрицательным. С этой целью перед обозначением положительного числа ставят знак +. Например, +5 обозначает просто число 5. Никакого различия между+5 и 5 нет.
Таким же образом, если какое-либо число, положительное, отрицательное или равное нулю, как-либо обозначено, например буквой а, то +а обозначает то же самое число. Например, +(-5) = — 5, +0 = 0 и т. д.
Целые и дробные положительные числа, противоположные им отрицательные числа и число 0 все вместе носят название рациональных чисел.
Введем теперь важное понятие абсолютной величины числа.
Определение:
Абсолютной величиной положительного числа и числа, равного нулю, называется само это число.
Абсолютной величиной отрицательного числа называется противоположное ему положительное число.
Например, абсолютная величина числа 5 равна 5, абсолютная величина —5 тоже равна 5.
Вообще, противоположные числа имеют одинаковую абсолютную величину.
Абсолютную величину числа а обозначают | а |. Так,
|—5| = 5; |5| = 5; |0| = 0.
Вычитание из меньшего положительного числа большего
Присоединение к целым числам дробных чисел дало возможность рассматривать действие деления двух целых чисел как возможное и в том случае, когда делимое «не делится» на делитель, т. е. в том случае, когда частное не является целым числом*).
Введение отрицательных чисел делает возможным действие, которое не имеет смысла, если оставаться в области обыкновенных чисел, т. е. чисел положительных и числа 0. Именно, введение отрицательных чисел делает возможным вычитание из меньшего положительного числа большего.
Действительно, что такое 10—15? Согласно определению действия вычитания 10—15 есть такое число, которое, будучи прибавлено к 15, дает в сумме 10. Ясно, что среди положительных чисел такого числа не существует, так как при прибавлении к числу 15
положительного числа в сумме получится число большее, чем 15, в то время как 10 меньше 15. Однако среди отрицательных чисел такое число найдется, именно —5. Действительно, согласно определению отрицательного числа, добавление к числу 15 числа —5 равносильно вычитанию числа 5. В результате получится 10.
*) Конечно, введение дробных чисел исторически и было вызвано именно тем, что практическая деятельность человека заставляла считать такое действие возможным. Так, например, разделить яблоко пополам можно, и не зная употребления дробей.
Подобным образом можно рассуждать и при других численных значениях уменьшаемого и вычитаемого.
Вывод. Если уменьшаемое меньше вычитаемого, то их разность есть отрицательное число, противоположное разности вычитаемого и уменьшаемого.
Применение отрицательных чисел при описании изменения переменной величины
В практической деятельности очень часто приходится иметь дело с переменными величинами, численные значения которых меняются в зависимости от обстоятельств. Например, уровень воды в реке повышается во время половодья или во время дождей и понижается в сухую погоду. Температура воздуха в данном месте все время меняется с течением времени. Площадь квадрата изменяется при изменении длины его стороны и т. д.
Для того чтобы составить представление об изменении переменной величины, нужно измерить или вычислить ряд ее значений. Так, чтобы судить об изменении уровня воды в реке, нужно измерять этот уровень через некоторые промежутки времени. Чтобы судить об изменении температуры воздуха в данном пункте, следует измерять ее термометром через некоторые промежутки времени. Чтобы судить об изменении площади квадрата при изменении его
стороны, следует вычислить эту площадь для ряда значений стороны и т. д.
Рассмотрим пример. Уровень воды в реке в течение суток измерялся через каждые 2 часа. Результат измерения сведен в следующую таблицу:
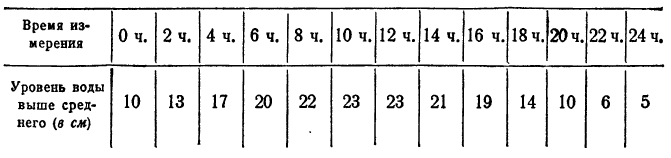
Из этой таблицы мы видим, что вода сначала поднималась, затем оставалась на одном уровне и, наконец, начала опускаться. Еще более полное представление об изменении уровня мы составим, если рассмотрим, как изменялся уровень воды за каждый из двухчасовых промежутков времени между двумя измерениями. Результат этого рассмотрения можно свести в такую таблицу:
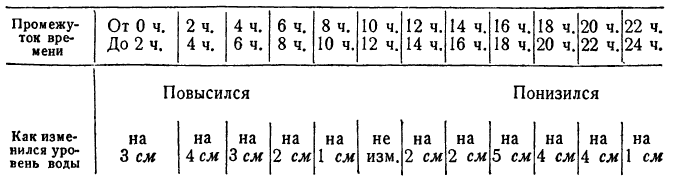
В этой таблице, кроме числа, показывающего величину изменения уровня воды, нам нужно указывать на направление этого изменения— уровень воды сначала повышался, затем стал понижаться.
Таблица сделается проще и нагляднее, если мы введем в рассмотрение наряду с положительными числами также и отрицательные числа следующим образом.
Пусть нам известны два значения переменной величины. При переходе от первого значения ко второму величина может увеличиться или уменьшиться. В обоих случаях величина изменения измеряется , разностью между большим и меньшим из сравниваемых значений. Для того чтобы получить второе Значение переменной из первого, нужно эту разность добавить или вычесть в зависимости от того, увеличивается переменная при переходе от первого значения ко второму или уменьшается. Поэтому целесообразно приписать этой разности знак минус в случае, если переменная величина уменьшается. Полученное таким образом число называется приращением переменной величины. Абсолютная величина приращения определяет величину изменения, а знак определяет направление изменения. Пользуясь приращением, можно записать предыдущую таблицу изменения уровня воды в следующей форме:
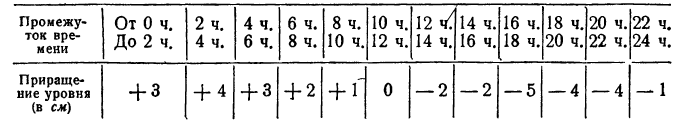
Мы поставили в таблице перед положительными приращениями знак +, чтобы противопоставить их отрицательным приращениям. Еще раз повторяем, что это делается только для большей наглядности, никакой разницы, например, между числами + 3 и 3 нет.
Определение:
Приращение переменной величины при
переходе от первого ее значения ко второму есть такое число, которое, будучи добавлено к первому значению, дает второе.
Иными словами, приращение есть разность между вторым и первым значением переменной. Если переменная возрастает при переходе от первого значения ко второму, то ее приращение положительно, если уменьшается, то ее приращение отрицательно. Наконец, если оба значения одинаковы, то приращение равно нулю.
Таким образом, отрицательные числа наряду с положительными числами и числом 0 удобно применять при описании изменения переменной величины, если дан ряд последовательных ее значений.
Применение отрицательных чисел к измерению величин, изменяющихся в двух противоположных направлениях
Всем известно употребление отрицательных чисел при измерении температуры. Учащиеся знакомы и с другим случаем употребления отрицательных чисел. В географии принято отсчитывать высоту географических пунктов от уровня океана. Эта высота считается положительной, если пункт расположен выше этого уровня, и отрицательной, если ниже. На физических картах часто отмечаются высоты наиболее замечательных пунктов. На карте Азии можно увидеть пометку —26 на изображении Каспийского моря. А на изображении впадины, расположенной к югу от восточных отрогов хребта Тянь-Шань, стоит пометка —298. Это означает, что уровень Каспийского моря на 26 м ниже уровня океана, а дно упомянутой впадины ниже уровня океана на целых 298 м.
В обоих рассмотренных нами примерах величины, для измерения которых привлекались наряду с положительными числами также и отрицательные, обладают следующим общим свойством. Обе эти величины, и температура, и высота над уровнем океана, могут изменяться в двух противоположных направлениях от некоторого значения, принятого -за начало отсчета (при измерении температуры за начало отсчета принимается температура тающего льда, при измерении высоты географических пунктов — уровень океана). Это делает возможным и удобным использование отрицательных чисел для измерения в направлении, противоположном тому, в котором результат измерения считается положительным.
Кроме величин, указанных в разобранных примерах, Существует очень много других величин, могущих изменяться в двух противоположных направлениях. Всякий раз при измерении таких величин целесообразно использовать отрицательные числа.
Так, при измерении времени относительно некоторого момента, принятого за начало отсчета, целесообразно считать положительным время событий, происшедших после начала отсчета, и отрицательным — время событий, происшедших до начала отсчета. При измерении сил, действующих на пружину, целесообразно считать положительными силы, растягивающие пружину, и отрицательными — силы, сжимающие пружину и т. д.
Пока мы ограничимся рассмотрением этих примеров.
В заключение заметим, что не при всяком измерении имеет смысл привлечение отрицательных чисел. Так, бессмысленно говорить, что число людей в комнате равно —2, бессмысленно употреблять отрицательные числа при измерении площади, объема, веса. Даже при
измерении температуры отрицательные числа лишены смысла при пользовании абсолютной шкалой, в которой за начало отсчета принята самая низкая возможная температура — так называемый абсолютный нуль (—273° по обычной шкале)*).
Вывод. Отрицательные числа наряду с положительными числами и с числом нуль служат для измерения величин, могущих изменяться в двух противоположных направлениях от некоторого значения, принятого за начало отсчета.
*) Тепловые явления объясняются беспорядочным движением мельчайших частиц — молекул, из которых образованы все вещества. Увеличение скорости этого движения соответствует повышению температуры. Абсолютный нуль соответствует такому состоянию, при котором движение молекул отсутствует.
Изображение чисел в виде точек на прямой линии
Числа имеют очень наглядное изображение в виде точек на прямой линии.
На прямой выбирается точка, которая принимается за начало отсчета, и задается некоторая единица масштаба, например 1 см.
Выбранная начальная точка разбивает прямую на две части. На одной из них изображаются положительные числа, на другой — отрицательные числа. Для изображения числа берется отрезок, длина которого равна абсолютной величине числа, и этот отрезок откладывается от начальной точки в ту или другую сторону в зависимости от знака изображаемого числа. Другой конец отрезка принимается за точку, изображающую данное число. За изображение числа 0 принимается сама начальная точка.
Прямая, точки которой изображают числа, носит название числовой оси. На рис. 3 изображена числовая ось, некоторые точки которой надписаны теми числами, которые они изображают.
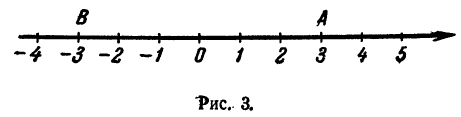
Для того чтобы различить части числовой оси, на которых изображаются положительные и отрицательные числа, на оси указывается направление движения от отрицательных чисел к положительным. На чертеже это направление указано стрелочкой.
Абсолютная величина числа есть расстояние от точки, изображающей это число, до начальной точки, измеренное в выбранном масштабе. Противоположные числа изображаются точками, лежащими на одинаковом расстоянии от начальной точки, но по разные стороны от нее.
Числовая ось называется также осью координат, а число, изображением которого является данная точка, называется координатой этой точки. Так, точка А на рис. 3 имеет своей координатой число 3, а точка В — число —3.
Таким образом, каждое рациональное число изображается некоторой точкой на числовой оси.
Сложение положительных и отрицательных чисел
В этом параграфе и в ближайших следующих будут даны правила арифметических действий над любыми рациональными числами.
Задача:
Уровень воды в реке измерялся в течение двух суток. За первые сутки уровень изменился, получив приращение а см, за вторые сутки,— получив приращение b см. Какое приращение
получил уровень воды за двое суток?
Решение:
При решении этой задачи допустим сначала, что числа а и b положительны, т. е. что в первые сутки уровень поднялся на а см и за вторые сутки также поднялся на b см.
Очевидно, что в этом случае уровень воды за двое суток поднялся на
Очевидно, что в этом случае уровень воды за двое суток
поднялся на (а + b) см. Таким образом, приращение уровня за двое суток получается сложением приращений уровня за каждые сутки. Сумма приращений уровня за первые сутки и за вторые сутки равна приращению уровня воды за двое суток.
Мы сделали этот вывод в предположении того, что числа а и b положительны. Сохраним то же истолкование суммы и при любых других значениях чисел а и b, а на основании этого выведем правила сложения для любых рациональных чисел.
Рассмотрим теперь ряд случаев, которые здесь могут представиться.
Случай 1. Число а=10; b =- 7. Вода поднялась на 10 см, затем опустилась на 7 см, В результате уровень получился выше начального уровня на 10 — 7=3 см. Таким образом, 10 + (-7)=10 -7 = 3.
Случай 2. Число а = — 7; b = 10. Вода опустилась на 7 см, затем поднялась на 10 см, В результате уровень воды оказался на 3 см выше начального уровня. Таким образом, (-7)+10 = 3.
Случай 3. Число а = 7; b =-10. Вода поднялась на 7 см, затем опустилась на 10 см. Результатом является понижение уровня на 3 см: 7+(-10) = — 3.
Случай 4, Число а = -10; b=+7. Вода опустилась на 10 см, затем поднялась на 7 см. Результатом является понижение уровня на 3 см: (—10) + 7 = —3.
Случай 5. Число а = 7; b = — 7. Уровень воды поднялся на 7 см, затем опустился на 7 см. В результате он вернулся к начальному уровню: 7 + (-7) = 0.
Случай 6. а = — 7; b = 7. Вода опустилась на 7 см, затем поднялась на 7 см. В результате уровень вернулся к исходному: (-7) + 7 = 0.
Случай 7. а= —10; b = — 7. Вода опустилась на 10 см, затем снова опустилась на 7 см. В результате вода опустилась на 17 см: (-10)+ (-7) = -17.
Случай 9. а = 0; b = — 7. Уровень воды не изменился за первые сутки, за вторые понизился на 7 см В результате вода опустилась на 7 см: 0+ (-7) = -7.
Таким же образом можно рассуждать и при любых других численных значениях для а и b.
Правило 1. Чтобы сложить два числа, из которых одно
положительное, а другое отрицательное, нужно найти разность их абсолютных величин и полученную разность взять со знаком слагаемого, имеющего большую абсолютную величину.
Правило 2. Чтобы сложить два отрицательных числа, нужно сложить их абсолютные величины и взять результат со знаком минус.
Правило 3. Сумма двух противоположных чисел равна нулю.
Правило 4. Сумма двух чисел, из которых одно равно нулю, равно другому слагаемому.
Свойства сложения
Как отмечалось в первой главе, действие сложения в применении к положительным числам обладает двумя важными свойствами, которые носят название переместительного и сочетательного законов. Эти законы выражаются следующими формулами:
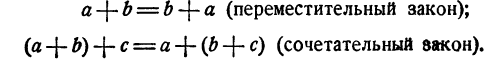
Переместительный и сочетательный законы сохраняются и при сложении любых рациональных чисел.
Справедливость переместительного закона непосредственно следует из правил, по которым выполняется сложение чисел. Действительно, согласно этим правилам, порядок слагаемых не оказывает влияния на результат, так как в этих правилах оба слагаемых совершенно равноправны.
Справедливость сочетательного закона также может быть доказана на основании правил сложения. Однако такое доказательство очень громоздко, так как при его проведении нужно рассмотреть огромное количество случаев, которые тут могут представиться. Поэтому мы поступим иначе. Вернемся к задаче, которая привела нас к правилам сложения, еще несколько усложнив ее условие.
Задача:
В течение первых суток приращение уровня воды составило а см, в течение вторых суток b см, в. течение третьих суток с см. Какое приращение получит уровень по истечении всех трех суток?
Решение:
Эту задачу можно решить двумя способами, Мы приведем эти два решения в той форме, в какой обычно решаются задачи по арифметике, т. е. в форме вопросов.
Способ 1. 1) Какое приращение получил уровень воды за первые двое суток?
Приращение уровня за первые сутки равно а см, за вторые сутки b см. Следовательно, за двое первых суток уровень воды получил приращение (a+b) см.
2) Какое приращение получил уровень воды за трое суток?
За первые двое суток уровень воды получил приращение (a+b) см, за третьи сутки с см. Следовательно, за трое суток уровень воды получил приращение [(a+b) + с] см.
Ответ. [(а+b)+с] см.
Способ 2. 1) Каково приращение уровня воды за вторые и третьи сутки?
За вторые сутки уровень воды получил приращение b см, за третьи с см. Следовательно, за вторые и третьи сутки приращение уровня равно (b + с) см.
2) Какое приращение получил уровень воды за все трое суток?
Приращение уровня складывается из приращения за первые сутки и из приращения за вторые и третьи сутки, т. е. оно равно [a+(b + c)] см.
Ответ. [a+(b + c)] см.
Сравнивая результаты решения по двум приведенным способам, мы приходим к выводу 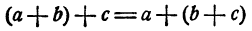 Таким образом, справедливость сочетательного закона установлена.
Таким образом, справедливость сочетательного закона установлена.
Вычитание
Вычитанием называется действие, обратное сложению, т. е. действие, посредством которого по данной сумме и одному из слагаемых определяется второе слагаемое. Таково определение действия вычитания в применении к положительным числам.
Это определение сохраняется и в применении к отрицательным числам. Названия «уменьшаемое», «вычитаемое» и «разность» тоже употребляются в прежнем смысле. Так, вычесть из числа -3 число
-5, это значит найти такое число, которое, будучи сложено с числом -5, дает в сумме -3. Очевидно, что таким числом является 2, ибо 2+(-5)=-3. Итак, -3 — (-5)=2.
Действие вычитания производится по следующему правилу.
Правило. Чтобы получить разность, достаточно к
уменьшаемому добавить число, противоположное вычитаемому.
Это правило записывается в виде следующей формулы:
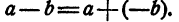
Дадим доказательство справедливости правила вычитания. Обозначим разность а — b через х. По определению вычитания х есть такое число, что х+b=а. Решим это уравнение относительно х, добавив к обеим частям равенства число — b. Мы рассуждаем так.
Если
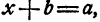
то
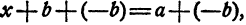
или
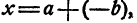
ибо 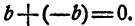 Проверим теперь полученное решение
Проверим теперь полученное решение
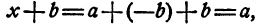
ибо (-b)+b=0Таким образом, x=a+(-b) действительно
удовлетворяет уравнению х+b=а
Итак х=а+(-b), т. е. а—b=a+(—b),
что и требовалось доказать.
Алгебраическая сумма
Мы условились производить несколько последовательных
действий сложения и вычитания в порядке их записи. Всякое отклонение от этого порядка указывается расстановкой скобок.
Определение:
Алгебраическое выражение, представляющее
собой запись нескольких последовательно проведенных действий
сложения и вычитания, называется алгебраической суммой.
По внешнему виду алгебраическая сумма состоит из нескольких алгебраических выражений (чисел, букв или более сложных выражений), соединенных .знаками + и -. Примерами алгебраической суммы могут служить выражения 2— 3 — 4+8-7, a — b — c + d+e и т. д.
На основании правила, установленного в предыдущем параграфе, действие вычитания можно заменить действием сложения с числом, противоположным вычитаемому.
Поэтому любая алгебраическая сумма может быть записана в виде суммы. Например,
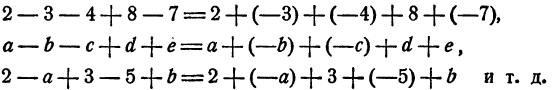
В такой записи все вычитаемые заменены противоположными им слагаемыми.
Слагаемые алгебраической суммы и числа, противоположные вычитаемым, называются членами алгебраической суммы. Так, членами алгебраической суммы а— b — c + d + e являются а, — b, — с, d и e.
Алгебраическая сумма есть сумма своих членов. На основании переместительного и сочетательного законов сложения члены алгебраической суммы можно переставлять в любом порядке и посредством расстановки скобок объединять в группы. Например,
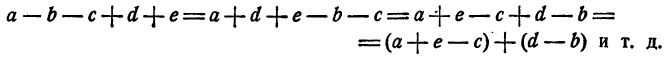
Указанное свойство алгебраической суммы удобно применять для вычисления численно заданной алгебраической суммы. Например,
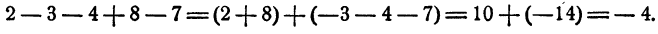
Употребление знаков неравенства
Часто бывает нужно сравнить числа по величине. Для записи результата сравнения употребляются специальные знаки > и < , заменяющие слова «больше» и «меньше». Так, 10 > 8 (десять больше восьми), 7<10 (семь меньше десяти) и т. д.
Понятия «больше» и «меньше», естественно, распространяются на любые рациональные числа. Например, чем холоднее воздух, тем меньше его температура. Так, температура —2° меньше, чем +1°, температура —5° меньше, чем—2°.
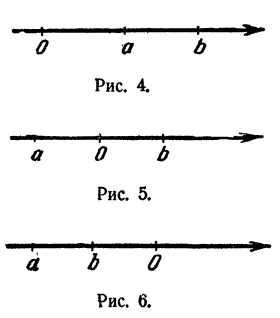
Из этих соображений вытекают
следующие правила сравнения чисел:
- Всякое положительное число больше всякого отрицательного
числа, всякое отрицательное число меньше всякого положительного числа. - Всякое положительное число больше нуля, нуль меньше всякого положительного числа.
- Всякое отрицательное число
меньше нуля, нуль больше всякого отрицательного числа. - Из двух различных отрицательных чисел меньше то, абсолютная величина которого больше а больше то, абсолютная величина которого меньше.
Во всех случаях неравенства а<b и b>а означают одно и
то же.
Согласно сформулированным правилам 5>0;—7<0; —19 <—7; 3>—4 и т. п.
Неравенство а>0 обозначает, что а есть положительное число.
Действительно, если а>0, то а не может быть равным нулю и не может быть отрицательным числом, ибо всякое отрицательное число меньше нуля. Следовательно, а положительно.
Таким же образом неравенство а<0 обозначает, что а есть отрицательное число.
Рассмотрим теперь геометрический смысл понятий «больше» и «меньше» в применении к любым рациональным числам.
На рис. 4, 5 и 6 изображена числовая ось, направленная слева направо. На каждом из рисунков отмечено начало отсчета, т. е. изображение числа 0 и изображения еще двух чисел а и b причем
каждый раз изображение числа b расположено правее изображения числа а. Покажем, что во всех трех случаях а<b.
На рис. 4 рассматривается случай, когда оба числа положительны. В этом случае очевидно, что а<b.
На рис. 5 число а отрицательное, b положительное. Следовательно, и здесь a<b.
На рис. 6 оба числа а и b отрицательны, причем абсолютная
величина числа а больше абсолютной величины числа изображающая а, находится от начала отсчета дальше, чем точка, изображающая число b. Следовательно, и в этом случае а<b.
Итак, если два -числа изображены на числовой оси, направленной слева направо, то из них большим является то, изображение которого расположено правее, а меньшим то, изображение которого расположено левее.
Из геометрического смысла неравенств легко вывести следующее свойство неравенств, очевидное для положительных чисел, но нуждающееся в доказательстве для любых рациональных чисел: если а<b и b<с, то а<с.
Действительно, изображая числа а, b и с на числовой оси,
направленной слева направо, мы увидим, что изображение числа а
расположено левее изображения числа b, а изображение числа b расположено
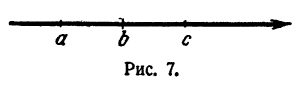
левее изображения числа с (рис. 7). Следовательно, изображение а расположено левее изображения с, и потому а<с.
Таким же oбразом устанавливается, что если а>b и b>с, то
а>с.
Неравенства одинакового направления часто соединяются в цепочку. Например, цепочка а<b<с обозначает, что а<b и b<с. При геометрическом изображении чисел а, b, с цепочка неравенств а<b<с обозначает, что изображение b расположено между изображениями а и с.
Знаки неравенств употребляются главным образом для записи границ, в которых могут находиться числа, участвующие в данной задаче или в данном рассуждении. Так, например, если а обозначает высоту сосны в метрах, то а должно удовлетворять неравенствам 0<a<50, ибо высота дерева есть положительное число и самая высокая сосна не достигает высоты 50 м.
Однако знаков > и < недостаточно для записи ограничений этого рода. Пусть а обозначает высоту в метрах некоторой горы, про которую известно только, что она расположена на территории СССР. Как записать неравенство, которому удовлетворяет число а, учитывая, что самая высокая гора в СССР — пик Сталина — имеет высоту 7495 м Записать а < 7495 было бы неверно, так как высота пика Сталина равна 7495 м. Можно записать а<7500 или даже а < 8000, но такая запись даст менее точное представление о высоте гор в СССР, чем знание высоты самой высокой горы. Здесь следует сказать: «а не больше 7495».
Слова «не больше» заменяются знаком 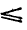 , который иногда читается «меньше или равно».
, который иногда читается «меньше или равно».
Итак, в нашем примере а 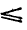 7495.
7495.
Таким же образом знак 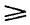 заменяет слова «не меньше» или, что то же самое, «больше или равно».
заменяет слова «не меньше» или, что то же самое, «больше или равно».
Знаки неравенства 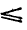 и
и 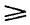 применяются главным образом к числам, одна из которых (или оба) обозначено буквой.
применяются главным образом к числам, одна из которых (или оба) обозначено буквой.
Кроме перечисленных знаков неравенства, употребляется знак 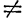 , который читается «не равно». Так, 3
, который читается «не равно». Так, 3 5 (три не равно пяти) и т. д. Этот знак употребляется в тех случаях, когда требуется подчеркнуть только неравенство двух чисел без указания о направленности этого неравенства»
5 (три не равно пяти) и т. д. Этот знак употребляется в тех случаях, когда требуется подчеркнуть только неравенство двух чисел без указания о направленности этого неравенства»
Направленные отрезки
Рассмотрим следующий пример. Через город H проходит шоссе. По этому шоссе из города выехал автомобиль и проехал 40 км. После остановки он проехал по тому же шоссе еще 30 км. На каком расстоянии от города оказался автомобиль?
Очевидно, что формулировка этой задачи неполная, так как в ней нет указания на то, в каком направлении проехал автомобиль последние 30 км; в том же, в котором он раньше проехал 40 км или в противоположном. В первом случае автомобиль окажется в 70 км от города, во втором — в 10 км.
Таким образом, для получения определенного ответа нужно в условие задачи к указанию пути в 30 км, пройденного автомобилем во второй прием, добавить указание о направлении его движения.
Таким же образом обстоит дело во всякой задаче, связанной с движением точки по прямой. Если известно исходное положение точки и известна длина отрезка, пройденного точкой, то нужно знать еще направление движения для того, чтобы знать конечное положение точки.
Отрезок на прямой линии, для которого задана не только длина, но и направление, называется направленным отрезком или вектором. У направленных отрезков следует различать начало и конец, так что
две точки, ограничивающие направленный отрезок, не равноправны.
Направленный отрезок обозначают двумя буквами, соответствующими его началу и концу. При этом буква, обозначающая начало, ставится впереди буквы, обозначающей конец.
Направленные отрезки считаются равными, если они имеют одинаковую длину и одинаковое направление. Так, отрезки АВ и CD (см. рис. 8) равны, а отрезки АВ и ВА не равны, хотя их длины равны.
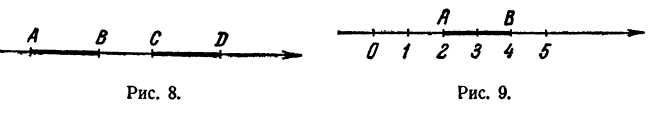
Для измерения направленных отрезков используются наряду с положительными числами числа отрицательные. Для этого прямой, на которой располагаются направленные отрезки, тоже придается некоторое направление.
Алгебраической величиной направленного отрезка на данной прямой называется его длина, измеренная в данном масштабе, взятая знаком +, если направление отрезка совпадает с направлением прямой, и взятая со знаком —, eсли эти направления противоположны.
Например, отрезок АВ имеет
алгебраическую величину 2, а отрезок ВА имеет алгебраическую величину — 2 (рис. 9).
Вообще отрезки, имеющие одинаковую длину, но противоположные направления, имеют в качестве алгебраических величин противоположные числа.
Особенно удобно рассматривать направленные отрезки на числовой оси. В этом случае алгебраическая величина направленного отрезка равна разности координаты конца отрезка и координаты его начала.
Действительно (рис. 10), длина отрезка, соединяющего точки с координатами а и b, равна сумме абсолютных . величин координат концов, если точки лежат по разные стороны от начала, или абсолютной величине разности абсолютных величин координат концов, если точки лежат по одну сторону от начала. В обоих случаях длина отрезка равна абсолютной величине разности координат концов.
Направление отрезка совпадает с направлением оси, если координата начала меньше координаты конца, и направление отрезка противоположно направлению оси, если координата начала больше координаты конца. В обоих случаях знак алгебраической величины отрезка совпадает со знаком разности координат его конца и начала. Таким образом, алгебраическая величина отрезка и разность координат его конца и начала совпадают по абсолютной величине и имеют одинаковые знаки. Следовательно, они равны.
Направленные отрезки применяются в задачах, связанных с движением. Перемещение за некоторый промежуток времени точки, движущейся по прямой линии, целесообразно рассматривать как направленный отрезок. Алгебраическая величина этого отрезка называется алгебраической величиной пути или величиной перемещения точки. Таким образом, величина перемещения двигающейся точки может быть как положительной, так и отрицательной. Величина перемещения положительна, если направление перемещения совпадает с выбранным направлением прямой, по которой происходит движение, и отрицательна, если эти направления противоположны.
Движение называется равномерным, если точка в равные промежутки времени проходит равные пути. Скорость равномерного движения измеряется алгебраической величиной пути, пройденного за единицу времени. Таким образом, скорость равномерного движения точки может измеряться как положительным, так и отрицательным числом. Положительная скорость указывает, что направление движения совпадает с направлением прямой, отрицательная,— что направление движения противоположно направлению прямой.
Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел выполняется по
следующему правилу.
Правило. Произведение двух неравных нулю чисел равно произведению их абсолютных величин, взятому со знаком , если оба множителя имеют одинаковые знаки, и со знаком
, если оба множителя имеют одинаковые знаки, и со знаком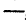 , если знаки множителей противоположны. Если один из сомножителей равен нулю или оба равны нулю, то и произведение равно нулю.
, если знаки множителей противоположны. Если один из сомножителей равен нулю или оба равны нулю, то и произведение равно нулю.
Например,
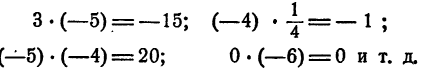
Сформулированное правило в случае, если хотя бы один из сомножителей является отрицательным числом, представляет собой определение действия умножения и не может быть доказано.
Однако легко на примерах показать его целесообразность.
Задача:
Автомобиль, едущий по шоссе с постоянной скоростью
v км/час, проехал через центр города H в 0 час. Где находится
автомобиль в момент времени t часов?
Решение:
Для определенности будем считать, что шоссе идет с юга на север. Рассмотрим его как числовую ось, направленную с юга на север, а автомобиль — как точку, равномерно двигающуюся по этой оси. За начало отсчета примем центр города H. Координату автомобиля обозначим буквой s. Так как автомобиль за 1 час проходит v километров, за t часов он проходит vt километров.
Следовательно, s = vt юга на север, а автомобиль — как точку, равномерно двигающуюся по этой оси. За начало отсчета примем центр города H. Координату автомобиля обозначим буквой s. Так как автомобиль за 1 час проходит v километров, за t часов он проходит vt километров. Следовательно, s = vt
Эта формула выведена в предположении, что v и t — положительные числа, только в этом случае проведенное выше рассуждение имеет смысл. Однако по смыслу задачи как v, так и t могут иметь и отрицательные значения. Мы уже условились считать скорость равномерного движения отрицательной, если движение происходит в направлении, противоположном выбранному направлению прямой. Мы условились и время считать отрицательным, если соответствующий момент предшествует моменту времени, принятому за начала отсчета.
Посмотрим, верный ли результат дает выведенная формула в случае, если v или t принимают отрицательные значения.
Положим, что v = —30; t=3.
В этом случае формула s = vt дает s = —90. Этот результат соответствует действительности. В самом деле,v=—30 означает, чтo автомобиль движется с севера на юг со скоростью 30 км/час и через 3 часа он окажется на 90 км к югу от города H, т. е. его координата будет равна—90, что и было получено из нашей формулы.
Положим теперь v=30, t=—3. В этом случае мы должны ответить на вопрос, где находился автомобиль за три часа до того, как он проехал через центр города H, двигаясь по шоссе со скоростью 30 км/час с юга на север. Очевидно, что он находился на 90 км к югу от центра города H, т. е. его кooрдината была равна — 90. Формула тоже дает 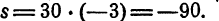
Положим, наконец, v = —30, t = —3. В этом случае автомобиль движется с севера на юг, и вопрос ставится о том, где он находился за 3 часа до того, как он проехал через центр города H. Очевидно, что он находился на 90 км к северу от начала отсчета, т. е. его координата равнялась 90 в соответствии с формулой
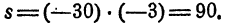
Таким образом, правило умножения позволяет распространить формулу s = v • t, выражающую зависимость между s, v, t, на любые значения скорости и времени.
Ответ. s = vt.
Целесообразность правила оправдывается и другими соображениями.
Одним из основных соображений является следующее. При действиях
над числами, а особенно над буквенными выражениями, играют важную роль законы действий, сформулированные для положительных чисел в § 6 гл. I. Из них к умножению относятся три закона:
1) переместительный закон умножения:
ab = bа;
2) сочетательный закон умножения:
(ab) с = а (bc);
3) распределительный закон умножения относительно
сложения:
(a+ b) с = ас + bc.
Все эти три закона остаются верными при действиях над любыми рациональными числами.
Справедливость переместительного закона непосредственно следует из правила умножения, так как в этих правилах порядок сомножителей никакой роли не играет.
Справедливость сочетательного закона устанавливается так. Абсолютная величина произведений (ab)c и a (bc), очевидно, равна произведению абсолютных величин чисел a, b и с. Знаки произведений (ab)c и а(bс) тоже одинаковы. Действительно, оба произведения положительны, если все три числа положительны или одно положительно, а два отрицательны. Оба произведения отрицательны, если все три сомножителя отрицательны или один отрицателен, а два положительны. Наконец, оба произведения равны нулю, если хотя бы один из сомножителей равен нулю. Таким образом, во всех возможных случаях
(ab) с = а (be).
Доказательство справедливости распределительного закона требует рассмотрения значительного числа частных случаев, связанных со знаками чисел a, b, а+b, с и с возможностями обращения одного из этих чисел в нуль. Поэтому мы ограничимся рассмотрением нескольких численных примеров:
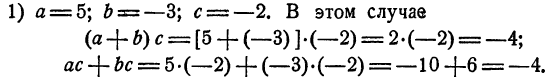
Мы получили одинаковые результаты.
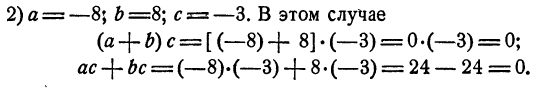
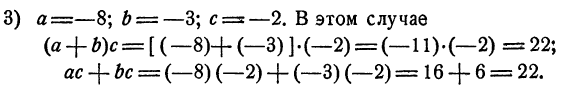
Отметим в заключение некоторые частные случаи умножения рациональных чисел.
Произведение любого числа а на 1 равно этому числу.
Действительно, как абсолютная величина такого произведения, так и знак совпадают с абсолютной величиной и знаком числа а.
Произведение любого числа а на целое положительное число m равно сумме m слагаемых, каждое из которых равно а. Для доказательства достаточно рассмотреть случай отрицательного а, ибо для а, положительного или равного нулю, справедливость этого утверждения известна. Пусть а = -b и b> 0. Тогда
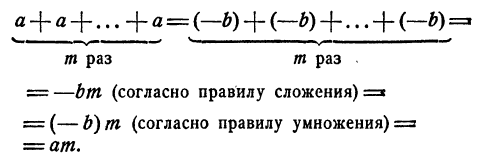
Наконец произведение любого числа а на —1 равно числу —а, противоположному числу а. Действительно, абсолютная величина произведения равна абсолютной величине а, а знак произведения противоположен знаку а. Следовательно,
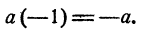
Основное свойство нуля
Согласно правилу умножения двух рациональных чисел число нуль в действии умножения играет особую роль. Именно, если один из сомножителей равен нулю, то и произведение равно нулю, каков бы ни был второй сомножитель.
Важную роль в алгебре играет обратное утверждение: если произведение двух чисел равно нулю, то по крайней мере один из сомножителей равен нулю. Для того чтобы убедиться в справедливости этого утверждения достаточно проверить, что произведение двух отличных от нуля сомножителей отлично от нуля. Здесь могут представиться три случая:
Случай 1. Оба сомножителя положительны.Тогда их произведение тоже положительно и, следовательно, не равно нулю.
Случай 2. Оба сомножителя отрицательны. Тогда их произведение положительно и, следовательно, не равно нулю.
Случай 3. Один сомножитель положителен, а другой отрицателен. Тогда их произведение отрицательно и, следовательно, не равно нулю.
Мы рассмотрели все возможные случаи, так как число, не равное нулю, или положительно, или отрицательно. И во всех случаях оказывается, что произведение отличных от нуля чисел отлично от нуля. Следовательно, если произведение равно нулю, то по крайней мере один из сомножителей равен нулю.
Умножение нескольких чисел и возведение отрицательного числа в степень
Пример:
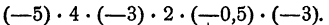
Решение:
Выполняем умножение, последовательно присоединяя множители но одному. Получим
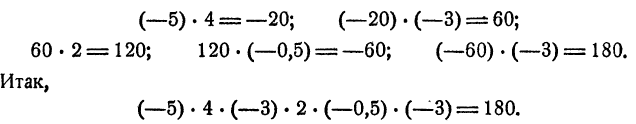
Ответ:180.
На каждом шагу приведенного вычисления мы умножаем абсолютную величину предшествующего результата на абсолютную величину присоединенного множителя,. Поэтому абсолютная величина произведения нескольких чисел равна произведению абсолютных величин сомножителей.
Далее, на каждом шагу знак результата совпадает со знаком предшествующего результата, если присоединяется положительный множитель, и знак последующего результата- противоположен знаку предшествующего, если присоединяется отрицательный множитель. Поэтому произведение нескольких чисел положительно, если все сомножители положительны или если число отрицательных сомножителей четно. Если же число отрицательных сомножителей нечетно, то произведение отрицательно.
Таким образом, мы пришли к следующему правилу умножения нескольких чисел:
Правило. Чтобы перемножить несколько чисел, нужно перемножить их абсолютные величины и взять результат со знаком  , если число отрицательных сомножителей четно, или со знаком
, если число отрицательных сомножителей четно, или со знаком 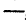 , если число отрицательных сомножителей нечетно.
, если число отрицательных сомножителей нечетно.
Заметим, что если хотя бы один из сомножителей, равен нулю, то и произведение равно нулю.
Из правила умножения нескольких сомножителей вытекает следующее правило для возведения отрицательных чисел в степень:
Правило. При возведении отрицательного числа в степень с четным показателем результат положителен. При возведении отрицательного числа в степень с нечетным показателем результат отрицателен. Абсолютная величина степени равна степени абсолютной величины основания с тем же показателем. Например,
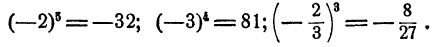
Действительно, степень отрицательного числа есть произведение равных ему сомножителей, число которых равно показателю степени. Если показатель степени есть четное число, то результат положителен, если показатель степени есть нечетное число, то результат отрицателен. Абсолютная величина степени равна произведению сомножителей, каждый из которых равен абсолютной величине основания, т. е. равна степени абсолютной величины основания с тем же показателем.
Отметим одно важное следствие: степень с четным показателем любого рационального числа не отрицательна. Это можно записать так: при любом а и при любом натуральном числе n
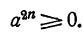
Действительно, любая степень положительного числа есть положительное число, любая степень числа 0 равна 0, и, наконец, степень счетным показателем отрицательного числа есть число положительное.
В частности, не существует числа, квадрат которого был бы равен отрицательному числу.
Деление
Действие деления для любых рациональных чисел сохраняет тот же смысл, который имеет это действие в применении к числам положительным. Именно, деление есть действие, посредством которого по данному произведению двух сомножителей и одному из них находится другой сомножитель. Названия «делимое», «делитель» и «частное» тоже понимаются в прежнем смысле. Таким образом, если делимое обозначить буквой b, делитель буквой а, то частное есть такое число х, что
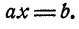
Если а = 0, то и ах = 0. Следовательно, при b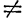 0 равенство 0 • х = b невозможно, а при b = 0 выполняется при любом значении x. Поэтому делить на нуль нельзя, так как это действие или невыполнимо, или не приводит к определенному результату (см. §7 гл.1).
0 равенство 0 • х = b невозможно, а при b = 0 выполняется при любом значении x. Поэтому делить на нуль нельзя, так как это действие или невыполнимо, или не приводит к определенному результату (см. §7 гл.1).
Рассмотрим подробнее уравнение ах =b в предположении, что а 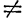 0
0
По правилу умножения абсолютная величина числа b равна произведению абсолютных величин чисел а и х. Следовательно, абсолютная величина х равна частному от деления абсолютных величин чисел b и а. В частности, если b= 0, то х = 0.
Нам остается определить знак числа х предположении, что b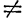 0 Здесь могут представиться 4 случая:
0 Здесь могут представиться 4 случая:
Случай 1. Числа а и b оба положительны. Тогда х тоже положителен.
Случай 2. Число а положительно, b отрицательно. Тогда х должен быть отрицательным числом.
Случай 3. Число а отрицательно, b положительно. Тогда х должен быть отрицательным числом.
Случай 4. Число а отрицательно, b отрицательно. Тогда х должен быть положительным числом.
Итак, абсолютная величина частного от деления двух чисел равна частному от деления абсолютной величины делимого на абсолютную величину делителя. Частное положительно, если делимое и делитель имеют одинаковые знаки, частное отрицательно, если делимое и делитель имеют разные знаки. Частное равно нулю, если делимое равно нулю. (Конечно, в этом правиле предполагается, что делитель отличен от нуля). Например,
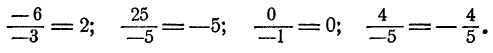
Подобно тому, как действие вычитания можно заменить действием сложения с числом, противоположным вычитаемому, действие деления можно заменить действием умножения на число, обратное делителю.
Это утверждение в применении к положительным числам известно из арифметики. В применении к любым рациональным числам оно нуждается в доказательстве. Итак, нам требуется доказать, что при
любом а 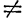 0
0
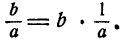
Обозначим 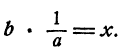 Тогда
Тогда
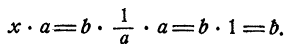
Следовательно, по определению частного х есть частное от деления b на а, т. е.
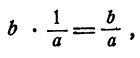
что и требовалось доказать.
Истолкование отрицательного ответа при решении задач
При алгебраическом решении задач (особенно в случае, если задача формулируется в общем виде, а лишь затем даются численные данные для исходных величин) часто получается отрицательный результат, который иногда не имеет смысла при буквальном понимании
вопроса, поставленного в задаче.
Например, если на вопрос «через сколько лет…» получается ответ «— 5», то этот ответ при буквальном понимании вопроса смысла не имеет. Действительно, фраза «через минус пять лет…» бессмысленна. Однако тот же ответ становится осмысленным, если его истолковать как «пять лет назад…».
Таким образом, имеет место следующее правило истолкования отрицательного ответа при решении задачи. Если отрицательный ответ на вопрос, поставленный в задаче, не имеет смысла при буквальном понимании вопроса, то иногда этот ответ получает смысл, если его абсолютную величину принять за ответ на вопрос, противоположный по смыслу вопросу, который поставлен в задаче.
Конечно, это правило не является всеобщим. Во-первых, часто бывает, что отрицательный ответ имеет смысл и при буквальном понимании вопроса. Например, ответ « — 5°> на вопрос «какова температура?» имеет смысл без всякого условного истолкования. Часто бывает так, что и условное истолкование отрицательного ответа невозможно по смыслу задачи. Например, ответ «— 5» на вопрос «сколько человек находилось в комнате?» лишен всякого смысла.
Графическое изображение зависимости между двумя переменными величинами
От геометрического изображения чисел в виде точек на числовой оси легко перейти к геометрическому изображению зависимости между двумя переменными величинами, применяя тот же прием, который применяется в курсе арифметики при построении диаграмм.
Рассмотрим один пример для того, чтобы напомнить это построение.
Пример. Температура воздуха измерялась в течение суток через каждые два часа. Результаты измерения сведены в следующую таблицу:

Построить диаграмму изменения температуры в течение суток.
Решение. Делается это следующим образом. На прямой линии, которую мы расположим горизонтально (рис. 11), строятся на одинаковых расстояниях точки, изображающие моменты времени измерений.
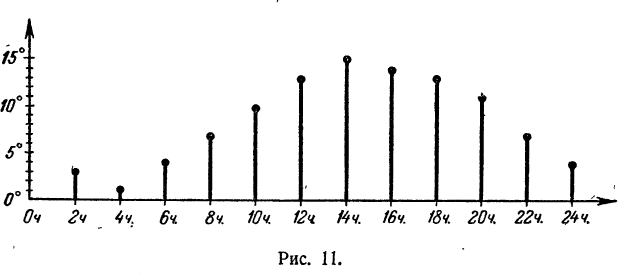
Таким образом, отрезки между этими точками изображают промежутки времени между двумя измерениями. На рис. 11 на горизонтальной оси нанесены деления, соответствующие двухчасовому промежутку времени.
От каждой из точек, изображающих моменты измерения, строится вверх перпендикуляр, длина которого в выбранном масштабе равна числу градусов температуры. Мы получаем чертеж, состоящий из ряда отрезков, длины которых наглядно показывают величину температуры в момент измерения. Этот чертеж и есть диаграмма, изображающая изменение температуры в зависимости от времени. Для сравнения длин отрезков с масштабом мы на перпендикуляре к оси, проведенном через точку, соответствующую нулю, нанесем деления, соответствующие градусам в выбранном масштабе.
Пример:
Пусть температура в течение суток изменялась согласно следующей таблице:
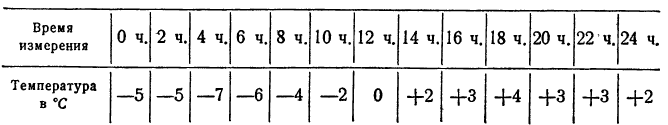
Как построить диаграмму в этом случае?
Решение:
Очевидно, что отрезки, изображающие отрицательную температуру, следует строить не вверх, а вниз, откладывая на перпендикулярах абсолютные величины числа градусов температуры. Диаграмма для рассматриваемой таблицы приведена на рис. 12, где точками изображены концы отрезков, соответствующих температуре.
Таким образом, при помощи диаграммы можно изобразить зависимость между величинами, принимающими как положительные, так и отрицательные значения. Диаграмма не теряет наглядности, если отбросить перпендикулярные отрезки; сохранив только их концы.
Представим теперь себе, что мы измеряем температуру не каждые два часа, а каждый час. При геометрическом изображении результатов этих измерений на чертеже появятся новые точки, расставленные между прежними. Если же производить измерения каждую минуту, точек будет настолько много, что различать их придется в сильную лупу — они будут отстоять друг от друга на 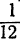 миллиметра.
миллиметра.
Если же представить себе, что измерение производится непрерывно, то точки диаграммы сольются в одну, более или менее плавную, линию. Эта линия носит название графика зависимости температуры от времени. Так называемый самопишущий термометр (термограф) чертит именно график температуры.
Прибор этот (в схематическом описании) состоит из вертикально расположенного барабана, который медленно вращается под действием часового
механизма. На барабан навертывается разграфленный лист бумаги. К этому листу прикасается перо, которое под влиянием температуры поднимается и опускается, подобно уровню жидкости в трубке термометра. Таким образом, в каждый момент времени перо стоит на высоте, соответствующей температуре в этот момент. При вращении барабана с течением времени перо чертит на бумаге линию, которая и представляет собой график температуры.
Подобно тому, как строится график зависимости температуры от времени, строятся графики, изображающие зависимость между двумя любыми переменными величинами, если значение второй переменной определяется, как только известно значение первой.
Для этого на плоскости
берутся две взаимно перпендикулярные
оси (рис. 13). Точка их пересечения
принимается за начало отсчета на обеих
осях. На одной из осей изображается значение первой переменной. В каждой из построенных точек проводится прямая, параллельная второй оси, и на этой прямой откладывается отрезок, длина (в своем масштабе) которого Рис. 13. равна абсолютной величине соответствующего значения второй переменной; отрезок откладывается в
направлении, совпадающем с направлением второй оси или в противоположном в зависимости от знака значения второй переменной.
Вторые концы этих отрезков и отмечаются на чертеже. Сами отрезки лучше не строить, так как это усложняет чертеж. В этом и нет необходимости, если бумага разграфлена на достаточно малые клетки.
Чем чаще брать значения первой переменной, тем чаще расположатся точки на чертеже.
Построенные точки соединяются линией, вообще говоря, искривленной. При соединении надо следить за тем, чтобы линия была по возможности плавной.
Построенная таким образом линия называется графиком зависимости.
Оси, по отношению к которым строится график, носят название осей координат. Одна из осей называется осью абсцисс, другая — осью ординат. Ось абсцисс обычно располагают горизонтально и направляют слева направо. За направление оси ординат обычно принимается направление снизу вверх. Алгебраические величины отрезков, откладываемых параллельно осям координат при построении точки, называются координатами точки. Одна из координат называется абсциссой, другая ординатой в соответствии с названиями осей. Точка пересечения осей называется началом координат.
Особенно интересным и важным для практического применения является построение графика зависимости, заданной при помощи уравнения, связывающего значения переменных друг с другом.
Для того чтобы построить график такой зависимости, нужно предварительно построить .таблицу соответствующих значений переменных. Для этого нужно произвольно задать ряд значений для одной из
переменных и вычислить на основании уравнения соответствующие значения второй переменной.
Составив таблицу, можно приступать к построению графика. Если при этом окажется, что точек построено мало, так что остается ещe неясным, как их следует соединять, нужно дополнить таблицу новыми значениями. Для построения графиков особенно удобна
миллиметровая бумага, которая разграфлена на квадратики со стороной в 1 мм.
Рассмотрим несколько примеров на построение графиков зависимостей.
Пример:
Зависимость между числами х ту задана посредством уравнения 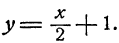 Построить график этой зависимости, принимая за единицу масштаба на обеих осях один и тот же отрезок.
Построить график этой зависимости, принимая за единицу масштаба на обеих осях один и тот же отрезок.
Решение:
Прежде всего вычисляем таблицу:
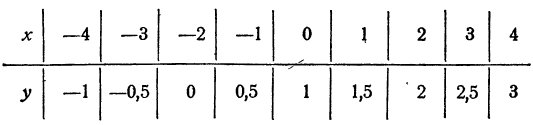
Теперь строим график (рис. 14). От точки оси абсцисс с
абсциссой —4 откладываем вниз отрезок длиною в 1 единицу масштаба и отмечаем его конец. От точки на оси абсцисс с абсциссой —3 откладываем вниз отрезок длины  и отмечаем конец; затем отмечаем точку на оси абсцисс с абсциссой —2; от точки с абсциссой —1
и отмечаем конец; затем отмечаем точку на оси абсцисс с абсциссой —2; от точки с абсциссой —1
откладываем отрезок длины 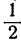 вверх и т. д.
вверх и т. д.
Построенный ряд точек укладывается на одну прямую линию, и мы смело соединяем их этой прямой. Таким образом, графиком зависимости 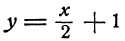 является прямая линия.
является прямая линия.
Мы сделали это заключение на основании вычисления всего лишь девяти точек. Однако мы не ошиблись. Так, измерив длину отрезка, соответствующего значению x = 0,5, мы видим из чертежа; что эта длина находится между 1,2 и 1,3. Более определенно высказаться
нам не позволяет точность построения. В действительности, если x = 0,5, то y = 1,25» Таким образом, в пределах точности чертежа мы получили правильный результат. Точно так же при х = 6 мы из
чертежа читаем, что у приближенно равно 4. В действительности, при х = 6, у = 4 точно.
Таким образом, вычислив несколько значений, мы получили правильное представление о зависимости между переменными х и y.
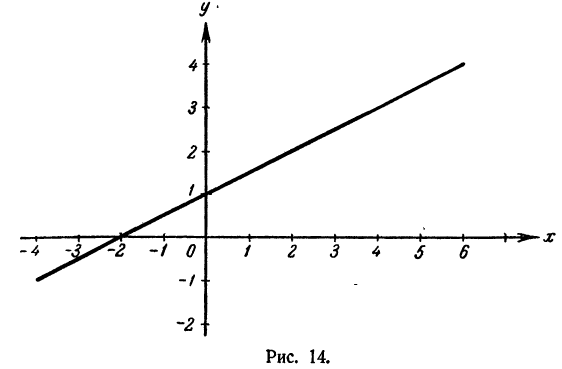
Пример:
Дано уравнение 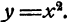 Построить график,
Построить график,
выражающий зависимость между числами х и у.
Решение:
Примем за единицу масштаба по обеим осям 1 см. Строим таблицу
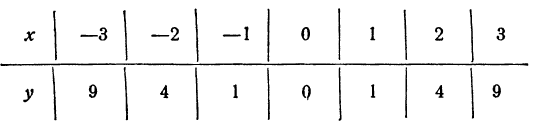
Мы не берем значения х больше 3 по абсолютной величине, так как значения у очень быстро растут, и мы были бы не в состоянии поместить график на чертеже в выбранном масштабе.
Построив точки, соответствующие этой таблице, мы можем подумать, что две ветви, графика сходятся в начале координат под углом. На всякий случай пополняем таблицу еще двумя промежуточными значениями x = 0,5 и х = — 0,5:
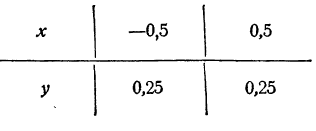
Построив соответствующие точки, мы видим, что в действительности график около начала координат плавно закругляется. Теперь мы можем соединить точки.
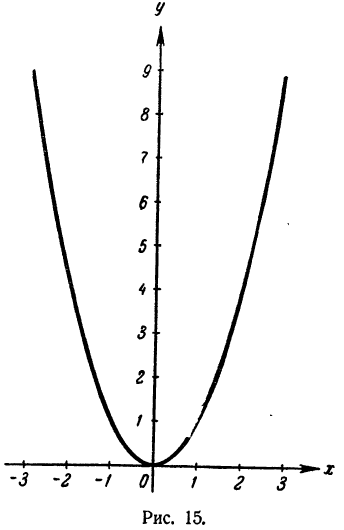
Линия, изображающая зависимость 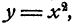 называется параболой (рис. 15).
называется параболой (рис. 15).
Пример:
Сумма длин двух сторон прямоугольника, сходящихся в одной вершине, равна 10 см. Построить график зависимости площади этого прямоугольника от длины одной из его сторон.
Решение:
Обозначим буквой х длину одной из сторон. Тогда длина другой стороны будет равна 10 — х. Площадь у, очевидно, равна х (10 — х). Таким образом, нам нужно построить график зависимости у = x (10 — х). При этом, по смыслу задачи, х есть положительное число, не большее 10.
Вычислим таблицу, придавая х целые значения от 0 до 10, включив и крайние значения, хотя они и не имеют геометрического смысла в данной задаче:
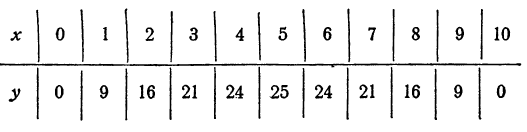
После вычисления мы видим, что для того чтобы график поместился на чертеже, следует, выбрав единицу масштаба по оси абсцисс, принять за единицу масштаба по оси ординат меньший отрезок. Мы примем за единицу по оси ординат отрезок, в 5 раз меньший, чем единица по оси абсцисс (рис. 16).
Что мы можем прочитать из этого графика?
Во-первых, мы видим, что наибольшая площадь прямоугольников равна 25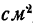 и она получается при x = 5 см, т. е. когда прямоугольник превращается в квадрат, сторона которого равна 5 см.
и она получается при x = 5 см, т. е. когда прямоугольник превращается в квадрат, сторона которого равна 5 см.
Во-вторых, мы видим, что ветви графика опускаются к оси абсцисс при приближении к краям. Это значит, что если сторона прямоугольника очень мала или очень близка к 10 (тогда вторая сторона очень мала), то и площадь будет очень малой.
Поставим следующий вопрос. Как нужно выбрать сторону прямоугольника, чтобы его площадь равнялась 12  ? Алгебраическое решение этой задачи сводится к решению относительно буквы х уравнения x (10 — x)=12. Такого рода уравнения мы решать еще не умеем. Однако из графика можем, хотя бы приближенно, определить х. Именно, х приближенно равно 1,4 или 8,6. В первом случае вторая сторона приближенно равна 8,6, во втором 1,4. Таким образом, прямоугольник со сторонами 1,4 и 8,6 приближенно удовлетворяет условию. Действительно, 1,4-8,6=12,04.
? Алгебраическое решение этой задачи сводится к решению относительно буквы х уравнения x (10 — x)=12. Такого рода уравнения мы решать еще не умеем. Однако из графика можем, хотя бы приближенно, определить х. Именно, х приближенно равно 1,4 или 8,6. В первом случае вторая сторона приближенно равна 8,6, во втором 1,4. Таким образом, прямоугольник со сторонами 1,4 и 8,6 приближенно удовлетворяет условию. Действительно, 1,4-8,6=12,04.
На основании рассмотренных примеров мы можем сделать следующие выводы:
Во-первых, график является очень наглядным изображением зависимости. После построения графика формула «оживает», настолько ясным становится ход изменения одной переменной в зависимости от изменения другой.
Во-вторых, график дает средство для приближённого решения задач, точное решение которых затруднительно.
Положительные и отрицательные числа
Числовая прямая (ось)
Представим себе, что на числовом луче (черт. 31) с началом  вправо, как обычно, отмечены точки 1, 2, З и т . д., соответствующие числам натурального ряда.
вправо, как обычно, отмечены точки 1, 2, З и т . д., соответствующие числам натурального ряда.
Продолжим наш луч в противоположную сторону — влево — таким образом, чтобы получилась прямая линия. От начала  отложим влево расстояния 1, 2, 3 и т. д. и отметим полученные точки значками (—1), (—2), (—3) и т. д.
отложим влево расстояния 1, 2, 3 и т. д. и отметим полученные точки значками (—1), (—2), (—3) и т. д.
Таким же образом, в случае надобности, будем поступать и с дробными числами: отложив, например, отрезок длины 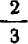 влево от точки
влево от точки  , мы получим точку отрезка, около которой можно поставить значок
, мы получим точку отрезка, около которой можно поставить значок 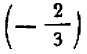 . Вообще, каково бы ни было число
. Вообще, каково бы ни было число  , откладывая расстояние
, откладывая расстояние  влево от точки
влево от точки  , мы получим точку, около которой поставим значок
, мы получим точку, около которой поставим значок 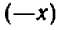 . Вместо «точка со значком
. Вместо «точка со значком 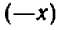 » будем просто говорить «точка
» будем просто говорить «точка 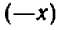 «.
«.
Точка 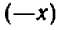 симметрична точке
симметрична точке 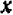 относительно начала
относительно начала  . Само начало симметрично самому себе: таким образом, точка
. Само начало симметрично самому себе: таким образом, точка 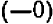 совпадает с точкой
совпадает с точкой  . Значки
. Значки 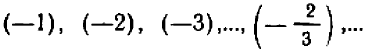 и им подобные можно рассматривать как числа. Те числа, которые изображаются точками, лежащими вправо от
и им подобные можно рассматривать как числа. Те числа, которые изображаются точками, лежащими вправо от  , называются положительными; новые числа (с которыми мы теперь впервые знакомимся), изображаемые точками, лежащими левее
, называются положительными; новые числа (с которыми мы теперь впервые знакомимся), изображаемые точками, лежащими левее  , называются отрицательными.
, называются отрицательными.
Особняком стоит число 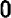 (нуль): оно не считается ни положительным, ни отрицательным.
(нуль): оно не считается ни положительным, ни отрицательным.
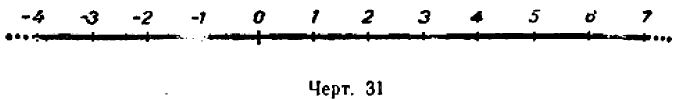
Прямая, па которой отмечены точки, соответствующие всевозможным, положительным и отрицательным, числам, называется числовой осью. Числовая ось состоит из положительной полуоси (луча) и отрицательной полуоси (луча), обе полуоси имеют общую вершину — начало  .
.
Если две точки симметричны относительно начала  , то соответствующие нм числа (их координаты) называют числами взаимно противоположными, Так, число
, то соответствующие нм числа (их координаты) называют числами взаимно противоположными, Так, число 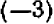 противоположно числу
противоположно числу 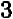 , число
, число 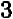 — противоположно числу
— противоположно числу 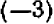 .
.
Чтобы подчеркнуть, что положительные числа изображаются точками, лежащими вправо от начала  , можно было бы при положительных числах ставить знаки
, можно было бы при положительных числах ставить знаки 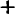 ; например,
; например, 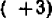 означало бы то же, что и
означало бы то же, что и 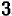 . Но ради краткости этого обычно не делают.
. Но ради краткости этого обычно не делают.
Расстояние точки от начала  называется абсолютным значением числа, соответствующего этой точке. Можно еще иначе сказать, что абсолютное значение числа, отличного от нуля, есть длина отрезка, образованного началом
называется абсолютным значением числа, соответствующего этой точке. Можно еще иначе сказать, что абсолютное значение числа, отличного от нуля, есть длина отрезка, образованного началом  и точкой, изображающей число. Таким образом, абсолютное значение положительного числа (или нуля) не отличается от самого числа; абсолютное же значение отрицательного числа есть число, противоположное данному.
и точкой, изображающей число. Таким образом, абсолютное значение положительного числа (или нуля) не отличается от самого числа; абсолютное же значение отрицательного числа есть число, противоположное данному.
Абсолютное значение числа, очевидно, никогда не может быть отрицательным; оно равно нулю лишь в том единственном случае, если само число равно нулю.
В дальнейшем , пользуясь в алгебре буквами, мы будем нередко давать им также и отрицательные значения.
Между двумя различными положительными числами  и
и  , как мы видели, может быть поставлен знак
, как мы видели, может быть поставлен знак  или
или  , смотря по тому, расположена ли точка
, смотря по тому, расположена ли точка  на числовом луче левее или правее, чем точка
на числовом луче левее или правее, чем точка  . Это же правило распространяется (по определению) и на всю числовую ось — в применении к положительным числам, отрицательным числам и нулю.
. Это же правило распространяется (по определению) и на всю числовую ось — в применении к положительным числам, отрицательным числам и нулю.
Отсюда вытекает следующее:
Всякое отрицательное число меньше всякого положительного.
Всякое положительное число больше нуля, всякое отрицательное — меньше нуля. И обратно: если число больше нуля, то оно положительно; если меньше нуля, то отрицательно.
Из двух положительных чисел больше то, у которого больше абсолютное значение. Из двух отрицательных чисел больше то, у которого абсолютное значение меньше.
Например, число 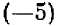 меньше, чем число
меньше, чем число 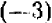 ;
;
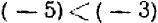 .
.
Каковы бы ни были рассматриваемые числа (положительные, отрицательные или нуль), всегда справедливы утверждения:
1) если 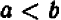 , то
, то  ,
,
2) если 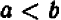 и
и  , то
, то  .
.
Ссылаясь на числовую прямую, объясните сами, почему это так.
Сложение положительных и отрицательных чисел
С отрицательными числами можно производить те же арифметические действия, что и с положительными.
Рассмотрим эти действия начиная со сложения.
На числовой прямой ясно видно, что значит «к  прибавить
прибавить  ». Мы сначала находим точку
». Мы сначала находим точку 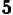 ; затем от нее вправо откладываем отрезок, равный
; затем от нее вправо откладываем отрезок, равный 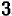 , и после этого сразу видим, что получилась точка
, и после этого сразу видим, что получилась точка 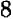 :
: 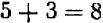 .
.
Вообще, чтобы к некоторому числу  прибавить положительное число
прибавить положительное число  , приходится на числовой оси от рассматриваемой точки
, приходится на числовой оси от рассматриваемой точки  вправо отложить отрезок длины
вправо отложить отрезок длины  и тогда полученная точка указывает, какова сумма
и тогда полученная точка указывает, какова сумма 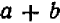 .
.
Посмотрим теперь, что значит «к данному числу прибавить отрицательное число», например, к 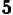 прибавить
прибавить 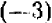 . Тогда на числовой прямой от точки
. Тогда на числовой прямой от точки 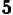 откладывают отрезок длины
откладывают отрезок длины 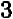 влево.
влево.
Получается результат: 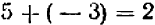 .
.
Вообще, чтобы к некоторому числу  прибавить отрицательное число
прибавить отрицательное число 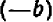 , на числовой оси от рассматриваемой точки
, на числовой оси от рассматриваемой точки  откладывают отрезок длины
откладывают отрезок длины  влево: тогда конец отрезка укажет, какова сумма
влево: тогда конец отрезка укажет, какова сумма 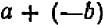 .
.
Что касается нуля, то его прибавление ничего не изменяет: не надо идти ни вправо ни влево.
При сложении двух чисел с одинаковыми знаками их абсолютные значения складываются и сохраняется общий знак. При сложении двух чисел с разными знаками из большего абсолютного значения следует вы честь меньшее абсолютное значение и взять тот знак, который стоит при числе с большим абсолютным значением.
Заслуживает особенного внимания тот случай, когда два слагаемых взаимно противоположны, т. е. имеют одинаковые абсолютные значения, но разные знаки; в этом случае сумма оказывается равной нулю : например, 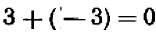 .
.
Итак: сложение каких угодно чисел (положительных, отрицательных, нуля) подчинено законам переместительному 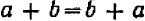 и сочетательному
и сочетательному 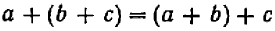 . Эти законы позволяют при сложении нескольких чисел переставлять между собою слагаемые и объединять их в какие угодно группы.
. Эти законы позволяют при сложении нескольких чисел переставлять между собою слагаемые и объединять их в какие угодно группы.
Таким образом часто удается облегчить запись и выполнение действий.
Весьма употребителен следующий способ группировки: собирают вместе все положительные слагаемые и вместе все отрицательные слагаемые; затем остается из одной суммы вычесть другую и при результате поставить надлежащий знак.
Вычитание положительных и отрицательных чисел
Попробуем решить уравнение 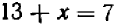 .
.
Нам нужно найти такое число 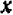 , чтобы, прибавив его к числу
, чтобы, прибавив его к числу 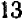 , получить число
, получить число 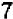 . Среди положительных чисел такого числа, очевидно, нет: положительных корней уравнение не имеет. Но среди отрицательных чисел можно найти число, удовлетворяющее уравнению. Именно, можно положить
. Среди положительных чисел такого числа, очевидно, нет: положительных корней уравнение не имеет. Но среди отрицательных чисел можно найти число, удовлетворяющее уравнению. Именно, можно положить 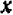 , равным
, равным 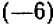 . В самом деле, мы видим, что
. В самом деле, мы видим, что 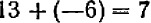 . Итак, найден отрицательный корень данного уравнения.
. Итак, найден отрицательный корень данного уравнения.
Чтобы сделать решение уравнения более наглядным, достаточно себя спросить: на сколько единиц от точки 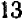 нужно по числовой осн передвинуться влево, чтобы прийти в точку
нужно по числовой осн передвинуться влево, чтобы прийти в точку 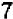 ?
?
Решая уравнение 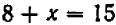 , мы ставим перед собой вопрос: какое число нужно прибавить к
, мы ставим перед собой вопрос: какое число нужно прибавить к 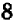 , чтобы получить
, чтобы получить 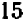 ? Такая задача решается посредством действия, обратного сложению, т. е. посредством вычитания.
? Такая задача решается посредством действия, обратного сложению, т. е. посредством вычитания.
Мы получаем: 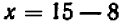 .
.
Рассмотрим теперь буквенное уравнение: 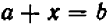 .
.
При решении этого уравнения мы ставим перед собой вопрос: какое число  нужно прибавить к
нужно прибавить к  , чтобы получить
, чтобы получить  ? Геометрически это значит: на сколько единиц нужно передвинуться по оси вправо из точки
? Геометрически это значит: на сколько единиц нужно передвинуться по оси вправо из точки  что бы попасть в точку
что бы попасть в точку  ? Ответ — положительный или отрицательный — можно дать всегда, прибегая, если нужно, к числовой оси.
? Ответ — положительный или отрицательный — можно дать всегда, прибегая, если нужно, к числовой оси.
Каковы бы ни были числа  и
и  (положительные, отрицательные или нуль), уравнение
(положительные, отрицательные или нуль), уравнение 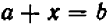 имеет единственное решение. Это решение называется разностью чисел
имеет единственное решение. Это решение называется разностью чисел  и
и  и обозначается:
и обозначается: 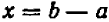 .
.
Положим, например, что 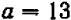 ,
, 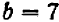 . Так как уравнение
. Так как уравнение 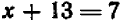 имеет решение
имеет решение 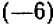 , то, значит, разность чисел
, то, значит, разность чисел 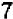 и
и 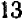 равна
равна 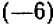 :
: 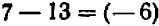 .
.
Вместо уравнения 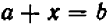 можно было бы рассматривать уравнение
можно было бы рассматривать уравнение 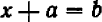 . Их корни одинаковы, так как
. Их корни одинаковы, так как 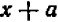 означает то же, что и
означает то же, что и 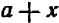 .
.
Легко указать удобное правило вычитания:
Чтобы вычесть некоторое число, достаточно прибавить число, ему противоположное.
Пусть, например, требуется из 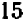 вычесть
вычесть 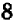 . Чтобы выполнить это действие, мы должны решить уравнение
. Чтобы выполнить это действие, мы должны решить уравнение 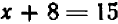 , т. е. узнать из какой точки оси нужно передвинуться вправо на
, т. е. узнать из какой точки оси нужно передвинуться вправо на 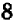 единиц, чтобы прийти в точку
единиц, чтобы прийти в точку 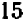 .
.
Но мы получим интересующую нас точку, если из точки 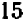 передвинемся на
передвинемся на 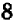 единиц влево (в обратном на правлении), а это как раз означает, что к
единиц влево (в обратном на правлении), а это как раз означает, что к 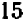 мы прибавим
мы прибавим 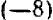 . Итак,
. Итак, 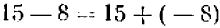 .
.
И точно так же 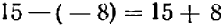 .
.
В общем виде указанное правило записывается следующим образом:
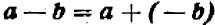 ,
, 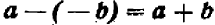 .
.
Мы видим, что вычитание всегда может быть заменено сложением.
Например: 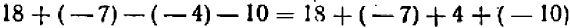
Прибавляя или вычитая нуль, мы не изменяем числа.
Поэтому можно свободно опускать члены, равные нулю. В частности, нуль опускают в выражениях вида  . Пишут
. Пишут 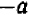 , и это обозначает
, и это обозначает  :
: 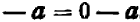 .
.
Числовое значение выражения 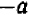 противоположно числовому значению
противоположно числовому значению  . При этом само
. При этом само  может быть каким угодно (положительным или отрицательным) числом. Например, выражение
может быть каким угодно (положительным или отрицательным) числом. Например, выражение 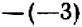 обозначает
обозначает 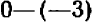 , т. е.
, т. е. 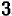 ; это — число, про противоположное числу
; это — число, про противоположное числу 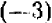 .
.
Необходимо усвоить, что выражение  необязательно положительно и выражение
необязательно положительно и выражение 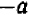 необязательно отрицательно. В самом деле, если мы дадим букве
необязательно отрицательно. В самом деле, если мы дадим букве  отрицательное значение, то будем иметь, наоборот:
отрицательное значение, то будем иметь, наоборот:  ,
, 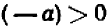 .
.
Отметим еще, что всегда (при всех значениях  ):
): 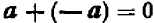 .
.
Умножение положительных и отрицательных чисел
Правило. 1) При умножении двух чисел с одинаковыми знаками (т. е. двух положительных чисел или двух отрицательных) достаточно пере множить их абсолютные значения.
2) При умножении двух чисел с разными знаками (т. е. одного положительного и одного отрицательного) нужно перемножить их абсолютные значения и затем перед полученным произведением поставить знак минус.
Таким образом: если оба множителя — положительные, то и произведение их, получаемое по известным правилам арифметики, оказывается положительным.
Если один из множителей отрицательный, то произведение их отрицательное. Если оба множителя отрицательные, то произведение снова положительное.
Например: 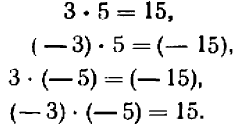
В частности, умножить данное число на 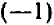 значит заменить его числом противоположным, например:
значит заменить его числом противоположным, например: 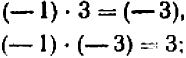 и вообще при любом
и вообще при любом  :
: 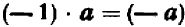 .
.
Что касается случая, когда один из множителей равен нулю (или равны нулю оба), то в этом случае произведение также равно нулю.
Законы умножения, переместительный, сочетательный и распределительный, справедливы не только в том случае, если множители положительные, но и в том случае, если они какие угодно (положительные, отрицательные, равные нулю).
Предположим, что числа  и
и  — положительные.
— положительные.
Тогда четыре формулы 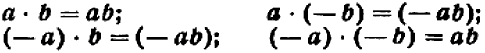 полностью охватывают правило умножения положительных и отрицательных чисел. Но эти формулы справедливы также и при каких угодно (положительных, отрицательных или равных нулю) значениях букв
полностью охватывают правило умножения положительных и отрицательных чисел. Но эти формулы справедливы также и при каких угодно (положительных, отрицательных или равных нулю) значениях букв  и
и  .
.
Рассмотрим, например, последнюю формулу 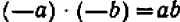 . Положим в ней
. Положим в ней 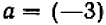 ,
, 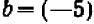 ; тогда
; тогда 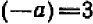 ,
, 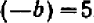 . По правилам умножения левая часть
. По правилам умножения левая часть 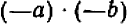 равна
равна 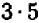 , т. е.
, т. е. 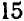 ; правая часть
; правая часть 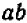 равна
равна 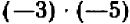 , т. е. тоже
, т. е. тоже 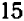 .
.
Вот другое рассуждение: мы видели, что 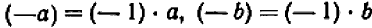 ; в таком случае
; в таком случае 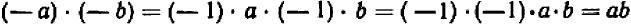
Произведение нескольких чисел, отличных от нуля, положительно или отрицательно, смотря по тому, является ли число отрицательных множителей четным или нечетным.
Теорема:
Если произведение двух чисел равно нулю, то непременно хотя бы одно из чисел равно нулю. Короче:
если 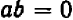 , то или
, то или 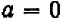 или
или 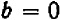 .
.
Доказательство:
Посмотрим, в самом деле, может ли случиться так, что ни одно из данных чисел  и
и  не равно нулю, а произведение
не равно нулю, а произведение  равно нулю?
равно нулю?
Допустим, что ни множитель  , ни множитель
, ни множитель  не равны нулю. Тогда каждое из этих чисел или положительное, или отрицательное. Возможны только четыре различных случая:
не равны нулю. Тогда каждое из этих чисел или положительное, или отрицательное. Возможны только четыре различных случая:
Случай 1. 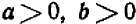 .
.
Случай 2. 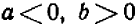 .
.
Случай 3. 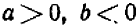 .
.
Случай 4. 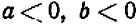 .
.
Но согласно правилу знаков в случаях 1 и 4 произведение 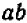 должно быть положительным, а в случаях 2 и 3 — отрицательным и, следовательно, ни в одном из случаев оно не равно нулю.
должно быть положительным, а в случаях 2 и 3 — отрицательным и, следовательно, ни в одном из случаев оно не равно нулю.
Необходимо твердо запомнить следующее: произведение двух множителей в том, и только в том, случае равно нулю, если хотя бы один из множителей равен нулю.
То же самое справедливо и в случае произведения нескольких множителей.
Деление положительных и отрицательных чисел
Деление есть действие, обратное умножению. Разделить  на
на  значит решить уравнение
значит решить уравнение  .
.
Мы умеем решать это уравнение и записываем решение в виде
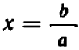 при условии, что делимое (числитель)
при условии, что делимое (числитель) 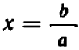 — положительное число (или нуль), а делитель (знаменатель)
— положительное число (или нуль), а делитель (знаменатель)  — положительное число (но не нуль).
— положительное число (но не нуль).
Решим теперь уравнение  , предполагая, что делимое
, предполагая, что делимое  и делитель
и делитель  могут иметь какие угодно знаки. Пусть, например, абсолютное значение числа
могут иметь какие угодно знаки. Пусть, например, абсолютное значение числа  равно
равно  , а абсолютное значение числа
, а абсолютное значение числа  равно
равно  .
.
Возможны только четыре случая:
1.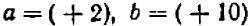 . Тогда
. Тогда 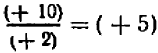 , так как
, так как 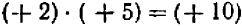 .
.
2.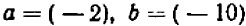 . Тогда
. Тогда 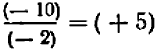 , так как
, так как 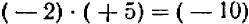 .
.
3.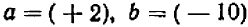 . Тогда
. Тогда 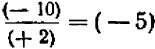 , так как
, так как 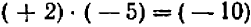 .
.
4.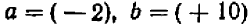 . Тогда
. Тогда 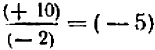 , так как
, так как 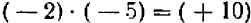 .
.
Отсюда следует:
Если делимое (числитель дроби) и делитель (знаменатель дроби) отличны от нуля, то для нахождения частного (значения самой дроби) достаточно разделить абсолютное значение делимого на абсолютное значение делителя; что касается знака частного, то он — положительный или отрицательный, смотря по тому, одинаковы или различны знаки делимого и делителя.
Далее:
Если делимое (числитель дроби) равно нулю, а делитель (знаменатель дроби) отличен от нуля, то частное (дробь) равно нулю.
В самом деле, раз произведение 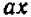 равно нулю, то должен равняться нулю один из множителей: но множитель
равно нулю, то должен равняться нулю один из множителей: но множитель  отличен от нуля; значит
отличен от нуля; значит 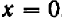 .
.
Обратно: если частное (дробь) равно нулю, а делит ель (знаменатель дроби) отличен от нуля, то делимое (числитель) равно нулю.
Действительно, раз множитель 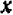 равен нулю, го произведение
равен нулю, го произведение 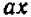 также равно нулю.
также равно нулю.
Остается заметить, что деление на нуль невозможно — по тем же соображениям, которые были изложены раньше.
Каждое не только положительное, но и отрицательное число  имеет обратное число
имеет обратное число 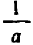 ; только число нуль не имеет обратного.
; только число нуль не имеет обратного.
Все действия с положительными и отрицательными числами
Рассмотрим здесь вопрос о выполнимости четырех арифметических действий.
Выполнимо ли сложение? Другими словами, если задано два числа  и
и  , то всегда ли можно по известным математическим правилам составить их сумму?
, то всегда ли можно по известным математическим правилам составить их сумму?
В арифметике дается утвердительный ответ на этот вопрос при условии, что слагаемые  и
и  положительны. В алгебре указывается правило сложения каких угодно чисел (положительных, отрицательных, равных нулю).
положительны. В алгебре указывается правило сложения каких угодно чисел (положительных, отрицательных, равных нулю).
Итак, сложение всегда выполнимо.
Перейдем к вычитанию. Верно ли, что всякое число  можно вычесть из всякого числа
можно вычесть из всякого числа  ?
?
Арифметика указывает, как вычесть меньшее число из большего; но с помощью правил арифметики нельзя вычесть большее число из меньшего. В курсе арифметики вычитание по этому не всегда выполнимо. Иначе обстоит дело в алгебре. После введения отрицательных чисел устанавливается, что вычитание сводится к сложению: 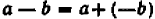 . Чтобы вычесть
. Чтобы вычесть  из
из  , достаточно к
, достаточно к  прибавить число, противоположное
прибавить число, противоположное  . Так как у всякого числа имеется ему противоположное, то в алгебре (после введения отрицательных чисел) вычитание становится всегда выполнимым.
. Так как у всякого числа имеется ему противоположное, то в алгебре (после введения отрицательных чисел) вычитание становится всегда выполнимым.
Об умножении можно сказать то же, что о сложении: в алгебре исчерпывающим образом указываются правила умножения любого числа на любое. Значит, и умножение всегда выполнимо.
Обратимся, наконец, к делению. Покуда учащийся (скажем, начальной школы) знает только целые числа, он не всегда может выполнить деление. Например,  «не делится» на
«не делится» на  . Но после введения дробных чисел становится возможным деление любого положительного числа (целого или дробного) на любое положительное:
. Но после введения дробных чисел становится возможным деление любого положительного числа (целого или дробного) на любое положительное: 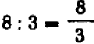 . После введения отрицательных чисел возникает вопрос: всегда ли можно любое число (положительное, отрицательное или равное нулю) разделить на любое (такое же)?
. После введения отрицательных чисел возникает вопрос: всегда ли можно любое число (положительное, отрицательное или равное нулю) разделить на любое (такое же)?
Правила деления непроизвольны: они с неизбежностью вытекают из правил умножения, по отношению к которому деление является обратным действием. Оказывается, что деление всегда выполнимо — с одним исключением: именно, даже после введения отрицательных чисел остается невозможным деление на нуль.
Подведем итоги: все четыре арифметических действия всегда вы полнимы, кроме деления на нуль. Другими словами: каковы бы ни были числа  и
и  (положительные, отрицательные, равные ну лю), во всех случаях можно вычислить значения выражений
(положительные, отрицательные, равные ну лю), во всех случаях можно вычислить значения выражений 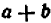 ,
,  ,
, 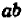 ,
,  за единственным исключением: выражение
за единственным исключением: выражение  не имеет никакого числового значения, если
не имеет никакого числового значения, если  равно нулю. В этом последнем случае говорят также, что выражение «не имеет смысла», или «теряет смысл», или не «существует».
равно нулю. В этом последнем случае говорят также, что выражение «не имеет смысла», или «теряет смысл», или не «существует».
Если встречаются более сложные выражения, требующие выполнения деления, то необходимо подразумевать, что входящие буквы имеют лишь такие значения, при которых делители не обращаются в нуль.
Рассмотрим, например, выражение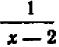 .
.
Его числовое значение может быть вычислено при любом значении 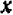 , кроме значения
, кроме значения 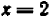 . При этом же значении знаменатель (делитель) обращается в нуль, и выражение «не имеет смысла».
. При этом же значении знаменатель (делитель) обращается в нуль, и выражение «не имеет смысла».
Координатная плоскость
Мы видели, что пары положительных чисел 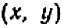 изображаются точками, расположенными внутри прямого угла
изображаются точками, расположенными внутри прямого угла 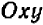 .
.
Станем теперь давать буквам 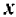 и
и 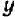 не только положительные, но вообще какие угодно значения (положительные, отрицательные и нуль) и посмотрим, как тогда можно будет изображать пары чисел
не только положительные, но вообще какие угодно значения (положительные, отрицательные и нуль) и посмотрим, как тогда можно будет изображать пары чисел 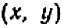 .
.
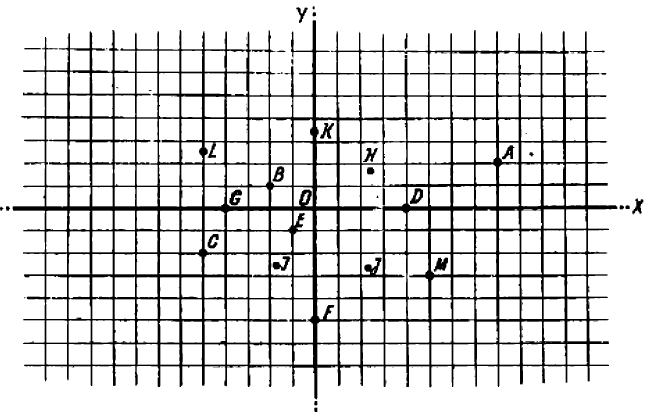
Пусть на клетчатой бумаге (черт. 33) проведены две прямые: числовая ось  — горизонтальная, и числовая ось
— горизонтальная, и числовая ось  —вертикальная. На оси
—вертикальная. На оси  положительные значения буквы
положительные значения буквы 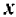 изображаются точками, расположенными вправо от начала
изображаются точками, расположенными вправо от начала  отрицательные значения — точками, расположенными влево; на числовой оси
отрицательные значения — точками, расположенными влево; на числовой оси  точно так же значения буквы
точно так же значения буквы 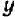 , смотря по знаку, отмечаются вверх или вниз. Пара чисел
, смотря по знаку, отмечаются вверх или вниз. Пара чисел 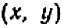 изображается точкой
изображается точкой  , лежащей на пересечении прямых, вертикальной и горизонтальной, проходящих через отмеченные точки.
, лежащей на пересечении прямых, вертикальной и горизонтальной, проходящих через отмеченные точки.
Числа 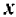 и
и 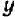 называются координатами точки
называются координатами точки 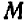 : первое число
: первое число 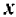 (откладываемое по горизонтальной оси
(откладываемое по горизонтальной оси  ) называется абсциссой точки
) называется абсциссой точки  , а второе число
, а второе число 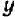 (откладываемое по вертикальной оси
(откладываемое по вертикальной оси  )— ординатой точки
)— ординатой точки  . Чтобы точку, координаты ее часто
. Чтобы точку, координаты ее часто
пишут в надлежащем порядке в скобках после названия точки: например, 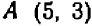 .
.
Мы имеем теперь возможность давать абсциссе 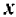 и ординате
и ординате 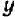 какие угодно — как положительные, так и отрицательные — значения. Оси
какие угодно — как положительные, так и отрицательные — значения. Оси  и
и  делят плоскость на четыре прямых угла: основной угол, расположенный вправо и вверх от начала
делят плоскость на четыре прямых угла: основной угол, расположенный вправо и вверх от начала  ; дальше, в порядке вращения вокруг начала
; дальше, в порядке вращения вокруг начала  против часовой стрелки, идут второй, третий и четвертый углы (черт. 34).
против часовой стрелки, идут второй, третий и четвертый углы (черт. 34).
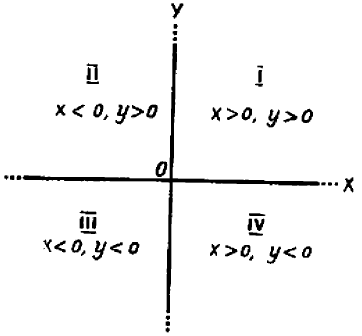
По знакам координат 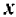 и
и 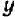 точки
точки  легко узнать, в каком из четырех углов она находится, именно:
легко узнать, в каком из четырех углов она находится, именно:
если 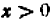 ,
, 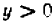 , то
, то  находится в первом углу (
находится в первом углу ( );
);
если  ,
, 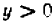 , >> >> во втором >> (
, >> >> во втором >> ( );
);
если  ,
, 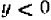 , >> >> в третьем >> (
, >> >> в третьем >> (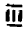 );
);
если  ,
, 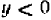 , >> >> в четвертом >> (
, >> >> в четвертом >> (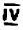 ).
).
Если абсцисса 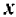 равна нулю, то точка
равна нулю, то точка  расположена на оси
расположена на оси 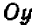 ; если равна нулю ордината
; если равна нулю ордината 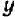 , то точка
, то точка 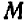 — на оси
— на оси 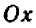 .
.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
