Оглавление:
При введении понятия о степени подразумевалось, что показатель степени — целое положительное число. Все правила действий над степенями были выведены в этом предположении.
В математике наряду со степенями с целыми положительными показателями рассматриваются также и степени с нулевым, отрицательным и дробным показателями. Более того, исследование некоторых вопросов, имеющих очень большое значение, требует рассмотрения степеней с иррациональными показателями.
В этой главе будет введено понятие о степени с любым вещественным показателем и будет показано, что все правила действий над степенями, выведенные для целых положительных показателей, сохраняются и для любых вещественных показателей.
Понятие о степени с нулевым и отрицательным показателем
Определение. Если а ≠ 0, то а⁰ = 1. Нулевая степень числа, отличного от нуля, равна единице.
Например, 2°= 1; (0,75)°= 1; (—√3)° = 1. Выражение 0° смысла не имеет.
Определение:
Если а ≠ 0 и q — целое положительное число, то
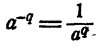
Целая отрицательная степень числа, отличного от нуля, равна единице, деленной на степень того же числа с показателем, равным абсолютной величине отрицательного показателя. Например,
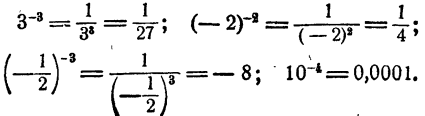
Теорема:
При любых целых положительных m и n справедливо правило деления степеней
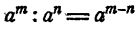
Доказательство:
Если m > n, утверждение в доказательстве не нуждается.
Если m = n, справедливость утверждения вытекает из определения нулевого показателя.
Если m < n, справедливость утверждения вытекает из определения целого отрицательного показателя.
Теорема доказана.
Определение нулевого и отрицательного показателей возникло в связи с желанием обобщить установленное ранее правило деления степеней одной и той же величины. Это правило
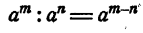
было выведено в предположении, что m и n— целые положительные числа и что m > n.
Допустим, что правило деления степеней можно применять и.тогда, когда показатель степени делимого равен показателю степени делителя и когда» показатель степени делимого меньше показателя степени делителя.
Пусть m = n, тогда
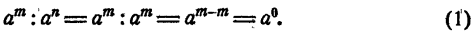
С другой стороны,

Сравнение результатов (1) и (2) показывает, что a° = 1
Пусть m < n , т. е. n = m + q, где q — положительное число.
Тогда имеем
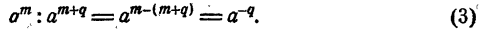
С другой стороны, посредством сокращения получаем

Сравнение результатов (3) и (4) показывает, что целесообразно считать
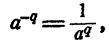
где q — целое положительное число.
Рассуждения, которые приведены выше, не являются, конечно,
доказательствами того, что 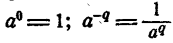 Эти рассуждения проведены только для того, чтобы показать, что принимаемые нами определения нулевого и отрицательного показателя подсказаны нам опытом деления степеней с одним и тем же основанием и единственно возможны, если мы желаем сохранить правило деления степеней для случая, когда показатель степени делимого не превосходит показателя степени-делителя.
Эти рассуждения проведены только для того, чтобы показать, что принимаемые нами определения нулевого и отрицательного показателя подсказаны нам опытом деления степеней с одним и тем же основанием и единственно возможны, если мы желаем сохранить правило деления степеней для случая, когда показатель степени делимого не превосходит показателя степени-делителя.
Замечание:
Не следует думать, что введением отрицательного показателя дробное выражение 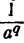 превращается в целое
превращается в целое 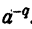 . Выражение
. Выражение 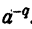 является лишь другой формой записи выражения
является лишь другой формой записи выражения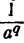
Понятие о степени с дробным показателем
Определение:
Если a > 0 и числа m и n натуральные, то
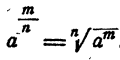
Пример:
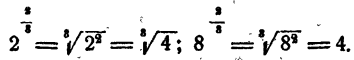
Определение дробного показателя возникло в связи с желанием обобщить правило извлечения корня на случай, когда показатель подкоренного количества не делится на показатель корня. Правило
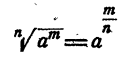
было выведено в предположении, что m и n натуральные и m делится на n. Теперь, это правило можно применять и тогда, когда m и n— любые натуральные числа.
Известно, что рациональная дробь может быть представлена в различных видах. Например, 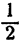 может быть представлена как
может быть представлена как 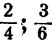 и т. п. Выражение с дробным показателем не зависит oт того, в каком виде представлен показатель. Пусть
и т. п. Выражение с дробным показателем не зависит oт того, в каком виде представлен показатель. Пусть
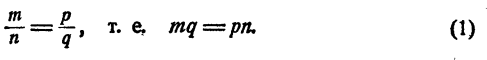
Тогда
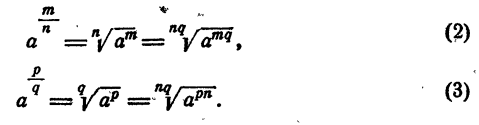
В силу (1) правые части равенств (2) и (3) тождественны. Поэтому
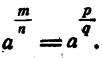
Определение дробного показателя не распространяется на степени с отрицательными основаниями, так как тогда выражения с дробными показателями не обладали бы столь простым и важным свойством, которое указано.
Пример:
Допустим, что определение дробного показателя распространено на степени с отрицательным основанием. Тогда
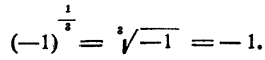
В то же время
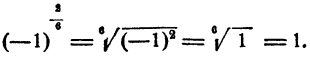
Замечание:
Не следует думать, что введением дробного показателя иррациональное выражение 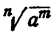 превращается в рациональное
превращается в рациональное 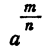 . Если выражение
. Если выражение 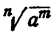 иррациональное, то и выражение
иррациональное, то и выражение 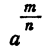 тоже иррациональное. Выражение
тоже иррациональное. Выражение 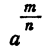 является лишь другой формой записи выражения
является лишь другой формой записи выражения 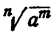
Понятие о степени с дробным отрицательным показателем
Определение:
Если а — положительное число, то
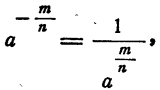
где m и n— любые натуральные числа.
То есть дробная отрицательная степень положительного числа равна единице, деленной на степень того же числа с показателем, равным абсолютной величине отрицательного показателя. Например,
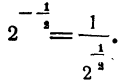
Теорема:
При любом целом х
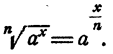
Доказательство:
Если x > 0 справедливость утверждения вытекает из определения дробного показателя.
Если х = 0, то
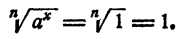
С другой стороны,
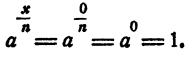
Пусть x < 0. Положим х = — m,m > 0. Имеем :
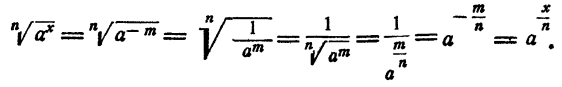
Действия над степенями с рациональными показателями
В этом параграфе буквы m, n, р, q обозначают целые положительные числа, буква r, а также r₁— любые рациональные числа.
Теорема:
Произведение степеней с одинаковыми основаниями равно степени с тем же основанием и с показателем, равным сумме показателей.
Короче: при умножении степеней с одинаковыми основаниями показатели степеней складываются, т. е.
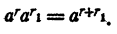
Доказательство:
Переместительный закон умножения справедлив для любых действительных чисел. При любых рациональных r и r₁ степени 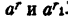 —действительные числа, поэтому
—действительные числа, поэтому
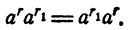
Для доказательства теоремы достаточно рассмотреть следующие случат
Случай 1. r = 0; r₁ — любое рациональное число. Имеем
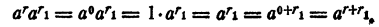
Случай 2.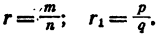 Имеем
Имеем
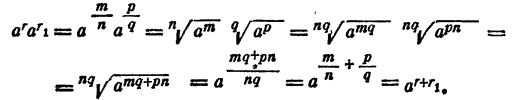
Случай 3. 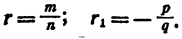 Имеем
Имеем
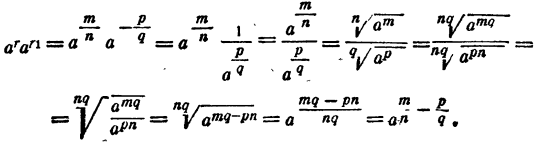
Случай 4. 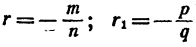 имеем
имеем
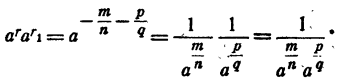
На основании доказанного в случае 2
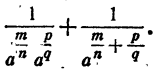
Значит,
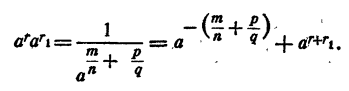
Методом математической индукции можно показать, что теорема верна для любого количества множителей.
Пример:
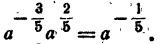
Пример:
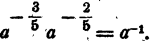
Теорема:
Частное от деления степеней с одинаковыми основаниями равно степени с тем же основанием и с показателем, равным разности показателей делимого и делителя.
Короче; при делении степеней с одинаковыми основаниями показатели степеней вычитаются, т. е.
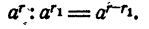
Доказательство:
На основании правила умножения степеней
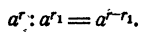
Отсюда по определению деления
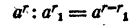
Пример:
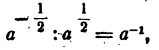
Пример:
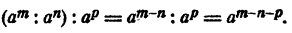
Теорема:
Степень произведения двух чисел равна произведению степеней сомножителей, т. е.
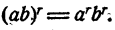
Доказательство:
Возможны три случая:
Случай 1. r = 0. Имеем
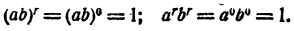
Следовательно,
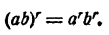
Случай 2. 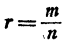 . Имеем
. Имеем
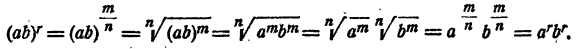
Случай 3. 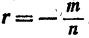 Имеем
Имеем
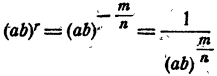
На основании доказанного в случае 2
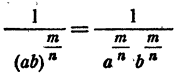
Значит,
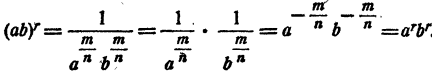
Методом математической индукции можно показать, что теорема верна для любого количества множителей.
Теорема:
Степень дроби равна частному от деления степени числителя с показателем, равным показателю дроби на степень знаменателя с показателем, равным показателю дроби.
Короче: степень дроби равна частному от деления степени числителя на степень знаменателя, т. е.
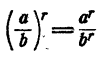
Доказательство:
Возможны три случая:
Случай 1. r = 0. Имеем
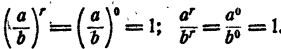
Следовательно,
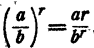
Случай 2. 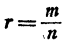 Имеем
Имеем
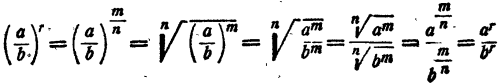
Случай 3. 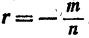 Имеем
Имеем
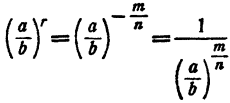
На основании доказанного в случае 2
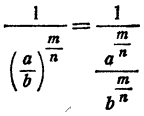
Значит,
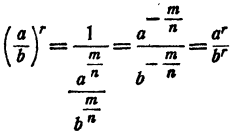
Пример:
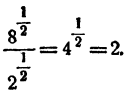
Теорема:
Результат возведения степени в степень равен степени с тем же основанием и с показателем, равным произведению показателей, участвующих в действии.
Короче: при возведении степени в степень показатели перемножаются, т. е.
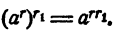
Доказательство:
Возможны шесть случаев:
Случай 1. r = 0. Имеем
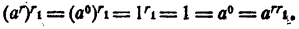
Случай 2. r₁=0. Имеем
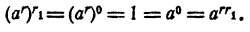
Случай 3. r > 0; r₁ > 0. Положим 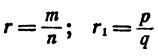 Тогда
Тогда
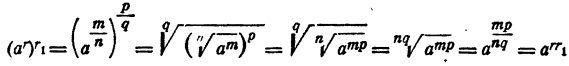
Случай 4, r < 0, r₁ > 0. Положим r = — r₂r₂, > 0. Тогда
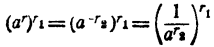
На основании теоремы 4 и доказанного в случае 3
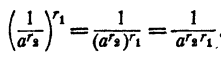
Значит,
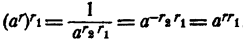
Случай 5. r > 0; r₁ < 0. Положим r₁ = — r₃, r₃, > 0. Тогда
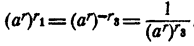
На основании доказанного в случае 3
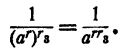
Значит,
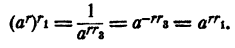
Случай 6. r < 0; r₁ < 0. Положим r = -r₂, r₁ = — r₃, r₂ > 0, r₃ >0. Тогда
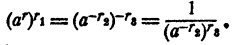
На oсновании доказанного в случае 4
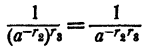
Значит,
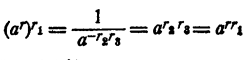
Следствие. 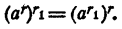
Пример:
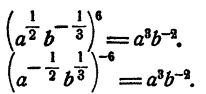
Из доказанных теорем вытекает, что для степеней с любыми рациональными показателями справедливы следующие правила, которые были ранее установлены для степеней с натуральными показателями:
1) правило умножения степеней;
2) правило деления степеней;
3) правило возведения произведения в степень;
4) правило возведения дроби в степень;
5) правило возведения степени в степень.
Пример:
Вычислить при а = 2,5 и b= 20
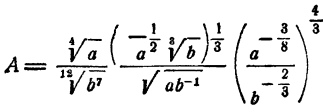
Решение:
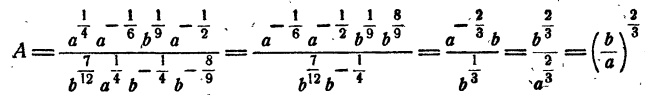
При а = 2,5; b = 20 имеем 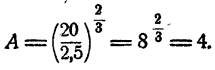
Ответ. А = 4
Степень с рациональным показателем
Теорема:
Пусть r рационально, тогда
1) если а > 1 и r > 0, то 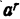 > 1; .
> 1; .
2) если 0 < a < 1 и r > 0 , то 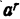 < 1
< 1
3) если а > 1 и r < 0, то 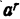 < 1;
< 1;
4) если 0 < a < 1 и r < 0, то 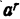 > 1
> 1
Доказательство:
1) Пусть а > 1 и 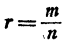 , где m и n— натуральные числа. Тогда
, где m и n— натуральные числа. Тогда

Так как 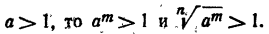
2) Пусть а< 1 и 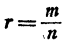 . Положим
. Положим 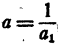 тогда a₁ > 1. Имеем
тогда a₁ > 1. Имеем
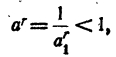
так как по доказанному в п. 1) 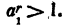
3) Пусть а > 1 и 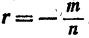 , тогда
, тогда
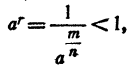
так как по доказанному в п. 1) 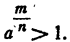
4) Пусть а < 1 и 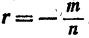 , тогда
, тогда
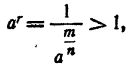
так как 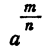 < 1 (по доказанному в п; 2).
< 1 (по доказанному в п; 2).
Теорема:
Если а > 1 и рациональное r больше рационального r₁, то  если же 0 < а < 1, то
если же 0 < а < 1, то  , т. е. если а > 1 то при возрастании r возрастает и степень
, т. е. если а > 1 то при возрастании r возрастает и степень 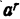 , а если 0 < a < 1, то при возрастании r степень
, а если 0 < a < 1, то при возрастании r степень 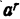 убывает.
убывает.
Доказательство:
Пусть a > 1 и r > r₁ Рассмотрим разность
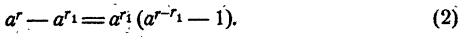
Так как 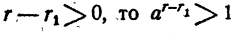 и, следовательно,
и, следовательно, 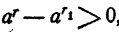 , т. е.
, т. е.
Пусть а < 1 и r > r₁. Рассмотрим разность
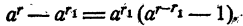
Так как 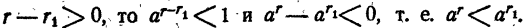
Теорема:
Если c > 0, то последовательность 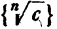 имеет пределом единицу, т. е.
имеет пределом единицу, т. е.
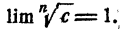
Доказательство:
Имеем последовательность
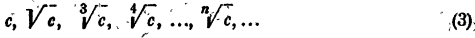
При с = 1 утверждение проверяется легко. Остается рассмотреть два случая: c > 1 и c < 1.
Предположим сначала, что с > 1. Тогда каждый член последовательности (3) больше единицы. Обозначим
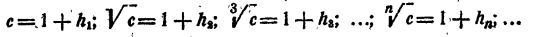
Тогда последовательность (3) может быть переписана так:
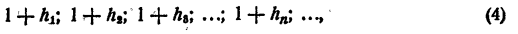
где 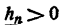 при любом n.
при любом n.
Пусть теперь n >1 тогда (см. теорему 1 § 9 гл. V)
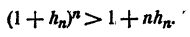
Но 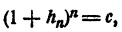 значит,
значит,
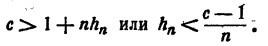
Последнее неравенство показывает, что по любому заданному положительному e можно указать столь большой номер N, что при всех n >N число 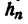 будет меньше e. Действительно, чтобы
будет меньше e. Действительно, чтобы 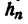 было меньше е, достаточно, чтобы
было меньше е, достаточно, чтобы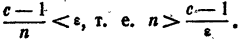 Таким образом, за N можно принять любое целое число, бoльшее
Таким образом, за N можно принять любое целое число, бoльшее 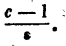 Отсюда вытекает, что
Отсюда вытекает, что 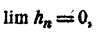 а тогда
а тогда
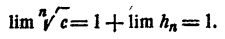
Пусть теперь подкоренное выражение c₁ меньше единицы. Положим 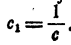 Тогда последовательность
Тогда последовательность
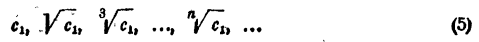
примет такой вид:
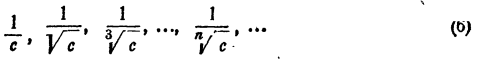
или, что все равно,
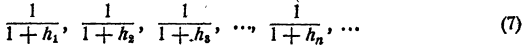
Последовательность (4), составленная из знаменателей последовательности (7), как показано, стремится к единице, значит, и последовательность (7) стремится к единице, т. е. опять
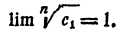
Понятие о степени с иррациональным показателем
Пусть а — какое-нибудь положительное число и а — иррациональное. Какой смысл следует придать выражению 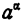 ?
?
Чтобы сделать изложение более наглядным, проведем его на частном примере. Именно, положим а = 2 и а = 1,624121121112…. Здесь, а — бесконечная десятичная дробь, составленная по такому закону: начиная с четвертого десятичного знака, для изображения а употребляются только цифры 1 и 2, и при этом количество цифр 1, записываемых подряд перед цифрой 2, все время увеличивается на одну. Дробь а непериодическая, так как иначе количество цифр 1, записываемых подряд в его изображении, было бы ограниченным. Следовательно, а — иррациональное число.
Итак, какой же смысл следует придать выражению
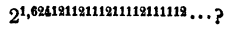
Чтобы ответить на этот вопрос, составим последовательности значений а с недостатком и избытком с точностью до 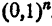 . Получим
. Получим
1,6; 1,62; 1,624; 1,6241; …, (1)
1,7; 1,63; 1,625; 1,6242; … (2)
Составим соответствующие последовательности степеней числа 2:

Последовательность (3) возрастает, так как возрастает последовательность (1) (теорема 2 § 6).
Последовательность (4) убывает, так как убывает последовательность (2).
Каждый член последовательности (3) меньше каждого члена последовательности (4), и, таким образом, последовательность (3) ограничена сверху, а последовательность (4) ограничена снизу.
На основании теоремы о монотонной ограниченной последовательности каждая из последовательностей (3) и (4) имеет предел. Если теперь окажется, что разность последовательностей (4) и (3) сходится к нулю, то из этого будет вытекать, что обе эти последовательности, имеют общий предел.
Разность первых членов последовательностей (3) и (4)
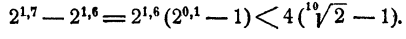
Разность вторых членов
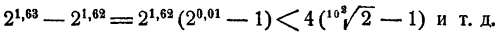
Разность n-х членов
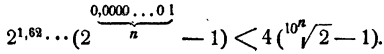
На основании теоремы 3 § 6
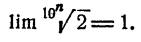
Итак, последовательности (3) и (4) имеют общий предел. Этот предел является единственным вещественным числом, которое больше всех членов последовательности (3) и меньше всех членов последовательности (4), его и целесообразно считать точным значением 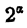 .
.
Из сказанного вытекает, что и вообще целесообразно принять следующее определение:
Определение:
Если a > 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых есть рациональные приближения а с недостатком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с избытком.
Если a < 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых — рациональные приближения а с избытком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с недостатком.
.Если а= 1, то степенью его с иррациональным показателем а является 1.
Пользуясь понятием предела, это определение можно сформулировать так:
Степенью положительного числа с иррациональным показателем а называется предел, к которому стремится последовательность рациональных степеней этого числа при условии, что последовательность показателей этих степеней стремится к а, т. е.
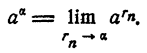
Пример:
Вычислить с точностью до 0,1 число 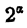 , если а= 1,624121121112 … (а то же, что и выше).
, если а= 1,624121121112 … (а то же, что и выше).
Решение:
Для приближенного вычисления 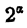 заметим, что
заметим, что
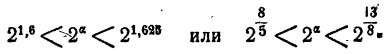
Далее,
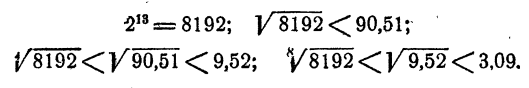
Таким образом, 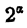 < 3,09.
< 3,09.
Испытанием уходим, что (3,03)⁵ = 255,3954324543 < 256. Поэтому 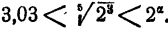 . Выходит, что
. Выходит, что
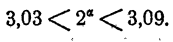
Число 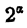 вычислено с точностью до: 0,06.
вычислено с точностью до: 0,06.
Свойства степени с любым вещественным показателем
Теорема:
1) Если а > 1 и а > 0, то 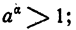
2) если 0 < а < 1 и а>0, то 
3) если а > 1 и а < 0, то 
4) если 0 < а < 1 и а<0, то 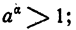
Доказательство:
1) Это утверждение доказано для случая, когда о рационально (теорема 1 § 6).
Пусть о иррациональное. Рассмотрим последовательность {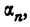 } десятичных приближений а с недостатком с точностью до
} десятичных приближений а с недостатком с точностью до 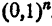 . Среди членов этой последовательности должны находиться, и положительные числа, так как если бы
. Среди членов этой последовательности должны находиться, и положительные числа, так как если бы  при всех n, то и
при всех n, то и 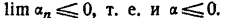
Пусть 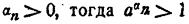 (теорема 1 §6). Но
(теорема 1 §6). Но 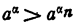 Значит,
Значит,
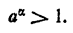
2) Положим 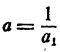 , тогда a₁ >. 1. По доказанному
, тогда a₁ >. 1. По доказанному 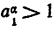 , значит,
, значит,
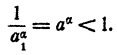
3) Пусть а > 1; а < 0. Положим 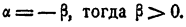 . Рассмотрим
. Рассмотрим
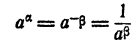
По доказанному в п. (1) 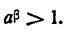 Значит,
Значит,
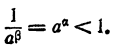
4) Пусть а<1; а<0. Положим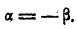 . Тогда
. Тогда
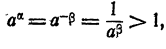
так как 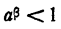 (по доказанному в п. 2).
(по доказанному в п. 2).
Теорема:
Если а > 1 и число а больше 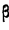 , то
, то 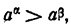 т. е. при а > 1 функция
т. е. при а > 1 функция 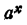 возрастает.
возрастает.
Если 0 < a < 1 и a > 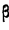 то
то 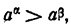 , т. е. при 0 < a < 1 функция
, т. е. при 0 < a < 1 функция 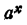 убывает.
убывает.
Доказательство:
Пусть 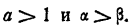 . Рассмотрим разность
. Рассмотрим разность
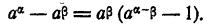
Так как 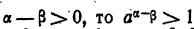 , то и, следовательно,
, то и, следовательно, 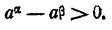 . Пусть
. Пусть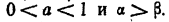 Рассмотрим
Рассмотрим
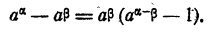
Так как
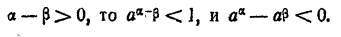
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
